Четырёхмерный гиперкуб. Программа Transformator 4D / Habr
В данной статье хотелось бы поговорить о четырехмерном гиперкубе (тессеракте), и его построение в программе Transformator 4D.
Как мы знаем из геометрии, квадрата – это правильный четырехугольник у которого все углы и стороны равны. Куб можно охарактеризовать следующим образом, это выпуклая фигура, обязательно замкнутая и состоящая из групп параллельных линий расположенных относительно друг друга на противоположных краях фигуры и, соединенных друг с другом под прямым углом. Следовательно гиперкуб — это n-мерная аналогия квадрата у которого n=2 и, куба у которого n=3.
Рассмотрим рисунок 1. На нем изображена точка, которая есть гиперкуб размерностью равной 0. Далее если сдвинуть точку на единицу длины, что приведет к получению отрезка единичной длины и как следствие гиперкуба размерностью единица. После чего сдвинуть отрезок на ту же единицу длины, но перпендикулярно в направлении исходного отрезка, и продолжить эту операцию до замыкания контура, то получится квадрат – гиперкуб размерностью в два.
Рис.1
В евклидовом пространстве тессеракт характеризуется как объемная оболочка состоящая из точек: +-1, +-1, +-1, +-1, что можно записать в виде:
Отсюда видно, что тессеракт ограничен 8-ю гиперплоскостями, пересечение которых с самим тессерактом задает его трехмерные грани, они же являются просто кубами, и в конечном итоге получаем:
- 8-мь трехмерных граней,
- 24-и двумерных,
- 32-а ребра,
- 16-ть вершин.

Основой работы программы являются именно аффинные преобразования, это действия над объектом путем перемещения, масштабирования, поворота. Пользователь может сам составлять объекты, в формате файла txt, и анимировать его движение. Программа может выводить частные случаи аффинных преобразований в пространстве, и проекции для любого заданного тела.
Как задавать фигуры
В директории с программой создается папка FIGURES. Каждая фигура задается при помощи двух файлов: первый FigureX.txt, где находятся координаты вершин, второй FigureXm.txt, где находится матрица смежности этих вершин. Х – номер фигуры.
Характеристика файла FigureX.txt:
Координаты первой вершины по Х, находятся в первой строке.
Координаты второй вершины по У, находятся во второй строке.
и т.д. Последняя строка «х» — конец данных.
Характеристика файла FigureXm: Матрица смежности, показывает номера вершин из первого файла.
При запуске программа требует файл acrTrans2FA. txt. Файл описывает четырехмерную фигуру и аффинные преобразования в отдельности для каждого полигона.
txt. Файл описывает четырехмерную фигуру и аффинные преобразования в отдельности для каждого полигона.
По сути можно построить объект отдельные части которого подвергаются разным преобразованиям, и каждую субмодель представить отдельным цветом.
После указания каждого полигона нужно указать аффинные преобразования этого полигона.
Пример: Сборка развертки куба на основе построения квадрата.
Рис. 2
1 Замкнутые полигоны
6 Шесть полигонов
4 4 точки в первом полигоне
1 1 0 Цвет полигона №1
0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
0 Аффинных преобразований отсутствуют — квадрат №1
4 4 точки — квадрат №2
0.5 0.5 0.5 Цвет полигона №2
0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
2 Два преобразования
2 1 -1 0 0 0 Смещение на -1 по х
6 1 0 -1 0 0 0 0 Разворот по оси zx
4 4 точки в квадрате №3
0. 1 0.1 0.1 Цвет полигона 3
1 0.1 0.1 Цвет полигона 3
0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
6 1 0 1 0 0 0 0 Разворот вокруг y от x к z
2 1 1 0 0 0 Смещение на 1 по x
4 Квадрат №4
0.6 0.1 0.7 Цвет полигона 4
0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
2 Два преобразования
2 1 0 -1 0 0 Смещаем вниз по y
6 1 0 0 0 -1 0 0 Перемещение вокруг x от z к y
4 Квадрат №5
1 0 0 Цвет полигона 5
0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
2 Два преобразования
6 1 0 0 0 1 0 0 Перемещение вокруг x от y к z
2 1 0 1 0 0 Смещаем вверх по y
4 Квадрат №6
0.25 0.5 0.5 Цвет полигона №6
0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
4 Четыре преобразования
2 1 0 -1 0 0
6 1 0 0 0 -1 0 0 Перемещение вокруг x от z к y
2 1 0 -1 0 0 Смещение вниз для квадрата №6
6 1 0 0 0 -1 0 0 Вращение относительно нижнего ребра четвертого квадрата.

Квадрат №6: описывает два поворота, так как одно из его ребер является общим с квадратом №4, поэтому изначально вращается квадрат №4, после происходит смещение на 1 вниз, и далее вращение вокруг этого же ребра.
Выглядит это так:
Рис.3
Как задать описание тессеракта:
Рис.4
Тессеракт можно развернуть в восемь кубов, так же как куб можно развернуть в шесть квадратов. Развертка тессеракта называется сетью. Для гиперкуба существует 261 вариант сетей, ниже показан самый распространенный.
Исходя из основ сборки куба, также можно написать программу сборки тессеракта или обратного.
Интересно знать
В фильме «Куб 2: Гиперкуб» — восемь незнакомых людей просыпаются в комнатах, имеющих форму куба. Комнаты находятся внутри четырёхмерного гиперкуба. Комнаты постоянно перемещаются путём «квантовой телепортации», и если перелезть в соседнюю комнату, то вернуться в прежнюю уже маловероятно. В гиперкубе пересекаются параллельные миры, время в некоторых комнатах течёт по-разному, а некоторые комнаты являются смертельными ловушками.
Используемый источник: damateur.narod.ru
Скутер 50 куб.см Feiling FL50QT-4D (серия № 252) Китай (Auto-Che.ru)
Скутер 50 куб.см Feiling FL50QT-4D (серия № 252) производится в Китае на заводе Zhejiang Lingyu Vehicle Industry Co., Ltd. Предприятие расположено в городе Тайчжоу (провинция Чжэцзян, Китай).
FL50QT-4D
Общие сведения
| Модель | FL50QT-4D |
| Бренд | Feiling |
| Информационный бюллетень | № 252 |
| Тип ТС | Скутер 50 куб.см |
| VIN |
|
| Страна изготовления | Китай |
Информация о производителе
| Предприятие-изготовитель | Zhejiang Lingyu Vehicle Industry Co., Ltd. |
| Бренды |
|
| Город | Тайчжоу |
| Провинция (Регион) | Провинция Чжэцзян |
| Страна местонахождения производства | Китай |
| Число моделей техники данного производителя* | 17 моделей (всего 88 описаний) |
| * Число моделей техники производства Zhejiang Lingyu Vehicle Industry Co., Ltd., найденных в базе данных сайта Auto-che.ru | |
Технические характеристики
| № | Модель двигателя | Рабочий объем двигателя | Мощность двигателя | Завод-изготовитель двигателя | ||
|---|---|---|---|---|---|---|
| 1 | 139QMB | 50 куб. см см | 0,1 л | 2.0 кВт | 3 л.с. | Zhejiang Lingyu Vehicle Industry Co., Ltd. |
| Динамические характеристики | ||
|---|---|---|
| Максимальная скорость | 50 км/ч | 32 миль/час |
| Производительность | ||
|---|---|---|
| Пассажировместимость (включая водителя) | 1 | |
| Веса и давление на грунт | ||
|---|---|---|
| Снаряженная масса | 83 кг | 0,1 т |
| Полная масса | 158 кг | 0,2 т |
| Размеры | ||
|---|---|---|
| Габаритная длина | 1820 мм | |
| Габаритная ширина | 655 мм | |
| Габаритная высота | 1045 мм | |
| Ходовая часть и подвеска | ||
|---|---|---|
| Число осей | 2 | |
| Колесная база | 1310 мм | |
| Колеса и шины | ||
|---|---|---|
| Число шин | 2 | |
| Размерность шин | передн.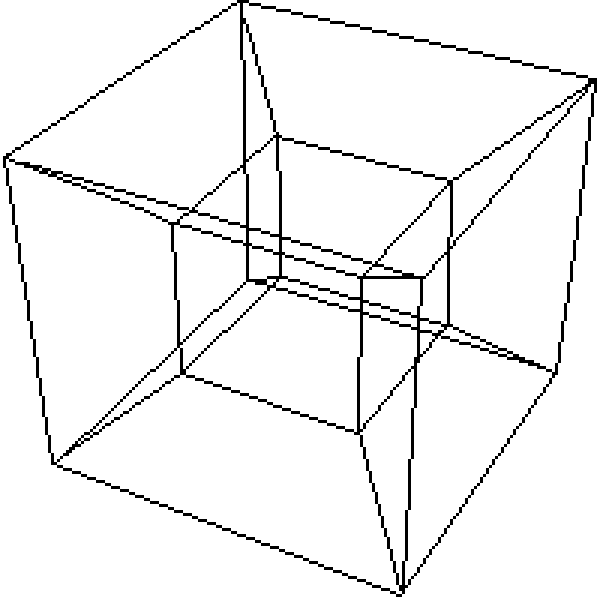 3.50-10 задн. 3.50-10 3.50-10 задн. 3.50-10 | |
Riya RY50QT-31 (серия № 284)
- Скутер 50 куб.см Riya
- Двигатель: 139QMB-E
- Рабочий объем, куб.см: 50
- Мощность, кВт: 2.4
- Число мест, чел.: 1
- Полная масса, кг: 160
Yiying YY50QT-15D (серия № 275)
- Скутер 50 куб.см Yiying
- Двигатель: 139QMB-D
- Рабочий объем, куб.см: 50
- Мощность, кВт: 2.2
- Число мест, чел.: 1
- Полная масса, кг: 152
Qisheng QS50QT (серия № 274)
- Скутер 50 куб.см Qisheng
- Двигатель: 1P39QMB
- Рабочий объем, куб.см: 50
- Мощность, кВт: 2.2
- Число мест, чел.: 1
- Полная масса, кг: 160
Brilliant Math & Science Wiki
Аррон Кау внес
Содержание
- Введение
- Свойства тессерактов
- Визуализация тессерактов
- Смотрите также
На изображении ниже мы видим одну попытку представить схему гиперкуба, хотя изображение обманчиво в том смысле, что относительные размеры и углы на этом изображении искажены.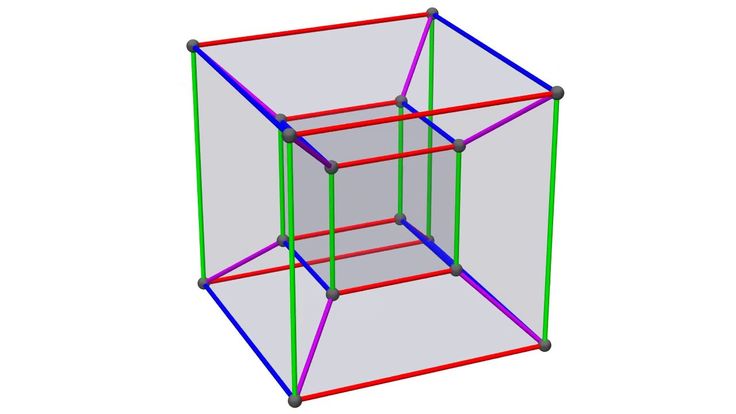 Каждый четырехугольник на изображении ниже, образованный четырьмя вершинами гиперкуба, является квадратом (хотя на диаграмме они не выглядят квадратами!) Точно так же каждая пара прямых, которые встречаются в вершине, находятся под прямым углом друг к другу ( как и следовало ожидать в квадрате или кубе). Невозможно идеально представить гиперкуб в двух измерениях или даже построить его в трех измерениях.
Каждый четырехугольник на изображении ниже, образованный четырьмя вершинами гиперкуба, является квадратом (хотя на диаграмме они не выглядят квадратами!) Точно так же каждая пара прямых, которые встречаются в вершине, находятся под прямым углом друг к другу ( как и следовало ожидать в квадрате или кубе). Невозможно идеально представить гиперкуб в двух измерениях или даже построить его в трех измерениях.
Квадрат представляет собой двумерную замкнутую фигуру с линиями одинаковой длины, пересекающимися под прямым углом. Куб — это трехмерная фигура с линиями одинаковой длины, пересекающимися под прямым углом. Для квадрата две линии встречаются в каждой вершине (угле). Для куба, поскольку мы добавили еще одно измерение, у нас есть три линии, пересекающиеся в каждой вершине.
Тессеракт представляет собой четырехмерную замкнутую фигуру с линиями одинаковой длины, которые пересекаются друг с другом под прямым углом. Поскольку мы добавили еще одно измерение, четыре линии сходятся в каждой вершине под прямым углом. Как и в случае с кубом, каждая двумерная грань тессеракта представляет собой квадрат. На самом деле тессеракт имеет трехмерные «грани», каждая из которых представляет собой куб.
Как и в случае с кубом, каждая двумерная грань тессеракта представляет собой квадрат. На самом деле тессеракт имеет трехмерные «грани», каждая из которых представляет собой куб.
Вы можете вычислить свойства тессеракта, экстраполируя идею квадрата и куба (см. задачи ниже). Однако они также перечислены за кнопкой здесь:
Гиперкуб обладает следующими свойствами:
- 16 вершин (0D: точки)
- 32 ребра (1D: линии)
- 24 грани (2D: квадраты)
- 8 ячеек (3D: кубики)
20 8 12 16
Сколько углов имеет гиперкуб (четырехмерный куб)?
Сколько двумерных граней имеет тессеракт (четырехмерный куб)?
Примечание: Грань — это плоская двумерная поверхность, являющаяся частью границы многогранного объекта.
Трудно визуализировать объекты в более высоких измерениях. Выше мы видели пару различных представлений выше. Вот еще один, в котором более наглядно показано свойство, заключающееся в том, что все строки в тессеракте имеют одинаковую длину. Хотя это изображение помогает нам увидеть, что все двумерные грани тессеракта являются квадратами, на этом рисунке труднее увидеть, что все трехмерные ячейки являются кубами:
Каждое отдельное представление помогает нам развить некоторую интуицию относительно взаимосвязей в форме. Возможны многие другие представления, каждое со своими компромиссами.
Выберите один или несколько
Ф я г л С ЧАС Дж Д
Если вы возьмете твердый четырехмерный гиперкуб и разрежете его одной плоской трехмерной гиперплоскостью, какое поперечное сечение может быть , а не ?
* Квадрат
* Гиперплоскость
Цитировать как: Тессеракт. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/tesseract/
Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/tesseract/
МАТЕМАТИКА 1332 Введение в математику (M 302), Раздел 3, 3.6 Четырехмерные кубы и треугольники
Чтобы доказать, что вы узнали кое-что о 4D, я прошу вас хорошо понимать два 4D-объекта: 4D-куб и 4D-треугольник (или симплекс). В этом разделе мы собираемся использовать так называемый комбинаторный подход . Мы будем думать об объектах как о построенных из объектов более низкого измерения, как если бы они были строительными блоками. Затем большая часть нашей работы сводится к подсчету количества объектов каждого типа и обсуждению того, как эти строительные блоки собираются вместе.
Для начала вспомните, что прямо перед последним экзаменом я просил вас узнать о границах объектов.
- граница объекта — это все точки объекта, примыкающие к частям объекта, и точки, которые не объекта.
 Подойти к этим точкам объекта можно как с снаружи , так и с внутри объекта.
Подойти к этим точкам объекта можно как с снаружи , так и с внутри объекта.
Для начала мы определим 0D-куб как одну вершину, а 1D-куб — как отрезок линии (который имеет границу из двух вершин).
Теперь представьте, что вы строите квадрат из частей 0D и 1D. Подумайте о 4 ребрах и 4 вершинах, соединенных вместе в форме квадрата, поэтому получается квадрат из проволоки. Затем вы затеняете середину 2D-областью.
Вот некоторые факты:
- Для краткости я скажу: «Двумерный квадрат состоит из 4 вершин, 4 ребер и одной грани».
- В каждой вершине мы видим, что встречаются два ребра. Используя формулы из последнего модуля, мы могли бы сказать, что «количество вершин будет равно \(\frac{4\cdot2}{2}=4\), поскольку имеется четыре ребра с двумя вершинами в каждом, и мы соединяем вместе две вершины за раз».
Затем подумайте о построении 3D-куба, по существу, построив пустой ящик, а затем вставив 3D-объем.
Вот некоторые факты:
- Для краткости я скажу: «Трехмерный куб состоит из 8 вершин, 12 ребер, 6 граней и одного заполнения».
- В каждой вершине сходятся три ребра. Используя формулы из последнего блока, мы могли бы сказать, что «количество вершин будет равно \(\frac{6⋅4}{3}=8\), потому что есть шесть квадратных граней с четырьмя вершинами в каждой, и мы соединяя вместе три вершины за раз».
Это большое видео. Целая лекция о том, как можно держать 3D-границу 4D-куба в руках, очень сильно щуриться, пользоваться маркером и пытаться представить форму 4D-куба.
Другими словами, вот частично разобранная трехмерная граница четырехмерного куба.
Вот некоторые факты:
- Для краткости я скажу, что четырехмерный куб состоит из 16 вершин, 32 ребер, 24 граней, 8 трехмерных заполнений и 1 четырехмерного «гиперзаполнения».
- На границе 8 кубов, мы склеиваем две грани за раз, вокруг каждого края соединяются три куба, вокруг каждой вершины соединяются четыре куба.
 Таким образом, используя формулы из последнего модуля, будет \(\frac{8⋅8}{4}=16\) вершин, \(\frac{8⋅12}{3}=32\) ребер и \ (\frac{8⋅6}{2}=24\) лиц.
Таким образом, используя формулы из последнего модуля, будет \(\frac{8⋅8}{4}=16\) вершин, \(\frac{8⋅12}{3}=32\) ребер и \ (\frac{8⋅6}{2}=24\) лиц. - Чтобы закончить сборку границы на картинке, вы должны покинуть трехмерный мир и войти в четвертое измерение. Только после этого вы сможете закончить склеивание пар двумерных граней вместе. Затем вы вводите объект с «гиперобъемом», и теперь у вас есть 4D-куб.
Вы заметили, что можно построить одномерный куб из двух нулевых кубов, двумерный куб из четырех одномерных кубов, трехмерный куб из шести двухмерных кубов и т. д.? В общем, вы можете построить куб n измерений, используя 2 n кубов на одно измерение меньше.
То же самое я могу сказать и о треугольниках.
- Треугольник 0D представляет собой одну вершину.
- Треугольник 1D состоит из 2 треугольников 0D, а затем вы окрашиваете край.
- 2D-треугольник состоит из 3 1D-треугольников, а затем вы заштриховываете область.


 Подойти к этим точкам объекта можно как с снаружи , так и с внутри объекта.
Подойти к этим точкам объекта можно как с снаружи , так и с внутри объекта. Таким образом, используя формулы из последнего модуля, будет \(\frac{8⋅8}{4}=16\) вершин, \(\frac{8⋅12}{3}=32\) ребер и \ (\frac{8⋅6}{2}=24\) лиц.
Таким образом, используя формулы из последнего модуля, будет \(\frac{8⋅8}{4}=16\) вершин, \(\frac{8⋅12}{3}=32\) ребер и \ (\frac{8⋅6}{2}=24\) лиц.