Эволюция стратегия: Стратегии : evo_lutio

Содержание

Стратегии : evo_lutio — LiveJournal

В Сети популярна вот эта шутка про стратегии:

Но в своей жизни многие люди думают, что стратегии выглядят именно так.

Вчера я по случаю посмотрела начало российского сериала «Короли игры»(2007).

В первые же 10 минут там показали как раз такую вот «стратегию» с ловлей комара на соль, водку, палку и камень.

Короли игры — это команда «стратегов», которые помогают людям достигать желаемого, когда им уже отказали.

То есть эта команда создает такой контекст, чтобы воля других разворачивалась в пользу клиента.

Но это по задумке. А в реализации у этой команды получается как раз ловля комара на соль, воду, палку и камень.

Самая первая ситуация — дочь состоятельной матери, которая против маминой воли хочет увеличить грудь силиконовыми имплантами.

Мать не может ее отговорить и нанимает супер-стратегов, чтобы они помешали планам дочки.

Дальше разворачивается настоящий квест.

Дочь едет на операцию, подходит к остановке и там сидит один из команды, громко рассказывая «приятелю» про какую-то свою девушку.

Приятель громко интересуется, какая же у его девушки грудь.

«Грудь супер, — кричит стратег, чтобы услышала девушка. — Маленькая, настоящая, без силикона!»

Наевшись соли вместо сахара, наш комар, то есть нерадивая дочь своей матери, садится в автобус. Воля ее пошатнулась, мучают сомнения и информационная жажда, она жадно шарит глазами по автобусу и читает на обложке журнала, который ей сунули под нос все те же хитрые «стратеги»: «Риски пластической хирургии!».

В глазах ее троится, будто она хлебнула водки вместо воды.

Жажду свою она не утолила, а лишь расшатала себя больше.

В расшатанном состоянии она добрела до клиники. И что же? Врач опаздывает.

Мы видим, что врачу искусственно создали препятствие, выследив его машину и устроив аварию на дороге.

И вот об это препятствие, об эту услужливо подложенную палку, спотыкается наш расшатанный комар.

Пока героиня сомневается ждать врача или нет, ее добивают камнем.

К ней выходит еще один «стратег», назвавшись юристом клиники, он провожает ее в кабинет и зачитывает ей договор, где перечислены послеоперационные ужасы, за которые клиника не несет ответственности.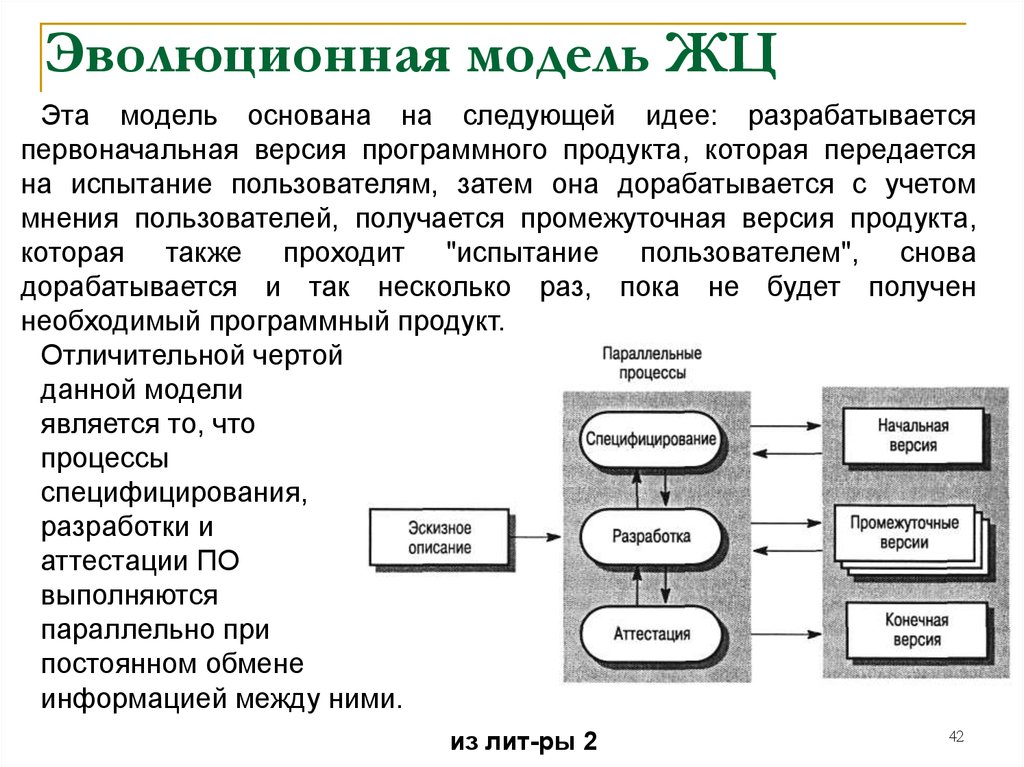 Выслушав список возможных уродств и болезней, девушка больше не хочет силиконовую грудь. Ее комар, то есть желание импланта, подыхает.

Как же стратегу удалось захватить кабинет неприятеля на глазах администратора?

А он прикинулся газовой службой, получил ключи и дальше уже разыграл этот спектакль, пока администратор болтала по телефону.

Точно так же, как и в истории с комаром, хватило бы одного юриста, одного камня, а лучше свернутой газеты, которым его можно было прихлопнуть. Но «короли игры» не ищут легких путей, их стратегия должна быть максимально сложной и запутанной, включать в себя множество каскадерских трюков, часть из которых будут выполнять жертвы.

Комар должен обязательно поесть соли, потом обязательно напиться водки, потом непременно спотыкнуться о палку и, наконец, удариться головой о камень.

Ничего, что в реальности комары не едят соль, не пьют водку, не спотыкаются и не ударяются головой. Автор стратегии представляет на месте комара кого-то вроде себя, но только намного глупей и послушней.

И все стратегии Победителей скроены по этому лекалу.

Чуть проще или такие же сложные, но это всегда история, где нет второго субъекта, а есть лишь послушная проекция самого «стратега».

Совсем другое дело стратеги.

Вот когда хищник оценивает силы неприятеля в этой истории и в этой, он не придумывает за неприятеля его ходов.

В первом случае он видит Выскочку и решает познакомиться поближе, чтобы этой Выскочке подыграть в нужном себе направлении. Не направлять человека, а открыть его решето и посмотреть, что из этого решета может пригодиться.

Во втором случае он смотрит на поле боя дольше, чтобы понять кто с кем в союзе, а кто в оппозиции.

Он сразу увидел, что мать невесты — Штурман, рассмотрел ее характер в динамике, не только персиковое платье, потому что только для моих двоечников персиковое платье означает стремление немедленно отдаться первому встречному, а в жизни все не так. Балкон удобен тем, что видно, кто к кому подходит, кто бегает, кто на месте стоит, кто в стороне, кто в центре. На поле так и надо смотреть, отстраненно, со стороны, представляя, что вы смотрите с балкона или на карту местности. И себя на этом поле тоже нужно видеть так же, как отдельную фигуру, видя слабости вашей позиции и сильные стороны.

Хищник не придумывал за мать невесты ее ходы. Он думал лишь о том, чем вызвать ее расположение.

Чтобы вызвать расположение человека, нужно увидеть его интерес.

Люди в короне и с внешним локусом имеют не интерес, а нужду, голод. Вот почему хищник в одну минуту пленяет таких людей.

Люди без короны, с нормальным локусом имеют нормальный интерес. И они тоже проникаются симпатией к рыбаку, а он проникается симпатией к ним, потому что они умеют видеть обратную связь и общаться в границах.

Вот это стратегия, противоположная стратегии Победителя.

Победитель гоняется за человеком с копьем как за добычей, он овеществляет другого. А рыбацкая стратегия — самому предложить добычу, увидев в другом субъекта.

Если другой — Победитель, он сам будет гоняться за рыбаком, сливая все. Только рыбак не возьмет слитое, а хищники могут взять, часть или все, смотря какой хищник, у хищников разная степень этичности.

Если другой имеет нормальный локус контроля, он не будет гоняться с копьем, он попытается предложить встречную добычу и, если рыбаку интересно, возникнет обмен.

С хищником будет то же самое. Если вы не погонитесь за ним, а предложите ему что-то интересное для него, он согласится на равноценный обмен.

То есть хищник — существо безопасное, если у вас нет короны.

Опасен хищник только для человека с большой короной и с плохими границами.

Если хотите, давайте эту тему обсудим.

А еще приведите примеры смешных «стратегий» с женских и мужских тренингов, курсов, из блогов, все равно откуда.

Только ссылки закрашивайте.

Эволюция желаний: стратегии выбора потенциальных партнеров

Forbes Woman публикует отрывок из книги Дэвида Басса «Эволюция сексуального влечения. Стратегии поиска партнеров» издательства «Альпина Паблишер».

Как в процессе эволюции формировались требования мужчин и женщин к представителям противоположного пола и их стратегии выбора потенциальных партнеров? Как объяснить с точки зрения развития человечества существование и моногамии, и случайных связей? Как все эти феномены меняются со временем? На эти вопросы в своей книге пытается ответить эволюционный психолог Дэвид Басс. Forbes Woman приводит два отрывка из произведения, в которых автор пытается объяснить, действительно ли стоит винить СМИ и рекламу в возникновении сегодняшних стандартов красоты.

Читатели Forbes Woman могут воспользоваться 10%-ной скидкой на любые книги «Издательской группы «Альпина» по промо-коду forbes до 31 августа 2017 года.

Эволюционные корни мужских требований

Большое значение, которое мужчины придают внешности женщины, — вовсе не общий закон животного мира. У многих других видов, например у павлинов, именно самки оценивают внешность самцов, а не наоборот. Точно так же не универсально мужское предпочтение молодости. Самцы некоторых других приматов, например орангутангов, шимпанзе и японских макак, предпочитают более зрелых самок, которые уже продемонстрировали свои репродуктивные способности, они практически не проявляют сексуального интереса к юным самкам из-за их более низкой фертильности. Мужчины имеют дело с уникальным набором адаптивных задач, и их эволюционная сексуальная психология также уникальна. Они предпочитают молодость из-за центральной роли брака в сексуальном поведении людей. Их предпочтения связаны с будущим репродуктивным потенциалом женщины, а не с возможностью зачатия в данный момент. Они придают так много значения внешности, поскольку она несет большое число надежных признаков репродуктивного потенциала партнерши.

Мужчины всего мира хотят иметь привлекательных, молодых и сексуально верных жен, которые сохраняют верность на протяжении длительного периода. Возникновение этих предпочтений нельзя приписать западной культуре, капитализму, узости взглядов белых англосаксов, СМИ или промыванию мозгов с помощью рекламы. Они универсальны для всех культур, и нет такой культуры, где они бы не присутствовали. Это глубоко укоренившиеся психологические адаптации, которые управляют нашими решениями в сфере поиска партнера, точно так же, как наши эволюционные вкусовые предпочтения определяют решения в сфере питания.

Как это ни странно, предпочтения мужчин-гомосексуалистов лишь доказывают глубину этих возникших в процессе эволюции психологических механизмов. Тот факт, что внешность занимает центральное место в предпочтениях геев, а юность — главный атрибут их стандартов красоты, позволяет утверждать, что даже различия в сексуальной ориентации не могут изменить этих фундаментальных мужских адаптаций.

Такие предпочтения расстраивают некоторых своей несправедливостью. Мы можем лишь ограниченно изменять свою внешность, и одни люди рождаются, или становятся, более красивыми, чем другие. Красота недемократична. Женщина не может изменить свой возраст, и ее репродуктивная ценность с возрастом снижается гораздо быстрее, чем у мужчин, — эволюция обошлась с женщинами жестоко, по крайней мере в этом отношении. (Далее мы увидим, как эволюция жестоко обошлась с мужчинами, которых в среднем ожидает более ранняя смерть.) Женщины борются с увяданием с помощью косметики, пластической хирургии и занятий фитнесом. Этим пользуется косметическая индустрия, бюджет которой в США составляет $8 млрд в год.

После прочитанной мною лекции о половых различиях предпочтений в отношении партнера одна женщина заметила, что мне не стоит распространяться об этом, поскольку такая информация расстраивает женщин. На ее взгляд, женщинам и без того тяжело живется в мире, где доминируют мужчины, а тут еще ученые с рассказами о том, что их проблемы в сфере поиска партнера связаны с эволюционной психологией мужчин. Однако утаивание правды вряд ли поможет, точно так же, как утаивание предпочтения спелых и сочных фруктов, вряд ли изменит наши пристрастия. Предъявлять мужчинам претензии за то, что они предпочитают красивых, молодых и верных жен, все равно что предъявлять претензии тем, кто ест мясо, за то, что они предпочитают животный белок. Убеждать мужчин в том, что их не должны возбуждать признаки юности и здоровья, все равно что убеждать их не чувствовать сладкий вкус, когда на языке оказывается сахар.

У многих сохраняется идеалистическая уверенность в том, что стандарты красоты искусственны и навязываются обществом, что красота — это нечто исключительно поверхностное, что представители разных культур придают очень разное значение внешности и что западные стандарты — порождение СМИ, родителей, цивилизации или прочих социальных факторов. Однако стандарты привлекательности вовсе не искусственны — они отражают признаки молодости и здоровья, а следовательно, репродуктивной ценности. Красота не поверхностна. Она говорит о внутренних репродуктивных способностях организма. Хотя современные технологии репродуктивной медицины помогают женщинам сохранять способность к деторождению в более зрелом возрасте, чем это было возможно в прошлом, мужские предпочтения в отношении женщин с явными признаками репродуктивных способностей продолжают действовать, хотя они и возникли очень давно в мире, который больше не существует.

Впрочем, культура, экономические условия и технологический прогресс играют важную роль в оценке мужчинами девственности. Там, где женщины менее зависимы от мужчин экономически, как в Швеции, на сексуальную свободу смотрят сквозь пальцы, и мужчины не требуют девственности от потенциальных жен. Эти перемены отражают чувствительность некоторых мужских предпочтений к особенностям культуры и контекста.

Несмотря на культурные вариации, в долговременных отношениях сексуальная верность для мужчин является важнейшим условием. Хотя многие западные мужчины не могут требовать от партнерш девственности, они обычно настаивают на верности. Методы контроля рождаемости, возможно, и сделали это предпочтение неважным с точки зрения гарантии отцовства, но тем не менее оно сохраняется. Мужчины не перестают требовать верности от жен просто потому, что те принимают противозачаточные таблетки. Это постоянство указывает на важность нашей эволюционной сексуальной психологии — психологии, которая возникла с ориентацией на важнейшие условия первобытного мира, но продолжает сохранять свою власть и в нынешнем мире сексуальных отношений.

Влияние СМИ на стандарты красоты

Рекламщики широко эксплуатируют привлекательность красивых молодых женщин. Некоторые даже утверждают, что именно СМИ и Мэдисон-авеню формируют единый стандарт красоты, к которому все должны стремиться. Считается, что реклама внушает неестественные, идеализированные компьютерные образы красоты и заставляет людей стремиться к ним. Такая интерпретация, возможно, в какой-то мере и верна, особенно когда нам демонстрируют неестественно худеньких моделей, однако в то же время она как минимум отчасти ошибочна. Стандарты красоты не являются чем-то необоснованным — это надежные признаки репродуктивной ценности. Рекламщикам ни к чему навязывать нам какие-то стандарты красоты, они просто используют все, что помогает продавать товары. Они сажают юную девушку с чистой кожей и правильными чертами лица на капот автомобиля последней модели или показывают, как несколько привлекательных женщин с любовью смотрят на мужчину, пьющего пиво известной марки, поскольку эти образы включают определенные психологические механизмы мужчин и таким образом помогают продавать машины или пиво, а не потому, что рекламщикам хочется установить определённый стандарт красоты.

Тем не менее у медиаобразов, воздействию которых мы ежедневно подвергаемся, есть потенциально опасные последствия. В одном исследовании группам мужчин показывали фотографии очень привлекательных женщин и женщин средней привлекательности, а затем просили оценить преданность своим романтическим партнершам. Мужчины, которые рассматривали фотографии красивых женщин, находили своих партнерш менее привлекательными, чем мужчины, которые рассматривали фотографии женщин средней привлекательности. Еще важнее то, что мужчины из первой группы ниже оценивали свою преданность, удовлетворенность, серьезность и близость отношений со своими реальными партнершами. Аналогичные результаты были получены в другом исследовании, где мужчины рассматривали журнальные фото обнаженных моделей: они также ниже оценивали привязанность к своим партнершам.

Причина таких изменений отношения заключается в нереалистичном характере данных изображений. Нескольких привлекательных женщин, снимающихся в рекламе, выбирают из тысяч претенденток. Во многих случаях делаются тысячи фотографий выбранной модели. Известно, например, что в журнале Playboy делают около 6000 снимков девушки, появляющейся на развороте. Из этих тысяч фотографий лишь несколько отбирают для разворота и рекламы. А потом эти снимки обрабатывают в фоторедакторе. В результате мужчины видят не то, что есть в действительности, а искусно обработанные изображения самых привлекательных женщин в самых привлекательных позах на самом привлекательном фоне. Сравните эти фотографии с тем, на что смотрел первобытный мужчина, живший в группе не более чем из 150 человек. Вряд ли в таких условиях ему удавалось видеть сотни или хотя бы десятки привлекательных женщин. Однако, будь у него доступ к множеству привлекательных фертильных женщин, он вполне мог бы захотеть сменить партнершу и его преданность реальной спутнице снизилась бы.

У нас те же самые механизмы оценки, которые выработались в древние времена у наших предков. Однако сегодня на эти психологические адаптации воздействуют десятки образов привлекательных женщин, с которыми мужчины ежедневно сталкиваются в нашей визуально насыщенной среде — в интернете, журналах, на рекламных плакатах, телевидении и в кино. Эти образы не соответствуют реальным женщинам в реальной социальной среде. Они, можно сказать, лишают нас адаптаций, выработанных для иных условий поиска партнера. Иногда они способны приносить несчастье, разрушая существующие реальные отношения. Доступ к тысячам объявлений потенциальных партнеров на таких интернет-ресурсах и приложениях, как Tinder, Match.com и OKCupid, может сбивать с толку и заставлять думать, что можно найти кого-то получше, стоит только просмотреть достаточно много вариантов.

Под влиянием этих образов мужчины теряют удовлетворенность и преданность существующим партнершам. Они потенциально вредны и для женщин, так как вызывают бесконтрольное и нездоровое состязание за идеальную фигуру, которая якобы привлекательна для мужчин, но на деле далека от того, что предпочитает большинство. Беспрецедентный уровень распространения расстройств пищевого поведения, таких как нервно-психическая анорексия, а также расцвет пластической хирургии, например абдоминопластика и увеличение груди, в определенной мере зависят от этих медиаобразов. Некоторые женщины идут на немыслимые жертвы, чтобы стать тем, что они считают мужским идеалом. Но к таким последствиям при- водит вовсе не создание каких-то новых стандартов красоты. Стандарты женской красоты у мужчин существуют давно, так же как и механизмы соперничества за партнера у женщин, а СМИ просто эксплуатируют их с невиданным и нездоровым размахом.

Какую бы роль ни играла красота тела и лица в мужских предпочтениях, эти качества помогают решить только один набор адаптивных задач, стоящих перед мужчинами, — поиск способных к деторождению женщин и вступление с ними в сексуальный контакт. Однако выбор репродуктивно ценной партнерши не гарантирует, что эта ценность будет принадлежать только одному муж- чине. Следующая важнейшая адаптивная задача — гарантия отцовства.

Стратегии эволюции — Scholarpedia

Ханс-Георг Бейер (2007), Scholarpedia, 2 (8): 1965.

doi:10.4249/scholarpedia.1965

редакция #199317 [ссылка/цитировать эту статью]

Постпубликационная деятельность

Куратор: Ханс-Георг Бейер

Авторы:

0,29 —

Николаус Хансен

0,29 —

Ижикевич Евгений Михайлович

0,14 —

Роберт Вюнше

0,14 —

Бенджамин Броннер

Доктор Ханс-Георг Бейер, Форарльбергский университет прикладных наук

Стратегии эволюции (ЭС) являются подклассом вдохновленных природой методы прямого поиска (и оптимизации), принадлежащие к классу Эволюционные алгоритмы (ЭА), которые используют мутацию, рекомбинацию, отбор, применяемый к популяции особей, содержащих возможные решения, чтобы итеративно развиваться все лучше и лучше решения. * = \mathrm{argopt}_{{\mathbf{y} \in \mathcal{Y}}} \, f(\mathbf{y}), \] функция $f(\mathbf{y})$, которую необходимо оптимизировать, также упоминается как целевая (или целевая) функция, может быть представлена в математическом форму, с помощью моделирования или даже с точки зрения измерений, полученных из реальные объекты. ES также может быть применен к набору целевых функций в контексте многоцелевой оптимизации (см. также Многокритериальные эволюционные алгоритмы и Многокритериальный поиск).

Содержимое

1 Версии Canonical ES
2 Пример: ($\mu/\mu_I, \lambda$)-$\sigma$-Самоадаптация-ES
3 Варианты принципов проектирования ES и оператора
4 Пример: простой $(\mu+\lambda)$-ES для комбинаторных задач упорядочения
5 Стратегии развития адаптации ковариационной матрицы CMA-ES
6 Каталожные номера
7 Внешние ссылки
8 См. также

Канонические версии ES

выбор запятой ($ \mu < \lambda $ должно выполняться), или как родители, так и потомство, называется плюс-выбор . Выбор основан на рейтинге пригодности людей. $F(\mathbf{y})$, взяв $\mu $ лучших особей (также называется усеченным выбором). В общем, \[ \mbox{ES индивидуальный} \quad \mathbf{a} := (\mathbf{y}, \mathbf{s}, F(\mathbf{y})) \] содержит вектор параметров объекта $\mathbf{y} \in \mathcal{Y}$ для оптимизации, набор параметров стратегии $\mathbf{s}\ ,$, необходимых особенно в самоадаптирующиеся ЭС и наблюдаемая приспособленность человека $F(\mathbf{y})$ эквивалентна целевой функции $f(\mathbf{y})\ ,$, т.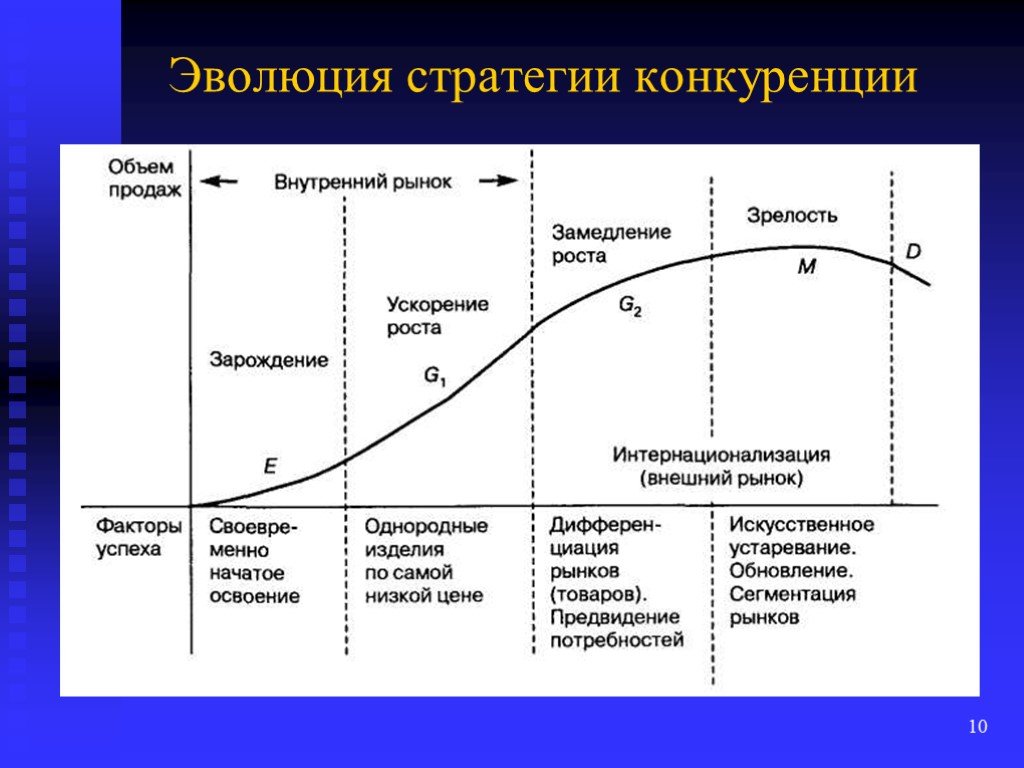 е. $F(\mathbf{y}) \equiv f(\mathbf{y})$ в простейшем случае.

Различие между $F(\mathbf{y})$ и $f(\mathbf{y})$ необходимо, так как $F(\mathbf{y})$ может быть результатом локального оператор поиска, который применяется к $f(\mathbf{y})$-функции быть оптимизированным, или даже может быть результатом другого ES (см. Мета-ES ниже). Кроме того, наблюдаемое $F(\mathbf{y})$ может быть результатом зашумленный $f(\mathbf{y})$-процесс оценки.

Концептуальный алгоритм $(\mu/\rho \; \stackrel{+}{,} \;\lambda)$-ES приведен ниже:

$(\mu/\rho \; \stackrel{+}{,} \; \lambda)$-Самоадаптация-Эволюция-Стратегия

Инициализировать родительскую популяцию $\mathbf{P}_\mu = \{ \mathbf{a}_1, \ldots, \mathbf{a}_{\mu} \}\ .$
Создание $\lambda$ потомков $\tilde{\mathbf{a}}$, формирующих популяцию потомков $\tilde{\mathbf{P}}_\lambda = \{ \tilde{\mathbf{ a}}_1, \ldots, \tilde{\mathbf{a}}_\lambda\}$, где каждое потомство $\tilde{\mathbf{a}}$ генерируется:
1. Выбрать (случайно) $\rho$ родителей из $\mathbf{P}_\mu$ (если $\rho = \mu$ вместо этого взять всех родительских особей).
2. Рекомбинация $\rho$ выбранных родителей $\mathbf{a}$ для формирования рекомбинантной особи $\mathbf{r}\ .$
3. Мутировать набор параметров стратегии $\mathbf{s}$ рекомбинантного $\mathbf{r}\ .$
4. Измените набор целевых параметров $\mathbf{y}$ рекомбинантного $\mathbf{r}$, используя набор параметров мутированной стратегии для управления статистическими свойствами мутации параметров объекта.
Выберите новую родительскую популяцию (используя детерминированный выбор усечения) из
- популяция потомков $\tilde{\mathbf{P}}_\lambda$ (обозначается как запятая -отбор, обычно обозначается как «$(\mu,\lambda)$-отбор «), или
- потомок $\tilde{\mathbf{P}}_\lambda$ и родительская $\mathbf{P}_\mu$ популяция (обозначается как плюс -отбор, обычно обозначается как «$(\mu + \lambda)$-выбор»)
Перейти к 2. до
критерий завершения выполнен.

В зависимости от области поиска и целевой функции $f(\mathbf{y})\ ,$ рекомбинация и/или мутация параметры стратегии могут встречаться или не встречаться в конкретных реализациях алгоритм. Например, $(\mu/1 + \lambda)$-ES, или, что то же самое, $(\mu + \lambda)$-ES не использует рекомбинацию. Он рисует своих новых $\mu$ родителей для следующего поколения как от старых $\mu$ родителей, так и от $\lambda$ потомство (полученное от этих родителей), взяв лучшее $\mu$ особей (относительно наблюдаемого $F(\mathbf{y})$).

$\mathrm{N}_l(0,1)$ и $\mathbf{N}_l(\mathbf{0}, \mathbf{I})$ обычно (0, 1) распределенные случайные скаляры и векторы соответственно, реализующие операция мутации для параметра стратегии $\sigma$ и $n$-мерный вектор параметров объекта $\mathbf{y}.$ Обе операции мутации применяются к соответствующие рекомбинанты $\langle \sigma \rangle$ и $\langle \mathbf{y} \rangle.$ Измененный параметр стратегии $\sigma_l$ контролирует силу параметра объекта мутация (в этом примере $\sigma_l$ — это просто стандартное отклонение нормально распределенных случайных составляющих). Эта мутация аддитивно применяется к рекомбинантному $\langle \mathbf{y} \rangle.$ Изменение силы мутации $\сигма$ согласно (I), позволяет
самонастройка силы мутации: Поскольку $\sigma_l$ человека контролирует генерацию $\mathbf{y}_l,$ индивидуума, выбирающего конкретный индивидуум $\mathbf{a}_l$ в соответствии с его пригодностью $F(\mathbf{y}_l)$ приводит к наследованию соответствующее значение $\sigma_l$.

{\mu} a_{m;\lambda}, \qquad\qquad\mbox{(II)} \] где «$m;\lambda$» обозначает $m$-й лучший потомство особи (последнего поколения). Этот тип рекомбинация называется глобальный промежуточный рекомбинации и обозначается нижним индексом $I$, присоединенным к число смешивания $\rho\ .$ Кроме промежуточного рекомбинация есть и другие типы, например. дискретная рекомбинация где родительские компоненты передаются по координатам случайным образом к рекомбинантному.

Простые реализации $(\mu/\mu_I, \lambda)$-$\sigma$-Самоадаптация-ES для Mathematica и Matlab/Octave можно найти здесь.

Варианты ES и принципов проектирования оператора

В то время как $(\mu/\mu_I,\lambda)$-ES в уравнении. (я) использует изотропно распределенные мутации для вектора параметров объекта $\mathbf{y}\ ,$ более продвинутые ES используют адаптация ковариационной матрицы (CMA) методы (CMA-ES), позволяющие для коррелированных мутаций в пространствах поиска с действительными значениями. \gamma \right]\mbox{-ES} \] с $\lambda’$ субпопуляциями $(\mu/\rho, \lambda)$-ES работают независимо в течение ряда поколений $\gamma$ (время изоляции). Такие стратегии используются в смешанной структуре и параметрах. оптимизационные задачи и для эволюционного изучения стратегии параметры (например, размер популяции, параметры мутации) внутренняя петля эволюции.

Производительность ЭС на конкретном классе задач зависит решающее значение для дизайна ES-операторов (мутация, рекомбинация, выбора) и от того, каким образом ES-операторы адаптировались в процессе эволюции (схемы адаптации, например, $\sigma$-самоадаптация, адаптация ковариационной матрицы, и т. д.). В идеале они должны быть спроектированы таким образом. что они гарантируют эволюционируемость системы во всем весь процесс эволюции. Вот некоторые принципы и общие методические рекомендации:

Отбор осуществляется путем усечения популяции аналогично тому, что делают селекционеры при разведении животных или растений.
Типичные коэффициенты усечения $\mu/\lambda$ в стратегиях с запятой -выборка в непрерывных пространствах поиска находятся в диапазоне от 1/7 до 1/2.
Использование плюс -отбора (своего рода элитарного отбора) в сочетании с операторами вариации, позволяющими достичь любой точки в конечных дискретных пространствах поиска за конечное время, гарантирует стохастическую сходимость для глобального оптимизатора. Однако, поскольку это результат, справедливый только для бесконечного времени работы, нельзя делать общие выводы относительно поведения ES за конечное время.
Использование плюс — выбор рекомендуется для задач комбинаторной оптимизации.
Эволюция ЭС обычно моделируется на уровне фенотипа . Задача, которую нужно оптимизировать, обычно представляется в ее естественном представлении проблемы, пытаясь соблюсти принцип сильной причинности. Это означает, что операторы вариации (мутации и рекомбинации) должны выполнять шаги поиска таким образом, чтобы небольшие шаги поиска приводили к небольшим изменениям пригодности, и наоборот. n\) (целочисленных) пространствах поиска.
Рекомбинация применяется везде, где это возможно и полезно. Он использует $\rho=2$ или более родительских особей для создания одного рекомбинанта (случай $\rho > 2$ называется мультирекомбинацией ). Основная цель рекомбинации — сохранение общих компонентов родителей, т. е. передача (полезных) сходств следующему поколению и ослабление действия вредоносных компонентов родительских генов (эффект генетической репарации).

Обратите внимание, что не всегда возможно соблюдать все принципы проектирования в конкретные приложения. Нарушение некоторых из этих принципов не обязательно приводит к неэффективным стратегиям. 9* = \ mathrm {argopt} _ {\ mathbf {y}} f (\ mathbf {y}) \) где $\mathbf{y}$ — вектор, описывающий перестановку $n$ компонентов. Например, $\mathbf{y} = (1, 3, 9, 2, \ldots)$ описывает порядок компонентов, например, порядок номеров городов, которые посещает продавец последовательно (задача коммивояжера) или порядок работы в задаче планирования рабочего места таким образом, что общая стоимость $е(\mathbf{у})$ минимальны. В ЭС эта оптимизационная задача обычно представлена в ее естественное представление задачи , т. е. операторы вариации действуют непосредственно в порядке $\mathbf{y}\ .$ Индивидуум определяется как $\mathbf{a} = (\mathbf{y}, F(\mathbf{y}))\ .$ ЭС генерирует потомство $\лямбда$ в соответствии с \[ \для всех l=1, \ldots, \lambda : \;\; \begin{случаи} & m \leftarrow \mbox{rand}\{1, \mu\}, \\[2 мм] & \mathbf{y}_l \leftarrow \mbox{PerMutate}( \mathbf{y}_{m; \, \mu+\lambda}), \\[2mm] & F_l \leftarrow F(\mathbf{y}_l) \end{случаи} \] представляющие шаги 2 и 3 концептуального алгоритма ES. ES выбирает случайным образом родитель из набора $\mu$ лучших индивидуумов из обоих родители и потомство последнего поколения (обозначены $\mathbf{y}_{m; \, \mu+\lambda}$ обозначение). Затем этот родитель мутировал случайной перестановкой. Простые операторы перестановки показан на рисунке 1.

Рисунок 1: Четыре оператора перестановки: слева направо и сверху вниз: инверсия, вставка, 2-обмен и сдвиг.

Представляют собой элементарные шаги перемещения, определяющие определенный поиск окрестности (количество состояний, до которых можно добраться за один шаг). В отличие от мутаций в непрерывных пространствах поиска, всегда существует минимальный шаг поиска (представляющий наименьшую возможную мутацию). Производительность различных операторов перестановки зависит от оптимизационная задача, которую необходимо решить. Попытка обеспечить 9п\) пространства поиска. CMA-ES имеет предложены А. Гавельчиком, Н. Хансеном и А. Остермайером в середина 1990-х. Его принципиальное отличие от $(\mu/\mu_I, \lambda)$-$\sigma$-Самоадаптация-ES Примером является форма распределения мутаций, которая генерируется в соответствии с ковариационной матрицей $\mathbf{C}$, которая адаптировал в ходе эволюции. Таким образом, мутации могут адаптироваться к местным условиям. форма фитнес-ландшафта и приближение к оптимуму могут быть значительно возросла. Он использует специальную статистику, накопленную за поколений для управления эндогенными параметрами, специфичными для стратегии (ковариационная матрица $\mathbf{C}$ и глобальный шаг размер $\сигма$). Это в отличие от (мутативного) $\sigma$-подход к самоадаптации рассматривался ранее. Упрощенный (но хорошо работающий) экземпляр дочернего обновления формулы стратегии $(\mu/\mu_I, \lambda)$-CMA для небольшие размеры популяции $\lambda$ (небольшие, по сравнению с размерность пространства поиска $n$) читает

$(\mu/\mu_I, \лямбда)$-CMA-ES

\[\mbox{(L1):} \quad \для всех l=1, \ldots, \lambda : \;\; \begin{случаи} & \mathbf{w}_l \leftarrow \sigma \sqrt{\mathbf{C}} \, \mathbf{N}_l(\mathbf{0}, \mathbf{1}),\\[2 мм] & \mathbf{y}_l \leftarrow \mathbf{y} + \mathbf{w}_l, \\[2мм] & F_l \leftarrow F(\mathbf{y}_l), \end{случаи} \] \[\mbox{(L2):} \quad \mathbf{y} \leftarrow \mathbf{y} + \langle \mathbf{w} \rangle, \] \[\mbox{(L3):} \quad \mathbf{s} \leftarrow \left(1-\frac{1}{\tau}\right)\mathbf{s} + \sqrt{\frac{\mu}{\tau} \left(2-\frac{1}{\tau}\right)} \, \ frac {\ langle \ mathbf {w} \ rangle {\ sigma}, \] \[\mbox{(L4):} \quad \mathbf{C} \leftarrow \left(1-\frac{1}{\tau_{\mathrm{c}}}\right)\mathbf{C} + \frac{1}{\tau_{\mathrm{c}}} \mathbf{s} \mathbf{s}^T, \] \[\mbox{(L5):} \quad \mathbf{s}_\сигма \leftarrow \left(1-\frac{1}{\tau_\sigma}\right) \mathbf{s}_\sigma + \ sqrt {\ frac {\ mu} {\ tau_ \ sigma} \left(2-\frac{1}{\tau_\sigma}\right)} \, \langle \mathbf{N}(\mathbf{0}, \mathbf{1}) \rangle , \] \[\mbox{(L6):} \quad \ сигма \ стрелка влево \ сигма \ exp \ влево [ \ гидроразрыва {\ | \mathbf{s}_{\sigma} \|^2 — n} {2 н \sqrt{п} } \верно]. 2\ .\) Остальные (L5) и (L6) используются для управления размером глобального шага. $\sigma$ с использованием кумулятивной адаптации размера шага (CSA) метод с постоянной времени $\tau_\sigma = \sqrt{n}$ ($\mathbf{s}_\sigma = \mathbf{0}\,$ изначально выбрано). Рекомбинантный $\langle \mathbf{N}(\mathbf{0}, \mathbf{1}) \rangle$ рассчитывается с использованием уравнения (II). 9Т. \] Чтобы в полной мере воспользоваться этим обновлением, константы времени $\тау\,$ $\тау_{\mathrm{c}}\,$ и $\tau_\sigma$ должны быть выбраны соответственно (см. Хансен и др., 2003).

Ссылки

Бейер, Х.-Г. и Швефель, Х.-П. (2002). Стратегии эволюции: всестороннее введение. В Natural Computing, 1(1):3-52.

Бейер, Х.-Г. (2001). Теория эволюционных стратегий. Серия «Естественные вычисления». Спрингер, Берлин, 2001 г.

Хансен, Н. и Остермайер, А. (2001). Полностью дерандомизированная самоадаптация в стратегиях эволюции. В Evolutionary Computation, 9(1):159-195.

Хансен, Н. и Мюллер, С.Д. и Комуцакос, П. (2003). Снижение временной сложности стратегии дерандомизированной эволюции с адаптацией ковариационной матрицы (CMA-ES). В Эволюционные вычисления, 11(1):1-18.

Рехенберг, И. (1994). Эволюционная стратегия ’94. Frommann-Holzboog Verlag, Штутгарт (на немецком языке).

Швефель, Х.-П. (1995). Эволюция и поиск оптимума. Уайли, Нью-Йорк, штат Нью-Йорк.

Внутренние ссылки

Ян А. Сандерс (2006) Усреднение. Scholarpedia, 1 (11): 1760.
Томаш Даунарович (2007) Энтропия. Scholarpedia, 2(11):3901.
Роб Шрайбер (2007) MATLAB. Scholarpedia, 2(7):2929.
Фрэнк Хоппенстедт (2006 г.) Модель «хищник-жертва». Scholarpedia, 1 (10): 1563.

Внешние ссылки

Веб-сайт Ханса-Георга Бейера
Эволюционные_алгоритмы — термины и определения
Веб-сайт, посвященный стратегии развития, кафедры бионики Берлинского технического университета
Веб-сайт Николауса Хансена с материалами, связанными с CMA-ES
Х. -П. Двухфазное сопло Швефеля, созданное с помощью (1+1)-ES
Следование скользящему оптимуму с помощью (15,100)-ES
Коллекция демонстраций стратегии развития (см. ниже)
Стратегии развития в действии: анимация с использованием MS Windows

См. также

Эволюционные алгоритмы, эволюционные вычисления, Эволюционное программирование, Эволюционная робототехника, Развивающееся оборудование, Развивающиеся интеллектуальные системы, Генетические алгоритмы, генетическое программирование

Стратегии эволюции — Scholarpedia

Ханс-Георг Бейер (2007), Scholarpedia, 2(8):1965.

doi:10.4249/scholarpedia.1965

редакция #199317 [ссылка/цитировать эту статью]

Постпубликационная деятельность

Куратор: Ханс-Георг Бейер

Авторы:

0,29 —

Николаус Хансен

0,29 —

Ижикевич Евгений Михайлович

0,14 —

Роберт Вюнше

0,14 —

Бенджамин Броннер

Доктор Ханс-Георг Бейер, Форарльбергский университет прикладных наук

Стратегии эволюции (ЭС) являются подклассом вдохновленных природой методы прямого поиска (и оптимизации), принадлежащие к классу Эволюционные алгоритмы (ЭА), которые используют мутацию, рекомбинацию, отбор, применяемый к популяции особей, содержащих возможные решения, чтобы итеративно развиваться все лучше и лучше решения. Его корни восходят к середине 1960-х годов, когда П. Бинерт, И. Рехенберг и Х.-П. Швефель в Техническом университете Берлина, Германия разработала первые основанные на бионике схемы эволюции оптимальные формы тел с минимальным сопротивлением в аэродинамической трубе с использованием теории Дарвина принцип эволюции. 9* = \mathrm{argopt}_{{\mathbf{y} \in \mathcal{Y}}} \, f(\mathbf{y}), \] функция $f(\mathbf{y})$, которую необходимо оптимизировать, также упоминается как целевая (или целевая) функция, может быть представлена в математическом форму, с помощью моделирования или даже с точки зрения измерений, полученных из реальные объекты. ES также может быть применен к набору целевых функций в контексте многоцелевой оптимизации (см. также Многокритериальные эволюционные алгоритмы и Многокритериальный поиск).