Правила игры Эволюция: время летать
Код товара: 14963
850 ₽
42 новых карты, которые позволят крокодилу взлететь!
Говорит Птеродактиль-1, слона вижу хорошо, захожу на цель!
Дополнение к Эволюции «Время летать» планировалось ещё с прошлого года. Тогда все думали, что в нём появятся птицы (и спорили, можно ли будет забираться в их гнёзда). Птицы появились. А кроме них пришла ещё целая толпа разных новых животных, из которых можно будет собрать даже сумчатого летающего скунса-удильщика с развитым интеллектом.
Во что теперь может мутировать хомячок?
Появились новые свойства:
-
Полёт как средство улететь от особо злобных и тяжелых хищников.
- Живорождение: новый путь тянуть карты и ставить маленьких существ на стол.
- Засада — новый путь съесть кого-нибудь вкусного и голодного.
- Чернильное облако: классная штука для тех, кто привык прятаться в нору после еды.
- Новый тип паразита, живущего там же, где коммуникация, то есть между животными (его нельзя скинуть отбрасыванием хвоста!).
- Метаморфоза: штука, которая уменьшает животное за еду. Можно сбрасывать парные свойства, например, симбиоз.
- Интеллект: теперь умное животное может убежать от зоркого хищника, спрятаться под водой от водоплавающего, или даже, будучи большим, притаиться за деревом, спасаясь от не менее крупного.
-
Раковина: эта штука, в которой нужно жить. Есть в ней нельзя, зато можно прятаться. Если кого-то с раковиной съедают, она остаётся на столе, пока в неё не заселится ещё кто-то.
- Специализации для тех, кто хочет спасти вымирающего дронта.
- И карта удильщика, позволяющая превратить маленькое существо без свойств в опасного хищника и сожрать атакующего.
Здорово! А что с балансом?
Один из основных вопросов к дополнению — это будет ли стабилизирован слегка шатающийся баланс первой версии игры. Так вот, пока понятно, что ситуация с балансом примерно такая же: дополнение добавляет непредсказуемости, но коренным образом ситуацию не улучшает. Тем не менее, играть становится веселее.
Что в комплекте?
В маленькой коробке (в половину размера базовой) лежат 42 новых карты, один шестигранный кубик и новые фишки еды. В «Эволюцию» с дополнением «Время летать» можно играть вшестером. Для игры обязательно наличие базовой версии.
Елена
« Купила молодому человеку в качестве подарка. Ему очень нравится эта игра!:) »
Дорогие друзья, перед вами дополнение к настольной игре «Эволюция».
Перед началом игры вам необходимо объединить карты дополнения и карты из базового набора в одну колоду и тщательно перемешать ее. Дополнение не влияет на основу правил игры, однако некоторые новые свойства значительно меняют игровой процесс. Мы рекомендуем до начала игры ознакомиться с особенностя-ми применения этих карт, описанными ниже. Обратите также внимание, что теперь некоторые из свойств базовой колоды указаны в качестве альтернативного (второго) свойства карты. Эти свойства играются так же, как они описаны на картах базового набора.
Используя базовый набор игры с дополнением, можно увеличить число игроков до шести человек. Однако если вы играете этим набором карт вдвоем или втроем, мы рекомендуем сократить состав колоды. Для этого вам нужно будет просто убрать половину карт — в базовой колоде и в дополнении четное число карт каждого типа.
Если базовая версия игры «Эволюция» давала возможность создавать животных с приблизительно 50 тысячами различных комбинаций свойств, то теперь число возможных комбинаций превышает 50 миллионов.
Это число, по всей видимости, больше, чем число видов живых существ на Земле. Так что не будем терять времени и проверим, какие из них окажутся наиболее приспособленными.
Правила игры
| Количество игроков | От 2 до 6 игроков |
| Возраст игроков | От 11 лет |
| Время игры | От 45 До 80 минут |
| Вес | 0.13 кг |
| Производитель | Правильные игры |
Эволюция
Как хомяк вырос до мамонта и съел кита
1 390 ₽
Эволюция подарочная
Увлекательная генная инженерия
2 890 ₽
Эволюция.
Невероятно красивая игра про эволюцию
3 550 ₽
Эволюция. Новый мир
Мы поначалу не знали, какую выбрать обезьяну
2 790 ₽
Эволюция. Растения
Травы зверям!
990 ₽
Эволюция. Биология для начинающих
Развиваемся проще
2 190 ₽
Эволюция. Случайные мутации
Мутируй или исчезай!
1 450 ₽
Доп
Эволюция.
Континенты
Второе дополнение к Эволюции
890 ₽
Эволюция.Трава и Грибы
Мухомор, который съел динозавра
990 ₽
Доп
Эволюция: Новый мир. Эффект бабочки
Один взмах крылом
1 690 ₽
Эволюция. КлиматЗвери выживают среди вулканов, пустынь и метеоритов
2 390 ₽
Эволюция. Полет
Встаём на крыло
1 690 ₽
Океаны
Морские глубины
3 490 ₽
Интернет-аукцион Мешок
Интернет-аукцион МешокЗагрузка .
..
-
- Основной раздел
- Как работает аукцион
- Зачем регистрироваться?
- Как покупать?
- Как продавать?
- Частые вопросы
- Корзина
- Продать
- Регистрация
- Недавние
- Лоты
- Разделы
- Поиски
- Избранные
- Лоты
- Разделы
- Поиски
-
- Недавние
- Лоты
- Разделы
- Поиски
- Избранные
- Лоты
- Разделы
- Поиски
- Покупаю
- Главная страница
- Избранные лоты
- Торгуюсь сейчас
- Я купил
- Не купил
- Подписка на новые лоты
- Запросы лотов у продавцов
- Предложения продавцов
- Продать
- В продаже
- Сделки
- Завершенные торги
- Пополнить счет
- Спрос
- Настройки продавца
- Мой магазин [подробнее]
- Активация
- Настройка
-
- Покупаю
- Избранные лоты
- Торгуюсь сейчас
- Я купил
- Подписка на новые лоты
- Запросы лотов у продавцов
- Предложения продавцов
- Продаю
- Продать
- В продаже
- Сделки
- Завершенные торги
- Пополнить счет
- Спрос
- Настройки продавца
«>
Продаю
Увлеченным Антиквариат и ИскусствоВидео, ФильмыВинтажКниги, журналы, газетыКоллекционноеМузыкаСделано своими руками Электрическое Бытовая техникаЭлектроника и ОптикаВидео, Фото, КиноКомпьютерная техникаТелефоны Себе и любимым Драгоценности и украшенияДетскоеКрасота и здоровьеОдежда, Обувь и АксессуарыСпорт-снаряжениеЧасыК Новому году Все в дом Видео, ФильмыДомашний очаг, Сад, ДачаКниги, журналы, газетыМузыкаСтроительство и РемонтФлора и Фауна Передвигаемся ВоздухоплаваниеАвто, Мото, ЗапчастиПлавсредства Остальное Для бизнесаНедвижимостьУслугиРазное Или так: Рекомендуемые |
Рекомендованные лоты: (показать все)
Набирают популярность 2 марки ГерманияБеларусь БелоруссияРСШопенвкладыш turboзарубежное кинолегендыкрупные серьгикотенокномермостыточный резистор1 гривнатранспортный жетонPC DVD ROMКЗDEEP PURPLEКлеймоРетроКОСТЯНОЙ ФАРФОРКамерунПарагвайЛЗХСиглаблескконаковоигра для PССунь Ятсенмакизарядное устройстволетасоветское золотосердцеслужбаКрасный крестцент1 шиллинг1электрорадиоизделия Еще… Вход:
|
Используйте тематические разделы слева или строку поиска сверху.
00 р.
00 р.Все права защищены 1999-2022 Мешок
Sun, 04 Dec 2022 21:11:41 +0300
3.1: Оператор эволюции времени — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 107223
- Андрей Токмаков
- Чикагский университет
Давайте начнем с самого начала, получив уравнение движения, которое описывает волновую функцию и ее эволюцию во времени через временной пропагатор.
Мы ищем уравнения движения для квантовых систем, эквивалентные уравнениям Ньютона — или, точнее, уравнениям Гамильтона — для классических систем. Вопрос в том, если мы знаем волновую функцию в момент времени \(| \psi (\vec{r}, t_o ) \rangle \), как она меняется со временем? Как мы определяем \(| \psi (\vec{r}, t ) \rangle \), для некоторого более позднего времени \(t > t_o\)? Мы воспользуемся здесь нашей интуицией, основанной в основном на соответствии с классической механикой. Чтобы свести обозначения к минимуму, в последующем обсуждении мы не будем явно показывать пространственную зависимость волновой функции.
Начнем с предположения причинности : \(| \psi (t_o) \rangle \) предшествует и определяет \(| \psi (t) \rangle \), что имеет решающее значение для вывода детерминированного уравнения движения. Также, как обычно, мы предполагаем, что время является непрерывной переменной:
\[\lim _ {t \rightarrow \ tau _ {0}} | \пси (т) \rangle = | \psi \left( t _ {0} \right) \rangle \label{2.
1}\]
Теперь определите «оператор смещения времени» или «пропагатор», который воздействует на волновую функцию вправо и тем самым распространяет систему вперед во времени:
\[| \psi (t) \rangle = U \left( t , t _ {0} \right) | \psi \left( t _ {0} \right) \rangle \label{2.2}\]
Мы также знаем, что оператор \(U\) не может зависеть от состояния системы \(| \psi (t) \rangle \). Это необходимо для сохранения вероятности, т. е. для сохранения нормировки системы. Если
\[| \psi \left( t _ {0} \right) \rangle = a _ {1} | \varphi _ {1} \left( t _ {0} \right) \rangle + a _ {2} | \varphi _ {2} \left( t _ {0} \right) \rangle \label{2.3}\]
, затем
\[\begin{align} | \psi (t) \rangle & = U \left( t , t _ {0} \right) | \psi \left( t _ {0} \right) \rangle \\[4pt] & = U \left( t , t _ {0} \right) a _ {1} | \varphi _ {1} \left( t _ {0} \right) \rangle + U \left( t , t _ {0} \right) a _ {2} | \varphi _ {2} \left( t _ {0} \right) \rangle \\[4pt] & = a _ {1} (t) | \varphi _ {1} \rangle + a _ {2} (t) | \varphi _ {2} \rangle \end{align}.
{- 1}\).
{- 1} \left( t , t _ {0} \right) &= U \left( t _ {0} , t \right) . \label{2.12} \end{align}\]Уравнение движения для U
Найдем уравнение движения, описывающее оператор эволюции во времени, используя замену системы для бесконечно малого временного шага, \(\delta t\): \(U( t+ \дельта t)\). Поскольку
\[\lim _ {\delta t \rightarrow 0} U ( t + \delta t , t ) = 1 \label{2.13}\]
Мы ожидаем, что для достаточно малых \(\delta t\) , \(U\) будет меняться линейно с \(\delta t\). Это основано на аналогии с представлением о детерминированном движении в классических системах. Установив \(t_0\) в 0, так что \(U(t,t_o) = U(t)\), мы можем написать
\[U ( t + \delta t ) = U (t) — i \шляпа {\Omega} (t) \delta t \label{2.14}\]
\(\шляпа{\Omega}\) — зависящий от времени эрмитов оператор, необходимый для того, чтобы \(U\) было унитарным. Теперь мы можем написать дифференциальное уравнение для развития во времени \(U(t,t_o)\), уравнение движения для \(U\):
\[\dfrac {d U (t)} {d t } знак равно \lim _ {\delta t \rightarrow 0} \dfrac {U ( t + \delta t ) — U (t)} {\delta t} \label{2.
15}\]
Итак, из уравнения \ref{ 2.14} имеем:
\[\ dfrac {\ парциальное U \ влево ( т , т _ {0} \ вправо)} {\ парциальное т} = — я \ шляпа {\ Omega} U \ влево ( т , т _ {0} \ справа) \label{2.16}\]
Теперь вы можете видеть, что оператору нужен комплексный аргумент, иначе плотность вероятности не сохранится; он будет расти или распадаться. Скорее, он колеблется в различных состояниях системы.
Заметим, что \(\hat {\Omega}\) имеет единицы частоты. Поскольку квантовая механика фундаментально связывает частоту и энергию как \(E = \hbar \omega\), и поскольку гамильтониан является оператором, соответствующим энергии и отвечающим за эволюцию во времени в гамильтоновой механике, мы пишем
\[\шляпа {\Omega} = \dfrac {\шляпа {H}} {\hbar} \label{2.17}\]
С этой заменой у нас есть уравнение движения для
\[\mathrm { я} \hbar \dfrac {\partial} {\partial t} U \left( t , t _ {0} \right) = \ hat {H} U \left( t , t _ {0} \right) \ label{2.18}\]
Умножение справа на \(| \psi(t_o) \rangle \) дает TDSE:
\[i \hbar \dfrac {\partial} {\partial t} | \psi \rangle = \шляпа {H} | \psi \rangle \label{2.
{\dagger} \left( t , t _ {0} \right)\), действует влево: 9{\prime \prime} \right) + \ldots \label{2.23}\]
Этот подход опасен, так как мы неправильно рассматриваем \(H\) как оператор. Глядя на второй член в уравнении \ref{2.23}, мы видим, что это выражение интегрируется по обоим возможным временным упорядочениям двух гамильтоновых операций, что было бы правильным, только если гамильтонианы в разное время коммутируют: \( H(t’ ),H(t»)] =0\)
Теперь поступим более осторожно, предполагая, что гамильтонианы в разные моменты времени не коммутируют. Интегрирование уравнения \ref{2.18} непосредственно из \(t_0\) в \(t\) дает 9{\prime} \leq \tau \leq t\)
Что представляет собой это выражение? Представьте, что вы начинаете в состоянии \(| \psi _ {0} \rangle = | \ell \rangle\) и хотите описать, как человек движется к целевому состоянию \(| \psi \rangle = | k \rangle\ ). Возможные пути, по которым можно сдвигать амплитуду и развивать фазу, изображенные в терминах этих временных переменных, следующие:
Первый член в уравнении \ref{2.
26} представляет все действия гамильтониана, которые действуют на прямую связь \( | \ell \rangle\) и \(| k \rangle\). Второй член описывает возможные переходы из \(| \ell \rangle\) в \(| k \rangle\) через промежуточное состояние \(| m \rangle\). Выражение для \(U\) описывает все возможные пути между начальным и конечным состоянием. Каждый из этих путей интерферирует так, как это диктуется приобретённой фазой наших собственных состояний при зависящем от времени гамильтониане. 9{\prime} \rightarrow \tau} \end{array} \right.\label{2.28}\]
Таким образом, это выражение говорит вам о том, как квантовая система развивается в течение заданного интервала времени, и допускает любые возможные траектория от начального состояния к конечному через любое количество промежуточных состояний. Каждый член разложения объясняет большее количество возможных переходов между различными промежуточными квантовыми состояниями на этой траектории.
Сравните упорядоченную по времени экспоненту с традиционным расширением экспоненты: 9{t} d \tau _ {1} H \left( \tau _ {n} \right) H \left( \tau _ {n — 1} \right) \ldots H \left( \tau _ {1} \right) \label{2.
{\dagger} \left( t , t _ {0} \right)\), действует влево, то мы получим 9{\dagger} ( t , \tau ) H ( \tau )\label{2.31}\]
Здесь \(H(\tau_i)\) действуют слева.
Чтения
- Коэн-Таннуджи, К.; Диу, Б.; Лало Ф., Квантовая механика. Wiley-Interscience: Париж, 1977; п. 1340.
- Мерцбахер Э., Квантовая механика. 3-е изд.; Уайли: Нью-Йорк, 1998; Ч. 14.
- Мукамель, С., Принципы нелинейной оптической спектроскопии. Издательство Оксфордского университета: Нью-Йорк, 1995; Ч. 2.
- Сакураи, Дж. Дж., Современная квантовая механика, исправленное издание. Эддисон-Уэсли: Рединг, Массачусетс, 19 лет.94; Ч. 2.
Эта страница под названием 3.1: Time-Evolution Operator распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Андреем Токмаковым посредством исходного контента, отредактированного в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Андрей Токмаков
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- № на стр.
- Теги
- источник@https://tdqms.uchicago.edu
- пропагатор времени
- оператор эволюции времени
- унитарные операторы
Эволюция времени | Основная квантовая механика
Фильтр поиска панели навигации Oxford AcademicEssential Quantum MechanicsФизика конденсированного состоянияКвантовая физикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicEssential Quantum MechanicsФизика конденсированного состоянияКвантовая физикаКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Cite
Bowman, Gary E.
,
«Эволюция времени»
,
Essential Quantum Mechanics
(
Oxford,
2007;
online edn,
Oxford Academic
, 1 Jan. 2008
), https://doi.org/10.1093/acprof:oso/9780199228928.003 .0011,
, по состоянию на 4 декабря 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicEssential Quantum MechanicsФизика конденсированного состоянияКвантовая физикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicEssential Quantum MechanicsФизика конденсированного состоянияКвантовая физикаКнигиЖурналы Термин поиска на микросайте
Advanced Search
Abstract
Зависящее от времени уравнение Шредингера является отправной точкой главы.
Для независимого от времени гамильтониана квантовое состояние может эволюционировать во времени с помощью стандартного унитарного оператора эволюции во времени. После получения этого оператора предоставляется алгоритм, с помощью которого состояние может быть изменено во времени и определены вероятности измерения. Пример со спином 1/2 конкретно иллюстрирует эволюцию во времени. Все это находится в тесной связи с обсуждением унитарных операторов в главе 10. Зависимость значений математического ожидания от времени образует следующую тему, за которой следует понятие постоянная движения , которая тщательно противопоставляется константе стационарного состояния. Соотношения неопределенностей энергия-время, которые опираются на совершенно иную концептуальную основу, чем «стандартные» соотношения неопределенностей, занимают оставшуюся часть главы. Пример со спином 1/2 иллюстрирует соотношение неопределенности энергия-время.
Ключевые слова: нестационарное уравнение Шредингера, гамильтониан, оператор эволюции во времени, математическое ожидание, постоянная движения, соотношения неопределенности энергия-время
Предмет
Квантовая физика Физика конденсированного состояния
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic.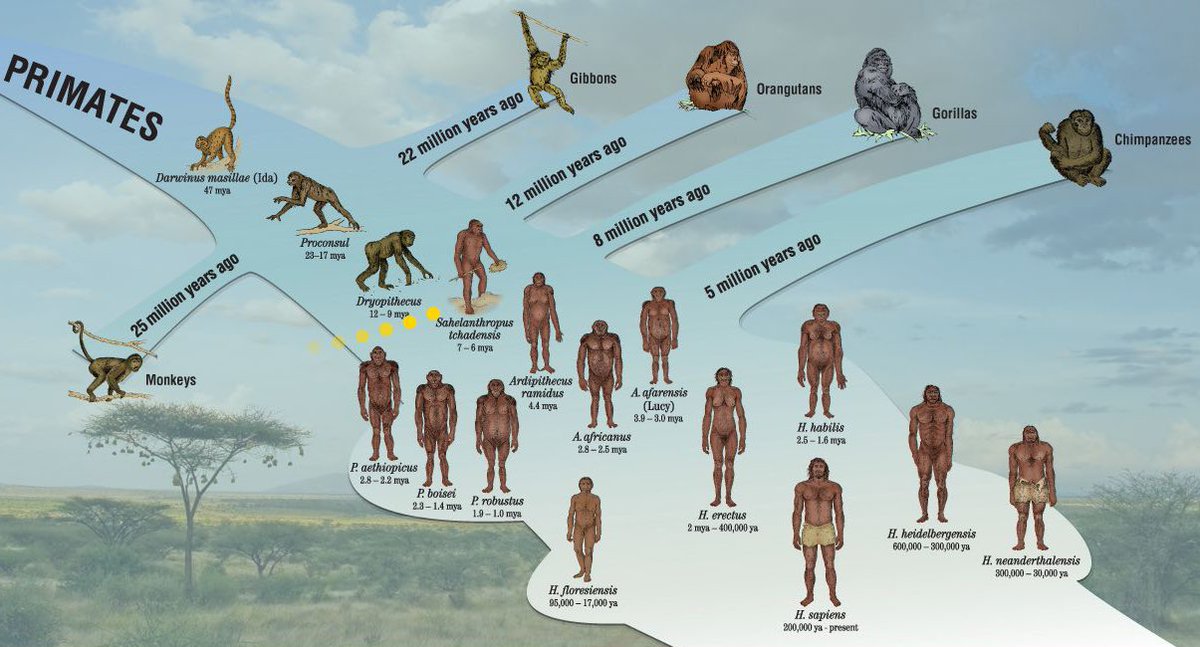
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т.