Алгоритм игры в кости: 🎲🐍 Моделируем игру в кости на Python с помощью метода Монте-Карло

Математика обмана: почему казино всегда в плюсе

Никакого мошенничества, или Почему казино всегда в плюсе

Все игры в казино — рулетка, кости, карты, автоматы — основаны на законах случая. И если в покере или блек-джеке (в России игра известна даже далеким от казино людям как очко) мастерство и опыт игрока могут повлиять на результат, то шансы любителей остальных развлечений равны. Гарантированный выигрыш есть только у одного игрока — казино.

Фото

Julian Nedev / Alamy via Legion Media

Рулетка

В рулетке прибыль заведения гарантирует секция зеро, а в американском варианте еще и дабл зеро. Колесо, или «вертушка», разделено на 37 ячеек, в 36 из них проставлены числа от 1 до 36, а в последней — зеро (в США ячеек 38, из которых две нулевые). Ставить можно на конкретные числа или группы чисел или на «равные шансы»: черное-красное и чет-нечет. Прибыль при выпадении чисел намного выше, чем при угадывании цвета или четности.

via Legion Media

Фото

Andrew Hasson / Alamy

Не будь ячейки зеро, вероятность выигрыша для игрока, поставившего, скажем, на черное, была бы 18/36, или 50%. Но из-за еще одной ячейки она сокращается до 18/37. Другими словами, у заведения появляется «дополнительная» доля шанса на выигрыш — 1/37, то есть 2,7%. В американском варианте из-за второго зеро расхождение вдвое больше и составляет 5,4%.

Когда человек ставит на конкретное число, игорный дом тоже остается в плюсе, несмотря на то что выигрыш вроде бы щедро выплачивается из расчета 35 к 1. Шансы игрока проиграть составляют 36 из 37, а шансы выиграть — только 1 из 37. То есть с каждого рубля, поставленного на конкретный номер, казино получит

или те же 2,7%. Это не означает, что игроки всегда в минусе, но шансов уйти с лишними деньгами у них намного меньше, чем проиграть имеющиеся.

Кости, или крэпс

Правила игры незамысловаты: игрок (шутер) кидает две кости, и, если сумма очков на них равна 7 или 11, он выигрывает, если 2, 3 или 12 — проигрывает. Когда на кубиках выпадает другая сумма, шутер бросает их до выигрышной или проигрышной комбинаций. Остальные участники делают ставки, пытаясь угадать, как лягут кости.

Фото

commercial images / Alamy via Legion Media

Казалось бы, все честно, ведь казино вообще напрямую не участвует в игре. Тем не менее игорный дом и тут остается в прибыли — размер ставок определен так, что участники получают выигрыш меньше «положенного», то есть рассчитанного по законам теории вероятностей. Например, шансы, что на кубиках выпадут комбинации 6+6 или 1+1, составляют

но ставка за них выдается из расчета 30 к 1. Если бы размер выигрыша был пропорционален вероятности, то размер куша вычислялся бы из расчета 35 к 1. Точно так же казино занижает выигрыши для других комбинаций, забирая себе разницу.

«Однорукие бандиты»

Казино в первую очередь ассоциируется с рулеткой и покером, но, по статистике, 61% посетителей игорных домов проводят время, сражаясь с «однорукими бандитами» (данные Американской игорной ассоциации за 2013 год). Правила игры на автоматах предельно просты, а несерьезная минимальная ставка делает их доступными даже для самых бедных игроков.

Фото

ADS / Alamy via Legion Media

Когда-то давно «бандиты» были механическими, и, дергая ручку, игрок спускал пружину, которая раскручивала барабаны с картинками. Сегодня колесики и шестеренки заменил компьютерный чип, а вишенки, лимоны или карточные номиналы отображаются на экране. Как и раньше, выигрышной считается комбинация из трех одинаковых картинок.

Формально игровые автоматы работают честно и останавливают барабаны, подчиняясь командам от генератора случайных чисел. На деле каждый «бандит» запрограммирован возвращать игрокам определенный процент вложенных денег — обычно от 80 до 90%, хотя в казино Лас-Вегаса установлена доля до 98%.

Противоречия здесь нет: момент остановки каждого барабана действительно определяется случайным числом. Но компьютер не использует выданное значение непосредственно. Вместо этого машина производит расчет по определенному алгоритму: умножает, делит и переводит с языка цифр на язык картинок по заранее составленным таблицам. И именно здесь закладывается процент выигрышных результатов: изменяя параметры таблицы, можно сделать «бандита» более или менее «щедрым».

Стратегии чертова колеса

Попыткам обмануть фортуну не одна сотня лет. В Интернете можно бесплатно, а иногда и за немалые деньги познакомиться с десятками «стопроцентно выигрышных стратегий» игры в рулетку (почему-то игрокам кажется, что «взломать» проще всего именно колесо). Бороться с теорией вероятностей бесполезно, но люди упорно пытаются.

Мартингейл НЕ РАБОТАЕТ

Одна из самых старых стратегий игры в рулетку требует от игрока ставить на красное или черное (или чет-нечет) и удваивать ставку при проигрыше. Рано или поздно игрок угадывает и срывает банк.

Схема кажется логичной, но в действительности суммарный выигрыш не превысит размера изначальной ставки. Пусть игрок ставит на черное и угадывает на шестом обороте (игроки говорят — спи՛не). Тогда его баланс выглядит так:

На каждом шаге шансы угадать составляют

из-за зеро, поэтому при достаточно большом количестве спинов игрок оказывается в минусе. Кроме того, любителям мартингейла зачастую приходится делать много попыток и каждый раз удваивать расход. Если деньги закончатся раньше, чем «стратег» угадает, он потеряет огромную сумму. Наконец, владельцы казино прекрасно знают о мартингейле, и размер максимальной ставки во всех игорных домах ограничен. Поставив почти максимум и проиграв, человек лишается шанса вернуть деньги.

Стратегия с позитивной прогрессией НЕ РАБОТАЕТ

В отличие от любителей мартингейла и подобных ему схем, игроки, использующие так называемые стратегии с позитивной прогрессией, повышают ставки после выигрыша и чаще всего понижают после проигрыша. Схемы с позитивной стратегией не дают быстро проиграться, но обогатиться с их помощью тоже не получится, потому что у казино всегда больше шансов, какие бы ставки ни делал игрок. Баланс при использовании таких стратегий выглядит примерно следующим образом:

Любимый номер НЕ РАБОТАЕТ

Игрок все время ставит на один и тот же номер, надеясь, что выигрыш в размере 35 к 1 покроет его расход. «Стратеги» не учитывают, что номера выпадают равномерно только при бесконечно большом количестве оборотов. А в реальной игре с высокой вероятностью за 36 спинов выбранный номер не сыграет ни разу — просто потому, что какой-нибудь другой номер выпадет дважды (кстати, именно на этом факте основана система Биарриц, тоже весьма популярная у посетителей казино). Если бы любители 36 раз подряд ставить на одно и то же число провели несложный расчет, они бы стали более прижимистыми.

Обозначим вероятность того, что за 36 спинов номера ни разу не совпадут, как

Выберем любой номер в качестве любимого и будем «сверять» его с выпадающими числами. Вероятность того, что любой следующий спин даст непарный номер, равна

(так как есть еще зеро, в знаменателе дроби будет не 36, а 37). Вероятность, что любой из последующих оборотов опять не даст пары, составляет

дальше

и так далее. Чтобы узнать, с какой вероятностью все номера за 36 спинов будут различными, нужно перемножить все эти вероятности. В общем виде формула выглядит так:

где ! — факториал (m! — это перемножение всех чисел от 1 до m ), n — число поворотов колеса.

Фото

Mira / Alamy via Legion Media

За счет огромного знаменателя получится настолько маленькое число, что на экране обычного калькулятора не хватит места, чтобы его показать. Например, для 36 спинов знаменатель дроби равен 285273917723723876056171083405292782327767461712708093041, а само значение составляет 0,000000000000000000000000000000000000000000000000000000003505. То есть шансов, что за 36 спинов номера ни разу не повторятся, практически нет.

Вероятность, что за любое выбранное количество оборотов мы получим хотя бы одну пару, равна

Если подсчитать этот параметр для конкретного количества спинов, то при четырех оборотах колеса шансы на минимум одну «двойню» составят 15%, при 7 оборотах — 45%, а при 18 — уже 99,3%!

Система Биарриц НЕ РАБОТАЕТ

Схема основана на том факте, что за 36 раундов игры в рулетку некоторые числа, скорее всего, выпадут два и более раз. В классическом варианте схемы игроки некоторое время наблюдают за колесом, не делая ставок. Обнаружив повторяющиеся номера, они начинают последовательно ставить именно на них или, наоборот, не ставят фишки на эти числа.

Математических оснований у системы Биарриц нет: вероятность, что шарик остановится на определенном номере, никак не зависит от того, попадал ли он на него на предыдущих спинах. Но интуитивно люди связывают будущие исходы с уже случившимися («в одно дерево молния дважды не попадает»), поэтому схема по-прежнему популярна.

Несовершенство колеса РАБОТАЕТ

Если рулеточное колесо работает идеально, шансы на выигрыш у казино всегда выше. Но в реальной жизни идеальное встречается редко, и в случае рулетки на этом можно заработать. Что и сделал в 1837 году английский инженер Джозеф Джаггер. Он наблюдал за колесами в Монте-Карло и обнаружил, что одно уравновешено неидеально. Девять чисел — 7, 8, 9, 17, 18, 19, 22, 28, 29 — выпадали чаще остальных.

Джаггер начал ставить на «залипающие» номера и за четыре дня выиграл 370 000 долларов. Владельцы сообразили, в чем дело, и поменяли колеса местами, но инженер раскусил подвох. Тогда хозяева стали по ночам переставлять ячейки, и выигрышными каждый день оказывались другие числа. Джаггер прервал карьеру игрока и уехал из Монте-Карло с 325 000 долларов — 5 млн долларов по нынешним деньгам.

Есть данные, что еще нескольким людям удалось найти несовершенные колеса при помощи статистического анализа. Сегодня выискивать недостатки колес в открытую невозможно — в казино не жалуют таких «исследователей».

Точный расчет РАБОТАЕТ

Этот метод предлагает угадывать, в какой ячейке окажется шарик, основываясь не на теории вероятностей, а на законах физики. При помощи нехитрого оборудования можно установить скорость шарика и скорость вращения колеса, непосредственно измерив их. Сопоставив эти значения, легко вычислить, когда и где остановится шарик. В 2004 году трое игроков, вооруженные лазерным сканером, компьютером и мобильными телефонами, выиграли в казино Ritz в Лондоне 1,3 млн фунтов. Игорный дом подал иск против счастливчиков, но суд решил, что ответчики не влияли на движение шарика и колеса, а значит, выигрыш законен.

Игровой автомат

Серия неудач НЕ РАБОТАЕТ

Идея похожа на идею стратегии Биарриц: шанс на выигрыш особенно высок после длинной серии неудач. Подсознательно человеку кажется, что нельзя все время проигрывать и после черной полосы он непременно сорвет банк. Создатели автоматов подстегивают эту надежду: «бандиты» запрограммированы с повышенной частотой выдавать выигрышные комбинации на уровень выше или ниже основной строки. Игрок видит, что барабан «чуть-чуть не докрутился», и снова и снова бросает жетоны в монетоприемник.

Фото

Eric Nathan / Alamy via Legion Media

Странности

Обидные совпадения

Любители лотерей тоже часто недооценивают мощь теории вероятностей. В сентябре 2009 года в розыгрыше национальной лотереи Болгарии выпали числа 4, 15, 23, 24, 35 и 42. Через четыре дня эти шесть чисел выпали вновь. Организаторов лотереи заподозрили в мошенничестве, было проведено расследование, установившее, что все честно. Подсчет показывает, что вероятность повторения шестерки чисел в Болгарской лотерее, которая проводится уже 52 года дважды в неделю, очень высока.
Результат каждого розыгрыша может совпасть с результатом любого из проводившихся ранее. Количество пар «шестерок», которые можно составить из всех розыгрышей, вычисляется по формуле:

где n — это число розыгрышей

Из двух розыгрышей можно составить только одну пару, из трех — 3, из четырех — 6, из пяти — 10, а из ста — уже 4950. При таком количестве сочетаний (возможных пар) вероятность, что какие-то из них окажутся одинаковыми, существенна. Чтобы она превысила 50%, достаточно провести 4404 розыгрыша — в случае Болгарской лотереи, на это потребуется меньше 43 лет.

Совпадение розыгрышей в лотереях не такая уж редкость. Например, в 2010-м в ходе двух тиражей национальной лотереи Израиля, 21 сентября и 16 октября, выигрышными были одни и те же числа.

_{Материал опубликован в журнале «Вокруг света» № 11, ноябрь 2014}

Ирина Якутенко

---

Теги

• наука
• Математика
• физика
• психология

Лучшие стратегии игры в кости с биткойнами

Любите свои игры в кости? Как зачинщик всей криптовалюты в пространстве онлайн-гемблинга, эта игра заслуживает всей любви и признания. Сегодня мы смотрим на лучшее Стратегии биткойн-дайс так что вы можете быть в выигрыше, когда грохочет и катится на BC Игра, На игра до н. э., игроки могут выбирать из классических игральных костей или хэш-дайсов. 

Что такое биткойн-дайс?

Биткойн кости, также называемая крипто-кубиками, представляет собой вероятностную игру, в которую играют с биткойнами или другими криптовалютами. Вы делаете ставку на следующее число, которое выпадет в игре, и насколько близко оно будет к предыдущему числу. Чем ближе число, тем выше шанс на победу.

Мы рассмотрим четыре лучшие стратегии игры в кости на Биткойн: Стратегия Мартингейла, Стратегия обратного Мартингейла, Стратегия Даламбера и Стратегия Пароли. Следуйте этим правилам, и вы быстро окажетесь на пути к победе. 

Мартингейл Стратегия

Стратегия Мартингейла, восходящая к 18 веку, покорила французов и распространилась со скоростью лесного пожара. Стратегия заключается в удвоении вашей ставки после каждого проигрыша, так что, когда вы действительно выиграете, ваши потери будут компенсированы, и вы, надеюсь, получите некоторую прибыль. Если вы выиграете; однако вы сохраняете ставку на прежнем уровне.

Чтобы объяснить это дальше:

Например:

Начиная с вашей начальной ставки в 0.01 BTC. Если вы выиграете, вы снова поставите 0.01 BTC. Однако, если вы проиграете, вы сделаете ставку в 2 раза больше своей первоначальной ставки, что приведет к ставке 0.02 BTC на следующий раунд.  Повторите.

Если это продолжится, это будет выглядеть так:

Ставка 0.01 BTC. 

Терять.

Ставка 0.02 BTC.

Терять.

Ставка 0.04 BTC.

Терять.

Ставка 0.08 BTC.

Win.

Ставка 0.08 BTC, или вы можете вернуться к первоначальной ставке, а затем еще немного. 

2. Обратная Мартингейл Стратегия

Как вы могли уже догадаться, стратегия обратного мартингейла является полной противоположностью предыдущей. Таким образом, в то время как первоначальная стратегия заключалась в удвоении вашей ставки в случае проигрыша, эта стратегия сосредоточена на уменьшении вдвое вашей ставки в случае выигрыша. Это позволяет игрокам сохранить половину своего выигрыша, пока они делают ставку на другую половину. 

Чтобы объяснить это дальше:

Например:

Начиная с вашей начальной ставки в 0.01 BTC. Если вы проигрываете, вы снова ставите 0.01 BTC. Однако, если вы выиграете, вы поставите половину своей первоначальной ставки, что приведет к ставке 0.005 BTC на следующий раунд. Повторите.

Если это продолжится, это будет выглядеть так:

Ставка 0.01 BTC. 

Терять.

Ставка 0.01 BTC.

Win.

Ставка 0.005 BTC.

Терять.

Ставка 0.005 BTC.

Win.

Ставка 0.0025 BTC.

3. Стратегия Даламбера

Лучшие стратегии игры в кости с биткойнами

Почти столь же популярная, как и ее аналог Мартингейл, стратегия Даламбера немного более рискованна. Это также легко реализовать. После того, как вы сделали ставку и проиграли, вы увеличиваете ставку на единицу, пока не выиграете. И когда вы выигрываете, вы уменьшаете ставку на единицу.  

Чтобы объяснить это дальше:

Например:

Начиная с вашей начальной ставки в 0.02 BTC. Если вы проигрываете, вы ставите 0.03 BTC. Однако, если вы выиграете, вы уменьшите свою ставку на 1, что приведет к ставке 0.02 BTC на следующий раунд. Повторите.

Если это продолжится, это будет выглядеть так:

Ставка 0.02 BTC. 

Терять.

Ставка 0.03 BTC.

Win.

Ставка 0.02 BTC.

Терять.

Ставка 0.03 BTC.

Терять.

Ставка 0.04 BTC.

4. Стратегия Пароли

Стратегия Пароли использует выигрышные серии. Таким образом, каждый раз, когда вы выигрываете, вы удваиваете свою ставку в следующем раунде. И в случае проигрыша вы сбрасываете сумму ставки, ИЛИ если вы выиграете серию из 3 побед. Эта стратегия направлена ​​на низкий риск и максимальное использование ваших выигрышей.

Чтобы объяснить это дальше:

Например:

Начиная с вашей начальной ставки в 0.01 BTC. Если вы проиграли или выиграли 3 раза подряд, вы ставите 0. 01 BTC. Однако, если вы выиграете, вы удвоите свою ставку, что приведет к ставке 0.02 BTC на следующий раунд. Повторите.

Если это продолжится, это будет выглядеть так:

Ставка 0.01 BTC. 

Терять.

Ставка 0.01 BTC.

Win.

Ставка 0.02 BTC.

Win.

Ставка 0.03 BTC.

Терять.

Ставка 0.01 BTC.

Будьте готовы к рок-н-роллу

Теперь, когда вы заряжены этими лучшие стратегии игры в кости на биткойн попробуй их в одной из замечательных игр в кости игра до н.э. может предложить. Будьте уверены, что все их игры доказуемо справедливый и на основе некоторых серьезных алгоритмов. Пришло время побеждать!

Алгоритм быстро имитирует бросок загруженных игральных костей | MIT News

Быстрая и эффективная генерация случайных чисел уже давно является важной задачей. На протяжении веков азартные игры полагались на бросок кости, подбрасывание монеты или перетасовку карт, чтобы внести некоторую случайность в процесс. Во второй половине ХХ века эту роль стали брать на себя компьютеры для приложений в криптографии, статистике и искусственном интеллекте, а также для различных симуляций — климатических, эпидемиологических, финансовых и т. д.

Исследователи Массачусетского технологического института разработали компьютерный алгоритм, который может, по крайней мере, для некоторых задач, производить случайные числа с лучшим сочетанием скорости, точности и низких требований к памяти, доступных на сегодняшний день. Алгоритм, названный Fast Loaded Dice Roller (FLDR), был создан аспирантом Массачусетского технологического института Ферасом Саадом, научным сотрудником Кэмероном Фриром, профессором Мартином Ринардом и главным научным сотрудником Викашем Мансингка, и он будет представлен на следующей неделе на 23-й Международной конференции. по искусственному интеллекту и статистике.

Проще говоря, FLDR — это компьютерная программа, которая имитирует бросок игральной кости для получения случайных целых чисел. У игральных костей может быть любое количество граней, и они «нагружены» или взвешены, чтобы некоторые стороны выпадали с большей вероятностью, чем другие. Заряженный кубик по-прежнему может давать случайные числа — поскольку нельзя заранее предсказать, какая сторона выпадет, — но случайность ограничивается заданным распределением вероятностей. Можно, например, использовать загруженные игральные кости, чтобы смоделировать исход игры в бейсбол; в то время как у более сильной команды больше шансов на победу, в определенный день любая команда может оказаться на вершине.

С FLDR кости «идеально» загружены, что означает, что они точно достигают заданных вероятностей. Например, с четырехгранным кубиком можно расположить числа так, чтобы числа 1, 2, 3 и 4 выпадали ровно в 23%, 34%, 17% и 26% случаев соответственно.

Чтобы смоделировать бросок загруженных игральных костей с большим количеством граней, команде Массачусетского технологического института сначала пришлось использовать более простой источник случайности — компьютеризированную (двоичную) версию подбрасывания монеты, дающую либо 0, либо 1, каждый с 50-процентной вероятностью. Эффективность их метода, ключевой критерий разработки, зависит от того, сколько раз им приходится подключаться к этому случайному источнику — другими словами, от количества «бросков монеты» — для имитации каждого броска костей.

В знаменательной статье 1976 года ученые-компьютерщики Дональд Кнут и Эндрю Яо разработали алгоритм, который мог имитировать бросок загруженных игральных костей с максимальной теоретически достижимой эффективностью. «Хотя их алгоритм был оптимально эффективен с точки зрения времени, — объясняет Саад, имея в виду, что буквально ничто не может быть быстрее, — он неэффективен с точки зрения пространства или компьютерной памяти, необходимой для хранения этой информации». На самом деле объем требуемой памяти растет экспоненциально, в зависимости от количества сторон игральной кости и других факторов. Это делает метод Кнута-Яо непрактичным, говорит он, за исключением особых случаев, несмотря на его теоретическую важность.

FLDR был разработан для большего удобства. «Мы почти так же эффективны по времени, — говорит Саад, — но на порядки лучше с точки зрения эффективности использования памяти». FLDR может использовать до 10 000 раз меньше места для хранения данных, чем подход Кнута-Яо, при этом занимая не более чем в 1,5 раза больше времени на одну операцию.

На данный момент основным конкурентом FLDR является метод Alias, который десятилетиями был доминирующей технологией в этой области. При теоретическом анализе, согласно Фриру, FLDR имеет одно явное преимущество перед Alias: он более эффективно использует случайный источник — «подбрасывание монеты», если продолжить эту метафору, — чем Alias. Кроме того, в некоторых случаях FLDR быстрее, чем Alias, генерирует броски загруженных игральных костей.

FLDR, конечно, все еще совершенно новый и еще не нашел широкого применения. Но его разработчики уже думают о способах повышения его эффективности за счет разработки как программного, так и аппаратного обеспечения. У них также есть конкретные приложения, помимо общей, постоянной потребности в случайных числах. В чем FLDR может помочь больше всего, предполагает Мансингка, так это в повышении эффективности так называемого моделирования Монте-Карло и методов вывода Монте-Карло. Точно так же, как FLDR использует подбрасывание монеты для имитации более сложного броска взвешенных многогранных игральных костей, моделирование методом Монте-Карло использует бросок игральной кости для создания более сложных моделей случайных чисел.

Организация Объединенных Наций, например, проводит симуляции сейсмической активности, которые показывают, когда и где на земном шаре происходят землетрясения, толчки или ядерные испытания. Организация Объединенных Наций также осуществляет вывод по методу Монте-Карло: запуск случайных симуляций, которые генерируют возможные объяснения фактических сейсмических данных. Это работает путем проведения второй серии моделирования методом Монте-Карло, в котором случайным образом проверяются альтернативные параметры для лежащего в основе сейсмического моделирования, чтобы найти значения параметров, которые с наибольшей вероятностью воспроизводят наблюдаемые данные.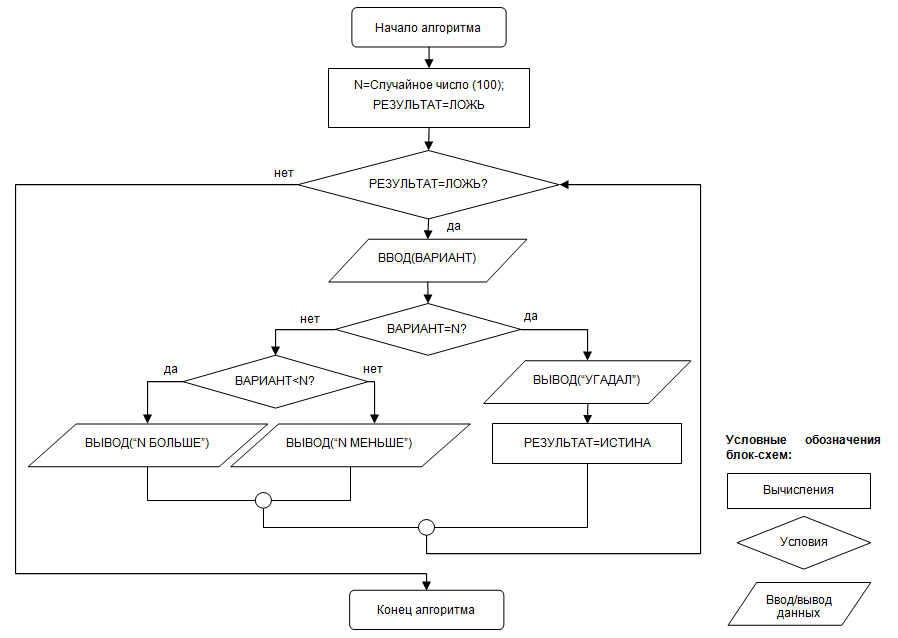 Эти параметры содержат информацию о том, когда и где на самом деле могли произойти землетрясения и ядерные испытания.

«Вывод методом Монте-Карло может потребовать в сотни тысяч раз больше случайных чисел, чем моделирование методом Монте-Карло», — говорит Мансингка. «Это одно большое узкое место, где FLDR действительно может помочь. Алгоритмы моделирования и логического вывода Монте-Карло также занимают центральное место в вероятностном программировании — новой области ИИ с широкими приложениями».

Райан Рифкин, директор по исследованиям Google, видит большой потенциал FLDR в этом отношении. «Алгоритмы вывода Монте-Карло занимают центральное место в современной разработке ИИ… и в крупномасштабном статистическом моделировании», — говорит Рифкин, не участвовавший в исследовании. «FLDR — это чрезвычайно многообещающая разработка, которая может привести к ускорению основных строительных блоков генерации случайных чисел и может помочь Google сделать вывод Монте-Карло значительно быстрее и более энергоэффективным».

Несмотря на кажущееся светлое будущее, FLDR так и не появился на свет. Намеки на это впервые появились в предыдущей статье тех же четырех исследователей Массачусетского технологического института, опубликованной на симпозиуме в январе, в которой был представлен отдельный алгоритм. В этой работе авторы показали, что если для компьютерной программы, моделирующей бросок загруженных игральных костей, выделить заранее определенный объем памяти, их алгоритм может определить минимально возможную «ошибку», то есть насколько близко человек подходит к совпадению. назначенные вероятности для каждой стороны кости.

Если не ограничивать память заранее, ошибку можно свести к нулю, но Саад заметил вариант с нулевой ошибкой, который использовал значительно меньше памяти и был почти таким же быстрым. Сначала он подумал, что результат может оказаться слишком тривиальным, чтобы о нем беспокоиться. Но он упомянул об этом Фриру, который заверил Саада, что по этому пути стоит идти. FLDR, который в этом же отношении безошибочен, возник из этих скромных истоков и теперь имеет шанс стать ведущей технологией в области генерации случайных чисел. Это не так уж и просто, учитывая, что мы живем в мире, в значительной степени управляемом случайными процессами — принцип, применимый как к распределению галактик во Вселенной, так и к результатам энергичной игры в кости.

вероятность — самый быстрый способ генерировать случайное целое число из правильных бросков костей

Задавать вопрос

спросил 1 год, 6 месяцев назад

Изменено 1 год, 6 месяцев назад

Просмотрено 183 раза

$\begingroup$

Учитывая, что у меня есть игральные кости с равными $n \in \mathbb{N}$ гранями, и я хочу сгенерировать целое число в диапазоне $[0, r), r \in \mathbb{N}$ с такая же вероятность. Я могу бросить кости любое количество раз и остановиться в любой момент после просмотра результатов. Как лучше всего сделать это, чтобы я сделал наименьшее количество ожидаемых бросков костей?

Интуитивно, мы можем сделать это с жадностью, чтобы каждый раз, когда число возможных исходов превышает $r$, мы выбрасывали эти исходы и перебрасывали их, когда происходит отклонение. В коде это будет что-то вроде (в коде числа на кубиках имеют нулевой индекс):

 определение dice_rand(r, n):
   cur_val = 0
   максимальное_значение = 1
   пока верно:
      cur_val = n * cur_val + roll_dice(n)
      максимальное_значение = n * максимальное_значение
      d = пол (max_val / r)
      если cur_val < d * r:
         этаж возврата (cur_val / d)
      cur_val = cur_val - d * r
      max_val = max_val - d * r
 

Теперь у меня возникла проблема с вычислением ожидаемого числа бросков костей для описанного выше алгоритма. Кроме того, как мне доказать, что приведенный выше алгоритм является наиболее эффективным?

• вероятность
• алгоритмы
• ожидаемое значение

$\endgroup$

14

$\begingroup$

Любой алгоритм, бросающий $r$-гранный кубик вместе с $n$-гранным кубиком, неизбежно «потратит» случайность (и в худшем случае будет работать вечно), если только «каждое простое число, делящее [$r$], также не делит [ $n$]", согласно лемме 3 в "Моделирование игры в кости с помощью кости" Б.