Math.ru
Григорий Александрович Гальперин, Александр Николаевич ЗемляковМ.: Наука, 1990. 288 с.
ISBN 5-02-014080-5; Тираж 130000 экз.
Серия Библиотечка «Квант», выпуск 77
| |||||||||||
Рассказывается о поведении бильярдного шара на столе произвольной формы без луз. Описание этого поведения приводит к решению разнообразных вопросов математики и механики: задач о переливании жидкости, об освещении зеркальных комнат, об осциллографе и фигурах Лиссажу и др.
На доступном школьникам языке вводятся понятия конфигурационного
и фазового пространства, понятия геодезических на простейших двумерных поверхностях, предлагаются (с решениями) многочисленные интересные задачи.
Содержание
Предисловие.
Введение.
Часть I. БИЛЬЯРДЫ В ВЫПУКЛЫХ ОБЛАСТЯХ С КРИВОЛИНЕЙНОЙ ГРАНИЦЕЙ.
Глава 1. Бильярд в круге.
§ 1. Шар в круглом бильярде без луз.
§ 2. Теорема Якоби. Применение к теории чисел.
§ 3. Теорема Пуанкаре о возвращении. Конфигурационное и фазовое пространства. Парадокс Цермело и модель Эренфестов.
Глава 2. Бильярд в эллипсе.
§ 4. Эллипс и его бильярдные свойства. Каустики.
§ 5*. Задача об освещении невыпуклой области.
§ 6. Экстремальные свойства бильярдных траекторий. Принцип Ферма и теорема Биркгофа.
Часть II. ГЕОМЕТРИЯ И ФИЗИКА ПРЯМОУГОЛЬНОГО БИЛЬЯРДА.
Глава 3. Геометрия прямоугольного бильярда.

§ 8. Top и его обмотки.
§ 9. Бильярд в прямоугольнике и тор.
Глава 4. Физика прямоугольного бильярда.
§ 10. Фигуры Лиссажу.
§ 11. Бильярд в прямоугольнике и осциллограф.
§ 12. Задача о пеленге.
Часть III. ГЕОМЕТРИЯ И АРИФМЕТИКА СТОЛКНОВЕНИЙ.
Глава 5. Одномерный «газ» из двух молекул.
§ 13. Два упруго сталкивающихся шара на отрезке.
§ 14. Два шара на отрезке: сведение к бильярду в треугольнике.
§ 15. Два шара на полупрямой: сведение к бильярду в угле.
Глава 6. Одномерный «газ» из большого числа молекул.
§ 16. Три упругих шара на прямой.
§ 17. n упругих шаров на прямой.
§ 18*. Число столкновений между молекулами одномерного «газа».
Глава 7**. Многомерный «газ».
§ 19. Конфигурационное пространство «газа» из n молекул в пространстве и сосуде.
§ 20. Сведение «газа» в пространстве и сосуде к бильярду.
§ 21. Рост числа столкновений между молекулами «газа».
Часть IV. БИЛЬЯРДЫ В МНОГОУГОЛЬНИКАХ И МНОГОГРАННИКАХ.
Глава 8. Геометрия многоугольного бильярда.
§ 22. Бильярды в «торических» многоугольниках.
§ 23. Склейка поверхностей из многоугольников.
§ 24. Бильярды в рациональных многоугольниках и поверхности.
Глава 9. Поведение бильярдных траекторий в многоугольниках.
§ 25. Траектории в рациональных многоугольниках и обмотки кренделей.
§ 26. Может ли непериодическая траектория в выпуклом многоугольнике не быть всюду плотной в нем?
Заключение.
Список литературы.
| |||||||||||
Постоянный адрес этой страницы: http://math.ru/lib/bmkvant/77
Бильярд. Практическое пособие для правильного изучения теории и техники бильярдной игры
Новое поступление
Продано
Год издания:
1890
Книги нет в наличии
Бесплатно доставим
в любую точку России
Характеристики
Описание
Варианты оплаты
Варианты доставки
Характеристики
Год издания:
1890
Размер:
19,8х14,3 см
Состояние:
отличное
Переплёт:
В индивидуальном подарочном переплёте. Полностью выполнен из кожи, декорирован золотым тиснением по передней крышке и корешку. «Мраморные» форзацы. Тройной крапчатый обрез. Имеется зелёная закладка-ляссе в тон переплёту.
Издательство:
СПб.: типография и хромолитография А. Траншель, 1890. — [2], IV, 122 с.: ил.
Описание
Редкое русское издание по бильярдному спорту.
Книга адресована любителям бильярда, «ищущим в игре не азарта и спекуляции, а развлечения и моциона, то есть спорта, а не промысла». В настоящее время содержание книги в равной степени будет полезно как любителю, так и настоящему «гурману», интересующемуся историей бильярда. Книга предназначена для усовершенствования техники, представляет собой сборник полезных рекомендаций и наставлений. На момент выпуска книги в России, несмотря на значительное число поклонников бильярда в нашей стране, практически не существовало крупных сочинений, популяризирующих бильярдный спорт.
Теория игры, физико-математические законы бильярда преподнесены в популярной форме; объяснена терминология. Издание иллюстрировано. Рисунки поясняют, какие бывают типы бильярда, как правильно держать кий и т.д. Даны графические задачи.
Особое внимание автор уделил описанию средств по противоборству шулерам и трюкачам.
Книга состоит из нескольких разделов. В начале книги приводится исторический обзор, в котором рассматривается происхождение терминологии и актуальная для того времени литература бильярдной игры.
Во втором разделе рассматривается оборудование бильярда: борта, лузы, доска, шары, кегли, кий, машинка, мазик, барак, орехи, счеты, рулетка, лилипут, бикс. Автор указывает также цены на все эти принадлежности.
В разделах по теории и технике бильярдной игры собраны основополагающие сведения о движении шара, направлении и действии удара и применение теории на практике. Проанализированы удары, описаны меры предупреждения шулерства, тактические советы, уделено внимание физиологии игрока.
Значительное место в книге отведено описанию правил игры и многообразию бильярдных партий, в том числе исторических, давно вышедших из моды. В книге можно познакомиться с систематикой партий и узнать, как играется московская партия, карамболь, подчерпнуть базовые представления о таких партиях, как волчья, вист-пирамида, швейцарская пулька, колокольня, чухонская, тамбовская, гусарская, коммерческая и партия à la russe.
В книге имеется словарь терминов на русском, немецком и французском языках.
Редкое русское издание по игре в бильярд. Представляет коллекционный и исторический интерес. Подарочно оформленное издание.
Варианты оплаты
Букинистический интернет-магазин «KnigAnt» предлагает купить книгу «Бильярд. Практическое пособие для правильного изучения теории и техники бильярдной игры» с оплатой следующими способами.
- Наличными при получении. Финансовые документы (кассовый и товарный чек с печатью продавца) отправляются с антикварным изданием, либо вручаются по желанию Вашему представителю.
- Оплата по счету – на расчетный счет магазина с оформлением соответствующих бухгалтерских документов. При желании заключается договор. Отправляются с книгой.
- Платежной системой – удобной для Вас, по указанным реквизитам магазина, только полная предоплата, финансовые документы (кассовый и товарный чек с печатью продавца) отправляются с книгой.
- Оплата картой – мы принимаем к оплате:
По Москве
Антикварное издание 1898 года печати, курьер бесплатно привезет по указанному адресу в удобное для Вас время. Доставка возможна даже в день принятия заказа. Жители Москвы могут выбрать несколько изданий, для просмотра и подбора наиболее подходящего варианта. Оплата принимается только в рублях!
Доставка возможна даже в день принятия заказа. Жители Москвы могут выбрать несколько изданий, для просмотра и подбора наиболее подходящего варианта. Оплата принимается только в рублях!
В Санкт-Петербург
Выбранное антикварное издание будет доставлено нашему представителю в Санкт-Петербург, у которого Вы сможете оформить покупку. Или оформить доставку после полной оплаты заказа одним из способов указанных в пункте «доставки в города России».
В города России
Только после полной предоплаты и получения денежных средств магазином.
- СДЭК, Почта России, ЕMS – Почта России.
- Любой другой транспортной компанией, по согласованию сторон.
Доставка по России осуществляется
за наш счет!
При удаленной покупке, мы можем осуществить показ издания по
видеосвязи, чтобы оценить его отличное состояние!
Задача о бильярдном столе – Mathigon
Обзор и цель На этом уроке учащиеся изучат знаменитые задачи о бильярдном столе, анализируя закономерности и создавая визуальные представления. Они будут исследовать взаимосвязь между траекторией бильярдного шара на идеализированном (без трения) бильярдном столе и размерами стола.
Они будут исследовать взаимосвязь между траекторией бильярдного шара на идеализированном (без трения) бильярдном столе и размерами стола.
Кроме того, учащиеся изучат количество клеток, которые пересекает мяч, и количество сделанных им подборов по отношению к наименьшему общему кратному и наибольшему общему множителю размеров стола.
Desmos Classroom Link
Задача с бильярдным столом • Конструктор занятий от DesmosTeacher.desmos.com/activitybuilder/custom/636c07fdf3cdb514dcce32d9
Разминка 9 0006 Используйте этот холст, чтобы показать учащимся диаграммы и объяснить проблему.Представьте себе бильярдный стол с четырьмя лузами в каждом углу (A, B, C, D).
Вы устанавливаете биток из вершины А и бросаете его под углом 45 градусов поперек стола, по закону отражения он отскакивает под тем же углом.
Предположим, что трения нет и мяч никогда не останавливается, пока не упадет в одну из угловых луз.
На заднем плане показана квадратная сетка, позволяющая учащимся рисовать повороты на 90 градусов при каждом ударе. Предложите им нарисовать путь, чтобы выяснить, в каком углу (лузе) окажется мяч в каждом случае?
Предложите им нарисовать путь, чтобы выяснить, в каком углу (лузе) окажется мяч в каждом случае?
Вот рисунки:
Обсудите с учащимися, что влияет на положение лузы, в которую попадает шар. Они, вероятно, видят, что это напрямую связано с размерами бильярдного стола. Спросите студентов, что их интересует сейчас. Пусть поделятся своими наблюдениями о сложности разных маршрутов.
Пусть придумают задачу: «Как узнать, в каких лузах окажется бильярдный шар для стола n x m?» Они также могут задать такие вопросы, как количество попаданий (отскоков) или количество клеток на пути (длина пути).
Основная деятельностьЗная размеры стола, можете ли вы предсказать конечный пункт назначения мяча?
Вы можете сгруппировать учащихся и напомнить им попробовать решить эту задачу со столами разного размера. Системный подход, как всегда, может помочь. Дайте им время поработать над проблемой.
Поделитесь с классом некоторыми работами учеников. Предложите учащимся рассказать о своих наблюдениях.
Предложите учащимся рассказать о своих наблюдениях.
Учащиеся могут начать понимать, что для таблицы n x m
- если и n, и m нечетные числа, бильярдный шар попадает в лузу C.
- , если n нечетно, а m равно четный, шар попадает в лузу B.
- Если n четно, а m нечетно, шар попадает в лузу D.
Спросите их о случае, когда и n, и m четны? Этот случай кажется более сложным, так как ответ все время меняется. Если они еще этого не сделали, вы можете попросить их понаблюдать за такими случаями, как «2 x 3, 4 x 6 и 8 x 12» или «6 x 10 и 10 x 14».
В этом примере карман назначения тот же. Пусть они представят эти размеры в виде дробей:
46=812=23{4 \более 6} = {8 \более 12} = {2 \более 3}64=128=32
610=??and1014 =??{6 \более 10 }={? \over ?} и {10 \over 14}={? \over ?}106=??and1410=??
Мяч движется по той же траектории, что и в простейшей форме измерений.
В первом наборе шарик попадает в D. Так как простейшая форма 2 на 3, задача переходит к четному на нечетный случай.
Так как простейшая форма 2 на 3, задача переходит к четному на нечетный случай.
Во втором наборе шарик попадает в C, так как простейшие формы стали нечетными по нечетным случаям.
Это как играть в ту же игру на уменьшенной модели того же стола.
Выполнение этих наблюдений может занять время и более длительные обсуждения в классе. Чтобы уточнить их наблюдения и обобщения, попросите их предсказать, что происходит в таблице
- 25 х 30
- 42 х 50
- 17 х 19
- 100 х 300
Теперь , вы можете спросить, почему паритет определить конечную лузу бильярдных шаров?
Первый подход
Вы можете предложить раскрасить точки сетки поочередно в сетках разных размеров. Вот пример:
Спросите учащихся, меняется ли путь бильярдного шара с фиолетовых точек на зеленые точки.
Поскольку это не так, нам нужно только выяснить, какой из четырех углов будет того же цвета, что и нижний левый угол. И это зависит только от соотношения размеров стола!
Второй подход
Что произойдет, если мы увеличим размер таблицы вместо уменьшения в предыдущем подходе? Попросите учащихся добавить столько столов одинакового размера, сколько необходимо, чтобы создать прямой путь для мяча в одну из крайних луз. Здесь важным моментом является то, что каждая добавленная таблица является зеркальным отражением предыдущей таблицы.
Здесь важным моментом является то, что каждая добавленная таблица является зеркальным отражением предыдущей таблицы.
Итак, когда биток приближается к краю стола, он проходит сквозь зеркало, а не отскакивает от него. Давайте посмотрим на пример 2 на 3, чтобы лучше понять идею.
Спросите учащихся, почему этот подход работает.
Поиск эффективных стратегий, например, упрощение дробей помогло нам решить любопытный случай с четными x четными таблицами, а теперь увеличение дробей помогает нам понять, почему.
Учащиеся могут начать использовать концепцию наименьшего общего кратного, чтобы определить, сколько столов вам нужно было сложить справа и сколько вы должны были сложить.
ЗакрытиеВ завершение урока обсудите это
- Может ли мяч упасть обратно в стартовую лузу?
- Если одно из двух заданных чисел кратно другому, какова форма арифметического бильярдного пути?
- Для каких чисел арифметическая бильярдная дорожка заканчивается в углу, противоположном начальной точке?
Как билет на выход, вы можете поделиться этим холстом, чтобы спросить, всегда ли бильярдный шар падает в лузу.
Эти петли могут удивить учеников. Пусть они подумают о других примерах, когда шар начинается в любой точке сетки бильярдного стола m x n.
Узнать большеВ начале этого исследования студентов попросили придумать свои собственные вопросы о бильярдном столе. Если эти вопросы еще не возникли сами собой, задайте их
- Определите формулу для количества клеток, пройденных шариком, в таблице n x m.
Количество клеток, которое проходит шарик, пока не окажется в лузе, равно наименьшему общему кратному m и n (НОК (n,m)). Когда m и n взаимно просты (НОК (n,m) = 1), то количество квадратов, которые пересекает мяч, равно m x n.
- Определите фактическую длину пути.
Используя теорему Пифагора, поскольку каждая единичная диагональ квадрата составляет √2 единицы длины, можно умножить LCM на √2, чтобы получить фактическую длину пути.
- Определите количество попаданий мяча до того, как он окажется в лузе.

Формула для общего числа совпадений в таблице m x n с GCF(m,n) = 1: m+n−2m + n-2m+n−2.
Полипады для этого урокаЧтобы назначить их своим классам в Mathigon, сохраните копию в своей учетной записи Mathigon. Нажмите здесь, чтобы узнать, как поделиться Polypads со студентами и как просмотреть их работу.
Бильярдный стол Intro – Polypadpolypad.org/J5mfsONRP3ZmnQ
Разминка бильярдного стола — Polypadpolypad.org/emfS63bpQuR6RQ#
Бильярдный стол S_WU — Polypadpolypad.org/ewbepHCGu9OKWA#poly угольники
Футляр Even x Even – Polypadpolypad .org/u6rncmPQqe7gcA
Бильярдный стол, действие 2. Подход 1 – Polypadpolypad.org/nh2ecPaHCWlEw
Примеры бильярдных задач – Polypadpolypad.org/ZjTyXvEYk50asA 900 07 Бильярдный стол LCM – Polypad
polypad.org/eWPHNyvN3p4tlw
Закрытие бильярдного стола – Polypadpolypad.org/5fentuIPdZvkrA
Regis Petit – Physics of Billiards
Regis Petit – Physics of Billiards – Theory of the Game| Французский | Дом | Бильярд | Гидравлический домкрат | ХНС | Относительность | Ботаника | Музыка | Орнито | Метео | Ссылки/Контакты |
| Теория игры | Искусство | Библиография |
Содержание этой главы
(Начало/Следующий абзац)- Книга «Бильярд: теория игры»
- Второе издание книги
- Содержание
- Заказать книгу
1.
 Книга «Бильярд: теория игры» (предыдущий/следующий абзац)
Книга «Бильярд: теория игры» (предыдущий/следующий абзац) Помимо размышлений и анализа наших главных чемпионов, полезно вернуться к тому, что можно сравнить с трактатом о бильярде.
Книга «Бильярд — Теория игры» [на английском языке: «Бильярд: теория игры»], сертифицированная Федерацией французского бильярда, представляет собой современную версию науки о бильярде, в основном основанную на книге Кориолиса. Эта версия исправляет многие ошибки книги (см. CORIOLIS errata n2 в нашей библиографии), дополняет и обобщает уравнения в трехмерном векторном выражении, полезном для разработчиков программного обеспечения.
Первое издание 1996 г., первое издание в январе 1997 г. (128 страниц).
2. Второе издание книги
(предыдущий/следующий абзац) Помимо строгости и качества, эта основополагающая книга представляет собой полный и современный синтез теории бильярда, сертифицированный Федерацией французского бильярда.
Второе издание 2004 г. (исправленная и дополненная версия), первое издание в июне 2004 г. (192 страницы).
(исправленная и дополненная версия), первое издание в июне 2004 г. (192 страницы).
Второе издание 2004 г. (обновленная версия от июня 2006 г.), первое издание в июне 2006 г. (192 страницы).
Примечание. В обновленной версии от июня 2006 г. исправлено 32 страницы текста по сравнению с исправленной и расширенной версией от июня 2004 г. Эти исправления касаются незначительных моментов (ссылка на страницу, пунктуация, добавление примечаний и т. д.), а также грубой ошибки на страницах. 155 и 173 в следующей математической формуле:
Вместо : W = (1 — t / t arrêt_translation) Wc
Читать : W = ( 1 — (t — tc) / (t arrêt_translation — тк) ) Туалет
3. Содержание
(предыдущий/следующий абзац)- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- ГЛАВА 1 — ОБЩЕЕ ДВИЖЕНИЕ ШАРА НА ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
- Поступательная и вращательная скорости
- Качение без скольжения
- Траектория
- Экстремум траектории и чистое скользящее состояние
- Кривизна
- Путь скольжения, пройденный мячом
- Выстрел в прыжке
- ГЛАВА 2 — ГОРИЗОНТАЛЬНЫЙ УДАР
- Начальная скорость
- Траектория
- Начальная поступательная скорость
- Автоматическое разделение битков
- Влияние удара снизу/сверху по центру на движение мяча
- Расстояние скольжения
- Удельные поступательные скорости
- Z-компонента вектора спина
- ГЛАВА 3 — НАКЛОННЫЙ ХОД
- Начальная скорость
- Траектория
- Автоматическое разделение битков
- Влияние удара снизу/сверху по центру на движение мяча
- Мяч ударный
- Трение с полотном для мячей
- Расстояние скольжения для ничейного броска
- Начальное отклонение
- Окончательный прогиб
- Выстрел в прыжке
- ГЛАВА 4 — УДАР МЯЧА
- Начальная скорость
- Траектория
- Кривизна
- Расстояние скольжения перед качением без скольжения
- Начальное отклонение
- Окончательный прогиб
- Полнота попадания мяча и точки прицеливания
- Полнота удара по мячу и окончательное отклонение
- Соотношение вращения/скорости и окончательное отклонение
- Практическое упражнение
- Движение прицельного шара
- Полезность и бесполезность английского
- Бильярдная стратегия
- ГЛАВА 5 — ВТОРОЙ УДАР ШАРА
- Начальная скорость
- Окончательный прогиб
- ГЛАВА 6 — НЕРАВНЫЕ МАССЫ, НЕСОВЕРШЕННАЯ УПРУГОСТЬ И ТРЕНИЕ МЕЖДУ ШАРАМИ
- 6.
 1. Неравные массы
1. Неравные массы - 6.2. Несовершенная эластичность между шариками
- 6.3. Трение между шариками
- 6.
- ГЛАВА 7 — ПОДУШКА(И) ШАРОВ УДАР
- Начальная скорость
- Траектория
- Расстояние скольжения
- Точки прицеливания
- Начальное отклонение
- Окончательный прогиб
- Конечная поступательная скорость
- Z-компонента вектора спина
- Влияние высоты подушки
- Измерение параметров (N) и (fi)
- Шариковые подушки ударные
- Удар мячом о подушку после удара мячом о мяч
- ГЛАВА 8 — УДАР МЯЧОМ, ЗАСТРЕВШИМСЯ О ПОДУШКЕ
- Состояние ответного поцелуя
- Начальная скорость каждого шара
- Траектория каждого мяча
- Окончательное отклонение каждого шарика
- ГЛАВА 9 — КОНТАКТ БЕЗ СКОЛЬЖЕНИЯ
- 9.
 1. Наклонный ход кия
1. Наклонный ход кия - 9.2. Удар мячом
- 9.3. Удар мячом-подушкой
- 9.4. Удар мячом, застрявшим в подушке
- 9.5. Адгезия мяча и ткани
- 9.
- ГЛАВА 10 — КАТАНИЕ ШАРОВ
- Поступательная и вращательная скорости
- Траектория
- Измерение параметров (fc) и (fz)
- Расстояния, пройденные шарами до остановки
- ГЛАВА 11. МОДЕЛЬ ДЛЯ РАЗРАБОТЧИКОВ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- ЗАКЛЮЧЕНИЕ
- МАТЕМАТИЧЕСКОЕ ПРИЛОЖЕНИЕ
- ГЛОССАРИЙ И ОБОЗНАЧЕНИЯ
- СПИСОК РИСУНКОВ
- ССЫЛКИ
- ФРАНЦУЗСКО-АНГЛИЙСКИЙ ИНДЕКС
4. Для заказа книги
(Предыдущий/Начальный абзац) Название на французском языке: Billard — Theorie du jeu» [на английском языке: «Billiards — Theory of the Game»]
Второе издание
Сертифицировано Федерацией французского бильярда [Оглавление и предметный указатель переведены на английский язык]
Автор: Régis PETIT
Издатель: CHIRON, 2004.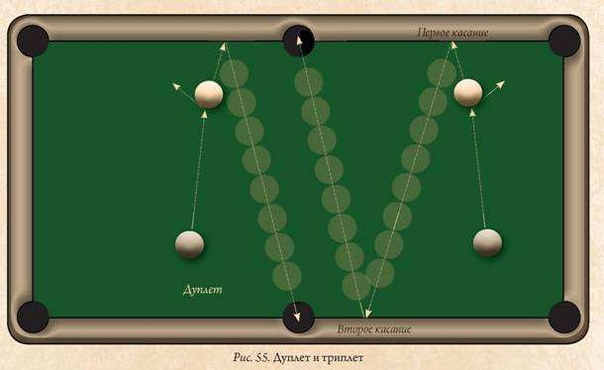

 49)
49)
 1. Неравные массы
1. Неравные массы 1. Наклонный ход кия
1. Наклонный ход кия