Сколько штук газоблока в кубе?
Всё на свете имеет свою меру. Дорога измеряется в километрах, вода и прочие напитки – в литрах, а такие стройматериалы как кирпич, шлакоблок, газобетон – в кубах.
В каталоге интернет магазина цена газоблока указывается за куб, а не поштучно. Однако многих интересует вопрос, сколько в 1 куб штук газоблока? Попробуем разобраться.
Что такое куб?
Прежде чем узнать, сколько газоблоков в кубе, давайте выясним, что же такое собственно – куб?.
Куб представляет собой условный объем материала, который получится, если сложить этот самый материал в квадратный ящик со сторонами равными 1 метру.
Если знания школьного курса геометрии еще свежи в вашей памяти, то вы вспомните, что формула куба равна произведению высоты на ее длину и ширину. Так как в классическом кубе все стороны равны 1, то и их произведение тоже будет равно единице. Таким образом, и получается 1 кубический метр стройматериалов.
Условным он является потому, что в действительности никто не строит ящиков с такими размерами.
Они существуют лишь в нашем воображении. Однако хоть и воображаемые, кубы являются незаменимым инструментом для того, чтобы рассчитать, сколько штук газоблоков в 1 куб метре.
Сколько газоблоков в 1 куб метре?
Один большой кубический метр, заполненный блоками, фактически представляет сумму объемов всех этих блоков или их произведение, ведь, например,
2+2+2+2+2+2+2+2+2+2+2 = 2×11
Чтобы узнать, сколько штук газоблока в 1 кубе, нужно выполнить всего 2 простых арифметических действия:
- Узнать сколько кубов в газоблоке отдельно взятом, то есть в 1 штуке. Для этого воспользуемся уже известной формулой: высота*ширина*длина. Число должно получиться дробное, ведь объем одного блока невелик.
- Разделить 1 на полученное в первом действии число, например,
- Число которое получится и будет ответом на вопрос сколько штук газоблока в 1 кубе.
Сколько газоблоков в кубе 200 300 600
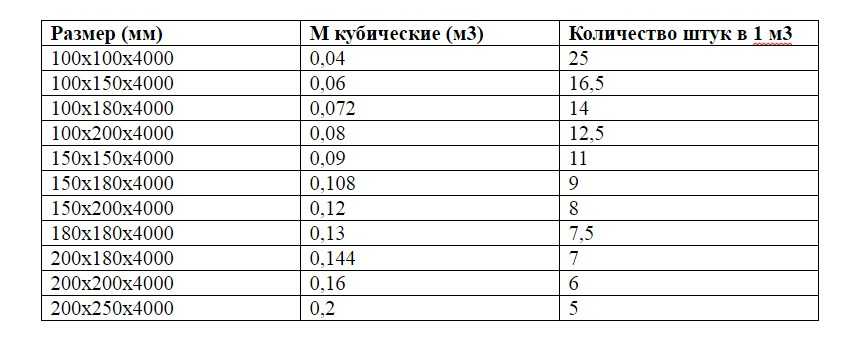
Узнать, сколько газоблоков в 1 кубе, невозможно, если вы не знаете, каковы размеры одной единицы.
А они, как известно, бывают разными. В каталоге интернет магазина Керамикфест указаны параметры каждого вида газобетонных блоков.
Давайте рассчитаем в качестве примера, сколько газоблоков в 1 кубе популярных марок газобетона
При проведении вычислений не забудьте миллиметры перевести в метры, для чего все числа нужно разделить на 1000.
0,2×0,2×0,6 = 0,024 – это объем одного блока Аерок Обухов Classic
1 ÷ 0,024 = 41,66 – столько штук в одном кубе
0.288×0.2×0.6 = 0,03456 – это объем одного блока Аэрок Обухов EcoTerm
1 ÷ 0,03456 = 28,93 – столько штук в одном кубе
Сколько кубов газоблока в поддоне?
Погрузка газобетонных блоков осуществляется поддоно-нормами. Никто не отгружает газоблоки поштучно.
Количество блоков на поддоне зависит от размеров одного блока и у разных производителей может варьироваться от 40 до 180. Поэтому эту информацию следует уточнять у менеджера при заказе.
Также тем, кто хочет купить газоблок, сколько штук в кубе, тоже может помочь посчитать консультант в магазине.
Читайте также: Какая должна быть стена из газобетона?
Редизайн «Два в Кубе»
Многие из вас знают, что я «наделал» достаточно дизайнов в сфере настолок. Meeple House, OMGames, Beaver Games, Board Game Family, Бабани Play, Table Top Time, Nastolio, YouLost, Клуб «Другое место» и тд. — все это большая семья настольщиков, которым я смог помочь и помогаю до сих пор 🙂 И я благодарен им за доверие и любовь к моим работам.Но была у меня мечта… сделать дизайн тому, кто многих из нас познакомил с миром настолок. И да, я говорю об Алексее Зуйкове и его видеоблоге «Два в Кубе».
Новая шапка для группы во ВконтактеНеожиданное «здравствуйте»
Благодаря моему другу и коллеге Илье Мурсееву, Лёша сам вышел на меня и попросил сделать ребрендинг его блога.
Все это должно быть приурочено к 9 годам его блога.
Я был безумно рад! Я давно грезил ребрендингом для «Два в Кубе» 🙂 НО! Передо мной встала серьезная задача. Ребрендинг — это всегда болезненно и страшно, как для самого блогера, так и для его аудитории.
Инстаграм, Сбербанк, Слэк, Вконтакте и многие другие тому доказательство. Тут чистая психология — сначала отрицание, а потом принятие. Нам сложно принять новое, но потом от этого нового невозможно отказаться. Я знал, что так будет и в этот раз, но все же сильно волновался 🙂
Снимаю шляпу перед мужеством и смелостью Лёши, который доверился мне в этом вопросе.
Алексей Зуйков. Игрокон 2019Ставим задачу
Оказалось, что до меня уже были попытки ребрендинга.
Но все они (по тем или иным причинам) не понравились Лёше. Тут-то я понял, что «клиент» капризный малый XD весьма строг и выборочен. И это очень хорошо! Нам дизайнерам нельзя давать расслабляться.
Обсудив детали, стало ясно — узнаваемость сохраняем; цветовую гамму наследуем. В остальном Лёша попросил максимального минимализма. Ну не прям максимального, но все же минимализма 🙂
Конкретно от меня требовалось:
- Ребрендинг лого
- Разработка шапок для ВК и Ютубчика
- И видео обложки (под разные форматы видосиков)
Задача ясна 🙂 Беремся за перо!
Начинаем работу
Как и при строительстве дома, мы начинаем с фундамента — логотипа 🙂
Блог «Два в Кубе» закристаллизовался в нашем сердце в виде двух кубиков, которые повернуты к нам гранями «2» и «3» соответственно.
В исходном варианте, кубики летят не очень красиво (с точки зрения композиции). Само их положение говорит больше про «разлетание» в разные стороны, нежели про объединение.
Они прижаты к черной рамке, при этом на удивление выглядят мелко. Магия дизайна 🙂 Не иначе.
Ну и самый главный момент — они растровые 🙂 Логотип никогда не переводился в вектор, что давало свои ограничения и сложности.
Приступаем к исправлению данных моментов.
Этапы созревания логотипа Покрутив кубы, я нашел хороший ракурс.
Они стали плотнее, цельнее и дружнее.
Да, многие из вас сделают справедливое замечание, что теперь логика — один кубик над другим пропала.
И тут я отвечу, что это было интересным решением, но больше портило внешнюю эстетику. Да простят меня поклонники и сам Лёша 🙂
Я сохранил цвета, но, по просьбе Лёши, добавил оранжевому больше желтого. Это дало яркости новому стилю.
Шапки для соц. сетей
Мое видение логотипа, попало в точку. Моя идея зашла почти с первых набросков и мы достаточно быстро нашли финальный стиль.
А вот с шапками все было чуть сложнее 🙂
Оригинальная шапка/заставка Оригинальная заставка любима всем.
Но давайте будет откровенны, она слишком устарела. Когда-нибудь она должна уйти на покой, как старый бабушкин ковер со стены 🙂
Я решил начать с сохранения стиля, но полным его обновлением.
1 вариантВышло вроде бы неплохо, но какое-то г..вно. Скучно, грустно и по-детски.
2 вариант Добавим немного солнца, подумал я. И полилась какая корейская версия «Два в Кубе».
Поискав положения и композицию, я пришел к китайско-японской версии шапки. В нем что-то было и Лёше этот вариант даже понравился, но и он и я посчитали его пустоватым.
Дальше были бесконечные поиски. Что-то не нравилось мне, что-то не нравилось Лёше. Я даже начал паниковать, что потерял хватку и сноровку. В таких случая очень помогает смена деятельности, что я и сделал — переключился на обложки для видео.
Но перед ними я все же сделал еще один выстрел в сердечко Алексея.
25 вариант Но вновь промахнулся.
Хотя идея мне самому (почему-то) очень нравилась.
Переключаемся на обложки для видео
Изучаем нынешние обложки видео на канале. Тут, к сожалению, тоже нужно многое поменять.
Одна из старых обложекГлавная проблема — это мелкий текст, огромный логотип, и не до конца раскрытая идея видосика. Мне всегда не понятно, что именно будут делать с игрой в данном видео? Обзор? Летсплей? Уничтожение?
Нужно это исправить. И тут дело не только в разработке дизайн-концепции обложки. От меня требовалось сделать шаблон, по которому Лёша мог бы создавать новые обложки.
1 вариант и финальный вариант Не поверите, но мой первый заход сразу попал в точку.
Алексею понравилась идея с размытием, понравились шрифты и концепция в целом. Мы лишь немного подвигали некоторые объекты и вот он — финальный вариант.
Вариант для обложки «Играем» был утвержден и я принялся за доработку автоматики шаблона.
Куча слоев и папокФотошоп это не только прога для удаления прыщей с носа, но и инструмент для серьезной автоматизации. Я создал специальный файл формата «PSDT», который и является шаблоном, Открывая его, создается новый файл со всеми стиля и слоями, но который не влияет на исходный шаблон. Поломать шаблон невозможно 🙂
Это очень удобно, если вы часто генерите контент в одном формате.
У меня так сделаны шаблоны для шапок всех соц. сетей, обложки для видосиков на Meeple House и многое другое.
Слои, которые трогать не нужно, я заблокировал. Красным пометил слои, с которыми можно и нужно взаимодействовать.
Фоновоя картинка была специальным смарт-объектом. Изменяя ее, автоматом менялся блюр на плашке.
Логотипы партнеровВ отдельную папку слоев я поместил смарт-картинку партнеров выпусков, менять которую Лёша может самостоятельно в пару кликов.
Иконка кол-ва игроков Так же я создал отдельную иконку для обозначения кол-ва участников (игроков) в выпуске.
Там тоже все легко меняется, не нарушая дизайн.
теперь беремся за обложку для «Обзоров». Концепцию сохраняем, но меняем логику и расположение элементов.
Обложка для видео «Обзоры»Шаблон работал как и предыдущий — содержал кучу слоев и папок.
Не волнуйтесь, я сделал видеоинструкции, где все пояснил на пальцах, что бы Лёша не запутался в этой фотошопной магии 🙂
Возвращаемся к шапкам
Мозг освежился 🙂 Открыв чистый хост, у меня сразу возникла классная идея.
1 вариант новой концепции Из логотипа вылетали катинки и компоненты настольных игр.
Лёша идею оценил, но попросил изменить часть картинок и сделать возможным их менять.
Спустя некоторое время мы нашли идеальный вариант и обложка для ВК была готова. Я снова сделал шаблон, что бы Лёша мог менять содержимое картинок.
Теперь приступаем к адаптации под Ютубчик. Там все было еще проще 🙂
Шапка для ЮтубчикаПара мелочей
Дополнительно я подготовил послойный логотип для видео-заставки и иконки кубов для подписчиков-спонсоров.
Да-да, видео заставку Лёша делает сам.
Я пока познаю азы этого дела. Но рано или поздно займусь и этим ремеслом 🙂
Работа была закончена. Я даже немного взгрустнул, так как процесс мне доставил море удовольствия и хотелось продолжения.
Я благодарен судьбе Илье Мурсееву, что он свел меня с таким прекрасным человеком. Уверен, это не последний проект с Лёшей 🙂 Мы что-нибудь интересненькое еще замутим.
Спасибо, что осилили этот пост. Буду рад вашему стрелочному лайку и комментарию. Другие работы можно посмотреть в моем инстике.
Мир, дружба, жвачка!
Расчет энергии между двумя кубами — блог Wolfram
В моем последнем сообщении в блоге мы обсуждали трехмерные конфигурации зарядов с острыми краями.
Читатель Rich Heart прокомментировал это и спросил, может ли Mathematica вычислить силу между двумя заряженными кубами, как это сделали Бенгт Форнберг и Ник Хейл и в приложении к главе книги Ллойда Н. Трефетена.
Ответ на вопрос из поста: Да, можем; То есть да, Mathematica может.
На самом деле довольно просто решить более общую задачу, чем два соприкасающихся куба одинакового размера:
- Мы можем иметь дело с двумя кубами с разной длиной ребер L 1 L 2
- Мы можем вычислить силу для любого разделения X , где X — расстояние между центрами двух кубов (включая случай проникающих кубов; представьте себе плазму)
- Мы будем использовать метод, который можно обобщить на многомерные кубы без необходимости делать больше вложенных интегралов
Вместо расчета силы между двумя кубами мы рассчитаем полную электростатическую энергию системы из двух кубов.
Тогда сила представляет собой просто отрицательный градиент полной энергии относительно X . Электростатическая энергия (в соответствующих единицах) определяется как:
(В следующих расчетах мы будем опускать постоянные [относительно X ] предфакторы Q 1 L 1 -3 Q 2 L 2 -3 или Q 1 Q 2 . через другую можно, но очень утомительная и трудоемкая операция. Вместо этого, чтобы не выполнять вложенный шестимерный интеграл, мы помним преобразование Лапласа 1 / √ с .
Это означает, что по модулю числового коэффициента функция, обратная квадратному корню, является самообратной по отношению к преобразованию Лапласа.
Использование этого интегрального преобразования для этого термина (( x 1 — ( x — x 2 )) 2 + ( Y 17)) 2 + ( Y 1 –.
2 ) 2 + ( z 1 – z 2 ) 2 ) ½ превращает интегралы в двумерные трехмерные вложенные множители. (Только один из двойных интегралов зависит от X ; это означает, что на данный момент обобщение на два четырехмерных куба является прямым.) Мы вычисляем функцию Vs, которую необходимо проинтегрировать за с , чтобы получить полную энергию взаимодействия. Все три двойных интеграла могут быть выполнены в закрытой форме, и остается выполнить только одномерный интеграл за с .
Теперь мы должны выполнить оставшийся интеграл по s . Формы последних выражений сначала предполагают замену переменной с → q = с ½ , чтобы получить более красивое подынтегральное выражение.
Множитель q -5 в последнем выражении предполагает, что мы выполняем частичное интегрирование, поэтому мы определяем правило для выполнения частичного интегрирования и применяем это правило рекурсивно для удаления всех высших отрицательных степеней д .
(Мы опускаем полностью интегрированные части частичного интегрирования, потому что все они исчезают.)
И мы определяем некоторые функции для применения этого правила к суммам и произведениям с числовыми коэффициентами.
Результирующее выражение теперь имеет больше терминов, но более простую структуру. Одно слагаемое в Vq после частичного интегрирования даст гораздо больше слагаемых. Этот процесс удаляет все термины, содержащие q -5 , q -4 , q -3 и q -2 , и сохраняет только 5 q 9015 -2 терминов, содержащих 5 q 1 -2 .0049 -1 . Вот пример частичного интегрирования одного слагаемого из 264 слагаемых.
Выполнение частичного интегрирования увеличивает размер наших q -интегрантов с 264 до 1196.
Вот три из них выбраны случайным образом.
Беглый осмотр терминов показывает, что существует только четыре различных типа по отношению к их q — зависимость, не более чем с коэффициентом q -1 .
Поскольку наша цель состоит в том, чтобы выполнить оставшийся интеграл по q , мы определяем функцию быстрого интегрирования с сопоставлением с образцом для четырех типов подынтегральных выражений, которые встречаются в Vq2List (это будет намного быстрее, чем использование Integrate). Один представляет собой просто интеграл Гаусса, а остальные три интеграла содержат функции ошибок, умноженные на гауссиан.
Теперь у нас есть закрытая форма для потенциала. Проведем быструю численную проверку интегрирования путем сравнения интегрирования с численно выполненным интегралом по q :
Теперь мы можем легко вычислить результирующую силу. Результат относительно большой. Проверка явной формы показывает термины, содержащие arcsinh, и термины, содержащие arctan. Мы упрощаем эти термины по отдельности:
Результирующее выражение стало меньше более чем в 10 раз.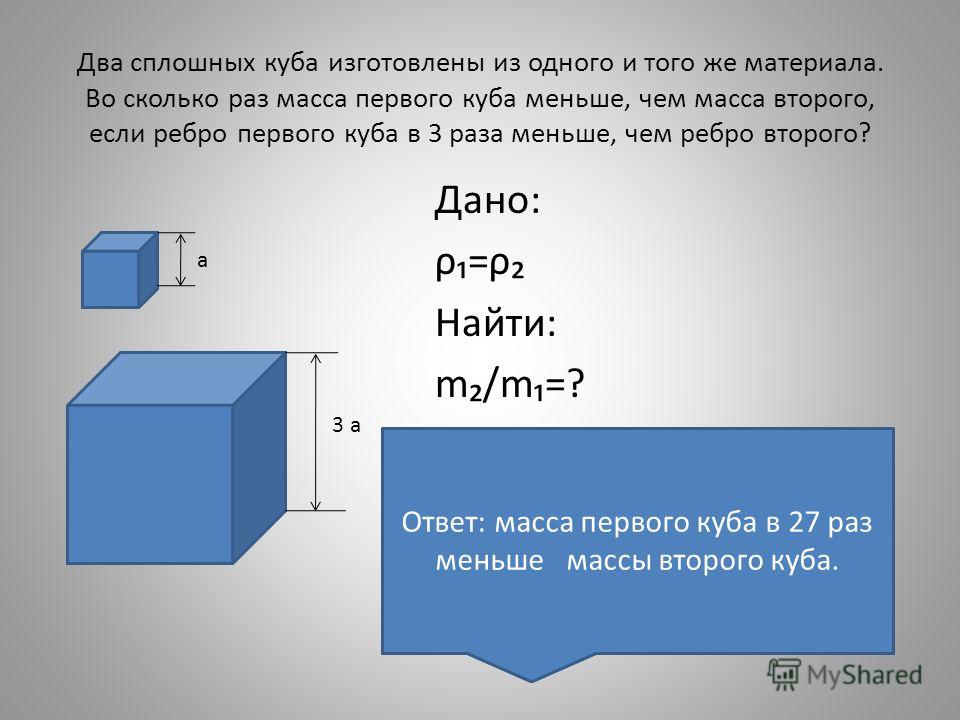
Вот некоторые из 68 показанных слагаемых V2.
Вот два графика полной энергии взаимодействия и силы между двумя кубами в зависимости от длины ребра L 2 второго куба и расстояния разделения Х . (Мы предполагаем, что длина ребра первого куба равна единице). для нулевого разделения (концентрические кубы) сила исчезает из-за симметрии. А острый пик на X = 1/2 для малых L2 — это максимум напряженности поля в центре грани единичного куба.
Давайте кратко рассмотрим поведение двух кубов, находящихся на большом расстоянии друг от друга. Срок пропорциональный X 5 дает первую поправку к закону Кулона.
Для быстрой проверки мы сравним эти старшие члены с интегрированием по ряду подынтегральной функции.
Теперь, в остальном, давайте выделим два куба с одинаковой длиной ребра. Из-за наличия устранимых сингулярностей мы не можем просто заменить L2 → L1 , а должны быть немного осторожнее.
Разлагая в ряд, оказывается, что все неопределенные члены обращаются в нуль в пределе L2 → L1 .
Это дает следующий окончательный результат для потенциала взаимодействия двух одинаковых кубов, разделенных расстоянием X . После еще нескольких упрощений мы получаем результат, умещающийся на одной странице. (Теперь мы включаем префакторы [ L -3 ] 2 .)
0049 -1 f ( x ) где безразмерное x определяется как x = X / L . Вот краткий обзор функции f ( x ) и ее первых двух производных. Вторая производная уже не является гладкой функцией при x = 1.
∞ .
В разложении ряда около x = 1 мы видим вершину второй производной, отраженную в различных значениях коэффициента ( x – 1) 3 0 .
Разница коэффициентов всего 2 π /3.
Мы получаем силу между двумя кубами, дифференцируя В С относительно Х . (По аналогии с хорошо известным ньютоновским законом силы между двумя однородными сферическими объектами, естественное название для этого зависящего от расстояния закона силы было бы законом силы Кубона.)
А вот точное выражение для силы между двумя кубами касаясь друг друга вдоль лица (что означает X = L ). Мы используем Ряды вместо подстановки в FC из-за неопределенных выражений, возникающих в процессе подстановки.
А вот искомое числовое значение из 100 цифр.
Существуют различные способы представления этого выражения; вот некоторые из них.
Вот еще несколько сокращенных версий, которые лучше показывают алгебраическую и трансцендентную часть результата.
Имея зависимость силы между двумя кубами от расстояния, возникает естественный вопрос: какова сила между двумя проницаемыми кубами и как она соотносится с силой между двумя кубами? сферы? Сила между двумя проницаемыми однородно заряженными сферами была рассчитана Кермодом, Мустафой и Роули.
(Мы снова игнорируем префакторы).
Мы будем использовать сферу того же объема, что и единичный куб.
Вот графики полной энергии взаимодействия и силы между двумя сферами. Синие кривые относятся к двум кубам, а красные — к двум сферам. (Две вертикальные линии обозначают радиус сферы и длины половин ребер.)
Мы видим, что максимальная сила между двумя кубами немного больше, чем максимальная сила между двумя сферами равного объема. Максимальная сила между двумя равными сферами возникает, когда центры двух сфер разнесены на расстояние, равное радиусу сферы.
Максимальная сила между двумя кубами возникает, когда центры двух кубов разнесены примерно на 68% длины ребра куба, и максимальная сила между двумя кубами в этом случае составляет около На 3,5% меньше, чем максимальная сила между двумя сферами одинакового объема.
Итак, теперь, когда у нас есть зависящая от расстояния кубонская сила между двумя кубами, что мы можем вычислить с ее помощью? Например, мы могли бы построить ньютоновскую колыбель с мягкой оболочкой, используя заряженные проницаемые кубы.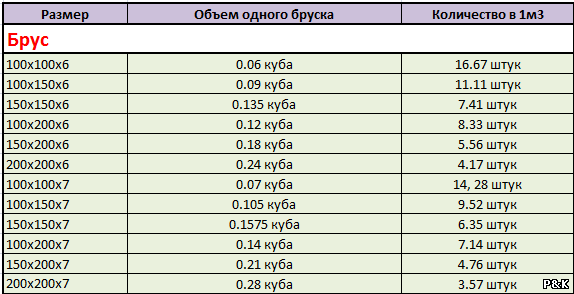
Мы предполагаем, что струны очень длинные, так что все кубы движутся в 1D, и моделируем гравитационную силу как линейную силу, возвращающую кубу положение покоя.
Предположим, что единичные кубы изначально расположены в позициях x n ] = n ∆ для некоторого заданного начального расстояния ∆.
Вот пример (скачайте CDF в конце поста, чтобы взаимодействовать с ним):
Поскольку кубы проницаемы, изначально вытянутый куб совершает около 50 колебаний через другие кубы, прежде чем соседние трубки начинают двигаться с большей амплитудой.
Загрузите этот пост в формате вычисляемого документа (CDF).
Сумма и разность кубов
Горячая математикаСумма или разность двух кубов может быть разложена на произведение биномиальный умножить на трехчлен.
Это,
Икс
3
+
у
3
знак равно
(
Икс
+
у
)
(
Икс
2
−
Икс
у
+
у
2
)
и
Икс
3
−
у
3
знак равно
(
Икс
−
у
)
(
Икс
2
+
Икс
у
+
у
2
)
.
Мнемоникой для знаков факторизации является слово «МЫЛО», буквы обозначают «Тот же знак», что и в середине исходного выражения, «Противоположный знак» и «Всегда положительный».
Это, Икс 3 ± у 3 знак равно ( Икс [ Тем же подписать ] у ) ( Икс 2 [ Противоположный подписать ] Икс у [ Всегда Положительный ] у 2 )
Пример 1:
Фактор
27
п
3
+
д
3
.
Попробуйте записать каждое из условий в виде куба выражения.
27 п 3 + д 3 знак равно ( 3 п ) 3 + ( д ) 3
Используйте факторизацию суммы кубов, чтобы переписать.
27 п 3 + д 3 знак равно ( 3 п ) 3 + ( д ) 3 знак равно ( 3 п + д ) ( ( 3 п ) 2 − 3 п д + д 2 ) знак равно ( 3 п + д ) ( 9п 2 − 3 п д + д 2 )
Пример 2:
Фактор
40
ты
3
−
625
в
3
.