Д 1 формула: Дискриминант. Формула дискриминанта.

Как решать квадратные уравнения? Формулы и Примеры

Поможем понять и полюбить математику

Начать учиться

647.3K

В 8 классе на алгебре начинается самое интересное — вот, например, квадратные уравнения. Так что приготовься запоминать алгоритм их решения!

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

• x² — 2x + 6 = 0
• x² — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x² ), а значит уравнение называется приведенным.

• 2x² − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Запоминаем!

У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.

Пример 1. Превратим неприведенное уравнение: 8x² + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x² + 2,5x — 1,125 = 0.

Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике

Добро пожаловать в школу магии.

О нет! Мальчик-молния случайно попал в школьные часы. Теперь они отстают.

Мы все можем задержаться в школе

Жми на стрелки сверху, чтобы путешествовать в истории→

‌

Одна ученица когда-то была в школьной кладовке и видела там схему часов

Но в кладовку просто так не попадёшь→

‌

Реши два примера от волшебной статуи на входе в кладовку

\frac{1}{7} + \frac{3}{7} =\frac{4}{7}\frac{5}{7}\frac{4}{14}\frac{2}{7}

\frac{4}{15} — \frac{1}{15} =\frac{1}{3}\frac{1}{5}\frac{3}{30}\frac{1}{10}

‌

Деталь можно сделать из проволоки и формы для заливки металла. Найди их на картинке

‌

Теперь осталось взять инструменты у садовника! Он обменяет их на волшебные бобы для его сада

‌

Для починки часов нужны: молоток, отвертка и плоскогубцы.

Ты можешь либо одолжить у садовника набор, либо отдельные инструменты, либо и то, и другое. Какое минимальное количество волшебных бобов ты можешь отдать садовнику?

Ответ:562 боба400 бобов553 боба

‌

Деталь имеет форму прямоугольника со сторонами 5 см и 12 см.

2

‌

Мальчик-молния выплавил деталь, часы должны работать! Но они почему-то не идут… Кажется, одной шестерёнки не хватает — она куда-то упала

‌

В коробке, шкатулке, ящике и банке находятся пыльца, волчий корень, золото и шестерёнка. Шестерёнка и пыльца не в коробке, ёмкость с волчьим корнем стоит между ящиком и ёмкостью с золотом, в банке не волчий корень и не шестерёнка. Шкатулка стоит около банки и ёмкостью с пыльцой. В какой ёмкости что находится?

Соедини ёмкости с содержимым на картинках ниже

ШестерёнкаЗолотоВолчий кореньПыльца

‌

Дальше узнаешь свои результаты →

‌

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax² + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax² + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:
Если b = 0, то квадратное уравнение принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0. Если c = 0, то квадратное уравнение выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2 + bx = 0. Если b = 0 и c = 0, то квадратное уравнение выглядит так ax2 = 0. Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax² + c = 0, при b = 0;
• ax² + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax

² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0

2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x² = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x² = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6x² = 0

   x² = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax

² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

• перенесем c в правую часть: ax² = — c,
• разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х2= -c/a, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8x² + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8x² = — 5

2. Разделим обе части на 8:

   x² = — 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x² + 5 = 0 не имеет корней.

Как решить уравнение ax

² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5x² + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = −0,125,
   х = −0,125/0,5

4. Разделить:

   х = −0,25

5. Значит корни исходного уравнения — 0 и −0,25.

Ответ: х = 0 и х = −0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b² − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

, .

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b²−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x² + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 28² — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x² = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6x² = 0 | *(-1)

   6x² — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6x² = 54

   х² = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x²— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x²— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x²— 10 = 39

   x²= 39 + 10

   x²= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x²— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)² — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b² — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax² + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)²— 4ac = 4n² — 4ac = 4(n²— ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n² -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n²— ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n²— ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Формула Виета

---

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x² + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

 

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x² + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x² − 6x + 8 = 0.

Как решаем:

1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

   Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

   Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

3. Значит числа 4 и 2 — корни уравнения x² − 6x + 8 = 0. p>

    

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x² — 4 x — 6 = 0, чем 1100x² — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x² — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x²— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x² — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов.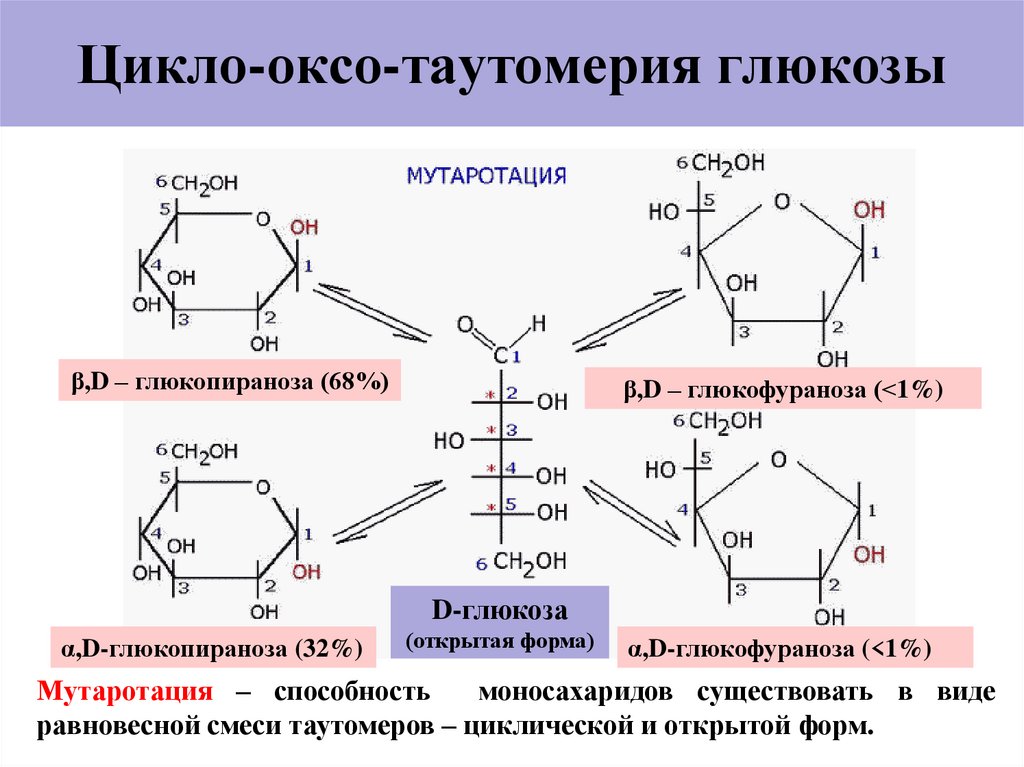 Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x² + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x²— 3x + 7 = 0 перейти к решению 2x² + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x²— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

249.6K

Основные геометрические фигуры

К следующей статье

527.5K

Как решать задачи с процентами

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k² − ac, а корни по формулам и .

Примеры

Решим квадратное уравнение x² + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.

Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.

n = 2k

Например, число 10 можно представить как 2 × 5.

10 = 2 × 5

В этом произведении k = 5.

---

Число 12 можно представить как 2 × 6.

12 = 2 × 6

В этом произведении k = 6.

---

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7.

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.

В уравнении x² + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = 3² − 1 × (−16) = 9 + 16 = 25

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x² + 6x − 16 = 0 являются числа 2 и −8.

В отличие от стандартной формулы для вычисления дискриминанта (D=b² − 4ac), в формуле D₁ = k² − ac не нужно выполнять умножение числа 4 на ac.

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

---

Пример 2. Решить квадратное уравнение 5x² − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−3)² − 5 × 1 = 9 − 5 = 4

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

---

Пример 3. Решить квадратное уравнение x² − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−5)² − 1 × (−24) = 25 + 24 = 49

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

---

Пример 5. Решить квадратное уравнение

Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k. Получается, что

Найдём дискриминант по формуле D₁ = k² − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .

Вычислим второй корень уравнения:

---

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax² + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

b = 2k

Заменим в уравнении ax² + bx + c = 0 коэффициент b на выражение 2k

ax² + 2kx + c = 0

Теперь вычислим дискриминант по ранее известной формуле:

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac

Вынесем в получившемся выражении за скобки общий множитель 4

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac = 4(k² − ac)

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k² − ac.

В выражении 4(k² − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k² − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k² − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

D₁ = k² − ac

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax² + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k² − ac)

Но ранее было сказано, что выражение k² − ac обозначается через D₁. Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Задания для самостоятельного решения

Задание 1. Решить уравнение:

Решение:

Ответ: 1; 0,6

Показать решение

Задание 2. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 3. Решить уравнение:

Решение:

Ответ: 1; −1,4

Показать решение

Задание 4. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 5. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 6. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 7. Решить уравнение:

Решение:

Ответ:

Показать решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Репетиторство по математике для экспертов в Великобритании

Формула арифметической последовательности используется для вычисления члена n ^th и суммы арифметической прогрессии. Арифметическая последовательность — это последовательность, в которой общая разность между любыми двумя последовательными членами остается постоянной. Если мы хотим найти какой-либо термин/сумму терминов в арифметической последовательности, мы можем использовать формулу арифметической последовательности. Давайте разберемся с формулой арифметической прогрессии на решенных примерах.

Что такое формула арифметической последовательности?

Арифметическая последовательность имеет вид: а, а + d, а + 2d, а + 3d, …… до n членов. Первый член — это а, общая разница — d, n = количество терминов. Для расчета с использованием формул арифметической последовательности сначала определите первый член, количество членов и общую разность последовательности. Существуют различные формулы, связанные с арифметическим рядом, используемым для вычисления члена n ^th , суммы или общей разности данной арифметической последовательности.

• n ^й срок есть, а _n = а ₁ + (n — 1) d
• Сумма n членов равна S _n = (n/2) [2a ₁ + (n — 1) d] (или) (n/2) [a ₁ + a _n ]
• Общая разность, d = a _n — a _{n — 1}

В этих формулах a ₁ = первый член, d = общая разность и n = количество членов.

Арифметическая последовательность Формула

Формулы арифметической последовательности задаются следующим образом:

Формула 1: Формула арифметической последовательности для нахождения n ^th членов задается как

a _{n 9001 7 = а 1 + (н — 1) d}

где,

• a _n = n ^th срок,
• a ₁ = первый член и
• d — общая разность

Формула 2: Сумма первых n членов арифметической последовательности вычисляется по одной из следующих формул:

• S _n = (n/2) [2a ₁ + (n — 1) d] (когда мы знаем первый член и общую разность)
• S _n =(n/2) [a ₁ + a _n ] (при первом и последнем членах)

где,

• S _n = сумма n слагаемых,
• a ₁ = первый член,
• a _n = n ^th срок и
• d — общая разница между последовательными терминами

Формула 3: Формула для вычисления общей разности арифметической прогрессии имеет вид

а _н = н ^-й срок,

a _{n — 1} = (n — 1) ^-й срок и

d — общая разница между последовательными терминами

Применение формулы арифметической последовательности

Мы используем формулу арифметической прогрессии каждый день или даже каждую минуту, даже не осознавая этого. Ниже приведены несколько примеров практического применения формулы арифметической последовательности

• Складывание чашек, стульев, мисок или карточного домика.
• Места на стадионе или в зрительном зале располагаются в арифметической последовательности.
• Секундная стрелка на часах движется в арифметической последовательности, а также минутная и часовая стрелки.
• Недели в месяце следуют арифметической последовательности, как и годы. Каждый високосный год можно определить, прибавив 4 к предыдущему високосному году.
• Количество свечей, задуваемых в день рождения, с каждым годом увеличивается как арифметическая прогрессия.

Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

 

Примеры с использованием формулы арифметической последовательности

Пример 1: Используя формулу арифметической последовательности, найдите 13 ^th член в последовательности 1, 5, 9, 13…

Решение:

Найти: 13 ^-й -й член данной последовательности.

Поскольку разница между последовательными терминами одинакова, данная последовательность образует арифметическую последовательность.

a = 1, d = 4

По формуле арифметической прогрессии 004 срок, n = 13

a _n = 1 + (13 — 1)4

a _n = 1 + (12)4

a _n = 1 + 48

a _n = 49

☛ Также проверьте: Калькулятор арифметической последовательности

Ответ: 13 член последовательности равен 49. 9000 5

Пример 2: Найти первый член арифметической прогрессии где 35-й ^-й -й член равен 687, а общая разность 14.

Решение:

Найти: Первый член арифметической последовательности

Дано: a _n = n 9000 3-й срок, д = 14

Используя формулу арифметической последовательности,

a _n = a ₁ + (n − 1)d

687 = a ₁ + (35 — 1)14

90 002 687 = а ₁ + ( 34)14

687 = a ₁ + 476

a ₁ = 211

Ответ: Первый член последовательности равен 211.

90 002 Пример 3: Найдите сумму следующего арифметического ряд: 3 + 7 + 11 + ……. (до 25 слагаемых).

Решение:

Найти сумму первых 25 членов арифметической прогрессии 3, 7, 11, …….

Дано: a ₁ = 3, d = 4, n = 25

данная арифметическая последовательность равна 3, 7, 11,….

Используя формулу арифметического ряда:

S _n = (n/2) [2a + (n — 1) d]

Сумма первых 25 членов

S ₂₅ =(25/ 2 ) [2 x 3 + (25 — 1) 4]

= (25/2) [6 + 24 x 4]

= 25/2 × 102

= 1275

Ответ: Сумма данного арифметического ряда равна 1275.

Часто задаваемые вопросы о формуле арифметической последовательности

Что такое формула арифметической последовательности в алгебре?

Формула арифметической последовательности относится к формуле для вычисления общего члена арифметической последовательности и суммы n членов арифметической последовательности.

• Общий член арифметической последовательности: a _n = a ₁ + (n — 1) d
• Сумма первых n членов арифметической прогрессии равна _n = (n/2) [2a ₁ + (n — 1) d]

где a ₁ = первый член и d = общая разность последовательности.

Что такое n в формуле арифметической последовательности?

В формуле арифметической последовательности для нахождения общего термина a _n = a ₁ + (n — 1) d, ‘n’ относится к номеру термина в данной арифметической последовательности. Например, ₂ представляет 2 ^-й -й член последовательности.

Что такое формула арифметической последовательности для суммы n членов?

Сумма первых n членов арифметической последовательности определяется как S _n = (n/2) [2a ₁ + (n — 1) d], где S _n = сумма n членов , a ₁ = первый член, а d — общая разность.

Что такое формула арифметического ряда?

Арифметический ряд есть не что иное, как сумма нескольких или всех членов арифметической прогрессии. Таким образом, формула арифметического ряда:

• S _n = (n/2) [2a ₁ + (n — 1) d] [ИЛИ]
• S _n = (n/2) [a ₁ + a _n ]

Здесь a ₁ — первый член арифметического ряда, а d — его общая разность.

Как использовать формулу арифметической последовательности?

Чтобы использовать формулу арифметической последовательности, сначала определите первый член (a ₁ ) и общую разность (d) последовательности. Затем подставьте их в соответствующую формулу (из n ^-й член или сумма) и упростить.

В чем разница между явной формулой и рекурсивной формулой арифметической последовательности?

Явная формула используется для нахождения любого члена арифметической прогрессии, если мы знаем только его первый член и общую разность. Но рекурсивная формула может быть использована для нахождения термина только тогда, когда известны его предыдущий термин и общая разность.

• Явная формула для арифметической последовательности: a _n = a ₁ + (н — 1) д
• Рекурсивная формула для арифметической последовательности: a _n = a _{n — 1} + d

Арифметические последовательности

Горячая математика

Ан арифметическая последовательность это последовательность числа, которое увеличивается или уменьшается на постоянную величину каждый член.

Мы можем написать формулу для н й член арифметической прогрессии в виде

а н «=» г н + с ,

где г это общая разница . Как только вы узнаете общую разницу, вы можете найти значение с подключив 1 для н и первый член последовательности для а 1 .

Пример 1:

{ 1 , 5 , 9 , 13 , 17 , 21 , 25 , … }

представляет собой арифметическую прогрессию с общей разностью 4 .

(С

5 − 1 «=» 4 ,

9 − 5 «=» 4 ,

и т. д.)

Чтобы найти следующий 3 условия, мы просто продолжаем добавлять 4 :

25 + 4 «=» 2929 + 4 «=» 33 33 + 4 «=» 37

Итак, следующий 3 условия 29 , 33 , и 37 .

Чтобы найти формулу для н й термин, мы заменяем н «=» 1 , а 1 «=» 1 и г «=» 4 в

а н «=» г н + с

найти с .

1 «=» 4 ( 1 ) + с с «=» − 3

Итак, формула для н й член последовательности

а н «=» 4 н − 3 .

Пример 2:

{ 12 , 9 , 6 , 3 , 0 , − 3 , − 6 , … }

представляет собой арифметическую прогрессию с общей разностью − 3 .

(С

9 − 12 «=» − 3

6 − 9 «=» − 3

и т. д. Обратите внимание, что, поскольку последовательность убывающая, общая разность отрицательна.)

Чтобы найти следующий 3 условия, мы просто продолжаем вычитать 3 :

− 6 − 3 «=» − 9− 9 − 3 «=» − 12 − 12 − 3 «=» − 15

Итак, следующий 3 условия − 9 , − 12 , и − 15 .

Чтобы найти формулу для н й термин, мы заменяем н «=» 1 , а 1 «=» 12 , и г «=» − 3 в

а н «=» г н + с

найти с .

12 «=» − 3 ( 1 ) + с с «=» 15

Итак, формула для н й член этой последовательности

а н «=» − 3 н + 15 .

Пример 3:

{ 2 , 3 , 5 , 8 , 12 , 17 , 23 , .