D формула: Дискриминант. Формула дискриминанта.

Умножение и деление чисел в Excel

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Еще…Меньше

Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.

Умножение чисел

Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.

Умножение чисел в ячейке

Для выполнения этой задачи используйте арифметический оператор

* (звездочка).

Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.

Умножение столбца чисел на константу

Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.

1. Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.

   Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2.

   Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.

2. Перетащите формулу вниз в другие ячейки столбца.

   Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.

Перемножение чисел в разных ячейках с использованием формулы

Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.

Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6)

перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).

Деление чисел

Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.

Деление чисел в ячейке

Для этого воспользуйтесь арифметическим оператором / (косая черта).

Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.

Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01.

12.1936 и отобразит в ячейке значение «1-дек».

Примечание: В Excel нет функции DIVIDE.

Деление чисел с помощью ссылок на ячейки

Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.

Пример:

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

Копирование примера

1. Создайте пустую книгу или лист.

2. org/ListItem»>

   Выделите пример в разделе справки.

   Примечание: Не выделяйте заголовки строк или столбцов.

   Выделение примера в справке

3. Нажмите клавиши CTRL+C.

4. Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.

5. Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».

	A	B	C
1	Данные	Формула	Описание (результат)
2	15000	=A2/A3	Деление 15000 на 12 (1250).
3	12

Деление столбца чисел на константу

Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.

	A	B	C
1	Данные	Формула	Константа
2	15000	=A2/$C$2	3
3	12	=A3/$C$2
4	48	=A4/$C$2
5	729	=A5/$C$2
6	1534	=A6/$C$2
7	288	=A7/$C$2
8	4306	=A8/$C$2

org/ItemList»>

1. В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2.

2. Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.

Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Умножение столбца чисел на одно и то же число

Умножение на процентное значение

Создание таблицы умножения

Операторы вычислений и порядок операций

Создание простой формулы в Excel

Excel

Формулы и функции

Формулы

Формулы

Создание простой формулы в Excel

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Еще…Меньше

Вы можете создать простую формулу для с суммы, вычитания, умножения и деления значений на вашем компьютере. Простые формулы всегда начинаются со знака равной(=),за которым следуют константы, которые являются числами и операторами вычислений, такими как «плюс»(+),«минус» (— ),«звездочка»*или «косая черта»(/)в начале.

В качестве примера рассмотрим простую формулу.

1. Выделите на листе ячейку, в которую необходимо ввести формулу.

2. Введите = (знак равенства), а затем константы и операторы (не более 8192 знаков), которые нужно использовать при вычислении.

   В нашем примере введите =1+1.

   Примечания: 

   • org/ListItem»>

     Вместо ввода констант в формуле можно выбрать ячейки с нужными значениями и ввести операторы между ними.

   • В соответствии со стандартным порядком математических операций, умножение и деление выполняются до сложения и вычитания.

3. Нажмите клавишу ВВОД (Windows) или Return (Mac).

Рассмотрим другой вариант простой формулы. Введите =5+2*3 в другой ячейке и нажмите клавишу ВВОД или Return. Excel перемножит два последних числа и добавит первое число к результату умножения.

Использование автосуммирования

Для быстрого суммирования чисел в столбце или строке можно использовать кнопку «Автосумма».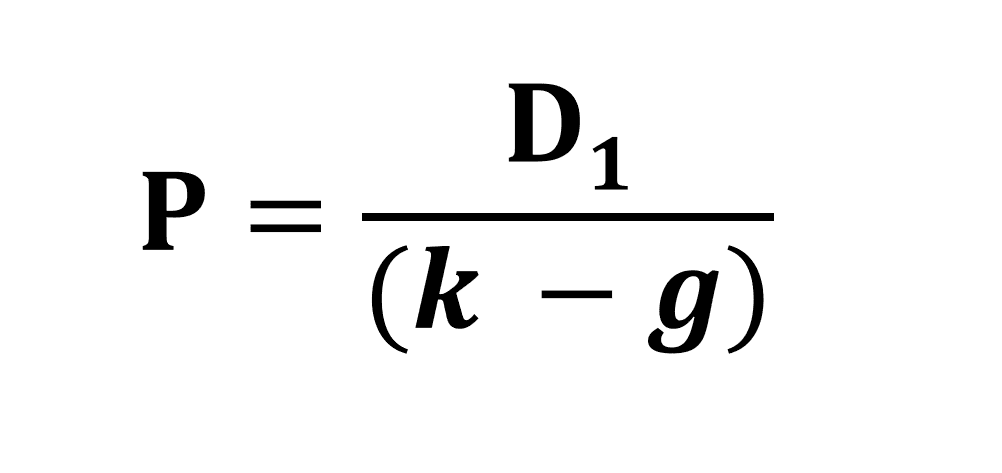 Выберите ячейку рядом с числами, которые необходимо сложить, нажмите кнопку Автосумма на вкладке Главная, а затем нажмите клавишу ВВОД (Windows) или Return (Mac).

Когда вы нажимаете кнопку Автосумма, Excel автоматически вводит формулу для суммирования чисел (в которой используется функция СУММ).

Примечание: Также в ячейке можно ввести ALT+= (Windows) или ALT++= (Mac), и Excel автоматически вставит функцию СУММ.

Приведем пример. Чтобы сложить числа за январь в бюджете «Развлечения», выберите ячейку B7, которая непосредственно под столбцом чисел. Затем нажмите кнопку «Автоумма». Формула появится в ячейке B7, а Excel выделит ячейки, которые вы суммируете.

Чтобы отобразить результат (95,94) в ячейке В7, нажмите клавишу ВВОД. Формула также отображается в строке формул вверху окна Excel.

Примечания: 

• Чтобы сложить числа в столбце, выберите ячейку под последним числом в столбце. Чтобы сложить числа в строке, выберите первую ячейку справа.

• Создав формулу один раз, ее можно копировать в другие ячейки, а не вводить снова и снова. Например, при копировании формулы из ячейки B7 в ячейку C7 формула в ячейке C7 автоматически настроится под новое расположение и подсчитает числа в ячейках C3:C6.

• Кроме того, вы можете использовать функцию «Автосумма» сразу для нескольких ячеек. Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.

Скопируйте данные из таблицы ниже и вставьте их в ячейку A1 нового листа Excel. При необходимости измените ширину столбцов, чтобы видеть все данные.

Примечание: Чтобы эти формулы выводили результат, выделите их и нажмите клавишу F2, а затем — ВВОД (Windows) или Return (Mac).

Данные
2
5
Формула	Описание	Результат
=A2+A3	Сумма значений в ячейках A1 и A2	=A2+A3
=A2-A3	Разность значений в ячейках A1 и A2	=A2-A3
=A2/A3	Частное от деления значений в ячейках A1 и A2	=A2/A3
=A2*A3	Произведение значений в ячейках A1 и A2	=A2*A3
=A2^A3	Значение в ячейке A1 в степени, указанной в ячейке A2	=A2^A3
Формула	Описание	Результат
=5+2	Сумма чисел 5 и 2	=5+2
=5-2	Разность чисел 5 и 2	=5-2
=5/2	Частное от деления 5 на 2	=5/2
=5*2	Произведение чисел 5 и 2	=5*2
=5^2	Число 5 во второй степени	=5^2

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи

Оглавление:

• Формулы сокращенного умножения
• Квадратное уравнение и формула разложения квадратного трехчлена на множители
• Свойства степеней и корней
• Формулы с логарифмами
• Арифметическая прогрессия
• Геометрическая прогрессия
• Тригонометрия
• Тригонометрические уравнения
• Геометрия на плоскости (планиметрия)
• Геометрия в пространстве (стереометрия)
• Координаты
• Таблица умножения
• Таблица квадратов двухзначных чисел
• Расширенная PDF версия документа «Все главные формулы по школьной математике»

 

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

 

Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению. ..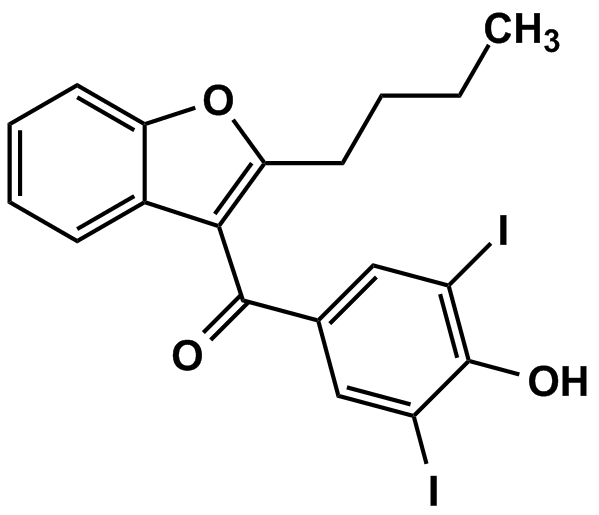

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам.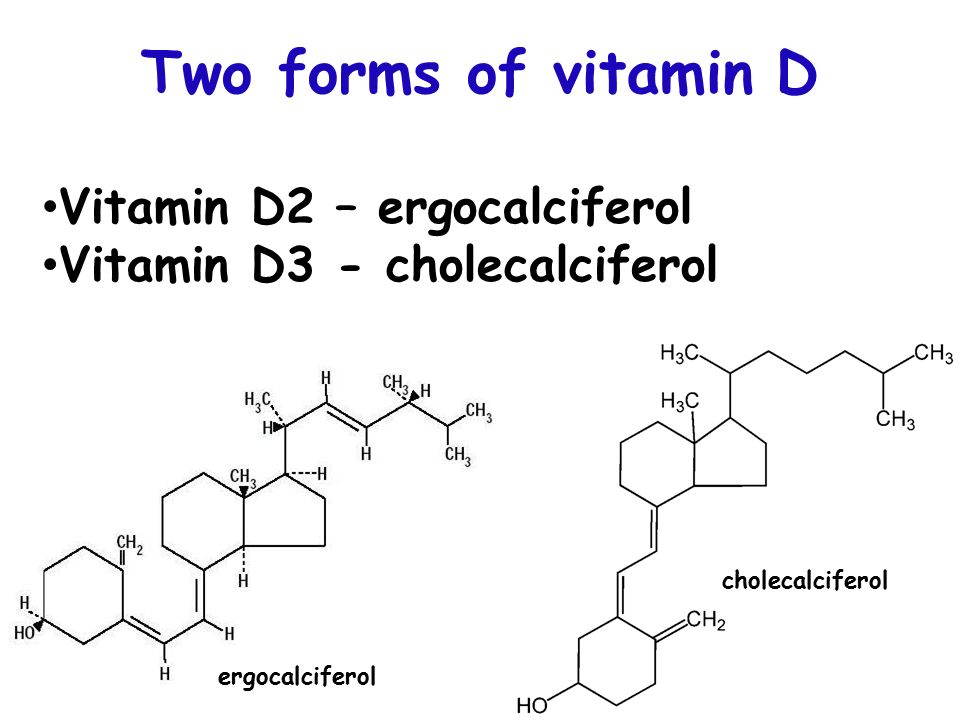 Икс вершины:

Игрек вершины параболы:

 

Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

 

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

 

Арифметическая прогрессия

К оглавлению. ..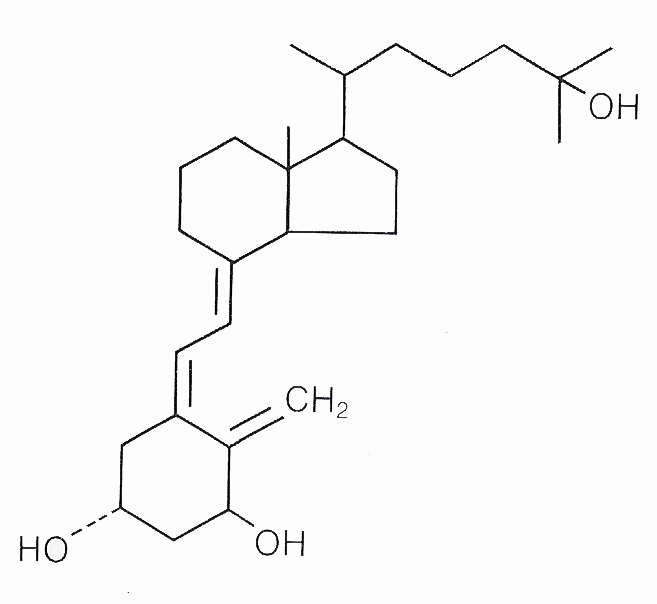

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

 

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

 

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

 

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

 

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

 

Тригонометрические уравнения

К оглавлению. ..

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

 

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.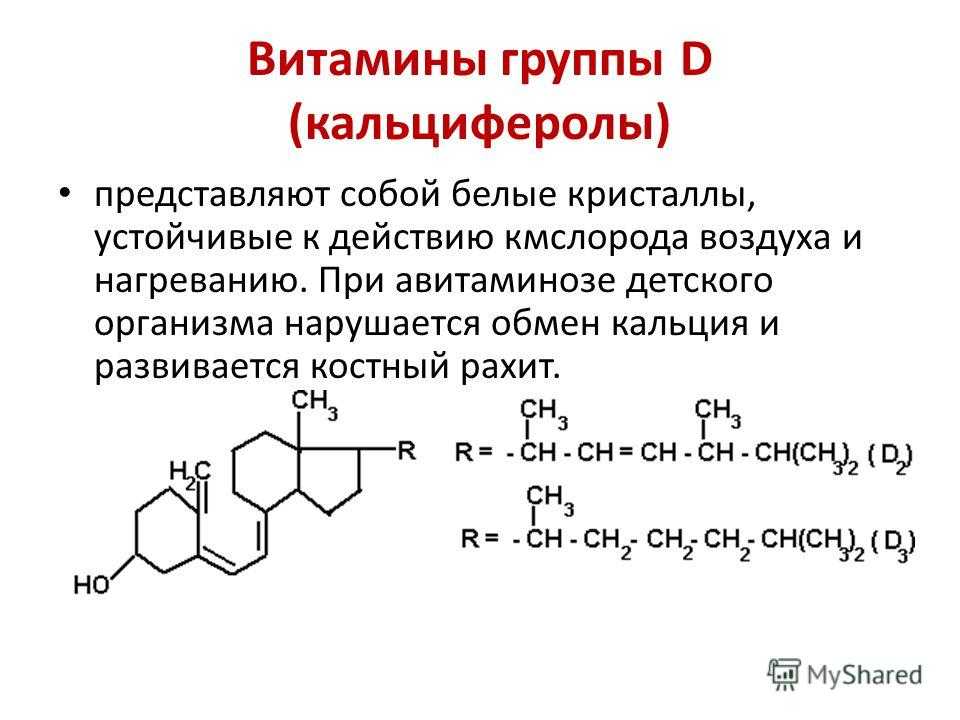 е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

 

Геометрия в пространстве (стереометрия)

К оглавлению. ..

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

 

Координаты

К оглавлению. ..

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

 

Таблица умножения

К оглавлению…

 

Таблица квадратов двухзначных чисел

К оглавлению…

 

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

К оглавлению…

Формула отношения долга к собственному капиталу (D/E) и ее интерпретация

Что такое отношение долга к собственному капиталу (D/E)?

Отношение долга к собственному капиталу (D/E) используется для оценки финансового рычага компании и рассчитывается путем деления общей суммы обязательств компании на ее собственный капитал. Соотношение D/E является важным показателем в корпоративных финансах. Это показатель того, в какой степени компания финансирует свою деятельность за счет долга, а не собственных ресурсов. Отношение долга к собственному капиталу — это особый тип соотношения заемных средств.

Основные выводы

• Отношение долга к собственному капиталу (D/E) сравнивает общие обязательства компании с ее акционерным капиталом и может использоваться для оценки степени ее зависимости от долга.
• Коэффициенты D/E варьируются в зависимости от отрасли и лучше всего используются для сравнения прямых конкурентов или для измерения изменения зависимости компании от долга с течением времени.
• Среди аналогичных компаний более высокий коэффициент D/E предполагает больший риск, в то время как особенно низкий показатель может указывать на то, что бизнес не использует заемное финансирование для расширения.
• Инвесторы часто изменяют соотношение D/E, чтобы учитывать только долгосрочные долговые обязательства, поскольку они сопряжены с большим риском, чем краткосрочные обязательства.

Соотношение долга к собственному капиталу

Формула соотношения D/E и расчет

Долг/Собственный капитал знак равно Всего обязательства Общий акционерный капитал \begin{aligned} &\text{Долг/Собственный капитал} = \frac{ \text{Общая сумма обязательств} }{ \text{Общая сумма акционерного капитала} } \\ \end{align} ​Долг/Собственный капитал = Общая сумма акционерного капиталаСуммарные обязательства​​

Информацию, необходимую для расчета коэффициента D/E, можно найти в балансе листинговой компании. Вычитание стоимости обязательств в балансе из общей суммы активов, показанной там, дает значение акционерного капитала, которое представляет собой измененную версию этого уравнения баланса:

Ресурсы знак равно Обязательства + Акционерный капитал \begin{align} &\text{Активы} = \text{Обязательства} + \text{Акционерный капитал} \\ \end{align} ​Активы=Обязательства+Акционерный капитал​

Эти категории баланса могут включать статьи, которые обычно не считаются заемным или собственным капиталом в традиционном смысле кредита или актива. Поскольку соотношение может быть искажено нераспределенной прибылью или убытками, нематериальными активами и корректировками пенсионного плана, обычно необходимы дальнейшие исследования, чтобы понять, в какой степени компания зависит от долга.

Чтобы получить более ясную картину и облегчить сравнение, аналитики и инвесторы часто изменяют коэффициент D/E. Они также оценивают коэффициент D/E в контексте коэффициентов краткосрочного левериджа, прибыльности и ожиданий роста.

Мелисса Линг © Investopedia 2019

Как рассчитать отношение D/E в Excel

Владельцы бизнеса используют различное программное обеспечение для отслеживания коэффициентов D/E и других финансовых показателей. Microsoft Excel предоставляет шаблон балансового отчета, который автоматически рассчитывает финансовые коэффициенты, такие как коэффициент D/E и коэффициент долга. Или вы можете ввести значения общих обязательств и акционерного капитала в соседние ячейки электронной таблицы, скажем, B2 и B3, а затем добавить формулу «=B2/B3» в ячейку B4, чтобы получить коэффициент D/E.

О чем говорит соотношение D/E?

Коэффициент D/E показывает, сколько долгов компания взяла на себя по отношению к стоимости ее активов за вычетом обязательств. Долг должен быть погашен или рефинансирован, налагает процентные расходы, которые, как правило, не могут быть отложены, и может обесценить или уничтожить стоимость собственного капитала в случае дефолта. В результате высокое соотношение D/E часто связано с высоким инвестиционным риском; это означает, что компания в основном полагается на заемное финансирование.

Рост, финансируемый за счет долга, может способствовать увеличению прибыли, и если дополнительное увеличение прибыли превышает связанное с этим увеличение затрат на обслуживание долга, то акционеры должны ожидать выгоды. Однако, если дополнительные затраты на заемное финансирование перевешивают дополнительный доход, который оно генерирует, цена акций может упасть. Стоимость долга и способность компании обслуживать его могут варьироваться в зависимости от рыночных условий. В результате заимствование, которое вначале казалось разумным, впоследствии может оказаться убыточным при различных обстоятельствах.

Изменения в долгосрочной задолженности и активах, как правило, больше всего влияют на коэффициент D/E, потому что вовлеченные числа, как правило, больше, чем для краткосрочной задолженности и краткосрочных активов. Если инвесторы хотят оценить краткосрочный левередж компании и ее способность выполнять долговые обязательства, которые должны быть выплачены в течение года или меньше, они могут использовать другие коэффициенты.

Например, денежный коэффициент оценивает краткосрочную ликвидность компании:

Денежный коэффициент знак равно Наличные + Рыночные ценные бумаги Краткосрочные обязательства \begin{aligned} &\text{Коэффициент наличности} = \frac{ \text{Наличные} + \text{Рыночные ценные бумаги} }{ \text{Краткосрочные обязательства} } \\ \end{align} Соотношение денежных средств = краткосрочные обязательства Денежные средства + Рыночные ценные бумаги​​

То же самое и с коэффициентом текущей ликвидности:

Текущее соотношение знак равно Краткосрочные активы Краткосрочные обязательства \begin{aligned} &\text{Current Ratio} = \frac{ \text{Краткосрочные активы} }{ \text{Краткосрочные обязательства} } } \\ \end{align} ​Коэффициент текущей ликвидности = краткосрочные обязательства – краткосрочные активы​​

Пример отношения D/E

Рассмотрим исторический пример от Apple Inc. (AAPL). Ниже мы видим, что за финансовый год (FY), закончившийся 2017, общая сумма обязательств Apple составила 241 миллиард долларов (округлено), а общий акционерный капитал — 134 миллиарда долларов, согласно отчету компании 10-K.

Используя приведенную выше формулу, соотношение D/E для Apple можно рассчитать следующим образом:

Долг справедливости знак равно $ 241 , 000 , 000 $ 134 , 000 , 000 знак равно 1,80 \begin{align} \text{Отношение долга к собственному капиталу} = \frac { \$241 000 000 }{ \$134 000 000 } = 1,80 \\ \end{align} Долг к собственному капиталу = 134 000 000 долларов США 241 000 000 долларов США​= 1,80​

Результат означает, что у Apple было 1,80 доллара долга на каждый доллар собственного капитала. Но само по себе это соотношение не дает инвесторам полной картины. Важно сравнить соотношение с другими аналогичными компаниями.

Изменение отношения D/E

Не все долги одинаково рискованны. Долгосрочный коэффициент D/E фокусируется на более рискованном долгосрочном долге, используя его значение вместо общей суммы обязательств в числителе стандартной формулы:

Долгосрочный коэффициент D/E = Долгосрочный долг ÷ Акционерный капитал

Краткосрочный долг, конечно, также увеличивает левередж компании, но, поскольку эти обязательства должны быть выплачены в течение года или раньше, они не так рискованны. Например, представьте себе компанию с краткосрочной кредиторской задолженностью (заработная плата, кредиторская задолженность, векселя и т. д.) на 1 миллион долларов и долгосрочной задолженностью на 500 000 долларов по сравнению с компанией с краткосрочной кредиторской задолженностью на 500 000 долларов и долгосрочной кредиторской задолженностью на 1 миллион долларов. срочная задолженность. Если акционерный капитал обеих компаний составляет 1,5 миллиона долларов, то отношение D/E у них равно 1. На первый взгляд риск от левериджа идентичен, но на самом деле вторая компания более рискованна.

Как правило, краткосрочная задолженность обычно дешевле долгосрочной и менее чувствительна к изменениям процентных ставок, а это означает, что процентные расходы и стоимость капитала второй компании, вероятно, выше. Если процентные ставки выше, когда наступает срок погашения долгосрочного долга и его необходимо рефинансировать, процентные расходы возрастут.

Наконец, если мы предположим, что компания не объявит дефолт в течение следующего года, то более ранняя задолженность не должна вызывать беспокойства. Напротив, способность компании обслуживать долгосрочный долг будет зависеть от ее долгосрочных деловых перспектив, которые менее очевидны.

Коэффициент D/E для личных финансов

Коэффициент D/E также может применяться к личным финансовым отчетам, выступая в качестве личного коэффициента D/E. Здесь собственный капитал относится к разнице между общей стоимостью активов человека и его совокупным долгом или обязательствами. Формула личного отношения D/E немного отличается:

Долг/Собственный капитал знак равно Всего личных обязательств Личные активы − Обязательства \begin{align} &\text{Долг/Собственный капитал} = \frac{ \text{Общая сумма личных обязательств} }{ \text{Личные активы} — \text{Обязательства} } \\ \end{align} ​Долг/Собственный капитал = Личные активы — Обязательства. Итого Личные обязательства​​

Личное соотношение D/E часто используется, когда физическое лицо или малый бизнес подают заявку на кредит. Кредиторы используют показатель D/E для оценки способности соискателя кредита продолжать выплаты по кредиту в случае временной потери дохода.

Например, потенциальный ипотечный заемщик с большей вероятностью сможет продолжать выплаты в период продолжительной безработицы, если у него больше активов, чем долга. Это также верно для человека, подающего заявку на кредит для малого бизнеса или кредитную линию. Если у владельца бизнеса хорошее личное соотношение D/E, более вероятно, что он сможет продолжать выплачивать кредит до тех пор, пока его инвестиции, финансируемые за счет долга, не начнут окупаться.

Соотношение D/E и передаточное отношение

Коэффициенты заемных средств представляют собой широкую категорию финансовых коэффициентов, из которых наиболее известен коэффициент D/E. «Гиринг» — это термин, обозначающий финансовый рычаг.

Коэффициенты заемных средств в большей степени ориентированы на концепцию кредитного плеча, чем другие коэффициенты, используемые в бухгалтерском учете или инвестиционном анализе. Основополагающий принцип обычно предполагает, что некоторые рычаги хороши, но слишком большие подвергают организацию риску.

Отношение долга к собственному капиталу наиболее полезно при сравнении прямых конкурентов. Если коэффициент D/E компании значительно выше, чем у других компаний в этой отрасли, то ее акции могут быть более рискованными.

Ограничения отношения D/E

При использовании коэффициента D/E очень важно учитывать отрасль, в которой работает компания. Поскольку разные отрасли имеют разные потребности в капитале и темпы роста, значение коэффициента D/E, обычное для одной отрасли, может быть тревожным сигналом в другой.

Акции коммунальных предприятий часто имеют особенно высокие коэффициенты D/E. Как строго регулируемая отрасль, делающая крупные инвестиции, как правило, со стабильной нормой прибыли и генерирующая стабильный поток доходов, коммунальные предприятия занимают большие суммы и относительно дешево. Высокие коэффициенты левериджа в медленно растущих отраслях со стабильным доходом представляют собой эффективное использование капитала. Компании в секторе потребительских товаров, как правило, имеют высокие коэффициенты D/E по тем же причинам.

Аналитики не всегда согласны в том, что определяется как долг. Например, привилегированные акции иногда считаются акционерным капиталом, поскольку выплата дивидендов по привилегированным акциям не является юридическим обязательством, а привилегированные акции имеют приоритет ниже всех долговых обязательств (но выше обыкновенных акций) в отношении их требований на корпоративные активы. С другой стороны, обычно стабильные привилегированные дивиденды, номинальная стоимость и права ликвидации делают привилегированные акции более похожими на долговые обязательства.

Включение привилегированных акций в общий долг увеличит коэффициент D/E и сделает компанию более рискованной. Включение привилегированных акций в долю собственного капитала коэффициента D/E увеличит знаменатель и снизит коэффициент. Это особенно сложный вопрос при анализе отраслей, особенно зависящих от финансирования привилегированными акциями, таких как инвестиционные фонды недвижимости (REIT).

Каково хорошее соотношение долга к собственному капиталу (D/E)?

То, что считается «хорошим» соотношением долга к собственному капиталу (D/E), будет зависеть от характера бизнеса и его отрасли. Вообще говоря, отношение D/E ниже 1 считается относительно безопасным, тогда как значения 2 и выше могут считаться рискованными. Компании в некоторых отраслях, таких как коммунальные услуги, производство потребительских товаров и банковское дело, обычно имеют относительно высокие коэффициенты D/E. Обратите внимание, что особенно низкий коэффициент D/E может быть отрицательным, предполагая, что компания не использует заемное финансирование и свои налоговые преимущества. (Расходы на деловые проценты обычно не облагаются налогом, а выплаты дивидендов облагаются корпоративным и подоходным налогом.)

На что указывает соотношение D/E, равное 1,5?

Соотношение D/E, равное 1,5, означает, что рассматриваемая компания имеет 1,50 доллара долга на каждый доллар собственного капитала. Для иллюстрации предположим, что активы компании составляют 2 миллиона долларов, а обязательства — 1,2 миллиона долларов. Поскольку собственный капитал равен активам за вычетом обязательств, собственный капитал компании составит 800 000 долларов. Таким образом, его отношение D/E составит 1,2 миллиона долларов, деленное на 800 000 долларов, или 1,5.

О чем сигнализирует отрицательное отношение D/E?

Если у компании отрицательное соотношение D/E, это означает, что у нее отрицательный акционерный капитал. Другими словами, обязательства компании превышают ее активы. В большинстве случаев это будет считаться признаком высокого риска и стимулом для обращения за защитой от банкротства.

Какие отрасли имеют высокие коэффициенты D/E?

В секторе банковских и финансовых услуг относительно высокий коэффициент D/E является обычным явлением. Банки несут более высокие суммы долга, потому что они владеют значительными основными фондами в виде филиальных сетей. Более высокие коэффициенты D/E также могут преобладать в других капиталоемких секторах, в значительной степени зависящих от заемного финансирования, таких как авиалинии и промышленные предприятия.

Как можно использовать коэффициент D/E для измерения рискованности компании?

Постоянно растущий коэффициент D/E может затруднить для компании получение финансирования в будущем. Растущая зависимость от долга может в конечном итоге привести к трудностям в обслуживании текущих кредитных обязательств компании. Очень высокие коэффициенты D/E могут в конечном итоге привести к дефолту по кредиту или банкротству.

Итог

Отношение долга к собственному капиталу (D/E) может помочь инвесторам определить компании с высокой долей заемных средств, которые могут представлять риски во время спадов в бизнесе. Инвесторы могут сравнить коэффициент D/E компании со средним показателем по отрасли и показателями конкурентов, чтобы получить представление о зависимости компании от долга. Но не все высокие коэффициенты D/E указывают на плохие перспективы для бизнеса. Фактически долг может позволить компании расти и получать дополнительный доход. Но если компания все больше зависит от долга или чрезмерно зависит от своей отрасли, потенциальные инвесторы захотят продолжить расследование.

Что такое и как рассчитать d Коэна?

Что такое d Коэна?

Коэффициент Коэна d представляет собой тип размера эффекта между двумя средними значениями. В этом отношении размер эффекта является количественной мерой величины разницы между двумя средними значениями.

Значения d Коэна также известны как стандартизированная разность средних (SMD).

Поскольку значения стандартизированы, можно сравнивать значения различных переменных.

Что такое d-формула Коэна?

На самом деле существует несколько d-формул Коэна. В этом руководстве я объясню два основных: Cohen’s d и Cohen’s d _s .

В частности, формулы представляют собой разницу между двумя средними значениями, деленную на объединенное стандартное отклонение (SD).

Коэффициент d Коэна (равные размеры групп)

Формула d Коэна основана на двух группах с одинаковым размером групп (n). Следовательно, поскольку это предполагается, в уравнении не требуется n.

Формулу для Коэна d можно увидеть ниже.

В этом отношении используется объединенное SD, поскольку SD населения обычно неизвестно. Объединенное SD рассчитывается на основе выборки 90 159 90 160 SD с использованием приведенного ниже уравнения.

Компоненты формулы:

• M ₁ = среднее значение группы 1 (например, контрольной группы)
• M ₂ = Среднее значение группы 2 (например, экспериментальной группы)
• SD ₁ = стандартное отклонение группы 1
• SD ₂ = стандартное отклонение группы 2

Коэновская d

_s (неравные размеры групп)

В отличие от первой формулы вариант Коэна d _s может учитывать неравные размеры групп. Следовательно, чтобы использовать это, необходимо знать размеры группы (n).

Формула для d Коэна _s аналогична формуле d Коэна, однако вычисление объединенного стандартного отклонения отличается.

На этот раз объединенное SD рассчитывается следующим образом.

Компоненты этих формул:

• M ₁ = среднее значение группы 1 (например, контрольной группы)
• M ₂ = Среднее значение группы 2 (например, экспериментальной группы)
• SD ₁ = стандартное отклонение группы 1
• SD ₂ = стандартное отклонение группы 2
• n ₁ = Размер группы 1
• n ₂ = размер группы 2

Расчет d Коэна на примере

Теперь вы знаете формулы, давайте воспользуемся ими в примере.

Формула d Коэна

Мы хотим рассчитать d Коэна между двумя группами: мужчинами и женщинами. В частности, в крови двух групп определяли количество определенного белка. У женщин уровень белка был выше (1,062 ± 0,339), чем у мужчин (0,528 ± 0,382).

Следовательно, четыре компонента уравнения таковы:

• M ₁ = 0,528
• М ₂ = 1,062
• SD ₁ = 0,382
• СО ₂ = 0,339

Самый простой способ вычислить значения d — сначала вычислить объединенное стандартное отклонение. Таким образом, получение этих значений и ввод их в уравнение показаны ниже.

Это даст объединенное значение SD 0,361 .

Итак, теперь мы можем подставить это значение в уравнение Коэна d вместе со средними двумя группами. Полное уравнение показано ниже.

Подставив все это в калькулятор, мы получим значение d, равное 9.0135 1.479 .

Формула Коэна d

_s

Давайте воспользуемся теми же примерными данными, но добавим другие номера групп. Скажем, было 16 женщин и только 13 мужчин.

Таким образом, данные, которые нужно ввести в уравнение, будут:

• M ₁ = 0,528
• М ₂ = 1,062
• SD ₁ = 0,382
• СО ₂ = 0,339
• n ₁ = 13
• н ₂ = 16

Опять же, давайте начнем с расчета объединенного SD. Поскольку сейчас мы используем формулу Коэна d _s , объединенные расчеты SD будут следующими.

При тщательном расчете объединенное значение стандартного отклонения получается равным 0,359 .

Теперь, если ввести это в общее уравнение, это будет выглядеть так.

Если ввести это в калькулятор, получится значение 1,489 .

Онлайн-калькулятор Коэна d

Если вы все еще пытаетесь рассчитать значения d с помощью формулы, мы создали калькулятор Коэна d.

Чтобы использовать калькулятор, просто введите среднее значение группы и значения стандартного отклонения, и величина d-эффекта будет рассчитана для вас.

Как интерпретировать размеры эффекта d Коэна

Проще говоря, вы можете думать о значениях d Коэна как о стандартном отклонении между двумя группами. Значение 1 указывает, что средние значения двух групп отличаются на 1 стандартное отклонение.

В нашем предыдущем примере значение 1,479 указывает, что средние различия между мужской и женской группами различаются на 1,479.стандартные отклонения, что, как вы увидите, является довольно большим эффектом.

Что такое малый, средний и большой размер эффекта?

После расчета значений d люди часто указывают, какой размер эффекта: малый, средний или большой.

Сам Коэн разделил значения d на три подгруппы (0,2, 0,5 и 0,8). Однако эти значения являются лишь общими интерпретациями и не должны использоваться строго.

Маленький: d = 0,2

Малый размер эффекта считается слишком маленьким, чтобы его можно было различить невооруженным глазом.

Коэн привел в качестве примера небольшой размер эффекта разницу в росте между 15- и 16-летними девочками.

Medium: d = 0,5

Medium Размер эффекта достаточно велик, чтобы его можно было увидеть невооруженным глазом.

Развивая это, Коэн объяснил, что разница в росте между 14- и 18-летними девочками будет рассчитана как средний размер эффекта.

Большие: d = 0,8

Большие размеры эффекта — действительно очевидные различия между группами.

Следуя примерам Коэна, он описал этот размер, наблюдаемый при сравнении роста 13- и 18-летних девочек.

Ссылки

Коэн, Дж. (1988). Статистический анализ мощности для поведенческих наук . Нью-Йорк, штат Нью-Йорк: Routledge Academic.

Лакенс, Д. (2013). Расчет и отчет о размерах эффекта для облегчения кумулятивной науки: практическое руководство по t-тестам и дисперсионному анализу. Границы психологии, 4:863. doi:10.3389/fpsyg.2013.00863

Formula D Oral: применение, побочные эффекты, взаимодействие, изображения, предупреждения и дозировка аллергия, сенная лихорадка или другие респираторные заболевания (такие как синусит, бронхит).

Гвайфенезин — отхаркивающее средство, которое помогает разжижать и разжижать слизь в легких, облегчая отхаркивание слизи. Декстрометорфан — это средство от кашля, которое воздействует на определенную часть мозга (центр кашля), уменьшая позывы к кашлю. Этот продукт также содержит противоотечное средство, которое помогает облегчить симптомы заложенности носа. Это лекарство обычно не используется при продолжающемся кашле из-за курения, астме, других длительных проблемах с дыханием (таких как эмфизема) или кашле с большим количеством слизи, если не указано иное. вашим доктором. Не было доказано, что продукты от кашля и простуды безопасны или эффективны для детей младше 6 лет. Не используйте этот продукт для лечения симптомов простуды у детей младше 6 лет, если только это не предписано врачом. Некоторые продукты (например, таблетки/капсулы пролонгированного действия) не рекомендуются для детей младше 12 лет. Спросите своего врача или фармацевта для получения более подробной информации о безопасном использовании вашего продукта. Эти продукты не излечивают простуду и не сокращают ее продолжительность и могут вызывать серьезные побочные эффекты. Чтобы снизить риск серьезных побочных эффектов, внимательно следуйте всем указаниям по дозировке. Не используйте этот продукт, чтобы вызвать у ребенка сонливость. Не давайте другие лекарства от кашля и простуды, которые могут содержать те же или подобные ингредиенты (см. также раздел «Взаимодействие с лекарствами»). Спросите у врача или фармацевта о других способах облегчения симптомов кашля и простуды (например, об употреблении достаточного количества жидкости, использовании увлажнителя или солевых капель/спрей для носа).

Как использовать жидкую формулу D

Если вы принимаете безрецептурный препарат, прочитайте все инструкции на упаковке перед приемом этого лекарства. Если у вас есть какие-либо вопросы, проконсультируйтесь с вашим фармацевтом. Если ваш врач прописал это лекарство, принимайте его в соответствии с указаниями.

Принимайте таблетки, капсулы или жидкие формы внутрь независимо от приема пищи. Следуйте указаниям по дозировке на этикетке или принимайте по назначению врача. Пейте много жидкости, когда вы используете это лекарство, если иное не указано вашим доктором. Жидкость поможет разжижить слизь в легких. Это лекарство можно принимать во время еды, если возникает расстройство желудка.

Если вы используете жидкую форму, используйте прибор для измерения лекарств, чтобы тщательно измерить предписанную дозу. Не используйте бытовую ложку. Если ваша жидкая форма представляет собой суспензию, хорошо встряхните бутылку перед каждой дозой.

Если вы принимаете таблетки или капсулы пролонгированного действия, проглатывайте лекарство целиком. Не раздавливайте и не разжевывайте таблетки или капсулы. Это может разрушить длительное действие препарата и усилить побочные эффекты.

Дозировка зависит от вашего возраста, состояния здоровья и реакции на терапию.

Неправильное использование этого лекарства (злоупотребление) может привести к серьезному вреду (например, повреждению головного мозга, судорогам, смерти). Не увеличивайте дозу и не принимайте это лекарство чаще, чем рекомендовано вашим врачом или инструкциями на упаковке, без одобрения вашего врача.

Сообщите своему врачу, если ваше состояние длится более 1 недели, если оно ухудшается или сопровождается головной болью, которая не проходит, лихорадкой или сыпью. Это могут быть симптомы серьезной медицинской проблемы, и их следует проверить у врача.

Побочные эффекты

Могут возникнуть головокружение, головная боль, тошнота, нервозность или проблемы со сном. Если какой-либо из этих эффектов сохраняется или ухудшается, немедленно обратитесь к врачу или фармацевту.

Если ваш врач прописал это лекарство, помните, что ваш врач пришел к выводу, что польза для вас больше, чем риск побочных эффектов. Многие люди, использующие это лекарство, не имеют серьезных побочных эффектов.

Немедленно сообщите своему врачу, если у вас есть какие-либо серьезные побочные эффекты, в том числе: психические изменения/изменения настроения (например, спутанность сознания, галлюцинации), дрожь (тремор), слабость, учащенное/замедленное/нерегулярное сердцебиение.

Очень серьезная аллергическая реакция на этот препарат встречается редко. Однако немедленно обратитесь за медицинской помощью, если заметите какие-либо симптомы серьезной аллергической реакции, в том числе: сыпь, зуд/отек (особенно лица/языка/горла), сильное головокружение, затрудненное дыхание.

Это не полный список возможных побочных эффектов. Если вы заметили другие эффекты, не перечисленные выше, обратитесь к врачу или фармацевту.

В США: позвоните своему врачу, чтобы получить медицинскую консультацию о побочных эффектах. Вы можете сообщить о побочных эффектах в FDA по телефону 1-800-FDA-1088 или на сайте www.fda.gov/medwatch.

В Канаде: позвоните своему врачу, чтобы узнать о побочных эффектах. Вы можете сообщить о побочных эффектах в Министерство здравоохранения Канады по телефону 1-866-234-2345.

Меры предосторожности

Прежде чем принимать это лекарство, сообщите своему врачу или фармацевту, если у вас аллергия на него; или если у вас есть какие-либо другие аллергии. Этот продукт может содержать неактивные ингредиенты, которые могут вызывать аллергические реакции или другие проблемы. Поговорите с вашим фармацевт для получения более подробной информации.

Перед использованием этого лекарства сообщите своему врачу или фармацевту свою историю болезни, особенно о: проблемах с дыханием (таких как астма, эмфизема), диабете, определенных проблемах с глазами (глаукома), проблемах с сердцем, высоком кровяном давлении, проблемах с почками, гиперактивности. щитовидная железа (гипертиреоз), проблемы с мочеиспусканием (например, из-за увеличения простаты).

Этот препарат может вызвать у вас головокружение. Алкоголь или марихуана (марихуана) могут усилить головокружение. Не садитесь за руль, не пользуйтесь механизмами и не делайте ничего, что требует бдительности, пока вы не сможете делать это безопасно. Ограничьте алкогольные напитки. Поговорите со своим врачом, если вы употребляете марихуану (каннабис).

Жидкие препараты этого продукта могут содержать сахар, аспартам и/или спирт.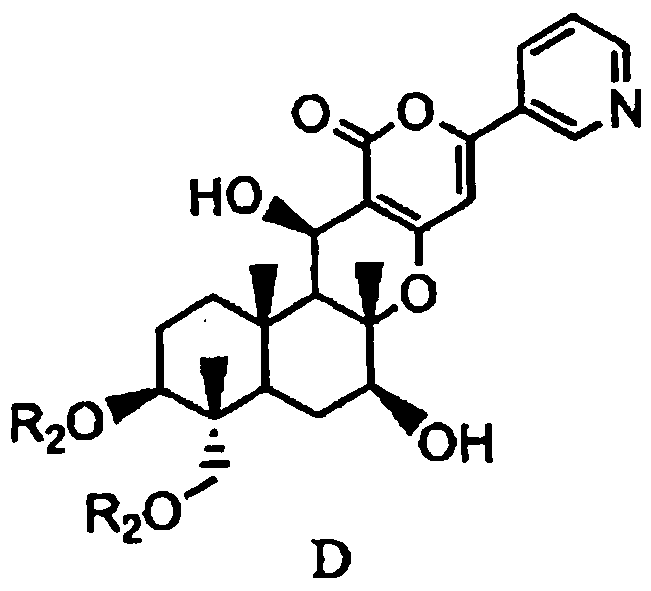 Рекомендуется соблюдать осторожность, если у вас диабет, алкогольная зависимость, заболевание печени, фенилкетонурия (ФКУ) или любое другое состояние, которое требует от вас ограничения/избегания этих веществ в вашем рационе. Спросите своего врача или фармацевта о безопасном использовании этого продукта.

Пожилые люди могут быть более чувствительны к побочным эффектам этого препарата, особенно к головокружению, затрудненному мочеиспусканию, учащенному/нерегулярному сердцебиению, проблемам со сном, спутанности сознания или изменениям психики/настроения.

Во время беременности это лекарство следует использовать только в случае крайней необходимости. Обсудите риски и преимущества с вашим врачом.

Это лекарство может проникать в грудное молоко. Перед кормлением грудью проконсультируйтесь с врачом.

Взаимодействия

Взаимодействия с лекарствами могут изменить действие ваших лекарств или увеличить риск серьезных побочных эффектов. Этот документ не содержит всех возможных лекарственных взаимодействий. Составьте список всех продуктов, которые вы используете (включая рецептурные и безрецептурные препараты и растительные продукты), и поделитесь им со своим врачом и фармацевтом. Не начинайте, не останавливайте и не изменяйте дозировку любых лекарств без разрешения врача.

Прием некоторых ингибиторов МАО с этим лекарством может вызвать серьезное (возможно, смертельное) взаимодействие с лекарственными средствами. Избегайте приема изокарбоксазида, метаксалона, метиленового синего, моклобемида, фенелзина, прокарбазина, разагилина, сафинамида, селегилина или транилципромина во время лечения этим лекарством. Большинство ингибиторов МАО также не следует принимать за две недели до лечения этим препаратом. Спросите своего врача, когда начинать или прекращать прием этого лекарства.

Некоторые продукты, которые могут взаимодействовать с этим препаратом: бета-блокаторы (такие как метопролол, атенолол), гуанетидин, некоторые ингаляционные анестетики (такие как галотан), метилдопа, ролапитант, трициклические антидепрессанты (такие как амитриптилин, дезипрамин).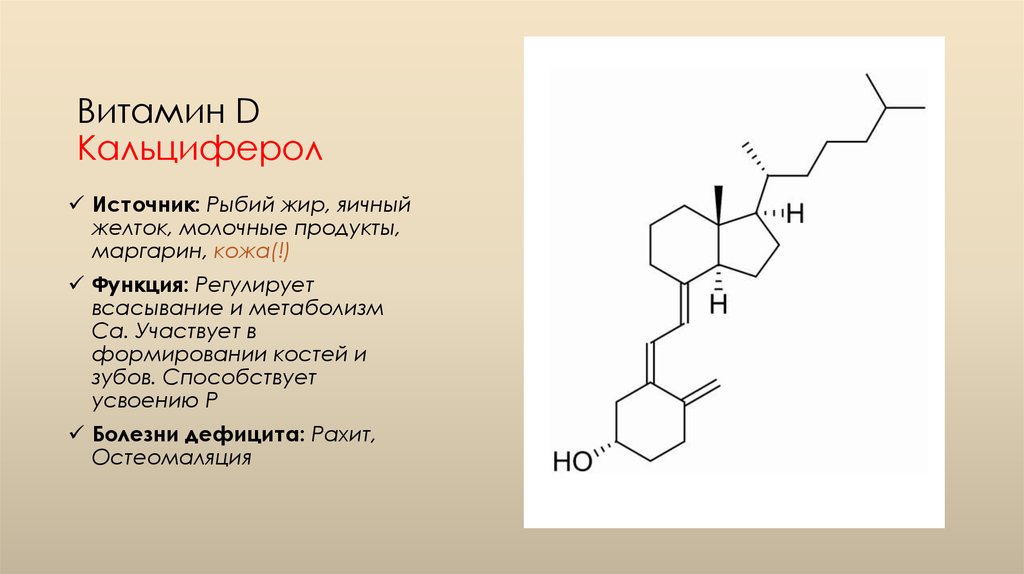

Гвайфенезин доступен как по рецепту, так и без рецепта. Внимательно проверьте этикетки на всех ваших лекарствах, чтобы убедиться, что вы не принимаете более одного продукта, содержащего гвайфенезин.

Проверьте этикетки на всех ваших лекарствах (таких как средства от кашля и простуды, диетические средства), поскольку они могут содержать ингредиенты, которые могут увеличить частоту сердечных сокращений или кровяное давление. Спросите своего фармацевта о безопасном использовании этих продуктов.

Это лекарство может мешать некоторым медицинским/лабораторным тестам (включая уровни 5-HIAA/VMA в моче, сканирование мозга на предмет болезни Паркинсона), что может привести к ложным результатам тестов. Убедитесь, что персонал лаборатории и все ваши врачи знают, что вы принимаете этот препарат.

Взаимодействует ли Formula D Liquid с другими препаратами, которые вы принимаете?

Введите свое лекарство в средство проверки взаимодействия WebMD

Передозировка

Если у кого-то произошла передозировка и появились серьезные симптомы, такие как потеря сознания или затрудненное дыхание, позвоните по номеру 911. В противном случае немедленно позвоните в токсикологический центр. Жители США могут позвонить в местный токсикологический центр по телефону 1-800-222-1222. Жители Канады могут позвонить в провинциальный токсикологический центр. Симптомы передозировки могут включать: возбуждение, спутанность сознания, галлюцинации, судороги.

Если ваш врач прописал это лекарство, не делитесь им с другими.

Посещайте все регулярные медицинские и лабораторные осмотры.

Если вам прописали это лекарство по регулярному графику и вы пропустили дозу, примите его, как только вспомните. Если приближается время приема следующей дозы, пропустите пропущенную дозу. Примите следующую дозу в обычное время. Не удваивайте дозу, чтобы наверстать упущенное.

Хранить при комнатной температуре вдали от света и влаги. Не хранить в ванной. Не замораживайте жидкие формы этого лекарства. Держите все лекарства подальше от детей и домашних животных.

Не смывайте лекарства в унитаз и не выливайте их в канализацию, если это не предписано. Правильно утилизируйте этот продукт, когда он просрочен или больше не нужен. Проконсультируйтесь с вашим фармацевтом или местной компанией по утилизации отходов.

Изображения

Далее

Ссылки по теме

Обзор препаратов

Вы когда-нибудь покупали жидкость Formula D?

Да, за последние 3 месяца

Да, за последние 6 месяцев

Да, за последний год

Не покупал, но рассматриваю

Не планирую покупать

Этот опрос проводится отделом маркетинговых исследований WebMD.

Купон на бесплатный RX

Сэкономьте до 80% на рецептах.

Доступные купоны

Сэкономьте до 80% на своем рецепте с помощью WebMDRx

Выбрано из данных, включенных с разрешения и защищенных авторским правом First Databank, Inc. Этот материал, защищенный авторским правом, был загружен из лицензированного поставщика данных и не предназначен для распространения. , за исключением случаев, когда это разрешено применимыми условиями использования.