Ряд из фишек домино и тримино
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Жарова Д.С. 1
1Гимназия №30 г. Петрозаводск
Ильящук В.А. 1
1Гимназия №30 г. Петрозаводск
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Находясь летом на даче, наша семья очень любит играть в различные настольные игры. Они позволяют не только скоротать и весело провести время в кругу семьи, но и развивают мыслительные способности. Одной из таких игр является игра «Домино».
Стандартный набор домино включает в себя 28 костяшек, каждая из которых представляет собой прямоугольную плитку.
Этим летом нашей семье подарили разновидность этой игры под названием «Тримино». Костяшки в этой игре представлены в треугольной форме, в углах которой проставлены цифры от 0 до 5. Одна костяшка ставится к другой своей гранью так, чтобы каждая и двух цифр данной грани соответствовала такой же цифре соседней костяшки.
Играя в эту игру, меня заинтересовал вопрос, а можно ли используя все фишки тримино или домино, выложить их в один ряд? Это и стало целью моей исследовательской работы.
Цели исследования: выяснить, можно ли из всех фишек стандартного набора домино и тримино выложить одну линию.
Задачи исследования:
Изучить литературу и ресурсы Интернет по теме исследованияПопытаться составить линию из фишек игр домино и тримино
Объяснить причину невозможности составления ряда из определенных наборов фишек
Выяснить, какое минимальное количество фишек нужно убрать при невозможности составления ряда.
Гипотеза
Из всех фишек игр тримино и домино можно составить одну линию
Объект исследования: игры домино и тримино
Предмет исследования: применение теории графов для составлениялинии из фишек игр домино и тримино
Нахождение информации в Интернете и литературных источниках
Использование теории графов в решении задач исследования
Эксперимент
Теоретическая часть
Домино́ — настольная игра, в процессе которой выстраивается цепь костяшек («костей», «камней»), соприкасающихся половинками с одинаковым количеством точек, обозначающим число очков.
Тримино (треугольное домино) — настольная игра, состоящая из 56 костяшек домино треугольной формы. В углах костяшек выписаны цифры от 0 до 5, которые идут в возрастающем порядке по часовой стрелке, и все костяшки разные.
В углах костяшек выписаны цифры от 0 до 5, которые идут в возрастающем порядке по часовой стрелке, и все костяшки разные.
Граф
– система объектов (вершин) и связок (рёбер), соединяющих некоторые пары этих объектов.Связный граф – граф, у которого каждая вершина имеет минимум одну связь.
Путь в графе — последовательность вершин, в которой каждая вершина соединена со следующим ребром
Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечётной степени. Узнав всю необходимую информацию, я перешла к практической части своего исследования.
Четная вершина графа – вершина, из которой исходит четное количество связей.
Нечетная вершина графа
Практическая часть
Ряд из фишек домино
Для начала я решила составлять линии из фишек домино, так как они имеют более простую форму связей. При этом я рассматривала наборы последовательно, начиная с 0 – 1 до 0 – 6.
Первыми я взяла фишки, содержащие числовые значения равные только 0 и 1. Без особого труда я составила ряд. Тоже самое произошло и с набором фишек от 0 до 2
Пробуя экспериментальным путем, составить линию из набора фишек от 0 до 3, я столкнулась с тем, что ряд у меня не получался. Тогда я обратилась к теории графов. Составим графы для наборов 0 – 1 и 0 – 2. В вершины этого графа мы поместим значения, которые могут располагаться на фишке домино, а линии (связи) показывают сами фишки домино.
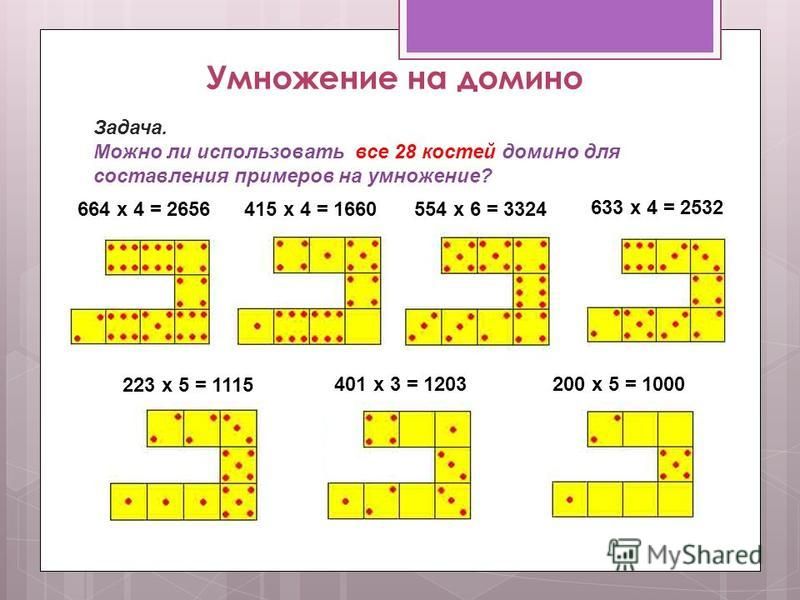
Теперь обратим внимание на граф, составленный для набора фишек от 0 до 3. Все вершины (их 4) имеют нечётное количество связей, а это значит, что пройти по данному графу одним путем невозможно. Поэтому и фишки домино данного набора нельзя выстроить в одну цепочку. Если мы уберем из набора одну фишку, то количество вершин с нечетной степенью станет ровно 2, поэтому обход нужно начинать с одной из них. На фотографии представлен такой ряд.
У графа из набора с числовыми значениями от 0 до 4 все вершины имеют четную степень, поэтому ряд можно построить, начиная из любой фишки.
Составим граф для ряда с числовыми значениями от 0 до 5. Данный граф имеет все вершины с нечётным количеством связей, поэтому ряд из фишек домино данного набора построить нельзя, но если мы уберем из графа две связи (эти связи не должны быть из одной вершины), то количество вершин с нечетными степенями станет ровно 2 и обход такого графа возможен. В моем примере я убрала связи 0-5 и 3-4, тогда обход нужно начинать или из 1, или из 2. Пример такого ряда на рисунке.
Граф для ряда с числовыми значениями от 0 до 6 имеет 0 вершин с нечётным количеством связей, поэтому ряд можно построить. Начинать обход такого графа возможно из любой вершины, а значит и ряд из фишек домино можно составлять из любого значения.
Вывод: используя полный набор фишек домино, можно их выстроить в один ряд.
Ряд из фишек тримино
Далее я перешла к составлению рядов из фишек игры тримино. По аналогии с фишками домино, будем составлять графы для каждого набора по отдельности. Вершинами такого графа будут не значения, а сами фишки, т.к. каждая фишка имеет один вход и два выхода.
Рассмотрим граф для фишек из набора от 0 до 1, т.е. только те фишки, у которых имеются только цифры 0 или 1. Таких фишек ровно 4. Количество вершин с нечетными степенями в таком графе ровно 2, поэтому составить ряд было довольно легко.
Граф для ряда с числовыми значениями от 0 до 2 не имеет вершин с нечётным количеством связей, поэтому ряд можно построить.
У графа из набора фишек с числовыми значениями от 0 до 3 имеется 8 вершин с нечётным количеством связей, поэтому ряд из этих фишек построить нельзя. При этом нечетные степени имеют фишки, на которых либо все три цифры одинаковые, либо все три цифры различные. При составлении такого ряда у меня получилось убрать 5 фишек, но я пока не могу утверждать, что это количество минимальное.
При составлении такого ряда у меня получилось убрать 5 фишек, но я пока не могу утверждать, что это количество минимальное.
Граф для ряда с числовыми значениями от 0 до 4 имеет 0 вершин с нечётным количеством связей, но несмотря на это, у меня не получилось построить ряд. Чтобы ряд получился, мне пришлось убрать 9 фишек. И опять я не могу утверждать, что это количество минимальное.
Я попыталась найти ответ на вопрос, почему у меня это не получилось. Мое объяснение следующее: фишка тримино в отличие от фишки домино имеет 2 выхода, поэтому продолжать ряд можно не только вдоль одной прямой, но и повернув этот ряд. Я попробовала это сделать и у меня получилось.
Рассматривая граф для полного набора фишек тримино (от 0 до 5), можно заметить, что он повторяет ситуацию набора фишек от 0 до 3. Только 30 вершин будут иметь четную степень, остальные 26 – нечетную. По-прежнему нечетную степень будут иметь вершины, где все цифры одинаковые или все цифры разные.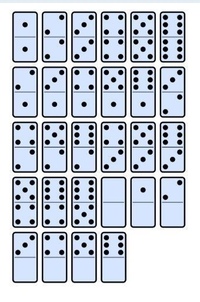 А это значит, что ряд составить нельзя. Для этой ситуации также я пока не знаю ответа на вопрос, какое минимальное количество фишек нужно убрать, чтобы получился ряд.
А это значит, что ряд составить нельзя. Для этой ситуации также я пока не знаю ответа на вопрос, какое минимальное количество фишек нужно убрать, чтобы получился ряд.
В ходе выполнения данной работы я познакомилась новым для меня разделом математики – теорией графов. Этот раздел не изучается в школьном курсе математики. Я узнала, что с помощью построения графов можно решать достаточно большое количество задач.
Составляя графы и выстраивая ряды из фишек домино и тримино, я познакомилась с эйлеровым путем в графе и узнала, что обойти граф можно только в том случае, если все вершины у графа четные или количество нечетных вершин равно 2. В первом случае обход можно начинать с любой вершины, а во втором случае – только с вершины с нечетной степенью. Данная теория полностью нашла подтверждение в моей работе.
Гипотеза, выдвинутая в начале работы, частично подтвердилась. Из полного набора фишек домино можно составить ряд, а из полного набора фишек тримино – нет. Это объясняется тем, что при составлении графа для полного набора количество вершин с нечетными степенями больше двух.
Из полного набора фишек домино можно составить ряд, а из полного набора фишек тримино – нет. Это объясняется тем, что при составлении графа для полного набора количество вершин с нечетными степенями больше двух.
На данный момент я продолжаю своё исследование. Я хочу понять, как можно вычислить минимальное количество фишек, которые нужно убрать при составлении ряда из некоторых наборов фишек.
Кроме этого в процессе игры в тримино я заметила, что фишки выстраиваются не только в ряд, но и из них можно получать некоторые фигуры. На рисунке представлены фигуры, которые получились у меня. В дальнейшем я хочу узнать, можно ли составить из всех фишек игры тримино одну сплошную фигуру. Если нет, то какое максимальное количество фишек я могу для этого использовать.
Список литературы и интернет источников
Гарднер М. Лучшие математические игры и головоломки, или самый настоящий математический цирк/ М. Гарднер; пер. с англ. М.И. Антипина. – М.: АСТ, Астрель, 2009. 255 с.
Гарднер; пер. с англ. М.И. Антипина. – М.: АСТ, Астрель, 2009. 255 с.
Мельников О.И. Теория графов в занимательных задачах. Изд.3, испр. и доп. 2009. 232 с.
Оре О. Графы и их применение: Пер. с англ. 1965. 176 с.
https://ru.wikipedia.org/wiki/Домино
http://cyclowiki.org/wiki/Треугольное_домино
https://function-x.ru/graphs1_relations.html
https://ru.wikipedia.org/wiki/Эйлеров_цикл
Просмотров работы: 419
Правила игры в домино козел
Научится играть в классическое домино козёл не так уж и сложно, как это может показаться. Всё что нужно сделать так это подробно прочитать правила игры для начинающих что здесь написаны. Инструкция с правилами проиллюстрирована фото-примерами, так правила намного легче воспринимать. После прочтения этой статьи у вас не будет возникать вопроса «Как играть в настольное домино?»
Сколько должно быть костей в наборе домино
Количество костей в одном наборе домино должно быть 28 штук. В китайских домино костей больше, а в классическом домино в коробке ровно 28 штук костяшек.
В китайских домино костей больше, а в классическом домино в коробке ровно 28 штук костяшек.
Играть на весь экран с компьютером
Играть с живым человеком
Скачать эту игру на компьютер
Скачать на Андроид (телефон, планшет)
Скачать на iPhone, iPad
Кстати, многие ошибочно спрашивают сколько в комплекте фишек, доминошек, правильно называть кости, камни или просто домино.
Дубли в домино — это парные кости с одинаковыми числами точек с обоих сторон, в наборе с 28 костей дублей должно быть 7 штук: 0–0, 1–1, 2–2, 3–3, 4–4, 5–5, 6–6. Сколько дублей в домино — 7 штук.
Как играть в домино козёл
Мы разобрались что такое дубли в домино и сколько всего должно быть костяшек для игры в «Козла» (28 штук). Приступаем непосредственно к тому как нужно играть в домино козёл.
1 Перемешиваем кости
Высыпаем кости на стол так чтобы очки (точки) на костях не было видно. Хорошенько перемешиваем кости, теперь эта куча камней называется «Базар».
2 Берем домино
Дальше игроки по очереди берут кости с Базара, нужно брать так чтобы другие игроки не увидели числа (точки) на твоих домино.
По сколько домино раздавать на игрока?
Зависит от того сколько будет играть людей, максимум можно 4 игрока.
- 2 игрока — берут по 7 костей каждый;
- 3–4 игрока — берут по 5 костей каждый;
Базар — это закрытые лишние домино что остались после того как все игроки взяли в руки домино. Когда нечем ходить, игроки с Базара добирают домино.
После того как все взяли в руки домино, начинается игра.
3 Первый ход
Первый камень на центр стола кладет игрок, у которого в руке есть дубль с меньшим количеством очков, 0–0, 1–1, 2–2 и так далее. Если ни у кого нет дублей, ставится простая кость с меньшим количество очков, например, 0–1, 0–2 и так далее.
На примере, у двух игроков самой меньшой костью за количеством очков оказалось 2-2.
4 Второй ход
После первого игрока остальные кладут по очереди свои кости. Если у игрока есть несколько вариантов домино для ходьбы, например, 2-6 и 2-3, он сам решает какую кость класть. На примере второй игрок походил камнем 2-6.
5 Что делать когда нечем ходить?
Твоя очередь класть кость на стол, а у тебя на руках нет подходящего домино. Тогда игрок ищет на «Базаре» подходящие домино. Каждый открытый камень с «Базара» игрок берет себе в руку.
5 Конец игры
Игра заканчивается когда у одного из игроков закончатся кости или когда получается «Рыба». Все остальные игроки с костями на руках начинают подсчитывать очки.
Подсчет очков
Перед началом игры игроки договариваются до какой суммы очков они будут играть в домино, например, 300 очков. Это значит что победит тот, кто наберет первым 300 очков. После каждой сыгранной партии победителю записываются очки с камней что остались на руках у проигравших игроков.
Какая кость сколько дает очков?
- Пустышка или пусто-пусто (0–0) — считают за 25 очков;
- Кость 6–6 — считают за 50 очков;
- Все остальные камни дают сколько очков, сколько на них точек. Например, кость 1–4 — это 5 очков, кость 6–4 — это 10 очков, 3–5 — это 8 очков и т.
 д.
д.
Что означает рыба в домино?
Иногда в домино складывается такая ситуация что не у кого из игроков на руках нет камня который можно поставить для продолжения игры и на Базаре закончились кости для подбора, такую ситуацию называют Рыбой в домино.
Рыбу не стоит считать ничьей. Когда настает рыба, побеждает в партии тот игрок, у которого на руках после подсчета оказалось меньше всего очков.
Что такое пустышка и пусто пусто в домино?
Ноль, пустышка, пусто, лысый, голый так называют камень 0-0, это кость на которой нет очков (точек).
Если ты дошел до этой части статьи, значит ты прочитал все правила как играть в настольное домино. Чтобы закрепить и понять все что написано в этой статье, попробуй поиграть в домино что находятся внизу. И запомни никогда не говори фишки, правильно будет кости, камни или доминошки 🙂
Правила домино — The Regency Chess Company, лучший интернет-магазин шахмат
Главная › Правила домино
Благодаря очень простой настройке и набору правил домино, возможно, является самой интуитивно понятной игрой для игры на достаточно большой поверхности и поэтому стало популярным во всем мире. В зависимости от варианта существует определенное количество плиток одинаковой формы с двумя наборами точек, представляющих целые числа. Самая простая из этих разновидностей — игра «блок», в которую играют сетом «двойная шестерка».
В зависимости от варианта существует определенное количество плиток одинаковой формы с двумя наборами точек, представляющих целые числа. Самая простая из этих разновидностей — игра «блок», в которую играют сетом «двойная шестерка».
Обычно в эту игру играют две пары игроков. Есть 28 костяшек домино: по одной на каждую возможную пару целых чисел от нуля до шести, включая двойные. Как правило, в наборе «двойное n» есть одна плитка на пару целых чисел между нулем и n.
Каждый игрок берет шесть тайлов из центральной колоды тайлов лицевой стороной вниз. Те тайлы, которые остались невыбранными, остаются вне игры и называются «спящими» тайлами. Самая высокая двойная комбинация разыгрывается той рукой, в которой она находится, начиная цепочку из костяшек домино изначально длиной один. Каждый игрок переходит к:
- поместите двойную плитку, известную как «дуплет», перпендикулярно соответствующему номеру на любом конце цепочки или;
- поместите недвойную плитку концом к соответствующему номеру на любом конце цепочки, или;
- стучите, чтобы указать, что ни один ход не может быть сыгран.

Например, при наличии в игре тайла три/пять, тайл два/три можно разыграть тремя различными способами, каждый из которых имеет одинаковый эффект.
Это продолжается до тех пор, пока:
- один игрок не сбросит фишки, сыграв последнее оставшееся домино (или в более строгом формате, пока не сбросятся оба игрока из пары), или;
- никто не может продвинуться вперед, и та пара, у которой наименьшая общая сумма на своих костяшках домино, побеждает в своего рода патовой ситуации.
Как вести счет в домино
В конце игры очки начисляются выигравшей паре. Для этого существует множество популярных способов:
- победившей паре начисляется очко за игру;
- победители набирают количество очков, равное сумме оставшихся доминошек соперников. В этом варианте игры повторяются до тех пор, пока пара не наберет 100 очков или, как некоторые предпочитают, 121 очко;
- в случае пата, победителям присуждается количество очков, равное разнице между тайлами соперника и их собственными.

Существуют бесконечные популярные модификации этих правил; например, существует любое количество комбинаций количества игроков и количества домино, данного каждому, в зависимости от присутствующих игроков и доступных ресурсов.
Более интересным изменением является игра в ничью. Каждый игрок берет меньшее количество плиток, возможно, каждый играет индивидуально. Когда игрок не может продолжить, он убирает одну плитку из стопки лицевой стороной вниз в центре до тех пор, пока не будут взяты все плитки, после чего их ход пропускается. Когда все плитки в игре, можно наслаждаться игрой с большей уверенностью.
Кросс-домино
Кросс-домино — это вариант, который следует традиционному формату, но более двухмерный. Первоначальная двойная фигура, изначально сыгранная как в обычной игре, должна иметь по одной костяшке домино на каждой из ее четырех сторон, прежде чем игра может продолжаться обычным образом. При необходимости для облегчения этого из стопки берутся плитки, после чего есть четыре конца, на которые можно положить домино.
С более крупными наборами, например с двойными девятью наборами, это может быть распространено на еще более крупные деревья, где каждый дублет расположен перпендикулярно, из которого формируются две новые цепочки. Это известно как домино «двойная девятка» и приводит к сложным, компактно разветвленным деревьям.
Все пятерки
Наряду с обычными и понятными способами подсчета очков в выигранных играх существует более уникальная арифметика, в которой очки начисляются в виде нескольких пятерок в системе, известной как все пятерки. Кроме того, очки начисляются как на протяжении всей игры, так и в конце:
- всякий раз, когда игрок кладет плитку на одном конце, так что сумма очков на обоих концах кратна пяти, это число добавляется к его счету. где:
- У недуплетов внешняя половина плитки определяется как конец;
- Дублеты, сыгранные крест-накрест, имеют обе половины, так что, например, двойная четверка на одном конце и одинарная двойка на другом считаются за десять
- всякий раз, когда игрок играет таким образом, но не записывает свой добавленный счет, ближайший к нему игрок может вместо этого потребовать очки, объявив «маггинс»;
- каждый проигравший игрок берет разницу между своим счетом и счетом победителя в конце, округляет ее до пяти и присуждает победителю: то есть итоговые очки представляют собой сумму округленных разностей.

В эту игру чаще всего играют до 100.
Дальнейшая адаптация играет таким же образом, но в отношении кратных трем, а также кратных пяти. Напрямую это называется все пятерки и тройки.
Доминирование домино — H.O.M.E.
Домино — классическая игра, которой люди всех возрастов пользуются уже сотни лет. Это игра, которую легко освоить, но может быть сложно освоить. В игре используется набор прямоугольных плиток, известных как домино. Каждая плитка имеет две стороны, и каждая сторона отмечена определенным количеством точек. Пятна на плитках обычно располагаются по схеме, похожей на пятна на шестигранной игральной кости.
Существует множество различных наборов домино с разным количеством плиток. Наиболее распространенным набором является набор «двойная шестерка», который содержит 28 плиток. Этот набор состоит из семи двойных и 21 одинарного. Двойные плитки — это плитки с одинаковым количеством точек на каждой стороне, а одинарные — с разным количеством точек на каждой стороне.
Цифры на плитках варьируются от нуля (или пробела) до шести. На пустых плитках нет пятен, и они используются для заполнения промежутков между плитками. Набор «двойная шестерка» — самый легкий доступный набор домино, и его часто используют новички.
Для более опытных игроков доступны более крупные наборы. Набор двойной девятки содержит 55 плиток, а набор двойной двенадцати содержит 91 плитку. Набор «двойная двенадцать» — самый тяжелый из доступных наборов домино, и он часто используется в профессиональных турнирах.
В наборе «двойной-двенадцать» тринадцать мастей, каждая из которых состоит из тринадцати членов. Масти пустые, один, два, три, четыре, пять, шесть, семь, восемь, девять, десять, одиннадцать и двенадцать. Каждая масть содержит одну плитку с каждой возможной комбинацией точек. Например, масть шестерок содержит плитки с шестью точками на одной стороне и нулем точек на другой, шестью точками на одной стороне и одной точкой на другой, шестью точками на одной стороне и двумя точками на другой, и так далее. до шести точек с одной стороны и шести точек с другой.
до шести точек с одной стороны и шести точек с другой.
В домино можно играть по-разному, с разными правилами и вариациями. Некоторые популярные игры включают Draw, Block, Mexican Train и All Fives. Каждая игра имеет свой собственный набор правил и стратегий, и игроки должны использовать свои навыки и рассудительность, чтобы перехитрить своих противников.
Домино — классическая игра, которой люди всех возрастов наслаждались на протяжении веков. В нее играют с набором прямоугольных плиток, каждая из которых имеет две стороны, отмеченные определенным количеством точек. Наиболее распространенным набором является набор «двойная шестерка», который содержит 28 плиток. Для более опытных игроков доступны более крупные наборы, такие как набор «двойная девятка» и «двойной набор двенадцать». Независимо от используемого набора, домино — это игра, для победы в которой требуются навыки, стратегия и немного удачи.
Количество домино в наборе
Домино — популярная игра, в которую играют во всем мире. Они бывают разных наборов, но наиболее распространенным является набор «двойная шестерка», который содержит 28 костяшек домино. Возникает вопрос, почему в наборе ровно 28 костяшек?
Они бывают разных наборов, но наиболее распространенным является набор «двойная шестерка», который содержит 28 костяшек домино. Возникает вопрос, почему в наборе ровно 28 костяшек?
Во-первых, каждая костяшка домино представляет собой прямоугольную плитку с двумя половинками, разделенными центральной линией или «полосой». Каждая половина плитки содержит определенное количество точек, от нуля до шести. Пятна на одной половине плитки называются «пипсами», а другая половина остается пустой.
Во-вторых, очки на домино расположены так же, как и на шестигранных костях. Однако, поскольку используются глухие концы без пятен, возможны семь граней. Таким образом, набор костяшек домино «двойная шестерка» содержит все уникальные комбинации ячеек от нуля до шести на каждой половине, в результате чего всего получается 28 частей.
Чтобы уточнить, вот список из 28 различных костяшек домино в наборе «двойная шестерка»:
– 0-0
– 0-1
– 0-2
– 0-3
– 0-4
– 0 -5
– 0-6
– 1-1
– 1-2
– 1-3
– 1-4
– 1-5
– 1-6
– 2-2
– 2-3
– 2-4
– 2-5
– 2-6
– 3-3
– 3-4
– 3-5
– 3-6
– 4-4
– 4-5
– 4-6
– 5-5
– 5-6
– 6-6
Причина, по которой в наборе «двойная шестерка» 28 костяшек домино, заключается в том, что он содержит все уникальные комбинации ячеек от нуля до шести на каждой половине, что в сумме дает 28 костяшек.
Источник: orientaltrading.com
Количество костяшек домино для начала
Играя в домино, важно начать с правильного количества костей. Каждый игрок должен начать с 6 костяшек домино, которые он вытягивает из перетасованной стопки костей. Эти плитки обычно сделаны из кости или пластика и имеют разное количество точек на каждом конце. Количество точек на каждом конце плитки указывает на ее значение или «количество пунктов».
Начиная с 6 костяшек домино, игроки могут размещать на доске различные плитки, что дает им больше возможностей для стратегического геймплея. Это также гарантирует, что у каждого игрока равные шансы на победу, поскольку все они начинают с одинакового количества плиток.
Важно отметить, что для некоторых вариантов домино может потребоваться разное количество плиток для начала. Однако в наиболее распространенной версии игры каждый игрок должен начинать с 6 костяшек домино, чтобы обеспечить честную и приятную игру.
Количество костей домино в наборе из 12 костей
Набора из 12 костей домино не существует. Тем не менее, существует тип набора домино под названием «двойное двенадцать», который содержит в общей сложности 91 домино. Этот набор является самым тяжелым из доступных наборов домино, в котором на каждой части домино есть два числа в диапазоне от 0 (или пустого) до 12. Набор разделен на тринадцать мастей, включая пустые, 1, 2, 3, 4, 5. , 6, 7, 8, 9, 10, 11 и 12, по тринадцать человек в каждой масти. Важно отметить, что набор «двойная двенадцать» — это не то же самое, что набор из 12 костяшек домино, а скорее особый тип набора домино, который содержит всего 91 элемент.
Тем не менее, существует тип набора домино под названием «двойное двенадцать», который содержит в общей сложности 91 домино. Этот набор является самым тяжелым из доступных наборов домино, в котором на каждой части домино есть два числа в диапазоне от 0 (или пустого) до 12. Набор разделен на тринадцать мастей, включая пустые, 1, 2, 3, 4, 5. , 6, 7, 8, 9, 10, 11 и 12, по тринадцать человек в каждой масти. Важно отметить, что набор «двойная двенадцать» — это не то же самое, что набор из 12 костяшек домино, а скорее особый тип набора домино, который содержит всего 91 элемент.
Количество костяшек домино в наборе из 6
Набор из 6 костяшек не является стандартным размером для костяшек домино. Стандартный размер набора домино — набор «двойная шестерка», состоящий из 28 плиток. Эти плитки имеют прямоугольную форму и размеры около 2 дюймов на 1 дюйм. Плитка изготовлена из прочных материалов, таких как дерево, пластик или слоновая кость. Каждая плитка разделена на два квадрата, или «конца», причем каждый квадрат имеет разное количество точек, или «зернышек», в диапазоне от 0 до 6.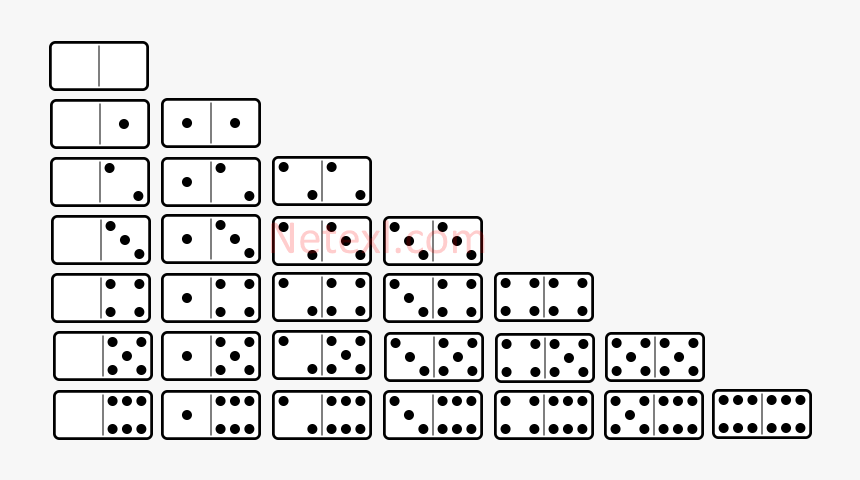

 д.
д.