Фигура с 5 углами: «Как называется фигура с пятью и шестью углами?» — Яндекс Кью

Пентагон (фигура) | это… Что такое Пентагон (фигура)?

Толкование

Пентагон (фигура)

Правильный пятиугольник

Правильный пятиугольник или пентагон (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Содержание 1 Свойства 2 Построение 3 Получение с помощью полоски бумаги 4 Интересные факты 5 См. также

Свойства

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

• Высота правильного пятиугольника:

• Площадь правильного пятиугольника:

• Радиус вписанной окружности правильного пятиугольника:

• Радиус описанной окружности правильного пятиугольника:

Построение

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

1. Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в
   C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Интересные факты

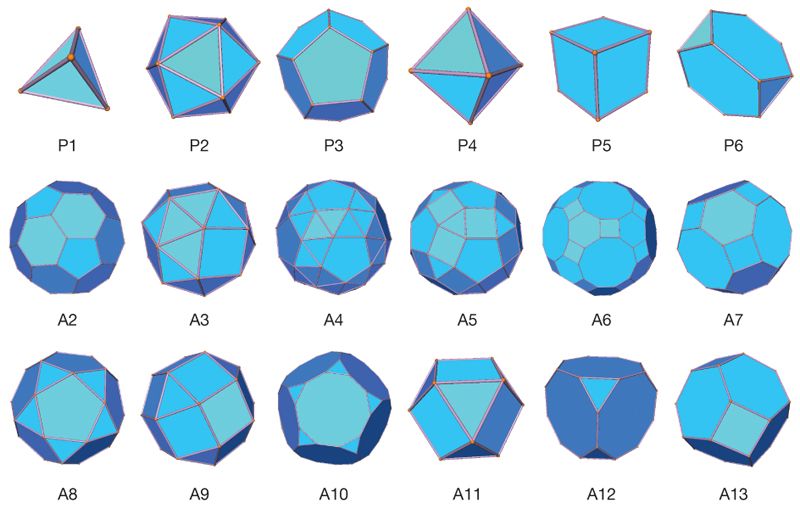
• Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.

Пентагон

• Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
• Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.

См.

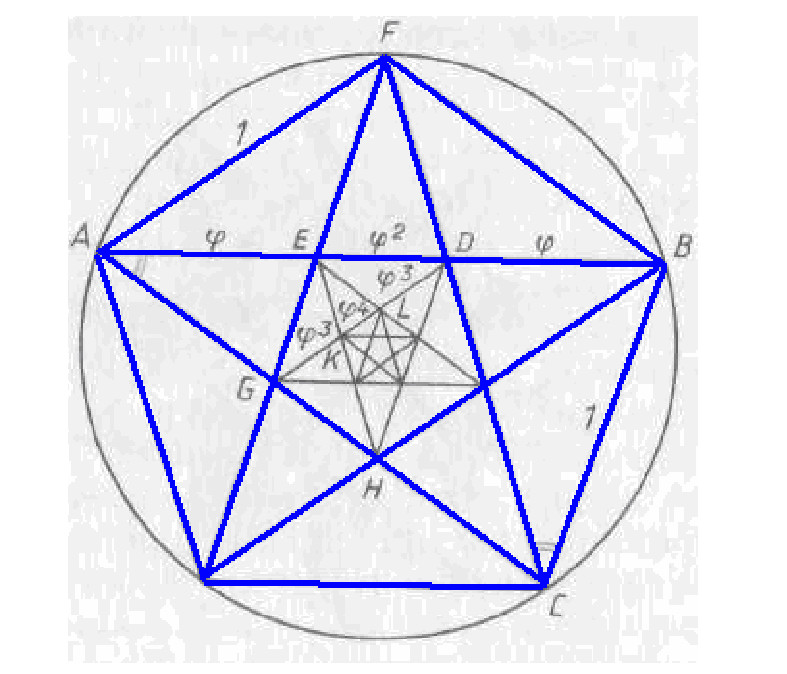
также

• Золотое сечение
• Пятиугольник
• Пентаэдр
• Пентаграмма
• Государственный Знак Качества СССР

Правильные многоугольники
Треугольник | Четырёхугольник | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Семнадцатиугольник | 257-угольник | 65537-угольник
(См. также: Многоугольник, Теорема Гаусса — Ванцеля)

Wikimedia Foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

• Пентагон (многоугольник)
• Пентадеканолид

Полезное

Пентагон (фигура) | это… Что такое Пентагон (фигура)?

Толкование

Пентагон (фигура)

Правильный пятиугольник

Правильный пятиугольник или пентагон (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Содержание 1 Свойства 2 Построение 3 Получение с помощью полоски бумаги 4 Интересные факты 5 См. также

Свойства

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

• Высота правильного пятиугольника:

• Площадь правильного пятиугольника:

• Радиус вписанной окружности правильного пятиугольника:

• Радиус описанной окружности правильного пятиугольника:

Построение

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

1. Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку
   G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Интересные факты

• Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.

Пентагон

• Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
• Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.

См.

также

• Золотое сечение
• Пятиугольник
• Пентаэдр
• Пентаграмма
• Государственный Знак Качества СССР

Правильные многоугольники
Треугольник | Четырёхугольник | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Семнадцатиугольник | 257-угольник | 65537-угольник
(См. также: Многоугольник, Теорема Гаусса — Ванцеля)

Wikimedia Foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

• Пентагон (многоугольник)
• Пентадеканолид

Полезное

Определение, форма, свойства, типы, формула и пример

Пятиугольник — это геометрическая фигура, имеющая пять сторон и пять углов. Здесь «пента» обозначает пять, а «гон» обозначает угол. Пятиугольник является одним из видов многоугольников. Сумма всех внутренних углов правильного пятиугольника равна 540 градусов.

Содержание:

• Определение
• Форма
• Правильный и неправильный пятиугольник
• Выпуклый и вогнутый пятиугольник
• Свойства
• Район
• Периметр
• Пример
• Равносторонний пятиугольник
• Циклический пятиугольник
• Часто задаваемые вопросы

В геометрии мы изучаем различные типы фигур. Двумерная форма, состоящая из прямых линий и внутренних углов, известна как многоугольник. Примеры полигонов:

• Треугольник (трехсторонний многоугольник)
• Четырехугольник (четырехсторонний многоугольник)
• Пятиугольник (пятиугольник)
• Шестиугольник (шестигранный многоугольник)
• Гептагон (семиугольник)
• Octagon (восьмиугольник) и так далее.

В этой статье вы можете подробно узнать о пятистороннем многоугольнике, называемом «пятиугольник», с правильным определением, формой, сторонами, свойствами, а также его периметром и площадью формулы пятиугольника.

Определение Пентагона

Пятиугольник – это многоугольник с 5 сторонами и 5 углами. Слово «пентагон» состоит из двух слов, а именно Penta и Gonia, что означает пять углов. Все стороны пятиугольника соединяются друг с другом, образуя фигуру. Следовательно,

Количество сторон пятиугольника = 5

Форма пятиугольника

Как и другие многоугольники, такие как треугольник, четырехугольник, квадрат, прямоугольник и т. д., пятиугольник также является многоугольником, который содержит пять сторон и пять углов.

В зависимости от сторон, углов и вершин существуют различные типы пятиугольников, например

• Правильный и неправильный пятиугольник
• Выпуклый и вогнутый пятиугольник

Правильный и неправильный пятиугольник

Если пятиугольник правильный , то все стороны равны по длине и пять углов имеют одинаковую меру. Если у пятиугольника не равные длина стороны и мера угла, то он известен как неправильный пятиугольник .

Обычный пятиугольник

Как определено выше, правильный пятиугольник содержит пять конгруэнтных сторон. Таким образом, мы можем легко найти периметр этого типа пятиугольника. Это видно из приведенного ниже рисунка.

Здесь все пять сторон равны, поэтому периметр правильного пятиугольника в пять раз больше длины любой из его сторон.

Также мы можем разделить правильный пятиугольник на пять подобных треугольников, как показано ниже.

Таким образом, мы можем сказать, что площадь правильного пятиугольника равна 5-кратной площади треугольника со сторонами, равными пятиугольнику.

Выпуклый и вогнутый пятиугольник

Если все вершины пятиугольника направлены наружу, он известен как выпуклый пятиугольник . Если у пятиугольника есть хотя бы одна вершина, указывающая внутрь, то пятиугольник известен как вогнутый пятиугольник .

Свойства Пентагона

Вот некоторые свойства пятиугольника:

• В пятиугольнике сумма внутренних углов равна 540°.
• Если все стороны равны и все углы равны, то это правильный пятиугольник. В противном случае он нерегулярен.
• В правильном пятиугольнике каждый внутренний угол равен 108°, а каждый внешний угол равен 72°.
• У равностороннего пятиугольника 5 равных сторон.
• Сумма внутренних углов прямоугольного пятиугольника равна 540°.

Площадь Пентагона

Для правильного пятиугольника со стороной и длиной апофемы формула для нахождения площади пятиугольника дается как

Площадь пятиугольника, A = (5/2) × длина стороны × квадратные единицы апофемы

Если дана только длина стороны пятиугольника, то

Площадь = 5s ² / (4 tan 36°) Квадратные единицы

Если дан только радиус пятиугольника, то

Площадь =(5/2)r ² sin 72° Квадратные единицы

Периметр Пентагона

Поскольку все стороны «а» правильного пятиугольника имеют одинаковую меру, периметр или окружность пятиугольника записывается как

.

Периметр пятиугольника, P = 5a единиц

Пентагон Решенная проблема

Вопрос:  Найдите площадь и периметр правильного пятиугольника со стороной 5 см и длиной апофемы 6 см.

Решение:

Дано:

Сторона пятиугольника, а = 5 см

Длина апофемы = 6 см

Мы знаем, что

Площадь пятиугольника, A = (5/2) × Длина стороны × Квадратные единицы Апофема

Замещающая сторона = 5 см, Апофема = 6 см в формуле,

А = (5/2) × 5 × 6

А = 5 х 5 х 3

А = 75

Следовательно, площадь пятиугольника равна 75 см ²

Периметр пятиугольника, P = 5a единиц

Р = 5(5)

П = 25 см

Следовательно, периметр пятиугольника равен 25 см.

Основываясь на свойствах пятиугольников, в геометрии существуют и другие типы пятиугольников. Они:

1. Равносторонний пятиугольник

Многоугольник с пятью сторонами одинаковой длины называется равносторонним пятиугольником. Однако все пять внутренних углов пятиугольника могут принимать различные значения. Таким образом, они позволяют ему образовывать семейство пятиугольников. Следовательно, правильный пятиугольник уникален с точностью до подобия. Потому что это равносторонний и равноугольный (поскольку его пять углов равны) пятиугольник.

2. Циклический пятиугольник

Если все вершины пятиугольника лежат на окружности, то такой пятиугольник называется вписанным. Правильный пятиугольник — лучший пример вписанного пятиугольника. Площадь циклического пятиугольника может быть представлена ​​как одна четвертая квадратного корня из одного из корней септического уравнения. Здесь коэффициенты уравнения являются функциями сторон пятиугольника. Это относится как к правильным, так и к неправильным пятиугольникам.

Линия симметрии пятиугольника:

Что касается линейной симметрии, то каждый многоугольник имеет определенное количество линий симметрии. Например, квадрат имеет 4 оси симметрии. Точно так же правильный пятиугольник имеет 5 осей симметрии.

Оставайтесь с нами с BYJU’S — обучающим приложением, чтобы изучать все интересные понятия математики, а также просматривать видео, чтобы учиться с легкостью.

Часто задаваемые вопросы о Пентагоне – Часто задаваемые вопросы

Сколько сторон у пятиугольника?

Как указано в названии, «пента» означает 5, а «гон» означает угол. Таким образом, пятиугольник имеет 5 сторон и 5 углов.

Какие бывают пятиугольники?

Различные типы пятиугольников:
Простой пятиугольник
Сложный пятиугольник
Правильный пятиугольник
Неправильный пятиугольник
Вогнутый пятиугольник
Выпуклый пятиугольник
Равносторонний пятиугольник
Циклический пятиугольник

Что такое неправильная форма?

Если пятиугольник не имеет одинаковой длины стороны и угла, то он известен как неправильный пятиугольник.

Какие есть 12 видов многоугольников?

В геометрии 12 видов многоугольников:
Треугольник (трехсторонний многоугольник)
Четырехугольник (четырехсторонний многоугольник)
Пятиугольник (пятисторонний многоугольник)
Шестиугольник (шестисторонний многоугольник)
Семиугольник (семисторонний многоугольник)
Октагон (восьмиугольник)
Нонагон (девятиугольник)
Декагон (десятиугольник)
Икосагон (двадцатиугольник)
Триаконтагон (тридцатиугольник)
Гектагон (100-угольник)
Chiliagon (многоугольник с 1000 сторонами)

Как называется фигура с 12 сторонами?

12-сторонняя фигура или двенадцатигранный многоугольник называется додекагоном. Внутренний угол правильного двенадцатиугольника равен 150 градусам.

Как называется фигура с 99 сторонами?

В геометрии эннеаконтагон, эненеконтагон или 90-угольник — это девяностоугольный многоугольник.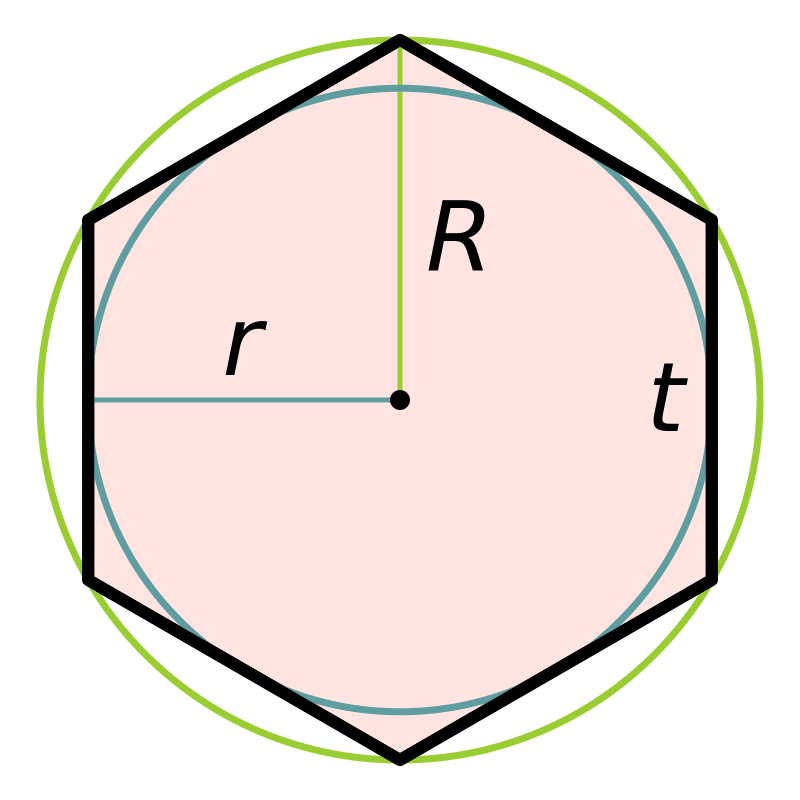 Таким образом, 99-сторонняя форма называется нонаконтакайнонагоном или эннеаконтанонагоном. Здесь эннеаконта — это префикс количества сторон, пронумерованных от 9 доот 0 до 99.

Форма пятиугольника — определение, свойства | Стороны пятиугольника

Пятиугольник представляет собой 5-сторонний многоугольник . Эта пятигранная фигура имеет пять прямых сторон и пять внутренних углов, которые в сумме составляют 540°. Давайте узнаем больше о форме пятиугольника, свойствах пятиугольника, объектах формы пятиугольника и некоторых примерах формы пятиугольника в этой статье.

1.	Что такое Пентагон?
2.	Стороны и углы пятиугольника
3.	Недвижимость Пентагона
4.	Формулы Пентагона
5.	Объекты в форме пятиугольника
6.	Типы Пентагона
7.	Часто задаваемые вопросы о Пентагоне

Что такое Пентагон?

Пятиугольник представляет собой двумерную геометрическую фигуру с пятью сторонами и пятью углами. Определение пятиугольника гласит, что это двумерный многоугольник, который имеет 5 сторон и 5 углов. Обратите внимание на приведенный ниже рисунок, на котором показана форма пятиугольника.

Стороны и углы пятиугольника

Как видно из приведенного выше рисунка, пятиугольник имеет 5 сторон и 5 внутренних углов. Слово «пентагон» происходит от греческого слова, в котором «пента» означает пять, а «гон» означает угол. Если это правильный пятиугольник, то все его стороны равны по длине, а все внутренние углы равны 108°. В случае неправильного пятиугольника внутренние углы имеют разную величину, но все они в сумме составляют 540°.

Свойства Пентагона

Ниже приведены основные свойства пятиугольника, которые помогают идентифицировать многоугольник как пятиугольник.

• Пятиугольник имеет 5 сторон и 5 углов.
• В пятиугольнике можно провести 5 диагоналей, и это можно рассчитать по формуле Диагонали пятиугольника: = n × (n − 3) ÷ 2 = 5 × (5 − 3) ÷ 2 = 5
• Сумма всех внутренних углов пятиугольника равна 540°, а сумма внешних углов пятиугольника равна 360°.
• В случае правильного пятиугольника каждый внутренний угол равен 108°, а каждый внешний угол равен 72°. Это можно рассчитать по формулам: Внутренний угол правильного пятиугольника: 540° ÷ n = 540° ÷ 5 = 108° Внешний угол правильного пятиугольника: = 360° ÷ n = 360° ÷ 5 = 72°

Формулы Пентагона

Есть много формул, связанных с пятиугольником. Несколько основных из них приведены ниже.

• Диагонали пятиугольника: = n × (n − 3) ÷ 2 = 5 × (5 − 3) ÷ 2 = 5
• Сумма внутренних углов пятиугольника: = 180° × (n − 2) = 180° × (5 − 2) = 540°
• Каждый внешний угол правильного пятиугольника: = 360° ÷ n = 360° ÷ 5 = 72°
• Каждый внутренний угол правильного пятиугольника: = 540° ÷ n = 540° ÷ 5 = 108°
• Площадь правильного пятиугольника = 1/2 × Периметр × Апофема
• Периметр Пентагона = (сторона 1 + сторона 2 + сторона 3 + сторона 4 + сторона 5)

Объекты в форме пятиугольника

Есть много объектов в форме пятиугольника, с которыми мы сталкиваемся в повседневной жизни, например, форма бамии после того, как мы ее разрезаем, симметричная морская звезда и многие другие. Обратите внимание на следующий рисунок, на котором показаны несколько примеров правильной и неправильной формы пятиугольника.

Интересные факты о форме Пентагона

• Пентагон — это штаб-квартира Министерства обороны США в Вашингтоне, округ Колумбия, пример типичной формы Пентагона.
• Президент Рузвельт решил, что во время Второй мировой войны необходимо новое здание для военного министерства.
• Интересной особенностью формы Пентагона было то, что архитектор выбрал форму Пентагона для здания, что сократило расстояние, которое люди должны были пройти от одного офиса до другого.

Типы Пентагона

Правильный пятиугольник и неправильный пятиугольник

Пятиугольник можно разделить на правильный пятиугольник и неправильный пятиугольник на основе размеров его углов и длин сторон.

• В правильном пятиугольнике все внутренние углы равны и все стороны имеют одинаковую длину.
• В неправильном пятиугольнике все внутренние углы и стороны разной величины.

Выпуклый пятиугольник и вогнутый пятиугольник

• В выпуклом пятиугольнике все внутренние углы меньше 180°, а вершины направлены наружу.
• В вогнутом пятиугольнике один или несколько внутренних углов больше 180°, а вершины направлены внутрь.

Обратите внимание на приведенный ниже рисунок, чтобы различить правильные и неправильные пятиугольники, а также два других типа пятиугольников — вогнутые пятиугольники и выпуклые пятиугольники.

☛ Похожие статьи о Пентагоне

• Углы в Пентагоне
• Район Пентагона
• Калькулятор площади пятиугольника
• Декагон
• Пятиугольная пирамида

Часто задаваемые вопросы о Пентагоне

Что такое форма пятиугольника в геометрии?

Двумерная фигура с 5 сторонами известна как пятиугольник. Мы называем его 5-сторонним многоугольником, потому что он состоит из 5 сторон и 5 углов.

Как называется пятисторонняя фигура?

Пятиугольник называется пятиугольником. Если все пять сторон равны, то мы называем его правильным пятиугольником, а если любые две стороны различны по размеру, мы называем его неправильным пятиугольником.

Является ли пятиугольник параллелограммом?

Нет, пятиугольник — это не параллелограмм, это пятиугольник. Параллелограмм имеет только четыре стороны.

В чем сходство четырехугольника и пятиугольника?

Четырехугольник и пятиугольник являются многоугольниками, сумма внешних углов которых равна 360°.

Есть ли у пятиугольника параллельные стороны?

Правильный пятиугольник не имеет параллельных линий, но неправильный пятиугольник может иметь 1 или 2 пары параллельных линий.

Сколько углов в пятиугольнике?

Пятиугольник имеет пять внутренних углов и пять соответствующих внешних углов. В случае правильного пятиугольника каждый из этих пяти внутренних углов равен 108°, а каждый из 5 внешних углов равен 72°.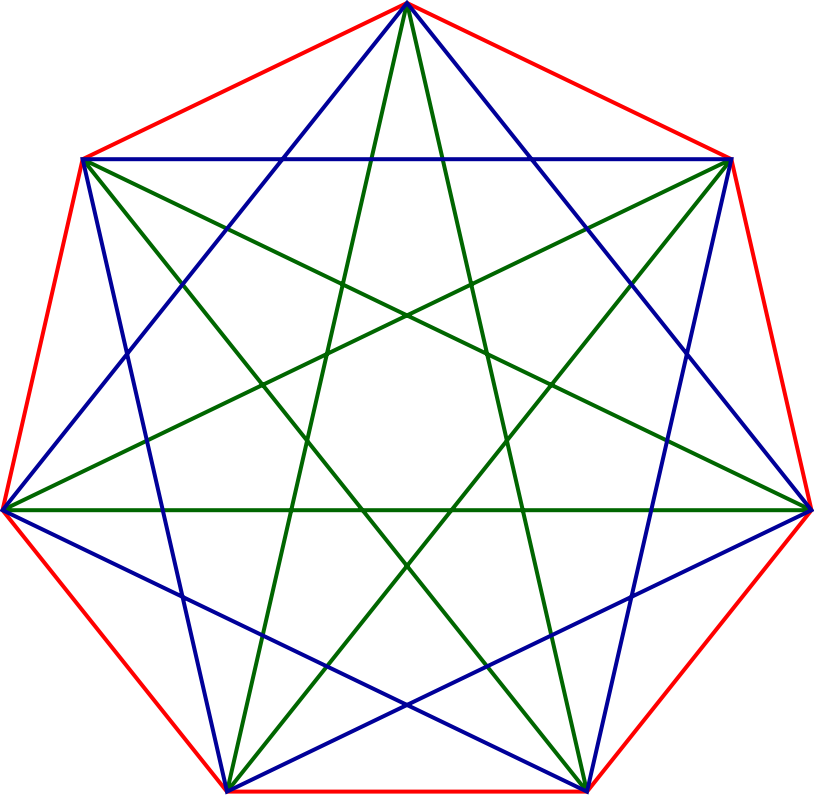

Сколько линий симметрии имеет фигура пятиугольника?

Правильный пятиугольник имеет 5 линий симметрии, тогда как неправильный пятиугольник не имеет линий симметрии.

Как найти внешний угол пятиугольника?

Каждый внешний угол правильного пятиугольника можно рассчитать по формуле 360 ÷ n, здесь n = 5, значит, 360 ÷ 5 = 72°. Следовательно, каждый внешний угол правильного пятиугольника равен 72°. В случае неправильного пятиугольника каждый внешний угол можно вычислить по значению соответствующего внутреннего угла. Так как внешний угол и внутренний угол образуют линейную пару, их сумма всегда будет 180°.

Что такое правильный пятиугольник?

Правильный пятиугольник — это пятиугольник, у которого все 5 сторон имеют одинаковую длину и все внутренние углы имеют одинаковую величину. Каждый внутренний угол правильного пятиугольника равен 108°, а каждый внешний угол правильного пятиугольника равен 72°.

Что такое свойство суммы углов Пентагона?

Свойство суммы углов многоугольника выражается с помощью формулы S = (n − 2) × 180°, где n равно количеству сторон в этом конкретном многоугольнике.