Фигура с 5 углами – Пентагон (фигура) - это... Что такое Пентагон (фигура)?

Содержание

Пентагон (фигура) — это… Что такое Пентагон (фигура)?

Пентагон (фигура)

Правильный пятиугольник

Правильный пятиугольник или пентагон (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

Высота правильного пятиугольника:

Площадь правильного пятиугольника:

Радиус вписанной окружности правильного пятиугольника:

Радиус описанной окружности правильного пятиугольника:

Построение

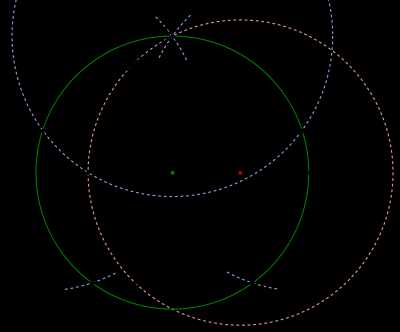
Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку
D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Интересные факты

Пентагон

Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.

См. также

Wikimedia Foundation. 2010.

Пентагон (многоугольник)
Пентадеканолид

Смотреть что такое «Пентагон (фигура)» в других словарях:

ПЕНТАГОН — (греч., от pente пять, и gonia угол). Геометрическая фигура, окруженная 5 ю сторонами и 5 ю углами: пятиугольник. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕНТАГОН греч., от pente, пять, и gonia, угол.… … Словарь иностранных слов русского языка
Пентагон — (Греч.) От pente пять , и gonia угол ; в геометрии плоская фигура с пятью углами. Источник: Теософский словарь … Религиозные термины
Пентагон-додекаэдр — Пентагондодекаэдр Индексы граней {2 1 0} Тип Неправильный многогранник Грань Неправильный пятиугольник Граней 12 Рёбер 30 Вершин 20 Граней при вершине … Википедия
Пентагон (многоугольник) — Пятиугольник многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого пятиугольника равна 540°. См.также Правильный пятиугольник Звезда (геометрическая фигура) Многоугольники … Википедия
ПЕНТАГОН — (Греч.) От pente пять , и gonia угол ; в геометрии плоская фигура с пятью углами … Теософский словарь
Пентаграмма — Пентаграмма … Википедия
Пентакль — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч. πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
Пентакл — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч. πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
Пифагорейский пентакл — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч. πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
Сатанинская звезда — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч. πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия

dic.academic.ru

Правильный пятиугольник | Формулы и расчеты онлайн

Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.

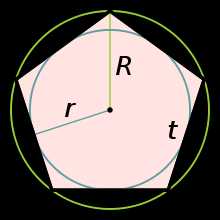
Правильный пятиугольник

Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного пятиугольника.

Обозначения на рисунке для правильного пятиугольника

n=5	число сторон и вершин правильного пятиугольника,	шт
α	центральный угол правильного пятиугольника,	радианы, °
β	половина внутреннего угла правильного пятиугольника,	радианы, °
γ	внутренний угол правильного пятиугольника,	радианы, °
a	сторона правильного пятиугольника,	м
R	радиусы правильного пятиугольника,	м
p	полупериметр правильного пятиугольника,	м
L	периметр правильного пятиугольника,	м
h	апофемы правильного пятиугольника,	м

Основные формулы для правильного пятиугольника

Периметр правильного пятиугольника

\[ L = 5a \]

Полупериметр правильного пятиугольника

\[ p = \frac{5}{2}a \]

Центральный угол правильного пятиугольника в радианах

\[ α = \frac{2}{5}π \]

Центральный угол правильного пятиугольника в градусах

\[ α = \frac{360°}{5} = 72° \]

Половина внутреннего угла правильного пятиугольника в радианах

\[ β = \frac{3}{10}π \]

Половина внутреннего угла правильного пятиугольника в градусах

\[ β = \frac{3}{10}180° = 54° \]

Внутренний угол правильного пятиугольника в радианах

\[ γ = 2β = \frac{3}{5}π \]

Внутренний угол правильного пятиугольника в градусах

\[ γ = \frac{3}{5}180° = 108° \]

Площадь правильного пятиугольника

\[ S = ph = \frac{5}{2}ha \]

Или учитывая формулу Площади правильного пятиугольника получим

\[ S = \frac{5}{2} · a · \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]

Отсюда получим апофему правильного пятиугольника

\[ h = \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]

В помощь студенту

Правильный пятиугольник	стр. 268

www.fxyz.ru

Правильный пятиугольник — Howling Pixel

Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

α=(n−2)n⋅180∘=35⋅180∘=108∘{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}

Площадь правильного пятиугольника рассчитывается по любой из формул:

S=54t2ctgπ5=55+254t2=512Rd=52R2sin⁡2π5=5r2tgπ5{\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}={\frac {5}{12}}Rd={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}},

где R{\displaystyle R} — радиус описанной окружности, r{\displaystyle r} — радиус вписанной окружности, d{\displaystyle d} — диагональ, t{\displaystyle t} — сторона.

Высота правильного пятиугольника:

h=tg72∘2t=5+252t≈1,539t{\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1{,}539t}

Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1+52{\displaystyle {\frac {1+{\sqrt {5}}}{2}}}.

t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R}

Радиус вписанной окружности:

r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t}

Радиус описанной окружности:

R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r}

d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t}

S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}}

Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)

Ss=Φ4=3Φ+2=35+72≈6,8541{\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541}

где Φ{\displaystyle \Phi } — отношение золотого сечения.

Построение

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе

Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.^[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.

Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.

Интересные факты

Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
В природе не существует кристаллов с гранями в форме правильного пятиугольника.
Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.

См. также

Примечания

↑ A one-dimensional ice structure built from pentagons. Nature Materials. 8 March 2009 (англ.)

5-ортоплекс

5-ортоплекс, или пентакросс, или триаконтадитерон, или триаконтидитерон — пятимерное геометрическое тело, правильный политоп, имеющий 10 вершин, 40 рёбер, 80 граней — правильных треугольника, 80 правильнотетраэдрических 3-гиперграней, 32 пятиячейниковых 4-гиперграней. 5-ортоплекс — это один из бесконечного множества гипероктаэдров — политопов, двойственных гиперкубам. 5-ортоплекс представляет собой пятимерную 16-ячейниковую гипербипирамиду.

5-полугиперкуб

5-полугиперкуб — это полуправильный пятимерный политоп, полученный из 5-гиперкуба (пентеракта) альтернацией (удалением чередующихся вершин). Его гиперграни — 10 16-ячейников и 16 5-ячейников. Его вершинная фигура — полностью усечённый 5-ячейник.

6-ортоплекс

6-ортоплекс, или гексакросс или гексаконтитетрапетон— шестимерное геометрическое тело, правильный шестимерный политоп, имеющий 12 вершин, 60 рёбер, 160 граней — правильных треугольника, 240 правильнотетраэдрических 3-гиперграней, 192 пятиячейниковых 4-гиперграни и 64 5-ячейки, имеющих форму правильного 5-симплекса. 6-ортоплекс — это один из бесконечного множества гипероктаэдров — политопов, двойственных гиперкубам. 6-ортоплекс — тело, двойственное гексеракту. 6-ортоплекс — 5-ортоплексовая гипербипирамида.

Гептеракт

Гептера́кт, также 7-куб или 7-гиперкуб, тетрадека-7-топ, тетрадекаэксон (тетрадекаэкзон) — аналог куба в семимерном пространстве.

Определяется как выпуклая оболочка 128 точек [±1,±1,±1,±1,±1,±1,±1]{\displaystyle [\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1]}.

Гирих (математика)

Мозаики «гирих» — это набор пяти плиток, использовавшихся для создания орнамента для украшения зданий в исламской архитектуре. Плитки использовались примерно с 12-го века и орнаменты существенно улучшились к моменту построения усыпальницы Дарб-и Имам в городе Исфахан в Иране (построена в 1453).

Пять плиток мозаики включают:

правильный десятиугольник с внутренними углами 144°;

удлиненный (неправильный выпуклый) шестиугольник с внутренними углами 72°, 144°, 144°, 72°, 144°, 144°;

галстук-бабочка (невыпуклый шестиугольник) с внутренними углами 72°, 72°, 216°, 72°, 72°, 216°;

ромб с внутренними углами 72°, 108°, 72°, 108°;

правильный пятиугольник с внутренними углами 108°.Все рёбра этих плиток имеют одну и ту же длину, а все углы кратны 36° (π/5 радиан). Четыре плитки (кроме пятиугольника) имеют двустороннюю (зеркальную) симметрию относительно двух перпендикулярных осей. Некоторые плитки имеют дополнительные симметрии. В частности, десятиугольник имеет десятикратную вращательную симметрию (вращение на 36°), а пятиугольник имеет пятикратную вращательную симметрию (вращение на 72°).

Собственно, гирих — это линии (орнамента), которым декорированы плитки. Плитки использовались для создания орнамента (гириха). На языке фарси слово گره означает «узел» . В большинстве случаев виден только гирих, (и другие украшения в виде цветов), но не границы самих плиток. Гирих является ломаными отрезками, пересекающими границы плиток по центру под углом 54° (3π/10) к ребру. Две перекрещивающиеся линии гириха пересекают каждое ребро плитки. Большинство плиток имеют единственный орнамент внутри, соответствующий симметрии плитки. Однако десятиугольник имеет два возможных орнамента гириха, один из которых имеет только пятикратную, а не десятикратную симметрию.

Десятиугольник

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.

Изотоксальная фигура

Многогранник, многоугольник или мозаика является изотоксальным или рёберно транзитивным, если его симметрии действуют транзитивно на его рёбрах. Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом.

Термин изотоксальный происходит от греческого τοξον, означающего дуга.

Многоугольник

Многоуго́льник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются.

Огранка (геометрия)

В геометрии огранка — это процесс удаления части многоугольника или многогранника без создания новых вершин.

Новые рёбра огранённого многогранника могут быть созданы вдоль диагоналей граней или внутренних диагоналей. Огранённый многогранник будет иметь две грани для каждого ребра и является новым многогранником или соединением многогранников.

Огранка является обратным или двойственным образованию звёздчатой формы. Для каждой звёздчатой формы некоторого выпуклого многогранника существует двойственная огранка двойственного многогранника.

Октеракт

Октеракт, или 8-гиперкуб, или гексадеказеттон — восьмимерный гиперкуб, аналог куба в восьмимерном пространстве. Определяется как выпуклая оболочка 256 точек [±1,±1,±1,±1,±1,±1,±1,±1]{\displaystyle [\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1]}.

Орден Нила

Орден Нила (Kiladate El Nile) — высшая государственная награда Египта.

Пентагон (значения)

Пентаго́н (от греч. πενταγωνον — пятиугольник):

Пентагон — правильный пятиугольник.

Пентагон — здание Министерства обороны США, имеющего форму правильного пятиугольника.

Пентагон — станция Вашингтонгского метро.

Пентагон (компьютер) — популярный в СССР домашний ПК, кустарный клон компьютера ZX Spectrum.

Пентагондодекаэдр

Пентаго́ндодека́эдр (от др.-греч. δωδεκάεδρον — «двенадцатигранник» и πενταγον «пятиугольник») — объёмная фигура с двенадцатью гранями в форме неправильных пятиугольников.

Пентаграмма

Пентагра́мма (пентальфа, пентагерон; греч. πεντάγραμμον от πέντε «пять» + γράμμα «черта, линия») — фигура, полученная соединением вершин правильного пятиугольника через одну; фигура, образованная совокупностью всех диагоналей правильного пятиугольника.

Пентаграмма — правильный пятиугольник, стороны которого продлены до точек пересечения, и образуют равнобедренные треугольники на его гранях, то есть — звёздчатая форма правильного пятиугольника.

Пентеракт

Пентеракт (англ. penteract) — пятимерный гиперкуб, аналог куба в пятимерном пространстве. Пентеракт имеет 32 вершины, 80 рёбер, 80 граней, 40 ячеек (кубов) и 10 4-мерных ячеек (тессерактов).

Слово «пентеракт» возникло путём комбинирования слов «тессеракт» и «пента» (от греч. πέντε — «пять»). Также может именоваться пентакуб, 5-гиперкуб, дека-5-топ или декатерон.

Пятиугольник

Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.

Символ Шлефли

Символ Шлефли — комбинаторная характеристика правильного многогранника, применяется для описания правильных многогранников во всех размерностях. Назван в честь швейцарского математика Людвига Шлефли, который внёс значительный вклад в геометрию и другие области математики.

Эннеракт

Эннеракт, или 9-гиперкуб, или октадекаиоттон — это девятимерный гиперкуб, аналог куба в девятимерном пространстве. Определяется как выпуклая оболочка 512 точек [±1,±1,±1,±1,±1,±1,±1,±1,±1]{\displaystyle [\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1]}.


Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

На других языках

This page is based on a Wikipedia article written by authors (here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

howlingpixel.com

Правильный пятиугольник | Треугольники

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A₂A₁A₅=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

∠A₁O A₂=360º:5=72º.

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

В треугольнике A₁OA₅

Проведём из вершины высоту OF.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A₁OA₅, то есть

OF — радиус вписанной в A₁A₂A₃A₄A₅окружности: OF=r.

Рассмотрим прямоугольный треугольник A₁OF.

По определению синуса,

откуда

Так как

то

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

По определению котангенса,

Подставив значение котангенса 36°, получаем:

Итак, формула радиуса вписанной в правильный пятиугольник окружности

Применив формулу

можно найти площадь правильного пятиугольника. Здесь

следовательно, формула для нахождения площади A₁A₂A₃A₄A₅

Все диагонали правильного пятиугольника равны.

Длина диагонали равна

www.treugolniki.ru

Правильный пятиугольник — WiKi

Свойства

Построение правильного пятиугольника

α=(n−2)n⋅180∘=35⋅180∘=108∘{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}

Площадь правильного пятиугольника рассчитывается по любой из формул:

Высота правильного пятиугольника:

h=tg72∘2t=5+252t≈1,539t{\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1{,}539t}

Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1+52{\displaystyle {\frac {1+{\sqrt {5}}}{2}}} .

t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R}

Радиус вписанной окружности:

r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t}

Радиус описанной окружности:

R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r}

d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t}

S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}}

Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)

Ss=Φ4=3Φ+2=35+72≈6,8541{\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541}

где Φ{\displaystyle \Phi } — отношение золотого сечения.

Построение

Построение правильного пятиугольника

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.

Пятиугольный узел на полоске бумаги

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе

Интересные факты

Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
В природе не существует кристаллов с гранями в форме правильного пятиугольника.
Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.

См. также

Примечания

ru-wiki.org

Правильный пятиугольник — это… Что такое Правильный пятиугольник?

Правильный пятиугольник

Правильный пятиугольник (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

Построение правильного пятиугольника

Площадь правильного пятиугольника рассчитывается по любой из формул:

где — радиус описанной окружности, — радиус вписанной окружности, — диагональ, — сторона.

Высота правильного пятиугольника:

Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу .

Радиус вписанной окружности:

Радиус описанной окружности:

Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного

где — отношение золотого сечения.

Построение

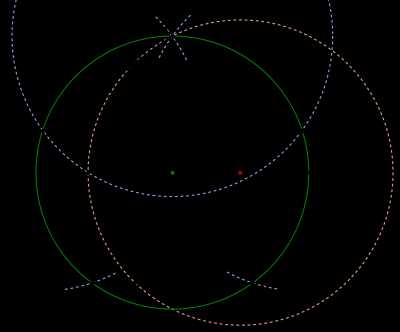Построение правильного пятиугольника

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью, как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Overhand knot of a paper strip

В природе

Интересные факты

Пентагон

Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
В природе не существует кристаллов с гранями в форме правильного пятиугольника.

См. также

Примечания

dic.academic.ru

Пятиугольник — Howling Pixel

Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.

Площадь пятиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.

Выпуклым пятиугольником называется пятиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Сумма внутренних углов выпуклого пятиугольника равна 540°.

∑i=15αi=(5−2)⋅180∘=3⋅180∘=540∘{\displaystyle \sum _{i=1}^{5}\alpha _{i}=(5-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }}

Любые 9 точек в общем положении содержат вершины выпуклого пятиугольника, и существует множество из 8 точек в общем положении, в котором нет выпуклого пятиугольника^[1]. Доказано также, что любые 10 точек на плоскости в общем положении содержат выпуклый пустой пятиугольник, и существует множество из 9 точек в общем положении, в котором нет выпуклого пустого пятиугольника^[2].

Правильный пятиугольник

Пентагоном или правильным пятиугольником называется пятиугольник, у которого все стороны и углы равны. Если провести в пентагоне диагонали, то он разобьётся на^[3]:

меньший пентагон (образуеся точками пересечения диагоналей) — в центре
Вокруг меньшего пентагона — пять равнобедренных треугольников двух видов (с отношением бедра к основанию, равным золотой пропорции):
- 1) имеют острые углы в 36° при вершине и острые углы в 72° при основании
- 2) имеют тупой угол в 108° при вершине и острые углы в 36° при основании

При соединении двух первых и двух вторых треугольников их основаниями получатся два «золотых» ромба (первый имеет острый угол в 36° и тупой угол в 144°). Роджер Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета (мозаики Пенроуза).

Звездчатые пятиугольники

Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника называется звёздчатым. Помимо правильного существует ещё один звёздчатый пятиугольник — пентаграмма.

Пентаграмма, как полагал Пифагор, представляет собой математическое совершенство, поскольку демонстрирует золотое сечение (φ = (1+√5)/2 = 1,618…). Если разделить длину любого цветного отрезка на длину самого длинного из оставшихся меньших отрезков, то будет получено золотое сечение φ.

φ=redblue=bluegreen=greenmagenta{\displaystyle \varphi ={\frac {\mathrm {\color {red}red} }{\mathrm {\color {Blue}blue} }}={\frac {\mathrm {\color {Blue}blue} }{\mathrm {\color {Green}green} }}={\frac {\mathrm {\color {Green}green} }{\mathrm {\color {Magenta}magenta} }}}

См. также

Примечания

↑ Kalbfleisch, J.D.; Kalbfleisch, J.G. & Stanton, R.G. (1970), «A combinatorial problem on convex regions», Proc. Louisiana Conf. Combinatorics, Graph Theory and Computing, vol. 1, Congressus Numerantium, Baton Rouge, La.: Louisiana State Univ., с. 180–188
↑ Harborth, Heiko (1978), «Konvexe Fünfecke in ebenen Punktmengen», Elem. Math. Т. 33 (5): 116–118
↑ Плитки Пенроуза

Гирих (математика)

Пять плиток мозаики включают:

правильный десятиугольник с внутренними углами 144°;

удлиненный (неправильный выпуклый) шестиугольник с внутренними углами 72°, 144°, 144°, 72°, 144°, 144°;

галстук-бабочка (невыпуклый шестиугольник) с внутренними углами 72°, 72°, 216°, 72°, 72°, 216°;

ромб с внутренними углами 72°, 108°, 72°, 108°;

Двуугольник

Двуугольник — многоугольник с двумя сторонами и двумя углами.

В Евклидовой геометрии двуугольник считается вырожденной фигурой, так как его две стороны совпадают.

В сферической геометрии четыре двуугольника образуются при пересечении двух больших окружностей.

Десятиугольник

Икосододекаэдр

Икосододека́эдр — полуправильный многогранник, состоящий из 32 граней (12 правильных пятиугольников и 20 правильных треугольников). В икосододекаэдре 30 одинаковых вершин, в которых сходятся два треугольника и два пятиугольника, а также 60 одинаковых рёбер, каждое из которых разделяет треугольник и пятиугольник. Двойственный к икосододекаэдру многогранник — ромботриаконтаэдр.

Для икосододекаэдра с длиной ребра a{\displaystyle a} можно выразить некоторые количественные характеристики:

Квадрат

Квадра́т — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны. Квадрат является одновременно частным случаем ромба и прямоугольника.

Многоугольник

Одноугольник

Одноугольник (генагон или моногон) — фигура в геометрии представляет собой многоугольник с одним краем и одной вершиной. Обозначается символом {1}. Имеет только одну сторону и только один внутренний угол.

Пентагон

Пентаго́н (англ. The Pentagon от греч. πεντάγωνον «пятиугольник») — штаб-квартира Министерства обороны США в здании, имеющем форму правильного пятиугольника. Находится по адресу: Арлингтон, Виргиния 22202, США.

Как символ американских военных часто «Пентагон» метонимически обозначает Министерство обороны США.

Пентагондодекаэдр

Пентаграмма

Правильный девятиугольник

Правильный девятиугольник — это правильный многоугольник с девятью сторонами.

Правильный пятиугольник

Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Правильный треугольник

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые (равны 90 градусам).

В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует.

Ромб

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны.

Ромбоид

В геометрии на плоскости, ромбоид — это параллелограмм, в котором смежные стороны имеют разные длины, и углы не являются прямыми.

Параллелограмм с равными сторонами (равносторонний) называется ромбом, но не ромбоидом.

Параллелограмм с прямыми углами называется прямоугольником, и тоже не является ромбоидом.

Термин ромбоид в настоящее время часто применяется к параллелепипедам, сплошным телам с шестью гранями, где каждая грань — это параллелограмм, и противоположные грани лежат в параллельных плоскостях.

Некоторые кристаллы имеют форму трёхмерных ромбоидов. Эти тела также иногда называют ромбоидными призмами. Термин часто используется в научной терминологии, как в двух-, так и в трёхмерном понимании.

Ромбоикосододекаэдр

Ромбоикосододекаэдр — полуправильный многогранник, состоящий из 12 правильных пятиугольников, 30 квадратов и 20 треугольников. Имеет икосаэдрический тип симметрии. В каждой из вершин сходятся треугольник, пятиугольник и 2 квадрата.

Ромбоикосододекаэдр можно представить либо как додекаэдр, усечённый по вершинам и рёбрам (при этом треугольники соответствуют вершинам додекаэдра, а квадраты — рёбрам), либо как икосаэдр, усечённый таким же образом (при этом пятиугольники соответствуют вершинам икосаэдра, а квадраты — рёбрам), либо же как усечённый икосододекаэдр, чем он по сути и является.

Усечённый икосаэдр

Усечённый икосаэдр — многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников. Имеет икосаэдрический тип симметрии. В каждой из вершин сходятся 2 шестиугольника и пятиугольник. Каждый из пятиугольников со всех сторон окружён шестиугольниками. Усечённый икосаэдр — один из самых распространённых полуправильных многогранников, так как именно эту форму имеет классический футбольный мяч (если представить его пятиугольники и шестиугольники, обычно окрашенные соответственно чёрным и белым, плоскими). Эту же форму имеет молекула фуллерена C60, в которой 60 атомов углерода соответствуют 60 вершинам усечённого икосаэдра.

Шестиугольник

Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы.

На других языках

howlingpixel.com

Пентагон (фигура) — это… Что такое Пентагон (фигура)?

Свойства

Построение

Получение с помощью полоски бумаги

Интересные факты

См. также

Смотреть что такое «Пентагон (фигура)» в других словарях:

Правильный пятиугольник | Формулы и расчеты онлайн

Обозначения на рисунке для правильного пятиугольника

Основные формулы для правильного пятиугольника

В помощь студенту

Правильный пятиугольник

Правильный пятиугольник — Howling Pixel

Свойства

Построение

Получение с помощью полоски бумаги

В природе

Интересные факты

См. также

Примечания

На других языках

Правильный пятиугольник | Треугольники

Правильный пятиугольник — WiKi

Свойства

Построение

Получение с помощью полоски бумаги

В природе

Интересные факты

См. также

Примечания

Правильный пятиугольник — это… Что такое Правильный пятиугольник?

Свойства

Построение

Получение с помощью полоски бумаги

В природе

Интересные факты

См. также

Примечания

Пятиугольник — Howling Pixel

Правильный пятиугольник

Звездчатые пятиугольники

См. также

Примечания

На других языках

Добавить комментарий Отменить ответ