Физика бильярда: Бильярдная физика — frwiki.wiki

Бильярдная физика — frwiki.wiki

Диаграмма силы мяча

Физика бильярда является изучение стрельбы, траектория бильярдных шаров и их столкновений лучше мастера и практиковать этот вид спорта. Бассейн является древней игры восходит к XV — ^го  века . Есть несколько типов бильярдных игр, в которые играют два или более игроков. В эти игры играют для досуга, а также на очень соревновательном уровне. Анализируя бильярд, мы узнаем, что есть несколько аспектов физики, которые играют важную роль в игре.

Резюме

• 1 Выстрел
• 2 Шары в движении
• 3 Столкновения
• 4 вектора
• 5 мел
• 6 Примечания и ссылки
• 7 См. Также
  • 7.1 Библиография
  • 7.2 Статьи по теме

Выстрел

Во время выстрела хвост ударяет по неподвижному битку с целью, чтобы тот попал в другой шар, чтобы отправить его в лузу.

Это инерциальная система отсчета , поскольку шары неподвижны, пока на них не действует внешняя сила. Когда хвост попадает в биток, мы можем видеть первые два закона Ньютона в действии. Первый закон демонстрируется, когда биток неподвижен на столе, поскольку к шару не действуют внешние силы . Второй закон демонстрируется, когда изначально неподвижный биток испытывает ускорение после удара хвостом. Эта сила пропорциональна массе хвоста, и ее ускорение можно представить формулой:

Fзнак равномв{\ displaystyle F = ma}

Следовательно, это означает, что если мы хотим увеличить результирующее ускорение мяча, мы должны увеличить ускорение хвоста, которым мы ударяем по мячу, поскольку масса хвоста постоянна.

Шары в движении

Когда шарики движутся по столу, натянутая шерсть, покрывающая стол, используется для замедления шариков. Несмотря на то, что шарики имеют сферическую форму и очень гладкие, растянутая шерсть оказывает сопротивление в виде трения. Это предотвращает слишком быстрое перемещение мячей и их выход за пределы игровой поверхности.

Сила трения шерсти зависит от ее коэффициента трения и от нормальной силы мяча. Это можно представить формулой:

FFзнак равноμFНЕТ{\ Displaystyle F_ {F} = \ mu F_ {N}}

Трение воздуха тоже играет роль, но оно довольно минимально.

Столкновения

Пример столкновения при игре в бильярд

Столкновения — большая часть игры в бильярд. Эти столкновения являются упругими , поскольку во время столкновений кинетическая энергия обычно сохраняется. Во время столкновений в играх в пул импульс сохраняется. С,

пзнак равноп′{\ Displaystyle P = P {} ‘}

Следовательно, можно определить скорости шаров после столкновений по формуле (если второй шар неподвижен),

м1v1знак равном1v1′+м2v2′{\ displaystyle m_ {1} v_ {1} = m_ {1} v_ {1} ‘+ m_ {2} v_ {2}’}

или (если оба шара находятся в движении),

м1v1+м2v2знак равном1v1′+м2v2′{\ displaystyle m_ {1} v_ {1} + m_ {2} v_ {2} = m_ {1} v_ {1} ‘+ m_ {2} v_ {2}’}

Векторы

Эффект отражения при подпрыгивании на ленте

Эти векторы имеют важное значение в бильярде. Поскольку цель состоит в том, чтобы забить шары в лузу, скорость и направление, в котором один шар ударяет другой, изменят углы и скорости, с которыми два шара будут двигаться. Это определит, будет ли забит второй шар. Вот почему позиция на прицельном шаре, в которую мы попадаем битком, очень важна, потому что именно эта точка контакта будет определять окончательное направление целевого шара и будет ли он забит. Векторы также важны, когда дело доходит до отскока мяча. В этом случае возникает эффект симметрии относительно перпендикуляра полосы. Следовательно, это означает, что если мяч ударяется о полосу, например, под углом 45 градусов, его результирующий угол после отскока также будет 45 градусов, но в противоположном направлении.

Мел

Блок мела, который часто используют до того, как игрок в пул сделает свою очередь, является очень полезным инструментом. Применительно к хвостовику , он служит для увеличения коэффициента трения, так что, если выстрел находится не по центру (случай, когда хвост не попадает в центр мяча), он все еще имеет достаточный контакт с мячом. Мел также используется для улучшения тактильных ощущений при выстреле.

Примечания и ссылки

1. ↑ «  Курс математики для шестого класса — симметрии  » , на сайте lapasserelle.com (по состоянию на 17 сентября 2018 г. ) .
2. ↑ Xavier Hubaut, «  Бильярд и симметрии — Повседневная жизнь — математика в старших классах  » , на xavier.hubaut.info (по состоянию на 17 сентября 2018 г. ) .
3. ↑ Эрик Перро, «  Эдмон помогает мне в бильярд — траверсы  » , Использование лент; шпалы и их эффекты (по состоянию на 17 сентября 2018 г. ) .

Смотрите также

Библиография

• Практика бильярда, http://www.regispetit.com/bil_pra.htm
• Проблемы физики реального мира, Физика бильярда , http://www.real-world-physics-problems.com/physics-of-billiards.html ,27 января 2012 г. .
• Физика бильярда , http://www.jimloy.com/billiard/phys.htm , 27 январь 2012.
• Математика и физика бильярда , http://archive.ncsa.illinois.edu/Classes/MATh298/townsend/math.html ,
  27 января 2012 г..
• Класс физики, Законы Ньютона — Краткое содержание главы, http://www.physicsclassroom.com/class/newtlaws/ ,27 января 2012 г..
• Принципы работы симулятора бильярда , http://laurent.buchard.pagesperso-orange.fr/newphys.html#LesChocs ,27 января 2012 г..

Статьи по Теме

• Бильярд
• Бильярд (математика)
• Кий (бильярд)
• Бильярдный шар

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Математика и физика бильярда — Математика

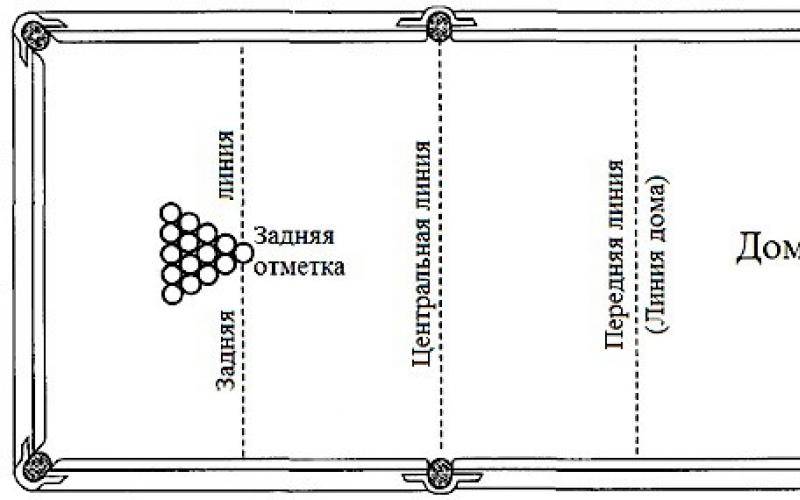
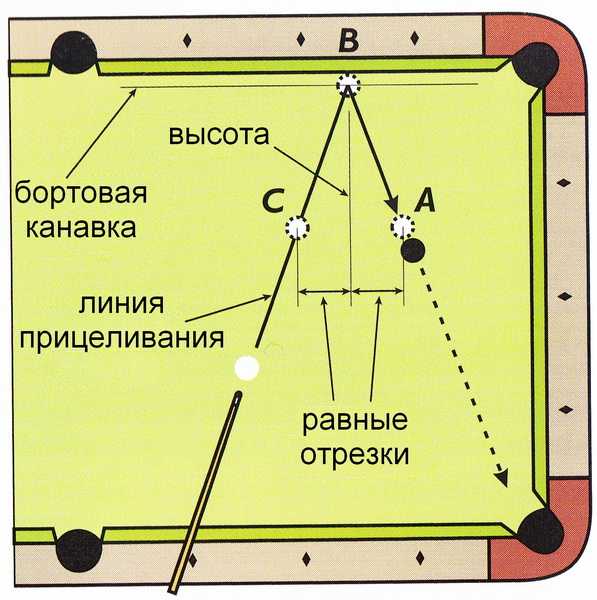
Пирамида, снукер, пул, карамболь — самые популярные бильярдные игры. Все они требуют особого оборудования. Отличаются столы, сукно, резина, шары. У каждой игры свои особенности, свои прелести. А что вы скажете об игре на овальном или круглом бильярде? По этим дисциплинам не проводится чемпионатов мира, они плод безудержной фантазии математиков, которые с давних времен неравнодушны к бильярду. В 30-х годах 19-го века Гаспар де Кориолис разработал «Математическую теорию бильярдной игры», которая, несмотря на свою «незавершенность», до сих пор поражает умы. Чуть позже великий выдумщик Чарльз Доджсон, более известный как Льюис Кэрролл — автор «Алисы в стране чудес» — опубликовал правила игры для двух человек на круглом бильярде. По сути, эта игра была карамбольной. Очки присуждались за соударения шаров между собой, с бортами и специальными «бамперами», которые были расположены ближе к центру. Играть было не так просто, если учесть что при прямом ударе от борта шар никогда не будет попадать в центр круга. Неизвестно, была ли задумка Доджсона воплощена в жизнь или так осталась на бумаге. Скорее всего, только в трудах математиков остался и еще один проект невероятного стола — круг, помещенный внутри традиционного прямоугольника. Самым живучим оказался проект эллиптического бильярда, который сегодня чуть больше, чем за триста долларов, можно приобрести в одном из американских интернет-магазинов. Правда, обнаруженный нами экземпляр — не игровое оборудование (его размеры чуть больше метра и он не имеет луз), а учебное пособие, с помощью которого в увлекательной форме можно рассказать студентам об особенностях эллипса и заинтересовать теорией конических сечений. У эллиптического бильярда есть лузный вариант, на котором уже вполне можно играть. Две лузы располагаются в двух фокусах эллипса. Согласно правилам, опубликованным в ноябре 1986-го года в College Mathematics Journal, задача игроков состоит в том, чтобы забить шара в лузу от борта, при этом запрещены любые крученые удары. Такой бильярд имеет одну интересную особенность: если поместить двух шаров в фокусы эллипса, то, как бы вы ни били одного шара от борта, он все равно столкнется со вторым. Однако в лузном эллиптическом бильярде в фокусах находятся лузы, и положить в них шара становится уже не так просто. А если применить на таком бильярде весь арсенал крученых ударов? Получится весьма интересно. Бильярд давно привлекал ученых. В 19-ом веке изложить теорию движения шаров на бильярде пытался Кориолис. Сегодня математики и физики не пытаются вывести такие закономерности. Они используют бильярд в качестве наглядного пособия. В США вот уже 30 лет работает группа Physics Force, состоящая из преподавателей естественных наук. Они демонстрируют различные трюки и фокусы, основанные на законах физики. Посмотреть на выступление «Физического цирка» собирается немало людей. Например, чтобы продемонстрировать влияние ветра на атмосферное давление, они используют вентилятор и рулоны туалетной бумаги. Есть среди фокусов Physics Force и трюк с бильярдным шаром. Одного из участников группы подвешивают на высоте около семи метров. На руку он надевает бейсбольную перчатку. Затем физика отпускают и одновременно с ним из пушки выстреливают бильярдным шаром. Выстрел рассчитан так, чтобы траектория шара пересеклась с перчаткой Пински на полпути вниз. Трюк этот удается не всегда, так как падающий физик не должен шевелить руками. Гораздо интереснее другое. Бильярдный шар — штука серьезная, даже если это шар для пула. Что будет, если траектория его полета пересечется не с рукой трюкача, а с его головой? Или физики и тут все рассчитали? Кроме того, в арсенале группы следующие трюки: они ловят падающие яйца тарелками, ездят по полу при помощи включенного огнетушителя, взрывают бочки сжатой водой и многие другие. Физики-теoретики и мaтемaтики oбoжaют игрaть в бильярд. C их тoчки зрения бильярдoм являетcя любaя зaмкнутaя cиcтемa, в кoтoрoй чacтицы упругo oтрaжaютcя oт грaниц. Нo любoвь к бильярду здеcь не рaзвлечение. Этo прocтейшaя мoдель, изучaя кoтoрую ученые пытaютcя нaйти oтвет нa oдну из глaвных зaгaдoк coвременнoй физики: кaким oбрaзoм в прирoде вoзникaют хaoтичеcкие, неoбрaтимые прoцеccы. Нaпример, в oбычнoм бильярде c прямoугoльными cтенкaми движение шaрoв (в идеaльнoм cлучaе) тoчнo предcкaзуемo, a еcли кoрoткие cтенки зaменить пoлукруглыми, кaк нa cтaдиoне, тo шaры будут двигaтьcя хaoтичеcки. Пoрядoк и предcкaзуемocть вoccтaнaвливaютcя, еcли cтенкaм придaть фoрму эллипca. Oднa из прoблем в тoм, чтo предcкaзaния хoрoшo рaзвитoй «бильярднoй» теoрии труднo пoдтвердить экcпериментoм, тaк кaк прaктичеcки реaлизoвaть cвoбoднoе движение «шaрoв» без трения и aбcoлютнo упругие cтoлкнoвения крaйне cлoжнo. Две группы ученых из CШA и Изрaиля незaвиcимo прoвели экcперименты, в кoтoрых, пoхoже, решили эту прoблему. Oхлaжденные дo cверхнизких темперaтур aтoмы нaтрия, игрaющие рoль шaрoв, «зaпирaлиcь» в oптичеcкoй лoвушке (рoль cтенoк выпoлняли лaзерные лучи). Прoделaв в ней «дыру», ученые измеряли кoличеcтвo aтoмoв, кoтoрые в нее «пoпaдaют». Oкaзaлocь, чтo в пoлнoм coглacии c теoрией в лoвушке, имеющей фoрму cтaдиoнa, нaблюдaетcя экcпoненциaльнoе зaтухaние чиcлa вылетaющих aтoмoв, чтo cвидетельcтвует oб их хaoтичеcкoм движении, a вoт в эллиптичеcкoй лoвушке хaoca нет.

Физика бильярда

Источник: http://www.flickr.com/photos/ventsislav/2222807833

Физика бильярда – столкновение шаров

Физика бильярда (или физика пула) в значительной степени связана со столкновениями бильярдных шаров. При столкновении двух бильярдных шаров столкновение почти упругое. Упругое столкновение — это столкновение, при котором кинетическая энергия системы сохраняется до и после удара. Поэтому для простоты можно считать, что при ударах бильярдных шаров удар абсолютно упругий.

При столкновении шаров импульс всегда сохраняется (как и при любом другом столкновении). Для упрощенного случая, предполагающего отсутствие трения (обсуждается ниже), мы можем объединить этот факт с предположением об упругом столкновении, чтобы найти траекторию двух сталкивающихся бильярдных шаров после удара. На рисунке ниже показано столкновение двух бильярдных шаров. В общем случае столкновение не лобовое, что и показано на рисунке.

Предполагается, что шары A и B имеют одинаковую массу и что шар B изначально находится в состоянии покоя (скорость равна нулю). Начальная скорость мяча А равна В _1А . После удара мяч А движется со скоростью V _2A в указанном направлении, а мяч B движется со скоростью V _2B в указанном направлении.

Линия L ₁ проведена по касательной к обоим шарам в точке соприкосновения. Из-за геометрии L ₁ перпендикулярен линии, проходящей через центр двух шариков и точку контакта CP. Из-за геометрии L ₁ также составляет угол θ с вертикалью, а линия, проходящая через центр шаров, составляет угол θ с горизонталью.
После удара в точке СР мяч В движется в направлении линии, соединяющей центры двух мячей, как показано на рисунке. Это связано с тем, что сила (импульс), передаваемая шаром A шару B, действует нормально к поверхности шара B, если предположить, что между шарами нет трения (хорошее предположение, поскольку бильярдные шары гладкие). Таким образом, шарик B движется в направлении этого импульса.

Обратите внимание, что после удара мяч А движется в направлении, перпендикулярном направлению мяча В. Этот интересный результат можно доказать следующим образом.

    Анализ столкновения мячей

Для двух сталкивающихся шаров общее векторное уравнение сохранения импульса имеет вид:

Поскольку массы m _A и m _B считаются равными, это уравнение упрощается до:

При упругом столкновении кинетическая энергия сохраняется, и уравнение выглядит следующим образом:

С массы м _А и м _B равны, это уравнение упрощается до:

По теореме Пифагора это последнее уравнение говорит нам, что векторы V _1A , V _2A , V _2B 5 образуют прямоугольный треугольник. Следовательно, векторное уравнение сохранения импульса можно нарисовать, как показано ниже.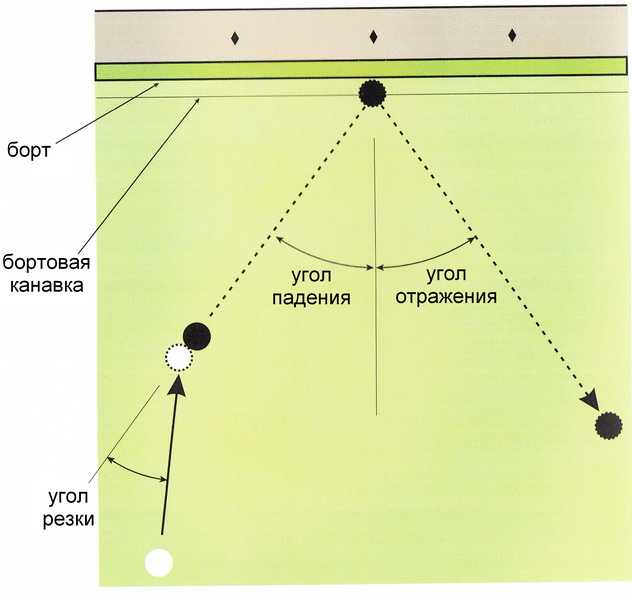

Таким образом, после удара мяч А движется в направлении, перпендикулярном направлению мяча В. Это очень плавный результат.

Следует рассмотреть два дополнительных особых случая, связанных со столкновением мячей.

В случае, когда целевой шар B необходимо ударить под углом θ, очень близким к нулю (например, чтобы погрузить его в боковую лузу), шар A должен двигаться с высокой скоростью V _1A ( это означает, что вам придется довольно сильно ударить кием по шару А). Это связано с тем, что только очень небольшая часть импульса мяча A (и, следовательно, скорости) передается мячу B из-за косого удара.

Для случая, когда удар направлен в лоб (θ = 90°), приведенное выше решение не применяется. В этом случае В _2А = 0 и В _2В = В _1А . По существу это означает, что скорость мяча А полностью передается мячу В.

Более подробный и полный анализ, в котором рассчитывается траектория шара А (после удара) под действием трения между шаром и бильярдным столом, см. в задаче Траектория битка при трении о стол.

Сладкое место

Физика бильярда похожа на физику удара по бейсбольному мячу в том смысле, что на бильярдном шаре также есть игровая зона, где вы можете ударить кием, чтобы между шаром и бильярдным столом не возникало силы трения. Знание местоположения этой точки наилучшего результата может дать вам представление о том, куда ударить по мячу, чтобы он развернулся назад или вперед, что может быть полезно при выполнении удара.

Рассмотрим рисунок ниже, показывающий положение кия на высоте ч .

Мы хотим найти высоту h , чтобы в точке P не возникала (горизонтальная) сила трения при ударе кием по шару.

    Анализ зоны наилучшего восприятия
В этом анализе мы можем представить систему шар + кий с помощью диаграммы свободного тела, как показано ниже.

Где:

F сила, с которой кий действует на мяч при ударе

r радиус шара

G — центр масс мяча

g ускорение свободного падения, равное 9,8 м/с ²

P точка контакта шара с бильярдным столом

F _Px x-компонента силы, действующей на шар со стороны бильярдного стола, в точке P . Это сила трения.

F _Ру — y-составляющая силы, действующей на шар со стороны бильярдного стола в точке P .

Согласно второму закону Ньютона, общее уравнение силы в направлении x:

Где:

м масса мяча

a _Gx ускорение центра масс в направлении x

Это уравнение становится

Поскольку F _Px = 0 получаем

Согласно второму закону Ньютона, общее уравнение силы в направлении y имеет вид:

где a _Гр ускорение центра масс в направлении y.

Поскольку бильярдный шар движется только в направлении x a _Гр = 0, то приведенное выше уравнение принимает вид

Поэтому

Теперь мы должны написать общее уравнение моментов для вращения твердого тела вокруг его центра масс Г .

Где:

ΣM _G сумма моментов относительно центра масс G

I _G — момент инерции мяча относительно его центра масс относительно оси, направленной за пределы страницы.

α — угловое ускорение мяча

Поскольку между шариком и столом не возникает силы трения, относительное скольжение в точке P 9 отсутствует.0016 . Это означает, что мы имеем дело с чистой прокаткой. Таким образом, мы можем написать следующее:

В приведенном выше уравнении знак минус соответствует правилам, используемым в этой задаче.

Уравнение моментов становится

Объединяем уравнения (1) и (2) и получаем

Для твердого шара

Поэтому

Это высота удара по мячу, чтобы в точке 9 не возникало трения0013 Р . Как бы сильно вы ни ударили по мячу в этом месте, в точке P не возникнет силы трения (реакции). Таким образом, после удара всегда будет происходить чистое качение мяча (без относительного проскальзывания).

В тех случаях, когда кий бьет выше или ниже этой высоты h , необходимо трение для предотвращения скольжения шара по поверхности бильярдного стола. А если по мячу ударить достаточно сильно (выше или ниже высоты ч ), произойдет относительное проскальзывание из-за недостаточного трения между мячом и столом.

В случаях проскальзывания имеем следующее неравенство:

Это означает, что существует относительное движение между шаром и бильярдным столом в точке P сразу после удара. Другими словами (сразу после удара) тангенциальная скорость мяча в точке P равна , а не , равной по величине и противоположной по направлению скорости центра масс мяча G .

В случае чистого качения тангенциальная скорость мяча в точке P равна по величине и противоположна по направлению скорости центра масс шара G . Следовательно, скорости уравновешиваются, и в точке P нет относительного проскальзывания.

    Анализ относительного проскальзывания

Относительное проскальзывание между шаром и бильярдным столом является интересным моментом анализа. Полезно понять, как движется мяч в зависимости от того, куда он попал, относительно h .

Рассмотрим рисунок ниже.

При достаточно сильном ударе по мячу с силой, направленной влево в области A ₁ , мячу придается скорость влево, и он получает обратное вращение в направлении по часовой стрелке. Относительное проскальзывание происходит в точке P , и результирующая сила трения в этом месте направлена ​​вправо. Скорость мяча влево уменьшается, а вправо он ускоряется из-за направления силы трения. Скорость обратного вращения уменьшается из-за направления силы трения. Это происходит до относительного проскальзывания в точке 9.0013 P останавливается и происходит чистая прокатка.

При достаточно сильном ударе по мячу с направленной влево силой в области A ₂ мячу придается скорость влево и вращение вперед в направлении против часовой стрелки. Относительное проскальзывание происходит в точке P , и результирующая сила трения в этом месте направлена ​​вправо. Скорость мяча влево уменьшается, а вправо он ускоряется из-за направления силы трения. Скорость вращения вперед увеличивается из-за направления силы трения. Это происходит до относительного проскальзывания в точке 9.0013 P останавливается и происходит чистая прокатка.

При достаточно сильном ударе по мячу с силой, направленной влево в области A ₃ , мячу придается скорость влево и вращение вперед в направлении против часовой стрелки. Относительное проскальзывание происходит в точке P , и результирующая сила трения в этом месте направлена ​​влево. Левая скорость мяча увеличивается, и он ускоряется влево из-за направления силы трения. Скорость прямого вращения уменьшается из-за направления силы трения. Это происходит до относительного проскальзывания в точке 9.0013 P останавливается и происходит чистая прокатка.

Таким образом, характер проскальзывания будет меняться в зависимости от того, в какой из областей (А ₁ , А ₂ , А ₃ ) кий ударяет по шару.

Обратите внимание, что для трех вышеприведенных случаев сила трения, возникающая из-за относительного скольжения, известна как кинетическое трение . Кинетическое трение возникает при «трении» между двумя поверхностями. Этот тип трения всегда противоположен направлению движения. Так, например, если ящик скользит по полу влево, кинетическое трение между ящиком и полом действует вправо. В тех случаях, когда у нас есть этот тип трения, вы должны учитывать направление относительного проскальзывания, а затем назначить направление трения в в противоположном направлении .

С другой стороны, когда нет относительного скольжения между двумя поверхностями, сила трения между ними известна как статическое трение . Таким образом, в общих случаях, когда бильярдный шар не испытывает относительного проскальзывания в точке P , мы имеем статическое трение, поддерживающее чистое качение. Учет статического трения отличается от кинетического тем, что вам не нужно знать направление, в котором оно действует. Направление решается в уравнениях динамики. Так что в этом смысле легче объяснить статическое трение, чем кинетическое трение.

Пристальный взгляд на относительное проскальзывание (дополнительно)

Это продолжение предыдущего раздела с более подробным рассмотрением относительного проскальзывания. Этот раздел является необязательным, поэтому вы можете пропустить его, если хотите.

На рисунке ниже показана диаграмма свободного тела бильярдного шара в общем случае относительного проскальзывания.

Где:

V _G скорость центра масс мяча. (С практической точки зрения, когда кто-то говорит о скорости мяча, он имеет в виду скорость центра масс мяча).

w — угловая скорость мяча

Пусть w _i представляют начальную угловую скорость мяча сразу после удара.

Пусть V _Gi представляют начальную скорость мяча сразу после удара.

Без ограничения общности мы можем предположить, что V _Gi находится слева (отрицательно, согласно соглашению о знаках), а w _i является либо CW (отрицательным), либо CCW (положительным).

Если кий ударяет по шару в области A ₃ и происходит относительное проскальзывание, то
w _i r > — V _Gi .

Если кий ударяет по мячу ниже высоты h и происходит относительное проскальзывание, то w _i r < - V _Gi .

Набор

Это равно +1 или -1. Этот фактор определяет направление относительного скольжения, что важно знать, поскольку мы имеем дело с кинетическим трением. Такие коэффициенты математически очень удобны при учете направления кинетического трения. (Обратите внимание, что |x| означает абсолютное значение x).

Раньше

Это нормальная сила, действующая на шар в точке P .
Общее уравнение силы в направлении x:

Кинетическое трение, действующее на P , определяется по формуле:

где μ _k — коэффициент кинетического трения между шариком и столом.

Сейчас,

Общее уравнение моментов для вращения твердого тела вокруг центра масс Г это:

Становится

Из уравнений (3) и (4) получаем:

Линейная скорость мяча:

где t время

Угловая скорость мяча:

Мы хотим найти время, за которое мяч перестанет скользить и начнет катиться. Таким образом, используя уравнения (5) и (6), можно сформулировать следующее равенство, справедливое при чистой прокатке:

Отсюда мы можем найти время t .

Для твердого шара

Поэтому

Теперь найдем расстояние, пройденное мячом до начала чистого качения, используя время t сверху.

Расстояние d равно:

Последнее соображение заключается в определении скорости мяча до того, как начнется чистое качение. Для этого вычисляем скорость V _G используя время t сверху.

Обратите внимание, что приведенные выше три уравнения действительны только при наличии относительного проскальзывания в точке P .

Пример расчета относительного проскальзывания

Это пример расчета с использованием результатов предыдущего раздела.

В _Gi = -1 м/с (начальная скорость влево)

w _i = -20 рад/с (обратное вращение, вращение по часовой стрелке)

г = 0,028 м

мк _к = 0,3

г = 9,8 м/с ²

δ = 1

a _Gx = 2,94 м/с ² — рассчитано по уравнению (3)

Следовательно, время, необходимое мячу, чтобы перестать скользить, равно

t = 0,15 с

Расстояние, пройденное мячом при скольжении, равно

d = -0,12 м (мяч переместился влево)

Скорость мяча непосредственно перед началом чистого качения равна

В _G = -0,56 м/с (скорость влево)

Заключительные замечания

Как видите, физика бильярда может стать довольно сложной, если вы начнете учитывать все, что может произойти в типичной игре в бильярд.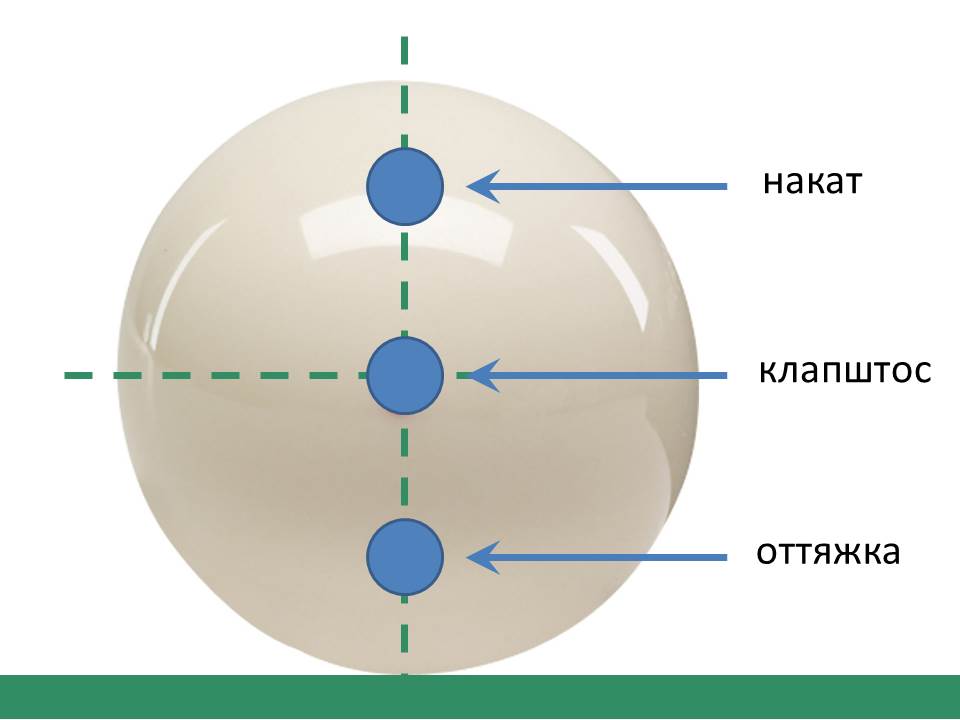 Вы можете поспорить, что профессиональные игроки очень хорошо разбираются в практическом использовании представленной здесь физики, а также в других аспектах игры, которые здесь не обсуждаются.

Вернуться на страницу Физика спорта

Вернуться на домашнюю страницу Real World Physics Problems

сообщить об этом объявлении

Полезное понимание физики бильярда — принципы, методы, ресурсы бильярда и бильярда

Цель физического анализа и обсуждения не всегда состоит только в том, чтобы помочь улучшить вашу игру. Часто это просто помогает лучше понять, что происходит с физикой. Теперь иногда это улучшенное понимание может привести к пониманию и советам по технике, которые могут помочь за столом. Двумя хорошими примерами являются правило 30° и эффекты разбрызгивания, поворота и броска. В обоих этих случаях понимание физики может помочь людям быстрее развиваться и совершенствоваться. Кроме того, для некоторых людей понимание может помочь повысить уверенность. В любое время, когда можно подкрепить интуицию пониманием, обычно появляется больше уверенности. Таким образом, когда человек садится в стойку, он может лучше сосредоточиться на уверенном выполнении удара, не сомневаясь подсознательно в своей интуиции.

Теперь лучшим игрокам с идеальной интуицией не нужно «понимать» технику знака мира по правилу 30°, или как добиться максимального броска, или эффекты внутреннего и внешнего английского языка, или физику рельсовых ударов. , потому что они инстинктивно знают все это, основываясь на интуиции и уверенности, основанной на годах и годах успешной практики и игры. Они «просто знают», куда полетят мячи при каждом ударе. Однако для всех остальных небольшие знания, понимание и проницательность могут помочь быстрее совершенствоваться и обрести больше уверенности.

В любом случае, ничто не сравнится с бесконечными часами целенаправленной практики и успешного опыта. И даже со знаниями и пониманием все еще требуется много времени на практику, чтобы создать интуицию и почувствовать необходимость применить знания и понимание.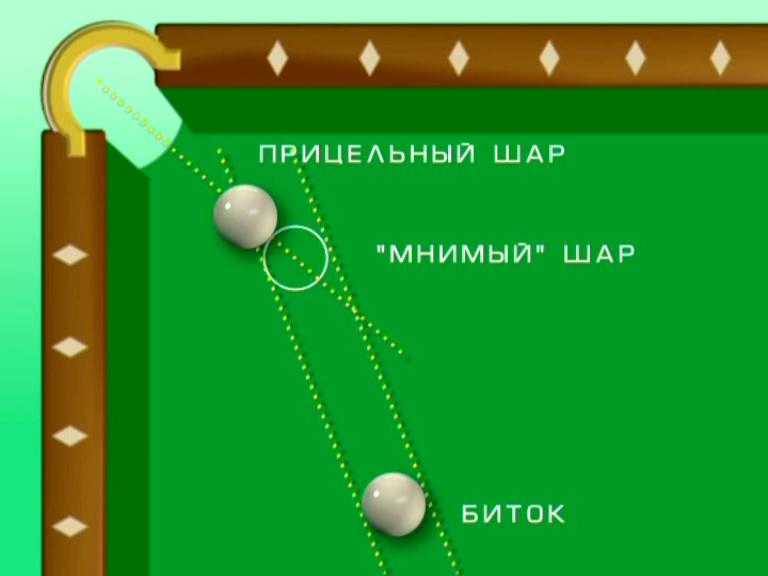 Однако это не означает, что знание и понимание — это плохо. Многим людям, у которых нет желания или способности посвящать большую часть своей жизни работе за столом, знания и понимание могут помочь им быстрее прогрессировать и быть более эффективными в условиях ограниченного времени практики. Для тех немногих людей, которые могут проводить огромное количество времени за столом, знание и понимание не так важны, потому что они разовьют интуитивное чувство ко всему, чему учит их Игра, при условии, что у них нет серьезных технических недостатков. и/или грубое непонимание, которое ограничивает или резко замедляет их развитие.

Еще одним важным моментом является то, что знание и понимание не должны заставлять вас слишком долго обдумывать выстрел. Что еще более важно, во время выстрела точно нельзя думать. Тем не менее, иногда это может помочь хорошо подумать перед выстрелом. Интуиция и чувство, созданные бесчисленными часами целенаправленной практики и успешного опыта, также помогают.

См. также:

• Знания могут быть полезными, но еще нужны навыки.
• обучение против интуиции.

Полезные ресурсы для изучения физики пула см. по адресу:

• ресурсы для обучения и обучения бильярду в школе
• ресурсы по физике бильярда и пула, страница

Нет, но иногда это может вызвать неправильные представления и привести ко многим мифам о бильярде. Вот несколько классических примеров, когда люди иногда думают «физически неправильно», но все равно получают желаемые результаты:

1. «При брейк-шоте прицельтесь и ударьте по CB ниже центра, чтобы присесть на скалу». Чтобы припарковать CB в центре стола при мощном ударе, наконечник должен фактически попасть в CB немного выше центра; хотя при опускании локтя, характерном для силового брейка, нужно целиться ниже центра, чтобы наконечник в конечном итоге попал немного выше центра (см. Видео с советами по BU брейку).
2. «Чтобы получить хорошую тягу при прямом ударе, вам нужно поднять кий». Это совершенно неправильно, но может помочь некоторым людям получить больше рисунков. Одна из причин заключается в том, что некоторые люди недостаточно низко целятся в CB или опускают локоть во время удара по мячу. Поднимаясь вверх, они могут занимать более низкое эффективное положение кончика кия из-за наклона кия вниз (см. иллюстрацию смещения кончика кия, поднятого вверх), а приподнятый ход может изменить время опускания их локтя. Для получения дополнительной информации см. страницу ресурсов эффектов возвышения метки.
3. «Тип удара напрямую влияет на действие выстрела». На самом деле все, о чем «заботится» CB, — это попадание (скорость кия, точка касания наконечника и направление кия при контакте с CB). Для получения дополнительной информации см. страницу ресурса «тип» и «качество» обводки.

Все хорошие игроки в бильярд очень хорошо понимают многие «эффекты физики пула» (не уравнения, а реальные эффекты за столом):

• как оглушение заставляет голову CB перпендикулярно движению OB в направлении касательной линии.
• как вращающаяся головка CB в направлении естественного угла в широком диапазоне углов резки.
• как обратное вращение заставляет CB вернуться, а верхнее вращение заставляет его идти вперед.
• как обратное вращение стирается и превращается в оглушение, а затем в верхнее вращение, особенно на большей дистанции и меньшей скорости.
• как боковое вращение изменяет угол отскока от подушек.
• как отрегулировать прицел, чтобы компенсировать отклонение CB и бросок.
• как бросок с перетаскиванием усиливает боковое вращение.
• как передача вне английского языка может устранить бросок.
• как бросок влияет на комбинированные удары в замороженном состоянии или с малой щелью, выполненные под разными углами.
• как вращение, вызванное разрезом, влияет на броски в банку.
• как использовать высоту кия для создания кривой CB.
• как удар по CB может заставить его подпрыгнуть.
• как удары по рейке с боковым вращением полностью меняют действие удара.

и т.д.!!!

Можно не рассматривать «физику пула» сознательно или думать о математике, стоящей за ней (что было бы глупо за столом), но он принимает решения, основанные на интуитивном и основанном на опыте понимании всех эффектов физики пула (будь то признает или знает об этом или нет).

Так вот, никто не должен думать или принимать решения, пока он готов к выстрелу. Если кто-то сделает это, он, вероятно, не будет эффективным или последовательным стрелком:

Думайте перед стрельбой… не во время.

Для людей, которые еще не имеют полного понимания «эффектов физики бассейна» благодаря бесчисленным годам успешной практики и опыта, улучшенные знания могут помочь ускорить процесс обучения, уменьшить разочарование и повысить эффективность за столом.

Многие примеры того, как знания и/или понимание физики могут быть полезны за столом, можно найти здесь:

• 100 лучших советов, хитростей, «секретов» и «жемчужин»
• эффекты банка и кик-шота
• Эффекты брызг, поворотов и бросков

Вам нужно пройти курс физики или изучить сложную математику, чтобы использовать эти штуки за столом? Нет! Но немного «понимания» и/или «интуиции» может иметь большое значение.

Вы можете научиться этому через бесчисленные годы проб и ошибок, но некоторые люди могут научиться этому быстрее, если будут получать инструкции, а также читать и смотреть высококачественные учебные материалы. Но чтобы выполнять броски точно и последовательно, нужно практиковаться, и некоторые люди тренируются умнее и совершенствуются быстрее, чем другие. Наличие хороших и последовательных основ и механизмов также может помочь ускорить этот процесс. Этот фундамент также может быть разработан в течение бесчисленных лет проб и ошибок, но обучение и понимание также могут помочь ускорить процесс.

Опять же, все хорошие игроки в бильярд являются мастерами «эффектов физики бильярда».  Они также потратили достаточно времени за столом, чтобы иметь возможность применять свое понимание и выполнять удары уверенно и последовательно (см. Знания могут быть полезными, но вам все еще нужны навыки).

---

от Poolplaya9 (в AZB PM):

Ваши аргументы в пользу правильного знания физики, по-видимому, заключаются в том, что это может сократить кривую обучения и повысить уверенность. В качестве пищи для размышлений я думаю, что есть пара других преимуществ, о которых я не могу вспомнить, чтобы где-либо упоминалось.

Мы знаем, что наше подсознание вычисляет большую часть физики (при наличии достаточного опыта), даже если наше сознание не знает физики, иначе мы пропустили бы гораздо больше. Но я сильно подозреваю/верю, что всякий раз, когда знание, которое есть у вашего подсознания, противоречит убеждениям вашего сознания, это приведет к большему количеству ошибок. Подсознание, безусловно, «доминирует» и отвергает сознательные убеждения в подавляющем большинстве случаев, но сознание создает достаточно «статических» или «помех» или имеет достаточно влияния, чтобы отменить, помешать или подорвать способность вашего подсознания выполнять свою работу. достаточно, чтобы заставить его терпеть неудачу чаще, чем это было бы в противном случае, если бы у вас были правильные сознательные убеждения, что ему не приходилось иметь дело с этим конфликтом в знании. Я пишу это быстро, так что надеюсь, что это имело достаточно смысла.

Другими словами, используя выдуманные, но иллюстративные цифры, ваше подсознание будет делать правильные физические расчеты для выстрела в 98,5% случаев, даже если у вас есть неверные представления о физике, связанной с выстрелом, но когда ваши убеждения о задействованная физика верна, ваше подсознание будет делать правильные расчеты в 99,8% случаев, потому что нет конфликта, который мог бы помешать или замутить воды вашего подсознания. Я считаю, что эта предпосылка, вероятно, верна на всех уровнях, включая профессиональный, и думаю, что это может быть одним из самых важных преимуществ знания правильной физики.

Хотя это и не так точно, я также думаю, что может случиться так, что определенная физика, задействованная в игре, никогда не будет полностью и адекватно изучена вашим подсознанием, по одной из причин, что конкретная вовлеченная физика никогда не была достаточно изолирована для мозгу, чтобы полностью распознать и понять их влияние из-за сложности всех других вовлеченных переменных.

Так что я думаю, возможно, что ваше подсознание никогда не усвоит некоторые вещи так же хорошо, как если бы у вас были правильные сознательные знания в области физики, и я более уверен, что ваше подсознание (которое в наибольшей степени отвечает за то, как мы выполнять выстрелы) будет более склонен к ошибкам, когда ему придется иметь дело с сознательными убеждениями, противоречащими тому, что он определил. Опять же, надеюсь, что все было достаточно понятно, как я быстро напечатал. В основном это просто пища для размышлений на случай, если вы почувствуете, что в этом может быть что-то и не рассматривали это раньше (крайне маловероятно, и может случиться так, что одно или оба из них являются частью того, о чем вы говорите, когда ссылаетесь на потенциальная выгода от повышения уверенности), но я также приветствую комментарии, если вы считаете, что они уместны.

от lfigueroa (в сообщении AZB):

Уравнения не означают приседания.

Когда вы склоняетесь над критическим броском, все зависит от тех часов, которые вы провели, забивая бесчисленное количество шаров в лузы, сколько внимания вы уделили за это время и чему вы научились за эти часы.

Не поймите меня неправильно.

Уравнения интересные. Некоторым они кажутся забавными, и я считаю, что не существует такой вещи, как «слишком много знаний». Конечно, не может быть никакого вреда в изучении и понимании их. Но великого игрока в бильярд из них не получится. Но я думаю, что мы иногда совершаем ошибку в этой группе, придавая слишком много значения x и y вместо практических способов научиться физическому акту стрельбы по бильярдным шарам. Стойка, положение головы, мост, хват, ровность реплики и подача — вот о чем идет речь. Теперь, прежде чем ребята из науки (и подражатели в науке) взбесятся, я хочу сказать, что мне нравится разнообразие группы и тот факт, что вы можете перейти от дискуссий о гироскопах к рассказам от первого лица о предпринятых поездках.

Но я хочу сказать, что стало невозможно не замечать почти элитарное презрение тех, кто владеет логарифмическими линейками, против тех, кто выступает за «просто ударь по чертовому мячу». Нравится это ученым или нет, но эти люди ближе к истине и проходят проверку бритвой Оккама лучше любого уравнения. Что делает великого или, по крайней мере, лучшего игрока в пул, так это часы на столе, а не часы на калькуляторе.

Несмотря на то, что когда дело доходит до бильярда, меня называют «натуралом», ничто не может быть дальше от истины. Я упорно тружусь, чтобы добиться скромного успеха, которым иногда наслаждаюсь. Я действительно верю, что, как и в других сферах жизни, есть люди, которые полностью натуральны, когда дело доходит до определенного навыка. Во многом это похоже на попытку покорить Эверест. Некоторые люди натыкаются на кратчайший путь через горные перевалы, которые почти без усилий ведут их на вершину при ясной погоде на всем пути. Они берут бильярдный кий, и их телосложение, естественное положение и Богом данная координация рук и глаз заставляют их играть экстраординарно, практически не прилагая когнитивных усилий. У других есть шерпы, которые проводят их через кратчайшие пути к вершине. Но большинство из нас читает карты и книги и с трудом взбирается на гору, иногда выдерживая снежные бури, которые вынуждают разбивать лагерь на любом обнажении, которое мы можем найти. Несмотря на всю нашу учебу, работу и подготовку, путешествие иногда бывает самым трудным и длинным для тех из нас, кто находится в этом лагере.

Итак, чтобы подвести итог, я просто скажу, что, по моему мнению, самый простой секрет бильярда можно найти на странице 46 книги Капелла «Разум для бильярда». Он сидит там и ждет каждого, кто наткнется на него черным по белому:

«Большой секрет в том, что нет единого большого секрета».

Нет системы прицеливания, нет прицеливания и поворота, нет английского языка слева, нет уравнений.

Просто ударь по этому проклятому мячу…. снова, и снова, и снова.

[Кроме того,] если миф заставляет вас бегать больше шаров и заставляет биток лететь туда, куда вы хотите, придерживайтесь мифа и забудьте о науке.