Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра..Общая формула для нахождения корней квадратного уравнения:
Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле
Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни
До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком.
Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».
Давайте попробуем разобраться,
что описывает дискриминант?В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить.
Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),
или парабола ветвями вниз (a<0).
Вершина параболы лежит посередине между корнями
Физический смысл дискриминанта:
Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).
Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
График функций всегда симметричен относительно начала координат.
Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах «+, -» или «-, +».
Неполное квадратное уравнение вида
одним из корней всегда имеет точку x=0.
В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!
Дискриминант онлайн
Примеры решенийРанг матрицы Умножение матриц Метод Гаусса Найти производную Найти интегралРешение СЛАУ методом Крамера Диф уравнения онлайнОпределитель матрицы Точки разрыва функции
ax2+bx+c=0
Формула дискриминанта:
D=b2-4ac
Онлайн-калькулятор предназначен для нахождения дискриминанта и корней функции для уравнений вида: ax2+bx+c=0.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Инструкция. Введите соответствующие коэффициенты:
a = b = c =
Вид: x2+x+1 Например для уравненияx2-8x+7=0 коэффициенты равны: a=1, b=-8, c=7
Как построить параболу
ax2+bx+c=0.
Виды дискриминантов
Формула дискриминанта зависит от степени многочленаanxn + an-1xn-1 + ... + a1x + a0 = 0.
Свойства дискриминанта
- Дискриминант равен 0, когда многочлен имеет кратные корни (равные корни).
- Дискриминант является симметрическим многочленом относительно корней многочлена и поэтому является многочленом от его коэффициентов; более того, коэффициенты этого многочлена целые независимо от расширения, в котором берутся корни.
Классификация дискриминантов
| D>0 | D=0 | D |
| При D > 0 корней — два. Формула для вычислений:
|
при D = 0 корень один кратности 2 (корни равны). Формула для вычислений:
|
при D < 0 вещественных корней нет. Существуют два комплексных корня. Формула для вычислений:
|
| При a > 0, x12. При a < 0, x1 > x2 Что означает, если дискриминант больше нуля: значит существуют вещественные корни, график квадратичной функции пересекает ось Х в двух местах. |
x1 = x2 = -b/2a
Что означает, если дискриминант равен нулю: значит существует один вещественный корень, график функции пересекает ось Х в одном месте. |
Что означает, если дискриминант меньше нуля: значит не существует вещественных корней, а только комплексные корни. График функции не пересекает ось Х.
|
Пример расчета для дискриминанта больше нуля
2x2+3x+1=0
Находим дискриминант: D=32-4·2·1=1
Корни уравнения: ;
Пример расчета для дискриминанта равного нулю
9/4x2+3x+1=0
Находим дискриминант:
D=32-4·9/4·1=0
Корни уравнения:
Пример расчета для дискриминанта меньше нуля
2x2+3x-4=0
Находим дискриминант: D=32-4·2·(-4)=41
Корни уравнения:
;
Результат:
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).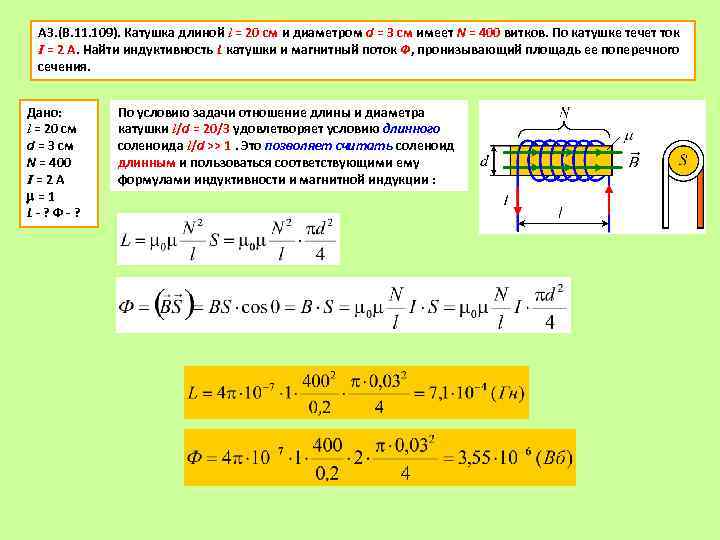
дискриминантных формул — что такое дискриминантные формулы? Примеры
Формулы дискриминанта используются для нахождения дискриминанта полиномиального уравнения. В частности, дискриминант квадратного уравнения используется для определения количества и характера корней. Дискриминант полинома – это функция, состоящая из коэффициентов полинома. Давайте изучим формулы дискриминанта вместе с несколькими решенными примерами.
Что такое дискриминантные формулы?
Дискриминантные формулы дают нам общее представление о природе корней. Дискриминант квадратного уравнения получается из квадратной формулы. Дискриминант обозначается D или Δ. Дискриминантные формулы для квадратного уравнения и кубического уравнения:
Дискриминантная формула квадратного уравнения
Дискриминантная формула квадратного уравнения ax 2 + bx + c = 0 есть, Δ (или) D = b 2 — 4ач. Мы знаем, что квадратное уравнение имеет максимум 2 корня, так как его степень равна 2.
Мы знаем, что квадратная формула используется для нахождения корней квадратного уравнения на оси 9.0013 2 + bx + c = 0. Согласно квадратичной формуле, корни можно найти, используя x = [-b ± √ (b 2 — 4ac) ] / [2a]. Здесь b 2 — 4ac — это дискриминант D, который находится внутри квадратного корня. Таким образом, квадратичная формула становится x = [-b ± √D] / [2a]. Здесь D может быть либо > 0, = 0, (или) < 0. Определим характер корней в каждом из этих случаев.
- Если D > 0, то квадратная формула принимает вид x = [-b ± √(положительное число)] / [2a], и, следовательно, в этом случае квадратное уравнение имеет два различных действительных корня.
- Если D = 0, квадратная формула принимает вид x = [-b] / [2a], и, следовательно, в этом случае квадратное уравнение имеет только один действительный корень.
- Если D < 0, то квадратная формула принимает вид x = [-b ± √(отрицательное число)] / [2a], и, следовательно, в этом случае квадратное уравнение имеет два различных комплексных корня (это связано с тем, что квадратный корень из отрицательного число приводит к мнимому числу. Например, √(-4) = 2i).
Например, √(-4) = 2i).Дискриминантная формула кубического уравнения
Дискриминантная формула кубического уравнения ax 3 + bx 2 + cx + d = 0 is, Δ (или) D = b 2 c 2 − 4ac 3 1 г − 27а 2
- . Если D > 0, все три корня действительны и различны.
- Если D = 0, то действительны все три корня, из которых хотя бы два равны между собой.
- Если D < 0, то два его корня — комплексные числа, а третий корень — вещественный.
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Закажите бесплатный пробный урок
Мы можем увидеть применение формул дискриминанта в следующем разделе.
Примеры использования дискриминантных формул
Пример 1: Определить дискриминант квадратного уравнения 5x 2 + 3x + 2 = 0. Также определить природу его корней.
Решение:
Данное квадратное уравнение 5x 2 + 3x + 2 = 0.
Сравнивая это с ax 2 + bx + c = 0, мы получаем a = 5, b = 3, и c = 2.
Используя дискриминантную формулу,
D = b 2 — 4ac
= 3 2 — 4(5)(2)
= 9 — 40
= -31
Ответ: Дискриминант равен -31. Это отрицательное число, поэтому данное квадратное уравнение имеет два комплексных корня.
Пример 2: Определить дискриминант квадратного уравнения 2x 2 + 8x + 8 = 0. Также определить характер его корней.
Решение:
Данное квадратное уравнение равно 2x 2 + 8x + 8 = 0.
Сравнивая это с ax 2 + bx + c = 0, мы получаем a = 2, b = 8 и c = 8.
Используя дискриминантную формулу,
D = b 2 — 4ac
= 8 2 — 4( 2)(8)
= 64 — 64
= 0
Ответ: Дискриминант равен 0 и, следовательно, данное квадратное уравнение имеет два комплексных корня.
Пример 3: Определить природу корней кубического уравнения x 3 — 4x 2 + 6x — 4 = 0.
Решение:
Данным кубическим уравнением является x 3 — 4x 2 + 6x — 4 = 0.
Сравнивая это с , b = -4, c = 6 и d = -4.
Использование дискриминантной формулы,
D = B 2 C 2 -4AC 3 -4B 3 D-27A 2 D 2 + 18ABCD
). (6) 2 − 4(1)(6) 3 − 4(-4) 3 (-4) − 27(1) 2 (-4) 2 + 18(1)(-4)(6)(-4)= -16
Ответ: Поскольку дискриминант является отрицательным числом, данное кубическое уравнение имеет два комплексных корня и один действительный корень.
Часто задаваемые вопросы о формулах дискриминанта
Что такое формулы дискриминанта?
Дискриминант полиномиального уравнения – это функция, выраженная через его коэффициенты. Дискриминант уравнения используется для определения характера его корней. Дискриминантные формулы следующие:
- Дискриминантная формула квадратного уравнения ax 2 + bx + c = 0 is, Δ (или) D = b 2 — 4ac.
- Дискриминантная формула уравнения куба − 27a 2 d 2 + 18abcd.
Как вывести дискриминантную формулу квадратного уравнения?
Выведем дискриминантную формулу квадратного уравнения ax 2 + bx + c = 0. По квадратичной формуле решения этого уравнения находятся с помощью x = [-b ± √ (b 2 — 4ac) ] / [2a]. Здесь b 2 — 4ac находится внутри квадратного корня, и, следовательно, мы можем определить природу корней, используя свойства квадратного корня (например, квадратный корень из положительного числа является действительным числом, квадратный корень из a отрицательное число является мнимым числом, а квадратный корень из 0 равен 0).
Таким образом, дискриминант квадратного уравнения равен b 2 — 4ач.
Каковы применения формулы дискриминанта?
Формула дискриминанта используется для определения природы корней квадратного уравнения. Дискриминант квадратного уравнения ax 2 + bx + c = 0 равен D = b 2 — 4ac.
- Если D > 0, то уравнение имеет два действительных различных корня.
- Если D = 0, то уравнение имеет только один действительный корень.
- Если D < 0, то уравнение имеет два различных комплексных корня.
Что такое дискриминантная формула кубического уравнения?
Дискриминантная формула кубического уравнения ax 3 + bx 2 + cx + d = 0 обозначается Δ (или) D и находится по формуле Δ (или) D = b 2 c 2 − 4ac 3 − 4b 3 d − 27a 2 d 2 + 18abcd.
Формула, правила, дискриминант квадратного уравнения
Дискриминант широко используется в случае квадратных уравнений и используется для определения природы корней.
Хотя найти дискриминант для любого многочлена не так просто, существуют формулы для нахождения дискриминанта квадратных и кубических уравнений, которые облегчают нашу работу.
Давайте узнаем больше о дискриминанте и его формулах, а также поймем связь между дискриминантом и природой корней.
| 1. | Что такое дискриминант в математике? |
| 2. | Дискриминантная формула |
| 3. | Как найти дискриминант? |
| 4. | Дискриминант и природа корней |
| 5. | Часто задаваемые вопросы о дискриминанте |
Что такое дискриминант в математике?
Дискриминант полинома в математике является функцией коэффициентов полинома. Полезно определить тип решений полиномиального уравнения, не находя их. т. е. он различает решения уравнения (как равные и неравные; действительные и недействительные), отсюда и название «дискриминант».
Дискриминантная формула
Дискриминант (Δ или D) любого полинома выражается через его коэффициенты. Вот дискриминантные формулы для кубического уравнения и квадратного уравнения.
Давайте посмотрим, как использовать эти формулы для нахождения дискриминанта.
Как найти дискриминант?
Чтобы найти дискриминант кубического уравнения или квадратного уравнения, мы просто должны сравнить данное уравнение с его стандартной формой и сначала определить коэффициенты. Затем подставляем коэффициенты в соответствующую формулу, чтобы найти дискриминант. 9{2}-4 а в}}{2 а}\). Здесь выражение, которое находится внутри квадратного корня квадратной формулы, называется дискриминантом квадратного уравнения
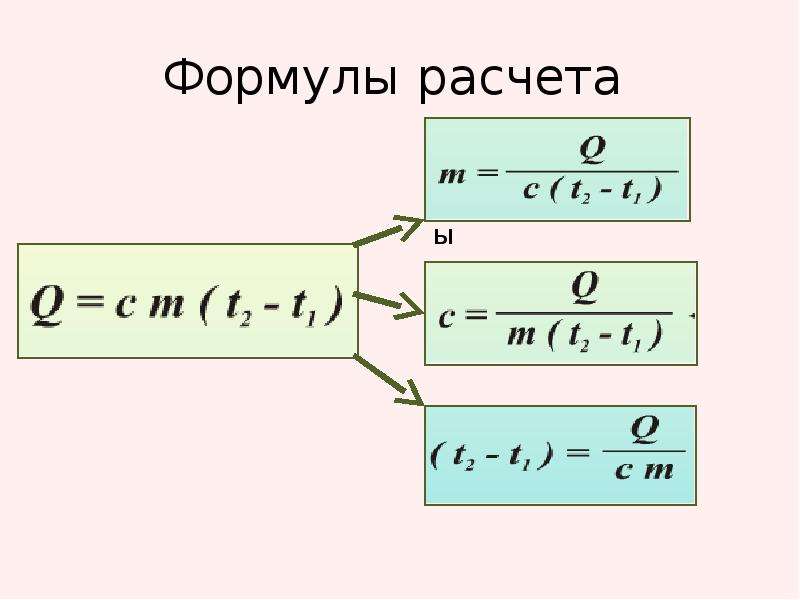
Пример: Найти дискриминант квадратного уравнения 2x 2 — 3x + 8 = 0.
Сравнивая уравнение с ax 2 + bx + c = 0, получаем a = 2, b = — 3 и c = 8. Таким образом, дискриминант равен 9.0379 Δ ИЛИ D = b 2 — 4ac = (-3) 2 — 4(2)(8) = 9 — 64 = -55 .
Дискриминант кубического уравнения
Дискриминант кубического уравнения ax 3 + bx 2 + cx + d = 0 выражается через a, b, c и d. т.е.,
- Δ или D = B 2 C 2 — 4AC 3 — 4B 3 D — 27A 2 D 2 + 18ABCD 9662666 2 D 2 + 18ABCD 6666666666666666666666666666666666666666666666666666666666666666666 2 D 2 + 18ABCD D
Пример: Найти дискриминант кубического уравнения x 3 — 3x + 2 = 0.
Сравнивая уравнение с ax 3 + bx 2 + cx + d = 0, мы имеем a = 1, b = 0, c = -3 и d = 2.
Таким образом, его дискриминант равен
Δ или D = b 2 c 2 − 4ac 3 − 4b 3 d − 27a 2 d 918ab014 2 2 = (0) 2 (-3) 2 — 4(1)(-3) 3 — 4(0) 3 (2) — 27(1) 2 (2) 2 + 18(1)(0)(-3)(2)
= 0 + 108 — 0 — 108 + 0
= 0
Дискриминант и природа корней
Корни квадратного уравнения ax 2 + bx + c = 0 — это значения x, которые удовлетворяют уравнению. Их можно найти по квадратичной формуле: x = \(\dfrac{-b \pm \sqrt{D}}{2 a}\). Хотя мы не можем найти корни, просто используя дискриминант, мы можем определить природу корней следующим образом.
Если дискриминант положительный
Если D > 0, квадратное уравнение имеет два разных действительных корня. Это связано с тем, что при D > 0 корни задаются как x = \(\dfrac{-b \pm \sqrt{\text {Положительное число}}}{2 a}\) и квадратный корень из положительного число всегда приводит к действительному числу.
Таким образом, когда дискриминант квадратного уравнения больше 0, оно имеет два корня, которые являются различными и действительными числами.
Если дискриминант отрицателен
Если D < 0, квадратное уравнение имеет два разных комплексных корня. Это связано с тем, что при D < 0 корни задаются как x = \(\dfrac{-b \pm \sqrt{\text {Отрицательное число}}}{2 a}\) и квадратный корень из отрицательного число всегда приводит к мнимому числу. Например, \(\sqrt{-4}\) = 2i. Таким образом, когда дискриминант квадратного уравнения меньше 0, оно имеет два корня, которые являются различными и комплексными числами (недействительными).
Если дискриминант равен нулю
Если D = 0, квадратное уравнение имеет два равных действительных корня . Другими словами, когда D = 0, квадратное уравнение имеет только один действительный корень. Это связано с тем, что при D = 0 корни задаются как x = \(\dfrac{-b \pm \sqrt{\text {0}}}{2 a}\), а квадратный корень из 0 равен 0 , Тогда уравнение превращается в x = -b/2a, который является только одним числом.
Таким образом, когда дискриминант квадратного уравнения равен нулю, оно имеет только один действительный корень.
Корень есть не что иное, как координата x точки пересечения x квадратичной функции. График квадратичной функции в каждом из этих 3 случаев может быть следующим.
Важные замечания по дискриминанту:
Связанные темы:
- Решение квадратных уравнений
- Дискриминантный калькулятор
- Факторинг Квадратика
- Квадратные выражения
- Квадратичная функция
Часто задаваемые вопросы о дискриминанте
Что такое дискриминант?
Дискриминант в математике определяется для многочленов и является функцией коэффициентов многочленов. Он говорит о природе корней или, другими словами, различает корни. Например, дискриминант квадратного уравнения используется для нахождения:
- Сколько у него корней?
- Являются ли корни реальными или ненастоящими?
Что такое дискриминантная формула?
Существуют разные формулы дискриминанта для разных полиномов:
Как вычислить дискриминант квадратного уравнения?
Чтобы вычислить дискриминант квадратного уравнения:
- Определите a, b и c, сравнив данное уравнение с ax 2 + bx + c = 0,
- Подставляем значения в дискриминантную формулу D = b 2 − 4ac.
Что делать, если дискриминант = 0?
Если дискриминант квадратного уравнения ax 2 + bx + c = 0 равен 0 (т. е. если b 2 — 4ac = 0), то квадратная формула принимает вид x = -b/2a и, следовательно, квадратичная уравнение имеет только один действительный корень.
Что говорит нам положительный дискриминант?
Если дискриминант квадратного уравнения ax 2 + bx + c = 0 положителен (т. е. если b 2 — 4ac > 0), тогда квадратная формула становится x = (-b ± √(положительное число)) / 2a, и, следовательно, квадратное уравнение имеет только два действительных и различных корня.
Что говорит нам отрицательный дискриминант?
Если дискриминант квадратного уравнения ax 2 + bx + c = 0 отрицателен (т. е. если b 2 — 4ac < 0), то квадратная формула принимает вид x = (-b ± √(отрицательное число) )) / 2a и, следовательно, квадратное уравнение имеет только два комплексных и различных корня.