Формула д 0: Дискриминант. Формула дискриминанта.

Формула квадратного уравнения дискриминант равен 0. Будьте всегда в настроении

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Эта тема поначалу может показаться сложной из-за множества не самых простых формул. Мало того что сами квадратные уравнения имеют длинные записи, еще и корни находятся через дискриминант. Всего получается три новые формулы. Не очень просто запомнить. Это удается только после частого решения таких уравнений. Тогда все формулы будут вспоминаться сами собой.

Общий вид квадратного уравнения

Здесь предложена их явная запись, когда самая большая степень записана первой, и дальше — по убыванию. Часто бывают ситуации, когда слагаемые стоят вразнобой. Тогда лучше переписать уравнение в порядке убывания степени у переменной.

Введем обозначения. Они представлены в таблице ниже.

Если принять эти обозначения, все квадратные уравнения сводятся к следующей записи.

Причем коэффициент а ≠ 0. Пусть эта формула будет обозначена номером один.

Когда уравнение задано, то непонятно, сколько корней будет в ответе. Потому что всегда возможен один из трех вариантов:

• в решении будет два корня;
• ответом будет одно число;
• корней у уравнения не будет совсем.

И пока решение не доведено до конца, сложно понять, какой из вариантов выпадет в конкретном случае.

Виды записей квадратных уравнений

В задачах могут встречаться их разные записи. Не всегда они будут выглядеть как общая формула квадратного уравнения. Иногда в ней будет не хватать некоторых слагаемых. То что было записано выше — это полное уравнение. Если в нем убрать второе или третье слагаемое, то получится нечто другое. Эти записи тоже называются квадратными уравнениями, только неполными.

Причем исчезнуть могут только слагаемые у которых коэффициенты «в» и «с». Число «а» не может быть равно нулю ни при каких условиях. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполного вида уравнений будут такими:

Итак, видов всего два, кроме полных, есть еще и неполные квадратные уравнения. Пусть первая формула будет иметь номер два, а вторая — три.

Дискриминант и зависимость количества корней от его значения

Это число нужно знать для того, чтобы вычислить корни уравнения. Оно может быть посчитано всегда, какой бы ни была формула квадратного уравнения. Для того чтобы вычислить дискриминант, нужно воспользоваться равенством, записанным ниже, которое будет иметь номер четыре.

После подстановки в эту формулу значений коэффициентов, можно получить числа с разными знаками. Если ответ положительный, то ответом уравнения будут два различных корня. При отрицательном числе корни квадратного уравнения будут отсутствовать. В случае его равенства нулю ответ будет один.

Как решается квадратное уравнение полного вида?

По сути, рассмотрение этого вопроса уже началось. Потому что сначала нужно найти дискриминант. После того как выяснено, что имеются корни квадратного уравнения, и известно их число, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу.

Поскольку в ней стоит знак «±», то значений будет два. Выражение под знаком квадратного корня — это дискриминант. Поэтому формулу можно переписать по-другому.

Формула номер пять. Из этой же записи видно, что если дискриминант равен нулю, то оба корня примут одинаковые значения.

Если решение квадратных уравнений еще не отработано, то лучше до того, как применять формулы дискриминанта и переменной, записать значения всех коэффициентов. Позже этот момент не будет вызывать трудностей. Но в самом начале бывает путаница.

Как решается квадратное уравнение неполного вида?

Здесь все гораздо проще. Даже нет необходимости в дополнительных формулах. И не понадобятся те, что уже были записаны для дискриминанта и неизвестной.

Сначала рассмотрим неполное уравнение под номером два. В этом равенстве полагается вынести неизвестную величину за скобку и решить линейное уравнение, которое останется в скобках. В ответе будет два корня. Первый — обязательно равен нулю, потому что имеется множитель, состоящий из самой переменной. Второй получится при решении линейного уравнения.

Неполное уравнение под номером три решается переносом числа из левой части равенства в правую. Потом нужно разделить на коэффициент, стоящий перед неизвестной. Останется только извлечь квадратный корень и не забыть записать его два раза с противоположными знаками.

Далее записаны некоторые действия, помогащие научиться решать всевозможные виды равенств, которые превращаются в квадратные уравнения. Они будут способствовать тому, что ученик сможет избежать ошибок по невнимательности. Эти недочеты бывают причиной плохих оценок при изучении обширной темы «Квадратные уравнения (8 класс)». Впоследствии эти действия не нужно будет постоянно выполнять. Потому что появится устойчивый навык.

• Сначала нужно записать уравнение в стандартном виде. То есть сначала слагаемое с самой большой степенью переменной, а потом — без степени и последним — просто число.

• Если перед коэффициентом «а» появляется минус, то он может усложнить работу для начинающего изучать квадратные уравнения. От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.

• Таким же образом рекомендуется избавляться от дробей. Просто умножить уравнение на соответствующий множитель, чтобы знаменатели сократились.

Примеры

Требуется решить следующие квадратные уравнения:

х 2 − 7х = 0;

15 − 2х − х 2 = 0;

х 2 + 8 + 3х = 0;

12х + х 2 + 36 = 0;

(х+1) 2 + х + 1 = (х+1)(х+2).

Первое уравнение: х 2 − 7х = 0. Оно неполное, поэтому решается так, как было описано для формулы под номером два.

После вынесения за скобки получается: х (х — 7) = 0.

Первый корень принимает значение: х 1 = 0. Второй будет найден из линейного уравнения: х — 7 = 0. Легко заметить, что х 2 = 7.

Второе уравнение: 5х 2 + 30 = 0.

Снова неполное. Только решается оно так, как описано для третьей формулы.

После перенесения 30 в правую часть равенства: 5х 2 = 30. Теперь нужно выполнить деление на 5. Получается: х 2 = 6. Ответами будут числа: х 1 = √6, х 2 = — √6.

Третье уравнение: 15 − 2х − х 2 = 0. Здесь и далее решение квадратных уравнений будет начинаться с их переписывания в стандартный вид: − х 2 − 2х + 15 = 0. Теперь пришло время воспользоваться вторым полезным советом и умножить все на минус единицу. Получается х 2 + 2х — 15 = 0. По четвертой формуле нужно вычислить дискриминант: Д = 2 2 — 4 * (- 15) = 4 + 60 = 64. Он представляет собой положительное число. Из того, что сказано выше, получается, что уравнение имеет два корня. Их нужно вычислить по пятой формуле. По ней получается, что х = (-2 ± √64) / 2 = (-2 ± 8) / 2. Тогда х 1 = 3, х 2 = — 5.

Четвертое уравнение х 2 + 8 + 3х = 0 преобразуется в такое: х 2 + 3х + 8 = 0. Его дискриминант равен такому значению: -23. Поскольку это число отрицательное, то ответом к этому заданию будет следующая запись: «Корней нет».

Пятое уравнение 12х + х 2 + 36 = 0 следует переписать так: х 2 + 12х + 36 = 0. После применения формулы для дискриминанта получается число ноль. Это означает, что у него будет один корень, а именно: х = -12/ (2 * 1) = -6.

Шестое уравнение (х+1) 2 + х + 1 = (х+1)(х+2) требует провести преобразования, которые заключаются в том, что нужно привести подобные слагаемые, до того раскрыв скобки. На месте первой окажется такое выражение: х 2 + 2х + 1. После равенства появится эта запись: х 2 + 3х + 2. После того как подобные слагаемые будут сосчитаны, уравнение примет вид: х 2 — х = 0. Оно превратилось в неполное. Подобное ему уже рассматривалось чуть выше. Корнями этого будут числа 0 и 1.

Копьевская сельская средняя общеобразовательная школа

10 способов решения квадратных уравнений

Руководитель: Патрикеева Галина Анатольевна,

учитель математики

с.Копьево, 2007

1. История развития квадратных уравнений

1.1 Квадратные уравнения в Древнем Вавилоне

1. 2 Как составлял и решал Диофант квадратные уравнения

1.3 Квадратные уравнения в Индии

1.4 Квадратные уравнения у ал- Хорезми

1.5 Квадратные уравнения в Европе XIII — XVII вв

1.6 О теореме Виета

2. Способы решения квадратных уравнений

Заключение

Литература

1. История развития квадратных уравнений

1.1 Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

X 2 + X = ¾; X 2 — X = 14,5

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

1.2 Как составлял и решал Диофант квадратные уравнения.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96»

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х , другое же меньше, т.е. 10 — х . Разность между ними 2х .

Отсюда уравнение:

(10 + х)(10 — х) = 96

100 — х 2 = 96

х 2 — 4 = 0 (1)

Отсюда х = 2 . Одно из искомых чисел равно 12 , другое 8 . Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения

у(20 — у) = 96,

у 2 — 20у + 96 = 0. (2)

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).

1.3 Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ах 2 + b х = с, а > 0. (1)

В уравнении (1) коэфиценты, кроме а , могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

Задача 13.

«Обезьянок резвых стая А двенадцать по лианам…

Власть поевши, развлекалась. Стали прыгать, повисая…

Их в квадрате часть восьмая Сколько ж было обезьянок,

На поляне забавлялась. Ты скажи мне, в этой стае?»

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).

Соответствующее задаче 13 уравнение:

( x /8) 2 + 12 = x

Бхаскара пишет под видом:

х 2 — 64х = -768

и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:

х 2 — 64х + 32 2 = -768 + 1024,

(х — 32) 2 = 256,

х — 32 = ± 16,

х 1 = 16, х 2 = 48.

1.4 Квадратные уравнения у ал – Хорезми

В алгебраическом трактате ал — Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корнями», т.е. ах 2 + с = b х.

2) «Квадраты равны числу», т.е. ах 2 = с.

3) «Корни равны числу», т.е. ах = с.

4) «Квадраты и числа равны корням», т. е. ах 2 + с = b х.

5) «Квадраты и корни равны числу», т.е. ах 2 + bx = с.

6) «Корни и числа равны квадратам», т.е. bx + с = ах 2 .

Для ал — Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида

ал — Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал — Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.

Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).

Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Трактат ал — Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.

1.5 Квадратные уравнения в Европе XIII — XVII вв

Формулы решения квадратных уравнений по образцу ал — Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения.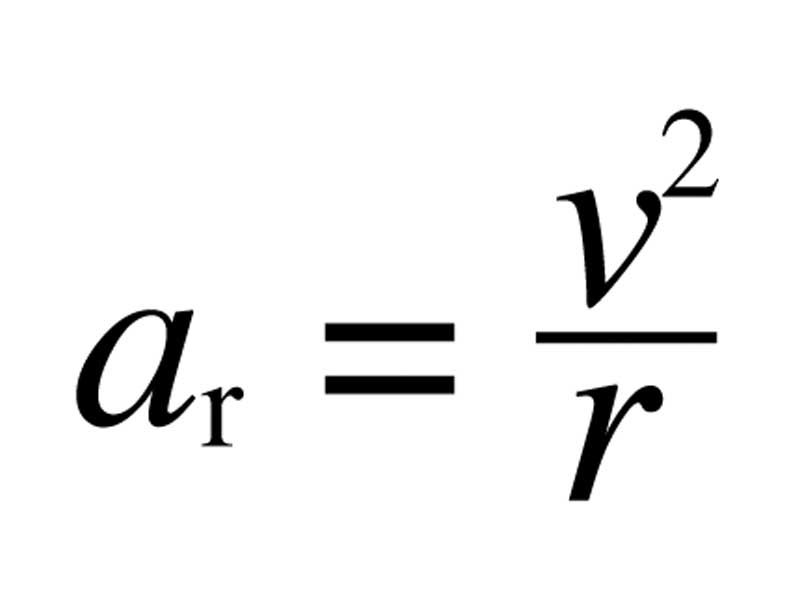 Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:

х 2 + bx = с,

при всевозможных комбинациях знаков коэффициентов b , с было сформулировано в Европе лишь в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

1.6 О теореме Виета

Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D , умноженное на A — A 2 , равно BD , то A равно В и равноD ».

Чтобы понять Виета, следует вспомнить, что А , как и всякая гласная буква, означало у него неизвестное (наше х ), гласные же В, D — коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место

(а + b )х — х 2 = ab ,

х 2 — (а + b )х + а b = 0,

х 1 = а, х 2 = b .

Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и по этому при решении уравнений рассматривал лишь случаи, когда все корни положительны.

2. Способы решения квадратных уравнений

Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.

Просто. По формулам и чётким несложным правилам. На первом этапе

надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно. Самое главное — правильно

определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения.

Выражение под знаком корня называется дискриминант . Как видим, для нахождения икса, мы

используем только a, b и с . Т.е. коэффициенты из квадратного уравнения . Просто аккуратно подставляем

значения a, b и с в эту формулу и считаем. Подставляем со своими знаками!

Например , в уравнении:

а =1; b = 3; c = -4.

Подставляем значения и записываем:

Пример практически решён:

Это ответ.

Самые распространённые ошибки — путаница со знаками значений a, b и с . Вернее, с подстановкой

отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы

с конкретными числами. Если есть проблемы с вычислениями, так и делайте!

Предположим, надо вот такой пример решить:

Здесь a = -6; b = -5; c = -1

Расписываем все подробно, внимательно, ничего не упуская со всеми знаками и скобками:

Часто квадратные уравнения выглядят слегка иначе. Например, вот так:

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок.

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду.

Что это означает?

Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с.

Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

Избавьтесь от минуса. Как? Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример.

Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета .

Для решения приведённых квадратных уравнений, т.е. если коэффициент

x 2 +bx+c=0,

тогда x 1 x 2 =c

x 1 +x 2 =− b

Для полного квадратного уравнения, в котором a≠1 :

x 2 + b x+ c =0,

делим все уравнение на а:

→ →

где x 1 и x 2 — корни уравнения.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте

уравнение на общий знаменатель.

Вывод. Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего

уравнения на -1.

3. Если коэффициенты дробные — ликвидируем дроби умножением всего уравнения на соответствующий

множитель.

4. Если икс в квадрате — чистый, коэффициент при нём равен единице, решение можно легко проверить по

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Формула дискриминанта 0: Дискриминант. Формула дискриминанта. — ЭкоДом: Дом своими руками

Содержание

Внеклассный урок — Формулы корней квадратного уравнения. Дискриминант

 

Формулы корней квадратного уравнения. Дискриминант.

  

Формула №1:

         —b ± √D
x =  ————,  где D = b² – 4ac.
             2a

Латинской буквой D обозначают дискриминант.

Дискриминант — это выражение, от которого зависит число корней данного уравнения.

Если D < 0, то уравнение не имеет корней.

Если D = 0, то уравнение имеет один корень.

Если D > 0, то уравнение имеет два корня.

Пример. Решим уравнение 12x² + 7x + 1 = 0.

Сначала вычислим дискриминант.

Мы видим, что а = 12, b = 7, c = 1.

Итак:

D = b² – 4ac = 7² – 4 · 12 · 1 = 49 – 48 = 1.

D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.

Чтобы найти корни, применим формулу корней квадратного уравнения:

         —b ± √D      -7 ± √1         -7 ± 1
x =  ———— = ———— = ————
             2a                24                 24

Находим оба значения x:

        -7 + 1        -6      -1          1
x₁ = ——— = —— = — = – —
           24           24       4          4

 

         -7 – 1       -8       -1         1
x₂ = ——— = —— = — = – — .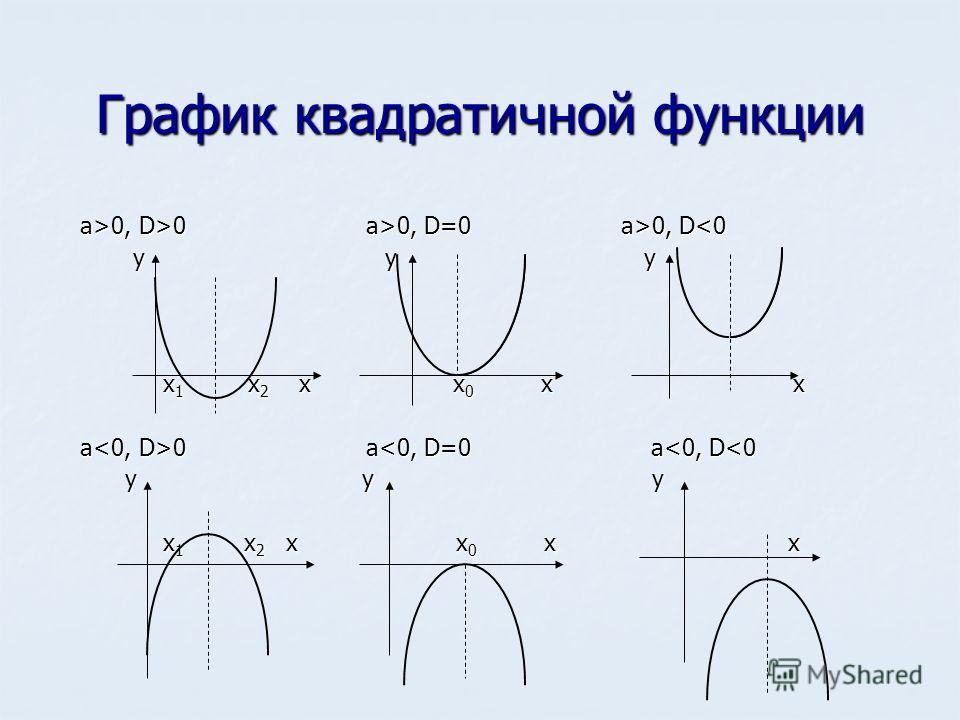
           24           24       3          3

 

                        1                   1
Ответ: x₁ = – —,    x₂ = – —
                        4                   3

 

Формула №2.

Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:

      —k ± √D₁
x = ————,   где D₁ = k² – ac
             a

Пример. Решим уравнение 5x² – 16x + 3 = 0.

Записываем -16x в виде 2 · (-8x). Тогда k = -8,  a = 5,  c = 3. Мы уже можем найти дискриминант D₁:

D₁ = k² – ac = (-8)² – 5 · 3 = 64 – 15 = 49.

Теперь находим оба значения x:

      —k ± √D₁       — (-8) ± √49      8 ± 7
x = ———— =  ————— = ———
             a                     5                  5

Отсюда:

          8 + 7       15
x₁ = ——— =  — = 3
            5            5

 

         8 – 7         1
x₂ = ——— =  — = 0,2
             5           5 

 

Ответ: x₁ = 3; x₂ = 0,2.

 

При решении квадратного уравнения по данным формулам целесообразно поступать следующим образом:

1) вычислить дискриминант и сравнить его с нулем;

2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней; если дискриминант отрицателен, то записать, что корней нет.

 

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k² − ac, а корни по формулам и .

Примеры

Решим квадратное уравнение x² + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.

Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.

n = 2k

Например, число 10 можно представить как 2 × 5.

10 = 2 × 5

В этом произведении k = 5.

---

Число 12 можно представить как 2 × 6.

12 = 2 × 6

В этом произведении k = 6.

---

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7.

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.

В уравнении x² + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = 3² − 1 × (−16) = 9 + 16 = 25

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x² + 6x − 16 = 0 являются числа 2 и −8.

В отличие от стандартной формулы для вычисления дискриминанта (D=b² − 4ac), в формуле D₁ = k² − ac не нужно выполнять умножение числа 4 на ac.

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

---

Пример 2. Решить квадратное уравнение 5x² − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−3)² − 5 × 1 = 9 − 5 = 4

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

---

Пример 3. Решить квадратное уравнение x² − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−5)² − 1 × (−24) = 25 + 24 = 49

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

---

Пример 5. Решить квадратное уравнение

Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k. Получается, что

Найдём дискриминант по формуле D₁ = k² − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2.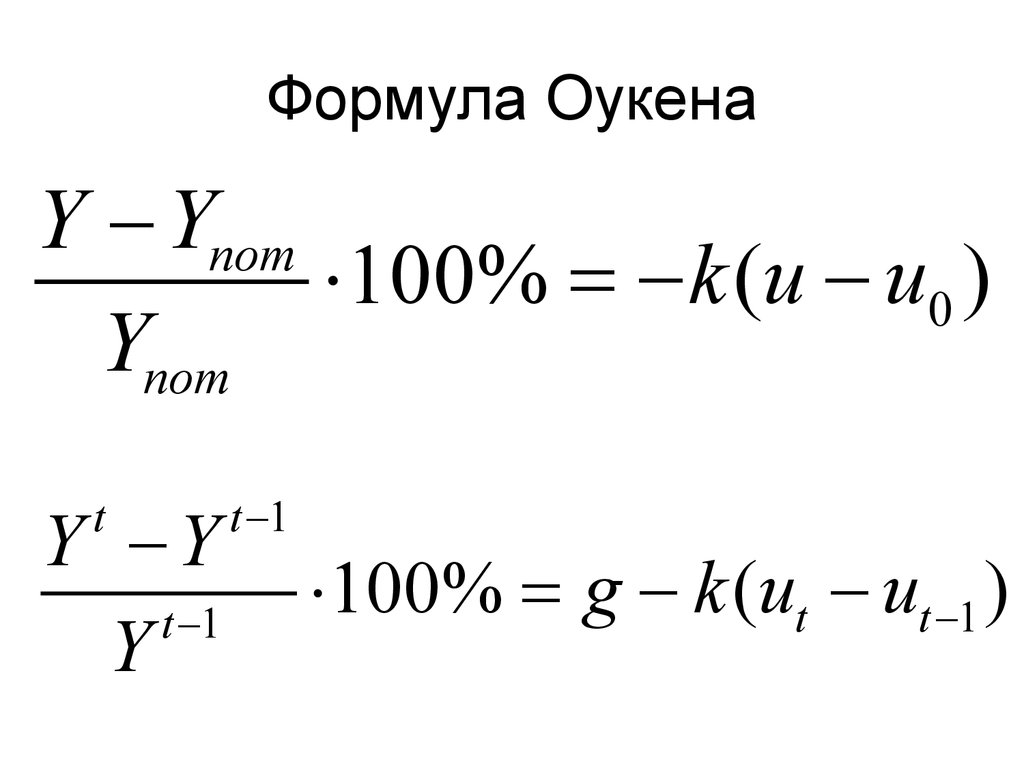 Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .

Вычислим второй корень уравнения:

---

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax² + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

b = 2k

Заменим в уравнении ax² + bx + c = 0 коэффициент b на выражение 2k

ax² + 2kx + c = 0

Теперь вычислим дискриминант по ранее известной формуле:

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac

Вынесем в получившемся выражении за скобки общий множитель 4

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac = 4(k² − ac)

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k² − ac.

В выражении 4(k² − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k² − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k² − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

D₁ = k² − ac

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax² + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k² − ac)

Но ранее было сказано, что выражение k² − ac обозначается через D₁. Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Задания для самостоятельного решения

Задание 1. Решить уравнение:

Решение:

Ответ: 1; 0,6

Задание 2. Решить уравнение:

Решение:

Ответ:

Задание 3. Решить уравнение:

Решение:

Ответ: 1; −1,4

Задание 4. Решить уравнение:

Решение:

Ответ:

Задание 5. Решить уравнение:

Решение:

Ответ:

Задание 6. Решить уравнение:

Решение:

Ответ:

Задание 7. Решить уравнение:

Решение:

Ответ:

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Что делать если дискриминант меньше нуля

Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

x_1;2 =

−b ± √ b 2 − 4ac

2a

Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

x_1;2 =

, где « D = b 2 − 4ac »

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай

D > 0
(дискриминант больше нуля)

D –> , где « D = b 2 − 4ac »
–> –> D = b 2 − 4ac
D = 5 2 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0

x_1;2 =

x_1;2 =

x_1;2 =

x₂ =−5 − 94x₁ =44x₂ =−144x₁ = 1x₂ = −324x₁ = 1x₂ = −312

Ответ: x₁ = 1; x₂ = −3

Вывод: когда « D > 0 » в квадратном уравнении два корня .

II случай

D = 0
(дискриминант равен нулю)

16x 2 − 8x + 1 = 0

D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0

x_1;2 =

x_1;2 =

x_1;2 =

x =

x =

Ответ: x =

Вывод: когда « D = 0 » в квадратном уравнении один корень .

III случай

D
(дискриминант меньше нуля)

D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D

x_1;2 =

x_1;2 =

Ответ: нет действительных корней

Вывод: когда « D » в квадратном уравнении нет корней .

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример 42.4. Решить уравнение: .

Решение. Найдем дискриминант: = 36 – 52 = -16.

.

Тогда .

Ответ:

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Дата добавления: 2014-12-27 ; Просмотров: 12919 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

1. Если дискриминант больше нуля, то уравнение имеет два корня.
2. Если дискриминант равен нулю, то уравнение имеет один корень.
3. Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-4) 2 – 4 · 3 · 2 = 16 – 24 = -8, D 2 – 6x + 9 = 0

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-6) 2 – 4 · 1 · 9 = 36 – 36 = 0, D = 0

Уравнение имеет всего один корень:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-4) 2 – 4 · 1 · (-5) = 16 + 20 = 36, D > 0

Дискриминант на 4 | Алгебра

Дискриминант, делённый на 4 — D/4 — удобно использовать для упрощения вычислений при решении квадратных уравнений, если коэффициент b при x — чётное число.

Формула дискриминанта, деленного на 4 —

   

Как и для случая с обычным дискриминантом, количество корней  квадратного уравнения зависит от знака D/4.

• Если D/4>0, квадратное уравнение имеет два корня:

     

• Если D/4=0, квадратное уравнение имеет один корень

     

• Если D/4<0, квадратное уравнение не имеет действительных корней.

Рассмотрим примеры решения квадратных уравнений с помощью формулы четверти дискриминанта.

   

   

Так как b=16 — чётное число, вместо обычного дискриминанта вычислим дискриминант, делённый на 4 (иногда его еще обозначают через D1):

   

Так как D/4>0, уравнение имеет два корня:

   

   

   

Ответ: -0,2; -3.

   

   

   

   

Поскольку D/4>0, уравнение имеет два корня:

   

   

   

   

Ответ: 9; 1/3.

   

   

   

   

Так как D/4=0, данное квадратное уравнение имеет один корень

   

Ответ: -2 1/3.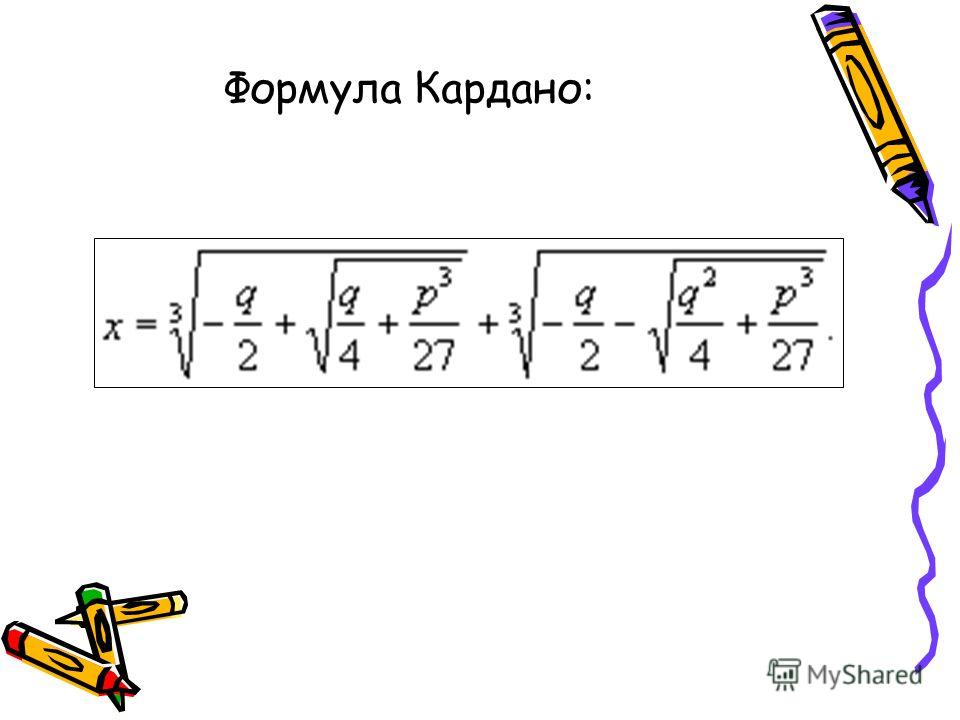

   

   

   

   

Так как D/4<0, уравнение не имеет корней в действительных числах.

Ответ: нет корней.

Для решения квадратных уравнений вполне достаточно помнить обычную формулу дискриминанта и связанные с ним формулы корней. И все же, дополнительное знание формулы четверти дискриминанта не будет лишним.

Во-первых, с меньшими (по модулю) числами проще работать. Во-вторых, эта формула иногда ускоряет процесс нахождения корней уравнения.

   

   

   

   

Если находить корни через формулу обычного дискриминанта, придётся раскладывать его на множители, выносить множитель из-под корня, затем общий множитель — за скобки и сокращать дробь.

Ответ:

   

 

Квадратное уравнение. Решение квадратных уравнений.

Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.

Решение квадратных уравнений. Дискриминант. Формула дискриминанта.

Теорема Виета.

Квадратным уравнением называется уравнение вида:

                 ,

где
x — переменная,
a,b,c — постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта

Формула дискриминанта:

.

О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

• D>0 — уравнение имеет 2 различных вещественных корня
• D=0 — уравнение имеет 2 совпадающих вещественных корня
• D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)

В общем случае корни уравнения равны:

                 .

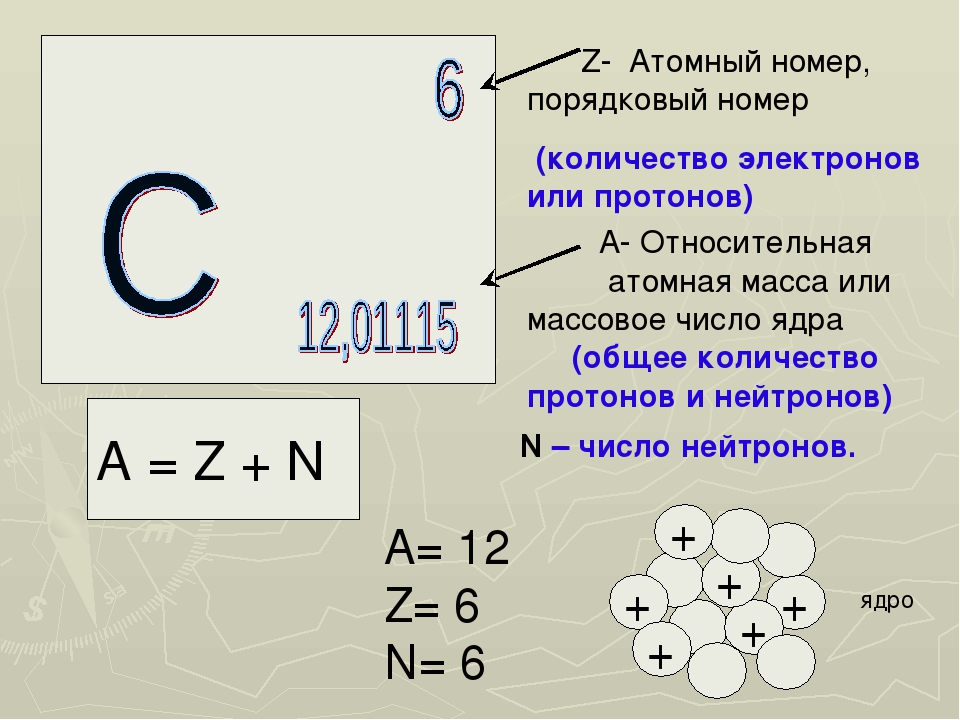
Очевидно, в случае с нулевым дискриминантом, оба корня равны

                 .

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

                

В таком случае корни уравнения вычисляются по формуле:

                

Теорема Виета.

Приведенным квадратным уравнением называется уравнение вида

                ,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

                 .

Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х²

Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта.

( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.

	Адрес этой страницы (вложенность) в справочнике dpva. ru:  главная страница  / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы.  / / Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа. Поделиться:    Квадратное уравнение. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.     Версия для печати. Квадратным уравнением называется уравнение вида:                  , где x — переменная, a,b,c — постоянные (числовые) коэффициенты. В общем случае решение квадратных уравнений сводится к нахождению дискриминанта Формула дискриминанта: . О корнях квадратного уравнения можно судить по знаку дискриминанта (D) : D>0 — уравнение имеет 2 различных вещественных корня D=0 — уравнение имеет 2 совпадающих вещественных корня D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет) В общем случае корни уравнения равны:                  . Очевидно, в случае с нулевым дискриминантом, оба корня равны                  . Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:                  В таком случае корни уравнения вычисляются по формуле:                  Теорема Виета о корнях квадратного уранения. Приведенным квадратным уравнением называется уравнение вида                 , то есть квадратное уравнение с единичным коэффициентом при старшем члене. В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:                  . Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х2 Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Квадратное уравнение

Квадратное уравнение

— это уравнение вида a x² + b x + c = 0, где a не равно 0.

Геометрический смысл

Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют точки пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.

Если коэффициент a положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.

Вывод формулы для решения квадратного уравнения

Формулу для решения квадратного уравнения a x² + b x + c = 0 можно получить так:

• перенесем c в правую часть a x² + b x = — c
• умножим уравнение на 4a (2a x)² + 4a b x = — 4a c
• добавим b² к обоим частям (2a x)² + 4a b x + b² = b² — 4a c
• в левой части выделим полный квадрат (2a x + b)² = b² — 4a c
• извлечем квадратный корень 2a x + b = ± √b² — 4a c
• перенесем b в правую часть 2a x = — b ± √b² — 4a c
• разделим уравнение на 2a
  

  x =	-b ± √b2 — 4a c
  	2 a

Дискриминант квадратного уравнения

Дискриминантом

квадратного уравнения называют число равное D = b² − 4ac

Квадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта:

• при D > 0 корней два, и они вычисляются по формуле
  

  x1,2 =	-b ± √D
  	2 a

• при D = 0 корень один (два равных или совпадающих корня), кратности 2:
• при D
  x_1,2 = -b ± i√-D2 a

Теорема Виета

Приведенным квадратным уравнением

называется уравнение, в котором коэффициент при x² равен единице. Такое уравнение может быть получено делением всего выражения на коэффициент a: x² + px + q = 0,
где p = ba, q = ca

Сумма корней приведённого квадратного уравнения

x² + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
      x₁ + x₂ = -p,      x₁x₂ = q.

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле

ax² + bx + c = a(x — x₁)(x — x₂)

Примеры решения квадратных уравнений

Например. Найти корни квадратного уравнения: 2x² + 5x + 3 = 0

D = 5² — 4·3·2 = 25 — 24 = 1

x1 =  —5 + √1  = -1, 2·2

x2 =  —5 — √1  = -1 1 2·2 2

Упражнения. Квадратные уравнения.

Дискриминанты и определение числа действительных корней квадратного уравнения

Что такое дискриминант?

Дискриминант — это величина, вычисляемая по квадратному уравнению. Он использует его, чтобы «различать» корни (или решения) квадратного уравнения.

Квадратное уравнение имеет вид: ax ² + bx + c

Дискриминант, D = b ² — 4ac

Примечание: это выражение внутри квадратного корня квадратной формулы

.

Дискриминант бывает в трех случаях;

Корпус 1:

b ² — 4ac> 0

Если дискриминант больше нуля, это означает, что квадратное уравнение имеет два действительных, различных (разных) корня .

Пример

х ² — 5х + 2 = 0

а = 1, б = -5, в = 2

Дискриминант, D = b ² — 4ac

= (-5) ² — ^{4 * (1) * (2)}

= 17

Следовательно, квадратное уравнение

имеет два действительных различных корня.

х ² — 5х + 2.

Корпус 2:

b ² — 4ac

Если дискриминант больше нуля, это означает, что квадратное уравнение не имеет действительных корней .

Пример

3x ² + 2x + 1 = 0

а = 3, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ^{2 —} 4 * (3) * (1)

= — 8

Следовательно, у квадратного уравнения 3x ² + 2x + 1 нет действительных корней.

Корпус 3:

b ² — 4ac = 0

Если дискриминант равен нулю, это означает, что квадратное уравнение имеет два действительных идентичных корня .

Пример

х ² + 2х + 1 = 0

а = 1, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ² — 4 * (1) * (1)

= 0

Следовательно, есть два действительных идентичных корня квадратного уравнения x ² + 2x + 1. 2 + bx + c #:

• Если #Delta> 0 # — полный квадрат, то #f (x) # имеет два различных рациональных вещественных нуля. 2-4ac)) / (2a) = (-b + -sqrt (Дельта)) / (2a) #

  , из которого вы можете понять, почему нули имеют тот характер, который они имеют для разных значений # Delta #.2 + 18abcd #

  • Если #Delta> 0 #, то #f (x) # имеет три различных действительных нуля.

  • Если #Delta = 0 #, то #f (x) # имеет либо один действительный ноль кратности # 3 #, либо два различных действительных нуля, один из которых имеет кратность # 2 #, а другой — кратность # 1 #.

  • Если #Delta

  Сколько корней?

  Когда вы решаете корни квадратного уравнения, есть несколько возможных результатов.

  • У вас может быть два вещественных числа. Если вы установите x равным любому решению, результат будет равен нулю оба раза.
  • Может быть только одно вещественное число.
  • Уравнение может иметь два решения комплексных чисел. Реальных числовых решений не существует.

  Не волнуйтесь; есть простой способ узнать, сколько существует решений, еще до того, как вы начнете использовать формулу. Просто взгляните на часть квадратной формулы b ² -4 ac .Этот небольшой кусок называется дискриминантом , и это ключевой вид нашей маленькой квадратичной экосистемы. Без него все развалится.

  • Если значение b ² -4 ac положительно, тогда существует два решения с действительными числами.
  • Если b ² -4 ac = 0, то существует только одно решение для вещественных чисел.
  • Если b ² -4 ac отрицательно, то существует два решения комплексных чисел.

  Все это происходит непосредственно из формулы корней квадратного уравнения. Если дискриминант положительный, то у вас есть, что приводит к двум ответам с действительными числами. Если он отрицательный, то да, что дает два сложных результата. И если b ² -4 ac равно 0, то у вас есть, поэтому у вас есть только одно решение.

  Пример задачи

  Сколько корней у x ² — 3 = 0?

  Чтобы использовать дискриминант, сначала отметим, что a = 1, b = 0 и c = -3.

  b ² — 4 ac = (0) ² — 4 (1) (- 3) = 12

  Итак, у нас есть два настоящих корня. Ха! Слишком легко.

  Хорошо, как насчет этого?

  Сколько корней имеет 2 x ² + 8 x + 8 = 0?

  Эй, прекрати с этой губой, подзаголовок. Почему бы просто не сказать «Пример задачи», как обычно? В любом случае, дискриминант для этого уравнения равен

  b ² — 4 ac = (8) ² — 4 (2) (8) = 64 — 64 = 0

  Это означает, что у нас есть один действительный числовой корень для этого уравнения.

  Тогда как вам этот?

  Сколько корней у 0,7731 x ² — 2,3812 x + 4,1111 = 0?

  Это просто подло — но мы все еще можем это сделать. Просто позвольте нам быстро найти наш калькулятор.

  b ² -4 ac = (-2,3812) ² -4 (0,7731) (4,1111) ≈ 5,6701 — 12,7132 = -7,0431

  Это отрицательное значение, поэтому у этого уравнения есть два комплексных корня . Кроме того, калькулятор находился в массажном кабинете Шмоопа, рядом с грудой учебников по алгебре.Если вам интересно.

  Что он там делал?

  В то время мы могли выполнять несколько задач одновременно. Знаешь, мы очень заняты.

  Дискриминант кубического уравнения

  Дискриминант квадратного уравнения

  a x ² + bx + c = 0

  это

  Δ = b ² — 4 ac .

  Если дискриминант Δ равен нулю, уравнение имеет двойной корень, то есть существует уникальный x , который делает уравнение нулевым, и он дважды считается корнем. Если дискриминант не равен нулю, есть два различных корня.

  Кубические уравнения также имеют дискриминант. Для кубического уравнения

  a x ³ + bx ² + cx + d = 0

  дискриминант равен

  Δ = 18 abcd — 4 b ³ d + b ²c² — 4 ac³ — 27 a ² d ².

  Если Δ = 0, уравнение имеет кратный корень, но в противном случае оно имеет три различных корня.

  Замена переменной может свести общее кубическое уравнение к так называемому «вдавленному» кубическому уравнению вида

  x ³ + px + q = 0

  , в этом случае дискриминант упрощается до

  Δ = — 4 p³ — 27 q ².

  Вот пара интересных связей. Идея сведения кубического уравнения к кубическому с углублением восходит к Кардано (1501–1576). То, что в этом контексте называется углубленной кубикой, известно как форма Вейерштрасса (1815–1897) в контексте эллиптических кривых. То есть эллиптическая кривая вида

  y ² = x ³ + ax + b

  Считается, что

  находится в форме Вейерштрасса. Другими словами, эллиптическая кривая имеет форму Вейерштрасса, если правая часть представляет собой углубленную кубику.

  Кроме того, эллиптическая кривая должна быть невырожденной, что означает, что она должна удовлетворять требованиям

  4 a³ + 27 b ² ≠ 0.

  Другими словами, дискриминант правой части отличен от нуля.В контексте эллиптических кривых дискриминант определяется как

  Δ = -16 (4 a³ + 27 b ²)

  , который совпадает с дискриминантом выше, за исключением коэффициента 16, который упрощает некоторые вычисления с эллиптическими кривыми.

  Примечание о полях

  В контексте решения квадратных и кубических уравнений мы обычно неявно работаем с действительными или комплексными числами. Предположим, что все коэффициенты квадратного уравнения действительны. Если дискриминант положительный, есть два различных действительных корня.Если дискриминант отрицательный, есть два различных комплексных корня, и эти корни являются комплексно сопряженными друг другу.

  Аналогичные замечания справедливы для кубических уравнений, когда все коэффициенты действительны. Если дискриминант положительный, существует три различных действительных корня. Если дискриминант отрицательный, имеется один действительный корень и комплексно сопряженная пара комплексных корней.

  В первом разделе я рассмотрел только, был ли дискриминант нулевым, и поэтому утверждения не зависят от поля, из которого берутся коэффициенты.2} — 4 \ left (1 \ right) \ left (1 \ right)}}} {{2 \ left (1 \ right)}} $$
  $$ = \ frac {{1 \ pm \ sqrt {- 3}}} {2} $$
  $$ = \ frac {{1 \ pm \ sqrt 3 i}} {2} = \ frac {1} {2} \ pm \ frac {{\ sqrt 3}} { 2} i $$

  Таким образом, корнями являются комплексные сопряжения $$ \ frac {1} {2} + \ frac {{\ sqrt 3}} {2} i $$ и $$ \ frac {1} {2} — \ frac { {\ sqrt 3}} {2} i $$

  Равные или двойные корни

  РАВНЫЕ ИЛИ ДВОЙНЫЕ КОРНИ

  Если дискриминант b ² — 4ac равен нулю,

  радикал в формуле корней квадратного уравнения обращается в ноль.

  В этом случае корни равны; таких корней

  иногда называют двойным корнем.

  Рассмотрим уравнение

  9x ² + 12x + 4 = 0

  Сравнивая с общей квадратичной, замечаем, что

  a = 9, b = 12 и c = 4

  Дискриминант

  Следовательно, корни равны.

  ПРОВЕРКА: По формуле

  Равенство корней проверено.

  Корни могут быть равны, только если трехчлен
  это. идеальный квадрат. Его коэффициенты равны.
  Факторизация трехчлена в

  9x ² + 12x + 4 = 0

  видим, что

  (3x + 2) ² = 0

  Поскольку множитель 3x + 2 возведен в квадрат, фактически имеем

  3x + 2 = 0

  дважды, а у нас

  дважды.

  Дело в том, что надо считать один и тот же корень
  дважды объясняет использование термина «двойной»
  корень «. Двойной корень квадратного уравнения — это
  всегда рационально, потому что двойной корень может возникнуть только тогда, когда радикал равен нулю.

  РЕАЛЬНЫЕ И НЕРАВНЫЕ КОРНИ Когда дискриминант положительный, корни

  должно быть настоящим. Также они должны быть неравными, поскольку
  равные корни возникают только тогда, когда дискриминант
  равно нулю.

  Рациональные корни.

  Если дискриминант — полный квадрат,
  корни рациональны. Например, рассмотрим
  уравнение

  3x ² — x — 2 = 0

  , в котором

  a = 3, b = -1 и c = -2

  Дискриминант

  Мы видим, что дискриминант 25 представляет собой полный квадрат. Идеальный квадрат указывает на то, что

  радикал в квадратной формуле может быть удален, что корни уравнения рациональны, и что трехчлен можно факторизовать.Другими словами, когда мы оцениваем дискриминант и обнаруживаем, что он представляет собой идеальный квадрат, мы знаем, что

  что трехчлен можно разложить на множители.

  Таким образом,

  , из которых

  Мы видим, что информация, полученная из
  дискриминант правильный. Корни настоящие,
  неравный и рациональный.

  % PDF-1.4
  %
  388 0 объект
  >
  эндобдж

  xref
  388 168
  0000000016 00000 н.
  0000004866 00000 н.
  0000004980 00000 н.
  0000006585 00000 н.
  0000006913 00000 н.
  0000007027 00000 н.
  0000007382 00000 п.
  0000007764 00000 н.
  0000012310 00000 п.
  0000012667 00000 п.
  0000012938 00000 п.
  0000013050 00000 п.
  0000013307 00000 п.
  0000013478 00000 п.
  0000013787 00000 п.
  0000014139 00000 п.
  0000014695 00000 п.
  0000015083 00000 п.
  0000015465 00000 п.
  0000015902 00000 н.
  0000020121 00000 п.
  0000020391 00000 п.
  0000020580 00000 п.
  0000020843 00000 п.
  0000021107 00000 п.
  0000021196 00000 п.
  0000021801 00000 п.
  0000021970 00000 п.
  0000022342 00000 п.
  0000022781 00000 п.
  0000022964 00000 н.
  0000023082 00000 п.
  0000023582 00000 п.
  0000023775 00000 п.
  0000027838 00000 п.
  0000028203 00000 п.
  0000028436 00000 п.
  0000033482 00000 п.
  0000033754 00000 п.
  0000033884 00000 п.
  0000034456 00000 п.
  0000034752 00000 п.
  0000034916 00000 п.
  0000035294 00000 п.
  0000035850 00000 п.
  0000036043 00000 п.
  0000036306 00000 п.
  0000036587 00000 п.
  0000036727 00000 н.
  0000039197 00000 п.
  0000039532 00000 п.
  0000039935 00000 н.
  0000044013 00000 п.
  0000044463 00000 п.
  0000044874 00000 н.
  0000045177 00000 п.
  0000045264 00000 п.
  0000050093 00000 п.
  0000050403 00000 п.
  0000050584 00000 п.
  0000050989 00000 п.
  0000051191 00000 п.
  0000055739 00000 п.
  0000056221 00000 п.
  0000056385 00000 п.
  0000056655 00000 п.
  0000057012 00000 п.
  0000060099 00000 п.
  0000064373 00000 п.
  0000064540 00000 п.
  0000064798 00000 н.
  0000069033 00000 п.
  0000069396 00000 п.
  0000069806 00000 п.
  0000070324 00000 п.
  0000070686 00000 п.
  0000070919 00000 п.
  0000071307 00000 п.
  0000071655 00000 п.
  0000072073 00000 п.
  0000072445 00000 п.
  0000077290 00000 п.
  0000081743 00000 п.
  0000087153 00000 п.
  0000112495 00000 н.
  0000113277 00000 н.
  0000113402 00000 н.
  0000116210 00000 н.
  0000118378 00000 н.
  0000120651 00000 н.
  0000121294 00000 н.
  0000122976 00000 н.
  0000123803 00000 н.
  0000125315 00000 н.
  0000150888 00000 н.
  0000151622 00000 н.
  0000152509 00000 н.
  0000157047 00000 н.
  0000157082 00000 н.
  0000157160 00000 н.
  0000171703 00000 н.
  0000172034 00000 н.
  0000172100 00000 н.
  0000172216 00000 н.
  0000172251 00000 н.
  0000172329 00000 н.
  0000191300 00000 н.
  0000191631 00000 н.
  0000191697 00000 н.
  0000191813 00000 н.
  0000191947 00000 н.
  0000192341 00000 п.
  0000192494 00000 н.
  0000192900 00000 н.
  0000193155 00000 н.
  0000193652 00000 н.
  0000193957 00000 н.
  0000194278 00000 н.
  0000194372 00000 н.
  0000195070 00000 н.
  0000195344 00000 н.
  0000195653 00000 н.
  0000195740 00000 н.
  0000196393 00000 н.
  0000196656 00000 н.
  0000196959 00000 н.
  0000197152 00000 н.
  0000197605 00000 н.
  0000197915 00000 н.

Исправление ошибки #Н/Д

Ошибка #Н/Д обычно означает, что формула не находит запрашиваемое значение.

Лучшее решение

Наиболее распространенной причиной ошибки #N/A является использование функций XLOOKUP, VLOOKUP, HLOOKUP, LOOKUP или MATCH, если формула не может найти указанное значение. Например, искомого значения нет в исходных данных.

В данном случае в таблице подстановки нет элемента «Банан», поэтому функция ВПР возвращает ошибку #Н/Д.

Решение. Убедитесь, что значение подстановки существует в исходных данных, или используйте обработчик ошибок, например IFERROR в формуле. Например, =IFERROR(FORMULA(),0), который говорит:

Вы можете указать «», чтобы не отображалось ничего, или подставить собственный текст: =ЕСЛИОШИБКА(ФОРМУЛА(),»Сообщение об ошибке»)

Если вы не знаете, что делать на этом этапе или какого рода помощь вам нужна, поищите похожие вопросы на форуме сообщества Excel или опубликуйте там свой вопрос.

Примечание:  Если вам нужна справка по ошибке #Н/Д для конкретной функции, например ВПР или ИНДЕКС/ПОИСКПОЗ, щелкните здесь.

Если вы хотите работать дальше, приведенный ниже контрольный список поможет вам определить возможные причины проблем в формулах.

Искомое значение и исходные данные относятся к разным типам. Например, вы пытаетесь использовать ссылку на функцию ВПР как число, а исходные данные сохранены как текст.

Решение. Убедитесь, что типы данных одинаковы. Чтобы проверить формат ячеек, выберите ячейку или диапазон ячеек, щелкните правой кнопкой мыши и выберите пункт «Формат ячеек >Число » (или нажмите клавиши CTRL+1) и при необходимости измените числовую формат.

Совет: Если вам нужно принудительно изменить формат для целого столбца, сначала примените нужный формат, а затем выберите Данные > Текст по столбцам > Готово.

Начальные и конечные пробелы можно удалить с помощью функции СЖПРОБЕЛЫ. В приведенном ниже примере в функции ВПР используется вложенная функция СЖПРОБЕЛЫ для удаления начальных пробелов из имен в ячейках A2:A7 и возврата названия отдела.

=ВПР(D2,TRIM(A2:B7),2,FALSE)

Примечание: 24 сентября 2018 г. — Формулы динамического массива — Если у вас есть текущая версия Microsoft 365 и вы находитесь на канале быстрого выпуска Insiders, вы можете ввести формулу в верхнюю левую ячейку выходного диапазона и нажать клавишу Enter, чтобы подтвердите формулу в виде формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.

По умолчанию функции, которые ищут данные в таблицах, должны использовать сортировку по возрастанию. Но у функций ВПР и ГПР есть аргумент интервальный_просмотр, который сообщает функции, что нужно искать точное совпадение, даже если таблица не отсортирована. Чтобы найти точное совпадение, укажите для аргумента интервальный_просмотр значение ЛОЖЬ. Помните, что значение ИСТИНА, сообщающее функции о том, что нужно искать приблизительное совпадение, может привести к возвращению не только ошибки #Н/Д, но и ошибочных результатов, как видно в следующем примере.

В этом примере возвращается не только ошибка #Н/Д для элемента «Банан», но и неправильная цена для элемента «Черешня». К такому результату приводит аргумент ИСТИНА, который сообщает функции ВПР, что нужно искать не точное, а приблизительное совпадение. Здесь нет близкого совпадения для элемента «Банан», а «Черешня» предшествует элементу «Персик». В этом случае при использовании функции ВПР с аргументом ЛОЖЬ будет отображаться правильная цена для элемента «Черешня», но для элемента «Банан» все равно будет указана ошибка #Н/Д, потому что в списке подстановок его нет.

Если вы используете функцию ПОИСКПОЗ, попробуйте изменить значение аргумента тип_сопоставления, чтобы указать порядок сортировки таблицы. Чтобы найти точное совпадение, задайте для аргумента тип_сопоставления значение 0 (ноль).

Чтобы исправить ошибку, убедитесь, что диапазон, на который ссылается формула массива, содержит такое же количество строк и столбцов, что и диапазон ячеек, в котором была введена формула массива. Или введите формулу массива в меньшее или большее число ячеек в соответствии со ссылкой на диапазон в формуле.

В данном примере ячейка E2 содержит ссылку на несовпадающие диапазоны:

=СУММ(ЕСЛИ(A2:A11=D2;B2:B5))

Чтобы формула вычислялась правильно, необходимо изменить ее так, чтобы оба диапазона включали строки 2–11.

=СУММ(ЕСЛИ(A2:A11=D2;B2:B11))

Примечание: 24 сентября 2018 г. — Формулы динамического массива — Если у вас есть текущая версия Microsoft 365 и вы находитесь на канале быстрого выпуска Insiders, вы можете ввести формулу в верхнюю левую ячейку выходного диапазона и нажать клавишу Enter, чтобы подтвердите формулу в виде формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.

В данном случае для месяцев с мая по декабрь указано значение #Н/Д, поэтому итог вычислить не удается и вместо него отображается ошибка #Н/Д.

Чтобы исправить ошибку, проверьте синтаксис используемой функции и введите все обязательные аргументы, которые возвращают ошибку. Вероятно, для проверки функции вам потребуется использовать редактор Visual Basic. Открыть этот редактор можно на вкладке «Разработчик» или с помощью клавиш ALT+F11.

Чтобы исправить ошибку, убедитесь в том, что книга, содержащая пользовательскую функцию, открыта, а функция работает правильно.

Чтобы исправить ошибку, убедитесь в том, что аргументы функции верны и расположены в нужных местах.

Чтобы исправить ошибку, нажмите клавиши CTRL+ALT+F9 для пересчета листа.

Если вы не знаете точно, какие аргументы использовать, вам поможет мастер функций. Выделите ячейку с формулой, а затем перейдите на вкладку « Формула» на ленте и нажмите клавишу INSERT FUNCTION.

Excel автоматически запустит мастер.

Щелкните любой аргумент, и Excel покажет вам сведения о нем.

Значение #Н/Д может принести пользу. Значения #Н/Д часто используются в диаграммах с такими данными, как в приведенном ниже примере, поскольку эти значения не отображаются на диаграмме. В примерах ниже показано, как выглядит диаграмма со значениями 0 и #Н/Д.

В предыдущем примере значения 0 показаны в виде прямой линии вдоль нижнего края диаграммы, а затем линия резко поднимается вверх, чтобы показать итог. В следующем примере вместо нулевых значений используются значения #Н/Д.

Дополнительные сведения об ошибке #Н/Д в конкретных функциях см. в следующих статьях:

• Исправление ошибки #Н/Д в функции ВПР

• Исправление ошибки #Н/Д в функциях ИНДЕКС и ПОИСКПОЗ

К началу страницы

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Преобразование чисел из текстового формата в числовой

Функция ВПР

ГПР

Функция ПРОСМОТР

Функция ПОИСКПОЗ

Общие сведения о формулах в Excel

Рекомендации, позволяющие избежать появления неработающих формул

Поиск ошибок в формулах

Сочетания клавиш в Excel

Все функции Excel (по алфавиту)

Функции Excel (по категориям)

Дискриминант.

2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра..

Общая формула для нахождения корней квадратного уравнения:

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни




До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),

или парабола ветвями вниз (a<0).

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).

Неполные квадратные уравнения

Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
График функций всегда симметричен относительно начала координат. Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах «+, -» или «-, +».
Неполное квадратное уравнение вида
одним из корней всегда имеет точку x=0.
В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!

Решение (корни) квадратного уравнения

• Определение квадратного уравнения и общее понятие о его корнях
• Геометрический смысл решения квадратного уравнения
• Три случая после нахождения дискриминанта квадратного уравнения
• Решение полных квадратных уравнений
• Теорема Виета
• Решение неполных квадратных уравнений
• Разложение квадратного трёхчлена на множители с применением корней квадратного уравнения
• Из истории решения квадратных уравнений
• Различные прикладные задачи на квадратные уравнения
• Онлайн калькулятор квадратных уравнений

Квадратным уравнением называется уравнение вида ax² + bx + c = 0, где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0.

Например, квадратным является уравнение

2x² — 3x + 1 = 0,

в котором a = 2, b = — 3, c = 1.

В квадратном уравнении ax² + bx + c = 0 коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.

Уравнения вида ax² + bx = 0,

где c =0,

ax² + c = 0,

где b =0, и

ax² = 0,

где a =0 и b =0,

называются неполными квадратными уравнениями.

Найти корни квадратного уравнения значит решить квадратное уравнение.

Для вычисления корней квадратного уравния служит выражение b² — 4ac, которое называется дискриминантом квадратного уравнения и обозначается буквой D.

Корни квадратного уравнения имеют следующие сферы применения:

— для разложении квадратного трёхлена на множители, что, в свою очередь, является приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.д.) в частности, при нахождении пределов, производных и интегралов;

— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения, чаще всего один, являются обычно конечным решением).

График квадратичного трёхлена ax² + bx + c — левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна оси 0y. Число точек пересечения параболы с осью 0x определяет число корней квадратного уравнения. Если точек пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает ось 0x, то квадратное уравнение не имеет действительных корней. На рисунке ниже изображены три упомянутых случая.

Как видно на рисунке, красная парабола пересекает ось 0x в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью 0x.

1. Если дискриминант больше нуля (), то квадратное уравнение имеет два различных действительных корня.

Они вычисляются по формулам:

и

.

Часто пишется так: .

2. Если дискриминант равен нулю (), то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня, которые равны .

3. Если дискриминант меньше нуля (), то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней в этой статье рассматривать не будем. В общем случае правильным решением является констатация того, что квадратное уравнение не имеет действительных корней.

Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.

Путём преобразования в квадратное уравнение следует решать и дробные уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, . О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.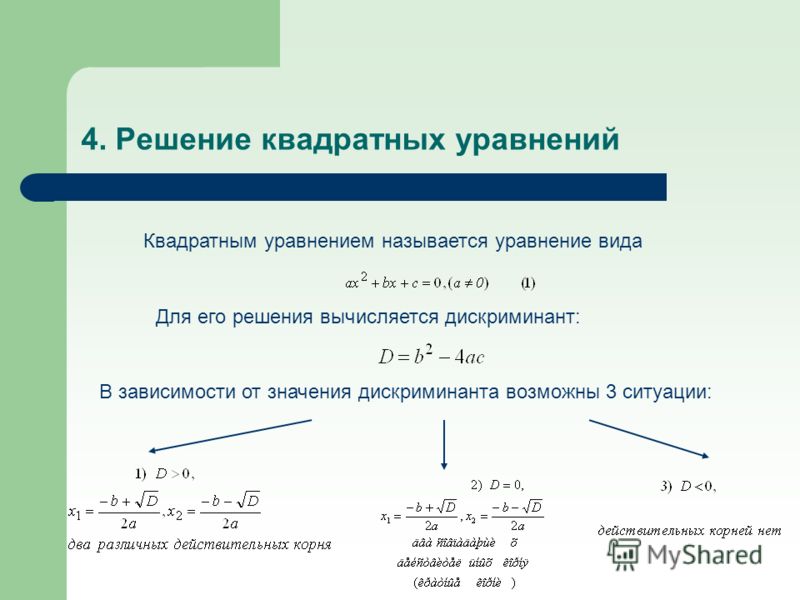

Пример 3. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Пример 4. Найти корни квадратного уравнения:

.

В примере 1 нашли дискриминант этого уравнения:

,

Решение квадратного уравнения найдём по формуле для корней:

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 5. Найти корни квадратного уравнения:

.

В примере 2 нашли дискриминант этого уравнения:

.

Применим формулу корней квадратного уравнения . Отсюда , . Найденные корни квадратного уравнения равны друг другу, а это значит, что уравнение имеет единственный корень:

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Корни приведённого квадратного уравнения

Пусть дано квадратное уравнение . Так как , то разделив обе части данного уравнения на a, получим уравнение . Полагая, что и , приходим к уравнению , в котором первый коэффициент равен 1. Такое уравнение называется приведённым.

Формула корней приведённого уравнения имеет вид:

.

Существуют формулы, связывающие корни квадратного уравнения с его коэффициентами. Они впервые были получены французским математиком Ф.Виетом.

Теорема Виета. Если квадратное уравнение ax² + bx + c = 0 имеет действительные корни, то их сумма равна — b/a, а произведение равно с/a:

Следствие. Если приведённое квадратное уравнение x² + px + q = 0 имеет действительные корни и , то

Пояснение формул: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Следовательно, теорему Виета можно применять и для поиска корней приведённого квадратного уравнения.

Пример 6. Написать приведённое квадратное уравнение, корнями которого являются числа 1 и -3.

Иначе говоря, надо найти числа p и q такие, чтобы квадратное уравнение

имело корни и .

По формулам Виета , . Требуемое в условии задачи уравнение имеет вид

---

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пример 7. Решить квадратное уравнение .

Решение. Чтобы решить данное неполное квадратное уравнение, разложим его левую часть на множители. Получим

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю: или . Решая уравнение , находим .

Следовательно, произведение обращается в нулю при и при . Поэтому числа 0 и 1/2 являются корнями неполного квадратного уравнения .

Пример 8. Решить квадратное уравнение .

Решение. Чтобы решить данное неполное квадратное уравнение, перенесём в его правую часть свободный член с противоположным знаком и разделим обе части уравнения на 3. Получим уравнение

.

Так как , то уравнение не имеет действительных корней. Следовательно, не имеет действительных корней и эквивалентное ему неполное квадратное уравнение .

Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно разложить на множители по следующей формуле:

.

Этот приём часто используется для упрощения выражений, особенно сокращения дробей.

Пример 9. Упростить выражение:

.

Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:

.

Корни квадратного уравнения будут следующими:

.

Разложим квадратный многочлен на множители:

.

Упростили выражение, проще не бывает:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 10. Упростить выражение:

.

Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:

.

Корни первого квадратного уравнения будут следующими:

.

Находим дискриминант второго квадратного уравнения:

.

Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:

.

Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Упрощать выражения путём решения квадратных уравнений требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде, он может быть получен в процессе предварительных преобразований выражения.

Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39).

Площадь большого квадрата равна (x + 5)². Она складывается из площади x² + 10x заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх квадратов со стороной 5/2, равной 25. Получается следующее уравнение и его решение:

Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?

Решение. Примем количество ткани в отрезке за x и получим уравнение:

Приведём обе части уравнения к общему знаменателю:

Произведём дальнейшие преобразования:

Получили квадратное уравнение, которое и решим:

Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.

Ответ: в отрезке 20 м ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках. Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом 2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?

Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:

Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение. Процесс записывается так:

Найдём дискриминант:

Найдём корни квадратного уравнения:

Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.

Ответ: в одном ящике взвешивают 12,5 кг ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Другие темы в блоке «Школьная математика»

Действия со степенями и корнями

Действия с дробями

Решение дробных уравнений с преобразованием в квадратное уравнение

Формула дискриминанта, количество решений при дискриминанте больше, меньше или равном нулю

Дискриминант — многозначный термин. В данной статье речь пойдёт о дискриминанте многочлена, который позволяет определить, есть ли у данного многочлена действительные решения. Формула для квадратного многочлена встречается в школьном курсе алгебры и анализа. Как найти дискриминант? Что нужно для решения уравнения?

Содержание:

• Квадратный многочлен, как искать его корни
  • Варианты расчётов для закрепления материала
  • Использование дискриминанта в вычислении корней
• Некоторые частные случаи
  • Приведенное уравнение второй степени
  • Чётный второй множитель
• Более высокий порядок дискриминанта
• Видео

Квадратный многочлен, как искать его корни

Квадратным многочленом или уравнением второй степени называется i * w ^ 2 + j * w + k равный 0, где «i» и «j» — первый и второй коэффициент соответственно, «k» — константа, которую иногда именуют «свободным членом», а «w» — переменная. Его корнями окажутся все значения переменной, при которых оно превращается в тождество. Такое равенство допустимо переписать, как произведение i, (w — w1) и (w — w2) равное 0. В этом случае очевидно, что если коэффициент «i» не обращается в ноль, то функция в левой части станет нулевой только в случае, если x принимает значение w1 или w2. Эти значения являются результатом приравнивания многочлена к нулю.

Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j — 4 * i * k. Зачем она используется?

1. Она говорит, имеются ли действительные результаты.
2. Она помогает их высчитать.

Как это значение показывает наличие вещественных корней:

• Если оно положительное, то можно найти два корня в области действительных чисел.
• Если дискриминант равен нулю, то оба решения совпадают. (1/2).
• Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
• Подстановка полученного результата в исходное равенство для проверки.

Некоторые частные случаи

В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:

1. многочлен раскладывается в разность квадратов при отрицательном свободном члене;
2. при положительной константе действительных решений найти нельзя.

Если свободный член нулевой, то корни будут {0; -j}

Но есть и другие частные случаи, упрощающие нахождение решения.

Приведенное уравнение второй степени

Приведенным именуют такой квадратный трёхчлен, где коэффициент перед старшим членом — единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе «k». 2 + 18 * i * j * k * m.

Допустим, дискриминант превосходит ноль. Это значит, что имеется три корня в области действительных чисел. При нулевом есть кратные решения. Если D < 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень — вещественный.

Видео

Наше видео подробно расскажет о вычислении дискриминанта.

дискриминантных формул — что такое дискриминантные формулы? Примеры

Формулы дискриминанта используются для нахождения дискриминанта полиномиального уравнения. В частности, дискриминант квадратного уравнения используется для определения количества и характера корней. Дискриминант полинома – это функция, состоящая из коэффициентов полинома. Давайте изучим формулы дискриминанта вместе с несколькими решенными примерами.

Что такое дискриминантные формулы?

Дискриминантные формулы дают нам общее представление о природе корней.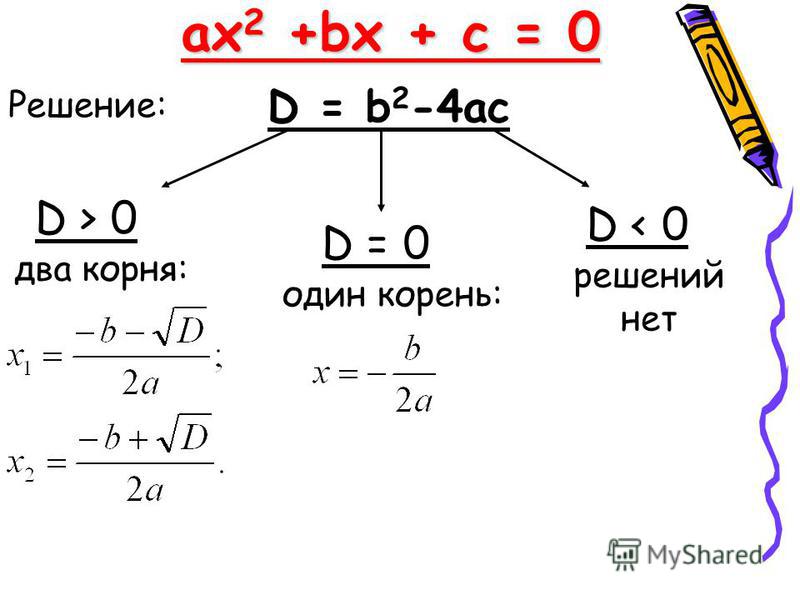 Дискриминант квадратного уравнения получается из квадратной формулы. Дискриминант обозначается D или Δ. Дискриминантные формулы для квадратного уравнения и кубического уравнения:

Дискриминантная формула квадратного уравнения

Дискриминантная формула квадратного уравнения ax ² + bx + c = 0 есть, Δ (или) D = b ²  — 4ач. Мы знаем, что квадратное уравнение имеет максимум 2 корня, так как его степень равна 2. Мы знаем, что квадратная формула используется для нахождения корней квадратного уравнения на оси 9.0013 2 + bx + c = 0. Согласно квадратичной формуле, корни можно найти, используя x = [-b ± √ (b ²  — 4ac) ] / [2a]. Здесь b ²  — 4ac — это дискриминант D, который находится внутри квадратного корня. Таким образом, квадратичная формула становится x = [-b ± √D] / [2a]. Здесь D может быть либо > 0, = 0, (или) < 0. Определим характер корней в каждом из этих случаев.

• Если D > 0, то квадратная формула принимает вид x = [-b ± √(положительное число)] / [2a], и, следовательно, в этом случае квадратное уравнение имеет два различных действительных корня.
• Если D = 0, квадратная формула принимает вид x = [-b] / [2a], и, следовательно, в этом случае квадратное уравнение имеет только один действительный корень.
• Если D < 0, то квадратная формула принимает вид x = [-b ± √(отрицательное число)] / [2a], и, следовательно, в этом случае квадратное уравнение имеет два различных комплексных корня (это связано с тем, что квадратный корень из отрицательного число приводит к мнимому числу. Например, √(-4) = 2i).

Дискриминантная формула кубического уравнения

Дискриминантная формула кубического уравнения ax ³  + bx ²  + cx + d = 0 is, Δ (или) D = b ² c ² − 4ac ^{3 1} г − 27а ² г ²  + 18abcd. Мы знаем, что кубическое уравнение имеет максимум 3 корня, поскольку его степень равна 3. Здесь

• . Если D > 0, все три корня действительны и различны.
• Если D = 0, то действительны все три корня, из которых хотя бы два равны между собой.
• Если D < 0, то два его корня — комплексные числа, а третий корень — вещественный.

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Закажите бесплатный пробный урок

Мы можем увидеть применение формул дискриминанта в следующем разделе.

Примеры использования дискриминантных формул

Пример 1: Определить дискриминант квадратного уравнения 5x ² + 3x + 2 = 0. Также определить природу его корней.

Решение:

Данное квадратное уравнение имеет вид 5x ² + 3x + 2 = 0.

Сравнивая это с ax ² + bx + c = 0, получаем и c = 2.

Используя дискриминантную формулу,

D = b ² — 4ac

= 3 ² — 4(5)(2)

= 9 — 40

= -31

Ответ: Дискриминант равен -31. Это отрицательное число, поэтому данное квадратное уравнение имеет два комплексных корня.

Пример 2:  Определить дискриминант квадратного уравнения 2x ²  + 8x + 8 = 0. Также определить характер его корней.

Решение:

Данное квадратное уравнение равно 2x ² + 8x + 8 = 0.

Сравнивая это с ax ² + bx + c = 0, мы получаем a = 2, b = 8 и c = 8.

Используя дискриминантную формулу,

D = b ²  — 4ac

= 8 ² — 4( 2)(8)

= 64 — 64

= 0

Ответ: Дискриминант равен 0 и, следовательно, данное квадратное уравнение имеет два комплексных корня.

Пример 3: Определить природу корней кубического уравнения x ³  — 4x ²  + 6x — 4 = 0.

Решение:

Данным кубическим уравнением является x ³  — 4x ²  + 6x — 4 = 0.

Сравнивая это с , b = -4, c = 6 и d = -4.

Использование дискриминантной формулы,

D = B ² C ² -4AC ³ -4B ³ D-27A ² D ² + 18ABCD

= (4) ² + 18ABCD

= (4) ² + 18ABCD

= (4) ² + 18ABCD

= (4). (6) ² − 4(1)(6) ³ − 4(-4) ³ (-4) − 27(1) ² (-4) ² + 18(1)(-4)(6)(-4)

= -16

Ответ: Поскольку дискриминант является отрицательным числом, данное кубическое уравнение имеет два комплексных корня и один действительный корень.

Часто задаваемые вопросы о формулах дискриминанта

Что такое формулы дискриминанта?

Дискриминант полиномиального уравнения – это функция, выраженная через его коэффициенты. Дискриминант уравнения используется для определения характера его корней. Дискриминантные формулы следующие:

• Дискриминантная формула квадратного уравнения ax ² + bx + c = 0 is, Δ (или) D = b ²  — 4ac.
• Дискриминантная формула уравнения куба − 27a ² d ²  + 18abcd.

Как вывести дискриминантную формулу квадратного уравнения?

Выведем дискриминантную формулу квадратного уравнения ax ² + bx + c = 0. По квадратичной формуле решения этого уравнения находятся с использованием x = [-b ± √ (b ²  — 4ac) ] / [2a]. Здесь b ²  — 4ac находится внутри квадратного корня, и, следовательно, мы можем определить природу корней, используя свойства квадратного корня (например, квадратный корень из положительного числа является действительным числом, квадратный корень из a отрицательное число является мнимым числом, а квадратный корень из 0 равен 0). Таким образом, дискриминант квадратного уравнения равен b ²  — 4ач.

Каковы применения формулы дискриминанта?

Формула дискриминанта используется для определения природы корней квадратного уравнения. Дискриминант квадратного уравнения ax ² + bx + c = 0 равен D = b ²  — 4ac.

• Если D > 0, то уравнение имеет два действительных различных корня.
• Если D = 0, то уравнение имеет только один действительный корень.
• Если D < 0, то уравнение имеет два различных комплексных корня.

Что такое дискриминантная формула кубического уравнения?

Дискриминантная формула кубического уравнения ax ³  + bx ²  + cx + d = 0 обозначается Δ (или) D и находится по формуле Δ (или) D = b ² c ² − 4ac ³ − 4b ³ d − 27a ² d ² + 18abcd.

Квадратное уравнение, Дискриминант, Парабола

Квадратные уравнения выглядят так: топор ^{2 92 — 4ac}}{2a}$}

Число D = b ² — 4ac называется «дискриминантом» .
Если D < 0, то квадратное уравнение не имеет действительных решений (имеет 2 комплексных решения).
Если D = 0, то квадратное уравнение имеет 1 решение $x = — \frac{b}{2a}$
Если D > 0, то квадратное уравнение имеет 2 различных решения.

Пример:
Решим квадратное уравнение: x ² + 3x — 4 = 0
a = 1, b = 3, c = -4 -32$ $y=2(x-3)(x+5)$ y-точка
$(0, -30)$ вершина в
$(-1, -32)$ x-отрезка на
$(3, 0)$ и $(-5, 0)$

Парабола

График квадратного уравнения называется параболой .
Если a > 0, то его вершина указывает вниз:

Если a < 0, то его вершина направлена ​​вверх: Если a = 0, то график представляет собой не параболу, а прямую линию.

Вершина параболы $x = -\frac{b}{2a}$.

Формулы Виета

Если x ₁ и x ₂ являются корнями квадратного уравнения ax ² + bx + c = 0 тогда:
$x_1 + x_2 = -\frac{b}{a}$
$x_1x_2 = \frac{c}{a}$
Эти формулы называются формулами Виета .
Мы можем найти корни x ₁ и x ₂ квадратного уравнения, решив уравнения уравнений.

Задачи на квадратные уравнения

Задача 1. Решите уравнение:
x ² — 4 = 0
Решение: x ² — 4 = (x — 2)(x + 2)
(x — 2)(x + 2) = 0
x — 2 = 0 или x + 2 = 0
Корни x = 2 или x = -2

Решение 2: a = 1, b = 0, c = -4
D = 0 ² — 4 ⋅ 1 ⋅ (-4) = 16
$x_1 = \frac{-b — \sqrt{D}}{2a} = \frac{- 0 — \sqrt{16}}{2 \cdot 1} = \frac{-4}{2} = -2$
$x_2 = \frac{-b + \sqrt{D}}{2a } = \frac{- 0 + \sqrt{16}}{2 \cdot 1} = \frac{4}{2} = 2$

---

Задача 2. Решить уравнение:
3x ² + 4x + 5 = 0
Решение: дискриминант D = 4 ² — 4⋅3⋅5 = 16 — 60 = -44 Таким образом, квадратное уравнение не имеет действительных корней.

---

Задача 3. Решить уравнение:
х ² + 4х — 5 = 0; х = ?
Решение: Дискриминант равен 4 ² — (-4⋅1⋅5) = 16 + 20 = 36 > 0
У уравнения два действительных корня: $\frac{-4 \pm \sqrt{36} {2}$
х = 1 или х = -5

---

Задача 4. Решить уравнение:
х ² + 4х + 4 = 0; х = ?
Решение: Дискриминант равен 4 ² — (4⋅1⋅4) = 16 — 16 = 0
Таким образом, существует одно действительное решение: $x = \frac{-4}{2}$
x = -2

---

Задача 5. Решите уравнение:
x ² — 13x + 12 = 0
Корни: 1, 12

---

Задача 6. Решить уравнение: 92 — 4ac}}{2a}$

Квадратные уравнения на нашем математическом форуме

Задачи на квадратные уравнения
Задачи по формулам Виета
Решение уравнений кубической и четвертой степени — 1

Форумы, посвященные квадратным уравнениям

Formula DRIFT — Расписание

Расписание

• Про
• ЛОНГ-БИЧ, КАЛИФОРНИЯ, США
• 01-02 апреля
• РАУНД 1: УЛИЦЫ ЛОНГ-БИЧ
• Подробнее

Купить билеты:

• Продано
• Про
• АТЛАНТА, ДЖОРДЖИЯ, США
• 06-07 мая
• РАУНД 2: AutoZone Дорога к чемпионату, представленному TYPE S
• Подробнее

Купить билеты:

• Продано
• Про ПРОСПЕК
• ОРЛАНДО, ФЛОРИДА, США
• 19-21 мая
• РАУНД 3: ОПАСЕН
• Подробнее

Купить билеты:

• Продано
• Про ПРОСПЕК
• АНГЛИШТАУН, НЬЮ-ДЖЕРСИ, США
• 9-11 июня
• РАУНД 4: ПЕРЧАТКА
• Подробнее

Купить билеты:

• Продано
• Про ПРОСПЕК
• СТ. ЛУИ, МИССУРИ, США
• 14-16 июля
• РАУНД 5: ПЕРЕКРЕСТОК
• Подробнее

Купить билеты:

• Продано
• Про
• МОНРО, ВАШИНГТОН, США
• 05-06 августа
• РАУНД 6: БРОСОК
• Подробнее

Купить билеты:

• Продано
• Про ПРОСПЕК
• ГРАНТСВИЛЛ, ЮТА, США
• 15-17 сентября
• РАУНД 7: ПОВЫШЕННЫЙ
• Подробнее

Купить билеты:

• Продано
• Про
• ИРВИНДЕЙЛ, КАЛИФОРНИЯ, США
• 14-15 октября
• РАУНД 8: БОЙ ЗА ТИТУЛ
• Подробнее

Купить билеты:

• Купить билеты

Завершение квадрата

» Завершение квадрата » вот где мы. ..

… возьмем квадратное уравнение следующим образом:		и превратите его в это:
ах 2 + Ьх + с = 0		а(х+ d ) 2 + е = 0

Для тех из вас, кто торопится, могу сказать, что: d = b 2a

и: e = c − б ² 4а


Но если у вас есть время, позвольте мне показать вам, как « Заполнить квадрат » самостоятельно.

Завершение квадрата

Допустим, у нас есть простое выражение вида x ² + bx. Наличие x дважды в одном и том же выражении может усложнить жизнь. Что мы можем сделать?

Что ж, немного вдохновившись геометрией, мы можем преобразовать его вот так:

Как видите x ² + bx можно переставить почти в квадрат. ..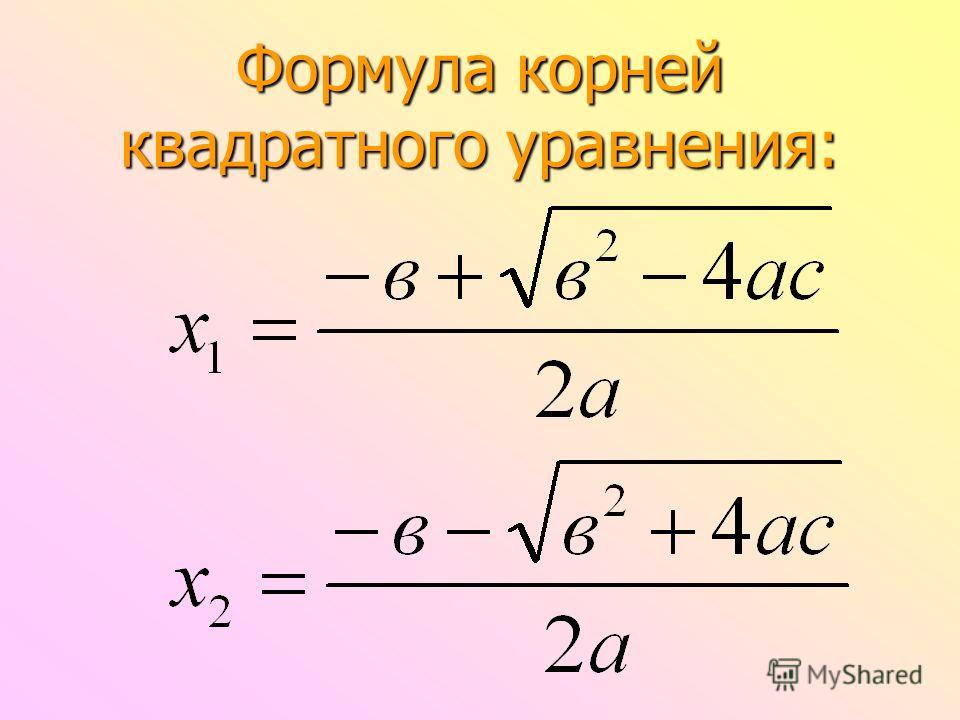

… и мы можем дополнить квадрат с помощью (b/2) ²

В алгебре это выглядит так:

x 2 + шт.	+ (б/2) 2	=	(х+b/2) 2
	«Заполните квадрат »

Итак, сложив (b/2) ² , мы можем завершить квадрат.

Результат (x+b/2) ² имеет x только один раз , что проще в использовании.

Сохранение равновесия

Теперь… мы не можем просто добавить (b/2) ² тоже без вычитая это тоже! В противном случае меняется все значение.

Итак, давайте посмотрим, как это сделать правильно на примере:

Начните с:
	(«b» в данном случае равно 6)
Заполните квадрат:
	Также вычесть новый термин
Упростите это, и все готово.

Результат:

x ² + 6x + 7   =   (x+3) ² − 2

И теперь x появляется только один раз, и наша работа выполнена!

Быстрый подход

Вот быстрый способ получить ответ. Вам может понравиться этот метод.

Сначала подумайте о желаемом результате: (x+d) ² + e

После расширения (x+d) ² получаем: x ² + 2dx + d ² + e

Теперь посмотрим, сможем ли мы превратить наш пример в эту форму, чтобы обнаружить d и e

Пример: попытаться вписать x

² + 6x + 7 в x ² + 2dx + d ² + e

Теперь мы можем «форсировать» ответ:

• Мы знаем, что 6x должно получиться как 2dx, поэтому d должно быть 3
• Далее мы видим, что 7 должно стать d ² + e = 9 + e, поэтому e должно быть −2

И мы получаем тот же результат (x+3) ² − 2, что и выше!

 

Теперь давайте рассмотрим полезное приложение: решение квадратных уравнений. ..

Решение общих квадратных уравнений путем заполнения квадрата

Мы можем дополнить квадрат до , решить квадратное уравнение (найти, где оно равно нулю).

Но общее квадратное уравнение может иметь коэффициент а перед х ² :

топор ² + Ьх + с = 0

Но с этим легко справиться… просто сначала разделите все уравнение на «а», а затем продолжайте:

х ² + (б/а)х + с/а = 0

шагов

Теперь мы можем решить квадратное уравнение за 5 шагов:

• Шаг 1 Разделите все члены на a (коэффициент x ² ).
• Шаг 2 Переместите числовое выражение ( c/a ) в правую часть уравнения.
• Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же значение в правую часть уравнения.

Теперь у нас есть что-то похожее на (x + p) ² = q, которое можно довольно легко решить:

• Шаг 4 Извлеките квадратный корень из обеих частей уравнения.
• Шаг 5 Вычтите число, оставшееся в левой части уравнения, чтобы найти x .

Примеры

Хорошо, несколько примеров помогут!

Пример 1: решить x

² + 4x + 1 = 0

Шаг 1 можно пропустить в этом примере, так как коэффициент при x ² равен 1

Шаг 2 Переместите числовой член в правую часть уравнения:

x ² + 4x = -1

Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив то же число в правую часть уравнения.

(б/2) ² = (4/2) ² = 2 ² = 4

x ² + 4x + 4 = -1 + 4

(x + 2) ² = 3

Шаг 4 Извлеките квадратный корень из обеих частей уравнения:

23 x 23 x 2 + 2 = ±√3 = ±1,73 (до 2 знаков после запятой)

Шаг 5 Вычтите 2 с обеих сторон:

x = ±1,73 – 2 = -3,73 или -0,27

А вот еще интересная и полезная штука. В конце шага 3 у нас было уравнение: (х + 2) 2 = 3 Это дает нам вершину (точка поворота) x 2 + 4x + 1: (-2, -3)

 

Пример 2: решить 5x

² – 4x – 2 = 0

Шаг 1 Разделить все члены на 5

x ² – 0,8x – 0,4 = 0

0509 Шаг 2 Переместите числовой член в правую часть уравнения:

x ² – 0,8x = 0,4

Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же самое число в правой части уравнения:

(b/2) ² = (0,8/2) ² = 0,4 ² = 0,16

x ² – 0,8x + 0,46 = 0,46

(x – 0,4) ² = 0,56

Шаг 4 Извлеките квадратный корень из обеих частей уравнения:

x – 0,4 = ±√0,56 = ±0,748 (до 3 знаков после запятой)

Шаг 5 Вычтите (-0,4) с обеих сторон (другими словами, добавьте 0,4):

x = ±0,748 + 0,4 = — 0,348 или 1,148

Почему «Завершить квадрат»?

Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу, чтобы решить квадратное уравнение?

Ну, одна причина указана выше, где новая форма не только показывает нам вершину, но и упрощает решение.

Бывают также случаи, когда форма ax ² + bx + c может быть частью более крупного вопроса , и перестановка его в виде a(x+ d ) ² + e упрощает решение, потому что только 9051 x упрощает решение однажды.

Например, «x» может быть функцией (например, cos(z) ), и ее изменение может открыть путь к лучшему решению.

Также завершение квадрата является первым шагом в выводе квадратичной формулы

Думайте об этом как о еще одном инструменте в вашем наборе математических инструментов.

 

364, 1205, 365, 2331, 2332, 3213, 3896, 3211, 3212, 1206

 

Сноска: значения «d» и «e»

Как я получил значения d и e из верхней части страницы?

Начните с
Разделить уравнение на a
Положите c/a на другую сторону
Добавить (b/2a) 2 с обеих сторон
«Заполни квадрат»
Теперь верни все обратно. ..
… на левую сторону
… к исходному множителю a x 2




И вы заметите, что у нас есть:

a(x+d) ² + e = 0

Где:d = б 2а

и: е = с — б ² 4a

Как вверху страницы!

 

Объяснение квадратичной формулы | Purplemath

ДискриминантДиск. и графики

Purplemath

Когда мне следует использовать квадратичную формулу?

Вы можете использовать Квадратную формулу в любое время, когда пытаетесь решить квадратное уравнение, если это уравнение имеет форму «(квадратичное выражение), которое установлено равным нулю».

Часто самый простой способ решить « x ² + bx + c = 0» для значения x — это разложить квадратное число на множители, установить каждый множитель равным нулю, а затем решить каждый фактор. Но иногда квадратное выражение слишком запутано, или оно вообще не учитывается, или, черт возьми, может быть, вам просто не хочется факторизовать. Хотя факторинг не всегда будет успешным, квадратичная формула всегда может найти ответы для вас.

Содержание продолжается ниже

Mathhelp.com

Практикуйте квадратичную формулу

. bx + c «, где « a «, « b » и « c » — просто числа; это «числовые коэффициенты» квадратного уравнения, которое они дали вам решить.

Квадратичная формула получается из процесса завершения квадрата и формально выражается как:

Что такое квадратичная формула?

Квадратная формула — это правило, согласно которому в любом уравнении вида x ² + bx + c = 0 решение x -значения уравнения задаются формулой:

Как использовать квадратичную формулу?

Чтобы использовать квадратную формулу, вы должны:

• Приведите уравнение к форме «(квадратичное) = 0».

• Расположите члены (уравнения) в порядке убывания (сначала квадратный член, затем член x и, наконец, линейный член).

• Вытяните числовые части каждого из этих терминов, а именно « a », « b » и « c » Формулы.

• Подставьте эти числа в формулу.

• Упростите, чтобы получить ответы.

Рекомендации: «2 a » в знаменателе формулы находится под всем, что указано выше, а не только под квадратным корнем. И это «2 a «, а не просто «2». Убедитесь, что вы не уронили квадратный корень или «плюс/минус» в середине ваших вычислений, иначе я могу гарантировать, что вы забудете «вставить их обратно» в своем тесте, и вы запутаетесь. себя вверх. Помните, что « b ² » означает «квадрат ВСЕХ b , включая его знак», поэтому не оставляйте b ² отрицательным, даже если b отрицательное, потому что квадрат отрицательного числа является положительным.

Другими словами, не делайте этого. Будьте небрежны и не пытайтесь срезать путь, потому что это только навредит вам в долгосрочной перспективе Поверьте мне в этом

Какой пример использования квадратичной формулы

использовать, чтобы подтвердить то, что я получаю от квадратичной формулы Формула должна дать мне те же ответы.

x ² + 3 x — 4 = ( x + 4)( x — 1) = 0

… так что я уже знаю, что решения = — 9 4 и x = 1.

Теперь, как бы мое решение выглядело в квадратичной формуле? Используя a = 1, b = 3 и c = −4, мой процесс решения выглядит следующим образом:

Таким образом, как и ожидалось, решение равно x = −4, x = 1.

Для этого конкретного квадратного уравнения факторизация, вероятно, будет более быстрым методом. Но Квадратичная формула — это метод plug-n-chug, при котором всегда будет работать как . У вас «заморозка мозгов» на тесте, и вы не можете ничего стоящего? Используйте формулу plug-n-chug; он всегда будет заботиться о вас!

---

Как квадратичная формула связана с пересечениями по оси x?

Решения квадратного уравнения, представленные Квадратичной формулой, являются точками пересечения x соответствующей параболы, изображенной на графике.

Как? Ну, когда y = 0, вы находитесь на оси x . Точки пересечения x на графике — это места, где парабола пересекает ось x . Вы применяете квадратичную формулу к уравнению x ² + bx + c = y , где y установлено равным нулю.

Глядя на приведенный выше пример, можно увидеть два решения уравнения x ² + 3 x − 4 = 0. Это говорит нам о том, что тогда должно быть два x — перехваты на графике. Построив график, мы получим следующую кривую:

Как видите, точки пересечения x (красные точки выше) соответствуют решениям, пересекая ось x в точке x = −4 и x = 1. Это показывает связь между построением графика и решением: когда вы решаете «(квадратичное) = 0», вы находите x -перехватов графика. Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратную формулу (при необходимости) для решения квадратного уравнения, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые x — точки пересечения имеют те же десятичные значения, что и решения, обеспечиваемые квадратичной формулой.

Обратите внимание, однако, что отображение графика калькулятором, вероятно, будет иметь некоторую ошибку округления, связанную с пикселями, поэтому вам нужно проверить, чтобы вычисленные и графические значения были достаточно близки; не ждите точного совпадения.

---

В (2)(−3) = −6 нет множителей, которые в сумме дают −4, поэтому я знаю, что этот квадрат нельзя разложить на множители. Я буду применять квадратную формулу. В этом случае a = 2, b = -4 и c = -3:

Тогда ответ равен x = -0,58, x = 2,58, округленное до двух знаков после запятой.

Можно ли округлить ответы квадратичной формулы?

В общем, нет, не стоит; обычно требуется, чтобы «решение» или «корни» или «нули» квадратного числа были в «точной» форме ответа. Вы можете использовать округленную форму при построении графика (при необходимости), но «ответ(ы)» из квадратичной формулы следует записывать в (часто беспорядочной) «точной» форме.

В приведенном выше примере точной формой является форма с квадратными корнями из десяти. Если вы хотите построить график x -перехватов или вам нужно упростить окончательный ответ в словесной задаче, чтобы он имел практическую («реальную») форму, вы можете использовать приближение калькулятора. Но если у вас нет веских оснований полагать, что ответ должен быть округленным, всегда выбирайте точную форму.

Подкрепляя концепцию: сравните решения, которые мы нашли выше для уравнения 2 x ² − 4 x − 3 = 0 с точками пересечения x графика: . Это всегда так. «Решения» уравнения также являются x -перехватами соответствующего графика.

Стр. 2 Стр. 3

---

URL: https://www.purplemath.com/modules/quadform.htm

Квадратичная формула и дискриминант: примеры

До сих пор мы использовали такие методы, как построение графиков, разложение на множители и применение свойства квадратного корня для нахождения точных решений некоторых квадратных уравнений. Мы также научились решать квадратные уравнения, дополняя квадрат.

Хотя некоторые из этих методов кажутся лучшим вариантом для решения любого типа квадратного уравнения, он может оказаться довольно сложным, если в данном квадратном уравнении участвуют дроби или десятичные дроби. Однако не бойтесь! Оказывается, есть решение для решения любая форма квадратного уравнения, выраженная в соответствии с приведенным выше определением. Это известно как квадратичная формула.

Квадратная формула — важный инструмент, используемый для определения решений любого заданного квадратного уравнения. Мы можем применить эту концепцию при решении квадратных уравнений, которые нельзя разложить на множители с помощью стандартных методов факторизации.

Обратите внимание, что мы действительно можем использовать Квадратную Формулу для нахождения решений любой формы квадратных уравнений, даже тех, которые можно разложить на множители.

Квадратная формула

Прежде чем мы углубимся в эту тему, давайте сначала вспомним стандартную форму квадратного уравнения.

Стандартная форма квадратного уравнения где

Имея это в виду, давайте теперь введем квадратную формулу.

Для квадратного уравнения вида, где решения даются квадратичной формулой ,

.

Обратите внимание, что квадратичная формула имеет « ±» знак. Это означает, что формула дает два решения, а именно

.

Учитывая, что квадратная формула сообщает нам корни данного квадратного уравнения, мы можем легко найти эти точки и построить график более точно.

Вывод квадратичной формулы

Квадратичная формула выводится путем завершения квадрата. В этом разделе шаг за шагом объясняется его вывод, как показано ниже.

Учитывая общую форму квадратного уравнения:

Шаг 1: Разделите выражение на

Шаг 2: С каждой стороны

Шаг 3: СТАВЕТ 40003

96999

679
679999999995
9000
67967999999995
969969696999 9 Фактор левой части и упрощение правой части

Шаг 5: Квадратный корень с каждой стороны

Не забудьте знак ‘±’!

Шаг 6: Вычтите с каждой стороны

Шаг 7: Упростить выражение

Примечание: . Этот метод завершения квадрата объясняется в деталях. Завершение квадратов . Это обсуждение содержит хорошо проработанные примеры, которые показывают, как этот вывод применяется к заданному квадратному уравнению. Проверьте это, если вы хотите изучить это более подробно!

Дискриминант

В следующих разделах мы рассмотрим свойства корней заданных квадратных уравнений. Мы познакомимся с новым понятием, называемым дискриминантом. Дискриминант играет решающую роль в понимании природы корней квадратного уравнения.

Прежде чем мы рассмотрим идею дискриминанта, нам нужно ознакомиться с несколькими важными терминами, которые помогут нам понять это обсуждение. Начнем с определения рационального и иррационального корня.

Рациональный корень — это решение, которое можно выразить как частное двух целых чисел.

Они представлены в виде где p и q — целые числа, где p — константа многочлена, а q — старший коэффициент.

Иррациональный корень — это решение, которое нельзя выразить как частное двух целых чисел. Они часто представлены бесконечно неповторяющимися десятичными знаками или сурдами.

Далее мы определим, что значит быть полным квадратом. Эта концепция имеет решающее значение, когда мы начинаем использовать квадратную формулу, поскольку она определяет, являются ли корни нашего данного квадратного уравнения рациональными или иррациональными, как мы скоро увидим!

Полный квадрат — это целое число, являющееся квадратом целого числа, то есть произведение некоторого целого числа на себя. Это принимает вид, где p — целое число. По сути, .

Примеры включают 9 (3 ² ), 16 (4 ² ), 25 (5 ² ) и т. д. дискриминант и его связь со свойствами корней.

Дискриминант и свойства корней

Чтобы найти количество корней в заданном квадратном уравнении, воспользуемся дискриминантом . Мы также можем определить тип корней выражения.

Дискриминант квадратного многочлена используется для определения количества и типа решений квадратного уравнения. Он описывается формулой

Обратите внимание, что это компонент внутри квадратного корня в квадратичной формуле.

Условие дискриминанта имеет три случая.

Случай 1: D > 0

Когда определитель больше нуля, или, другими словами, b ² – 4ac > 0 , мы получаем два действительных различных корня. Это может быть дополнительно классифицировано следующим образом.

1. Если b ² – 4ac – полный квадрат, то у нас есть два действительных рациональных корня;

2. Если b ² – 4ac не является полным квадратом, то у нас есть два действительных иррациональных корня.

График для этого случая показан ниже.

Дискриминантный случай, когда D > 0, StudySmarter Originals

Случай 2: D = 0

Когда определитель равен нулю, или, другими словами, настоящий корень.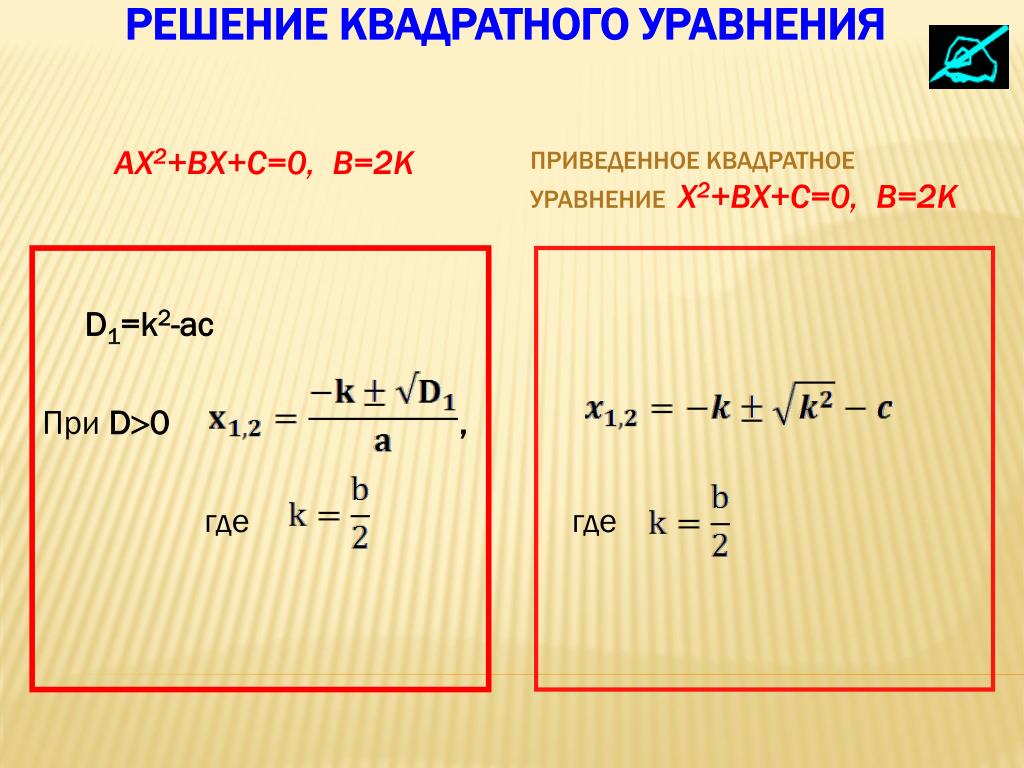 Это также известно как повторяющийся корень. График для этого случая показан ниже.

Дискриминантный случай, когда D = 0, StudySmarter Originals

Случай 3: D

< 0

Когда определитель меньше нуля или, другими словами, b ² – 4ac < 0 получаем два комплексно-сопряженных корня. Это означает, что наше решение имеет вид a + bi , где a — действительная часть, а b — мнимая часть. График для этого случая показан ниже.

Дискриминантный случай, когда D < 0, StudySmarter Originals

Напомним, что мнимая единица равна

Использование квадратичной формулы и дискриминанта для поиска корней

В этом разделе мы рассмотрим некоторые рабочие примеры, демонстрирующие применение квадратичной Формула и дискриминант для поиска решений заданного квадратного уравнения.

Два действительных рациональных корня

Решите следующее квадратное уравнение.

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу для оценки ее решений.

Решение

Шаг 1 : Найдите a, b и c

Шаг 2 : Вычислите дискриминант

Шаг 3 : Найдите решения

Используя квадратичную формулу, мы получаем

Обратите внимание, что составляющая внутри квадратного корня равна D, или, другими словами,

Здесь — идеальный квадрат, поэтому мы получаем пара рациональных корней

Таким образом, решения .

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 1, StudySmarter Originals

Два действительных иррациональных корня

Решите следующее квадратное уравнение.

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу, чтобы оценить их решения.

Решение

Шаг 1 : Найдите a, b и c

Шаг 2 : Вычислите дискриминант

Шаг 3 : Найдите решения

Используя квадратичную формулу, мы получаем

Здесь не полный квадрат, поэтому мы получаем пару иррациональных корней

Таким образом, решения .

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 2, StudySmarter Originals

Обратите внимание, что вы можете сохранить корни в точной форме и что десятичные разряды являются приблизительным ответом.

Один вещественный повторяющийся корень

Решите следующее квадратное уравнение.

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу, чтобы оценить их решения.

Решение

Шаг 1 : Определить a, b и c

Шаг 2: Вычислить дискриминант

Шаг 3 : Найдите решения

Используя квадратную формулу, мы получаем

Заметив, что

Таким образом, решение .

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 3, StudySmarter Originals

Два комплексных корня

Решите следующее квадратное уравнение.

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу, чтобы оценить их решения.

Решение

Шаг 1 : Идентифицируйте a, b и c

Шаг 2 : Вычислите дискриминант

3 Так как есть два комплексных корня < D,

3 .

Шаг 3 : Найдите решения

Используя квадратичную формулу, мы получаем

Заметив, что

Упрощая это, мы получаем

.

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 4, StudySmarter Originals

Обратите внимание, что на этом графике нет помеченных решений. Это связано с тем, что решения являются мнимыми и не могут быть отображены на стандартной декартовой плоскости. Декартова плоскость представлена ​​действительными числами, а не мнимыми числами! В этом случае мы можем по существу «предполагать» форму графика на основе коэффициента x ² , а точка пересечения с осью y задана исходным квадратным уравнением.

Дискриминант кубического уравнения

В этом разделе мы рассмотрим дискриминант кубического уравнения и определим типы корней выражения, учитывая значение его дискриминанта.

Для кубического уравнения (общего) вида

,

где a ≠ 0, дискриминант описывается формулой

.

Формула для вычисления дискриминанта кубических уравнений может быть довольно длинной. Вопросы, где может быть применена эта формула, часто редко встречаются в этой программе. Тем не менее, может быть полезно знать, как это делается для ясности.

Как и в квадратичном случае, дискриминант для кубических уравнений имеет три условия.

Случай 1: D > 0

Когда дискриминант больше нуля, мы получаем три (различных) действительных корня.

Допустим, у нас есть кубическое уравнение.

Здесь дискриминант равен .

Следовательно, у нас есть три различных действительных корня. Факторизация этого выражения дает

Таким образом, корни равны .

График показан ниже.

Пример 5, StudySmarter Originals

Случай 2: D = 0

Случай 2(a): (четкий тройной корень).

Допустим, у нас есть кубическое уравнение.

Здесь дискриминант равен .

Далее, .

Следовательно, у нас есть три повторяющихся действительных корня. Факторизация этого выражения дает

Таким образом, корни равны .

График показан ниже.

Пример 6, StudySmarter Originals

Случай 2(b): Если дискриминант равен нулю, а (отдельный) корень.

Допустим, у нас есть кубическое уравнение.

Здесь дискриминант равен .

Далее, .

Следовательно, у нас есть два повторяющихся действительных корня и один действительный корень. Факторизация этого выражения дает

Таким образом, корни равны .

График показан ниже.

Пример 7, StudySmarter Originals

Случай 3: D

< 0

Когда дискриминант меньше нуля, мы получаем один (различный) действительный корень и пару комплексно-сопряженных корней.

Допустим, у нас есть кубическое уравнение.

Здесь дискриминант.

Следовательно, у нас есть один действительный корень и два комплексно-сопряженных корня. Факторизация этого выражения дает

Таким образом, корни равны .

График показан ниже.

Пример 8, StudySmarter Originals

Квадратичная формула и дискриминант – основные выводы

• Квадратичная формула используется для определения решений заданного квадратного уравнения.