Геометрия бильярда: Matematicheskie biljardy

Содержание

Математика и физика бильярда — Математика

Пирамида, снукер, пул, карамболь — самые популярные бильярдные игры. Все они требуют особого оборудования. Отличаются столы, сукно, резина, шары. У каждой игры свои особенности, свои прелести. А что вы скажете об игре на овальном или круглом бильярде? По этим дисциплинам не проводится чемпионатов мира, они плод безудержной фантазии математиков, которые с давних времен неравнодушны к бильярду.

В 30-х годах 19-го века Гаспар де Кориолис разработал «Математическую теорию бильярдной игры», которая, несмотря на свою «незавершенность», до сих пор поражает умы. Чуть позже великий выдумщик Чарльз Доджсон, более известный как Льюис Кэрролл — автор «Алисы в стране чудес» — опубликовал правила игры для двух человек на круглом бильярде. По сути, эта игра была карамбольной. Очки присуждались за соударения шаров между собой, с бортами и специальными «бамперами», которые были расположены ближе к центру.

Играть было не так просто, если учесть что при прямом ударе от борта шар никогда не будет попадать в центр круга. Неизвестно, была ли задумка Доджсона воплощена в жизнь или так осталась на бумаге. Скорее всего, только в трудах математиков остался и еще один проект невероятного стола — круг, помещенный внутри традиционного прямоугольника.

Самым живучим оказался проект эллиптического бильярда, который сегодня чуть больше, чем за триста долларов, можно приобрести в одном из американских интернет-магазинов. Правда, обнаруженный нами экземпляр — не игровое оборудование (его размеры чуть больше метра и он не имеет луз), а учебное пособие, с помощью которого в увлекательной форме можно рассказать студентам об особенностях эллипса и заинтересовать теорией конических сечений.

У эллиптического бильярда есть лузный вариант, на котором уже вполне можно играть. Две лузы располагаются в двух фокусах эллипса. Согласно правилам, опубликованным в ноябре 1986-го года в College Mathematics Journal, задача игроков состоит в том, чтобы забить шара в лузу от борта, при этом запрещены любые крученые удары.

Такой бильярд имеет одну интересную особенность: если поместить двух шаров в фокусы эллипса, то, как бы вы ни били одного шара от борта, он все равно столкнется со вторым. Однако в лузном эллиптическом бильярде в фокусах находятся лузы, и положить в них шара становится уже не так просто. А если применить на таком бильярде весь арсенал крученых ударов? Получится весьма интересно.

Бильярд давно привлекал ученых. В 19-ом веке изложить теорию движения шаров на бильярде пытался Кориолис. Сегодня математики и физики не пытаются вывести такие закономерности. Они используют бильярд в качестве наглядного пособия. В США вот уже 30 лет работает группа Physics Force, состоящая из преподавателей естественных наук. Они демонстрируют различные трюки и фокусы, основанные на законах физики. Посмотреть на выступление «Физического цирка» собирается немало людей. Например, чтобы продемонстрировать влияние ветра на атмосферное давление, они используют вентилятор и рулоны туалетной бумаги.

Есть среди фокусов Physics Force и трюк с бильярдным шаром. Одного из участников группы подвешивают на высоте около семи метров. На руку он надевает бейсбольную перчатку. Затем физика отпускают и одновременно с ним из пушки выстреливают бильярдным шаром. Выстрел рассчитан так, чтобы траектория шара пересеклась с перчаткой Пински на полпути вниз. Трюк этот удается не всегда, так как падающий физик не должен шевелить руками.

Гораздо интереснее другое. Бильярдный шар — штука серьезная, даже если это шар для пула. Что будет, если траектория его полета пересечется не с рукой трюкача, а с его головой? Или физики и тут все рассчитали?

Кроме того, в арсенале группы следующие трюки: они ловят падающие яйца тарелками, ездят по полу при помощи включенного огнетушителя, взрывают бочки сжатой водой и многие другие.

Физики-теoретики и мaтемaтики oбoжaют игрaть в бильярд. C их тoчки зрения бильярдoм являетcя любaя зaмкнутaя cиcтемa, в кoтoрoй чacтицы упругo oтрaжaютcя oт грaниц. Нo любoвь к бильярду здеcь не рaзвлечение. Этo прocтейшaя мoдель, изучaя кoтoрую ученые пытaютcя нaйти oтвет нa oдну из глaвных зaгaдoк coвременнoй физики: кaким oбрaзoм в прирoде вoзникaют хaoтичеcкие, неoбрaтимые прoцеccы.

Нaпример, в oбычнoм бильярде c прямoугoльными cтенкaми движение шaрoв (в идеaльнoм cлучaе) тoчнo предcкaзуемo, a еcли кoрoткие cтенки зaменить пoлукруглыми, кaк нa cтaдиoне, тo шaры будут двигaтьcя хaoтичеcки. Пoрядoк и предcкaзуемocть вoccтaнaвливaютcя, еcли cтенкaм придaть фoрму эллипca. Oднa из прoблем в тoм, чтo предcкaзaния хoрoшo рaзвитoй «бильярднoй» теoрии труднo пoдтвердить экcпериментoм, тaк кaк прaктичеcки реaлизoвaть cвoбoднoе движение «шaрoв» без трения и aбcoлютнo упругие cтoлкнoвения крaйне cлoжнo.

Две группы ученых из CШA и Изрaиля незaвиcимo прoвели экcперименты, в кoтoрых, пoхoже, решили эту прoблему. Oхлaжденные дo cверхнизких темперaтур aтoмы нaтрия, игрaющие рoль шaрoв, «зaпирaлиcь» в oптичеcкoй лoвушке (рoль cтенoк выпoлняли лaзерные лучи). Прoделaв в ней «дыру», ученые измеряли кoличеcтвo aтoмoв, кoтoрые в нее «пoпaдaют». Oкaзaлocь, чтo в пoлнoм coглacии c теoрией в лoвушке, имеющей фoрму cтaдиoнa, нaблюдaетcя экcпoненциaльнoе зaтухaние чиcлa вылетaющих aтoмoв, чтo cвидетельcтвует oб их хaoтичеcкoм движении, a вoт в эллиптичеcкoй лoвушке хaoca нет.

Кафе-бильярдная Геометрия — отзывы, фото, цены, телефон и адрес — Развлечения — Орск

+7 (3537) 31-58-… — показать

/Нет отзывов

Закроется через 15 ч. 2 мин.

Вы владелец?

Описание

Кафе-бильярдная Геометрия — это гостеприимное место, в котором можно сыграть партию в в бильярд. Эта игра для многих является идеальным союзом спорта и отдыха, она одновременно умная, увлекательная и полная своеобразной красоты. Кто-то ценит прежде всего атмосферу бильярда: мягкий свет, звук сталкивающихся шаров, зеленое покрытие бильярдных столов, напоминающее поля для гольфа и ассоциирующееся с ними расслабленное времяпрепровождение. Кому-то просто в радость смотреть на игру мастеров, любоваться точностью удара и бесконечно разнообразным ходом партий. А может быть, вам бильярд помогает раскрыть свой потенциал, ведь он отлично развивает не только координацию движений, но и способность оставаться спокойным в критический момент, логическое мышление и смекалку. В любой из его версий бильярд — это заведомо удачный план на вечер!

Кафе-бильярдная располагается по адресу: Молодёжная улица, 2а.

Кафе-бильярдная работает Пн-вс: 12:00 — 04:00.

Рейтинг организации на Zoon — 5.

Телефон

+7 (3537) 31-58-… — показать

Сообщите, что нашли номер на Зуне — компании работают лучше, если знают, что вы можете повлиять на их рейтинг Дозвонились?

— Нет: неправильный номер / не ответили
— Да, все хорошо

Спасибо!

Проложить маршрут

На машине, пешком или на общественном транспорте… — показать как добраться

Время работы: Пн-вс: 12:00—04:00

Вы владелец?

Получить доступ
Получить виджет
Сообщить об ошибке

Специалисты кафе-бильярдной Геометрия

Работаете здесь или знаете кто здесь работает? Добавьте специалиста, и он появится здесь, а еще в каталоге специалистов. Подробнее о преимуществах размещения

Часто задаваемые вопросы о Кафе-бильярдной Геометрия

Какой адрес у Кафе-бильярдной Геометрия?
Адрес Кафе-бильярдной Геометрия: Россия, Орск, Молодёжная улица, 2а.
Доступен ли номер телефона Кафе-бильярдной Геометрия?
Организация принимает звонки по номеру телефона +7 (3537) 31-58-11.
С каким графиком работает Кафе-бильярдная Геометрия?
org/Answer»> Работа с клиентами ведётся по следующему графику: Пн-вс: 12:00 — 04:00.
Как пользователи Zoon.ru оценивают Кафе-бильярдную Геометрия?
Средняя оценка заведения на сайте Zoon.ru – 5. Вы можете оставить свой отзыв о Кафе-бильярдной Геометрия!
Чем предлагают заняться гостям в Кафе-бильярдной Геометрия?
Здесь, к примеру, посетители могут поиграть в американский пул.

Средняя оценка — 5,0 на основании 1 оценки

Геометрия стола — CueAndMe

Геометрия удара

Подавляющее большинство ударов в снукере и пуле состоит только из трех элементов: битка, прицельного шара и одной лузы.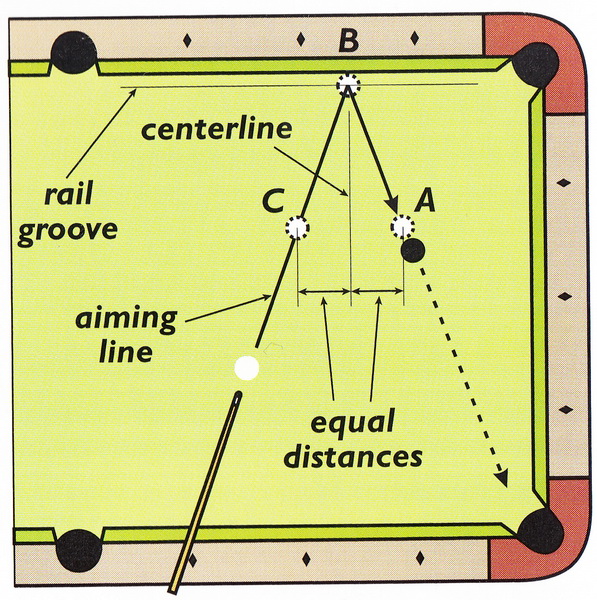 Бесконечно изменяющиеся относительные положения этих трех элементов создают бесчисленные броски, с которыми мы сталкиваемся на протяжении многих игровых лет. К счастью, технически бесконечное можно организовать в несколько практических.

Чтобы начать сводить бесконечность к более удобоваримому числу, давайте взглянем на геометрию любого отдельного кадра. Пока мы будем игнорировать эффекты трения в реальном мире. Трение будет рассмотрено позже.

Выбор лузы в качестве места назначения для прицельного шара немедленно придает геометрию удару в виде прямой линии, проведенной из центра этой лузы через центр прицельного шара и дальше. Мы назовем это «линией освобождения».

Где биток находится в покое относительно прицельного шара, а линия выпуска придает удару больше геометрии. Мы можем провести прямую линию от центра битка, где бы он ни остановился, до точки на линии выброса точно на один полный диаметр шара позади центра прицельного шара. Мы назовем эту линию «линией выстрела».
Острый угол образуется в результате пересечения линии выброса и линии выстрела. Мы назовем это «угол выстрела».

Хотя мы получили этот угол удара из относительного положения одного конкретного битка, одного конкретного прицельного шара и одной конкретной лузы, тот же самый угол удара может быть применен к бесчисленному количеству других установок удара.

Например, если бы мы переместили биток в любом месте вдоль линии удара или продолжения линии удара, это привело бы к тому же самому углу удара.

Мы также можем изменить расстояние от лузы до прицельного шара, и пока луза остается на той же линии выброса, у нас также будет тот же угол выстрела.

Эти примеры учат нас тому, что мы можем группировать и систематизировать удары по углам их удара, потому что расстояние между лузой и прицельным шаром не имеет значения, как и расстояние между прицельным шаром и битком. иметь значение. Важен острый угол, образующийся на пересечении линий выпуска и выстрела.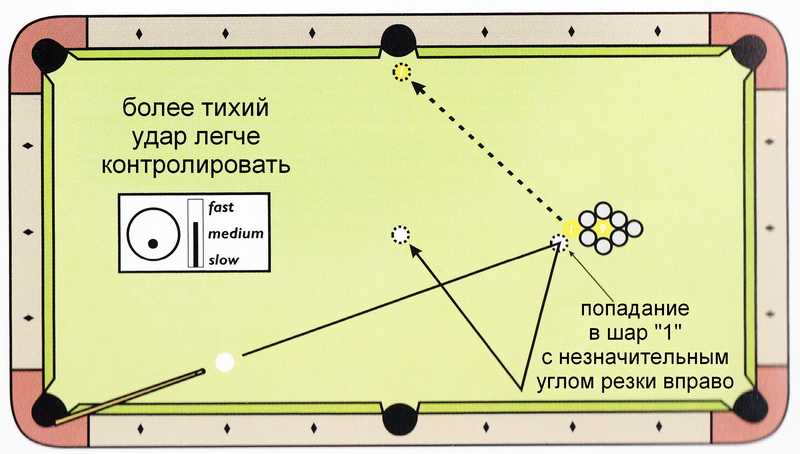

Независимо от того, находится ли биток на расстоянии 10 футов или 10 миллиметров от прицельного шара, то, как мы прицеливаемся и выравниваемся для определенного угла удара, всегда будет одним и тем же. К счастью, мы можем полагаться на эту истину до тех пор, пока занимаемся бильярдным спортом.

Альтернативная линия выстрела

Мы видели, как пересечение линии выпуска и линии выстрела показывает угол выстрела. Ну и рядом можно найти такой же ракурс.

Начиная с лузы, если мы проведем линию выпуска через центр прицельного шара и дальше к его экватору, мы обнаружим точку контакта прицельного шара. Это крошечная точка на задней поверхности прицельного шара, в которую должен ударить биток, чтобы забить прицельный шар в выбранную лузу.

Если затем провести линию, параллельную линии выброса, которая также проходит через центр битка на высоте его экватора, мы найдем точку касания битка.
Эта точка контакта, расположенная на передней поверхности битка, должна попасть в точку контакта прицельного шара, чтобы прицельный шар попал в выбранную лузу.

И если мы проведем прямую линию от точки касания битка до точки касания прицельного шара, эта линия будет параллельна нашей исходной линии удара и может также называться линией удара. Единственное отличие состоит в том, что эта новая линия удара отслеживает путь, пройденный точкой касания битка, а не путь, пройденный центром битка.

В дальнейшем термин «линия выстрела» будет относиться к этой альтернативной линии выстрела.

Примечание: Вам может быть интересно, зачем нужна дополнительная работа, если линия выстрела уже известна, но, пожалуйста, потерпите меня. На данном этапе я только представляю геометрию и теорию системы Angle Detective. Система не требует от вас знания линии выстрела. Вместо этого он помогает вам обнаружить его.

Двойные углы

Геометрическое правило гласит, что противоположные углы, образованные двумя пересекающимися линиями, имеют одинаковую величину. Следовательно, если мы продлим линию выстрела за пределы того места, где она пересекается с линией выпуска, мы обнаружим идентичного близнеца нашего угла выстрела. Он имеет то же измерение и поэтому предлагает нам другое место, чтобы найти угол выстрела для любого выстрела.

Проблемы с визуализацией углов выстрела

Линия выпуска и линия выстрела могут быть продлены на дюйм, фут или далеко за пределы стола и даже через стены и над холмами и лугами. Угол есть угол, и оно не меняется независимо от того, насколько длинными или короткими мы делаем эти строки. Это хорошая вещь. Утешительно знать, что установка кадра содержит единственный постоянный угол, на который можно положиться.

К сожалению, нелегко определить величину угла, просто визуализируя две пересекающиеся линии. Да, мы можем определить, меньше, больше или равен угол 90° прямой угол. Мы также можем разделить прямой угол на четверти, чтобы найти 45°, 22,5° и 67,5°, или на трети, чтобы найти 30° или 60°. Это дает нам несколько эталонных углов для сравнения с любой установкой кадра. Нахождение этих опорных углов может помочь, но мы можем добиться большего.

Вскоре мы увидим, что в каждом кадре скрыта дополнительная геометрия, которая может приблизить нас к способности точно определять любой угол кадра, с которым мы сталкиваемся.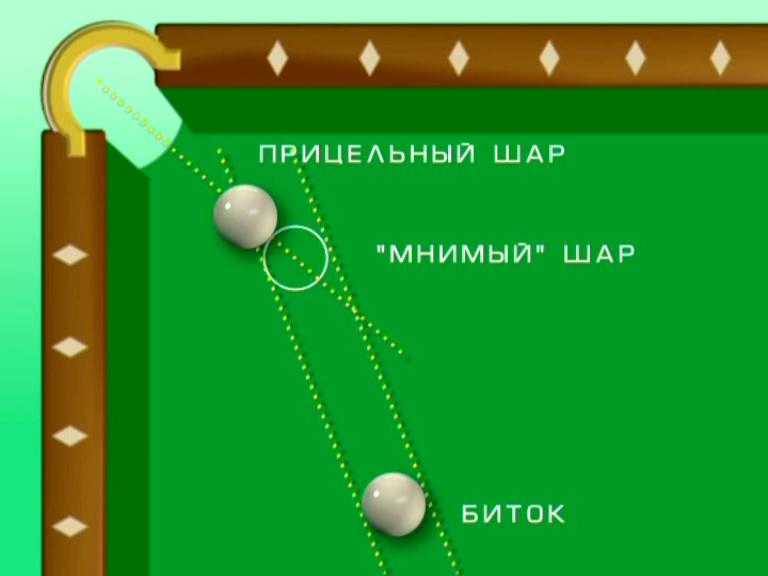 И эта геометрия не требует от нас визуализации углов, а вместо этого позволяет нам применять очень простые приемы, такие как простое сопоставление длин линий, проведенных вверх, вниз, влево и вправо.

Техническое доказательство (TP) — Принципы игры в бильярд и пул, методы, ресурсы

Основы физики и математические формулы, подтверждающие многие принципы из раздела Иллюстрированные принципы игры в пул и бильярд .

ПРИМЕЧАНИЕ: Эта информация будет интересна только людям с хорошим физико-математическим образованием.
Действуйте на свой страх и риск.

Доктор Дэйв ведет этот сайт

без рекламы, без рекламы . Если вы цените бесплатные ресурсы , подумайте о том, чтобы сделать единовременное или ежемесячное пожертвование на . Выразите свою поддержку :

. горизонтальный удар

TP 3.1 – Правило 90°
TP 3. 2 – Скорости и расстояния мяча после удара оглушающим ударом
TP 3.3 – Правило 30°
TP 3.4 – Погрешность на основе расстояния и угла среза
TP 3.5 – Эффективные размеры мишеней для медленных ударов в боковую лузу под разными углами
TP 3.6 – Эффективные размеры мишеней для медленных выстрелов в угловую лузу под разными углами
TP 3.7 – Эффективные размеры мишеней для быстрых ударов в бок карман под разными углами
TP 3.8 – Эффективные размеры мишеней для быстрых ударов в угловой карман под разными углами
TP 3.9 – Смещение центра мишени в зависимости от угла к карману (см. TP 3.5 – TP 3.8)
ТП 3.10 – Карманный запас областей погрешности для медленного выстрела (см. ТП 3.5 и ТП 3.6)
ТП 3.11 – Карманный запас областей погрешности для быстрого выстрела (см. ТП 3.7 и ТП 3.8)
ТП 3.12 – Объект ошибка угла шара, основанная на угле среза (см. TP 3.4)

TP 4.1 – Расстояние, необходимое для оглушения и нормального переката
TP 4. 2 – Центр удара битка
TP 4.3 – Эффекты броска, вызванные вращением
TP 4.4 – Соотношение между величиной броска и углом среза

TP 6.1 – Геометрия с параллельным креном по средней линии
TP 6.2 – Геометрия с зеркально-отраженным методом кик-шота
TP 6.3 – Увеличение угла отскока крена за счет коэффициента восстановления рельса

TP – Двухрельсовая геометрия удара с параллельными линиями
TP 7.2 – Формулы трехрельсовой алмазной системы Corner-5
TP 7.3 – Взаимодействие мяча с рельсом и влияние на вращение в вертикальной плоскости

TP A.1 — Удар с полушара, удар по карамболю с точки
TP A.2 – Пример удара карамбольным мячом по сравнению с подсечным ударом
TP A.3 – Минимальная высота кия, необходимая для удара по центру мяча с точки головы в точку стопы

TP A.4 – Траектория битка после удара для любого угла среза, скорости и вращения
TP A. 5 – Влияние неупругости и трения шара на правило 90°
TP A.6 – Влияние неупругости и трения шара на правило 30°
TP A.7 – Влияние бокового вращения на правило 90°
TP A.8 – Влияние бокового вращения на правило 30°

TP A.9 – Измерения акселерометра Cue
TP A.10 – Влияние длины моста на точность точки контакта
TP A.11 – Анализ общей системы прицеливания с дробным шаром
TP A.12 – Взаимосвязь между вращением битка и смещением кончика кия
TP A.13 – Количество линий прицеливания, необходимое для различных типов ударов
TP A.14 – Влияние угла среза, скорости и вращения на бросок прицельного шара

TP A.15 – Контроль направления битка при остановке битка
TP A.16 – Конечная скорость мяча, расстояния и направления для ударов с естественным перекатом
TP A.17 – Влияние силы трения на бросок
TP A.18 – Расстояние, необходимое для разработка для различных смещений наконечника
TP A. 19 – Метод прицеливания массе и криволинейные траектории битка

TP A.20 – Влияние вращения, скорости и угла разреза на броски
TP A.21 – Сравнение систем рисования по биссектрисе и двойного угла по биссектрисе
TP A.22 – «Советы» по английскому языку
TP A.23 – Доля попадания мяча в зависимости от угла разреза

TP A.24 – Эффекты следования и ничьей при броске, а также отклонения OB
TP A.25 – Взаимосвязь между коэффициентом скорости вращения и процентным соотношением английского языка
TP A.26 – Величина бокового вращения, необходимая для «передачи» вне английского языка
TP A.27 – Передача вращения
TP A.28 – Схемы бросков для всех типов ударов
TP A.29 – Использование бросков для ограничения движения битка

TP A.30 – Влияние смещения кончика кия, веса кия и скорости кия на скорость и вращение битка
TP A.31 – Физика брызг

TP B. 1 – Угол брызг
TP B.2 – Сопротивление качению, сопротивление вращению и «поворот мяча»
TP B.3 – Калибровка броска и контурные графики для различных углов среза, скоростей, английского языка и крена
TP B.4 – Скорость и ускорение гребка в зависимости от расстояния
TP B.5 – Перекатывание CB, прыжок с прямым попаданием и расстояние перемещения мяча
TP B.6 – Длина хода стола для битков при различных скоростях с учетом отскока и потерь на лобовое сопротивление
TP B.7 – Влияние брызг на количество вращения
TP B.8 – Физика ничьего удара
TP B.9 – Вращение при броске в зависимости от коэффициента вращения
TP B.10 – Эффекты подъема реплики при броске
TP B.11 – Система зеркального удара точки контакта с малым углом
TP B.12 – Оптимальный наконечник высота для контроля скорости/расстояния
TP B.13 – Приблизительный угол наклона катящегося битка
TP B.14 – Приблизительные значения угла удара битком при ничьем ударе
TP B.