Работа на НПК по математике «Танграм» (7 класс)
Муниципальное бюджетное образовательное учреждение Лицей № 20
Городская научно-практическая конференция обучающихся
«Первые шаги в науку»
Математика
«ТАНГРАМ»
Автор: Скрипюк
Дарья Константиновна
Класс: 6
ОУ: МБОУ «Лицей № 20»
Руководитель: Фролова Елена Ивановна
Учитель математики
МЕЖДУРЕЧЕНСК –2019 год
Содержание:
I. Введение…………………………………………………………………………………………………………… 3
Введение…………………………………………………………………………………………………………… 3
II. Основная часть…………………………………………………………………………………………………. 5
2.1. Почему игра получила такое название? 5
2.2. Возникновение головоломки «Танграм»…………………………………………………………… 5
2.3. Знаменитые люди и танграм ………………………………………. 7
2.4. Геометрические фигуры танграма…………………………………………………………………….. 8
2.5. Площадь и свойства площадей с использованием танграма………………………………. 9
2.6. Классификация……………………………………………………………………………….. ……………….
9
……………….
9
2.7. Правила составления головоломки «Танграм»………………………………………………… 12
III. Практическая часть………………………………………………………………………………………… 12
3.1. Изготовление Танграма………………………………………………………………………………….. 12
3.2. Танграм, не просто игра, а математическое развлечение………………………………….. 13
3.3. Двойной танграм……………………………………………………………………………………………. 16
IV. Заключение……………………………………………………………………………………………………… 18
V. Список литературы…………………………………………………………………………………………. 19
Приложение №1
Приложение №2
Приложение №3
«Очарование танграма таится в простоте материала
и в кажущейся непригодности его для создания фигурок,
обладающих эстетической
привлекательностью».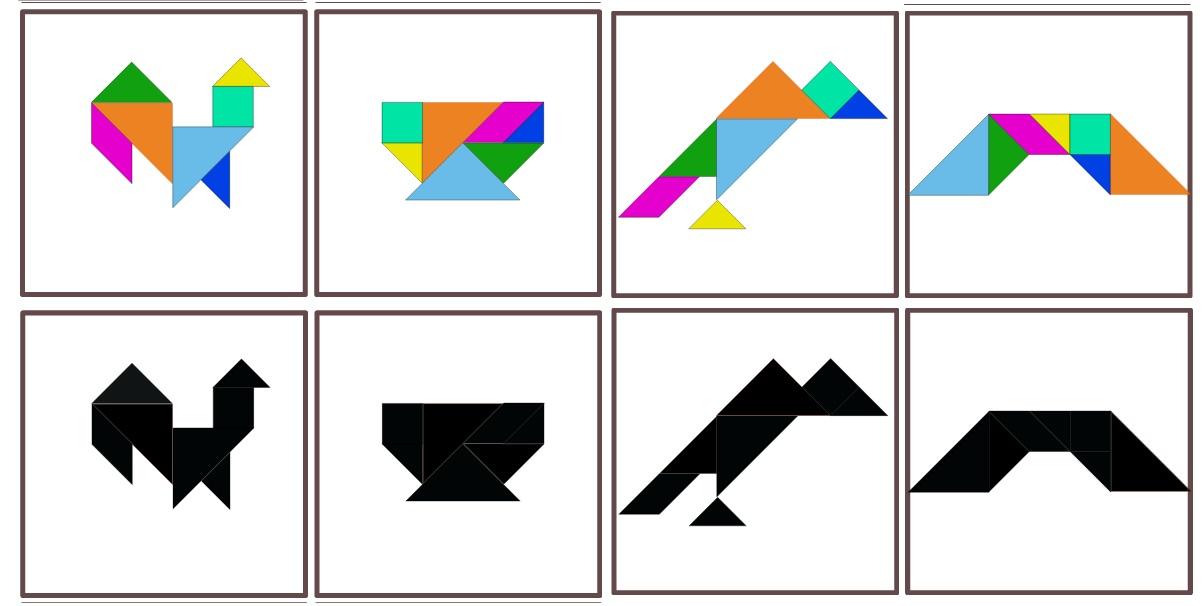
М. Гарднер
I. Введение.
Когда китайская головоломка «Танграм» попала мне в руки, я задумалась – это просто игра или что-то большее?
В процесс знакомства и овладения техникой складывания фигурки танграма у меня возникли вопросы: Как танграм может помочь в изучении математики? В решении логических и занимательных математических задач? Можно ли составлять фигуры из нескольких танграмов?
Чтобы разобраться в этих вопросах, мне предстояло изучить все комплектующие фигуры: измерить их размеры, вычислить площади, найти соотношения, установить возможности применения танграма.
Объект исследования: головоломка «Танграм».
Предмет исследования: возможность составления фигур, состоящих из двух и трех танграмов.
Цель работы – составить свои фигуры, состоящие из двух и более танграмов и использовать приложение в PowerPoint для тренировки в составлении фигур из двух танграмов.
Задачи:
·
Изучить
историю происхождения традиционной китайской игры-головоломки – танграм.
· Провести анкетирование среди одноклассников.
· Познакомиться с различными способами составления фигур.
· Создать коллекцию картин из нескольких танграмов.
· Разработать в приложение тренажер для тренировки в составлении фигур из нескольких танграмов.
· Узнать сферу применения «Танграма» в геометрии.
Методы исследования:
· изучение материалов по теме исследование;
· моделирование;
· конструирование;
· классификация.
- анализ полученных в ходе исследования результатов.
Проблемы, которые предстояло разрешить:
1.Сколько фигур можно построить из фрагментов танграма?
2.Какие виды фигур можно сконструировать из фрагментов двух танграмов?
3.Можно ли использовать эту головоломку в геометрии?
4.Используется ли танграм в настоящее время?
Гипотеза: Я предположила, что эта старинная головоломка поможет
мне при изучении геометрии.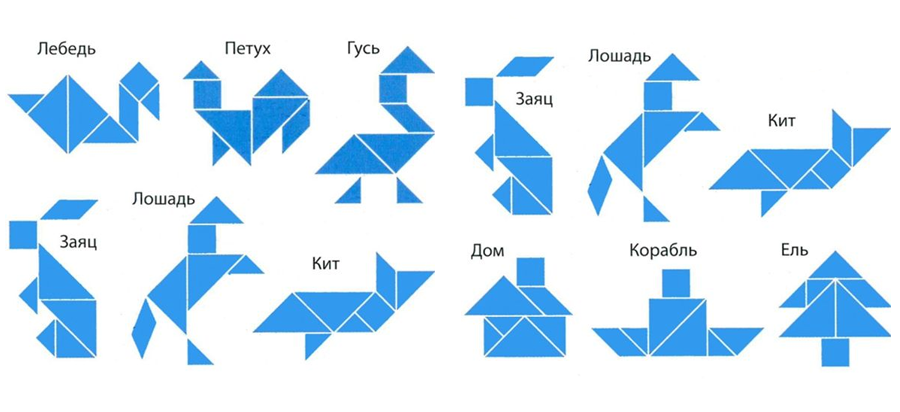
II. Основная часть
Танграм (по-китайски «Пиньинь» — семь дощечек мастерства) – головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.).
В Китае название “Танграм” неизвестно, а игра имеет название «ШИ-ЧАО-ТЮ», что в переводе «Хитроумный узор из семи частей».
2.1.Почему игра получила такое название?
Установить точное происхождение этого названия невозможно. Существует несколько версий, одна из них гласит, что название головоломке дали люди, живущие на берегах реки Танка в Китае. Они были известны купцам. Моряки из стран Запада, вероятно научились играть в танграм, общаясь с местными жителями, а затем привезли головоломку на родину.
В книге
«Китайский философский и математический танграм» (1817 г.) слово танграм —
трактуется, как старинное английское слово — обозначающие игрушка головоломка.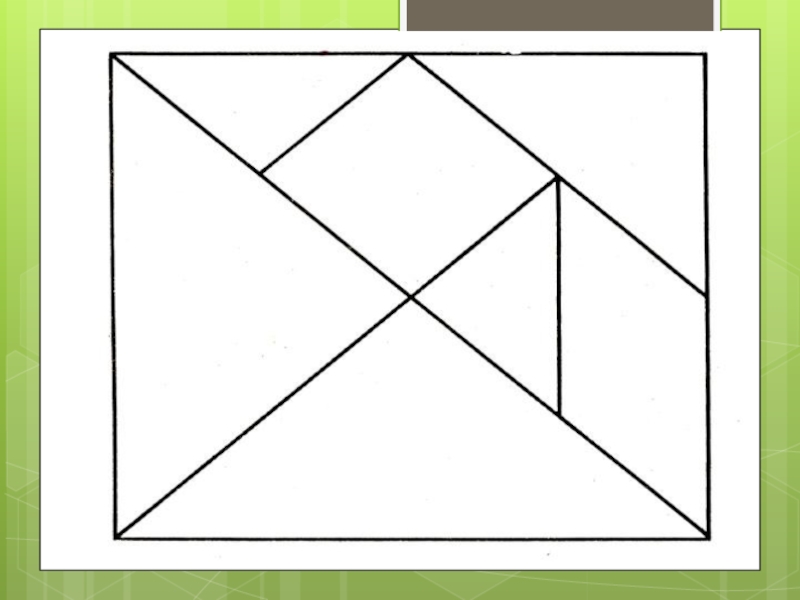
В Оксфордском словаре английского языка — название Танграм появляется со ссылкой на авторитетного Генри Э. Дьюдени, его версию принял составитель словаря Д.Мюррей. Он обнаружил, что слово танграм впервые встречается в словаре Вебстера издания 1864 г. По мнению Мюррея, само слово танграм было придумано в середине прошлого столетия неким американцем, образовавшим неологизм из слова Тан, что означает на кантонском диалекте китайский, и распространенного суффикса -грам (в переводе с греческого «буква») (как в словах анаграмма или криптограмма).
Танграм — очень древняя игра – головоломка. Существует целый ряд версий и гипотез возникновения игры “Танграм”.
Легенда первая: версия про разбитую плитку.
Более 4000 тысяч лет назад у одного человека из рук выпала
фарфоровая плитка и разбилась на семь частей. Расстроенный, он в спешке
старался ее сложить, но каждый раз получал все новые интересные изображения.
Это занятие оказалось настолько увлекательным, что впоследствии квадрат,
составленный из семи геометрических фигур, назвали Доской Мудрости.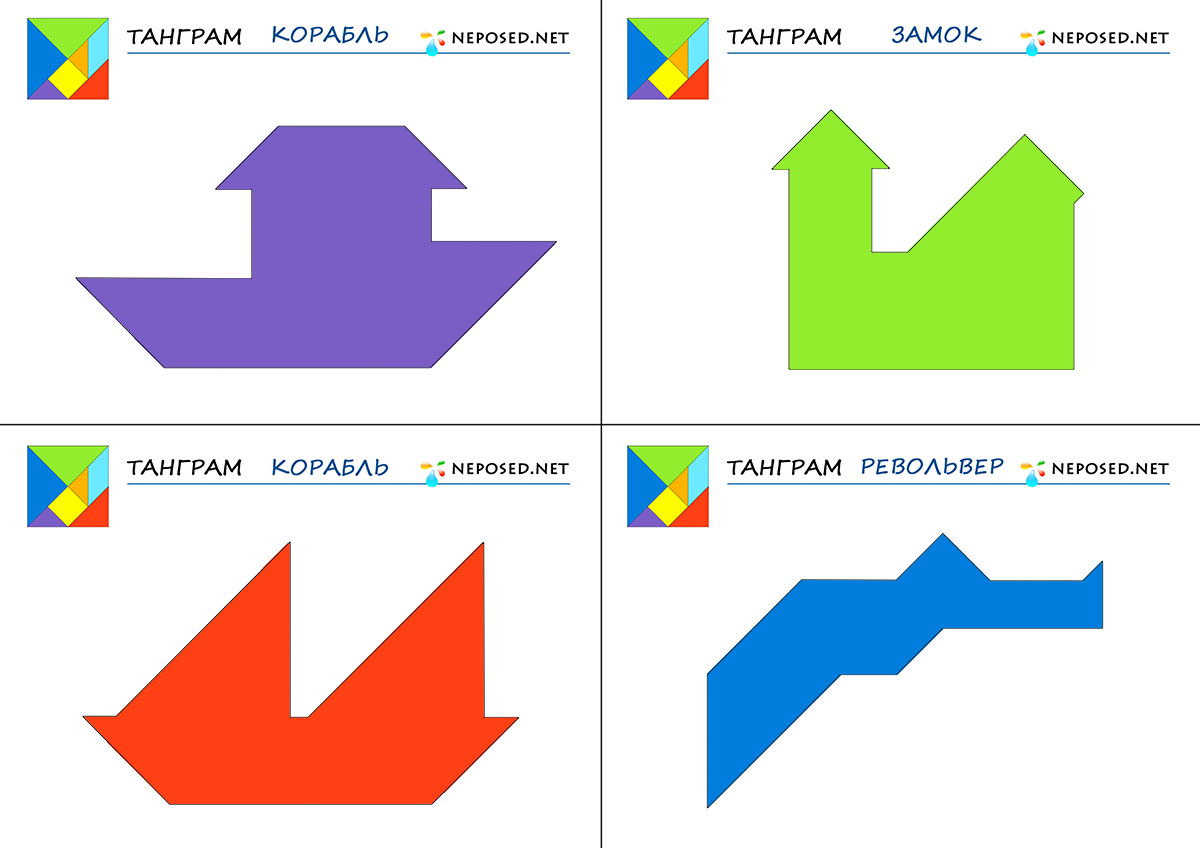
Легенда вторая: три мудреца придумали «Ши-Чао-Тю».
Появление этой китайской головоломки связано с красивой легендой. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло большее удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали «Ши-Чао-Тю»- квадрат, разрезанный на семь частей.
Легенда третья: семь книг Тана.
Местом где была изобретена игра, несомненно является Китай. Дата создания может быть определенна приблизительно XVIII век. Первой известной древней книгой по танграму является “Собрание фигур из семи частей” (Китай 1803 г.). Издана она была на рисовой бумаге. Книги, изданные в Европе, были лишь отчасти оригинальны, а в своей основе имели китайские источники. Приведем отрывок из этой книги: «В записках покойного профессора Челленора, попавших в руки автора, — утверждал Лойд, — имеются сведения о том, что семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур, были составлены в Китае более 4000 лет назад. Эти книги ныне стали столь большой редкостью, что за те сорок лет, которые профессор Челленор провел в Китае, ему лишь раз удалось видеть первое издание первого из семи томов (сохранившихся полностью) и несколько разрозненных фрагмента второго тома».
Согласно
легенде Лойда, Тан был легендарным китайским мудрецом, которому его
соотечественники поклонялись как божеству. Фигуры в своих семи книгах он
расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы
начинаются с символических изображений хаоса и принципа “инь и ян”. Затем
следуют простейшие формы жизни, по мере продвижения по древу эволюции
появляются фигуры рыб, птиц, животных и человека. По пути в различных местах
попадаются изображения того, что создано человеком: орудию труда, мебель,
одежда и архитектурные сооружения.
Фигуры в своих семи книгах он
расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы
начинаются с символических изображений хаоса и принципа “инь и ян”. Затем
следуют простейшие формы жизни, по мере продвижения по древу эволюции
появляются фигуры рыб, птиц, животных и человека. По пути в различных местах
попадаются изображения того, что создано человеком: орудию труда, мебель,
одежда и архитектурные сооружения.
Первое изображение танграма (1780) обнаружено на ксилографии японского художника Утомаро, где две девушки складывают фигурки.
На первых порах им пользовались не для развлечения, а для обучения геометрии. Слово «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии».
Появление
танграма на западе относят не ранее чем к началу XIX столетия, когда эти головоломки
попали в Америку на китайских и американских судах. Старейший такой экземпляр,
подаренный сыну американского судовладельца в 1802 году, сделан из слоновой
кости и хранится в шёлковом футляре (рис.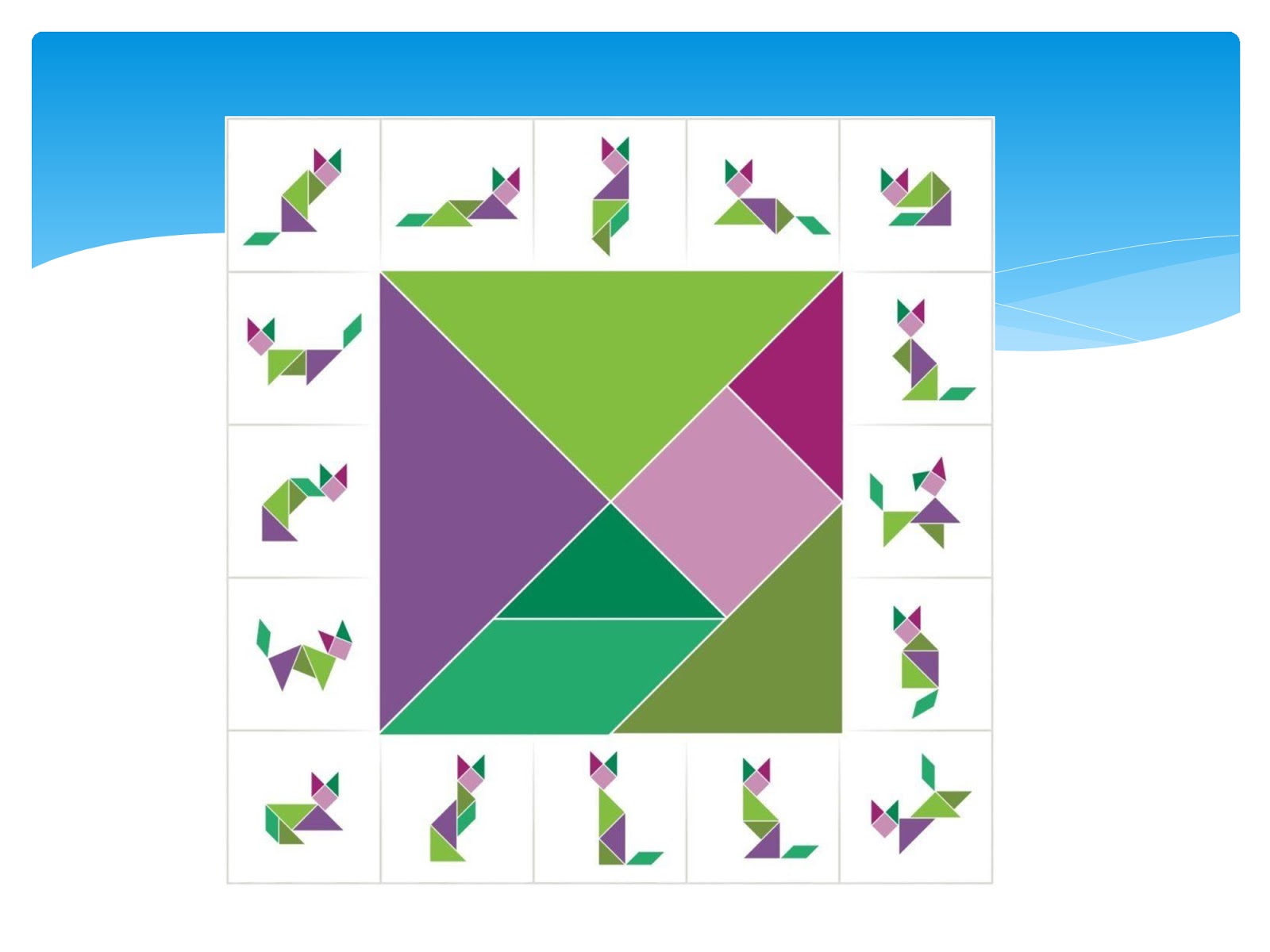 1).
1).
Рис.1 |
2.3.Знаменитые люди и танграм
Льюис Кэрролл
Все мы хорошо знаем книгу «Алиса в стране чудес» Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге «Модная китайская головоломка» он пишет, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость». Упоминание о любимой игре Наполеона, скорее всего не соответствует действительности, однако, и нет обратных доказательств, что, в свою очередь, позволяет существовать и такой красивой версии.
Эдгар А. По
Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке.
Роберт ван Гулик
Известный
писатель и дипломат Роберт ван Гулик в романе «Убивающие ногтями» построил весь
сюжет книги вокруг танграма.
Абдул — Вефа
Одним из первых научных трудов известных человечеству по решению задач на разрезание является трактат Абдул Вефа. Он являлся персидским астрономом. Жил в десятом веке в Багдаде. Сохранились лишь отдельные части этой книги и в том числе решение задачи как разрезать три одинаковых квадрата на 9 частей из которых в дальнейшем возможно сложить один большой квадрат. В дальнейшем решение этой задачи с условием использования минимального количества элементов было сделано англичанином Генри Э. Дьюдени. Он решил задачу Абдул Вефа с использованием 6 элементов, и это является минимальным решением на настоящее время.
2.4. Геометрические фигуры танграма.
Танграм состоит из: двух больших, двух маленьких и одного среднего треугольников, одного квадрата и одного параллелограмма.
Треугольник.
Три точки, не лежащие на
одной прямой, соединены отрезками, образуют геометрическую фигуру, которая
называется треугольником.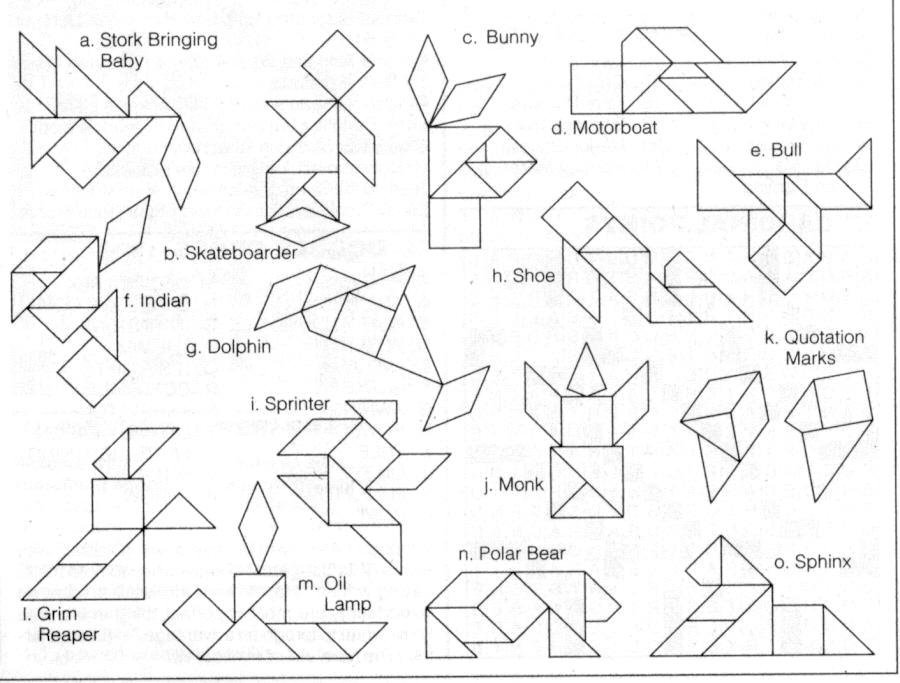 Точки- вершины треугольника, отрезки назовем
сторонами треугольника.
Точки- вершины треугольника, отрезки назовем
сторонами треугольника.
Треугольники бывают: прямоугольный, остроугольный, тупоугольный.
Прямоугольный треугольник-это треугольник, у которого один из углов равен 900.
Квадрат- прямоугольник, у которого стороны равны.
Параллелограмм- это четырехугольник, у которого противоположные стороны попарно параллельны.
Противоположные стороны параллелограмма равны.
2.5. Площадь и свойства площадей с использованием танграма.
Можно
чётко проследить свойство площадей на примере «Танграма». Собрав квадрат,
становиться ясно, что измерение части занимаемой той или иной фигурой, удобно
осуществлять квадратом, с заданной единицей длины стороны квадрата. Свойства
площадей: 1. Равные фигуры имеют равные площади. С помощью наложения треугольников
в танграме это хорошо просматривается. Треугольник аbd равен треугольнику adh.
Собрав квадрат,
становиться ясно, что измерение части занимаемой той или иной фигурой, удобно
осуществлять квадратом, с заданной единицей длины стороны квадрата. Свойства
площадей: 1. Равные фигуры имеют равные площади. С помощью наложения треугольников
в танграме это хорошо просматривается. Треугольник аbd равен треугольнику adh.
Треугольник hfi равен треугольнику dgc.
2.Чтобы найти площадь сложной фигуры надо найти сумму всех площадей входящих в неё фигур. В танграме S cbeg = S cgd + S hti, а так как площади этих треугольников равны, то S cbeg =2 S cgd. Siej=2S cgd. Таким S cbeg=S iej.
Вывод: Действительно тема площадей и свойств площадей прекрасно иллюстрируется танграмом.
Вид | Характеристика | Пример |
Связный танграм | с любого тана можно перейти на любой другой тан, переходя только через общие части сторон танов | |
Несвязный танграм | стороны танов не соприкасаются У этого танграма отсутствует даже какая-либо связная
часть, т. | |
Точно подогнанный танграм | связный танграм без дыр, составленный так, что если два тана соприкасаются, то совпадают либо катет с катетом, либо гипотенуза с гипотенузой элементарных треугольников, из которых они составлены. |
|
Замечательные фигурки получаются при объединении двух тематически связанных между собой танграмов, каждый из которых составлен из полного комплекта 7 танов, как на рис.2.
Рис.2. Женщина, толкающая коляску и Индейцы
Парные танграмы
Парные, или парадоксальные, танграмы — два танграма такие, что при их совместном рассматривании кажется, что один из них собран без одного тана.
На рис3. приведены два примера парных танграмов.
Рис.3. Парные танграмы: Монах со свечой и Монах с чашей
Самый известный парадокс
«Путник» – это два одинаковых человеческих силуэта, один из которых
стоит на ноге, а другой нет. Откуда взялась нога у человечка? Этот парадокс
обнаружил Генри Дьюдени. Если всмотреться внимательно, то первая фигура чуть толще
второй.
Откуда взялась нога у человечка? Этот парадокс
обнаружил Генри Дьюдени. Если всмотреться внимательно, то первая фигура чуть толще
второй.
Площадь «ноги» в точности равна площади избыточной полоски на животе, обозначенной отрезком АВ.
Ещё один фокус того же типа можно обнаружить, если сравнить фигуры квадратов.
А также фигуры чаши:
Суть головоломки заключается в конструировании на плоскости разнообразных предметных силуэтов, напоминающих животных, людей, предметы быта, транспорт, буквы, цифры, цветы и т. д. Всего насчитывают более 7000 различных комбинаций из одного танграма. Самые распространенные из них — фигуры животных, птиц и человека.
Правила:
· в каждую собранную фигуру должны входить все элементы;
· при составлении фигур элементы не должны налегать друг на друга;
· элементы фигур должны примыкать один к другому;
·
начинать нужно с того, чтобы найти место самого
большого треугольника.
В результате получается плоскостное силуэтное изображение. Оно условно, схематично, но образ легко угадывается по основным характерным признакам предмета: его строению, пропорциональному соотношению частей и форме.
III. Практическая часть
3.1. Изготовление Танграма:
Начертите на картонном листе или листе пористой резины квадрат 10см*10см и расчертите его как показано на схеме.
3.2. Танграм, не просто игра, а математическое развлечение
Сфера применения «Танграма» гораздо шире, чем просто игра. Из частей головоломки можно составлять изученные геометрические фигуры (треугольник, квадрат, параллелограмм, трапеция, прямоугольник), вычислять их площади, а также сравнивать эти фигуры с помощью наложения.
Взяв площадь маленького квадрата (q) за единицу (Sq=1), я накладывая
фигурки друг на друга определила площадь каждой из них. Таким образом,
выяснилось, что площадь больших треугольников равна удвоенной площади квадрата
(ST=2*Sq=2) , площадь среднего треугольника равна площади квадрата и удвоенной
площади маленького треугольника (Sĩ = Sq = 2* St =1), площадь параллелограмма
также равна площади квадрата (Sp=Sp=1) , площадь маленьких треугольников –
половина площади квадрата (St=1/2*Sq=1/2).
Так как два маленьких треугольника, сложенные определённым образом составляют квадрат, то возможно определить их углы (90, 45,45). Если эти два треугольника сложить иначе, то можно определить углы параллелограмма (135,135,45,45). Соединяя квадрат и маленькие треугольники, мы получаем большой треугольник и можем также определить его углы (45,45,90)
Составляя фрагменты танграма можно получить такие геометрические фигуры как треугольник, трапеция, прямоугольник, параллелограмм.
Сочетанием больших треугольников можно получить квадрат, параллелограмм, и треугольник. Из пяти оставшихся можно составить равнобедренный прямоугольный треугольник и квадрат.
С помощью двух танграмов, я проверила теорему Пифагора для равнобедренного прямоугольного треугольника.
В прямоугольном
треугольнике квадрат гипотенузы равен сумме квадратов катетов c2=a2+b2.
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Для этого я вырезала два танграма из квадратов со стороной равной гипотенузе треугольника. Путём наложения определила, что сумма площадей двух квадратов на катетах будет равна площади квадрата построенного на гипотенузе.
Площадь квадрата построенного на гипотенузе равна 8 площадям тана-квадрата.
Площади квадратов, построенных на катетах, равны. Площадь каждого из них равна 4 площадям тана-квадрата. 4+4=8 Площадь квадрата построенного на гипотенузе равна сумме площадей квадратов построенных на катетах.
Я думаю, что применять танграм можно при изучении свойств многоугольников, периметра прямоугольника и четырёхугольника и многих других.
Область
применения «Танграма» гораздо шире, чем просто головоломка. Из ее частей можно
составлять изученные геометрические фигуры (треугольник, квадрат, параллелограмм,
трапеция, прямоугольник), вычислять их площади, а также сравнивать эти фигуры с
помощью наложения.
3.3. Двойной танграм
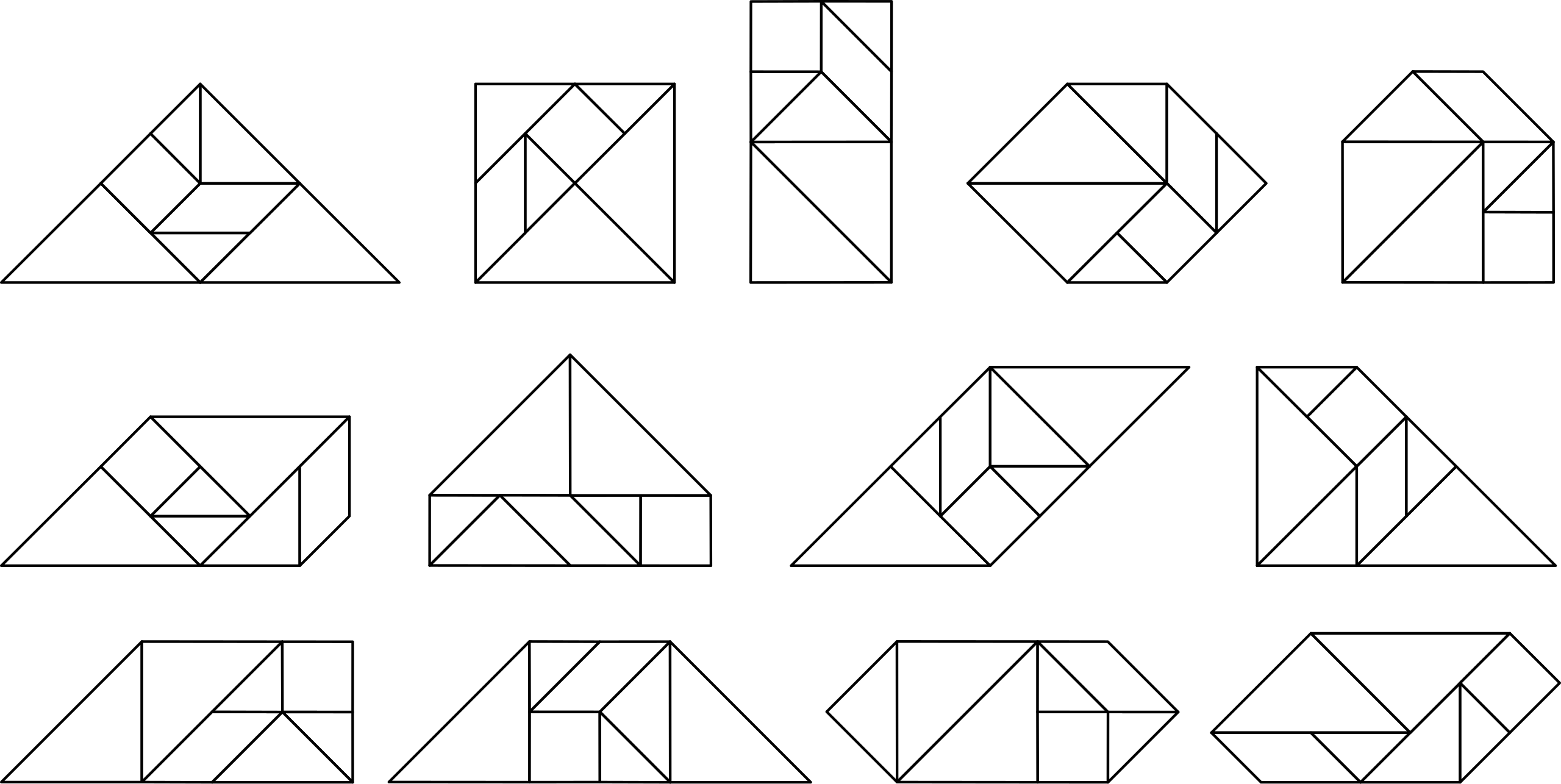
Сначала я собирала фигуры из одного танграма (см. прил. 1), но потом, попробовала составить фигуры из двух танграмов. Я собирала квадрат, у меня получилось 8 решений (см. прил. 2). Затем я собирала равнобедренный треугольник и получили 5 решений (см. прил. 2). Потом я составляла различные фигуры из двух танграмов (см. прил. 3 ).
Этапы создания и работы приложения для тренировки составления фигур из двойного танграма:
1. подбор рисунков, картинок для тренажера;
2. создание фоновой основы презентации;
3. создание 14 танов головоломки «Танграм»;
4. размещение контуров фигур на отдельные слайды;
5. сохранение данной игры, проверка;
6. при работе с тренажером, необходимо нажать на нужный элемент левой кнопкой мыши и переместить его, в нужную позицию;
7. составление предложенной фигуры из 14 элементов;
8. при необходимости можно воспользоваться подсказкой, нажатием на пробел;
9. для будущей корректной работы в тренажере при окончании работы не
нужно сохранять изменения.
для будущей корректной работы в тренажере при окончании работы не
нужно сохранять изменения.
Головоломка придумана 4 000 лет тому назад, но мода на нее не проходит до сих пор. Самые современные дизайнеры используют идею складывания элементов танграма в своих модных коллекциях.
Танграм во всех его проявлениях можно встретить начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном. Самое удачное применение танграма, пожалуй в качестве мебели. Есть и столы танграмы и трансформируемая мягкая мебель и знаменитые настенные полки фирмы Lago.
IV. Заключение
Танграм – одна из удивительных головоломок, которой способен увлечься
практически любой человек. Для математиков она служит неиссякаемым источником
геометрических соотношений. Учителя используют танграм как наглядное пособие.
Коллекционеры ценят танграмы из дерева и слоновой кости, а также исторические
издания, посвященные богатым коллекциям фигур.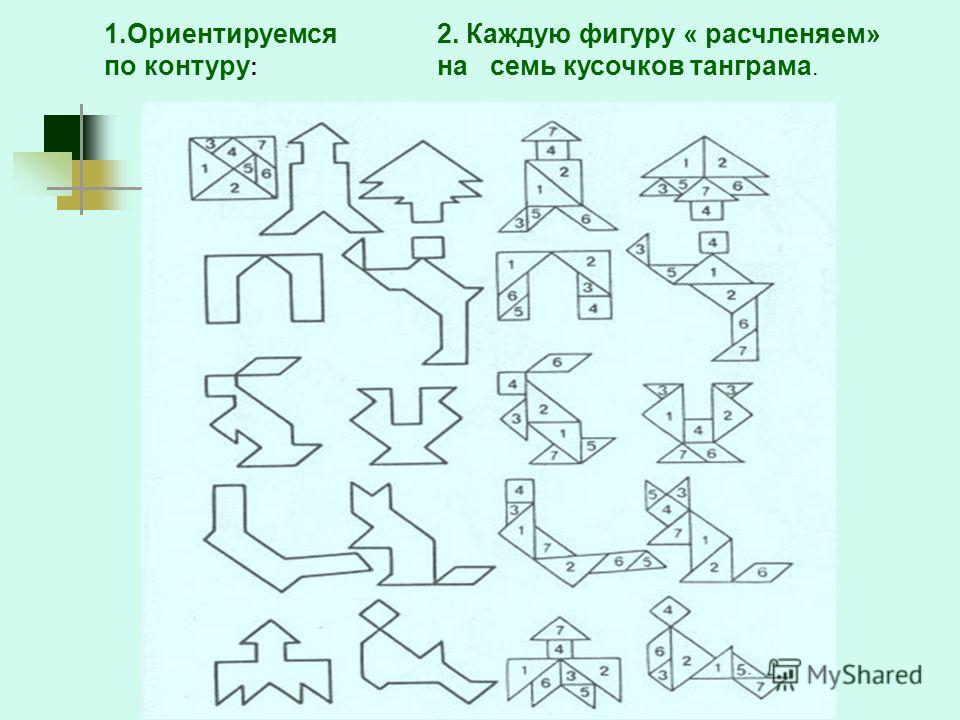 Можно играть танграмом, детали
которого вырезаны из листа бумаги, а для тех, кто признает только игры с
клавиатурой и экраном, есть всевозможные компьютерные программы по танграмам.
Можно играть танграмом, детали
которого вырезаны из листа бумаги, а для тех, кто признает только игры с
клавиатурой и экраном, есть всевозможные компьютерные программы по танграмам.
В начале своей работы я предположила, что эта старинная головоломка поможет мне в учебе. Моя гипотеза подтвердилась, так как действительно с помощью «Танграма» я изучила полезные геометрические сведения.
А также результатом моей работы стала презентация – тренажер для сборки фигур из двух танграмов, которую можно использовать на дополнительных занятиях по математике.
Также дома у нас появилась интересная настольная игра. Эта элегантная старинная головоломка, удивляющая простотой деталей и многообразием фигур, которые можно из них составить, по-прежнему завораживает ценителей, каким бы ни был их возраст.
Мне кажется, что игры развивают детей, учат находить правильное решение, находить выход из трудной игровой ситуации. Игры не только занимают досуг, но и обучают.
Игры — головоломки – это хорошая разрядка от трудных ежедневных проблем и они просто интересны!
V. Список литературы
Список литературы
1. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.:Просвещение,1989.
2. Ленгдон Н.,Снейп Ч. С математикой в путь. — М.: Педагогика, 1987.
3. Ерганжиева геометрия: Учебное пособие для учащихся V-VI классов. – М.: Дрофа, 2011.
4. Мациевский культура. Игры: Учебное пособие. – Калининград: Изд-во КГУ, 2003.
5. «Занимательная геометрия», издательство «АСТ», Москва 2003.
Интернет ресурсы:
1. http://ru. Wikipedia/org/wiki/
3. http://puzzles.h2.ru/Puzzles/tangram.html
4. http://www.babylessons.ru/igra-golovolomka-tangram/
5. http://dic/academic.ru/ .
Задачи, головоломки, игры
Урок 18. Наглядная геометрия 5–6 классы ФГОС
Этот видеоурок будет посвящён решению задач с геометрическим содержанием. Также в нём будут головоломки и игры.
Конспект урока «Задачи, головоломки, игры»
Однажды великий итальянский учёный Галилео Галилей сказал: «Геометрия
является самым могущественным средством для изощрения наших умственных
способностей и даёт нам возможность правильно мыслить и рассуждать».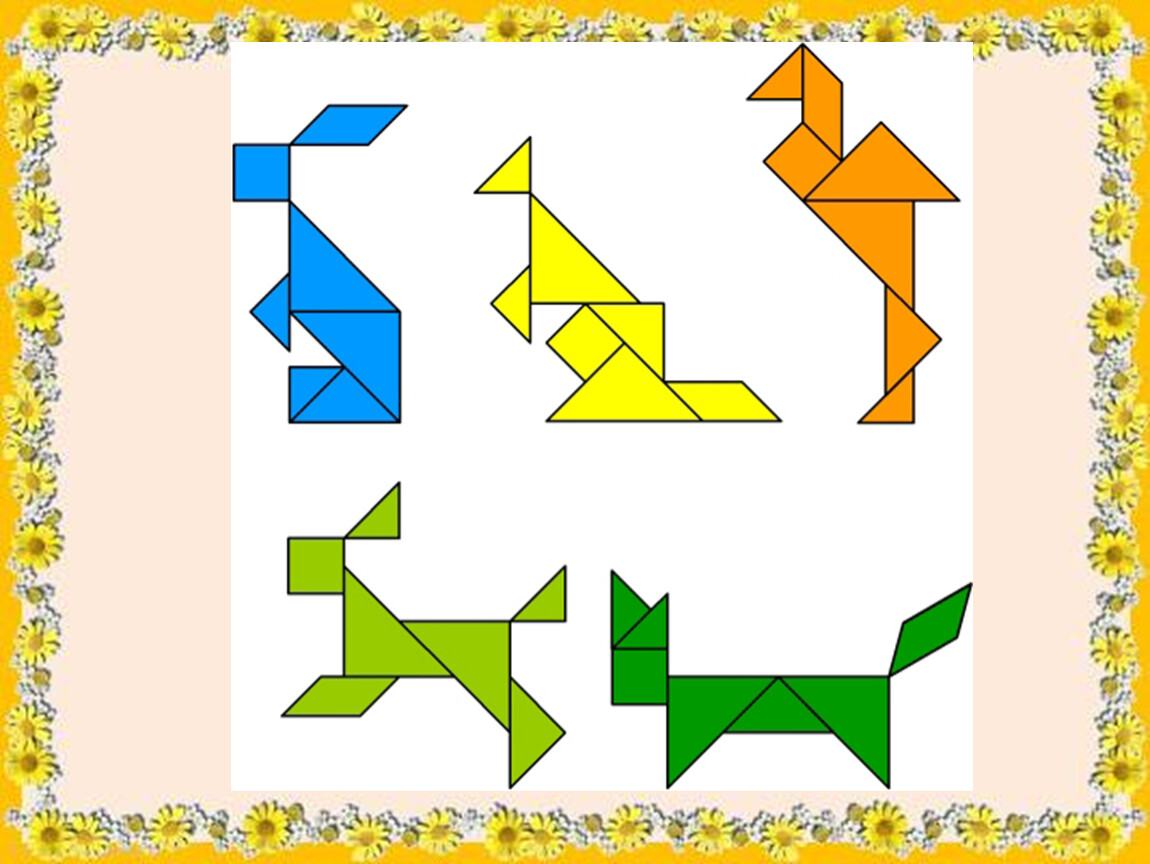
При выполнении заданий нам понадобится не только знание геометрии, но и хорошее воображение и сообразительность.
Задание первое. Начертите окружность и возьмите на ней 4 точки. Через каждые две из них можно провести прямую и притом только одну. Сколько различных прямых получается?
Решение.
Задание второе. На окружности отмечены 10 точек. Найдите число всех различных прямых, проходящих через каждые две точки из заданных на окружности.
Решение.
Задание третье. Найдите на рисунке 8 четырёхугольников.
Решение.
Задание четвёртое. На рисунке изображён прямоугольник со сторонами 6 см и 4 см. Его стороны разделили соответственно на 3 и на 2 равные части, по 2 см каждая. Найдите 18 разных прямоугольников.
Отметим, что квадраты также являются прямоугольниками.
Решение.
Задание пятое. Сколько разных треугольников изображено на рисунке?
Решение.
В первую очередь сосчитаем самые маленькие треугольники. Их 9.
Ещё есть 3 треугольника, длина сторон которых в 2 раза больше длины стороны маленького треугольника. И последний треугольник – самый большой.
Задание шестое. Разрежьте прямоугольник на две части так, чтобы из них можно было составить равнобедренный треугольник.
Решение.
Задание седьмое. Как расставить 16 стульев так, чтобы у каждой из четырёх стен комнаты стояло: а) по 4 стула; б) по 5 стульев?
Решение.
Задание восьмое. Как расставить 10 стульев так, чтобы у каждой стены комнаты стояло по 3 стула?
Решение.
Задание девятое. Можно ли из одного куска проволоки получить такую фигуру, которая изображена на рисунке?
Решение.
Задание десятое. На рисунке показаны 3 спички. Как удалить среднюю спичку из середины, не трогая её?
Решение.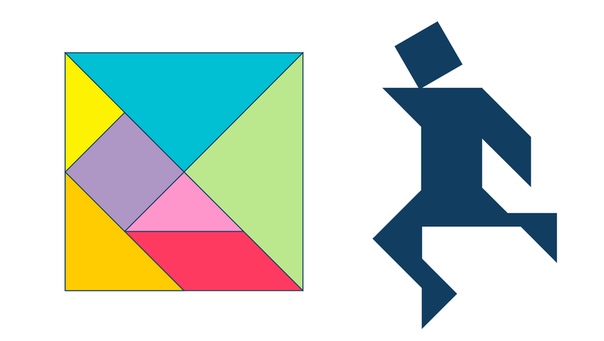 Чтобы ответить на вопрос
задачи, мы, не трогая среднюю спичку, переложим любую из крайних спичек на
другой край. Тогда получится, что спичка, которая была средней, станет крайней.
Чтобы ответить на вопрос
задачи, мы, не трогая среднюю спичку, переложим любую из крайних спичек на
другой край. Тогда получится, что спичка, которая была средней, станет крайней.
Задание одиннадцатое. Из спичек выложена фигура, изображённая на рисунке. Переложите 2 спички так, чтобы получилось 5 равных квадратов.
Решение.
Задание двенадцатое. На рисунке из спичек римскими цифрами выложено неверное равенство: . Переместите одну спичку так, чтобы равенство стало верным.
Решение.
Первый способ.
Второй способ.
Задание тринадцатое. Из 7 многоугольников, входящих в танграм, сложите фигуру, изображённую на рисунке.
Решение.
Задание четырнадцатое. У нас есть 10 квадратных карточек со сторонами 10, 9, 8, 7, 6, 5, 4, 3, 2, 1. Карточки, стороны которых чётны, – чёрного цвета, а стороны которых нечётны – белого.
Выложим на стол самую большую карточку со стороной десять, то есть
чёрную. Затем на неё положим карточку со стороной девять, то есть белую, но не
по центру, а в левом верхнем углу. На неё (в левый нижний угол) положим чёрную
карточку со стороной восемь. Потом на неё (в правый нижний угол) кладём
следующую по размеру карточку – белую карточку со стороной семь. Продолжите
далее этот процесс. Какой чёрно-белый рисунок получится после того, как будет
выложена последняя карточка?
Затем на неё положим карточку со стороной девять, то есть белую, но не
по центру, а в левом верхнем углу. На неё (в левый нижний угол) положим чёрную
карточку со стороной восемь. Потом на неё (в правый нижний угол) кладём
следующую по размеру карточку – белую карточку со стороной семь. Продолжите
далее этот процесс. Какой чёрно-белый рисунок получится после того, как будет
выложена последняя карточка?
Вы, наверное, обратили внимание, что положения карточек закручиваются внутрь против часовой стрелки.
Предыдущий урок 17 Зашифрованная переписка
Следующий урок 19 Фигурки из кубиков и их частей
Получите полный комплект видеоуроков, тестов и презентаций Наглядная геометрия 5–6 классы ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Знать цель китайской головоломки Танграм
Танграм — это еще один тип разборной головоломки, возникший в Китае.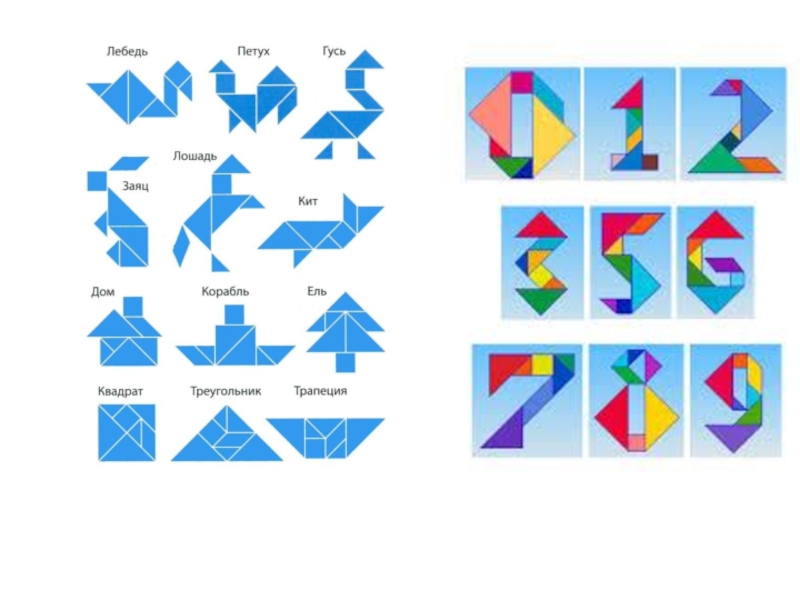 Никаких стандартных инструкций не дается, вместо этого вам нужно использовать свое творчество и пространственное мышление, чтобы формировать из него другие формы.
Никаких стандартных инструкций не дается, вместо этого вам нужно использовать свое творчество и пространственное мышление, чтобы формировать из него другие формы.
Чтобы узнать больше о китайском танграме, а также о некоторых увлекательных испытаниях, продолжайте читать ниже.
Какова цель китайской головоломки танграм?
Цель китайского танграма состоит в том, чтобы создать новую форму фигуры из семи многоугольников. Уникальная форма может быть формой животных, других многоугольников, людей, вещей и всего, что вы можете себе представить. Просто убедитесь, что каждая часть должна быть соединена, но не перекрывать друг друга.
Танграм изначально представляет собой многоугольник квадратной формы, разделенный на семь частей (также известный как « tans »). Таны состоят из треугольников, одного квадрата и одного параллелограмма, в каждом из которых есть прямоугольный треугольник.
Прямоугольный треугольник — это основная форма, необходимая для создания одного большого идеального квадрата, для которого он почти всегда является основой теоремы Пифагора.
Теорема Пифагора — это математическое уравнение, обычно используемое для решения геометрических задач. Это уравнение основано на гипотенузе двух прямоугольных треугольников, образующих квадрат.
Ниже указано место, где находится прямоугольный треугольник в каждом загаре.
Два больших прямоугольных треугольника. Один прямоугольный треугольник среднего размера. однако это не было доказано из-за отсутствия исторических документов.Как ты играешь в китайский танграм?
Играть в китайский танграм легко. Все, что вам нужно, это ваше место, чтобы делать свой танграм, многоугольники танграма и ваш творческий ум. Вы можете сослаться на заданные формы на самой коробке танграма или создать новые, основываясь на своем творчестве.
Не существует руководства или стандартной инструкции по игре в китайский танграм. Так что пусть ваш разум блуждает и представляет, как вы хотите, чтобы все выглядело.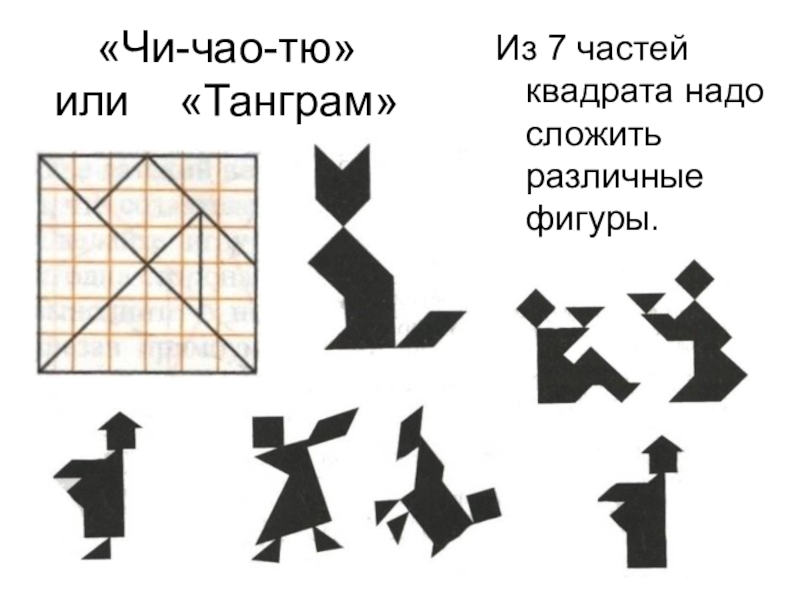
Вам может показаться, что это скучно и все такое. Вот почему я создал список испытаний танграма, которые вы можете выполнить сами, чтобы прокачать себя!
Список заданий Tangram
1. Пять изображений за 5 минутКак следует из названия игры, вам нужно создать пять изображений за 5 минут. В этой игре можно побить свои рекорды по времени или сделать это вместе с другом.
Если вы сделаете это с другом, я предлагаю договориться о последствиях для проигравшего. Это добавит азарта и веселья при этом.
Это задание можно выполнить, если вам скучно и вы устали ждать доставки еды. Это поможет вам почувствовать, что время бежит быстрее из-за острых ощущений, веселья и разочарования от проигрыша сразу.
Попробуйте!
2. Выполняйте задание по азбуке через месяцКаждый день формируйте по одной букве алфавита. Это отличная практика для ускорения ваших навыков танграма.
На первый взгляд это испытание может показаться простым, но внешность бывает обманчива. Различные углы и формы букв создают серьезную проблему и изюминку. Во-первых, вам нужно выяснить, как правильно разместить загар, чтобы сформировать его.
Различные углы и формы букв создают серьезную проблему и изюминку. Во-первых, вам нужно выяснить, как правильно разместить загар, чтобы сформировать его.
Создавайте по одному номеру в день в неделю. Как и в случае с алфавитом, это поможет вам тренировать свое творческое и пространственное мышление день за днем.
Вы можете следить за числовой формой текущей даты, которую вы играете. Это будет твой » танграм трофей дня », когда вы поняли, как его сформировать.
4. Парный танграмЭтот челлендж направлен на формирование образа танграма парами. Вы можете установить таймер в каждой команде, чтобы знать, кто сможет создать быстрее всех. Кто быстрее финиширует, тот и победитель. Последствия могут быть даны проигравшему, и это зависит от вашего внутреннего устройства, каким оно будет.
В нее можно играть как в « пари », если хотите.
Например, если у вас с другом возникает конфликт по поводу того, какое решение следует принять, эта игра может помочь уладить конфликт. Просто не стесняйтесь добавлять в игру другие правила, чтобы сделать ее более увлекательной и захватывающей.
Просто не стесняйтесь добавлять в игру другие правила, чтобы сделать ее более увлекательной и захватывающей.
Найдите лучший портрет, который у вас есть дома, и воссоздайте его с помощью танграма. Лучше всего искать что-то, что показывает все ваше тело, чтобы вы могли создать из него силуэт.
Вы также можете сфотографировать свой портретный танграм, а затем поместить его рядом с исходным изображением, чтобы запомнить его.
Это также может быть отличным подарком для ваших близких! Одновременная демонстрация ваших усилий и творчества будет для них очень много значить.
Так почему бы вам не попробовать прямо сейчас?
6. Зодиак TangramСоздайте свой знак зодиака, используя загар. Если вам посчастливилось закончить свой знак зодиака, попробуйте заполнить и другие зодиаки. Пожалуйста, создайте это, ожидая, когда любимый человек придет к вам на день рождения. Это может быть и вашим подарком себе!
Вы также можете попробовать это, используя свои китайские знаки зодиака или другие астрологические знаки, которые вы можете придумать.
Последствие Танграма — это групповое занятие, в котором один участник угадывает название предмета на своем лбу, используя помощь своих товарищей по группе. Загвоздка в том, что каждому члену группы не разрешается говорить или показывать подсказки к действию; вместо этого им нужно создать из него образ танграма. Побеждает самая быстрая группа, у которой решено больше всего задач.
Убедитесь, что в этой игре есть таймер, чтобы острые ощущения не умерли. Кроме того, настоятельно рекомендуется создать огромный танграм для повышения уровня сложности.
Я настоятельно рекомендую за несколько дней до этой игры создать свой огромный загар. Но тогда делать это с семьей или друзьями очень весело, потому что вы наверняка подумаете и вообразите, как вы будете играть с этим на запланированном мероприятии.
Кроме того, это поможет вам построить командную работу с самого начала, и вы сможете настроить ее по вкусу своей команды.
Если вы одновременно творческий писатель и разгадываете головоломки, вам обязательно понравится эта игра. Создайте короткую детскую историю в соответствии с вашими предпочтениями, а затем сделайте изображение, представляющее каждую сюжетную линию. Эта игра отлично развивает творческие способности и воображение ребенка. Вы также можете сфотографировать его, сохранить на своем компьютере, а затем распечатать из него сборник рассказов!
Это можно сделать как самостоятельный вызов, а также как индивидуальный подарок. Самостоятельный вызов, потому что вам нужно подтолкнуть себя к созданию сборника рассказов с нуля, во время индивидуального подарка, потому что готовый продукт может быть подарен вашим близким.
9. Угадай меня Попробуйте с трех попыток угадать необычный образ, сформированный вашим противником. Если вы не угадаете, что это такое, вы получите следствие. Я предлагаю иметь под рукой от 3 до 5 изображений, чтобы тот, кто подумал больше, стал победителем.
Ваш противник может угадать изображение, даже если оно еще не завершено, но как только ваш друг начнет угадывать, вы должны запустить таймер, чтобы добавить больше уровней сложности. Это ваша внутренняя договоренность о том, как долго это будет длиться, но я предлагаю, чтобы это было максимум 3 минуты.
Вот полное руководство «Угадай меня», которому вы можете следовать:
- Как претендент, вы должны собирать загары по одному. Вы можете провести от 30 секунд до одной минуты в каждом загаре, а затем позволить своему противнику угадать, что это такое.
- Как только ваш оппонент начал угадывать, его/ее время угадывания уже началось. Таким образом, ваш оппонент должен понять это до того, как истечет время.
- Если вам удалось закончить картинку, а ваш оппонент еще не начал угадывать, у него нет другого выбора, кроме как разгадать ее за 3 минуты. Если они не могут ответить правильно, они проигрывают. Претендент получает очко.
 Погладьте меня
Погладьте меня Затем создайте танграм-версию своего питомца! Это также может быть отличным подарком для других «меховых» родителей. Вам нужно найти портретное изображение домашнего животного, а затем создать его танграм-версию. Затем, пожалуйста, сфотографируйте готовое изделие и разместите его рядом с исходной фотографией.
Если вы хотите выйти на новый уровень своего творчества, используйте готовый танграм в качестве образца для вышивки крестиком, а затем оформите его в рамку.
Последнее слово
Играть в танграм легко. Вот почему.
- Специальное оборудование не требуется.
- Нет стандартных инструкций
- Дешевый
- Универсальный
- Это головоломка для всех возрастов
Лучше всего…
Вам просто нужно использовать свое творческое мышление, и все готово!
Не могли бы вы попробовать выполнить задания, которые я перечислил? Если да, что бы вы сделали?
Поделитесь им в комментариях ниже!
Координаты Танграма — Матигон
План урока и цель
Учащиеся смогут делать выводы о свойствах фигур, нарисованных на координатной сетке.
Танграм — это традиционная головоломка, состоящая из семи многоугольников, которые можно сложить в квадрат, а также собрать в бесчисленное множество других форм. Существует множество способов математического исследования частей танграма. На этом уроке учащиеся изучают творческие возможности, которые предоставляют танграмы, работая в системе координатной сетки и просматривая названия различных многоугольников. На сайте mathigon.org/tangram учащиеся могут использовать танграммы, чтобы создавать из танграмм различные формы.
Разминка
На этом полипадном полотне учащимся предлагается определить координаты семи частей танграма, расположенных в виде квадрата. Учащиеся могут перемещать фигуры по мере необходимости.
Решения:
- Большой розовый треугольник (1,1), (1,9), (5,5)
- Большой синий треугольник (1,9), (9,9), (5,5)
- Маленький Бирюзовый треугольник (3,3), (7,3), (5,5)
- Малый красный треугольник (9,5), (9,9), (7,7)
- Зеленый квадрат (5,5) , (7,3), (9,5), (7,7)
- Оранжевый параллелограмм (1,1), (5,1), (7,3), (3,3)
Основная деятельность
Есть несколько разных подходов к этому уроку с элементами танграма. Одна из возможностей состоит в том, чтобы задать открытый вопрос для исследования:
Одна из возможностей состоит в том, чтобы задать открытый вопрос для исследования:
- Какие четырехугольники можно составить из двух или более частей танграма?
Этот вариант может подойти учащимся, которые привыкли работать самостоятельно или в небольших группах над исследовательской задачей. Возможно, вам придется обсудить, можно ли повторно использовать части в фигуре или нет.
Более структурированный подход может состоять в том, чтобы предложить учащимся перечислить известные им четырехугольники и описать их свойства. Затем предложите им составить квадрат (кроме исходного квадрата, в котором используются все семь частей), прямоугольник, параллелограмм и трапецию (Великобритания)/трапецию (США). После того, как они создали свои фигуры на Polypad, предложите им определить координаты каждого угла их готовых фигур, выбрав начало координат и нарисовав отдельную ось для каждой фигуры, которую они делают. Необходимо позаботиться о том, чтобы углы фигур совпадали с точками сетки. Например, на изображении ниже показан прямоугольник, который должен быть под углом 45°, чтобы все вершины находились на сетке.
Например, на изображении ниже показан прямоугольник, который должен быть под углом 45°, чтобы все вершины находились на сетке.
Создав фигуру, они могут предложить своим одноклассникам нанести координаты и нарисовать контур фигуры, а затем решить, какие части танграма могут заполнить контур.
Обсуждение на протяжении всего урока может быть сосредоточено на следующих темах для обсуждения:
- Откуда вы знаете, что фигура является квадратом/прямоугольником/параллелограммом/трапецией (трапецией)?
- Как узнать, какие прямые параллельны/перпендикулярны/одинаковой длины?
- Есть ли фигуры, которые мы можем сделать более чем одним способом?
- Можем ли мы определить площадь любой из фигур, которые мы сделали?
- Можем ли мы сделать ромб (кроме квадратов)?
Возможные решения
На этом холсте Polypad показаны некоторые примеры четырехугольников, которые могут обнаружить учащиеся. Формы танграма имеют следующие площади:
- Большие треугольники: 16 квадратных единиц
- Средний треугольник: 8 квадратных единиц
- Маленький треугольник: 4 квадратных единицы
- Параллелограмм: 8 квадратных единиц
- Квадрат: 8 квадратных единиц
Учащиеся могут вычислить эти площади, используя формулы площади для каждой фигуры, или рассчитав площади относительно маленьких треугольников, посчитав, сколько маленьких треугольников составляют каждую из других фигур.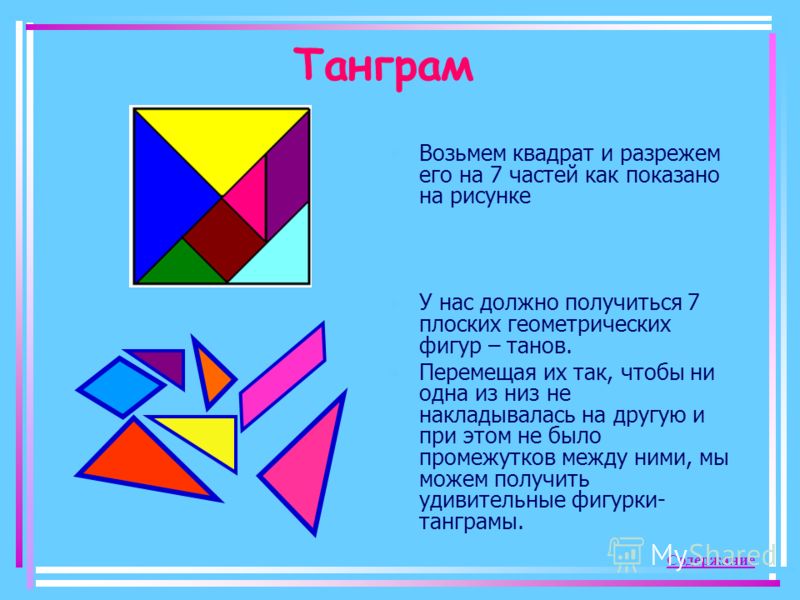

 е. он состоит из 7 несвязных частей.
е. он состоит из 7 несвязных частей.