Куб 4d: Фигура Куб 4D 16 золото ⋆ Чудо-Место

Содержание

Четырёхмерный гиперкуб. Программа Transformator 4D / Хабр

В данной статье хотелось бы поговорить о четырехмерном гиперкубе (тессеракте), и его построение в программе Transformator 4D.

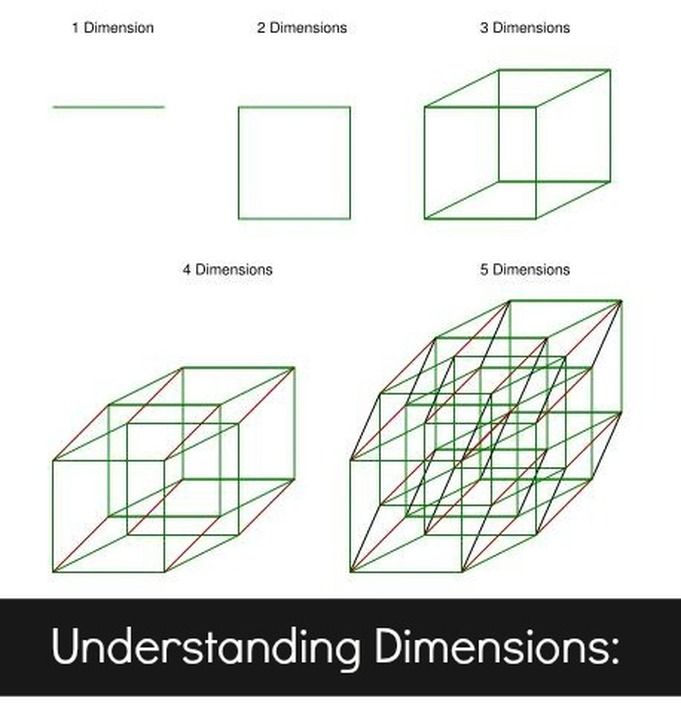
Как мы знаем из геометрии, квадрата – это правильный четырехугольник у которого все углы и стороны равны. Куб можно охарактеризовать следующим образом, это выпуклая фигура, обязательно замкнутая и состоящая из групп параллельных линий расположенных относительно друг друга на противоположных краях фигуры и, соединенных друг с другом под прямым углом. Следовательно гиперкуб — это n-мерная аналогия квадрата у которого n=2 и, куба у которого n=3.

Рассмотрим рисунок 1. На нем изображена точка, которая есть гиперкуб размерностью равной 0. Далее если сдвинуть точку на единицу длины, что приведет к получению отрезка единичной длины и как следствие гиперкуба размерностью единица. После чего сдвинуть отрезок на ту же единицу длины, но перпендикулярно в направлении исходного отрезка, и продолжить эту операцию до замыкания контура, то получится квадрат – гиперкуб размерностью в два.

Если продолжить построение, то сдвигая квадрат на ту же единицу длины обязательно в направлении перпендикулярному плоскости квадрата, получим куб или гиперкуб размерностью 3. И наконец если сдвинуть куб на единицу длины в четвертом измерении то получим четырехмерный гиперкуб. Такое процесс можно повторять на n-е количество измерений.

Рис.1

В евклидовом пространстве тессеракт характеризуется как объемная оболочка состоящая из точек: +-1, +-1, +-1, +-1, что можно записать в виде:

Отсюда видно, что тессеракт ограничен 8-ю гиперплоскостями, пересечение которых с самим тессерактом задает его трехмерные грани, они же являются просто кубами, и в конечном итоге получаем:

8-мь трехмерных граней,
24-и двумерных,
32-а ребра,
16-ть вершин.

Программа Transformator 4D предназначена для создания модели, путем считывания аффинных преобразований и последующим их созданием.

Основой работы программы являются именно аффинные преобразования, это действия над объектом путем перемещения, масштабирования, поворота. Пользователь может сам составлять объекты, в формате файла txt, и анимировать его движение. Программа может выводить частные случаи аффинных преобразований в пространстве, и проекции для любого заданного тела.

Как задавать фигуры

В директории с программой создается папка FIGURES. Каждая фигура задается при помощи двух файлов: первый FigureX.txt, где находятся координаты вершин, второй FigureXm.txt, где находится матрица смежности этих вершин. Х – номер фигуры.

Характеристика файла FigureX.txt:

Координаты первой вершины по Х, находятся в первой строке.

Координаты второй вершины по У, находятся во второй строке.
и т.д. Последняя строка «х» — конец данных.

Характеристика файла FigureXm: Матрица смежности, показывает номера вершин из первого файла.

При запуске программа требует файл acrTrans2FA. txt. Файл описывает четырехмерную фигуру и аффинные преобразования в отдельности для каждого полигона.

По сути можно построить объект отдельные части которого подвергаются разным преобразованиям, и каждую субмодель представить отдельным цветом.

После указания каждого полигона нужно указать аффинные преобразования этого полигона.

Пример: Сборка развертки куба на основе построения квадрата.

Рис. 2

1 Замкнутые полигоны
0 0 0 1 Координаты вектора проецирования
6 Шесть полигонов
4 4 точки в первом полигоне

1 1 0 Цвет полигона №1

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

0 Аффинных преобразований отсутствуют — квадрат №1

4 4 точки — квадрат №2
0.5 0.5 0.5 Цвет полигона №2

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

2 Два преобразования
2 1 -1 0 0 0 Смещение на -1 по х
6 1 0 -1 0 0 0 0 Разворот по оси zx

4 4 точки в квадрате №3
0. 1 0.1 0.1 Цвет полигона 3

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
2 Два преобразования
6 1 0 1 0 0 0 0 Разворот вокруг y от x к z
2 1 1 0 0 0 Смещение на 1 по x

4 Квадрат №4

0.6 0.1 0.7 Цвет полигона 4

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

2 Два преобразования
2 1 0 -1 0 0 Смещаем вниз по y
6 1 0 0 0 -1 0 0 Перемещение вокруг x от z к y

4 Квадрат №5
1 0 0 Цвет полигона 5

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

2 Два преобразования
6 1 0 0 0 1 0 0 Перемещение вокруг x от y к z
2 1 0 1 0 0 Смещаем вверх по y

4 Квадрат №6
0.25 0.5 0.5 Цвет полигона №6

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

4 Четыре преобразования
2 1 0 -1 0 0 Смещаем вниз по y
6 1 0 0 0 -1 0 0 Перемещение вокруг x от z к y
2 1 0 -1 0 0 Смещение вниз для квадрата №6
6 1 0 0 0 -1 0 0

Вращение относительно нижнего ребра четвертого квадрата.

Квадрат №6: описывает два поворота, так как одно из его ребер является общим с квадратом №4, поэтому изначально вращается квадрат №4, после происходит смещение на 1 вниз, и далее вращение вокруг этого же ребра.

Выглядит это так:

Рис.3

Как задать описание тессеракта:

Рис.4

Тессеракт можно развернуть в восемь кубов, так же как куб можно развернуть в шесть квадратов. Развертка тессеракта называется сетью. Для гиперкуба существует 261 вариант сетей, ниже показан самый распространенный.

Исходя из основ сборки куба, также можно написать программу сборки тессеракта или обратного.

Интересно знать

В фильме «Куб 2: Гиперкуб» — восемь незнакомых людей просыпаются в комнатах, имеющих форму куба. Комнаты находятся внутри четырёхмерного гиперкуба. Комнаты постоянно перемещаются путём «квантовой телепортации», и если перелезть в соседнюю комнату, то вернуться в прежнюю уже маловероятно. В гиперкубе пересекаются параллельные миры, время в некоторых комнатах течёт по-разному, а некоторые комнаты являются смертельными ловушками.

Используемый источник: damateur.narod.ru

4D Rubik’s Cube, классическая ретро-игра RBKube Rubik Cube 3D Месть Рубика, куб, 4D, Кубик Рубика, Классика png

Об этом PNG

Размер изображения: 512x512px
Размер файла: 204.75KB
MIME тип: Image/png

Скачать PNG ( 204.75KB )

изменить размер PNG

ширина(px)

высота(px)

Лицензия

Некоммерческое использование, DMCA Contact Us

org/ImageObject»> Мир, Кубик Рубика, Разумный спорт, Всемирные интеллектуальные игры, Игры разума, Speedcubing, Rubiks Revenge, Международная федерация Савате, площадь, куб, Federation Internationale De Savate png 512x512px 96.58KB
Кубик Рубика. Головоломка Кубо де Эспехос, Кубик Рубика., игра, лицо, прямоугольник png 512x512px 149.24KB
Art Illustrator Дизайнер Иллюстрации, Кубик Рубика, культура, нарисованный, текст png 2362x2362px 21.29MB
3 на 3 кубик Рубика, кубик Рубика, кубок профессора, кубик Рубика, симметрия, куб, игрушка png 1826x1920px 442.06KB
Головоломка Кубик Рубика Головоломка кубик Speedcubing, кубик Рубика, синий, игра, ребенок png 1080x1080px 814. 49KB
человек, держащий меч персонаж Minecraft, Minecraft Cinema 4D 3D рендеринг 3D компьютерная графика, Minecraft, 3D Компьютерная графика, логотип, игрушка png 1920x1080px 475.36KB
Евклидов куб. Трехмерное пространство Иллюстрация, кубик Рубика, угол, симметрия, кубики льда png 827x1122px 487.34KB
3×3 кубик Рубика, головоломка кубика Рубика, кубик Рубика, симметрия, кубик Вектор, кубики льда png 1826x1920px 268.17KB
Rubiks Cube Трехмерное пространство, Белый куб, угол, 3D компьютерная графика, черный белый png 743x800px 205.24KB
Рубикс Кубик Книжка-раскраска V-Cube 6, Кубик Рубика, игра, угол, белый png 564x592px 121. 18KB
желтый куб иллюстрация, куб евклидов, куб, угол, прямоугольник, оранжевый png 1600x1513px 100.87KB

Футболка с принтом Sheldon Cooper Rubik’s Cube, футболка, Футболка с принтом, кубик Рубика png 640x700px 167.21KB
Рубикс-головоломка Кубик Рубикс Волшебный карманный кубик, куб, игра, с днем рождения векторные изображения, алмазы png 1369x1382px 1.51MB
Куб, куб, кубик Рубика, 3D куб, куб, синий, угол, 3D компьютерная графика png 862x893px 379.5KB
Кубик Рубика Волшебный кубик-головоломка 3D Кубик Рубика-мести, кубик Рубикса, Кубик Рубика, Магический куб, Головоломка png 640x480px 277. 41KB
Рубикс Куб Арт, Рубик Куб, угол, симметрия, типография png 1593x1400px 959.29KB
белый куб, кубик рубика, кусочки белого куба, угол, белый, текст png 567x567px 174.47KB
3×3 Иллюстрация кубика Рубика, головоломка с кубиками Рубика, кубик Рубика, угол, белый, ребенок png 564x592px 117.97KB
Rubiks Cube Puzzle, Куб, игра, прямоугольник, симметрия png 812x773px 76.48KB
Пазлы Игра Месть Рубика, другие, Пазлы, Месть Рубика, Игры png 1697x2400px 178.56KB
Персонаж Майнкрафт, Майнкрафт Roblox Rendering Cinema 4D, Майнкрафт, игра, 3D компьютерная графика, фотография png 1920x1080px 586. 87KB
Рубикс Куб Детский, Буквы Куб, текст, игра в кости, мультфильм png 1000x1000px 133.61KB
Инфографика 3D компьютерная графика, кубик Рубика, 3D компьютерная графика, куб вектор, кубики льда png 6667x6667px 2.22MB
Пазлы Паззл 3D V-Cube 7 Кубик Рубика, куб, Пазлы, Пазз 3D, V-Cube 7 png 500x500px 243.64KB
черный пазл-куб, OLAP-куб Онлайн аналитическая обработка Rubik ‘s Cube Color, информационная статистика, угол, лицо, прямоугольник png 798x800px 156.3KB
Рубикс Кубик Рубикс Магия, Кубик, угол, прямоугольник, с днем рождения векторные изображения png 800x800px 77. 71KB
Cube Трехмерное пространство Shape, 3D Cube s, угол, прямоугольник, симметрия png 570x598px 27.32KB
Иллюстрация кубика Рубика, Кубик Рубика Профессорская реклама куба, Кубик Рубика, угол, прямоугольник, треугольник png 650x650px 122.63KB
Логотип Rubik’s Cube Puzzle, куб, Кубик рубика, пазл, логотип png 530x530px 82.66KB
Minecraft 3D-рендеринг, скин, 3D Компьютерная графика, видео игры, вымышленный персонаж png 800x600px 105.74KB
Cube Трехмерное пространство Shape, 3D Cube s, синий, угол, прямоугольник png 600x563px 13.69KB
org/ImageObject»> оптическая иллюзия бежевого цвета, геометрия иллюзии куба, элемент сборки трехмерного куба, угол, 3D компьютерная графика, треугольник png 600x600px 249.05KB
Рубикс Кубик Рубикс Волшебная головоломка кубик, Кубик головоломка игрушки, игра, лицо, прямоугольник png 2480x3508px 1.85MB
Младенческий куб, куб головоломки, ребенок, игрушка Блок, мультфильм png 2184x1746px 671.92KB
Рубикс Куб Бизнес Технологии, Рубик Куб, синий, симметрия, кубик Вектор png 778x671px 548.07KB
Кубик рубика, кубик рубика, угол, прямоугольник, симметрия png 650x527px 179.64KB
org/ImageObject»> Rubik ‘s Cube Mind игры Columbia High School Mind спорта, другие, Кубик Рубика, Игры разума, Высшая школа Колумбии png 512x512px 96.58KB
Икона Рубика, Кубик Рубика, фиолетовый, треугольник, пурпурный png 800x800px 232.51KB
Cube Трехмерное пространство 3D компьютерной графики, Cube, угол, 3D компьютерная графика, инкапсулированный PostScript png 1203x1266px 177.79KB
синий, красный и желтый кубик Рубика, кубик Рубика. Головоломка куба Speedcubing, кубический фон, игра, прямоугольник, симметрия png 1272x1287px 1.18MB
Геометрическая форма, куб, трехмерное пространство, кубик Рубика, логотип, черный, черный и белый, Линия, угол, черный, Черное и белое png 900x900px 60. 08KB
Cinema 4D Animated film Компьютерное программное обеспечение 3D компьютерная графика 3D моделирование, другое, 3D компьютерная графика, другие, компьютерные обои png 600x600px 189.49KB
три черно-коричневых стека портфелей, багажная сумка, винтажная одежда Travel, классические чемоданы, мебель, ретро, кожа png 610x640px 563.5KB
Рубикс Куб, куб, угол, 3D компьютерная графика, прямоугольник png 2038x2138px 143.23KB
синий кубик логотип, кубик блю рубикс, синий кубик, синий, угол, прямоугольник png 1800x1613px 110.92KB
Головоломка кубика рубика магия рубика, куб, Кубик Рубика, Головоломка, Магия Рубика png 610x646px 285. 15KB
Cinema 4D illustration, Cinema 4D 3D компьютерная графика Mental Ray 3D моделирование Компьютерное программное обеспечение, cinema 4d, 3D Computer Graphics, другие, логотип png 558x556px 87.62KB
Minecraft персонаж иллюстрации, Minecraft Cinema 4D рендеринг видео игры Компьютерные серверы, Minecraft, игра, компьютерная графика 3D, компьютерное программное обеспечение png 3000x2080px 1.38MB
Квадрат Сплошная геометрия Прямоугольник Куб, Куб, угол, треугольник, компьютерные обои png 650x540px 34.36KB
Кубик Рубика Головоломка Кубик, Кубик Рубика, игра, прямоугольник, симметрия png 692x800px 62.57KB

Feiling скутер 50 куб.

см FL50QT-4D производства Zhejiang Shunqi Vehicle Industry Co., Ltd. (Мото Китай)

FL50QT-4D

Китайский скутер мотороллер 50 куб.см Feiling FL50QT-4D производства Zhejiang Shunqi Vehicle Industry Co., Ltd. (производственное предприятие в г. Тайчжоу, провинция Чжэцзян, Китай; производит разнообразную мотоциклетную технику под маркой Feiling, Huatian, Jiaji, в том числе скутеры мотороллеры 50 куб.см). Экологический стандарт , двигатель 139QMB, всего мест 1 (вместе с водителем), шины передн. 3.50-10 задн. 3.50-10, макс. скорость 50 км/час, снаряженная масса китайского скутера 83 кг, бензин, колесная база 1310 мм, полная масса 158 кг.

Технические характеристики китайского скутера Feiling

Общая информация

Двигатель китайского скутера Feiling FL50QT-4D

Характеристики двигателя китайского скутера
Модель двигателя	139QMB
Рабочий объем двигателя, куб. см	50
Мощность двигателя, кВт (л.с.)	2.0 (3)
Производитель двигателя	Zhejiang Shunqi Vehicle Industry Co., Ltd.
Топливо	бензин
Экологический стандарт

Размеры и масса китайского скутера Feiling FL50QT-4D

Размеры и весовые характеристики китайского скутера
Габаритные размеры китайского скутера
Габаритная длина, мм	1820
Габаритная ширина, мм	655
Габаритная высота, мм	1045
Масса
Снаряженная масса китайского скутера, кг	83
Полная масса, кг	158
Количество мест
Число мест всего	1
База
Колесная база, мм	1310

Колеса и шины

Колеса и шины китайского скутера Feiling FL50QT-4D
Число осей	2
Число шин	2
Размерность шин	передн. 3.50-10 задн. 3.50-10

Прочие технические характеристики

Разные характеристики Feiling FL50QT-4D (скутер 50 куб.см)
Максимальная скорость	50
Число мест всего	1
Рулевое управление

См. также

Скутер 50 куб.см Feiling

Feiling FL50QT-3D (скутер 50 куб.см)

Изготовитель:	Zhejiang Shunqi Vehicle Industry Co., Ltd. (Китай)
Рабочий объем, куб.см:	50	Полная масса, кг:	160
Двигатель:	139QMB	Мощность, кВт:	2.0
Шины:	3.00-103.00-10	Топливо:	бензин
Скорость, км/ч:	50	Колесная база, мм:	1270
Число мест, чел. :	1	Число осей:	2
Снаряженная масса, кг:	85	Число шин:	2

Feiling FL50QT-9D (скутер 50 куб.см)

Изготовитель:	Zhejiang Shunqi Vehicle Industry Co., Ltd. (Китай)
Рабочий объем, куб.см:	50	Полная масса, кг:	170
Двигатель:	139QMB	Мощность, кВт:	2.0
Шины:	130/60-13120/70-12	Топливо:	бензин
Скорость, км/ч:	50	Колесная база, мм:	1385
Число мест, чел.:	1	Число осей:	2
Снаряженная масса, кг:	95	Число шин:	2

Feiling FL50QT-9C (скутер 50 куб. см)

Изготовитель:	Zhejiang Lingyu Vehicle Industry Co., Ltd. (Китай)
Скорость, км/ч:	50
Число мест, чел.:	1
Снаряженная масса, кг:	103
Полная масса, кг:	178
Габариты, мм:	1970 × 700 × 1090

Скутер 50 куб.см

Feiying FY50QT-3C (скутер 50 куб.см)

Изготовитель:	Guangzhou Panyu Huanan Motorcycle Enterprise Group Co., Ltd. (Китай)
Рабочий объем, куб.см:	50	Полная масса, кг:	158
Двигатель:	FY139QMB-3	Мощность, кВт:	2. 0
Шины:	90/90-1090/90-10	Топливо:	бензин
Скорость, км/ч:	45	Колесная база, мм:	1185
Число мест, чел.:	1	Число осей:	2
Снаряженная масса, кг:	83	Число шин:	2

Riya RY50QT-32 (скутер 50 куб.см)

Изготовитель:	Zhejiang Riya Motorcycle Co., Ltd. (Китай)
Рабочий объем, куб.см:	50	Полная масса, кг:	168
Двигатель:	139QMB-E	Мощность, кВт:	2.4
Шины:	3.50-103.50-10	Топливо:	бензин
Скорость, км/ч:	45	Колесная база, мм:	1280
Число мест, чел.:	1	Число осей:	2
Снаряженная масса, кг:	93	Число шин:	2

Haoda HD48QT-D (скутер 50 куб. см)

Изготовитель:	Guangdong Dafu Motorcycle Co., Ltd. (Китай)
Рабочий объем, куб.см:	48	Полная масса, кг:	172
Двигатель:	139QMA-2	Мощность, кВт:	2.2
Шины:	3.50-103.50-10	Топливо:	бензин
Скорость, км/ч:	50	Колесная база, мм:	1205
Число мест, чел.:	1	Число осей:	2
Снаряженная масса, кг:	97	Число шин:	2

Покрутить гиперкуб онлайн

☰ Оглавление

Первая страница
Онлайн инструменты ▽
- Редактор иконок favicon.ico онлайн
- Игра «Жизнь» онлайн
- Онлайн навигатор по множеству (фракталу) Мандельброта
- Онлайн конвертер PNG в favicon. ico
- Интерактивная схема солнечной системы
- Пересчёт дат в Юлианские дни
- Объяснение и онлайн-демо, как работает HTML5 canvas transform
- Онлайн генератор периодических фонов
- Онлайн конвертер цветов из HSV в RGB
- Онлайн URL-перекодировщик
- Онлайн генератор QR-кодов
- Покрутить 4D-гиперкуб
- Получение географических координат точки на карте
- «Сапёр» на бесконечном поле онлайн
- Черепаший язык онлайн
- Калькулятор индекса массы тела
- Для самых маленьких ▽
  - Рисовалка для детей до трёх лет
  - «Робот» для детей с трёх-четырёх лет
  - «Морской бой» для самых маленьких
- Простой чат
Инструменты ▽
- Docker ▽
  - Docker устанавливаем и разбираемся
  - Пример использования Docker для изучения Ruby on Rails
  - Пример использования Docker для запуска MySQL
  - Почему docker требует root-прав
- JavaScript ▽
  - Букмарклеты для JavaSctipt/HTML-разработчика
  - Использование «use strict» в JavaScript
  - Небольшая памятка по JavaScript
  - Простой минификатор/оптимизатор JavaScript
  - Мои плагины для хрома
- Python ▽
  - Сводная таблица методов основных типов данных Python 2 и 3
  - Инструменты для Python-разработчика
  - Удобная командная строка Python
  - Утечки памяти в Python: метод __del__ и сборка мусора
  - Работа с нитями в Python
- Файловая система ▽
  - FS: перемещение, переименование, архивирование
  - Монтирование sshfs с помощью systemd
- Shell ▽
  - Работа с историей команд bash
  - Консоль/bash. настройка
  - Отправка e-mail с картинками чистым shell скриптом
  - Конвертирование аудио
  - Конвертирование видео
- Управляем тактовой частотой процессора
- Совместный доступ к mercurial по SSH
- Передача файлов по сети
- Безопасное хранение и передача данных
- Нотификатор
- Xorg. Настройка
- Xorg. Настройка нестандартной клавиатуры
- Synergy: Много мониторов с одной клавиатурой и мышкой
- Ssh. Настройка
- Ssh. Настройка туннелирования через NAT и firewall
- Pidgin для хакеров
- Печать
- USB-Flash. монтирование
- Доступ к данным по MTP
- Настройка aspell
- Iptables. Port knocking
- Sudo, sudoers, visudo
- Swap в файле в Linux
- Добрый kill (gdb)
- Изменить размер tmp (tmpfs)
- Установка Arch Linux на USB-Flash
- Эмуляция в QEMU
- GRUB2 вручную
- Системные утилиты
- Настройка редактора vi
- Краткое руководство по vi
- HTML-валидатор
- VDS/VPS
  - Начальная настройка
  - Сборка nginx
  - Настройка nginx
  - Сборка uWSGI (Django+CGI)
  - Настройка uWSGI
- Управление сетью в Ubuntu с помощью netctl (Arch Linux)
- Настройка WiFi точки доступа под Linux
CS: Искусственный интеллект ▽
- Метрики в машинном обучении: precision, recall и не только
- Оценка точности классификатора
- Нейронные сети на простейших примерах
  - Что такое нейрон (очень коротко)
  - Пример задачи и демонстрация, как нейрон её решает
  - Пример обучения нейрона
  - Что осталось за сценой в задаче для одного нейрона
- Деревья принятия решений
- Байесовское машинное обучение
- Примеры кода numpy, scipy, matplotlib
  - Метод наименьших квадратов
  - Построение системы рекомендаций, на основе текстов
  - Диффузионные реакции (реакции с диффузией)
CS: Разное ▽
- RSA-шифрование на пальцах
- SQRT-декомпозиция
- О пользе рекурсии
- Дискретная бисекция
- Top-K из N (куча)
- Быстрое возведение в степень и подсчёт чисел Фибоначчи
- Алгебра логики
- Небольшая памятка по C++
- Проблема останова
- Примеры простейших серверов на Python
  - Простейший форкающийся сервер
  - Простейший prefork-сервер
  - Простейший многонитевой сервер
  - Многонитевой сервер с простым взаимодействием между нитями
  - Асинхронный сервер
- Кумулятивное вычисление статистических характеристик
- Пять задач, которые хорошо бы уметь решать за час
Теория относительности ▽
- Об этих заметках
- Пространство-время как геометрия
- Физическая интерпретация
- Универсальность скорости света
- Эквивалентность инерциальных систем отсчёта
- Относительность пространственных и временных интервалов
- Движение быстрее света
- Парадокс близнецов
- Заключение
Теория вероятностей ▽
- Как нас обманывает интуиция
- Парадокс Монти Холла
- Парадокс двух конвертов
Квантовая механика ▽
- Принцип неопределённости на классических примерах
Фракталы ▽
- Фрактальная размерность
- Фрактальные деревья
- Применение фракталов
- Комплексная размерность
Гиперкуб
Обучение и преподавание ▽
- О репетиторстве
- Типичные ошибки на экзаменах
- Лёгкая подготовка к экзаменам
- Как отвечать на экзамене
Как я худел
Личное ▽
- Обо мне (как бы резюме)
- Благодарности
- Мои ошибки
- Немного фотографий
- Копирование этих материалов

В четырёхмерном пространстве есть шесть взаимно-перпендикулярных плоскостей (в трёхмерном — их три).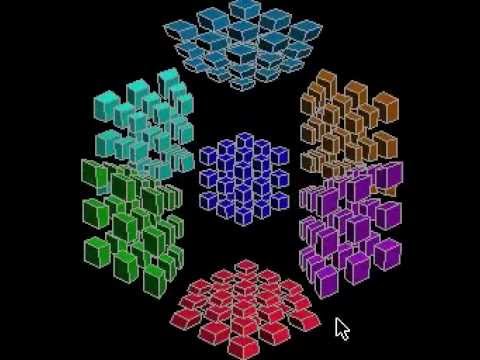 Вы можете крутить гиперкуб в любой из этих плоскостей. Используйте ползунки рядом с картинкой.

Кроме того, есть четыре профиля окраски.

При построении проекции предполагается, что четырёхмерный куб проецируется на трёхмерную гиперплоскость с помощью ортогональной проекции.

То есть если предположить, что четвёртая координата — это время, то мы рассматриваем куб в тот момент, когда наше трёхмерное пространство проходило через его центр (как четырёхмерной фигуры).

Далее проекция на трёхмерное пространство проецируется на плоскость экрана с помощью центральной проекции в предположении, что глаза наблюдателя находится на расстоянии 1500 пикселей от фигуры. (Да, расстояние в данном случае можно указать только в пикселях, чтобы пересчитать его в другие единицы, используйте характеристики вашего монитора.)

минимализм, Cinema 4D, куб, черный, HD обои

Выберите разрешение и загрузите эти обои

PC(720P, 1080P, 2K, 4K,8K):

1366×768
1920×1080
1440×900
1600×900
1280×800
1024×768
1280×1024
1536×864
1680×1050
1280×720
1360×768
360×640
2560×1440
2560×1080
1920×1200
1280×768
1024×600
800×600
1364×768
320×570
3840×2160
7680×4320

iMac:

iMac 21.

5″ LED-backlit 1080P:

1920×1080

iMac 21.5″ Retina 4K:

4096×2304

iMac 27″ Retina 5K:

5120×2880

MacBook:

MacBook Air 11.6″:

1366×768

MacBook Air 13″, MacBook Pro 15.4″:

1440×900

MacBook Pro 13.3″:

1280×800

MacBook Pro 15.4″ Retina:

2880×1800

MacBook Pro 16″:

3072×1920

MacBook Pro 17″:

1920×1200

MacBook Pro 13.3″ Retina, MacBook Air 13″ Retina, MacBook Air 13.3″(2020, M1):

2560×1600

Двойной монитор:

2732×768
3840×1080
2880×900
3200×900
2560×800
2048×768

Тройной монитор:

4098×768
5760×1080
4320×900
4800×900
3840×800
3072×768

Четырехместный монитор:

2732×1536
3840×2160
2880×1800
3200×1800
2560×1600
2048×1536

iPhone:

iPhone 2G, iPhone 3G, iPhone 3GS:

320×480

iPhone 4, iPhone 4s:

640×960

iPhone 5, iPhone 5s, iPhone 5c, iPhone SE:

640×1136

iPhone 6, iPhone 6s, iPhone 7, iPhone 8:

750×1334

iPhone 6 plus, iPhone 6s plus, iPhone 7 plus, iPhone 8 plus:

1242×2208

iPhone X, iPhone Xs, iPhone 11 Pro:

1125×2436

iPhone Xs Max, iPhone 11 Pro Max:

1242×2688

iPhone Xr, iPhone 11:

828×1792

iPhone 12 mini, iPhone 13 mini:

1080×2340

iPhone 12, iPhone 12 Pro, iPhone 13, iPhone 13 Pro, iPhone 14:

1170×2532

iPhone 12 Pro Max, iPhone 13 Pro Max, iPhone 14 Plus:

1284×2778

iPhone 14 Pro:

1179×2556

iPhone 14 Pro Max:

1290×2796

Android:

720×1280
1080×1920
480×854
480×800
540×960
600×1024
800×1280
1440×2560
320×480
1080×1812
1080×1800
720×1208
375×667
320×568
1440×2960
1080×2160

iPad:

iPad, iPad 2, iPad Mini:

768×1024, 1024×768

iPad 3, iPad 4, iPad Air, iPad Air 2, 2017 iPad, iPad Mini 2, iPad Mini 3, iPad Mini 4, 9.

7″ iPad Pro:

2048×1536, 1536×2048

10.5″ iPad Pro:

2224×1668, 1668×2224

11″ iPad Pro:

2388×1668, 1668×2388

12.9″ iPad Pro:

2732×2048, 2048×2732

10.9″ iPad Air:

2360×1640, 1640×2360

10.2″ iPad:

2160×1620, 1620×2160

8.3″ iPad mini:

2266×1488, 1488×2266

Surface & Android планшеты:

2736×1824
2048×1536
1024×600
1600×1200
2160×1440

1824×2736
1536×2048
600×1024
1200×1600
1440×2160

Ключевые слова обоев:

минимализм
Cinema 4D
куб
черный

Лицензия:

Некоммерческое использование, DMCA Связаться с нами

1920x1080px черно-синий куб обои, 3D, Cinema 4D, цифровое искусство, куб, HD обои
2560x1600px куб, черный, Cinema 4D, минимализм, HD обои
1920x1080px куб, Cinema 4D, 3D, аннотация, HD обои
1125x1500px вертикаль, неон, киберпанк, футуристический, самурай, Cinema 4D, научная фантастика, HD обои
7680x4320px киберпанк, киберпанк 2077, самурай, логотип, видеоигры, Cinema 4D, демон, киборг, талисман, HD обои
1920x1080px иллюстрация солнечной системы, минимализм, космическое искусство, планета, Photoshop, Cinema 4D, Земля, HD обои
org/ImageObject»> 1920x1080px синие и желтые абстрактные цифровые обои, Cinema 4D, куб, 3D, абстракция, голубой, оранжевый, HD обои
2560x1600px минимализм кинотеатр 4d куб черный, HD обои
5000x2812px черно-розовая звезда с принтом, текстиль, куб, Cinema 4D, 3D, HD обои
3840x2160px Cinema 4D, Atari, HD обои
1920x1080px Cinema 4D, OctaneRender от OTOY, абстрактные, 3D абстрактные, HD обои
2560x1440px черный и серый абстрактный куб, квадратный зеленый куб цифровые обои, произведения искусства, красочные, Джастин Маллер, Гранит, градиент, минимализм, куб, простой фон, цифровое искусство, аннотация, HD обои
org/ImageObject»> 1920x1080px иллюстрация серого куба, минимализм, куб, простой, произведения искусства, монохромный, простой фон, черный фон, аннотация, цифровое искусство, HD обои
1354x840px CGI, цифровая, Cinema 4D, HD обои
1920x1080px 3D, Photoshop, Cinema 4D, космос, HD обои
1920x1080px зелено-синий куб цифровой wallpaepr, Cinema 4D, Photoshop, куб, графический дизайн, аннотация, HD обои
1920x1080px черный куб, майнкрафт, куб, видеоигры, HD обои
1920x1080px обои фиолетовый и черный куб, цифровые обои фиолетовый куб, вселенная, аннотация, куб, градиент, пространство, космическое искусство, цифровое искусство, геометрия, шестиугольник, фиолетовый, фиолетовый, простой, HD обои
org/ImageObject»> 1920x1080px алмазные обои, Cinema 4D, бриллианты, драгоценности, HD обои
1920x1080px кино 4d куб 3d аннотация, HD обои
2560x1440px серая гора иллюстрация, серая гора цифровые обои, цифровое искусство, горы, Cinema 4D, низкополигональная, произведения искусства, HD обои
1920x1080px шестиугольник синий и черный цифровые обои, космос, минимализм, куб, 3D, синий, аннотация, HD обои
2880x1800px черно-серый ноутбук Samsung, Windows 10, технология, минимализм, черный, белый, HD обои
3840x2161px абстрактный, белый, узор, куб, квадрат, минимализм, HD обои
org/ImageObject»> 1920x1080px Cinema 4D, OctaneRender от OTOY, пейзаж, аннотация, HD обои
2606x1080px Американские боги, виртуальная реальность, сериал, Cinema 4D, HD обои
1920x1080px 3D, Cinema 4D, цифровое искусство, HD обои
1920x1080px 3D, Cinema 4D, цифровое искусство, HD обои
1920x1080px черный, минимализм, япония, HD обои
1920x1080px Кубик 3х3, иллюстрация кубика, минимализм, куб, простой фон, HD обои
1646x926px темный, черный, минимализм, HD обои
org/ImageObject»> 1920x1080px Кинотеатр 4D, куб, 3D, HD обои
1920x1080px белые светодиодные обои, цифровое искусство, минимализм, куб, крест, Halo Reach, аннотация, голубой, синий, простой, черный фон, HD обои
3440x1440px Dreamscape, пространство, аннотация, 3D аннотация, Cinema 4D, красочные, голубой, розовый, HD обои
2560x1600px Cinema 4D Графика, 3D,, шар, красочный, HD обои
1920x1080px узор, темно, текстура, черный, минимализм, HD обои
2560x1440px электронное устройство с круглой черной подсветкой, Poké Balls, Cinema 4D, 3D, CGI, рендеринг, абстракция, цифровое искусство, HD обои
org/ImageObject»> 1920x1080px игрушка мяча с черной и зеленой подсветкой, 3D, Cinema 4D, цифровое искусство, HD обои
1920x1080px черно-белый деревянный стол, иллюстрация, низкополигональная, Cinema 4D, городской пейзаж, HD обои
1920x1080px куб, блендер, черный, фары, белый, минимализм, HD обои
1920x1200px черные сотовые обои, минимализм, шестиугольник, HD обои
1920x1080px зеленые и белые полигональные горы цифровые обои, низкополигональная, 3D, Cinema 4D, цифровое искусство, горы, лес, река, небо, пейзаж, фотошоп, HD обои
1920x1080px игрушка красный и черный шар, 3D, Cinema 4D, цифровое искусство, HD обои
org/ImageObject»> 2606x1080px Американские боги, сериал, пирамида, Cinema 4D, HD обои
1920x1080px черно-красные обои, Cinema 4D, HD обои
1920x1080px Cinema 4D, абстракция, рендеринг, 3d дизайн, OctaneRender от OTOY, HD обои
1920x1080px 3D, Cinema 4D, цифровое искусство, HD обои
1920x1080px 3D, Cinema 4D, цифровое искусство, HD обои
1920x1080px 3D, Cinema 4D, цифровое искусство, HD обои
1920x1080px иллюстрация, низкополигональная, Cinema 4D, HD обои
org/ImageObject»> 1920x1080px черно-белый деревянный шкаф, темный, Стюарт Липпинкотт, stuz0r, цифровое искусство, простой, киберпанк, футуристический, утопия, Cinema 4D, OctaneRender, HD обои
1920x1080px stuz0r, Стюарт Липпинкотт, священник, Cinema 4D, темно, свет, HD обои
3840x2160px неон, НАСА, японский, простой, черный фон, минимализм, HD обои
1920x1080px 3D, Cinema 4D, цифровое искусство, HD обои
1920x1080px зеленое лиственное дерево в окружении безлистных деревьев, Cinema 4D, 3D, пейзаж, HD обои
1920x1080px Ассорти куб много, куб, минимализм, 3D, цифровое искусство, рендер, простой фон, HD обои
org/ImageObject»> 3840x2160px абстракция, Cinema 4D, 3D, рендер, цифровое искусство, HD обои
1920x1080px Покемон, красный, оранжевый, яркий, Cinema 4D, Poké Balls, мультфильм, простой фон, минимализм, HD обои
1920x1080px абстрактный, 1920×1080, черный, красный, куб и 4K, HD, HD обои
2120x1193px красно-черные обои, Minecraft, баннер, YouTube, Photoshop, Cinema 4D, HD обои

Похожий поиск:

Волшебный куб 4D

MagicCube4D — это полнофункциональный четырехмерный аналог кубика Рубика, а также десятки других красивых четырехмерных головоломок. На изображении выше показана головоломка 3 ⁴ в решенном состоянии. или щелкните здесь правой кнопкой мыши и выберите «Сохранить ссылку как»
Программа упакована в исполняемый файл jar, который должен работать в любой системе с установленной виртуальной машиной Java. Сохраните его на рабочем столе или в любом другом месте, если вы сможете найти его позже. Просто дважды щелкните по нему, чтобы запустить; установка не требуется. В Windows вы можете создать ярлык на рабочем столе, щелкнув правой кнопкой мыши и выбрав «Отправить > Рабочий стол» в раскрывающемся списке. Пожалуйста, прочтите FAQ для более полного описания головоломки. Польский FAQ здесь. Если он не запускается, вам может потребоваться установить текущую виртуальную машину Java. Щелкните здесь для получения последней версии.
Дон Хэтч и Мелинда Грин разрабатывала эту головоломку с 1988 года. Джей Беркенбилт и Позже к нам присоединился Ройс Нельсон и внес большой вклад. Дон и Джей первыми решили головоломку, широко используя макросы. Ройс был первым, кто решил головоломку без использования макросов. Для своего решения он расширил 3D Филипа Маршалла. «Окончательное решение кубика Рубика» в 4D. Вы можете изучите решение Ройса, если вам не хочется сначала пытаться решить его самостоятельно. Дон даже написал программу, которая может собирать кубики Рубика в любом количестве измерений, и создал альтернативную реализацию MC4D. Наконец, Mathologer на YouTube создал руководство по решению этой головоломки, которое делает решение этой головоломки на удивление простым.

Мелинда 2x2x2x2

Наконец-то первая в мире настоящая физическая 4D-извилистая головоломка! Это физическая версия 2 ⁴ . Посмотрите вводное видео ниже и посетите домашнюю страницу проекта, чтобы узнать больше и получить его для себя.

Страницы проекта

Список рассылки — Для общего обсуждения. Открыт для всех. Примечание. Мы перешли на Google Groups, когда Yahoo Groups перестали поддерживать свои архивы сообщений. Вот архивный файл, который мы получили от них здесь. Его формат не ясен, но Джошуа Дэниелс написал код, чтобы превратить его в архив сообщений HTML. Спасибо Джошуа!
Репозиторий исходного кода — это проект с открытым исходным кодом.
Отслеживание проблем. Пожалуйста, отправляйте сюда отчеты об ошибках и запросы на добавление новых функций.
Project Wiki — корень всей документации.
MagicCube4D Hall Of Fame — список всех решателей 4D-кубов и рекордных решений. Отправьте свой лог-файл, и мы вас тоже добавим!
Расширенный зал славы — за рекордные решения всех головоломок, кроме куба.

Сервер Hypercubers Discord — Дружественная группа, созданная участниками списка рассылки.

15 x 4 915
or in decimal as 1 756 772 880 709 135 843 168 526 079 081 025 059 614 484 630 149 557 651 477 156 021 733 236 798 970 168 550 600 274 887 650 082 354 207 129 600 000 000 000 000

For Для сравнения, в обычном 3D-кубике Рубика всего 43 252 003 274 489 856 000 уникальных позиций, что по-прежнему огромно. С другой стороны, четырехмерный куб имеет больше потенциальных позиций, чем общее количество атомов во Вселенной! Гораздо больше. Разговор об иголке в космическом стоге сена! Нажмите на следующую ссылку, чтобы узнать, как рассчитать перестановки 4D-куба. Удивительно, но хотя количество позиций 4D-куба пугающе велико, это не означает, что эту головоломку во много раз сложнее решить. Если вы уже можете собрать 3D-куб, значит, вы на полпути к решению этого. Здесь также применимы все техники, которые вы уже знаете.

Похожие головоломки

MagicCube5D — Ройс написал потрясающую 5D-версию этой головоломки, которую он и некоторые другие даже решили. После того, как вы попадете в зал славы 4D, вы можете попробовать 5D Зал Безумия. Вот видео, показывающее мировой рекорд кратчайшее 5D-решение Андраша Эчеки. И если 3 ⁵ с его 810 наклейками вас пугает, просто знайте, что Мэтью Ширин решил 7 ⁵ с 24010 наклейками!
Magic120Cell — автономный 4D-аналог Roice. Извилистая головоломка Мегаминкс. Этот монстр состоит из 120 гиперграней, каждая из которых представляет собой додекаэдр, выглядящий в точности как Мегаминкс. Он имеет в общей сложности 7 560 гиперстикеров и поистине поразительные 2,3 x 10 ⁸¹²⁶ возможных позиций, только одна из которых является решенным состоянием. Прежде чем двигаться дальше, мы должны остановиться и поразмыслить над тем, насколько велико это число, потому что вы действительно не видите такие числа каждый день. Помните выше, как есть больше 3 ⁴ позиций, чем частицы во Вселенной? Представьте себе, что каждая частица во Вселенной — это на самом деле крошечная вселенная, в каждой из которых столько же частиц, сколько в нашей. Это намного больше, верно? А теперь представьте, что все этих частиц во всех этих вселенных также представляют собой целую вселенную, подобную нашей. Гораздо больше, верно? Хорошо представьте, что вы повторяете это упражнение на 100 уровней в глубину, и только тогда мы приближаемся к количеству позиций в этой головоломке. MagicCube4D теперь также поддерживает этого монстра, но версия Roice лучше, если вы намерены сделать серьезную попытку его решить. Ноэль Чалмерс стал первым, кто разгадал этого монстра. Обязательно посмотрите таймлапс-видео Решение Ноэля на YouTube. Поздравляем Ноэль!
Ранняя реализация Джона Бейли 2 ⁴ в Javascript.
В 2010 году Андрей Астрелин присоединился к нашему сообществу и сразу же побил несколько наших самых заветных рекордов. Не удовлетворенный, он тогда написал и выпустил свою собственную семимерную версию ! MagicCube7D решает проблему визуализации такого многомерного объекта, начав с уже знакомой нам 4D-проекции, а затем частично развернув последние три измерения, используя умный фрактальный дизайн. Не только одна головоломка, этот удивительный фрагмент кода поддерживает все 12 кубов из 3 9от 0006 4 до 5 ⁷ . О, а потом он пошел и решил 3 ⁷ . Молодец Андрей!
Magic Cube 3D — Дэвид Вандершел написал трехмерный симулятор кубика Рубика, используя трехмерный эквивалент четырехмерной проекции и пользовательский интерфейс для четырехмерной головоломки. Может показаться странным создавать трехмерный аналог четырехмерного аналога трехмерной головоломки, но в этом есть логика, поскольку она помогает прояснить смысл работы и пользовательского интерфейса головоломок более высокого измерения.
MagicCube2D — Просто для развлечения и посмотреть, как будет выглядеть эквивалентная 2D-головоломка.
А Игра с 4D-строительными блоками от Хенрика Траппманна дает нам еще одно интересное занятие в 4-х измерениях.
Magic Cube 4D для Android, мобильная версия.
MagicTile от Roice позволяет вам складывать свои собственные 2D-гиперболические запутанные головоломки, в том числе удивительные Квартик Клейна, а также евклидов эллиптический бесконечные правильные многогранники и даже 4D косые многогранники! MagicTile — это красота.
Magic Hyperbolic Tile {6,3,3} от Андрея — это 3D-версия MagicTile от Roice, потому что она находится в трехмерном гиперболическом пространстве. Эта головоломка оказывается чертовски сложной, но в то же время невероятно красивой.
Magic Puzzle Ultimate также от Андрея — его версия MagicCube4D. Пользовательский интерфейс совершенно другой, и некоторые опытные пользователи предпочитают его. Он включает в себя некоторые уникальные и специальные головоломки, такие как столь желанные и очень сложные 24-ячеечные, 48-ячеечные, 600-ячеечные, а также усеченные, укороченные, ректифицированные и курносые версии многих из них, а также некоторые 5D и 6D головоломки.
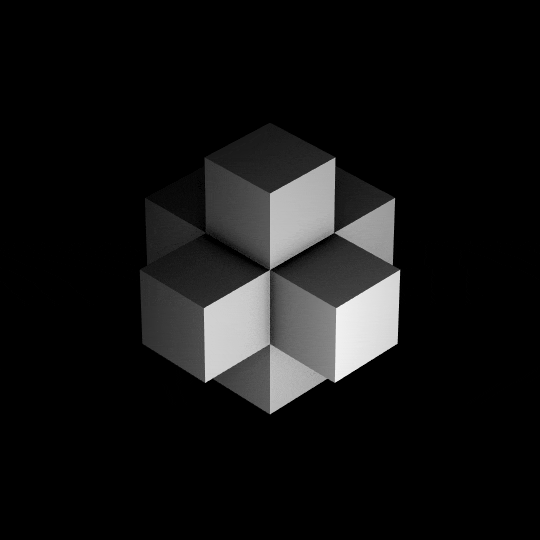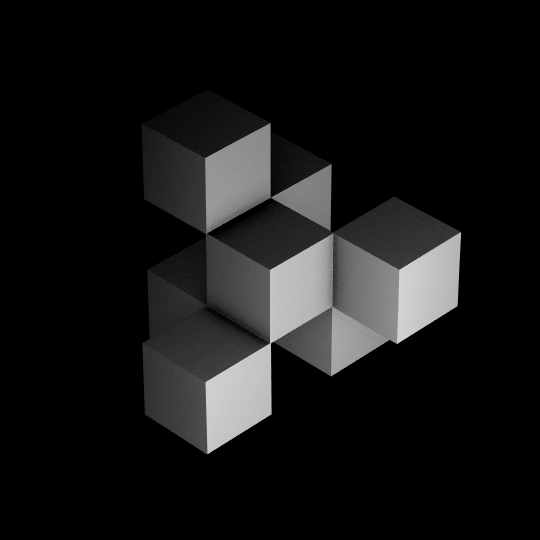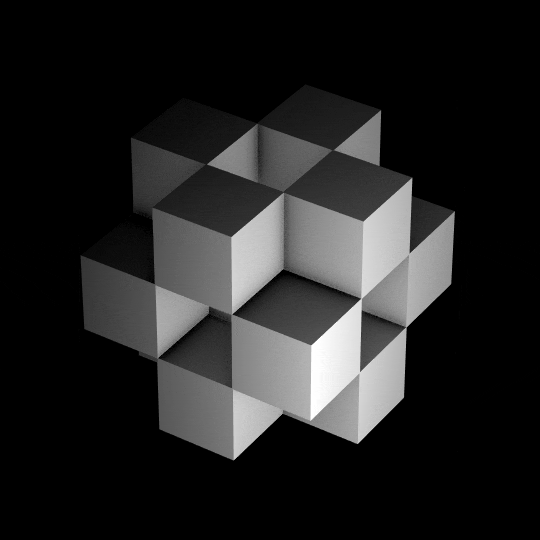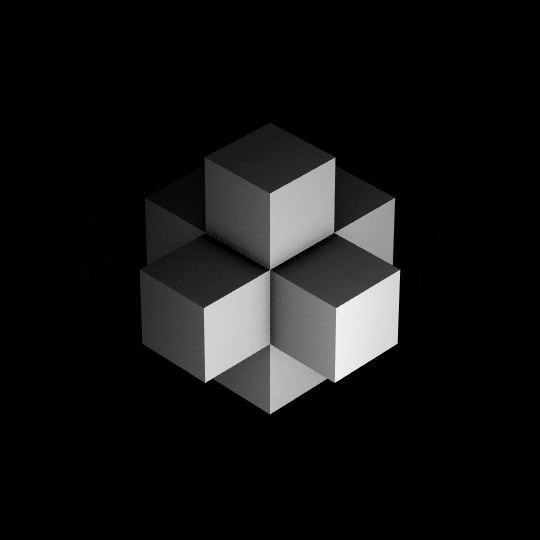
2D реализации 3D и Извилистые 4D-кубы Алекса.
Refle Cube из Нан Ма дает нам трехмерный кубик Рубика, в котором можно использовать только движения отражения и другие комбинации этой базовой идеи.
Light’s Out 3D Еще одна головоломка от Nan Ma поддерживает десятки симметричных многогранников. Нэн действительно хорошо разбирается в головоломках!
Eleven Cell от Nan Ma, пожалуй, самая невероятная головоломка из всех. Он основан на абстрактном многограннике. Что такое абстрактный многогранник, о котором вы говорите? Это обобщенный тип многогранника, полностью не ограниченный геометрией.
Hyperspeedcube от Эндрю Фаркаса — это современный, удобный для начинающих 3D- и 4D-симулятор кубика Рубика с настраиваемыми элементами управления мышью и клавиатурой и расширенными функциями для решения задач на скорость.

Ройс написал статью, в которой описал многие из вышеперечисленных головоломок и способ их извлечения из оригинального кубика Рубика. Она была принята в качестве обложки статьи в выпуск журнала Math Horizons за апрель 2018 года.

Лицензия

Бесплатное ПО, требуется указание авторства, в идеале включая ссылки на эту страницу.

Другие реализации 4D-кубиков

Java-апплет — только углы.
Дэн Веллеман Тессеракт Рубика для Mac.

Веб-страницы со ссылками на эту

Статья Slashdot Обязательно прокрутите страницу вниз, чтобы увидеть ветки обсуждения.
Упоминается в Статья Slashdot о 4D аналоге Мегаминкса.
И в Статья Slashdot о 5D-головоломке Ройса.
Страница со ссылками на головоломки Мефферта. Покупайте головоломки у него!
страница кубических ссылок Мэтт Янг
Кса Ли Страница отличных математических программ.
Филип Маршалл ИДЕАЛЬНОЕ РЕШЕНИЕ КУБИКА РУБИКА
Страница кубика Le Rubik для франкоговорящих любителей кубиков. также на их страница программного обеспечения
Персональные страницы Дон, Джей, Ройс и Мелинда. Черт, немного саморекламы никогда не помешает!
Страница-головоломка Яапа Ссылки
Страница многомерной геометрии Свалка геометрии. Отличный математический сайт.
Университет Дрекселя Библиотека математического форума Листинг Magic Cube 4D.
Страница Кубика Рубика Жорж Хелм
В разделе Ресурсы сайта Джошуа Белла Волшебные многогранники* Страница патентов.
Страница HyperDimension Исихама Ёсиаки.
Джошуа Белла Страница патентов на магические многогранники.
Tetraspace: Ссылки Гаррета Джонса на сайты о четвертом измерении.
Линукс Ссылки Страница головоломок.
FreshPorts поддерживает древняя сборка MC4D? Кто они???
В разделе «Ботанисты» CoMedia Веселая страница.
Собирайте свои собственные трехмерные пазлы с Абсолютный магический куб.
Комментарий с одной ссылкой на длинный Тема Reddit вызвала самый большой всплеск посетителей за год.
Краткий взгляд на Видео на YouTube, описывающее четвертое измерение, также вызвало хороший всплеск.
А Статья в новостях кибернета.
О Евсебее Страница ресурсов 4D.
У Джона Кемени блог.
У Уильяма Бадера страница решения куба.
Мэтью Кале хочет увидеть физическую версию. Теперь он наконец существует!
И в испанский японский и Страницы венгерского блогера.

Вернуться на главную страницу Superliminal.

Гиперкуб — Невозможный мир

В геометрии, гиперкуб является n -мерным аналогом квадрата ( n = 2) и куб ( n = 3). это закрытый выпуклая фигура, состоящая из групп противоположных параллелей сегменты линии, выровненные в каждом из измерений пространства, под прямым углом друг к другу.

Он также известен как tesseract . Тессеракт к кубу, как куб к квадрату; или, более формально, тессеракт можно описать как обычный выпуклый 4-многогранник, граница которого состоит из восьми кубических ячеек.

По данным Оксфорда Словарь английского языка, слово «тессеракт» было придумано и впервые использовано в 1888 году Чарльзом Говард Хинтон в своей книге «Новая эра мысли» , из ионического Греческий «τεσσερες ακτινες» («четыре луча»), ссылаясь на четыре линии от каждой вершины к другим вершинам. Поочередно, некоторые люди называют ту же фигуру «тетракубом».

n -мерный гиперкуб также называется n-кубом . Термин «Многогранник меры» также используется, но, по-видимому, относится только к гиперкуб с единичными сторонами (см. Коксетер 1973) и встречается редко.

Точка — это гиперкуб нулевой размерности. Если сдвинуть эту точку на одну единицу длины, он выметет отрезок, который является мерным многогранником измерение один. Если переместить этот отрезок, его длина будет перпендикулярна направление от себя; он заметает двумерный квадрат. Если переместить квадрат на единицу длины в направлении, перпендикулярном плоскости, на которой он лежит, он создаст трехмерный куб. Это можно обобщить на любое количество измерений. Например, если человек движется куб одной длины в четвертое измерение, он генерирует 4-мерное измерить многогранник или тессеракт.

Семейство гиперкубов — одно из немногих правильных многогранники, представленные в любом количестве измерений. Двойной Многогранник гиперкуба называется кросс-многогранником.

Элементы

Гиперкуб размерности n имеет 2 n «сторон» (a 1-мерная линия имеет 2 конечные точки; двумерный квадрат имеет 4 стороны или ребра; трехмерный куб имеет 6 граней; четырехмерный тессеракт имеет 8 ячеек). Количество вершин (точек) гиперкуба равно 2 ⁿ (куб имеет 2 ³ вершин, например).

Количество m -мерных гиперкубов на границе n -куба равно

Например, граница 4-куба содержит 8 кубов, 24 квадрата, 32 линии и 16 вершин.

**Элементы гиперкуба**
н-куб	Имена	Вершины (0 граней)	Кромки (1-сторонние)	Поверхности (2 стороны)	Ячейки (3-сторонние)	(4 стороны)	(5 сторон)	(6 сторон)	(7 граней)	(8 граней)
0-куб	Точка	1
1 куб	Дигон	2	1
2 куба	Квадрат	4	4	1
3 куба	Куб Шестигранник	8	12	6	1
4 куба	Тессеракт октахорон	16	32	24	8	1
5 кубов	Penteract дека-5-топ	32	80	80	40	10	1
6 кубов	Hexeract додека-6-топ	64	192	240	160	60	12	1
7 кубов	Гептеракт тетрадека-7-топ	128	448	672	560	280	84	14	1
8 кубов	Октеракт гексадека-8-топ	256	1024	1792	1792	1120	448	112	16	1
9 кубов	Eneneract октадека-9-топ	512	2304	4608	5376	4032	2016	672	144	18

Проекции на 2 измерения

Построение гиперкуба можно представить следующим образом: линия АВ.

2-мерный: две параллельные линии AB и CD можно соединить, чтобы получить квадрат с углами, отмеченными как ABCD.
Трехмерный: два параллельных квадрата ABCD и EFGH можно соединить превратитесь в куб с углами, отмеченными как ABCDEFGH.
4-мерный: два параллельных куба ABCDEFGH и IJKLMNOP могут быть соединены чтобы стать гиперкубом с углами, отмеченными как ABCDEFGHIJKLMNOP.

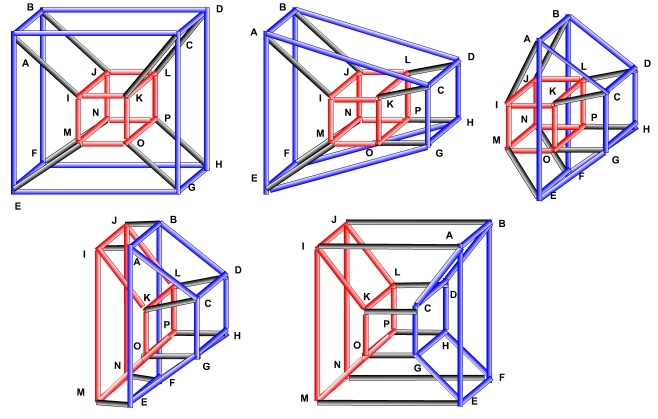
Эту структуру нелегко представить, но ее можно спроектировать тессеракты в трехмерные или двумерные пространства. Кроме того, проекции на 2D-плоскость стала более информативной, если изменить положение проецируемые вершины. Таким способом можно получить изображения, которые больше не отражают пространственные отношения внутри тессеракта, но которые иллюстрируют структура соединения вершин, например, в следующих примерах:

На первом рисунке показано, как тессеракт в принципе получается путем объединение двух кубов. Схема аналогична построению куба из два квадрата: сопоставьте две копии куба нижнего измерения и соедините соответствующие вершины. Второй рисунок объясняет тот факт, что каждое ребро тессеракта имеет одинаковую длину. Эта картина также позволяет человеческому мозгу чтобы найти множество кубов, которые хорошо связаны между собой. Третья диаграмма окончательно упорядочивает вершины тессеракта относительно расстояния вдоль края относительно нижней точки. Этот вид представляет интерес при использовании тессеракты как основа для сети топология для параллельного соединения нескольких процессоров вычисления: расстояние между двумя узлами не более 4 и существует много различные пути для балансировки веса.

Развертывание тессеракта

Тессеракт можно разложить на восемь кубов, так же как куб можно раскладывается на шесть квадратов. Развертку многогранника называют сетью. Существует 261 отдельная сеть тессеракта (см. рисунок рядом для примера). одна из 261 сети).

Гиперкуб в искусстве

Гиперкуб появился в научно-фантастической литературе с 1940 года, когда Роберт А. Хайнлайн в «И он построил кривой дом» , где он описал дом построен как развернутый тессеракт. Он рухнул, превратившись в настоящий 4-х мерный тессеракт. Затем тессеракт появляется во многих книгах и романах.

Фильм «Куб 2: Гиперкуб» рассказывает о восьми незнакомцах, запертых внутри. сеть гиперкубов.

Картина «Распятие (Corpus Hypercubus)» , Сальвадор Дали, 1954, изображает распятого Иисуса на сетке гиперкуба. Он представлен на Метрополитен-музей в Нью-Йорке.

Заключение

Так как гиперкуб является одной из простейших четырехмерных фигур, он наглядно показывает сложность и необычность четвертого измерения. То, что кажется невозможное в нашем трехмерном пространстве возможно в четвертом измерении, ибо например, невозможные фигуры. Бары четырехмерного невозможного треугольник можно соединить под прямым углом и он не будет искажаться от любой точки зрения, отличной от трехмерного невозможного треугольника (см. «Невозможный цифры в реальном мире»).

Статья основана на материалах Википедии.

© Идея и дизайн Влад Алексеев, 2001-2022. (невозможно.мир@gmail.com) | Политика конфиденциальности
Если у вас есть изображения невозможных фигур, которые не опубликованы на сайте, пришлите их мне.

Кубик Рубика-4 « The Mathematica Journal

Кубик Рубика имеет естественное продолжение в четырехмерном пространстве. В этой статье строятся основные понятия головоломки и реализуются в программе. Всем известный трехмерный кубик Рубика состоит из 27 единичных подкубов. Каждая грань определяет набор из девяти вложенных кубов, грань которых находится в той же плоскости, что и . Набор можно вращать вокруг нормали через центр . 4-куб Рубика (или 4D-гиперкуб) состоит из 81 единичного 4-подкуба, каждый из которых содержит восемь 3D-подкубов. Каждая 3-грань определяет набор из 27 4-подкубов, у которых есть куб в той же гиперплоскости, что и . Набор можно вращать вокруг нормали (плоскости), проходящей через центр . Проецирование всей 4D-конфигурации в 3D демонстрирует кубик Рубика-4 как четырехмерное расширение кубика Рубика. Начиная со случайной раскраски 4-куба, цель головоломки — вернуться к исходной раскраске 3-граней.

Основные понятия

Гиперкубы в малых измерениях

Чтобы понять четырехмерный гиперкуб, полезно сначала увидеть, как его низкоразмерные аналоги соотносятся друг с другом. Нульмерный гиперкуб (или 0-куб) — это точка с одной вершиной. Одномерный гиперкуб (или 1-куб) — это сегмент с двумя вершинами и одним ребром. Двумерный гиперкуб (или 2-куб) представляет собой квадрат с четырьмя вершинами, четырьмя ребрами и одной гранью (квадрат, включая его внутреннюю часть). Трехмерный гиперкуб представляет собой куб (или 3-куб) с восемью вершинами, ребрами, шестью квадратными гранями и одним объемом. Увеличение измерения удваивает количество вершин. В более общем смысле количество -кубов (точек, сегментов, квадратов и т. д.) в -кубе равно .

3D-куб может быть представлен в 2D-плоскости с использованием центральной проекции, определяемой пересечением плоскости с линией, соединяющей две точки и .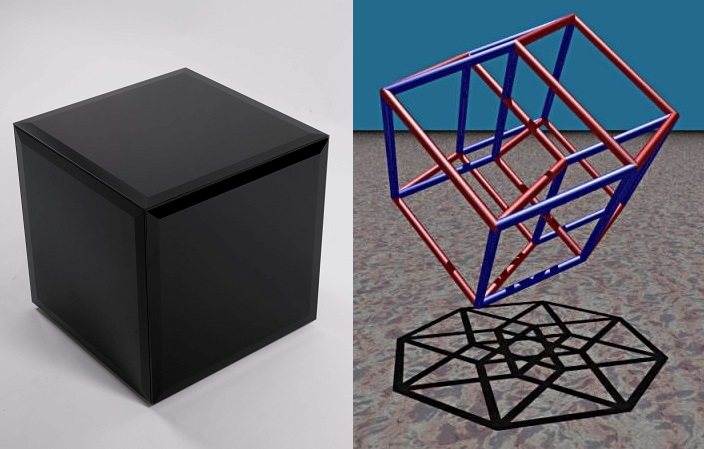 Эта проекция отображает точку в . Выберите, чтобы получить проекцию, показанную справа в
Рисунок 1. Пять граней перекрываются с шестой гранью, цена за потерю одного измерения.

Рис. 1. Куб и его изображение в центральной проекции.

4-куб

В целом, 4D-головоломка Рубика представляет собой 4-куб [1] (или 4-мерный гиперкуб или тессеракт) с вершинами, ребрами, квадратами, восемью кубами и одним 4-кубом. Восемь кубов называются ячейками , которые подобны шести квадратным граням трехмерного куба. Собственными гранями 4-куба являются его вершины, ребра, квадраты и клетки.

Каждая точка собственной грани находится на трехмерной гиперповерхности 4-куба. Ни одна точка правильной грани не находится строго внутри 4-куба; то есть гиперсфера в такой точке содержит точки внутри и точки вне 4-куба. В частности, ни одна внутренняя точка ячейки как трехмерного объекта не находится внутри гиперкуба; все точки клетки лежат на границе 4-куба.

16 вершин 4-куба могут быть определены как списки длины четыре всех возможных комбинаций
и .

24 квадрата 4-куба описываются индексами их вершин.

Помимо 4-куба, есть еще пять правильных многогранников в четырех измерениях. Файлы .csv и .m, содержащие информацию об этих многогранниках, приведены в [2]: положения вершин, индексы вершин для соответствующих граней и какие грани являются соседями.

Для отображения 4-куба в 3D центральная проекция из 4D в 3D аналогична центральной проекции из 3D в 2D; функция является естественным расширением ; см. рис. 2.

Рис. 2. Спроецированное изображение 4-куба посредством центральной проекции. Больший внешний куб является одной из ячеек 4-куба.

Вращение

Ось вращения в 3D представляет собой фиксированную линию. В 4D ось вращения в четырех измерениях представляет собой фиксированную плоскость [3]. Например, матрица вращения вокруг плоскости – определяется как:

(1)

Имеется шесть плоскостей вращения, объединенных парами осей координат, а именно –, –, –, –, –, –.

Вот первый, например, который оставляет точки на плоскости фиксированными.

Эта анимация показывает два последовательных поворота 4-куба, спроецированного в 3D.

Реализация кубика Рубика 4

Разделение кубика 4

Рассмотрим 4-куб с центром в начале координат , длиной стороны 3 и всеми правильными гранями положительной размерности, параллельными осям координат. Тогда его 16 вершин равны:

(2)

Восемь ячеек исходного 4-куба окрашены в разные цвета. Слово «начальный» означает, что повороты не применялись. Раскраска затрагивает каждую точку ячейки, включая ее внутренние 3D-точки.

Так же, как грани кубика Рубика делятся на девять квадратов путем деления каждого ребра на три, ребра кубика Рубика-4 также делятся на три. Затем исходный 4-куб разбивается на малые 4-кубы, каждый с длиной ребра 1. Граница (гиперповерхность) малого 4-куба содержит восемь маленьких кубиков, его ячеек.

Кубик Рубика 3 имеет 27 подкубиков в ; ни один квадрат центрального куба не окрашен, а некоторые квадраты других кубов окрашены. Эти 26 подкубов делятся на три типа в зависимости от того, находятся ли они в углу, на краю или в центре грани большего куба. На рис. 3 показаны по одному из каждого типа.

Рис. 3. Три вида кубиков: в центре квадратной грани, на краю и в вершине, с одним, двумя или тремя цветными квадратами.

Аналогично, 81 маленький 4-куб включает неокрашенный в центре и 80 частично окрашенных 4-кубов. Они подразделяются на четыре типа в зависимости от размера их пересечения с . Тип маленького 4-куба не меняется после вращения. Таблица 1 суммирует числа для каждого типа для и .

Таблица 1. Количество цветных квадратиков для и кубиков для для каждого типа маленького
кубика или ячейки.

Количество цветных квадратиков для кубика Рубика рассчитывается по данным таблицы 1:

Другой способ — подсчитать количество граней, умноженное на количество квадратов на грани: .

Маленькие 4-кубы с ненулевыми координатами образуют гиперповерхность . В частности, небольшой 4-куб с центром, заданным четырьмя ненулевыми координатами, содержит вершину . Снова из Таблицы 1 количество окрашенных маленьких клеток равно:

Это число также может быть получено как количество клеток, умноженное на количество маленьких клеток в ячейке : .

Мы определяем несколько глобальных переменных, которые будут использоваться здесь и далее. На рис. 4 показан разделенный 4-куб с 216 цветными мелкими ячейками.

Рис. 4. Центральная проекция гиперкуба, состоящего из 216 цветных маленьких ячеек.

Каждое ребро разделено на три части, так что длина 4-подкуба равна 1. Рассмотрим 4-подкуб с центром в . Тогда вершины 4-подкуба равны . Координаты центра каждого 4-подкуба представляют собой комбинацию одного из , 0 и . Когда значение не равно нулю ( или ), 4-подкубы обращены наружу в соответствующих направлениях. Другими словами, ненулевые значения в координатах обозначают обращенные наружу 4-подкубы.

216 цветных маленьких ячеек и начальное состояние

Для исходного состояния цвета ячеек задаются в соответствии с координатами их центров:

Например, в маленьком 4-кубике с центром два маленькие ячейки с вершинами и окрашены, потому что значения координат и отличны от нуля.

Геометрия из 216 маленьких цветных ячеек используется для управления головоломкой. Каждый элемент наборов данных состоит из четырех элементов: (1) вершин шести квадратов; (2) расположение центра малого 4-куба, которому принадлежит малая ячейка; (3) цвет; и (4) расположение центра маленькой ячейки. Вершины шести квадратов используются для рисования вложенных кубов, а расположение центров вложенных кубов используется для оценки полноты головоломки. Набор данных начального состояния получается с помощью следующих процедур. Сначала определяются номера вершин квадратов, составляющих каждую маленькую ячейку.

Затем выбираются 216 малых ячеек путем проверки всех возможных малых ячеек.

Этот список содержит 216 записей, каждая из которых содержит четыре компонента, соответствующие маленькой ячейке.

Например, вот запись 123 файла . Компонентами этой маленькой ячейки являются ее шесть квадратных граней, центр, цвет и текущая позиция.

устанавливает 4-куб для рисования.

Вот пример.

устанавливает ячейку (с 27 4-кубами) для рисования.

На рис. 5 показано начальное состояние кубика Рубика-4.

Рис. 5. Центральная проекция исходного состояния кубика Рубика-4 с восемью ячейками.

В трехмерном случае кубика Рубика блок представляет собой набор из девяти маленьких кубиков, центры которых имеют одну постоянную координату, , 0 или 1. Имеется девять блоков, по три на оси координат.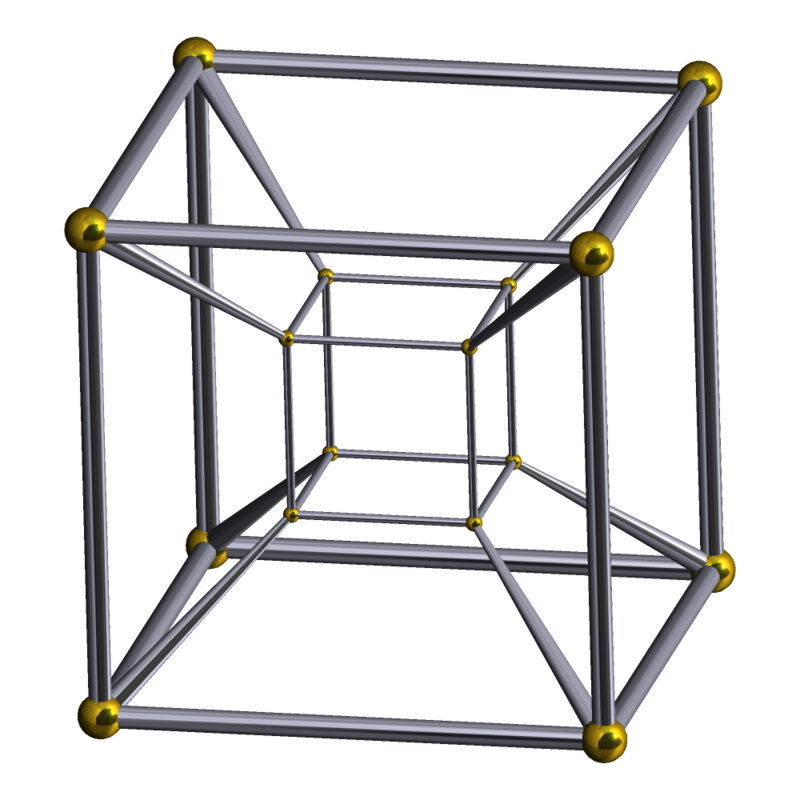 Естественный метод поворота среднего блока, например, того, который разрезается плоскостью на , состоит в том, чтобы повернуть блок вверху на , блок внизу на , а затем весь куб на .

В случае 4D блок представляет собой набор из 27 маленьких 4-кубов, центры которых имеют одну постоянную координату. Есть 12 блоков, по четыре на ось и три на выбор постоянной координаты, 0 или 1. При вращении маленькие 4-кубики в блоке меняют положение одновременно. Каждый блок представляет собой четырехмерную гиперпризму с высотой 1.

На рис. 6 показан пример блока ; ячейка напротив оранжевой ячейки не окрашена.

Рис. 6. Пример блока из 27 маленьких 4-кубов (оранжевый, ).

Блок вращается на или вокруг оси, которая является неподвижной плоскостью. Таким образом, информация, необходимая для действия с кубиком Рубика-4, это (1) блок, который нужно вращать; (2) ось вращения; и (3) угол. Для кубика Рубика ось вращения определяется автоматически выбором блока. Но для необходимо выбрать две оси координат для определения неподвижной плоскости. Одна является постоянной осью координат, используемой для выбора блока, а другая должна быть выбрана из оставшихся трех осей координат. Существует 108 возможных действий над : 12 вариантов блока, три варианта второй оси координат и три варианта угла: . Следовательно, для вращения в компьютерной программе «4 кубика Рубика» требуется 108 кнопок. В таблице 2 перечислены свойства кубика Рубика и кубика Рубика-4.

Таблица 2. Свойства кубика Рубика и кубика Рубика-4.

Окончательная форма

Программа для реализации кубика Рубика 4 в 3D основана на центральной проекции гиперкуба и матрицах вращения в 4D. Программа представлена в следующем разделе.

Реализация интерфейса состоит из трех частей: создание кнопок для поворотов, отображение текущего состояния и определение того, завершена ли головоломка.

Кнопки для поворотов размещены в сетках. Игрок может вращать блок, нажимая одну из кнопок. Строки соответствуют выбору оси координат блока, а столбцы соответствуют значениям координат для этой оси. Игрок может выбрать блок, выбрав одну из строк и один из столбцов. Например, нажатие кнопки, в которой строка пересекает столбец, выбирает блок на . Для каждого блока перечислены остальные три оси. Затем требуется выбор второй оси для проверки плоскости вращения. Наконец, необходимо выбрать одну из трех кнопок (вверх, по диагонали и вниз), чтобы определить угол поворота (▲), (■) и (▼). (0 рядов можно игнорировать — вместо этого игрок может выполнить эквивалентную пару действий в параллельных блоках.)

Когда цвета 27 вложенных кубов в ячейке совпадают, эта ячейка завершена. Головоломка решена, когда все ячейки заполнены.

Программа

Обсуждение

Хотя нам удалось реализовать кубик Рубика-4, некоторые проблемы еще предстоит решить. Мы стремились к простоте реализации, а не к эффективности. Поэтому в будущем стоит подумать о доработке приложения, чтобы получить более эффективный метод визуализации и интуитивно понятный интерфейс.

Программа перерисовывает 1296 квадратов после каждого поворота, поэтому важно эффективное кодирование. Существует большая избыточность в вычислении вершин 4-подкубов для каждого вращения. Остается выяснить, какой самый эффективный метод обработки вершин с помощью подкубов или 4-подкубов. Обратите внимание, что мы должны перенести вершины 4-подкубов в вершины подкубов, когда мы обрабатываем вершины 4-подкубов как набор данных, а не обрабатываем их как вложенные кубы.

Эффективная визуализация является общей проблемой для четырехмерной геометрии. В этой статье мы использовали центральную проекцию для представления 4-кубов. Однако предлагаемая проекция не полностью отражает особенности головоломки. Хотя существуют и другие проекции для представления 4-куба, наиболее подходящий метод пока не ясен.

Еще одно возможное улучшение — анимация вращения. Анимация вращения цветных маленьких 4-кубиков поможет игроку интуитивно понять их перестановку.

В этой головоломке важен интуитивно понятный интерфейс. Вопросы интерфейса и визуализации связаны между собой, и их развитие может дать новый метод понимания четырехмерного пространства.

Каталожные номера

[1]	HSM Коксетер, Введение в геометрию , 2-е изд., Hoboken: Wiley, 1989.
[2]	Т. Йошино. «Деятельность доктора Такаси Ёсино». (11 декабря 2017 г.) takashiyoshino.random-walk.org/basic-data-of-4d-regular-polytopes.
[3]	К. Миядзаки, М. Исии и С. Ямагути, Наука о многомерных формах и симметрии , Киото: Издательство Киотского университета, 2005 (на японском языке).
Т. Йошино, «4 кубика Рубика», Журнал Mathematica , 2017. dx.doi.org/doi:10.3888/tmj.19-8.

Об авторе

Профессия: наука о форме. Сфера интересов: скелетная структура планктона, неевклидова геометрия, гиперпространство, формирование узоров.

Такаси Йошино
Университет Тойо,
Кудзирай 2100, Кавагоэ, 350-8585, ЯПОНИЯ
tyoshino@toyo. jp

Четыре измерения1

0 Четыре измерения

ГЭС 0410

Эйнштейн для всех

Назад на страницу основного курса

Джон Д. Нортон
Кафедра истории и философии науки
Университет Питтсбурга

Одномерный интервал
Двумерный квадрат
Трехмерный куб
Четырехмерный куб: тессеракт
Стереовидение
Сводная таблица
Вместительный вызов
Запутанный вызов
Использование цветов для визуализации дополнительного измерения
Что вы должны знать

Мы уже видели, что нет ничего страшного таинственно о добавлении одного измерения к пространству, чтобы сформировать пространство-время. Тем не менее трудно устоять перед затянувшимся беспокойство по поводу идеи четырехмерного пространства-времени. проблема не в время часть четырехмерного пространства-времени; Это это четыре . Легко представить себе три оси трехмерного мерное пространство: вверх-вниз, поперек и задом наперед. Но куда нам поставить четвертую ось, чтобы сделать четырехмерное пространство?

Моя нынешняя цель — показать вам, что в все таинственное в четырех измерениях пространства-времени. Для этого я брошу временная часть полностью. Я просто рассмотрю четырехмерный пространство; то есть пространство точно такое же, как наше трехмерное пространство, но с одно дополнительное измерение. Каково это?

Без всяких усилий я могу визуализировать трехмерное пространство — и вы тоже можете. Что бы это быть как жить в трехмерном кубе? Чтобы его попросили визуализировать это как просят дышать или моргать. Это легко. Там мы сидим в куб с шестью квадратными стенками и восемью углами. Наш разум позволяет мы парим внутри.

Могу ли я представить, каково было бы жить в четырехмерный аналог куба, четырехмерный куб или «тессеракт»? Я не могу представить это с таким же легким непосредственность. Сомневаюсь, что и вы сможете. Но это только о единственное, что мы не можем сделать. В противном случае мы можем определить все свойства тессеракта и то, что это будет нравится жить в одном. Для этого существует множество техник. я покажет вам один ниже. Он включает в себя продвижение через последовательность измерений, экстраполируя естественные выводы в каждом шагнуть в четвертое измерение. Как только вы видели, как это делается для особого случая тессеракта у вас не будет проблем применяя его к другим случаям.

Дверь в четвертое измерение открывается.

Одномерный интервал

Одномерным аналогом куба является интервал. это формируется путем взятия безразмерной точки и ее перетаскивания на определенное расстояние. Это расстояние может быть 2 дюйма или 3 фута или что-то еще. Давайте позвоним расстояние «Л».

Интервал имеет длину L. Он ограничен двумя точками как его грани — две точки на обоих концах интервала.

Двумерный квадрат

Двумерный аналог куба — квадрат. это образованный перетаскиванием одномерного интервала на расстояние L в второе измерение.

Квадрат имеет площадь L ² . Он ограничен гранями на 4 стороны. Грани — это интервалы длины L. Мы знаем, что их четыре. их, поскольку его двумерные оси должны быть закрыты с обоих концов гранями.

Таким образом, у нас есть 2 измерения x 2 грани каждое = 4 грани. грани вместе образуют периметр длиной 4xL.

Трехмерный куб

Чтобы сформировать куб, мы берем квадрат и перетаскиваем его на расстояние L в третьем измерении.

Объем куба L ³ . Он ограничен гранями на 6 сторон. Грани представляют собой квадраты площадью L ² . Мы знаем, что есть 6 из них, так как его трехмерные оси должны быть закрыты с обоих концов лица.

Итак, у нас есть 3 измерения x 2 грани в каждой = 6 граней. грани вместе образуют поверхность площадью 6xL ². Рисование изображение трехмерного куба на двумерной поверхности одинаково легко. Берем две его грани — два квадрата — и соединяем углы.

Есть несколько способов сделать рисунок, который соответствует взгляду на куб под разными углами. На рисунке показано два способа сделать это. Первый дает косой обзор; второй смотрит по одной из осей.

Четырехмерный куб: тессеракт

Пока я надеюсь, что вы нашли наши конструкции полностью безупречный. Следующий шаг в четыре измерения можно сделать одинаково механически. Мы просто систематически повторяем каждый шаг выше. Единственный разница в том, что на этот раз мы не можем легко сформировать ментальную картину что мы строим. Но мы можем знать все его свойства!

Чтобы сформировать тессеракт, мы берем куб и перетаскиваем его расстояние L в четвертом измерении . Мы не можем точно представить как это выглядит, но это примерно так:

Тессеракт имеет объем L ⁴ . Он ограничен лица с 8 сторон. Грани представляют собой кубы объема L ³ . Мы знаем их 8, так как его четыре оси должны быть ограничены любой конец гранями — две кубические грани на ось. Еще раз, мы не можем визуализируйте все четыре из этих закрытых измерений. Мы можем в лучшем случае визуализировать три направления перпендикулярны друг другу. Затем мы каким-то образом добавим в четвертый (красный):

Итак, у нас есть 4 измерения x 2 грани в каждой = 8 граней. грани вместе образуют «поверхность» (на самом деле трехмерный объем) размером 8xL ³ в объеме. Рисование изображения четырехмерного тессеракта в трехмерном размерное пространство прямолинейно. Мы берем два его лица — два кубики — и соедините углы.

Есть несколько способов сделать рисунок, который соответствует взгляду на тессеракт под разными углами. Фигура показывает два способа сделать это. Первый дает косой обзор; секунда смотрит по одной из осей.

Итак, теперь мы, кажется, знаем все, что нужно знать о тессеракт! Мы знаем его объем в четырехмерном пространстве, как он выражается вместе из восьми кубов как поверхностей и даже каков объем его поверхность (8xL ³ ).

Стереовидение

«Чертежи» тессеракта плохо видны. Это потому, что они действительно должны быть трехмерными моделями в трехмерное пространство. Итак, что у нас есть выше, это два объемный чертежи трехмерных моделей четырехмерного тессеракт. Неудивительно, что он становится грязным!

Изображения ниже представляют собой стереопары. Если вы знакомы с тем, как их просматривать, вы увидите, что они дают вам хороший стереофонический вид трехмерной модели. Если это новое для вас, они берут практика, чтобы увидеть. Вам нужно расслабить свой взгляд, пока ваш левый глаз не смотрит на левое изображение и правый глаз смотрит на правое изображение.

Но как научиться этому? мне проще всего начать, если я сижу далеко от экрана и смотрю вдаль над верхней частью экрана. Я вижу два несколько размытых изображения на край моего поля зрения. Пока я не сосредотачиваюсь на них, они начинают дрейфовать вместе. Это то движение, которое вам нужно. Чем больше они дрейфуют вместе тем лучше. Я стараюсь усилить дрейф, насколько это возможно, пока осторожно перемещая свой взгляд к изображениям. Цель состоит в том, чтобы получить два изображения для слияния. Когда они это делают, я продолжаю смотреть на объединенные изображения, улучшается фокусировка и появляется полный трехмерный стереоэффект резко. Эффект поразителен и стоит небольших усилий.

Эту пару легче сплавить:

и этот немного сложнее:

Сводная таблица

Мы можем подытожить развитие свойств tesseract следующим образом:

Размер	Рисунок	Лицо	Том	Номер лица	Том поверхность/периметр
1	интервал	точка	л	1×2=2	два баллы
2	квадрат	интервал	л ²	2×2=4	4 л
3	куб	квадрат	л ³	3×2=6	6 л ²
4	тессеракт	куб	л ⁴	4×2=8	8 л ³

Вместительный вызов

Если бы вы жили в тессеракте, вы могли бы выбрать жить на своей трехмерной поверхности, как двухмерный человек могли бы выбрать жить в 6 квадратных комнатах, которые образуют двухмерный поверхность куба. Таким образом, ваш дом будет состоять из восьми кубов, образующих поверхность. из тессеракта. Представьте себе, что есть двери, где когда-либо две из эти кубики встречаются. Если вы находитесь в одной из этих комнат, сколько дверей будет Понимаете? Как бы выглядела следующая комната, если бы вы прошли через одну из двери? Через сколько дверей нужно пройти, чтобы добраться до самой дальней номер? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо окна снаружи тессеракта? Как насчет окон внутрь? тессеракт?

Некоторые из этих вопросов непростые. Чтобы ответить на них, перейдите вернемся к простому случаю трехмерного куба с гранями, состоящими из квадраты. Задайте аналогичные вопросы там и просто экстраполируйте ответы на тессеракт.

Запутанный вызов

Доступ к четвертому измерению делает возможным многое иначе это было бы совершенно невозможно. Чтобы увидеть, как это работает, мы будем использовать стратегия обдумывания процесса в трехмерном пространстве. затем мы воспроизвели его в четырехмерном пространстве.

Рассмотрим монету, лежащую в рамке на столешнице.

Монета не может быть удалена из рамки в пределах ограничивает двумерную поверхность стола. Теперь вспомните что у нас есть доступ к третьему измерению. Монета легко удалить, просто подняв его в третье измерение, высота над столом.

После этого мы можем свободно перемещать монету по своему усмотрению в более высокую слой, а затем опуститься обратно на столешницу за пределами рамы.

При подъеме следует обратить внимание на то, что движение вообще не двигает монету в двух горизонтальных направлениях двух объемное пространство. Таким образом, движение никогда не приближает его к кадру и там нет опасности столкновения с рамой.

Теперь повторите этот анализ для своего аналог в одном более высоком измерении, мрамор запертым в трехмерном ящике.

Мрамор можно удалить в точно так же, «подняв» его, на этот раз в четвертое измерение. Как и монета в рамке, ключ следует отметить, что при этом подъемном движении шарик положение в трех пространственных направлениях ящика без изменений. Мрамор никогда не приближается стены и нет опасности столкновения с ними.

Как только он поднимается в новое трехмерное пространство, он можно свободно перемещать в этом пространстве и опускать обратно в исходное трехмерное пространство, но теперь за пределы коробка.

=Теперь, наконец, рассмотрим два зацепленных колец в некотором трехмерном пространстве. Мы можем разделить их, используя доступ к четвертому измерению?

Это можно сделать точно так же процесс подъема одного из колец в четвертое измерение. В качестве прежде обратите внимание, что подъем не перемещает кольцо ни в одном из три направления трехмерного пространства, удерживающие первоначально связанные кольца. Так что движения рисков нет столкновения перемещаемого кольца с другим. Подъем просто поднимает перемещенное кольцо на новый трехмерный слой из четырех размерное пространство, в котором нет ни одной части другого кольца.

перемещенное кольцо может быть свободно перемещено в этот новый слой, и если мы с удовольствием опустился обратно в исходное трехмерное пространство в совсем другое место.

А теперь самое сложное. Мы знакомы в нашем трехмерное пространство с завязыванием узлов на веревке. Некоторые узлы просто кажущиеся клубки, которые могут довольно легко разойтись. Остальные настоящие и можно расстегнуть, только продев конец веревки в петлю. Так примите это за настоящий узел: тот, который не может быть развязаны любыми манипуляциями с веревкой, если мы не сможем ухватиться за заканчивается. (Представьте, если хотите, что каждый из них прикреплен к стене и нельзя удалить.)

Задача состоит в том, чтобы убедить сами понимаете, что в четырехмерном пространстве на веревках нет настоящих узлов. пространство. Основная помощь, которая вам понадобится, — это описанная выше манипуляция с связанные кольца. Для начала представьте, как бы вы использовали четвертый измерение, чтобы развязать какой-нибудь простой узел, который вы легко можете себе представить.

Использование цветов для визуализации дополнительных размер

Общая идея «поднятия» объекта в четвертое измерение все еще кажется неуловимым? Если да, то вот техника для визуализация этого может просто помочь. Хитрость заключается в том, чтобы представить, что различия в положении в дополнительном измерении пространства может быть представлено различия цветов.

Вот как это работает, когда мы начинаем с двухмерного пространства и подняться в третье измерение. Объекты в оригинале два мерное пространство черное. Когда мы поднимаемся через третий измерения, они последовательно приобретают синий цвет, зеленый и красный.

Теперь давайте применим цветной слой.

трюк к более раннему примеру подъема монеты из рамки. монета начинается в том же двухмерном пространстве, что и рамка. Мы поднимаем это в третье измерение в более высокое пространственный слой, который мы закодировали красным цветом. В этом высшем слой, монета может свободно перемещаться влево/вправо и вперед/назад без пересекающие рамку. Мы перемещаем его вправо, пока он не пройдет над рамой. Затем опускаем обратно вниз снаружи.

А теперь представьте, что мы не можем воспринимать третье измерение напрямую. Вот как мы представить побег монеты. Он начинается внутри кадра в пространство кадра. Затем он поднимается из рамы в третье измерение. В этот момент на это указывает призрачный красная монета. Его пространственное положение слева/справа и направление вперед/назад не изменилось.

Все, что изменилось, это его высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево или справа, или спереди и сзади, в этом красном слое уже не пересекает рамку и может двигаться прямо над ней. мы этого не увидим однако перемещайтесь по кадру. Насколько нам известно, это будет просто пройди через это.

Движение монеты в этом трехмерном побеге иллюстрируется призрачным красным монета.

Этот последний анализ монеты в кадр является шаблоном для работы с реальный случай шарика, заключенного в трехмерную коробку. Если шарик движется в любом из трех известных измерений (вверх/вниз, влево/вправо и вперед/назад), его движение пересекает стены ящик, и он не может убежать. Итак, мы поднимаем шарик в четвертый измерение, не меняя своего положения в трех привычных Габаритные размеры.

На рисунке это показано тем, что мрамор становится призрачным. красный. В красном поле шарик может двигаться вверх/вниз, слева/справа и спереди/сзади, не пересекая стенки коробки. Затем мрамор перемещается так, что проходит над одной из стен. это затем опустили из красного пространства обратно к исходным трем мерное пространство коробки, но уже вне стен.

То же анализ относится к связанным кольцам. Одно кольцо снято из трехмерного пространства исходной установки. В этом красное пространство, кольцо может свободно двигаться, не пересекаясь с другим звенеть. Мы отодвигаем его подальше от другого кольца, а затем опускаем обратно. в исходное трехмерное пространство. Теперь он не связан с другое кольцо.

Что следует знать

Свойства квадратов, кубов и тессерактов.
Как получить свойства тессеракта и других четырехмерные фигуры путем экстраполяции методов, используемых для получения свойства куба.

Авторское право Джон Д. Нортон. февраль 2001 г.; июль 2006 г., 2 февраля 2008 г.; 6 февраля 2012 г.; 30 апреля 2014. Январь 30, 2022.

Что такое тессеракт? Четырехмерный объект, который невозможно построить

16 июня 20214 мин. чтение

Тессеракт — четырехмерный гиперкуб с 24 гранями, 32 ребрами и 16 вершинами.
Его можно создать, утолщая куб в четвертом измерении.
Хотя физически построить тессеракт невозможно, мы можем визуализировать его в нашем трехмерном мире.

Идея четвертого пространственного измерения будоражила людей с момента ее зарождения. В физике три измерения представляют пространство (x, y, z), а четвертое измерение представляет время (t). Однако в абстрактной математической концепции может быть бесконечное количество пространственных измерений.

Давайте попробуем понять четвертое измерение. В геометрии четырехмерный аналог куба называется тессерактом. Это легко экстраполировать, глядя на более низкие измерения –

Нульмерный куб – это точка, вершина.
Одномерный куб представляет собой отрезок с двумя вершинами (по одной на каждом конце). Его можно создать, утолщая точку в одном измерении.
Двумерный куб представляет собой квадрат с 4 вершинами. Его можно создать, утолщая сегмент линии во втором измерении.
Трехмерный куб — это куб с 8 вершинами, созданный путем утолщения квадрата в третьем измерении.

Точно так же четырехмерный куб (также известный как гиперкуб или тессеракт) имеет 16 вершин. Его можно создать, утолщая куб в четвертом измерении. Но поскольку мы живем в трехмерном мире, построить четырехмерный объект невозможно.

В целом можно сказать, что тессеракт относится к кубу так же, как куб к квадрату. У него 24 грани, 32 ребра и 16 вершин.

Объект, изменяющийся в размерах от Точки до Тессеракта | Фото: Wikimedia Commons Это происходит потому, что наше воображение недостаточно сильно, чтобы спроецировать наше сознание в искусственный мир, который сильно отличается от нашего собственного.

Наш мозг устроен таким образом, чтобы преобразовывать двухмерный ввод в трехмерное изображение. Точнее, наши глаза отправляют в мозг пару двумерных изображений, из которых мозг строит двухмерную модель поля зрения с глубиной.

Это то, о чем лучше всего думает наш мозг. Трехмерное пространство легко визуализировать, потому что мы буквально видим его все время. Однако у нас нет прямого опыта высших измерений, и поэтому у людей нет четкого прототипа, который можно было бы использовать в качестве трамплина для его визуализации.

Справка: На что похоже четырехмерное пространство? | Джон Д. Нортон

Физики и математики, обученные работе с многомерными пространствами, с другой стороны, более способны, чем остальные из нас, визуализировать это в своем мозгу.

Давайте попробуем визуализировать тессеракт

Как куб можно спроецировать в двухмерное пространство, так и тессеракты можно спроецировать в трехмерное пространство.

Рисунок 2 | Изображение предоставлено: Wikimedia Commons

Поверхность трехмерного куба содержит 6 квадратных граней; аналогично гиперповерхность тессеракта содержит 8 кубических ячеек.

Тессеракт можно разложить на 8 кубов в трехмерном пространстве (рис. 2). Это похоже на разворачивание куба на 6 квадратов в двухмерном пространстве. Развертывание геометрического объекта [с плоскими сторонами] известно как сеть. Тессеракт имеет 261 сеть.

Существует два типа четырехмерных вращений:

1) Простые вращения : Трехмерная проекция Тессеракта (рис. 3), выполняющая простое вращение вокруг плоскости, делящей фигуру пополам сверху вниз и спереди слева. назад-вправо.

Рис. 3 | Альтернативная проекция тессеракта | Wikimedia Commons

2) Двойное вращение: Трехмерная проекция тессеракта (рис. 4), показывающая двойное вращение вокруг двух ортогональных плоскостей.

Рисунок 4 | Альтернативная проекция тессеракта | Wikimedia Commons

Тессеракт также можно показать с точки зрения устранения скрытого тома. Например, на рисунке 5 красное лицо ближе всего к четвертому измерению и имеет четыре кубические ячейки, сходящиеся вокруг него.

Рисунок 5 | Тессеракт с точки зрения устранения скрытого объема

Он был открыт в 1888 году

Слово «тессеракт» было придумано британским математиком и писателем-фантастом Чарльзом Говардом Хинтоном. Он впервые употребил это слово в 1888 году в своей книге «Новая эра мысли». Он также изобрел несколько новых слов для описания элементов четвертого измерения.

Прочтите: Может ли жизнь сформироваться в двумерной Вселенной?

С тех пор слово «тессеракт» используется в различных произведениях об искусстве, архитектуре и научной фантастике (таких как «Мстители» и «Агенты Щ.И.Т.»), где оно не имеет ничего общего с четырехмерным гиперкубом.

Недавние исследования

Человеческие пространственные представления не ограничены нашим трехмерным миром

Группа исследователей из Университета Иллинойса, США, провела исследование, чтобы выяснить, могут ли люди развить интуитивное понимание четырехмерного пространства. Они использовали виртуальную реальность (VR) для получения точных результатов.

Данные показывают, что люди без специальной практики могут научиться делать пространственные суждения о длине и угле между линейными сегментами, встроенными в 4D-пространство, просматриваемое в виртуальной реальности. Их решение включало данные как из трехмерной проекции, так и из четвертого измерения. Лежащие в основе представления были основаны на зрительных образах (установленных алгебраического характера), хотя и примитивных и недолговечных.

Общее количество возможных измерений во Вселенной

В то время как общая теория относительности рисует картину четырехмерной Вселенной, теория суперструн говорит, что она имеет 10 измерений, а расширенная версия, называемая М-теорией, говорит, что она имеет 11 измерений. В теории бозонных струн пространство-время является 26-мерным. Эти теории просто представляют собой математические уравнения. Они настолько сложны, что никто не знает их точную форму.

Прочтите: Что такое теория струн? Простой обзор

Эксперимент по изучению теоретических материалов в четырехмерном пространстве

Международная группа исследователей смогла разработать двухмерную экспериментальную систему, которая позволяет им анализировать физические свойства «материалов», которые, как предполагалось, существуют только в 4D пространство.

В частности, они продемонстрировали, что четырехмерные квантовые эффекты Холла можно эмулировать, используя фотоны, проходящие через двумерную решетку волноводов.

Чем полезно это исследование в нашем трехмерном мире? Допустим, квазикристаллы (широко используемые для покрытия некоторых сковородок с антипригарным покрытием) имеют скрытые размеры. Этот эксперимент может помочь нам понять физику этого скрытого измерения. Затем физику можно было бы использовать в качестве принципа проектирования нового фотонного оборудования.

Гиперкуб или Тессеракт — Галерея

diff-arch (дифференциал-арка) 7 мая 2019 г., 20:07

Привет всем,

Вот мой побочный проект, который я, к счастью, завершил сегодня!

Некоторое время, в основном после просмотра некоторых фильмов о супергероях Marvel и услышанного о «тессеракте» , я просмотрел его и был разочарован тем, что тессеракт фильма не имеет ничего общего с геометрической концепцией, что гораздо интереснее. . Дисней изображает тессеракт как простой светящийся синий куб с анимированной жидкой субстанцией внутри.

В геометрии тессеракт или гиперкуб является «четырехмерным аналогом трехмерного куба . Он относится к кубу так же, как куб к квадрату». (источник)

Вот что я придумал:

2019-05-07 19_58_42.gif1067×760 3,83 МБ

Гиперкуб создается анимированным компонентом GHPython.

12 лайков

Дэнсергрэм (Грэм Кнапп) 26 мая 2019 г., 20:11

Это очень круто. Я искал способ использовать 3D-срезы через 4D-формы и нашел это на Github: https://github.com/orybkin/Tesseract. Он использует Jupyter Notebook для визуализации трехмерного среза через 9 гиперкубов (не все видны сразу)

К сожалению, он работает на Cpython, а не на Ironpython, и использует Scipy для ключевых элементов, поэтому нет возможности легко интегрировать его с Rhino / GrassHopper 9.0009

1 Нравится

diff-arch (дифференциал-арка) 26 мая 2019 г. , 20:33

Очень классная штука, Грэм! Спасибо за ответ.

Дэнсергрэм (Грэм Кнапп) 26 мая 2019 г., 20:35

Если честно, это немного разочаровывает. Оказывается, трехмерный срез четырехмерного гиперкуба — это… куб!

арка дифференциала (дифференциал-арка) 26 мая 2019 г., 20:43

Ха-ха… что-то не так.

чанли (Крис Хэнли) 26 мая 2019 г. , 20:49

Дэниел Шиффман (автор Nature of Code, крутой чувак со всех сторон), тоже сделал одно на javascript.

2 отметок «Нравится»

(дифференциал-арка) 26 мая 2019 г., 20:58

Здорово! Я проверю это завтра.

ДэниелПайкер (Дэниел Пайкер) 26 мая 2019 г., 22:34

В последних выпусках Kangaroo есть новый компонент, который позволяет вам исследовать 4D-вращения — на вкладке «Утилиты» — Преобразование Мёбиуса .

Moebius_example.gh (7,2 КБ)

Он берет любую геометрию и стереографически проецирует ее из плоского трехмерного пространства в трехмерную сферу, вращает ее в четырехмерном пространстве, а затем проецирует обратно.

В 2-х измерениях существует много возможных конформных отображений (углы сохраняются, а окружности остаются круглыми), но в 3D эти преобразования Мёбиуса являются возможными только конформными преобразованиями.

Поскольку мы все равно смотрим только на 3D-срез или проекцию, я думаю, что иногда может быть более поучительно исследовать 4D-вращения через их влияние на знакомые 3D-объекты, а не просто многогранники более высокого измерения.

Вы также можете получить всевозможные интересные кривые и поверхности, перемещая или выстраивая в ряд точки или кривые с помощью этих четырехмерных вращений

4 отметок «Нравится»

(дифференциал-арка) 27 мая 2019 г.