Кубика 2: Как собрать кубик Рубика 2×2

Как собрать кубик Рубика 2х2

Кубик Рубик 2×2 — это двухуровневая версия головоломки. Изобретение принадлежит Эрнё Рубик (отсюда и название). Игра развивает логику и пространственное мышление, мелкую моторику, память. 

Схема сборки кубика Рубика 2х2х2 (иногда его называют Мини-кубик Рубика) достаточно простая для того, чтобы максимум через 20 минут, после того как Вы открыли эту инструкцию, ваш кубик приобрёл такой вид:

Рассмотрим, как собрать кубик Рубика 2 на 2.

Терминология

Куб 2×2 — это головоломка-куб без центральной и краевой частей, имеющий только 8 угловых частей.

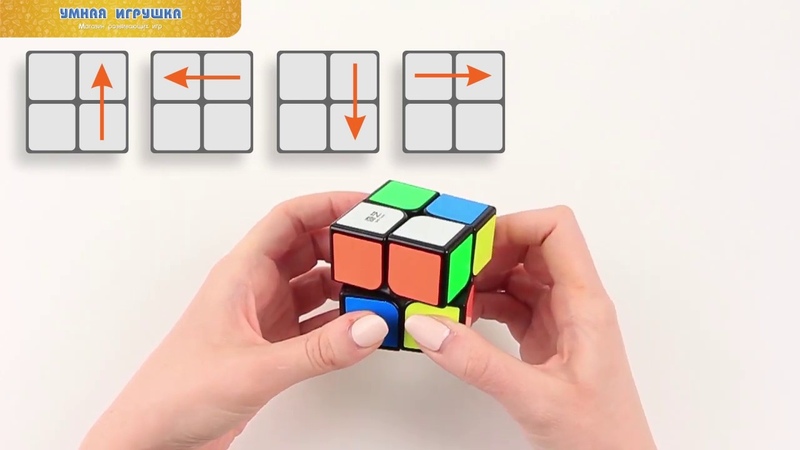
Для того чтобы научиться читать схемы сборки, нужно запомнить шесть букв. Они обозначают поворот или их последовательность. Указывают, какой именно ход следует сделать. Зная основы, любая формула кубик рубика 2×2×2 будет читаться легко.

Возьмите куб и держите перед собой:

• F (Ф) (спереди) — грань, обращенная к вам;
• B (Т) (тыл) — тыльная сторона;
• R (П) (справа) — правая;
• L (Л) (слева) — левая;
• U (В) (верх) — грань, находящаяся сверху;
• D (Н) (низ) — нижняя часть.

Цвет этих граней может быть любым. Названия они получили из-за расположения. Буква указывает, что вращать нужно по часовой стрелке на 90°.

Прописная буква, за которой следует знак апострофа (‘), указывает, что соответствующую грань нужно повернуть на 90° против часовой стрелки.

Буква, после которой стоит цифра «2», означает поворот на два оборота (180°). Не имеет значения, в какую сторону крутить.

Шаг 1. Первый (нижний) слой

Схема сборки кубика Рубика 2×2×2 на самом деле достаточно проста. Задача, которую нужно решить на первом шаге, — собрать нижний слой таким образом, что внизу были собраны четыре фигуры одного цвета. Другие два цвета должны быть идентичны с соседними кубиками.

Новичкам рекомендуется начинать сборку с белой стороны. Цель — сделать так, чтобы все квадратики этого цвета были на одной стороне. Прилегающие элементы должны соответствовать друг другу.

Найдите сторону, на которой есть только один белый угол. Это будет вершиной.

Теперь найдите белую фигуру, затем ту, у которой одна из сторон совпадает с вашей начальной белой фигурой. Например, если к начальной прилегает зеленая и красная, следующая фигура, которую вы ищете, должна быть зеленой или красной.

Шаг 2. Расположение кубиков верхнего слоя

Следующая задача — собрать элементы верхнего ряда. Для этого нужно вращать верхнюю часть кубик Рубика 2х2 до тех пор, пока один из элементов не станет в нужное положение — три цвета должны пересечься.

После того как угол зафиксирован, наша цель — собрать оставшиеся элементы. Это можно сделать двумя способами:

• менять местами соседние фигуры;
• менять местами части по диагонали.

Шаг 3. Вращения кубиков верхнего слоя

На этом шаге комбинации делать нужно попарно. Например, по часовой стрелке вращается один угол, затем другой — против часовой стрелки.

На данном этапе может показаться, будто все снова запуталось. Не обращайте внимания. Поворачивайте другой угол в противоположном направлении. Верхнюю грань следует между операциями вращать, пока нужный угол не станет в верхний правый.

Для трех углов можно применять иные комбинации.

Тренируйтесь, и у вас все получится собрать кубик 2×2.

У нас в каталоге магазина легко выбрать кубик рубика 2х2.

Как собрать кубик рубика 2х2 для начинающих, схема сборки

Содержание

Кубик Рубика 2х2 собрать легко – это на первый взгляд, но на самом деле он является довольно сложной головоломкой. Кубик 2х2 собирать так же сложно, как и 3х3. Но есть 100% схемы, алгоритмы сбора кубика, но кроме схем вам необходимо знать еще и язык вращения самого кубика. Далее мы вам расскажем обо всем подробнее.

Кубик Рубика — история

Рубик преподавал в университете студентам теорию математических групп и с помощью кубика наглядно показывал в чем суть этой теории. Он тогда не подозревал, что эта головоломка сделает его на столько популярным, но еще и миллионером.

Но известно, что Рубик был не первым, кто пытался создать такую головоломку. Вильям Гуфстафсон в 1958 году показал миру головоломку с гранями кубика 2х2 и 3х3, но эти кубики были очень не совершенной конструкции и известности не приобрели. А в 1970 году Ларри Николс запатентовал головоломку кубика 2х2, у которой кубики были соединены магнитами.

А уже в 1977 году Эрне Рубик запатентовал конструкцию головоломки 2х2, которая сейчас известна миллионам людей на всей планете. В настоящее время придумали уже более 10 различных модификаций кубика Рубика, но все-таки стоит начать изучать эту головоломку с кубика Рубика 2х2.

Кубик Рубика 2х2 — для новичков, схема сборки

Несмотря на то, что количество кубиков всего по 4 на каждой грани и 6 цветов, насчитывают более 3,5 миллионов вариантов сбора данной модели кубика Рубика.

Для быстрого сбора кубика Рубика 2х2, необходима внимательность, смекалка и пространственное мышление, ну или же вам на помощь приходит поэтапная схема сборки кубика Рубика 2х2 с картинками.

Эта вариация кубика собирается практически так же, как и кубик Рубика 3х3. Для сборки нижней грани вам понадобятся формулы сборки классического кубика Рубика 3х3.

Алгоритм сборки кубика Рубика 2х2 для начинающих

Спидкубинг кубика Рубика 2х2 – самая популярная дисциплина на соревнованиях. Даже профессиональные спидкуберы порой встают в стопор при сборе кубика Рубика 2х2. Одна малейшая ошибка и вы в тупике.

Сначала изучите самую простую схему сборки кубика. Алгоритм состоит всего из 3 этапов.

Шаг 1: сбор верхней грани

Изначально кубик полностью перемешан.

Сначала ищем кубик с цветом верхней грани на нижней грани и ставим кубик так, как нарисовано на рисунке ниже. Выбрав ваш вариант из трех предложенных, выполните вращение по указанной схеме.

Вариант 1

Вариант 2

Вариант 3

Как только нужный цвет встал на верхнюю грань, надо повторить точно такие же действия с другими тремя кубиками из верхнего слоя. После окончания манипуляций верхняя грань кубика 2х2 соберется полностью.

Шаг 2: сбор второй грани

Верхняя грань уже собрана, приступаем ко второму шагу нашего алгоритма.

Поверните кубик собранной гранью вниз (смотри рисунок ниже).

На предыдущем этапе мы выбирали верхнюю грань белого цвета, то после разворота кубика верхняя грань будет желтой. Необходимо повернуть верхнюю грань столько раз, чтобы желтый кубик занял правильную позицию – показана на рисунке. Чтобы этот момент получился – необходимо следовать алгоритму, который показан на рисунках ниже.

Может получиться так, что нужный желтый кубик встанет на верхнюю грань, а нижняя грань кубика «разлетится», тогда необходимо вращать верхнюю грань по часовой стрелке до тех пор, пока на его место не встанет другой кубик и еще раз пройти все этапы вращения, пока не соберется белая грань кубика, а желтый кубик, помещенный на верхней грани так и останется на своем месте.

После прохождения этих вращений, надо сделать тоже самое и с другими оставшимися тремя кубиками. После прохождения второго этапа у вас соберутся полностью 2 грани: верхняя и нижняя.

Шаг 3: сбор кубика 2х2 полностью

Прежде чем перейти к заключительному третьему этапу сборки, проверьте, что верхняя и нижняя грани собраны полностью, а боковые будут разобраны.

На третьем этапе надо проверить наличие на верхней грани парных кубиков – кубики одинаковых цветов, расположенных рядом. Если таковых нет, то следуйте инструкции, которая представлена ниже, и такие варианты появятся. Далее надо поместить парные кубики как показано на схеме ниже и проделать вращения еще раз.

Вот и кубик 2х2 собран полностью!

Если у вас получилось собрать кубик Рубика 2х2 с первого раза,  то советуем попробовать собрать кубик 3х3. Ну, а если вы все же ошиблись, то начните заново и внимательно следуйте указанным инструкциям.

Мировой рекорд сборки кубика Рубика 2х2

Мировой рекорд сборки кубика Рубика 2х2 составляет всего лишь 0,49 секунды и принадлежит он поляку Maciej Czapiewski.

Как собрать кубик рубика 2х2 — видео

кубиков (2) | Spelunky Вики

Посмотреть источник

Функция: Используется как часть игры в Магазинах

Можно принести в жертву на Алтаре Кали

Источник:

Дома игральных костей

Урон:

1 (Бросок)

Примечания:

• Всегда выпадает 1 или 6 при взбивании

• Владелец магазина Angers Shop, если его снова бросили во время игры или украли

Кости — предмет в Spelunky 2.

Свойства

Кости используются как часть мини-игры в Dice Houses, которой управляют либо владельцы магазинов, либо мадам Туск в Tide Pool. При броске кубика на лицевой стороне выпадает другое число. Это используется как часть мини-игры в Dice Houses, где игрок бросает два кубика и получает разные результаты в зависимости от того, какое число они складываются.

Есть трюк с игральными костями: если их подбросить в воздухе, они всегда будут выбрасывать 1 или 6. Это можно использовать для более легкого броска 7, чтобы заработать призы в Доме игральных костей или гарантировать определенные награды на алтаре. , так как каждый кубик будет иметь равные шансы выбросить любое число.

Принесение в жертву двух кубиков вместе на алтаре даст игроку награду, размер которой зависит от суммы.

Награды за Алтарь Dice Kali

Всего игральных костей	Награда
2	Змея
3	Алмаз
4	Телепак
5	Очки
6	Веревочная свая
7	Мачете
8	Паутина
9	Приготовленная индейка
10	Альпинистские перчатки
11	Вампир
12	Наемный рабочий

Обычный трюк с костями, используемый для более легкого броска семерок. Это не работает с Рукавицей Питчера, если только кости не брошены по диагонали вверх.

Общая информация

• Можно было поднять кость, пока она еще катилась в воздухе. Поскольку технически это другой предмет, он вечно вертелся в руке игрока, пока его не положили. Это было исправлено в версии 1.20.4a.
• Получение змеи при предложении двух кубиков с суммарным значением 2 является очевидным намеком на термин «Глаза змеи», относящийся к указанному значению на кубике.

Spelunky 2 предмета
Оборудование	Паста • Очки • Перчатки для скалолазания • Перчатка кувшина • Весенние туфли • Обувь с шипами • Компас • Компас пришельцев • Парашют • Уджатский глаз • Капала • Анх • Табличка судьбы • Отмычка • Четырехлистный клевер
Короны	Hedjet • Корона • Баклажановая корона • Настоящая корона
Спинка	Плащ • Плащ Влада • Реактивный ранец • Телепак • Ховерпак • Силовой ранец
Бонусы	Бомбы • Веревки • Маточное молочко • Приготовленная индейка • Эликсир
Полезные предметы	Веб-пушка • Дробовик • Замораживающий луч • Клон-пушка • Арбалет • Камера • Телепорт • Мотыга • Бумеранг • Мачете • Экскалибур • Сломанный меч • Плазменная пушка • Скипетр • Лук Хоу И • Деревянный щит • Металлический щит
Разное	Стрела Света • Идол • Идол Бивня • Горшок проклятия • Ушабти • Баклажан
Ловушки	Медвежий капкан • Мина
Нет записи в журнале	Ящик • Подарок • Сундук • Ключ • Золотой ключ • Запертый сундук • Стрелы • Факел • Карательный шар • Кубик • Горшок с золотом • Сокровище • Сумка игрока • Гигантская еда • Металлолом

Контент сообщества доступен по лицензии CC-BY-SA, если не указано иное.

Калькулятор вероятности игры в кости

Создано Wojciech Sas, PhD

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 13 февраля 2023 г.

Содержание:

• Многогранные кости
• Как рассчитать вероятность броска костей?
• Когда использовать калькулятор вероятности игры в кости?
• Играть или пасовать? — Давай сыграем в игру!
• Часто задаваемые вопросы

Калькулятор вероятности броска кости является отличным инструментом, если вы хотите оценить вероятность броска броска кости по многочисленным вариантам . В набор входит множество различных многогранных кубиков, так что вы можете исследовать вероятность выпадения 20-гранного кубика и обычного кубического кубика.

Итак, просто оценивайте шансы и играйте! Вы также найдете краткие описания каждой опции в тексте.

🔎 У тебя нет физических кубиков? Нет проблем — попробуйте наш калькулятор игры в кости!

Многогранный кубик

Все знают, что такое обычный 6-гранный кубик, и, скорее всего, многие из вас уже сыграли тысячи игр, в которых использовалась одна (или более) t Но знаете ли вы, что существует

различных типа штампа ? Из бесчисленных возможностей самые популярные кости включены в Набор игральных костей Dungeons & Dragons , который содержит семь различных многогранных игральных костей:

• Четырехгранные игральные кости , также известные как тетраэдр — каждая грань представляет собой равносторонний треугольник;
• 6-гранный кубик , классический кубик — каждая грань квадратная;
• 8-гранный кубик , также известный как октаэдр — каждая грань представляет собой равносторонний треугольник;
• 10-гранный кубик , также известный как пятиугольный трапецоэдр — каждая грань — воздушный змей;
• 12-гранная игральная кость , также известная как додекаэдр — каждая грань представляет собой правильный пятиугольник; и
• 20-гранный кубик , также известный как икосаэдр — каждая грань представляет собой равносторонний треугольник.

💡 Вы можете отточить свою стратегию D&D, используя калькулятор покупки очков Omni 5e.

Не волнуйтесь, мы учитываем каждый из этих кубиков в нашем калькуляторе вероятности. Вы можете выбрать то, что вам нравится, и, например, притвориться, что бросаете сразу пять 20-гранных кубиков!

Как рассчитать вероятность броска кубиков?

Что ж, вопрос сложнее, чем кажется на первый взгляд, но вскоре вы убедитесь, что ответ не так уж и страшен! Все дело в математике и статистике.

Прежде всего, мы должны определить

какую вероятность броска костей мы хотим найти . Мы можем выделить несколько, которые вы можете увидеть в этом калькуляторе вероятности игры в кости.

Прежде чем приступать к каким-либо вычислениям, давайте определим некоторые переменные, которые мы будем использовать в формулах. n – количество игральных костей, s – количество отдельных граней кости, p – вероятность выпадения любого значения с кости, а P – общая вероятность решения задачи. Существует простое соотношение — p = 1/s , поэтому вероятность выпадения 7 на 10-гранном кубике в два раза больше, чем на 20-гранном кубике.

1. Вероятность выпадения одного и того же значения на каждом кубике – при этом шанс выпадения определенного значения на одном кубике равен

   p , нам нужно только умножить эту вероятность на саму себя столько раз, сколько игральных костей. Другими словами, вероятность P равна p в степени n , или P = pⁿ = (1/s)ⁿ . Если мы рассмотрим три 20-гранных игральных кубика, вероятность выпадения 15 на каждом из них составит: P = (1/20)³ = 0,000125 (или P = 1,25·10⁻⁴ в экспоненциальной записи). И если вы заинтересованы в броске набора из любых одинаковых значений, просто умножьте результат на общее количество граней кости: P = 0,000125 · 20 = 0,0025 .

2. Вероятность выпадения всех значений, равных или превышающих y – задача аналогична предыдущей, но на этот раз p равна

   1/с , умноженная на все возможности, удовлетворяющие начальному условию . Например, допустим, у нас есть обычный кубик и y = 3 . Мы хотим, чтобы прокатанное значение было либо 6 , 5 , 4 , либо 3 . Тогда переменная p равна 4 · 1/6 = 2/3 , а окончательная вероятность равна P = (2/3)ⁿ .

3. Вероятность выпадения всех значений, равных или меньших y — этот вариант почти такой же, как и предыдущий, но на этот раз нас интересуют только числа, равные или меньшие нашей цели. Если мы возьмем одинаковые условия ( s=6 , y=3 ) и применим их в этом примере, мы увидим, что значения 1 , 2 , & 3 удовлетворяют правилам, и вероятность равна: P = (3 · 1/6)ⁿ = (1/2)ⁿ .

4. Вероятность выпадения ровно X одинаковых значений (равных y ) из набора — представьте, что у вас есть набор из семи 12-гранных игральных костей, и вы хотите узнать вероятность выпадения ровно двух 9с . Это как-то отличается от того, что было раньше, потому что только часть всего набора должна соответствовать условиям . Здесь на помощь приходит биномиальная вероятность. Формула биномиальной вероятности:

   P(X=r) = nCr · pʳ · (1-p)ⁿ⁻ʳ ,

   , где r — количество успехов, а nCr — количество комбинаций (также известное как « n выбрать r »).

   В нашем примере мы имеем n = 7 , p = 1/12 , r = 2 , nCr = 21 , поэтому окончательный результат: P(X=2) = 21 · (1 /12)² · (11/12)⁵ = 0,09439 или P(X=2) = 9,439% в процентах.

🙋 Более подробную информацию по этой теме вы можете найти в нашем калькуляторе биномиального распределения.

5. Вероятность выпадения как минимум X одинаковых значений (равных y ) из набора — задача очень похожа на предыдущую, но на этот раз результатом является сумма вероятностей для X =2,3,4,5,6,7 . Переходя к числам, мы имеем: P = P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) = 0,11006 = 11,006% . Как и следовало ожидать, результат немного выше. Иногда точная формулировка проблемы увеличивает ваши шансы на успех.

6. Вероятность выпадения точной суммы r из набора n s гранных игральных костей — общая формула довольно сложна:

P(r,n,s)=1sn∑k=0⌊(r−n)/s⌋(−1)k(nk)(r−s⋅k−1n−1)\scriptsize \начать{разделить} P (r, n, s) = \ frac {1} {s ^ n} \ sum ^ {\ lfloor (rn) / s \ rfloor} _ {k = 0} (-1) ^ k & \ binom {n} {k}\\ &\binom{r\!-s\!\cdot\!k\!-\!1}{n\!-\!1} \end{split}P(r,n,s)=sn1​k=0∑⌊(r−n)/s⌋​(−1)k​(kn​)(n−1r−s⋅k−1 ​)​

Однако мы также можем попробовать решить эту проблему вручную. Один из подходов состоит в том, чтобы найти общее количество возможных сумм. С парой обычных игральных костей мы можем получить 2,3,4,5,6,7,8,9,10,11,12 , но эти результаты не эквивалентны !

Взгляните; Есть только один способ получить 2 : 1+1 , но для 4 есть три различных возможностей: 1+3 , 2+2 , 3+1 и для 12 есть, опять же, только один вариант: 6+6 . Оказывается, 7 — наиболее вероятный результат с шестью вариантами: 1+6 , 2+5 , 3+4 , 4+3 , 5+2 и 902. 04 6+ 1 . Количество перестановок с повторениями в этом наборе равно 36 . Наш калькулятор перестановок может быть полезен для поиска перестановок для других типов игральных костей. Мы можем оценить вероятности как отношение благоприятных исходов ко всем возможным исходам: P(2) = 1/36 , P(4) = 3/36 = 1/12 , P(12) = 1/36 , P(7) = 6/36 = 1/6 .

Чем больше игральных костей, тем ближе функция распределения сумм к нормальному распределению. Как и следовало ожидать, по мере увеличения количества игральных костей и граней все больше времени уходит на оценку результата на листе бумаги. К счастью, это не относится к нашему калькулятору вероятности игры в кости!

7. Вероятность выпадения суммы из множества, не ниже X — как и в предыдущей задаче, нужно найти все результаты, соответствующие начальному условию, и разделить их на количество всех возможностей. Учитывая набор из трех десятигранных игральных костей, мы хотим получить сумму, по крайней мере равную 27 . Как мы видим, мы должны сложить все перестановки для 27 , 28 , 29 и 30 , то есть 10, 6, 3 и 1 соответственно. Всего из 1000 возможностей 20 хороших исходов, поэтому конечная вероятность: P(X ≥ 27) = 20/1000 = 0,02 .

8. Вероятность выпадения суммы из множества, не выше X — процедура точно такая же, как и в предыдущей задаче, но складывать нужно только суммы меньше или равные заданной. Имея тот же набор костей, что и выше, какова вероятность того, что выпадет не более 26 ? Если бы вы делали это шаг за шагом, потребовались бы годы, чтобы получить результат (суммировать все 26 сумм). Но, если подумать, мы только что вычислили дополнительное событие в предыдущей задаче. Суммарная вероятность дополнительных событий точно равна 1 , поэтому вероятность здесь равна: P(X ≤ 26) = 1 — 0,02 = 0,98 .

Когда использовать калькулятор вероятности игры в кости?

Существует множество настольных игр, в которых вы по очереди бросаете кости (или игральные кости), а результаты могут использоваться в различных контекстах. Допустим, вы играете в Dungeons & Dragons и атакуете. Класс брони вашего противника 17 . Вы бросаете 20-гранный кубик, надеясь, что выпадет как минимум 15 с вашим модификатором +2. Этого должно быть достаточно. При этих условиях вероятность успешной атаки равна 0,30 . Если вы знаете шансы на успешную атаку, вы можете выбрать, хотите ли вы атаковать эту цель или выбрать другую с лучшими шансами.

Или, может быть, вы играете в Поселенцы Катана и надеетесь, что на двух шестигранных кубиках выпадет ровно 8 , так как этот результат принесет вам драгоценные ресурсы. Просто воспользуйтесь нашим калькулятором вероятности в костях, и вы увидите, что вероятность составляет около 0,14 – вам лучше повезти на этом ходу!

Играть или пасовать? — Давай сыграем в игру!

Существуют различные виды игр, например, лотереи, где ваша задача состоит в том, чтобы сделать ставку в зависимости от шансов. Бросание игральных костей является одним из них. Хотя некоторые риски неизбежны, вы можете выбрать наиболее выгодный вариант и максимизировать свои шансы на победу. Взгляните на этот пример.

Представьте, что вы играете в игру, в которой у вас есть один из трех вариантов на выбор , а именно:

• Сумма пяти десятигранных костей не меньше 30 ;
• Сумма пяти 12-гранных игральных костей не превышает 28 ;
• Сумма пяти 20-гранных костей не меньше 59 .

Вы выиграете, только если выпадет выбранный вами вариант. Вы также можете отказаться, если чувствуете, что ничего из этого не произойдет. Интуитивно трудно оценить наиболее вероятный успех, но с нашим калькулятором вероятности в костях для оценки всех вероятностей требуется всего лишь мгновение ока.

Полученные значения:

• P₁ = 0,38125 для 10-гранной кости;
• P₂ = 0,3072 для 12-гранной кости; и
• P₃ = 0,3256 для 20-гранной кости.

Вероятность успешного прохода равна произведению дополнительных событий остальных вариантов:

• P₄ = (1-P₁) · (1-P₂) · (1-P₃) = 0,61875 · 0,6928 · 0,6744 = 0,2891 .

Мы видим, что самый благоприятный вариант — первый, а прохождение — наименее вероятное событие. Мы не можем гарантировать, что вы всегда будете выигрывать, но мы настоятельно рекомендуем вам выбрать для игры 10-гранный набор костей.

Часто задаваемые вопросы

Что такое вероятность?

Вероятность определяет, насколько вероятны определенные события . Простая формула для вероятности: число желаемых исходов/количество возможных исходов . В настольных играх или азартных играх вероятность выпадения костей используется для определения вероятности выпадения определенного числа , например, какова вероятность получения определенного числа одним кубиком?

Сколько возможных исходов может быть при бросании двух игральных костей?

Есть 36 исходов при бросании двух игральных костей . Для одной кости имеется шесть граней, и для любого броска существует шесть возможных исходов . Для две кости , вы должны перемножить количество возможных исходов вместе, чтобы получить 6 × 6 = 36 . При последующих бросаниях просто умножьте результат на 6 . Если вы используете игральные кости другой формы, вместо 6 введите число их граней .

Какова вероятность того, что при броске 2 игральных костей выпадет 7?

Это 1/6 или 0,1666667 . Предположим, что всего 7 встречается хотя бы один раз . Для 2 игральных костей имеется 6 способов бросить сумму 7 — (1,6), (2,5), (3,4), (4,3), (5,2), (6 ,1) . Общее количество комбинаций для пары кубиков равно 36 . Таким образом, вероятность суммирования до 7 равна 6/36 = 1/6 = 0,1666667 .

Сколько раз я выбрасываю 5 на паре игральных костей?

20 . Предположим, что пару игральных костей бросают 180 раз .