Логические игры по математике: 30 математических головоломок для проверки вашего ума (с ответами)

Логические задачи по математике

Старик, имевший трёх сыновей, распорядился,
чтобы они после его смерти поделили принадлежавшее ему стадо верблюдов так,
чтобы старший взял половину всех верблюдов,
средний — треть и младший — девятую часть всех верблюдов.
Старик умер и оставил 17 верблюдов.
Сыновья начали делёж, но оказалось, что число 17 не делится ни на 2, ни на 3, ни на 9.
В недоумении, как им быть, братья обратились к мудрецу.
Тот приехал к ним на собственном верблюде и разделил 17 верблюдов по завещанию.
Как он это сделал?

Ответ: Мудрец пустился на уловку. Он прибавил к стаду на время своего верблюда, тогда их стало 18. Разделив это число, как сказано в завещании (старший брат получил 18 х 1/2 = 9 верблюдов, средний 18 х 1/3 = 6 верблюдов, младший 18 х 1/9 = 2 верблюда), мудрец взял своего верблюда обратно (9 + 6 + 2 + 1 = 18). Секрет заключается в том, что части, на которые по завещанию должны были делить стадо сыновья, в сумме не составляют 1.

Действительно, 1/2 + 1/3 + 1/9 = 17/18.
—————————
Как разделить 5 яблок между пятью детьми так,
чтобы каждый получил по яблоку и одно яблоко осталось в корзине?

Ответ: Один ребенок берет яблоко вместе с корзиной.
—————————
Мул и ишак, груженные мешками, идут рядом.
Мул говорит ишаку: «Я потащу вдвое больше тебя, если возьму у тебя мешок.
А если ты возьмёшь мой мешок, то мы оба понесём поровну».
Сколько мешков несёт каждое животное?

Ответ: Мул несёт 7 мешков, ишак только 5.
—————————
Белка, делая запасы на зиму, наткнулась на большую кучу орехов.
Она трудилась три ночи, заполняя орехами своё гнездо.
Сколько орехов исчезло из кучи, если в первую ночь белка унесла вдвое меньше орехов,
чем в обе последующие (вместе взятые),
а в последнюю — на один орех меньше, чем в обе предыдущие?

Ответ: На 9 орехов. В первую ночь — 3, во вторую — 2, в третью — 4

—————————
В комнате четыре угла. В каждом углу сидит по кошке. Напротив каждой кошки по три кошки.
На хвосте каждой кошки по одной кошке. Сколько же кошек в комнате?

Ответ: В комнате всего четыре кошки.
—————————
Кот Васька спит, а во сне видит, что его окружили двенадцать серых мышей и одна белая.
Слышится Ваське во сне голос: «Ты должен съедать каждую тринадцатую мышку, считая все время в одном направлении, так, чтобы последней была съедена белая мышь».
Задумался Васька: с какой же мышки начинать?
Помогите коту решить задачу.

Ответ: Начинать счёт следует с шестой мыши, считая по ходу часовой стрелки от белой мыши (её не считая). Чтобы установить, с какой мыши начинать счёт, нарисуйте на кругу 12 точек и один крестик и начните с него счёт. Вычёркивайте каждую точку и крестик, когда до него дойдёт очередь. Делайте так до тех пор, пока не останется одна точка. Замените её белой мышью, а крестик укажет, с какой серой мыши начинать.

—————————
Ваня имеет столько же братьев, сколько и сестёр, а у его сестры вдвое меньше сестёр, чем братьев. Сколько сестёр и сколько братьев в той семье?

Ответ: 3 сестры и 4 брата.
—————————
Ваня наблюдает за утками, плавающими в деревенском пруду.
Одна утка плывёт перед двумя утками,
другая утка плывёт между двумя утками, и одна утка плывёт за двумя утками.
«Так много уток никогда ещё не было у нас в деревенском пруду», — думает Ваня.
Сколько уток видит Ваня?

Ответ: Мальчик видит в пруду 3 уток.
—————————
Сошлись два пастуха, Иван и Пётр. Иван и говорит Петру:
«Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!»

А Пётр ему отвечает: «Нет! Лучше ты мне отдай одну овцу тогда у нас будет овец поровну!»
Сколько было у каждого овец?

Ответ: Ясно, что овец больше у Ивана. Но на сколько у него больше, чем у Петра? Если Иван отдаст одну овцу не Петру, а кому-либо другому, то станет ли у обоих пастухов овец поровну? Нет, потому что поровну у них было бы только в том случае, если бы эту овцу получил Пётр. Значит, если Иван отдаёт одну овцу не Петру, а третьему лицу, то у него всё-таки будет больше овец, чем у Петра, но на сколько больше? Ясно, что на одну овцу, потому что если прибавить теперь к стаду Петра одну овцу, то у обоих станет поровну. Отсюда следует, что, пока Иван не отдаст никому ни одной своей овцы, у него в стаде на две овцы больше, чем у Петра. Теперь примемся за Петра. У него, как мы нашли, на две овцы меньше, чем у Ивана. Значит, если Пётр отдаст, скажем, одну свою овцу не Ивану, а кому-либо иному, то тогда у Ивана будет на три овцы больше, чем у Петра. Но пусть эту овцу получит именно Иван, а не третье лицо. Ясно, что тогда у него будет на четыре овцы больше, чем осталось у Петра. Но задача говорит, что у Ивана в этом случае будет ровно вдвое больше овец, чем у Петра. Значит, четыре и есть именно то число овец, которое останется у Петра, если он отдаст одну овцу Ивану, у которого будет восемь овец. А до предполагаемой отдачи, значит, у Ивана было 7, а у Петра 5 овец.

Дальше:    задачи на логику по математике >>>

Логические задачи по математике для 2 класс — задания на логику для 2 класса

Зачем второкласснику развивать логическое мышление?

Чтобы успешно реализовывать себя в жизни

Критическое мышление, умение правильно задавать вопросы, с удовольствием учиться новому и использовать полученные знания пригодится не только в будущей профессии, но и в жизни.

Грамотно мыслить, рассуждать и делать выводы

А ещё сравнивать, анализировать и выстраивать причинно-следственные связи — умения, которые необходимы каждому в течение всей жизни, в любой области знаний.

Различать правду и ложь

Логическое мышление помогает не только отыскивать ответы на свои вопросы в море информации, но и отделять главное от второстепенного, сопоставлять факты и отличать правду от вымысла.

Находить неординарные способы решения задач

Креативность, без преувеличения, — одно из важнейших качеств современного человека. Её можно и нужно развивать, и чем раньше начать это делать, тем эффективнее будет результат.

Как развивать логическое мышление ребенка во 2 классе?

Подвергай все сомнению

Важно не только научиться отделять правду ото лжи. На пути к этому есть и другие задачи: уметь анализировать информацию, различать факты и мнения, выстраивать причинно-следственные связи.

Связь логики и воображения

Воображение — важная составляющая в развитии логики. Ассоциации, данетки, поиск аналогов (нахождение похожих вещей по разным признакам) и новых применений обычным предметам — дети очень любят подобные логические игры.

«Нешуточные» задачки

Или, как их ещё называют, задачки с подвохом — отличный способ развития критического мышления. На первый взгляд кажется, что это только развлечение. На самом деле, такие задачи требуют творческого подхода и смены привычного алгоритма решения.

Примеры заданий на логику для 2 класса

Задача 1

Три друга — Шпагин, Мячиков и Нырялкин — занимаются в спортивных секциях. Один занимается фехтованием, второй — футболом, третий — плаванием. Известно, что фамилии друзей не совпадают с их увлечениями, а Нырялкин боится мяча.
Каким спортом занимается каждый из ребят?

Решить задачу

Задача 2

Степан, Ермолай, Аветик, Игорь и Виталик живут на разных этажах пятиэтажного дома. Известно, что Степан живёт выше Ермолая, но ниже Виталия. Аветик и Виталий живут не на соседних этажах. А Игорь не живёт на соседних этажах ни со Степаном, ни с Аветиком, ни с Виталием.
Кто из ребят живёт на пятом, а кто на первом этажах?

Решить задачу

Задача 3

Семья Шариковых (мама, папа, Полиграф и его младшая сестра Меланья) села за праздничный стол.
Сегодня мама приготовила гамбургеры, винегрет, торт «Наполеон» и картошку фри. Известно, что мама не ела картошку, а Полиграф ненавидит свёклу. Дети съели по гамбургеру и по куску «Наполеона», а папа с Полиграфом разделили между собой всю картошку фри.
Кто из семьи Шариков мог попробовать все праздничные блюда за этим столом?

Решить задачу

Решать задачи на логику для учеников 2 класса

Познакомьтесь с форматом курса «Математическое мышление». Пройдите сюжетную игру и решите три задачи на логику!

Решать задачи

Решать задачи

В Умназии дети развивают мышление в игровой форме, решая увлекательные сюжетные задачи по математике

Продуманная программа

Курсы математического мышления разработаны на базе множества источников, экспертизы методистов и педагогов, разделены на 10 тем с теорией и игровыми заданиями с объяснением

Увлекательные задания

Второклассник решает сюжетные игровые задачи по математике для изучения новых тем и закрепления пройденного по каждому курсу. Никакой скуки! Ни одно задание не повторяется!

Дипломы и награды

В конце каждого курса математической логики ребенок решает тест или проходит игру, получая сертификат в случае успешного выполнения. Вы будете уверены в его знаниях!

Развитие логического мышления во 2 классе

Возраст 8-9 лет — период формирования критического мышления. Ребенок многое ставит под сомнение, учится анализировать информацию, сопоставляет факты, составляет собственное мнение на основе изученного.

Существует большое количество игр и заданий на развитие критического мышления. В их числе: ТРИЗы (логические задачи, ответы на которые можно найти, задавая вопросы на «да» и «нет»), ассоциации и их разновидности (например, «Простые рисунки» — найти, что спрятано в рисунках из хаотичных линий) и другие задания на пересечении логики и воображения.

Купите курс математики для детей со скидкой 40 % уже сейчас

Решение задач с помощью логических игр

Детский сад

1 класс

2 класс

3 класс

4 класс

5 класс

6 класс

Решение задач с помощью логических игр

Знаете ли вы, что на Math Playground есть более 125 логических игр, которые помогут вам в изучении математики? Эти игры наполнены возможностями обучения, которые необходимы для развития широкого спектра навыков мышления. В наших логических играх представлены сценарии решения задач, которые помогают учащимся приобрести опыт в распознавании образов, аналитическом мышлении и других важных навыках решения задач.

Веселые игры, серьезные результаты

Тщательно продуманные задачи лежат в основе наших логических игр. Эти веселые, красочные головоломки предлагают гораздо больше, чем развлекательные задачи. Они дают учащимся возможность применять логическое мышление, развивать навыки пространственного мышления, планировать заранее и визуализировать стратегические ходы. Особенно важны навыки пространственного мышления. Задания на пространственное мышление являются инклюзивными и предлагают учащимся всех способностей рассуждать математически.

Исследуя игровую среду, учащиеся анализируют причинно-следственные ситуации и применяют стратегии проб и ошибок. Они собирают данные и принимают решения. Они могут даже рассуждать о числах. Когда учащиеся играют в наши логические игры, они участвуют в тех же процессах, что и математики, когда сталкиваются с новой проблемой, которую необходимо решить. Логическое мышление является важным навыком решения задач, необходимым для математического мышления, и мы, как учителя, должны помогать учащимся развивать этот набор навыков в классе.

Jelly Slice combines math and logic

Top 10 Problem Solving Skills

Sequential Reasoning
Creative Thinking
Spatial Reasoning
Computational Thinking
Geometric Thinking
Planning Strategies
Perseverance
Trial and Error
Testing Ideas
Analyzing Outcomes

Начало работы с логическими играми

Все логические игры на Math Playground организованы по классам. Лучший способ найти логические игры, подходящие для вашего возраста, — это посетить страницу своего уровня. Выберите игру и сыграйте пару уровней. Обратите внимание на тип используемого рассуждения. Вы можете спроецировать игру на доску и пригласить к участию весь класс. Позже вы можете предложить учащимся пройти игру самостоятельно. Продлите обучение, попросив учеников написать об игре. Им понравилось? Почему или почему нет? Как бы они сделали это веселее? Творческие учащиеся могут вдохновиться на разработку собственных игр. Возможности безграничны. В свободное время предложите учащимся изучить другие типы логических игр на Math Playground. У нас есть самые разные игровые темы, от приключений животных до исследования космоса. Все они имеют одну общую черту. Наши игры делают обучение веселым!

Попробуйте свои любимые логические игры:
Возвращение красного блока
Обрушение лабиринта
Логические магниты
Zippy Boxes
Jelly Slice

Логические головоломки | Brilliant Math & Science Wiki

Энди Хейс, Хуа Чжи Ви, Чимин Хим, и

способствовал

Содержимое

• Силлогизмы
• Сетки исключения
• Правдивцы и лжецы
• Криптограммы
• Арифметические головоломки
• Головоломка с переходом через реку
• Тур Пазлы
• Нонограммы
• Морские головоломки
• судоку
• Шахматные головоломки
• K-уровень мышления
• Другие головоломки

Основная статья: Пропозициональная логика

См. также: Логика предикатов

Один из простейших типов логических головоломок — силлогизм . В этом типе головоломки вам дается набор утверждений, и вы должны определить некоторую истину из этих утверждений. Эти типы головоломок часто можно решить, применяя принципы логики высказываний и логики предикатов. Следующий силлогизм принадлежит Чарльзу Лютвиджу Доджсону, более известному под псевдонимом Льюис Кэрролл.

У меня есть блюдо из картофеля. Верны следующие утверждения:

• Моя картошка, новая, не вареная.
• Весь мой картофель в этом блюде можно есть.
• Мой невареный картофель нельзя есть.

В этом блюде есть молодой картофель?

---

Первое и третье утверждения могут быть связаны транзитивным аргументом. Весь молодой картофель невареный, а невареный картофель непригоден для еды, поэтому молодой картофель не годится для еды.

Второе утверждение может быть выражено как эквивалентное противопоставление. Весь картофель в блюде годен для еды; если есть картофель, который нельзя есть, значит, его нет в блюде.

Затем снова применяется транзитивный аргумент. Молодой картофель не годится для еды, а несъедобного картофеля в тарелке нет. Таким образом, молодой картошки в блюде нет. \(_\квадрат\)

а) б) в) г)

Ниже приведены три утверждения, за которыми следуют три вывода. Примите три утверждения за истину, даже если они отличаются от общеизвестных фактов. Прочитайте утверждения и решите, какие выводы логически следуют из утверждений.

Заявления:
1. Все актеры — музыканты.
2. Ни один музыкант не является певцом.
3. Некоторые певцы умеют танцевать.

Выводы:
1. Некоторые актеры поют.
2. Некоторые танцоры — актеры.
3. Ни один актер не является певцом.

Варианты ответа:
а) Далее следует только вывод 1.
б) Далее следует только вывод 2.
в) Далее следует только вывод 3.
г) следует не менее 2 выводов.

Основная статья: Сетки на выбывание

Некоторые логические головоломки требуют, чтобы вы определили правильные пары для наборов объектов. Эти головоломки часто можно решить с помощью процесса исключения, и сетка исключения является эффективным инструментом для применения этого процесса.

Пример сетки исключений

Сетки исключений выровнены таким образом, что каждая строка представляет объект в наборе, а каждый столбец представляет объект, который должен быть соединен с объектом из этого набора. Флажки и метки X используются, чтобы показать, какие объекты являются парными, а какие нет.

младший ребенок третий ребенок второй ребенок старший ребенок

У мистера и миссис Тан четверо детей — три мальчика и девочка —
, каждому из которых нравится один из цветов — синий, зеленый, красный, желтый —
и одна из букв — P, Q , R, S.

1. Старшему ребенку нравится буква Q.
2. Младший ребенок любит зеленый цвет.
3. Альфреду нравится буква S.
4. У Бренды есть старший брат, которому нравится Р.
5. Тот, кто любит синий, не самый старый.
6. Тому, кто любит красный цвет, нравится буква П.
7. Чарльз любит желтый цвет.

Исходя из вышеизложенного, Дариус является \(\text{__________}.\)

Основная статья: Правдивцы и лжецы

Разновидностью головоломок на выбывание является головоломка о правде и лжеце , также известная как головоломка о рыцарях и лжецах . В этом типе головоломки вам дается набор людей и их соответствующие утверждения, и вам также говорят, что некоторые люди всегда говорят правду, а некоторые всегда лгут. Цель головоломки состоит в том, чтобы вывести истину из данных утверждений. 9Эти типы головоломок популяризировал математик \text{th}\) века Рэймонд Смаллян.

Только у А есть сокровище A и C имеют сокровище Только у B есть сокровище B и C имеют сокровище Только у C есть сокровище Во всех сундуках есть сокровища A и B имеют сокровище

Вы находитесь в комнате с тремя сундуками. Вы знаете, что по крайней мере в одном из них есть сокровища, а если в сундуке нет сокровищ, значит, он содержит смертельный яд.

В каждом сундуке есть сообщение, но все сообщения врут .

• Левый сундук: «В среднем сундуке сокровища».
• Средний сундук: «Во всех этих сундуках есть сокровища.»
• Правый сундук: «Только в одном из этих сундуков есть сокровища.»

В каких сундуках есть сокровища?

A — рыцарь, а B — лжец А — лжец, а Б — рыцарь Оба они лжецы Оба они рыцари

Есть два человека, A и B , каждый из которых либо рыцарь, либо лжец.

А говорит: «По крайней мере, один из нас — лжец».

Что такое A и B ?

\(\)
Детали и предположения:

• Рыцарь всегда говорит правду.
• Мошенник всегда лжет.

Основная статья: Криптограммы

Криптограмма — это головоломка, в которой числовые цифры в числовом предложении заменены символами, и цель головоломки — определить значения этих символов.

\[ \begin{массив} { l l l l l }
& & P & P & Q \\ & &P & Q & Q \\ + && Q & Q & Q \\ \hline & & 8 & 7 & 6 \\ \конец{массив} \]

В приведенной выше сумме \(P\) и \(Q\) представляют собой цифры. Каково значение \(P+Q\)?

\[ \overline{EVE} \div \overline{DID} = 0. \overline{TALKTALKTALKTALK\ldots} \]

Учитывая, что \(E,V,D,I,T,A,L\) и \(K \) — различные одиночные цифры, пусть \(\overline{EVE} \) и \(\overline{DID} \) — два взаимно простых трехзначных положительных целых чисел и \(\overline{TALK} \) быть 4-значным целым числом, таким, что приведенное выше уравнение верно, где правая часть представляет собой повторяющееся десятичное число.

Найдите значение суммы \( \overline{EVE} + \overline{DID} + \overline{TALK} \).

Основные статьи: заполнение пробелов и поиск оператора

Арифметические головоломки содержат ряд чисел, операций и пробелов по порядку, и цель головоломки состоит в том, чтобы заполнить пробелы для получения желаемого результата.

\[\huge{\Box \times \Box \Box = \Box \Box \Box}\]

Заполните поля выше цифрами \(1,2,3,4,5,6\), без повторяющихся цифр, так что уравнение верно.

Введите ответ, соединив все цифры в порядке их появления. Например, если ответ \(1 \times 23 = 456\), введите \(123456\) в качестве окончательного ответа.

Также попробуйте родственную задачу.

\[ \БОЛЬШОЙ{\begin{eqnarray} \ в коробке {\ phantom0} \; + \; \ в коробке {\ phantom0} \; «=» \ в коробке {\ phantom0} \\ \ в коробке {\ phantom0} \; — \; \ в коробке {\ phantom0} \; «=» \ в коробке {\ phantom0} \\ \ в коробке {\ phantom0} \; \раз\; \ в коробке {\ фантом0} \; «=» \ в коробке {\ phantom0} \\ \ в коробке {\ phantom0} \; \дел\; \ в коробке {\ phantom0} \; «=» \ в коробке {\ phantom0} \\ \end{eqnarray}} \]

Поместите одно из целых чисел \(1, 2, \ldots , 13\) в каждую из ячеек так, чтобы двенадцать из этих чисел использовались по одному разу для каждой (а одно число вообще не использовалось) и все четыре уравнения верны.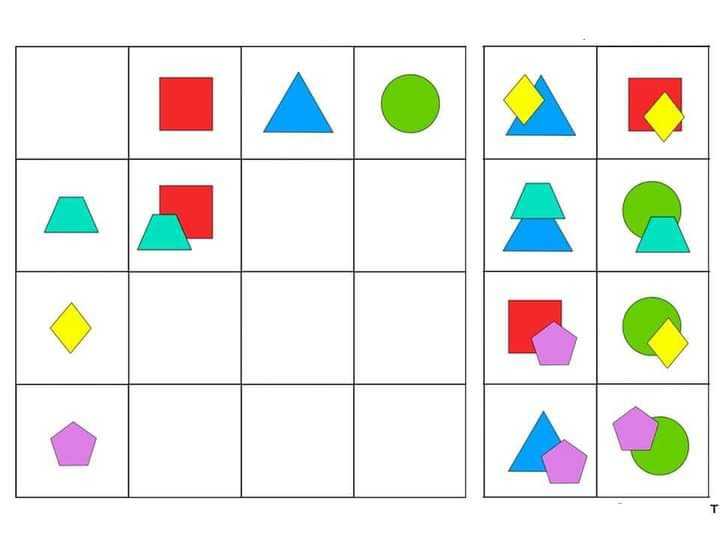

Какова сумма всех возможных значений пропущенного (неиспользованного) числа?

Основная статья: Головоломки с переходом через реку

В головоломке о переходе через реку цель состоит в том, чтобы найти способ переместить группу людей или объектов через реку (или какое-либо другое препятствие) и сделать это за наименьшее количество шагов или количество времени.

Известная задача о переходе через реку — это задача Ричарда Ховассе о мосте и факеле , написанная ниже.

Ночью к реке приходят четыре человека. Есть узкий мост, но он может вместить только двух человек одновременно. У них есть один фонарик, а так как сейчас ночь, фонарик приходится использовать при пересечении моста. Человек A может пересечь мост за одну минуту, B за две минуты, C за пять минут и D за восемь минут. Когда два человека пересекают мост вместе, они должны двигаться со скоростью более медленного человека. Вопрос в том, смогут ли они все перейти мост за 15 минут или меньше?

---

Предположим, что решение минимизирует общее количество крестиков. Это дает в общей сложности пять скрещиваний — три парных скрещивания и два одиночных скрещивания. Кроме того, предположим, что мы всегда выбираем самых быстрых для одиночного кросса.

Во-первых, мы показываем, что если два самых медленных человека (C и D) пересекают дорогу по отдельности, их общее время перехода равно 15. Для этого нужно взять людей A, C, D: D+A+C+A = 8+ 1+5+1=15. (Здесь мы используем A, потому что мы знаем, что использование A для пересечения C и D по отдельности является наиболее эффективным.) Но время истекло, а люди A и B все еще находятся на начальной стороне моста и должны перейти. Таким образом, два самых медленных (C и D) не могут пересекаться по отдельности.

Во-вторых, мы показываем, что для того, чтобы C и D пересеклись вместе, они должны пересечься на второй паре перекрестков: т. е. не C или D, поэтому A и B должны пересечься вместе первыми. Помните наше первоначальное предположение о том, что мы должны свести к минимуму пересечения, поэтому у нас есть пять пересечений — 3 парных пересечения и 2 одиночных пересечения. Предположим, что C и D пересекаются первыми. Но затем C или D должны вернуться, чтобы переместить факел на другую сторону, поэтому тот, кто пересек дорогу в одиночку, должен пересечь снова. Следовательно, они будут пересекаться отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечь дорогу раньше, иначе на стартовой стороне было бы всего три человека. Таким образом, поскольку есть только три варианта парного пересечения, а C и D не могут пересечься первым или последним, они должны пересечься вместе во втором, или среднем, парном пересечении.

Собирая все это вместе, A и B должны пересечься первыми, поскольку мы знаем, что C и D не могут, и мы минимизируем пересечения. Затем A должен пересечься следующим, так как мы предполагаем, что должны выбрать самого быстрого, чтобы совершить одиночное пересечение. Тогда мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны уйти. Затем мы решаем отправить назад самого быстрого, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься последней парой. Это дает нам B+A+D+B+B = 2+1+8+2+2 = 15.

Все четыре человека могут перейти через 15 минут. \(_\квадрат\)

Основная статья: Тур Пазлы

См. также: Путь Эйлера

В головоломке Tour цель состоит в том, чтобы определить правильный путь для объекта, чтобы пересечь график. Эти виды головоломок могут принимать несколько форм: шахматные туры, обходы лабиринта, эйлеровы пути и другие.

Найдите путь, ведущий от звезды в центре обратно к звезде в центре. Пути могут идти только в направлении стрелки.

Изображение предоставлено: Эрик Фиск

---

Путь решения обведен красным ниже.

Определите путь через приведенный ниже граф так, чтобы каждое ребро было пройдено ровно один раз .

---

Есть несколько возможных решений. Одно из возможных решений показано ниже, где ребра отмечены в порядке их пересечения.

Шахматный тур — интересная головоломка сама по себе, подробное описание которой приведено ниже.

Основная статья: Нонограммы

нонограмма — это головоломка на основе сетки, в которой рядом с прямоугольной сеткой дается ряд числовых подсказок. Когда головоломка собрана, в сетке формируется картинка.

Головоломка начинается с ряда чисел слева и над сеткой. Каждое из этих чисел представляет собой последовательную серию заштрихованных пробелов в соответствующей строке или столбце. Каждый последующий запуск отделяется от других запусков хотя бы одним пустым пространством. Головоломка завершена, когда все числа были удовлетворены. Основным методом решения этих головоломок является процесс исключения. Если головоломка составлена ​​правильно, никаких догадок не требуется.

Заполните нонограмму:

---

Одной из многих логических головоломок является головоломка «Морской бой» (иногда называемая «Бимару», «Юботу», «Морские корабли-пасьянсы» или «Солитер-морской бой»). Головоломка основана на игре Морской бой.

Пасьянс «Морской бой» был изобретен Хайме Пониачиком в Аргентине и впервые был опубликован в журнале Humor & Juegos.

Это пример решенной головоломки Морской бой. Головоломка состоит из маленьких квадратов 10 × 10, которые содержат следующее:

• 1 линкор 4 квадрата длиной
• 2 крейсера по 3 квадрата каждый
• 3 эсминцы 2 квадрата каждый
• 4 подводные лодки по 1 квадрату каждая.

Их можно ставить горизонтально или вертикально, но никогда по диагонали. Лодки размещены так, чтобы ни одна из лодок не касалась друг друга даже вертикально. Цифры рядом со строкой/столбцом обозначают количество клеток, занятых в строке/столбце соответственно. ⬤ указывает на подводную лодку, а ⬛ указывает на корпус корабля, а полукруги указывают на начало/конец корабля.

Цель игры — заполнить сетку водой или кораблями.

Основная статья: Судоку

A судоку головоломка на \(9\times 9\) сетка, в которой каждая строка, столбец и меньшая квадратная часть содержат каждую из цифр от 1 до 9, каждая не более одного раза. Каждая головоломка начинается с заполнения некоторых мест в сетке. Цель состоит в том, чтобы заполнить оставшиеся места в головоломке. Головоломка решается в основном через процесс исключения. Для решения не требуется никаких догадок, и для любой заданной головоломки должно быть только одно решение.

Решите головоломку судоку:

Головоломка, созданная генератором судоку Open Sky

---

Каждая строка должна содержать каждую из цифр от 1 до 9 ровно один раз. То же самое верно для столбцов и меньших квадратов \(3\x 3\).

Основная статья: Шахматные головоломки

См. также: Сокращенные партии, дебютные стратегии и ладейные стратегии

Шахматные головоломки основаны на правилах игры в шахматы и требуют от вас выполнения определенных действий или определения состояний доски.

Одним из видов шахматной головоломки является шахматный тур , связанный с головоломками тура, упомянутыми в разделе выше. Этот тип головоломки предлагает вам совершить путешествие по шахматной фигуре по доске, применяя правила движения этой фигуры.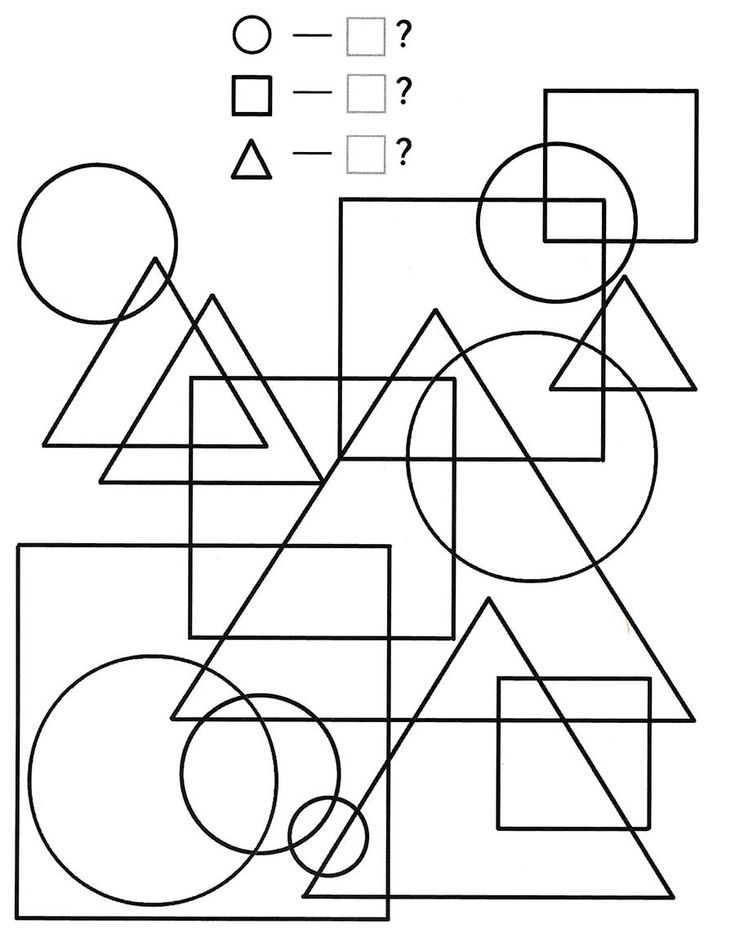

Дэн Сэм Ни у одного из них нет выигрышной стратегии

Дэн и Сэм играют в игру на доске \(5\x3\). Дэн ставит Белого рыцаря в угол, а Сэм ставит Черного рыцаря в ближайший угол. Каждый в свой ход перемещает своего рыцаря на клетки с , а не уже посещал любой из рыцарей в любой момент матча.

Например, ходит Дэн, затем Сэм, и Дэн хочет пройти на начальную клетку Черного рыцаря, но не может, так как эта клетка была занята ранее.

Когда кто-то не может двигаться, он проигрывает. Если начнет Дэн, кто выиграет, если оба игрока будут играть оптимально?

---

Это семнадцатая задача из набора «Стратегии выигрыша».

Благодаря четко определенному набору правил, игра в шахматы предлагает множество различных типов головоломок. Приведенная ниже задача показывает, что вы даже можете определить, чей сейчас ход, из определенного состояния доски (или, возможно, вы не можете).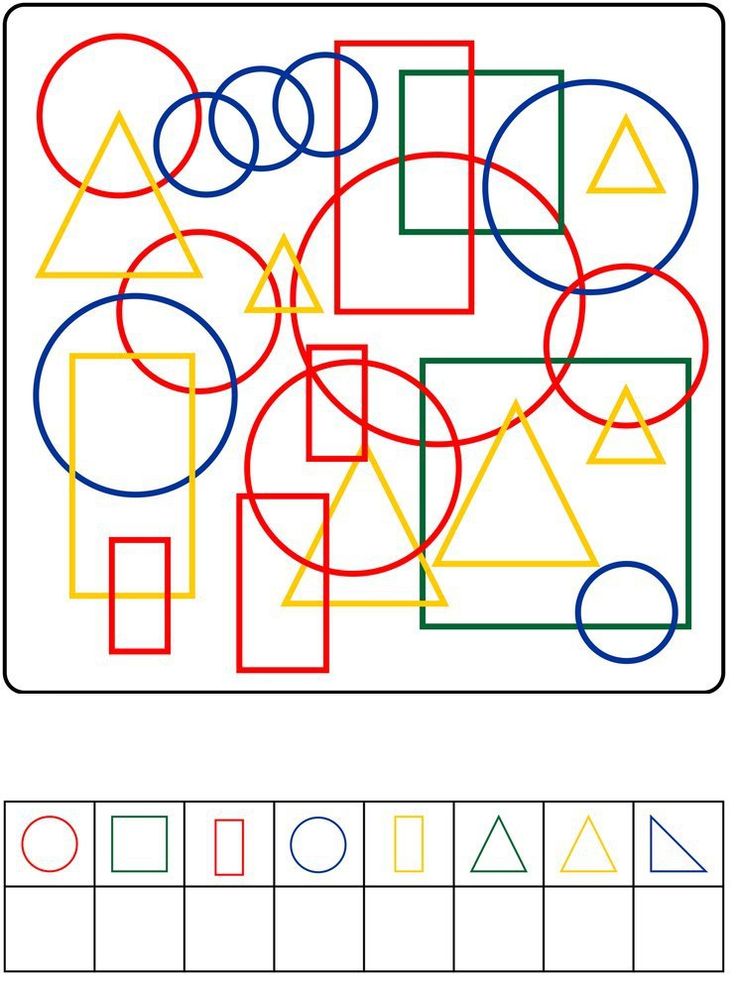

Ход белых Черный, чтобы двигаться Невозможно определить Это невозможная позиция

Чей сейчас ход?

Основная статья: Мышление K-уровня

См. также: Индукция — Введение

Мышление К-уровня — это название своего рода предположения в некоторых логических головоломках. В подобных головоломках в ситуации участвует несколько действующих лиц, и каждый из них совершенно логичен в принятии решений. Кроме того, каждый из этих действующих лиц осознает, что все остальные действующие лица в данной ситуации совершенно логичны в своих решениях.

Кальвин, Зандра и Эли учатся в математическом классе мистера Сильвермана. Мистер Сильверман вручает каждому из них запечатанный конверт с номером внутри.

Он говорит им, что у каждого из них есть положительное целое число, а сумма трех чисел равна 14. Каждый открывает свой конверт и проверяет свое число, не видя других чисел.

Кальвин говорит: «Я знаю, что у Зандры и Илая разные числа».
Зандра отвечает: «Я уже знала, что все три наших номера разные».
После короткой паузы Эли наконец говорит: «А, теперь я знаю, какой у каждого номер!»

Какое число получил каждый ученик?

Отформатируйте свой ответ, написав сначала номер Кальвина, затем номер Зандры и, наконец, номер Эли. Например, если у Кальвина 8, у Зандры 12, а у Эли 8, ответ будет 8128.

Два логика должны найти два различных целых числа \(A\) и \(B\), такие, что они оба находятся между 2 и 100 включительно, а \(A\) делит \(B\). Первый логик знает сумму \(A + B\), а второй логик знает разность \(B-A\).

Далее происходит следующее обсуждение:

Логик 1: Я их не знаю.
Логик 2: Я это уже знал.

Логик 1: Я уже знаю, что вы должны это знать.
Логик 2: Я думаю, что… я знаю… что ты собирался это сказать!

Логик 1: Я до сих пор не могу понять, что это за два числа.
Логик 2: Ой! Плохо… мой предыдущий вывод был необоснованным. Я этого еще не знал!

Какие два числа?

Введите ответ в виде десятичного числа \(A.B\).
\((\)Например, если \(A=23\) и \(B=92\), напишите \(23.92.)\)

---

Примечание: В этой задаче участники не участвуют в соревнование, кто первым найдет числа. Если у одного из них достаточно информации для определения чисел, он может промолчать. Поэтому ничего нельзя вывести из молчания. Единственная используемая информация — это явные объявления в диалоге.

Конечно, головоломки, описанные выше, не единственные типы головоломок, с которыми можно столкнуться. Ниже приведены еще несколько логических головоломок, не связанных с типами, описанными выше.

Вас просят угадать целое число от \(1\) до \(N\) включительно. \text{rd}\) это слишком низко, вы вышли.

При каком максимальном \(N\) вы гарантированно выполните это задание?

\(\)
Пояснение : Например, если вам было позволено угадать один раз слишком много и один раз слишком мало, вы могли бы гарантировать правильный ответ, если \(N=5\), но не для \( N>5\). Итак, в этом случае ответ будет \(5\).

Вы играете в игру с кучей \(N\) золотых монет.

Вы и ваш друг по очереди берете 1, 3 или 6 монет из стопки.
Победит тот, кто возьмет последнюю монету.

Для того, кто ходит первым, сколько существует выигрышных стратегий для \(N < 1000?\)

\(\)
Пояснение: Для \(1 \leq N \leq 999\), как при многих значениях \(N\) может ли первый игрок разработать выигрышную стратегию?

Цитировать как: Логические головоломки. Brilliant.org . Извлекаются из https://brilliant.