Задачки с числами
День рождения
Позавчера мне было 25. А в следующем году мне исполнится 28.
Какой день — день моего рождения?
Простая дедукция
Учитель сказал, что задумал два последовательных числа от 1 до 10. После этого он сообщил одному студенту одно из этих чисел, а второму – другое. Последовал такой разговор:
1-й студент: «Я не знаю другого числа.»
2-й студент: «Я тоже не знаю другог числа.»
1-й студент: «Теперь я знаю другое число.»
Найдите все 4 возможные комбинации из двух чисел.
Сложная дедукция
Эта задачка – одна из самых сложных в этом разделе.
Учитель сообщил, что задумал два натуральных числа больше единицы.
1-й студент: «Я не знаю сумму.»
2-й студент: «Я знал, что ты не знаешь. Сумма меньше 14.»
1-й студент: «Теперь я знаю эти числа.»
2-й студент: «Я тоже.»
Найдите эти два числа.
Сколько лет детям?
Два друга разговаривают:
— Питер, сколько лет твоим детям?
— Знаешь, Томас, у меня их трое. И если перемножить их возраста, то получится 36.
— Этого недостачно…
— Сумма их возрастов равна количеству бутылок пива, что мы сегодня выпили.
— Этого всё ещё недостаточно.
— Хорошо. Последнее, что могу сказать – старший сын носит зеленую кепку.
Сколько лет детям Питера?
Математический знак
Какой математический знак можно поставить между цифрами 5 и 9, чтобы получилось число больше, чем 5 и меньше, чем 9?
Дробь
Расставьте все 9 цифр: 1, 2, 3, 4, 5, 6, 7, 8, и 9 в числителе и знаменателе дроби, использовав каждую цифру один и только один раз, так чтобы получилась дробь равная 1/3.
Пятизначное число
Если приписать цифру 1 впереди некоего 5-тизначного числа, то получится число в 3 раза меньше, чем если приписать цифру 1 в конце этого же числа. Найдите это число.
Шифр
Найдите число, если:
- Это число состоит из 6 разных цифр.
- Чётные и нечётные цифры чередуются (ноль также может чередоваться и будет считаться четным числом).
- Каждые две соседние цифры отличаются больше, чем на 1.
- Число, состоящие из первых двух цифр, как и число, состоящие из средних двух цифр, делятся без остатка на число, составленное двумя последними цифрами.
У этой задачи существует больше одного варианта решения.
Кроссворд с числами
Составьте таблицу из трёх чисел, расположенных вертикально, и трёх – горизонтально, как показано на примере ниже. Числа можно брать только из приведённого списка. Можно использовать одно и то же число несколько раз. Составив таблицу, подсчитайте сумму всех цифр в ней. Какова максимальная сумма, которую можно получить?
Таблица Список чиселПример с использованием каждого из чисел: 40067 04802 78215 дважды
Сумма в этом примере: 73.
Но, конечно, этот результат можно улучшить.
Загадочное число
Найдите число обозначенное звёздочками, если известно следующее:
- Все 4 цифры неизвестого числа – разные.
- Ни одна из цифр не равна нулю.
- Ниже даны вспомогательные 4-х значные числа, где каждый «0» справа от числа означает, что в этом числе есть цифра, которая совпадает с одной из цифр искомого числа, но находится в другой позиции.
- Каждый «+» справа от числа означает, что в этом числе есть совпадающая цифра стоящая в той же позиции, как и цифра искомого числа.
6152 +0 4182 00 5314 00 5789 + ---------- ****
1996
Пользуясь цифрами: «1», «9», «9» и «6» и знаками арифметических операций: «+», «-», «х», «:», знаком извлечения корня и скобками, получите следющие результаты:
29, 32, 35, 38, 70, 73, 76, 77, 100 и 1000.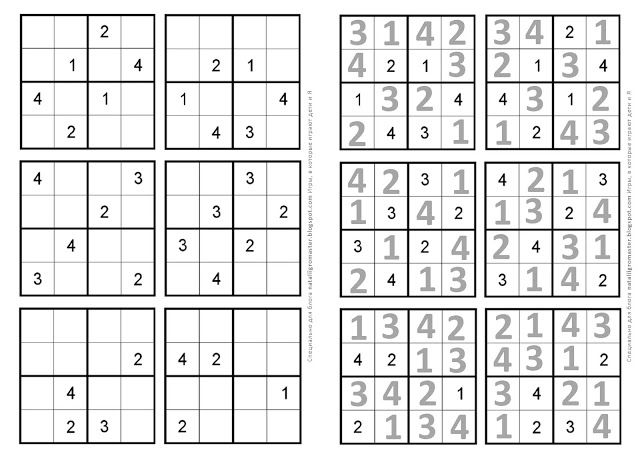
Все четыре цифры должны быть использованны только в заданном порядке, каждая цифра только один раз, и нельзя переворачивать цифры вверх ногами.
100
Используя четыре семёрки (7) и одну еденицу (1), получите число 100. Кроме 5-ти цифр, можно пользоваться обычными арифметическими операциями: «+», «-», «х», «:», знаком извлечения корня и скобками.
Уравнение
Переставьте только одну цифру, так чтобы получилось равенство:
101 – 102 = 1
Последовательности
Существует бесконечное множество формул (функций), которые удовлетворет заданная конечная последовательность чисел. Постарайтесь найти самые простые формулы для следующих последовательностей.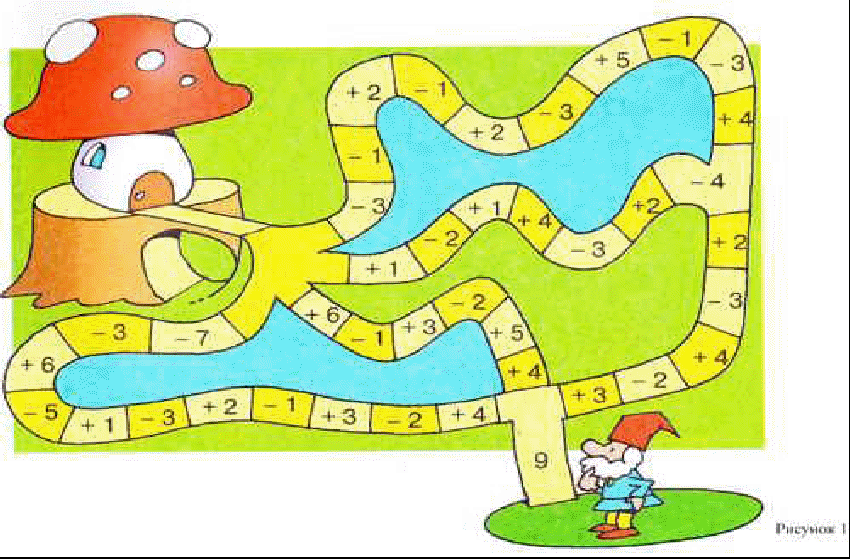
- 8723, 3872, 2387, ?
- 1, 4, 9, 18, 35, ?
- 23, 45, 89, 177, ?
- 7, 5, 8, 4, 9, 3, ?
- 11, 19, 14, 22, 17, 25, ?
- 3, 8, 15, 24, 35, ?
- 2, 4, 5, 10, 12, 24, 27, ?
- 1, 3, 4, 7, 11, 18, ?
- 99, 92, 86, 81, 77, ?
- 0, 4, 2, 6, 4, 8, ?
- 1, 2, 2, 4, 8, 11, 33, ?
- 1, 2, 6, 24, 120, ?
- 1, 2, 3, 6, 11, 20, 37, ?
- 5, 7, 12, 19, 31, 50, ?
- 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, ?
- 126, 63, 190, 95, 286, 143, 430, 215, 646, 323, 970, ?
- 4, 7, 15, 29, 59, 117, ?
- 2, 3, 2, 3, 2, 4, 2, 3, 2, 3, 2, 5, 2, 3, 2, 3, 2, 4, 2, 3, 2, 3, 2, 5, 2, 3, 2, 3, 2, 4, 2, 3, 2, 3, 2, 5, ?
- 4, 4, 341, 6, 4, 4, 6, 6, 4, 4, 6, 10, 4, 4, 14, 6, 4, 4, 6, 6, 4, 4, 6, 22, 4, 4, 9, 6, ?
Математические головоломки >>
Девиз
Наука не является и никогда не будет являться законченной книгой.
Альберт Эйнштейн
Головоломки со спичками — онлайн-задания от ЛогикЛайк с ответами для детей и взрослых
Занимательная математика / Головоломки и логические игры онлайн
Спички детям не игрушка! Исключение из правил – наши онлайн-головоломки. В курсе развития мышления более 300 заданий на перестановки.
У нас есть все, что вы искали!
Выберите возраст для старта
5-8 лет
9-14 лет
Взрослый (15+)
Можно менять вид Курса логики: «Пошаговый» или
«По разделам».
Задания со спичками ждут вас в рубрике «Головоломки с фигурами».
Рекомендуем попробовать разделы «Расположение и ориентация», «Расположи по
описанию», «2D-формы» и «3D-формы».
Играть со спичками на сайте ЛогикЛайк безопасно и полезно. В большинстве задач одним или несколькими движениями можно получить совсем иную картинку или правильное равенство.
Задания для разминки
Нужно переложить, добавить или убрать 1 или несколько спичек. На этой странице – мысленно, а можно решать онлайн.
После каждой головоломки мы указали свое решение. В некоторых заданиях может быть несколько
правильных вариантов ответа и это нормально.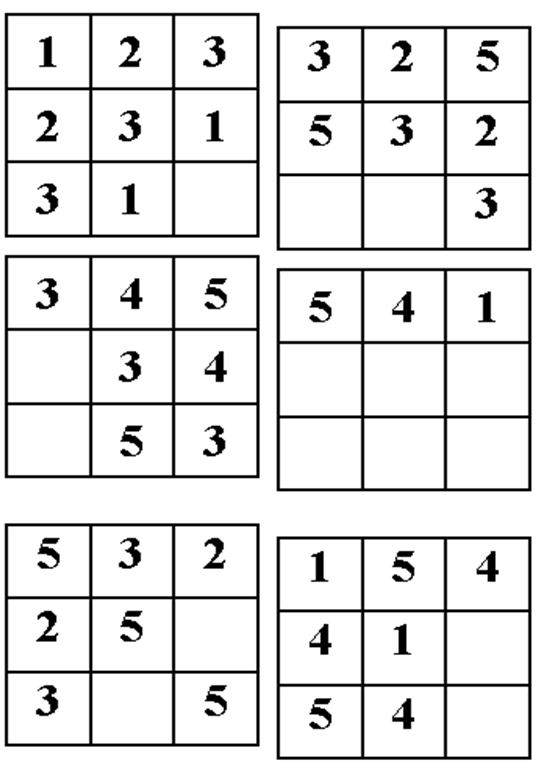
Задача 1
Переложите одну спичку так, чтобы пример был решен правильно.
Cмотреть ответ
Задача 2
Как можно переложить 1 спичку, чтобы равенство стало верным?
Узнать ответ
Когда ребенок выполняет задания со спичками, он:
- тренирует кратковременную память и воображение;
- учится применять нестандартные подходы к решению задач;
- развивает пространственное и логическое мышление.
3500+ интерактивных заданий
Ребёнок развивает логику и мышление в игровом формате.
К задачам! К задачам!
Задача 3
Нужно убрать 2 спички так, чтобы осталось 4 равных квадрата.
Узнать ответ
Задача 4
Как переложить 3 спички, чтобы получить 3 одинаковых квадрата?
Узнать ответ
Мы знаем, что гораздо удобнее, когда спички можно вращать и перемещать пальцем или по клику
мыши.
Головоломки, в которых нужно переместить более 2 спичек или других предметов, лучше решать в интерактивном формате.
Такой подход очень помогает начинающим «логикам», и большинству продвинутых любителей «спичечных» задач – тоже по душе.
Выбирайте лучшие курсы для развития логики, математического мышления и кругозора
Сложные головоломки
Легко решаете любую головоломку в уме? Попробуйте силы на более сложных задачах со спичками.
Задача 5
Уберите 3 спички так, чтобы осталось только 3 треугольника.
Узнать ответ
Задача 6
Переставьте 4 спички, чтобы получилось 3 квадрата.
Узнать ответ
Задача 7
Уберите 5 спичек так, чтобы осталось только 5 равных треугольников.
Узнать ответ
Мы задумали платформу ЛогикЛайк в первую очередь для детей и построили обучение от
простого к сложному.
Начать с экспертного уровня сложности не получится.
Но немного смекалки, и взрослый увидит интересные ему головоломки.
Подключайтесь к ЛогикЛайк!
Более 150 000 ребят и их родители уже развивают логику на Logiclike.com.
Начать обучение! Начать обучение!
Игра «Быки и коровы» и «Математические карты»
Классы: 2, 3, 4, 5, 6
Ключевые слова: математическая игра, занимательная математика, быки коровы
Игра “Быки и коровы”
Игра “БЫКИ–КОРОВЫ” — замечательная
логическая игра, не требующая специальных
приспособлений.
В нее можно играть в любых
ситуациях: дома, на даче, в поездках и даже в
ожидании очередей.
Игра развивает умение сравнивать и анализировать.
Играют двое. Каждый загадывает число из четырех неповторяющихся цифр (ноль в игре используется, но на первом месте стоять не может).
Задача противника отгадать число из 10 попыток.
Противник называет любое 4-хзначное число, у
которого цифры также не повторяются Его
необходимо написать под своим загаданным числом,
чтобы было удобно сравнивать цифры. При
совпадении цифр названного числа с загаданным
говорится “БЫК”. Бык означает, что цифра
отгадана и стоит в нужной позиции (например, в
задуманном числе первая цифра 3 и в названном
противником – тоже первая 3 – это бык.). Корова означает, что цифра отгадана, но она стоит не в
своей позиции. Путем логических рассуждений и
проверки ответов необходимо угадать все 4 цифры
числа и их порядок. Выигрывает тот, кто первым
угадает число противника. Например, загадано 3749 и
победитель называет 3749.
Игра с числами на самом деле не очень сложна, так как цифр всего 10 и повторяться они не могут. Ее могут освоить дети даже 8-9 лет.
Пример игры:
3749 – загаданное число
3589 – называет противник – ваш ответ – 2 быка. (3 и 9 стоят на своих местах)
7628 – называет противник – ваш ответ – 1 корова. (только 7 есть в числе, но не на своем месте).
Значит, из первого числа используются 2 цифры, а из второго только одна (но какие после первого ответа определить невозможно). Дальше, называя следующие числа, надо вычислить сами цифры и их порядок.
По двум ответам определить используется ли цифра 8 в загаданном числе нельзя – надо пробовать другие числа и сравнивать, какой ответ получаешь. Например, 8601 – ни одной цифры в загаданном числе нет. Значит, и в первом, и во втором числе цифры 6 и 8 можно зачеркнуть и дальше пробовать числа без этих цифр.
4973 – называет противник – ваш ответ –
4 коровы (т.
е. все цифры правильные, а вот их
порядок – нет). А вот ответ: 3 быка 1 корова быть не
может, так как если три цифры стоят на своем
месте, то и четвертая – тоже.
ИГРА “Быки и коровы” со словами
После освоения игры с числами интереснее перейти на игру со словами.
В русском языке очень много слов из 4 букв (играем всегда в значащие слова). А сочетание букв могут быть самые разные: и 3 согласных 1 гласная, и 2 на 2, и 1 на 3. Не используется только твердый знак и слова типа МАМА, ФАРА, РАМА, ОКНО, ТОРТ и т.д., где 2 одинаковые буквы. Принцип игры остается тем же: буква на своем месте – бык, буква есть в слове, но не на своем месте, — корова.
Играть можно на любом клочке бумаги, годится
даже пол-листочка или исписанный с одной стороны,
а заставляет сравнивать и логически мыслить, так
как надо все время заниматься перестановками и
анализом – где же все-таки бык и какой он?
Например, противник может загадать и пруд, и прут,
и порт – и замена даже одной буквы приводит
уже к новому слову, а иногда одни и те же буквы
могут быть в разном порядке – и будет два разных
слова, например, лето и тело.
Себе на
листочке сбоку для подсказки удобно выписывать
алфавит и проверять разные варианты подстановки
букв (тень, день, пень, лень…..)
Примеры игры:
* * * *
- рука – 1 к
- слон – пусто (нет ни одной буквы)
- гриб – 3 б
- горб – 1 б 1 к
- бусы – пусто
- грим – 3 б
- гриф – слово угадано.
* * * *
- луна – 1 б
- море – 1 к
- угол – 1 к
- порт – 1 к
- нора – 1 к
- стул – 1 к
- лень – пусто
- буря – 1 б 2 к
- рука – 1 б 1 к
- сруб – 3 к
- шуба – 2 б
- зубр – слово угадано.
Математические карты
Игра позволяет тренировать устный счет и таблицу умножения. Рекомендуется для учащихся начальной школы.
Делаются они так: берутся два набора чисел от 1 до 24 (для чисел удобно использовать старый настенный календарь). Всего 48 карт. На каждой карте (основа – картон) делается одно число в двух противоположных углах, чтобы тому, кто сидит напротив, было удобно смотреть на это же число (см. рисунок).
Правила: Каждому играющему дается по 4 карты. Начинающему игру дается пятая карта. Из своих 5 карт он выбирает одну, которую дает соседу в качестве задания.
Принцип игры такой: игрок из своих 4
карт, то есть чисел, используя любые
математические действия: +, — , *, : (сложение,
вычитание, умножение, деление) и ставя числа в
любом(!) порядке, должен получить ответ, который
дал ему сосед. Те числа-карты, которые он при этом
использовал вместе с ответом, игрок берет себе
как «взятку».
А в конце игры каждый считает,
сколько он набрал карт в своей стопочке. Эта игра
рассчитана на тренировку устного счета,
простейшего деления и умножения (все варианты до
24).
Например: первому игроку достались карты: 17, 4, 8, 9. А в качестве задания дали сделать 10 или 16.
- число10 получается очень легко: 8:4+17-9=10;
- число 16 сделать уже сложнее: (17-9)*(8:4)=16.
А если «поиграть» с этими числами, то можно получить еще целый набор ответов: 12, 14, 13, 23, 6, 4, 20… Например, 12 = 17 – 4 – (9 — 8). 14 = 17 – 4 + (9 – 8).
Преимущество игры в том, что
последовательность чисел и математических
действий не фиксирована, как в учебнике
математики, а играющий сам должен определить
их, перекладывая карточки в любом порядке, а
также то, что игра ведется в открытую и все
играющие тоже “ломают голову”, чтобы решить
данный пример.
Если скобки используются при записи примера, то устно можно про них ничего не говорить, просто называть действия в нужном порядке: для 16 (из примера выше): сначала из 17 вычитаю 9, получается 8; 8 делю на 4, и 8 умножаю на 2. Очень часто есть несколько вариантов получения ответа.
Иногда, конечно, бывает такая ситуация, когда ответ ну никак не получается, тогда взрослый проверяет это и просит, чтобы поменяли задание или меняет одну карту у игрока из неиспользованной колоды. Иногда решение может быть только из трех карт, тогда игрок берет себе во «взятку» не 5, а 4 карты.
В этой игре дети, например, очень хорошо тренируют простейшее деление и умножение (на 2, на 3, на 4), а также свойство 1: если на нее умножить или разделить — число не изменится.
Рекомендую попробовать и поиграть дома, а также
давать набор чисел и результат, который надо
получить, как дополнительное задание на уроках
математики.
Числовые логические головоломки — Griddlers.net
Судоку
Судоку — это логическая головоломка с размещением чисел. Цель состоит в том, чтобы заполнить сетку цифрами так, чтобы каждый столбец и каждая строка содержали цифры только один раз.
Нет блоков (латинский квадрат)
Латинский квадрат представляет собой массив n x n, заполненный n различными цифрами, каждая из которых встречается ровно один раз в каждой строке и ровно один раз в каждом столбце. Правило латинских квадратов:
|
Прямоугольные блоки
Наиболее распространенным ограничением являются прямоугольные блоки. Сетка 9×9 состоит из 9 блоков, как показано на рисунке. Прямоугольные блоки Правила:
|
Неправильные блоки (головоломки)
Головоломка играется так же, как судоку, за исключением того, что в сетке есть неправильные блоки, также известные как клетки. Правила неправильных блоков:
|
Диагональные варианты
Обычно добавляются ограничения на размещение цифр помимо обычных строк и столбцов. Одним из ограничений является диагональный вариант. Диагональные варианты Правило:
|
Комбинированные варианты
Варианты можно комбинировать. Прямоугольные блоки и диагональные варианты Правила:
|
Например: сетка может иметь как прямоугольные блоки, так и диагональные линии. Также может быть более 2 диагональных линий.Перекрывающиеся варианты
Перекрывающиеся варианты состоят из нескольких головоломок. Общие блоки выделяются другим цветом. Вот несколько примеров перекрывающихся судоку:
Double-Doku
Sensei
Gattai Near-2
Wing-3
Gattai-3
SOHEI
Butterfly
Flower-4
Samurai
Gattai-8
Killer
Каждая клетка заключает в себе 2 или более ячеек. Верхняя левая ячейка помечена суммой клеток, которая представляет собой сумму всех цифр решения для ячеек внутри клетки.Killer Sudoku Rules:
- Каждый столбец и каждая строка содержат цифры только один раз.
- Все цифры в клетке должны быть различны.
Больше/Меньше
Больше (или меньше) Судоку не имеет подсказок (цифр). Вместо этого есть «Больше, чем» (>) или «Меньше, чем» ( Правила «больше / меньше чем»:
|
Какуро
Какуро играется на сетке из заполненных и заштрихованных ячеек, «черных» и «белых» соответственно. Правило Какуро:
|
Сетка разделена на «входы» (линии белых ячеек) черными ячейками. Черные ячейки содержат косую черту от левого верхнего угла к правому нижнему и число в одной или обеих половинах. Эти числа называются «подсказками».Kalkuldoku
Сетка разделена на сильно очерченные клетки (группы ячеек). Числа в ячейках каждой клетки должны давать определенное «целевое» число при объединении с использованием указанной математической операции (сложения, вычитания, умножения или деления). Правила Kalkuldoku:
|
Футошики
Футошики разыгрываются на сетке, которая может отображать некоторые цифры в начале. Кроме того, есть «Больше, чем» (>) или «Меньше, чем» ( Правила Футошики:
|
Стриты
Стриты разыгрываются на сетке, частично разделенной черными ячейками на отсеки. Отсеки должны содержать стрит — набор последовательных цифр — но в любом порядке (например: 2-1-3-4). В черных ячейках также могут быть белые подсказки. Правила стрита:
|
Небоскреб
В головоломке «Небоскреб» числа расположены вдоль края сетки. Эти цифры означают количество зданий , которые вы бы увидели с этого направления, если бы существовал ряд небоскребов с высотой, равной элементам в этой строке или столбце. Например: если в строке 4 ячейки и если первое число в ячейке равно 4, вы увидите только один небоскреб, потому что 4-этажный небоскреб скрывает 1-этажный, 2-этажный и 3-этажный небоскребы. Небоскребы Правила:
|
Небоскребы с парками
В головоломке «Небоскребы» может быть парков (пустые ячейки). Небоскребы с парками Правила:
|
Сумма небоскребов
Числа вдоль края сетки суммы небоскребов указывают сумму высот видимых зданий. Sum Skyscrapers Правила:
|
Двоичный
Заполняйте сетку нулями (0) и единицами (1), пока не будет столько же нулей и единиц в каждой строке и каждом столбце. Бинарные правила:
|
Кирпичи
Кирпичи — еще один тип латинского квадрата. Сетка разбита на пары и выглядит как кирпичная стена. Кубики правила
|
Групповые игры — логические игры LSAT
Все ресурсы логических игр LSAT
5 диагностических тестов 77 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 … 27 28 Следующая →
LSAT Logic Games Help » Групповые игры
Учитель танцев составляет сет-лист для предстоящего танцевального вечера. Должно быть пять номеров, выполняемых последовательно. Номера могут быть соло, дуэтами или трио, состоящими из восьми учениц: Эми, Белль, Кэрри, Дана, Линда, Моник, Николь и Она. Каждый студент будет выступать только один раз, и сет-лист должен соответствовать следующим условиям:
Эми и Она должны выступить соло
Кэрри не может выступать под вторым номером, если Белль не выступит под четвертым
Николь и Линда должны выступить вместе
Она должна выступить за некоторое время до Даны должны быть соло
Если Дана — участница трио, выступающего вторым, что из следующего может быть правдой?
Возможные ответы:
Кэрри выступает вторым, а Эми — третьим
Кэрри выступает второй, а Николь — третьей
Она — третьей, Линда — четвертой
Белль играет первой, Линда — второй
Она — первой, Линда — пятой
Вторая Правильный ответ:
5 90 исполняет третий
Объяснение:
Как только мы узнаем, что Дана занимает второе место, мы можем поставить Ону на первое место.
Поэтому любой ответ, в котором кто-то, кроме Она, выступает первым ИЛИ где Она выступает где-то еще, кроме первого, не может быть верным. Мы знаем, что пятое место должно быть соло, поэтому ответ, согласно которому Линда выступает на пятом месте, должен быть автоматически неправильным, потому что ей всегда приходится выступать с Николь. Если мы поместим Кэрри на второе место с Даной, мы автоматически поместим Белль на четвертое место из-за нашего условного предложения. Если Эми выступает третьей, мы знаем, что она должна выступать одна. Это оставляет нас с Николь, Линдой и Моник на своих местах. Поскольку Николь и Линда должны выступать вместе, Моник должна выступать пятой в одиночку. Затем мы должны поместить Николь и Линду на четвертое место с Белль, поскольку Эми всегда выступает одна, а если поставить их на второе место с Даной и Кэрри, получится квартет. В этом сценарии Дана НЕ входит в трио, поэтому этот ответ неверен. Правильный ответ (Кэрри выступает второй, а Николь — третьей) дает следующий сет-лист: Первый: Она; Второй: Дана, Кэрри, Моник; Третье: Николь, Линда; Четвертое: Белль; Пятое: Эми.
Сообщить об ошибке
Учитель танцев составляет сет-лист для предстоящего танцевального вечера. Должно быть пять номеров, выполняемых последовательно. Номера могут быть соло, дуэтами или трио, состоящими из восьми учениц: Эми, Белль, Кэрри, Дана, Линда, Моник, Николь и Она. Каждый студент будет выступать только один раз, и сет-лист должен соответствовать следующим условиям:
Эми и Она должны выступать соло
Кэрри не может выступать под вторым номером, если Белль не выступит под четвертым0005
Николь и Линда должны выступить вместе
Она должна выступить раньше Даны
Первый и пятый номера должны быть соло
Что из следующего должно быть правдой?
Возможные ответы:
Не более двух дуэтов
Не менее трех дуэтов
Не более одного трио
Не менее трех соло
615Не более двух соло
Правильный ответ:Существует не более одной тройки
Объяснение:
Мы можем понять это из начальной настройки игры.
Если мы помещаем восемь танцоров в пять номеров, мы знаем, что на каждом месте должна быть одна девушка. Это заботится о пяти танцорах. У нас осталось три. Наши варианты: разместить все три под разными числами, получив соотношение 1:1:2:2:2, ИЛИ поместить два под одним числом, а одно под другим, получив соотношение 1:1:1:2:3. Следовательно, единственный правильный ответ состоит в том, что существует не более одного трио.
Сообщить об ошибке
Председатель правления создает финансовый комитет из группы из семи представителей: Харрис, Иннис, Дженкинс, Кензи, Лоуренс, МакГенри и Нин. Комитет должен соответствовать следующим ограничениям:
Если Харрис выбран в комитет, Иннис также должен быть выбран
Если выбран МакГенри, Харрис не может быть
Если выбран Нин, МакГенри также выбран, но Иннис не
Если выбирается Иннис, Кензи также выбирается
Если Дженкинс не выбран, выбирается Харрис
Что из следующего является возможным полным и точным списком представителей, НЕ избранных в комитет?
Возможные ответы:
NIN, Jenkins, Lawrence
Jenkins, Nin
Harris, Innis, Jenkins, Kenzi, Lawrence
Nin, Mchenry, Kenzi
, Jenkins, Lawrence, McHenry, Kenzi
, Jenkins, Lawrence, McHenry, Kenzi
, Jenkins, Lawrence, McHenry, Kenzi
, Jenkins, Lawrence, McHenry, Kenzi
, Jenkins, Lawrence, McHenry, Kenzi
.
ответ:
Дженкинс, Лоуренс, МакГенри, Нин
Объяснение:
Это простой вопрос списка, вывернутый наизнанку. Чтобы ответить на этот вопрос, нам нужно выяснить, кто выбран в комитет в каждом ответе, и исключить ответы на основе нарушений правил. Мы знаем, что Харрис и МакГенри не могут быть выбраны одновременно, а Нин и Иннис не могут быть выбраны одновременно. Если выбран Иннис, Кензи также должна быть выбрана, как и при выборе Харриса Иннис также должен быть выбран. Мы также знаем, что всегда должен быть выбран по крайней мере один из Харриса и Дженкинса, поэтому любой ответ, в котором они оба отсутствуют, неверен. Единственный правильный вариант оставляет этот комитет: Харрис, Иннис, Кензи.
Сообщить об ошибке
Председатель правления создает финансовый комитет из группы из семи представителей: Харрис, Иннис, Дженкинс, Кензи, Лоуренс, МакГенри и Нин. Комитет должен соответствовать следующим ограничениям:
Если Харрис выбран в комитет, Иннис также должен быть выбран
Если выбран МакГенри, Харрис не может быть
Если выбран Нин, МакГенри также выбран, но Иннис не
Если выбирается Иннис, Кензи также выбирается
Если Дженкинса не выбрали, Харриса выбрали
Если Харриса выбрали в комитет, что из следующего может быть правдой?
Possible Answers:
Innis is not chosen
Nin is chosen
Jenkins is chosen
McHenry is chosen
Kenzi is not chosen
Correct answer:
Jenkins is chosen
Пояснение:
Мы знаем, что когда выбирают Харриса, Иннис также должен быть выбран.
Если выбрана Иннис, Кензи также должна быть выбрана. Итак, самая маленькая возможная группа — это Харрис, Иннис и Кензи. Нин и Иннис не могут быть выбраны одновременно, поэтому Нин не может быть в этой группе. МакГенри и Харрис не могут быть выбраны одновременно, поэтому МакГенри также не может быть в этой группе. Единственный ответ, который может быть правдой, заключается в том, что выбран Дженкинс — Дженкинс не обязательно должен быть в этой группе, но может быть.
Сообщить об ошибке
Председатель правления создает финансовый комитет из группы из семи представителей: Харрис, Иннис, Дженкинс, Кензи, Лоуренс, МакГенри и Нин. Комитет должен соответствовать следующим ограничениям:
Если Харрис выбран в комитет, Иннис также должен быть выбран
Если выбран МакГенри, Харрис не может быть
Если выбран Нин, МакГенри также выбран, но Иннис не
Если выбирается Иннис, Кензи также выбирается
Если Дженкинс не выбран, выбирается Харрис
Какое наименьшее возможное число представителей выбрано в комитет?
Возможные ответы:
Один
Ноль
Два
Четыре
Три
Правильный ответ: 5 Один
Объяснение: Мы знаем, что если Дженкинса не выберут, то выберут Харриса. Сообщить об ошибке Председатель правления создает финансовый комитет из группы из семи представителей: Харрис, Иннис, Дженкинс, Кензи, Лоуренс, МакГенри и Нин. Комитет должен соответствовать следующим ограничениям: Если Харрис выбран в комитет, Иннис также должен быть выбран Если выбран МакГенри, Харрис не может быть Если выбран Нин, МакГенри также выбран, но Иннис не Если выбирается Иннис, Кензи также выбирается Если Дженкинс не выбран, Харрис выбран Если в комитете ровно три человека, может быть верно каждое из следующего, КРОМЕ: Возможные ответы: Харрис выбран, а Кензи выбрана Выбрана Кензи и выбран Лоуренс Выбран МакГенри и выбран Лоуренс Выбран Харрис и выбран Дженкинс Выбран Нин и выбран Дженкинс Правильный ответ: Выбран Харрис и выбран Дженкинс Объяснение: Единственный ответ, который может превышать трех человек, это Харрис и Дженкинс оба выбраны. Сообщить об ошибке Председатель правления создает финансовый комитет из группы семи представителей: Харрис, Иннис, Дженкинс, Кензи, Лоуренс, МакГенри и Нин. Комитет должен соответствовать следующим ограничениям: Если Харрис выбран в комитет, Иннис также должен быть выбран Если выбран МакГенри, Харрис не может быть Если выбран Нин, МакГенри также выбран, но Иннис не Если выбран Иннис, Кензи также выбран Если не выбран Дженкинс, выбран Харрис Должно быть верно все следующее, КРОМЕ: Возможные ответы: Харрис и Дженкинс не могут быть выбраны оба Нин и Иннис не могут быть выбраны оба МакГенри и Харрис не могут быть выбраны оба Nin и 900 нельзя выбрать обоих МакГенри и Иннис можно выбрать обоих Правильный ответ: Харриса и Дженкинса нельзя выбрать обоих Объяснение: Единственным ложным утверждением здесь является то, что Харрис и Дженкинс не могут быть выбраны оба — это не указано ни в одном правиле. Сообщить об ошибке Председатель правления создает финансовый комитет из группы семи представителей: Харрис, Иннис, Дженкинс, Кензи, Лоуренс, МакГенри и Нин. Комитет должен соответствовать следующим ограничениям: Если в комитет выбран Харрис, Иннис также должен быть выбран Если выбран МакГенри, Харрис не будет Если выбран Нин, также выбран МакГенри, но не Иннис Если выбран Иннис, Кензи также выбран Если Дженкинс не выбран, то выбран Харрис Если выбрана Нин, что из следующего является полным и точным списком всех других возможных представителей, которые также могут быть выбраны? Возможные ответы: McHenry, Jenkins, Lawrence McHenry, Jenkins, Kenzi, Lawrence McHenry, Jenkins, Kenzi 6666767676767676767676767676767676767. Чтобы ответить на этот вопрос, начнем с выбора Нин. Затем мы автоматически выбираем МакГенри и устраняем Инниса. Поскольку мы выбрали МакГенри, мы устраняем Харриса. Устранение Харриса заставляет нас выбрать Дженкинса. Остались только Кензи и Лоуренс, кого можно было выбрать, а кого нельзя было выбрать. Поэтому, если бы мы хотели создать максимально большой комитет, начиная с Нин, мы могли бы добавить МакГенри, Дженкинса, Лоуренса и Кензи. Сообщить об ошибке Четверо детей и четверо взрослых посещают бейсбольный матч и сидят в двух секциях. В каждой секции должны сидеть не менее трех членов группы — на первых местах и на трибунах. Взрослыми были Мэтью, Нора, Ольга и Питер. Детей звали Сара, Таня, Ульрик и Виктор. Применяются следующие правила: В каждой секции должен быть хотя бы один взрослый Нора и Сара не могут сидеть в одной секции Нора и Ульрик должны сидеть в одной секции Мэтью должен сидеть в первой секции Что из следующего может быть списком тех, кто сидел в каждой секции? Возможные ответы: Прайм: Ульрик, Мэтью, Ольга, Сара Трибуны: Питер, Нора, Виктор, Таня Прайм: Мэтью, Ульрик, Нора Ольга Прайм: Ульрик, Нора, Таня, Мэтью, Виктор, Петр Трибуны: Сара, Ольга Прайм: Ульрик, Ольга, Нора, Таня Трибуны: Петр, Сара, Виктор, Мэтью Прайм: Петр, Нора, Ульрик, Мэтью, Ольга Трибуны: Таня, Сара, Виктор Правильный ответ: Прайм: Мэтью, Ульрик, Нора Трибуны: Петр, Сара, Виктор, Таня, Ольга Объяснение: Убедитесь, что вы правильно поняли каждое правило, а затем примените правила, чтобы исключить все неправильные ответы. Сообщить об ошибке Четверо детей и четверо взрослых посещают бейсбольный матч и сидят в двух секциях. В каждой секции должны сидеть не менее трех членов группы — на первых местах и на трибунах. Взрослыми были Мэтью, Нора, Ольга и Питер. Детей звали Сара, Таня, Ульрик и Виктор. Применяются следующие правила: В каждой секции должен быть хотя бы один взрослый Нора и Сара не могут сидеть в одной секции Нора и Ульрик должны сидеть в одной секции Мэтью должен сидеть в первой секции Кто из следующих двух человек не может сидеть вместе? Возможные ответы: Victor and Sara Sara и Ulric Victor and Tania Nora and Ulric Matthew and Nora Правильный ответ: 95995995959595959595959595959595959595959005 . Сара не может быть в том же разделе, что и Нора, но Нора должна быть в том же разделе, что и Ульрик. В результате Саре запрещено находиться в одной секции с Ульриком, так же как ей запрещено находиться в одной секции с Норой. Сообщить об ошибке ← Предыдущая 1 2 3 4 5 6 7 8 9 … 27 28 Следующая → Уведомление об авторских правах 5 Диагностические тесты
77 практических тестов
Вопрос дня
Карточки
Learn by Concept В нашем классе мы узнаем, что (W.A.L.T.)… решателя проблем думают и пробуют, прежде чем сдаться или попросить о помощи полезных члена команды разговаривают и работают со своими партнерами гибких мыслителя отказываются от одной идеи и переходят к другой свободно мыслящих человека генерируют множество идей и делятся ими Вот некоторые из наших любимых игр.
Поэтому, если Харрис не выбран, Дженкинс. Это означает, что у нас всегда должен быть хотя бы один из этих двух в игре. Если будет выбран Харрис, это приведет к тому, что будут выбраны и несколько других членов, но если будет выбран Дженкинс, он может быть единственным представителем в комитете.
Когда выбирается Харрис, мы также должны выбрать Инниса, а затем Кензи. Выбор Дженкинса также потребует четырех человек в комитете. Другие ответы дают следующие группы: Харрис, Кензи, Иннис; Кензи, Лоуренс, Дженкинс; Нин, МакГенри, Дженкинс; МакГенри, Лоуренс, Дженкинс
Из правил мы знаем, что МакГенри и Харрис не могут быть выбраны одновременно, а Нин и Иннис не могут быть выбраны одновременно. Поскольку МакГенри должен быть выбран, когда выбрана Нин, Нин, следовательно, не может быть выбрана вместе с Харрисом. Нет правила, согласно которому МакГенри и Иннис не могут быть выбраны вместе.
Объяснение:
Каждый неверный ответ прямо нарушает хотя бы одно правило.
Объяснение: Все ресурсы LSAT Logic Games
Логические и стратегические игры | GATErocks
Наслаждаться! 7500
Название игры 7500. Цель игры состоит в том, чтобы сложить два четырехзначных числа, чтобы получить сумму, ближайшую к 7500, не превышая ее.
Чтобы сыграть в 7500, один человек пишет на доске два четырехзначных числа. Я использую один цвет для верхнего числа (синий) и другой цвет для нижнего числа (красный). Затем на своих листах игроки переставляют цифры в числах.
Цифры не могут менять строки. Синие цифры должны оставаться на своей линии. Красные цифры должны оставаться на своей линии.
Используя все 4 цифры в верхней строке и 3 или 4 цифры в нижней строке, составьте уравнение с суммой, близкой к 7500.
Помните, что в этой игре вы можете использовать только сложение, и ваш ответ не может быть больше 7500. Если ваш ответ близок к 7500, напишите свое уравнение и ответ на доске. Выигрывает тот, кто ближе всего к 7500.
Шахматы
Шахматы — отличная игра, если вы хотите использовать аналитическое и стратегическое мышление.
Игра в шахматы помогает нам лучше концентрироваться, визуализировать, думать наперед, взвешивать варианты и планировать.
Ищете видео о том, как играть в шахматы? Посмотрите этот… В нем есть основы, и это все, что вам нужно для начала: https://www.youtube.com/watch?v=KlTEQZ5Sy4E 9.0005
Думайте об этом, когда передвигаете свои фигуры:
Пешка = Пешка маленькая, но делает свою работу благодаря силе пешки! Пешка ходит вперед на одну клетку за раз, за исключением случаев взятия или первого хода. При первом ходе пешка возбуждается и может двигаться вперед на 1 или 2 клетки. При взятии пешка перемещается на одну клетку по диагонали.
Ладья (ладья) = Ладья движется вверх, вниз, из стороны в сторону, я сказал вверх, вниз, из стороны в сторону.
Ферзь = Ферзь представляет собой комбинацию ладьи и слона. Королева движется вверх, вниз, из стороны в сторону, я сказал вверх, вниз, из стороны в сторону и скользит.
Судоку
Судоку — логическая игра, использующая дедуктивное и аналитическое мышление. Чтобы играть в судоку, введите числа в пустые места, чтобы каждая строка, столбец и поле 3×3 содержали числа от 1 до 9. Повторяющихся чисел быть не может. В некоторых головоломках судоку используются цвета, а не числа, но у каждой головоломки судоку есть одно уникальное решение.
websudoku.com
sudokukingdom.com
funbrain.com/sudoku
www.primarygames.com
picsudoku.com
Логические головоломки
Что такое логические головоломки? Логические головоломки — это весело! Работая с подсказками и сеткой, используйте свои навыки дедуктивного мышления, чтобы решить головоломку. Соедините подсказки вместе, чтобы решить, что они говорят вам. Отметьте свою сетку «x» или «нет» для элементов, которые определенно не являются ответом, и «да» для элементов, которые являются.
Возможно, вам придется вернуться и прочитать подсказки несколько раз, чтобы понять, как все связано.
На этих сайтах много головоломок. В некоторые из этих логических головоломок играют онлайн, а некоторые нужно распечатать.
Logic-Puzzles.org
Таинственный Мастер
Логические головоломки для печати
Головоломки с логической сеткой
A-J-Z
Цель A-J-Z (Aces, Jumble, Zilch) — выяснить секретное число.
Один игрок (Парень с числами) записывает число и скрывает его на протяжении всей игры. Парень с числами должен сидеть на одном конце стола, напротив других игроков, чтобы никто не мог увидеть секретный номер. Трехзначные числа хороши для начала. Четырехзначные числа сложны. В номере не должно быть повторяющихся цифр.
Игроки по очереди угадывают число. Когда число угадывается, каждый записывает его на своей бумаге.
В другой колонке, рядом с догадкой, все игроки записывают оценку, которую дает за догадку Номерной Парень. A= Ace (цифра стоит на правильном месте) J = Jumble (цифра стоит не на том месте) Z = Zilch (цифры нет в номере). Например, если секретный номер 752, а вы угадали 592, ваша оценка AJZ.
Номер Парень должен написать счет в алфавитном порядке. Если баллы записаны в порядке номеров, в этой игре нет проблем. «А» всегда пишется первой, даже если это не оценка первой цифры. Требуется немного времени, чтобы привыкнуть к подсчету очков, когда вы являетесь цифровым парнем, но это должно быть написано именно так. Перед тем, как угадать число, игроки должны просмотреть предыдущие догадки в поисках подсказок и закономерностей.
Помните, что есть один и только один правильный ответ.
Вдохновитель — другое имя для Aces, Jumble, Zilch.
Игры для мозга
Вдохновитель
Взломщик кода
Крипто
Цель Крипто состоит в том, чтобы сложить, вычесть, умножить или разделить 5 чисел, чтобы получить целевое число.
Начните игру, написав на доске пять случайно выбранных однозначных чисел. Затем напишите на доске целевое число от 1 до 100.
Используя все пять цифр и любые математические операции, создайте математическое выражение, равное целевому числу.
Правила Крипто
1. Вы должны использовать все 5 номеров.
2. Вы можете использовать любую математическую операцию (сложение, вычитание, умножение или деление).
3. Вы можете использовать круглые скобки.
4. В уравнении может быть только один знак равенства. Поскольку обычно есть несколько способов достичь целевого числа, попробуйте составить более одного уравнения.
Вот пример, показывающий два уравнения, которые используют эти цифры и достигают целевого числа:
цифр: 5 7 4 3 8
целевое число: 20
решение A: (5 + 7 + 7 + 7) x (4 -3)
решение B: (8 — 3) x (7 — 4) + 5
Манкала
Манкала — настольная игра, появившаяся в 6 веке.