Тату механика: значение, фото татуировки, эскизы
Татуировки в стиле механика и биомеханика подчеркивает современное развитие общества. Мир стал невозможен без навороченных гаджетов и техники. Популярность данного вида татуировок обусловлена тем, что показывает безграничность человеческих возможностей. Изображения, относящиеся к этой категории, традиционно считаются мужскими, однако и здесь есть исключения. Некоторые девушки с удовольствием подбирают для себя красивые и женственные эскизы.
Содержание статьи:История возникновения
Татуировки в стиле биомеханика, или как их еще называют, просто механика, начали появляться в 80-х годах. Это было обусловлено ростом развития техники. Первоначальные эскизы не отличались выразительностью и выполнялись в черно-белых или дымчато-серых тонах. В дальнейшем, данный вид изображения претерпел ряд изменений, например, сами рисунки стали все изощреннее, а многие из них стали цветными.
Большую роль в развитии биомеханики как художественного стиля стал Ганс Гигер, который прославился благодаря своим эпатажным работам. Татуировки механика, фото которых зачастую захватывает дух, берут за основу рисунки Гигера. На них люди, вне зависимости от пола, представляли собой синтез человека и машины. Отличительными чертами его работ является наличие металлических платин, труб и проводов, вживленных в живые тела.
Татуировка механика с надписью на предплечье
Отличительные черты татуировки в стиле механика
Зачастую, данный стиль подразумевает изображение, связанное с прорастанием механизмов из человеческой плоти. В современных татуировках отдельно прорисовывают именно живую часть: мышцы, сосуды, сухожилия. В то время как в 80-х упор делался только на механизмы. Сейчас можно встретить разные варианты того, что произошло с кожей и мышцами. Могут быть изображены окровавленные края плоти, или обугленная кожа.
Рукав в стиле механика
Важно! Ганс Гигер, считающийся прародителем стиля механика, также причастен к культовому фильму 1979 года «Чужой». Им был создан ряд костюмов, а также именно ему принадлежит идея оформления внешнего вида пришельцев. Татуировка механика, значение которой различно, в зависимости от вида, берет свое начало напрямую от фильмов «Чухой» и «Терминатор», когда «Стальные» мышцы вошли в моду.
Татуировка ловец снов в стиле механика
Где лучше наколоть татуировку в стиле биомеханика?
Татуировка в таком стиле хорошо смотрится только тогда, когда занимает большой участок тела. Поэтому ее предпочтительнее накалывать на руках, ногах или груди:
- татуировки на плече. Такое расположение придает изображения дополнительную выразительность за счет рельефа мышц;
- рисунок на предплечье.
 Размещают татуировку механика, эскиз которой предполагается разместить на предплечье, с внутренней стороны. Также популярно расположение от кисти рук, до локтевого или плечевого сустава. Подобный рисунок отлично смотрится благодаря тому, что руки часто находятся в движении;
Размещают татуировку механика, эскиз которой предполагается разместить на предплечье, с внутренней стороны. Также популярно расположение от кисти рук, до локтевого или плечевого сустава. Подобный рисунок отлично смотрится благодаря тому, что руки часто находятся в движении; - татуировка на голени. Это наиболее типичный мужской вариант такого вида рисунка. Упор делается на голую торчащую кость, опоясанную проводами и винтами.
- изображение на бедре. Смотрится мягче, чем предыдущий вариант, его также можно скрыть под одеждой. Часто выбирают женщины.
- Татуировка биомеханика на груди. Расположение выбирают в области сердца, подчеркивая, что состоит оно из металла. Есть также еще один вариант расшифровки такого изображения – любовь к технике.
Татуировка в стиле биомеханика под кожей
Значение татуировки механика
Каждая татуировка несет свое особое значение, изображения в стиле механика не исключение. Можно считать, что все татуировки, изображающие синтез техники и человека несут общий смысл: единство живого и неживого, победа человека над техникой. Также существует мнение, что такие изображения символизируют возможности человека, его огромный потенциал. Но в итоге все сводится к тому, что смысл татуировки зависит от деталей: от расположения элементов, цветовых решений и т.д.
Также существует мнение, что такие изображения символизируют возможности человека, его огромный потенциал. Но в итоге все сводится к тому, что смысл татуировки зависит от деталей: от расположения элементов, цветовых решений и т.д.
Татуировка механика на плече
Отзыв:
Татуировку в стиле биомеханика хотел сделать давно. И тут подвернулся удобный случай. Эскиз был предложен мастером, мне полностью понравился. Набивать стали на ноге, от колена, до ступни. Изображение выполнено четко, с множеством мелких деталей, таких как шестеренки, проводки, разорванная кожа. Никакого особого смысла не вкладывал, просто круто смотрится.
Виктор, Архангельск.
Татуировка механика на груди и плече
Татуировка биомеханика. Женский вариант
Как уже уточнялось, не все девушки готовы пойти на то, чтобы занять татуировкой большую площадь тела. Да и изображение металла, роботов и разорванной плоти как-то присуще больше мужчинам. Однако многие девушки развеивают этот стереотип.
Однако многие девушки развеивают этот стереотип.
Это интересно. Многие дополняют традиционные элементы татуировки различными деталями. Так, можно встретить изображение в стиле биомеханика, на котором также изображены растения, травы, насекомые. Вполне вероятно, что такой подход скоро приведет к созданию нового стиля, основывающемуся на соединении не только человека и робота, но и живой природы.
Татуировка на груди механика — поршни в действии
Девушки выбирают эскизы, содержащие большое количество округлых, плавных элементов, которые придают татуировке женственность. Также пользуется популярностью среди женского пола расположение татуировки на боку, приоткрывая ребра с переплетенными между ними проводками и трубочками. Также в женские татуировки традиционно добавляют больше красок, цветовых решений, чтобы придать им больше женственности.
Отзыв:
Татуировку с изображением далеко не женского плана сделала сознательно.
Эскиз пришлось выбирать очень долго, еще больше времени ушло на то, чтобы найти хорошего мастера, который и помог мне воплотить в жизнь мою задумку. Идеальным местом для татуировки мне показалось бедро. Так у меня и появилось изображение проглядывающего сквозь кожу металла, кости, капилляров и проводов. Выполняли все в черно-белом варианте, с четкими контурами. По площади татуировка небольшая, ее легко прикрыть даже шортами или юбкой.
Виола, Пермь.
Видео-подборка татуировок механика
Понравилась статья? Расскажите друзьям: Оцените статью, для нас это очень важно:
Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.
Гостевая |
Чип и Дейл спешат на помощьСклад Механика |
|
|
Обьявление |
Обьявление Все, что не касается Гаечки и сериала «Чип и Дейл спешат на помощь», теперь будет публиковатся вот здесь luckytech. ru . Названия пока не пугайтесь… у меня всегда так — сложно выдумывать глобальные названия. (я до сих пор свой самолет никак не назвал! А уже несколько десятков вылетов на нем было… сколько раз разбивал…) ru . Названия пока не пугайтесь… у меня всегда так — сложно выдумывать глобальные названия. (я до сих пор свой самолет никак не назвал! А уже несколько десятков вылетов на нем было… сколько раз разбивал…)А по теме… тут да. Ничего нет :( | |
|
Гайка 2011. Создано: 11.12.2011. … Даже не хочется подсчитывать, сколько лет я не рисовал Гайку… | ||
|
Еще один светильник. Создано: 11.12.2011. | ||
|
Обьявление |
Обьявление | |
|
Обьявление |
Обьявление На складе открыт еще один раздел. Посвящен авиамоделизму | |
|
Фаза голосования 2009 |
Конкурс Золотая Гайка 2009 — Фаза голосования | |
|
Симулятор махолета спасателей. | ||
|
Снегурочка. Создано: 31.12.2009. | ||
|
Картина с Гайкой. Создано: 6.11.2009. | ||
|
Страница из журнала Барвінок. | ||
|
Фаза голосования |
Обьявление | |
|
Фаза голосования |
Конкурс Золотая Гайка 2008 — Фаза голосования — ЗАВЕРШЕНА | |
|
Обьявление! |
Конкурс Золотая Гайка 2008! | |
|
Самолет спасателей | ||
|
Как я рисовал Гайку 🙂 Создано: 07. | ||
|
Идущая Гайка Создано: 5.12.2007. | ||
|
Книга о Шестом спасателе. Создано: 02-03.2007. | ||
|
Детская раскраска 3. | ||
|
Летающая Гаечка 🙂 Создано: 24.02.2007. | ||
|
Летающий Чип 🙂 Создано: 23.02.2007. | ||
|
Детская раскраска 2. | ||
|
Детская раскраска 1. | ||
|
Новогодний! Создано: 31.12.2006. | ||
|
Маленький Рокки. Создано: 17.11. | ||
|
Гаечка за рулем. Создано: 22.10.2006. | ||
|
Чип. Создано: 22.10.2006. | ||
|
Гайка с гаечным ключом. Создано: 22. | ||
|
Раскраска Чип и Дейл. Найдено: 1.07.2006. | ||
|
Зошит для малювання (Альбом для рисования) Найдено: 1.07.2006. | ||
|
А как же Вжик?! Дата создания: 1.07.2006. | ||
|
Гайка в гостях у CDRR фэндома Дата создания: 30.06.2006. | ||
|
Нимнул и доктор Ливси 🙂 Дата создания: 01. | ||
|
Наклейки! | ||
|
Обложка одной книжечки | ||
|
Гайка провожает Дейла… Дата создания: 07.05.2006. | ||
|
Вертолет 🙂 | ||
|
Рисунок (MS Paint) Дата создания: 27.04.2006. | ||
|
Стена в моей комнате Дата создания: 24. | ||
|
Календарь на 2006 год Дата создания: 24.04.2006. | ||
|
Пасхальные наклейки Дата приобретения: 16.04.2006. | ||
|
Гайка с инструментами. | ||
|
Гайка с цветами. Дата создания: 07.04.2006. | ||
|
Кубики из спасателями. Дата создания: 07.04.2006. | ||
|
Чип и Дейл (плакат). Дата создания: 30.03.2006. | ||
|
Гаечка — проказница 🙂 Дата
создания: 30. | ||
|
Командир спасателей 🙂 Дата
создания: 24.03.2006. | ||
|
Моя хорошая Гаечка… Дата
создания: 23.03.2006. | ||
|
Последняя Гаечка… Дата
создания: 21.03.2006. | ||
|
Светильник с Гаечкой. Дата
создания: 02.03.2006. | ||
|
Сердитая Гаечка. Дата
создания: 20.02.2006. | ||
|
Гаечка. Дата создания:
20.02.2006. | ||
|
Гаечка в
профиль. Дата создания:
22.11.2005. | ||
|
Гаечка улыбается
🙂 Дата создания: 19.11.2005. | ||
|
«Святой»
Нимнул. | ||
|
Толстопуз в цвете
🙂 Дата создания: | ||
|
Толстопуз. Дата
создания: | ||
|
Рисунок Гайки на школьной
доске. Дата создания: 16.09.2005. | ||
|
Гаечка из
памяти. Дата создания: 16.09.2005. | ||
|
Гаечка улыбается. | ||
|
Гаечка с
подарком. Дата создания: 28.08.2005. | ||
|
Крот. Дата
создания: 24.08.2005. | ||
|
Мепс. | ||
|
Гаечка и
Толстопуз. Дата создания: 24.08.2005. | ||
|
Дейл —
козак. Дата создания: 21.08.2005. | ||
|
Гайка —
Украинка. Дата создания: 9.08.2005. | ||
|
Дейл и
Вжик. Дата создания: 05,06.08.2005. | ||
|
Наброски с Гаечкой
3. Дата создания: 05.08.2005. | ||
|
Спасатели. Дата
создания: 04-05.08.2005. | ||
|
Наброски с Гаечкой
2. Дата создания: 03,06.08.2005. | ||
|
Наброски с Гаечкой
1. Дата создания: 02,03. | ||
|
Рокки и Вжик — козаки
🙂 Дата создания: 01.08.2005. | ||
|
Чип и
Дейл. Дата создания: 01.08.2005. | ||
|
Рокки и
Вжик. | ||
|
Рисунок Гаечки на
фанере. Дата создания: | ||
|
Гаечка в
цвете. Дата создания: 09.07.05. | ||
|
Гайка. | ||
|
Выпускница
🙂 Дата создания: 01.07.2005. | ||
|
Третья перерисовка
Гаечки. Дата создания: 30.06.2005. | ||
|
Вторая перерисовка
Гаечки. | ||
|
Гаечка.
Дата создания: 05.06.2005. | ||
|
Первая перерисовка
Гаечки. | ||
Связи и их реакции — Теория и решение задач
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными. Тела, ограничивающие свободу перемещения других тел, называются по отношению к ним связями.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными. Ниже приведены примеры замены связей их реакциями. На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.
а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям
Рисунок 1.1
Подробнее про связи и реакции связей смотрите в нашем видео:
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1). Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня) (рисунок 1.2).
а – балка висит на двух тросах;б – действие тросов заменено силами Т1 и Т2;
в – связь «идеальный стержень»;
г – связь «идеальная нить»
Рисунок 1.2
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3, а или 1.3, б). Она может быть заменена либо силой R с углом α (рисунок 1.3, в), либо двумя силами, например, XA и YA (рисунок 1.3, г).
Рисунок 1.3
Всегда можно перейти от R и α к XA и YA (и наоборот):
XA = Rcosα; YA = Rsinα;
Шарнирно-подвижная опора (рисунок 1.4, а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (рисунок 1.4, б).
Рисунок 1.4
Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), их действие заменено силами XA, YA и RB.
Рисунок 1.5
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросим втулку – получим действие на стержень силы RD и момента MD.
Рисунок 1.6
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент MC (рисунок 1.7, б).
Рисунок 1.7
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA) и момент ΜA (рисунок 1.8).
Рисунок 1.8
На рисунках 1.9 – 1.15 показаны примеры замены сил, расположенных в пространстве, их реакциями.
Шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменена системой сил (рисунок 1.9, б) XA, YA и ZA, т.е. силой, неизвестной по величине и направлению.
Рисунок 1.9
На рисунке 1.10, а показан вал, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA, YA, ZA и XB, ZB (рисунок 1.10, б).
Рисунок 1.10
На рисунках 1.11 и 1.12 приведены примеры замены различных связей их реакциями.
Рисунок 1.11
Рисунок 1.12
>> Проекция силы на ось
Вся статика — теоретическая механика
Определение и роль статики в теоретической механике
- Статика
- – это раздел теоретической механики, в котором изучаются условия равновесия материальных тел, находящихся под действием сил, а также методы преобразования сил в эквивалентные системы.
Основной задачей статики является установление законов преобразования системы сил в эквивалентные системы. Методы статики применяются не только при изучении тел, находящихся в равновесии, но и в динамике твердого тела, при преобразовании сил в более простые эквивалентные системы.
Под состоянием равновесия, в статике, понимается состояние, при котором все части механической системы покоятся относительно некоторой инерциальной системы координат. Одним из базовых объектов статики являются силы и точки их приложения.
Понятие силы
- Сила
- , действующая на материальную точку с радиус-вектором со стороны других точек – это мера воздействия других точек на рассматриваемую точку, в результате которой она получает ускорение относительно инерциальной системы отсчета. Величина силы определяется по формуле:
,
где m – масса точки – величина, зависящая от свойств самой точки. Эта формула называется вторым законом Ньютона.
Подробнее, см. «Силы в теоретической механике».
Единицей измерения силы является один Ньютон:
.
В технике широко используется килоньютон:
.
Как следует из определения, сила – это векторная величина, которая, в трехмерном пространстве, имеет три проекции на оси координат. Также задать силу можно с помощью абсолютной величины (модуля) и направления. Для материальной точки, сила приложена к самой точке. Но если мы рассматриваем твердое тело, то кроме вектора силы нам нужно еще указать и точку ее приложения. Таким образом, действие силы на твердое тело характеризуется вектором силы и точкой ее приложения. Если выбрать систему отсчета, то действие силы на твердое тело определяется двумя векторами. Это вектор силы, и вектор, проведенный из начала системы отсчета в точку приложения силы.
- Система сил,
- действующих на тело – это совокупность векторов сил, приложенных к телу, и точек их приложения.
- Эквивалентные системы сил
- Две системы сил являются эквивалентными, если законы движения любых точек твердого тела совпадают при действии любой из этих систем.
- Эквивалентное преобразование системы сил
- – это переход от одной системы сил к эквивалентной ей системе.
- Система взаимно уравновешивающихся сил
- – это система сил, не меняющая уравнений движения или уравнений равновесия твердого тела. То есть это система, эквивалентная отсутствию сил.
- Равнодействующая
- – это одна сила, действие которой эквивалентно действию данной системы сил.
Закрепленные, скользящие и свободные векторы
Поскольку действие силы на твердое тело определяется двумя векторами, то часто под силой подразумевают множество, состоящее из двух векторов – вектора силы, и вектора точки ее приложения относительно выбранной системы координат. Такие множества подразделяются на три класса, для которых вводят специальные термины.
- Закрепленный вектор
- – это множество, состоящее из образующего вектора и точки его приложения. Два закрепленных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.
- Скользящий вектор
- – это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.
- Свободный вектор
- – это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.
- Линия действия силы
- – это прямая, проведенная через точку приложения силы параллельно ее направлению.
Если мы рассматриваем упругое тело, то сила – это закрепленный вектор. Деформации зависят не только от величин и направлений сил, но и от точек их приложения. Если мы рассматриваем движение или равновесие абсолютно твердого тела, то действующая сила является скользящим вектором. Перемещение ее точки приложения вдоль линии ее действия не меняет уравнений движения или уравнений равновесия. Угловая скорость вращения абсолютно твердого тела является свободным вектором. Она характеризует движение в целом, и ее значение одинаково во всех точках тела.
С математической точки зрения, статика – это алгебра скользящих векторов.
Проекции силы на оси координат
Сила в трехмерном пространстве
Вектор силы и ее проекции на оси пространственной системы координат.
Пусть у нас есть декартова система координат Oxyz. И пусть – единичные векторы, направленные вдоль ее осей , и , соответственно. Пусть – проекции вектора силы на оси координат. Тогда разложение силы на составляющие вдоль координатных осей имеет вид:
.
Абсолютное значение (модуль) силы:
.
Введем единичный вектор , направленный вдоль вектора силы . Тогда
.
Эта формула выражает тот факт, что вектор силы можно задать, указав ее модуль F и направление . Вектор имеет три проекции на оси координат: . Поскольку его длина равна единице: , то они связаны соотношением:
.
То есть единичный вектор имеет только две независимые компоненты. Таким образом, для задания вектора силы нужно знать три величины:
либо три проекции на оси координат ;
либо модуль F и направление , которое задается двумя независимыми величинами.
Введем углы между вектором силы и осями координат , и . Тогда проекции силы на оси координат определяются по формулам:
;
.
Косинусы углов называются направляющими косинусами.
- Направляющие косинусы
- вектора – это косинусы углов между вектором и осями координат. Они являются проекциями единичного вектора , сонаправленного с :
,
и связаны соотношением:
.
Сила на плоскости
Вектор силы и ее проекции на оси плоской системы координат.
Результаты, приведенные выше, можно применить и для плоской декартовой системы координат Oxy. В этом случае имеем:
;
;
;
;
;
;
.
Поскольку , то . Последнее уравнение представляет собой известную тригонометрическую формулу:
.
Для задания вектора силы , необходимо знать две независимые величины:
либо проекции вектора на оси координат ;
либо модуль F и направление , которое задается одним углом .
Аксиомы статики
Часть аксиом являются основными законами механики. Другая часть относится к законам преобразования сил, действующих на абсолютно твердое тело, и применяется только к задачам теоретической механики. По своей сути, они выражают собой тот факт, что действие силы на тело является скользящим вектором.
1. Аксиома инерции (закон инерции Галилея)
Существуют такие системы отсчета, в которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если тело покоилось в определенный момент времени, то оно будет покоиться и в последующие моменты.
Такие системы отсчета называются инерциальными. В механике, если это особо не оговорено, под системой отсчета подразумевается именно инерциальная система отсчета. Аксиому инерции иногда формулируют так.
1′. Аксиома инерции
В инерциальной системе отсчета, под действием взаимно уравновешивающихся сил, материальная точка находится в состоянии покоя или движется прямолинейно и равномерно, а первоначально покоившееся тело продолжает покоиться и в последующие моменты времени.
2. Аксиома равновесия двух сил
Две силы, приложенные к абсолютно твердому телу, являются уравновешенными тогда и только тогда, когда они равны по модулю, направлены в противоположные стороны и их линии действия совпадают.
3. Аксиома присоединения и исключения уравновешивающихся сил
Кинематическое состояние твердого тела не изменится, если к действующей на него системе сил прибавить или отнять уравновешенную систему сил.
То есть, прибавляя или исключая уравновешенную систему сил, мы получаем эквивалентную систему сил.
Следствие аксиом 2 и 3
Действие силы на твердое тело не изменится, если точку приложения силы перенести вдоль ее линии действия. То есть сила, приложенная к твердому телу, является скользящим вектором. Доказательство
4. Аксиома параллелограмма сил
Две силы, приложенные к телу в одной точке, можно заменить их равнодействующей силой, равной векторной сумме этих сил и приложенной к той же точке.
Верно и обратное. Любую силу можно разложить на две (и более) силы по правилу векторной суммы (по правилу параллелограмма), приложенных в той же точке, что и исходная сила.
То есть, если силы и приложены в одной точке, то их можно заменить равнодействующей , приложенной к той же точке. Сумму векторов можно найти двумя способами.
1) Можно вычислить проекции сил на оси прямоугольной системы координат:
.
Сложение сил по правилу параллелограмма
2) Можно сложить векторы по правилу параллелограмма (см. рисунок).
;
.
Здесь – угол между векторами и . Точкой обозначено скалярное произведение векторов.
5. Аксиома равенства действия и противодействия (3-й закон Ньютона)
Всякому действию соответствует равное и противоположно направленное противодействие.
То есть если мы возьмем все силы, действующие на тело 2 со стороны тела 1, и объединим их с силами, действующими на тело 1 со стороны тела 2, то получим уравновешенную систему сил.
6. Принцип отвердевания
Если деформируемое тело находится в равновесии, то его равновесие не нарушится, если тело считать абсолютно твердым.
Подробнее, см. «Аксиомы статики».
Система сходящихся сил
- Сходящиеся силы
- – это силы, линии действия которых пересекаются в одной точке.
Система сходящихся сил всегда имеет равнодействующую , равную векторной сумме этих сил:
,
и приложена в точке их пересечения.
Таким образом, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на оси координат:
;
.
Условия равновесия системы сходящихся сил
Если тело или система тел, на которые действует сходящаяся система сил, находится в покое, то равнодействующая этих сил равна нулю:
.
Это дает три уравнения равновесия:
.
Теорема о трех непараллельных силах
Если твердое тело находится в равновесии под действием трех сил, линии действия двух из которых пересекаются в одной точке, то все силы лежат в одной плоскости и являются сходящимися.
Следствие
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то эти силы являются сходящимися.
Параллельные силы
Ранее мы отмечали, что система сходящихся сил имеет равнодействующую. То есть такую систему можно заменить одной силой. Приведем еще важные примеры систем сил, имеющих равнодействующую.
Две силы одного направления
Две параллельные силы F1 и F2 имеют равнодействующую R.
Пусть мы имеем две однонаправленные параллельные силы и . Переместим точки их приложения вдоль линий их действия в точки A и B так, чтобы отрезок AB был перпендикулярен силам. Тогда система сил и имеют равнодействующую , приложенную в точке C. Направление равнодействующей совпадает с направлениями и . Абсолютная величина равна сумме сил:
.
Точка приложения C находится между A и B и делит отрезок AB обратно пропорционально модулям сил:
.
Две противоположно направленные силы
Две не равные противоположно направленные силы F1 и F2 имеют равнодействующую R.
Теперь рассмотрим противоположно направленные силы и , различающиеся по величине, . Пусть . Эта система также имеет равнодействующую , направление которой совпадает с направлением большей по модулю силы, а абсолютное значение равно абсолютному значению разности модулей сил:
.
Точка приложения C равнодействующей находится на продолжении отрезка AB, ближе к наибольшей по модулю силе . Расстояния до точек A и B также обратно пропорциональны и :
.
Момент силы относительно точки
Определение
- Моментом силы
- , приложенной к телу в точке A, относительно точки O, называется вектор , равный векторному произведению векторов и :
(2) . - Плечом силы
- относительно точки O, называется кратчайшее расстояние между линией действия этой силы и точкой O. Другими словами, плечо силы – это длина перпендикуляра, опущенного из точки O на линию действия силы.
Абсолютное значение момента силы относительно точки O равно произведению силы на плечо этой силы относительно выбранной точки O. Направление момента перпендикулярно плоскости, проходящей через точку O и линию действия силы.
Доказательство
Геометрическая интерпретация
Момент силы равен произведению силы F на плечо OH.
Пусть векторы и расположены в плоскости рисунка. Согласно свойству векторного произведения, вектор перпендикулярен векторам и , то есть перпендикулярен плоскости рисунка. Его направление определяется правилом правого винта. На рисунке вектор момента направлен на нас. Пусть α – угол между векторами и . Абсолютное значение момента:
.
Из точки O проведем перпендикуляр OH к линии действия силы . Из прямоугольника OAH имеем: . Тогда
.
То есть абсолютное значение момента силы относительно точки O равно произведению силы F на плечо |OH| этой силы относительно точки O.
Компоненты момента силы в декартовой системе координат
Выберем декартову систему координат Oxyz с началом в точке O. Найдем компоненты вектора момента силы в этой системе координат относительно ее начала.
.
Здесь – единичные векторы в направлении осей ; – координаты точки A в выбранной системе координат: .
Таким образом, момент силы имеет следующие компоненты:
(М.1) ;
(М.2) ;
(М.3) .
Компоненты представляют собой значения момента силы относительно осей , соответственно.
Свойства момента силы относительно центра
Момент относительно центра O, от силы, проходящей через этот центр, равен нулю.
Доказательство
Если точку приложения силы переместить вдоль линии, проходящей через вектор силы, то момент, при таком перемещении, не изменится.
Доказательство
Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство
То же самое относится и к силам, чьи линии продолжения пересекаются в одной точке.
Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство
Теорема Вариньона о моменте равнодействующей
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки равен векторной сумме моментов сил системы относительно той же точки.
Пара сил
Из предыдущих формул ⇑ видно, что если противоположно направленные силы имеют равные модули: , то система сил не имеет равнодействующей. Действительно, в этом случае . Пытаясь использовать предыдущие формулы, мы получим деление на нуль. Такую систему сил называют парой сил.
- Пара сил
- – это система из двух сил , равных по абсолютной величине, имеющих противоположные направления, приложенных к разным точкам тела и не лежащих на одной прямой.
- Плечо пары сил
- – это кратчайшее расстояние h между линиями действия сил, входящих в пару.
- Момент пары сил
- – это векторная сумма моментов сил, входящих в пару, вычисленная относительно любой точки. Абсолютное значение момента пары равно произведению силы на плечо пары:
.
Теорема о независимости выбора центра при вычислении момента пары
Векторная сумма моментов сил, составляющих пару, не зависит от выбора точки, относительно которой вычисляются моменты.
Теорема об эквивалентности пар
Две пары, имеющие равные векторы моментов, эквивалентны. То есть у пары можно менять модуль силы и длину плеча, оставляя неизменным ее момент.
Теорема о возможности перемещения пары
Пару сил можно переносить в любом направлении. Другими словами, если пару сил переместить параллельным переносом в любое положение, то она будет эквивалентна исходной паре.
Теорема о сложении нескольких пар
Система нескольких пар сил эквивалентна одной паре, вектор момента которой равен векторной сумме моментов исходных пар.
Условие равновесия пар
Система, состоящая только из нескольких пар, является уравновешенной, если векторная сумма моментов пар равна нулю:
.
Момент силы относительно оси
Часто встречаются случаи, когда нам нужно знать не все компоненты момента силы относительно выбранной точки, а только проекцию момента на выбранное направление.
- Момент силы относительно оси,
- проходящей через точку O – это проекция вектора момента силы относительно точки O, на направление оси.
Свойства момента силы относительно оси
Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство
Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство
Вычисление момента силы относительно оси
Момент силы относительно оси.
Пусть на тело, в точке A действует сила . Найдем момент этой силы относительно оси O′O′′.
Построим прямоугольную систему координат. Направим ось z вдоль O′O′′. Из точки A опустим перпендикуляр AO на O′O′′. Через точки O и A проводим ось Ox. Перпендикулярно Ox и Oz проводим ось Oy. Разложим силу на составляющие вдоль осей системы координат:
.
Сила пересекает ось O′O′′. Поэтому ее момент равен нулю. Сила параллельна оси O′O′′. Поэтому ее момент также равен нулю. По формуле (М.3) находим:
.
Заметим, что компонента направлена по касательной к окружности, центром которой является точка O. Направление вектора определяется правилом правого винта.
Условия равновесия
Главный вектор и главный момент
- Главный вектор
- – это векторная сумма всех сил, приложенных к телу.
- Главный момент
- относительно данного центра – это векторная сумма моментов всех сил, приложенных к телу относительно выбранного центра.
Подчеркнем, что величина главного момента зависит от выбора центра, относительно которого вычисляются моменты.
Пространственная система сил
Основная форма условий равновесия
Условия равновесия системы сил
Для того, чтобы твердое тело под действием произвольной системы сил находилось в равновесии, необходимо и достаточно, чтобы главный вектор и главный момент, относительно произвольной точки C, равнялись нулю:
;
.
Здесь – точка приложения силы , .
Доказательство
Это основная форма условий равновесия. Точка C может, как принадлежать телу, так и находится за его пределами. Обычно центр C выбирают так, чтобы сделать вычисления более простыми. Спроектировав каждое из этих векторных уравнений на три направления, получим шесть уравнений, из которых можно определить шесть неизвестных величин.
Вторая форма условий равновесия
Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
;
;
.
Доказательство
Третья форма условий равновесия
Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
;
;
;
.
Доказательство
Плоская система сил
- Плоская система сил
- – это система сил, расположенных в одной плоскости. То есть точки приложения всех сил расположены в одной плоскости, а направления сил параллельны этой плоскости.
Все изложенное для пространственной системы сил является применимым и для плоской системы. Направим оси x и y декартовой системы координат в плоскости действия сил, а ось z – перпендикулярно. Тогда z компоненты координат точек и сил равны нулю: . Также равны нулю x, y компоненты моментов сил относительно произвольной точки C: . То есть момент может иметь отличное от нуля значение только для z компоненты. Поскольку z компонента не входит в плоскую систему координат xy, то, в двумерном пространстве, момент силы уже не является вектором, а является скаляром (точнее псевдоскаляром). Его называют алгебраическим моментом силы относительно центра C (или просто моментом силы относительно центра C), и обозначают символом с маленькой буквы без знака вектора:
.
Величина является моментом силы относительно оси, проходящей через точку C перпендикулярно плоскости действия сил. Момент вычисляют как произведение модуля силы на плечо со знаком плюс или минус:
.
Если, при неподвижном центре C, сила стремится повернуть систему против часовой стрелки, то момент положителен . В противном случае – отрицательный: .
Величину момента от силы , приложенной в точке A, относительно центра C, также можно выразить через компоненты векторов по формуле:
,
где и – координаты точек A и C, соответственно.
Условия равновесия плоского тела
Для плоской системы сил можно составить три уравнения, из которых можно определить три неизвестных величины. Считаем, что сила приложена в точке .
Основная форма условий равновесия
;
;
.
Вторая форма условий равновесия
;
;
.
Третья форма условий равновесия
;
;
;
.
Связи и их реакции
Определения и свойства
- Свободное тело
- Тело называется свободным, если его перемещения ничем не ограничены.
- Несвободное тело
- Тело, перемещение которого ограничено другими телами, называется несвободным.
- Связи
- Тела, ограничивающие перемещения данного тела, называются связями.
- Реакции связей
- Силы, с которыми связи действуют на данное тело, называются реакциями связей.
Принцип освобождаемости
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.
Основные типы связей и их реакции
Плоские и пространственные задачи
Две гладкие не острые поверхности. Через точку соприкосновения проводим касательную плоскость к этим поверхностям. Реакция является силой, направленной перпендикулярно этой плоскости, то есть, направлена по нормали к обеим поверхностям в точке их соприкосновения.
Одна из гладких поверхностей является острием. Реакция является силой, направленной вдоль нормали не острой поверхности в точке соприкосновения.
Две шероховатые поверхности. То же самое, что и для гладких поверхностей, только в точке соприкосновения добавляем силу трения, лежащую в плоскости касания.
Невесомая нить и стержень. Реакция направлена вдоль нити или стержня. При этом на нить всегда действует сила растяжения. На стержень может действовать как растягивающая, так и сжимающая сила.
Плоские задачи
Следующие связи применяют только в плоских задачах.
Неподвижный шарнир. Реакция является силой, проходящей через ось шарнира. Обычно ее раскладывают на две составляющие параллельно осям координат.
Подвижный шарнир, или опора на катках. Реакция является силой, которая проходит через ось шарнира перпендикулярно опорной поверхности.
Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно оси, проходящей через точку соединения перпендикулярно плоскости фигуры. Силу обычно раскладывают на две составляющие параллельно осям координат.
Пространственные задачи
Цилиндрический шарнир или петля. Реакция является силой, проходящей через ось шарнира, перпендикулярно направлению оси. Обычно ее раскладывают на две составляющие параллельно осям координат.
Сферический подшипник или подпятник. Реакция является силой, проходящей через центр подшипника. Обычно ее раскладывают на три составляющие параллельно осям координат.
Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно этой точки. Силу и момент обычно раскладывают на три составляющие параллельно осям координат.
Силы трения
- Сила трения
- Пусть два тела находятся в соприкосновении. Сила трения – это сила, параллельная плоскости соприкосновения тел, которая возникает между телами при попытке сместить одно тело относительно другого, препятствующая их относительному смещению.
Трение скольжения
Сила трения скольжения Fтр = f·N.
Рассмотрим тело, которое скользит по поверхности другого тела с отличной от нуля скоростью v под действием внешней силы . Если поверхности абсолютно гладкие, то в точках соприкосновения тел возникает только сила давления N, перпендикулярная плоскости соприкосновения тел. Для шероховатых поверхностей, возникает еще сила трения , параллельная плоскости соприкосновения, направленная в сторону, противоположную скорости движения. Величина силы трения пропорциональна силе давления и не зависит от площади соприкосновения поверхностей:
(Т1) .
Здесь f – безразмерный коэффициент, который называется динамическим коэффициентом трения, или коэффициентом трения скольжения. Он зависит от материалов и обработки соприкасаемых поверхностей и почти не зависит от скорости относительного движения. При расчетах его считают постоянной.
- Сила трения скольжения
- – это сила трения, приложенная к точкам соприкосновения движущихся тел и параллельная плоскости их соприкосновения. То есть это сила, препятствующая скольжению одного тела по поверхности другого. При расчетах, под силой трения скольжения понимают равнодействующую всех сил трения, возникающих в точках соприкосновения тел.
Закон Амонта – Кулона
Сила трения скольжения направлена параллельно плоскости соприкосновения тел в сторону, противоположную их движению, которое возникло бы при отсутствии трения. Она не зависит от площади соприкосновения поверхностей, а зависит от силы давления N одной поверхности на другую, перпендикулярную плоскости соприкосновения тел:
.
Трение сцепления
Сила трения сцепления. Движение возможно при tg φ > f0.
Теперь рассмотрим статическую задачу. Пусть тело покоится, и на него действуют внешние силы с равнодействующей , приложенной под углом φ к нормали поверхности. Разложим ее на две составляющие: параллельную поверхности, и перпендикулярную . На тело также действуют сила реакции , перпендикулярная плоскости соприкосновения тел, и сила трения , которую при отсутствии скольжения называют силой сцепления. Сила сцепления направлена параллельно поверхности, препятствуя движению. Она может принимать значения от нуля до максимальной величины , определяемой аналогично (Т1):
(Т2) .
Здесь – статический коэффициент трения, который еще называют коэффициентом сцепления. Он не может быть меньше динамического коэффициента трения: .
Если , тело покоится. При этом сила трения сцепления меньше максимальной величины: . При , возникает движение. Когда , сила трения достигает предельной величины, возникает состояние предельного равновесия. Дальнейшее увеличение приводит к потере равновесия.
- Сила трения сцепления
- – это сила трения скольжения, когда относительное перемещение соприкасающихся тел отсутствует.
- Предельная сила трения
- – это максимальное значение силы трения сцепления.
- Предельное равновесие
- – это состояние равновесия, при котором значение силы трения сцепления равно ее максимальному значению.
Из условий равновесия имеем: . Подставим в (Т2):
.
Отсюда получаем, что система будет находиться в равновесии, если
.
Видно, что условие равновесия зависит от угла φ, под которым приложена равнодействующая внешних сил, и не зависит от ее величины. Введем предельный угол трения: . Эту величину также называют просто углом трения. Тогда, условие равновесия можно записать так:
.
Это неравенство определяет конус в пространстве, который называется предельным конусом трения, конусом трения, или конусом сцепления. Если направление силы выходит за пределы этого конуса, то система начинает движение. Если направление силы попадает в конус сцепления, то система остается в состоянии покоя. Такое явление называется заклиниванием механизма.
- Заклинивание механизма
- – это явление в механике, при котором система остается в состоянии покоя при любом, сколь угодно большом увеличении модуля внешней силы.
Условие возникновения движения при наличии трения
Для того чтобы тело начало движение, необходимо и достаточно, чтобы равнодействующая внешних сил находилась вне конуса трения.
Трение качения
Силы, возникающие при деформации, препятствуют качению тела круглой формы по плоской поверхности.
Рассмотрим случай, когда одно из тел круглой формы катится без проскальзывания по поверхности другого. С точки зрения механики, такие тела соприкасаются в одной точке A. Площадь их соприкосновения бесконечно мала, в результате чего возникает бесконечно большое давление, которое не могут выдержать реальные материалы. Поэтому вблизи точки соприкосновения тел возникает деформация, которая имеет место только в небольшом участке соприкасающихся тел. В основной части тел, удаленных от точек соприкосновения, деформация практически отсутствует, и их можно рассматривать как абсолютно твердые тела. Тогда систему сил, возникающую в результате соприкосновения, можно привести к некоторой равнодействующей силе . При этом оказывается, что точка ее приложения смещена относительно оси симметрии катящегося тела. Это приводит к появлению момента сил относительно точки A, расположенной на оси симметрии круглого тела. Изучение деформированного состояния выходит за рамки теоретической механики. Поэтому мы приводим лишь результаты, применяемые в расчетах.
Расчетная схема трения качения.
1. Поскольку деформации, для небольших значений внешних сил малы, то, считают, что они не влияют на геометрические характеристики тел. То есть считают, что тела округлой формы соприкасаются в одной точке.
2. В точке соприкосновения, на тело действуют:
сила давления , перпендикулярная соприкасающимся поверхностям;
сила сцепления , лежащая в касательной плоскости, проходящей через точку соприкосновения поверхностей;
момент силы трения , препятствующий движению.
Максимальное значение момента силы трения определяется по формуле:
,
где δ – коэффициент трения качения, который имеет размерность длины.
3. Коэффициент трения качения зависит от соприкасающихся материалов и состояния их поверхностей. Он не зависит от кривизны поверхностей и угловой скорости вращения тела. А при движении с проскальзыванием, не зависит от скорости скольжения.
Центр тяжести тела
Центр тяжести в пространстве
Пусть тело состоит из n материальных точек. И пусть на каждую точку Bi действует сила тяжести , . Все силы тяжести, действующие на точки, параллельны. Поэтому мы имеем дело с параллельной системой сил. Как и для системы из двух однонаправленных сил, такая система сил имеет равнодействующую. Найдем ее.
Пусть – главный вектор. Поскольку все силы имеют одинаковое направление, то введем единичный вектор , направленный вдоль сил:
. Отсюда .
Найдем момент сил тяжести относительно произвольно расположенного центра O.
,
где
(ЦТ1) .
Отсюда видно, что формула вычисления момента имеет вид формулы момента от одной силы , приложенной в точке C. Точка C, положение которой определяется формулой (ЦТ1), называется центром тяжести тела. Таким образом, равнодействующая отдельных сил тяжести точек тела равна главному вектору силы тяжести, приложенному в центре тяжести. Модуль P равнодействующей называют весом тела.
Если бы мы находили равнодействующую сил тяжести, выполняя эквивалентные преобразования сил, то мы бы нашли только линию действия равнодействующей. Далее, если повернуть тело на некоторый угол, то можно найти другую линию действия равнодействующей. При этом все, подобным образом построенные линии, пересекаются в одной точке, которая и является центром тяжести тела.
- Центр тяжести твердого тела
- – это точка, связанная с телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела, при любом положении тела в пространстве.
- Вес тела
- – это абсолютное значение равнодействующей сил тяжести частиц, составляющих тело.
Координаты центра тяжести определяются по формулам:
(ЦТ2) .
Здесь – абсолютное значение равнодействующей сил тяжести, или вес тела. – координаты точек тела. Эти формулы также можно записать в векторном виде.
.
Центр тяжести C связан с телом. Однако его положение может находиться за его пределами. Например, при наличии полости.
В случае, когда силы имеют другое происхождение, но также имеют одинаковое направление, то мы имеем дело с системой параллельных сил. В этом случае, точка C называется центром параллельных сил.
Для сплошного однородного тела, мы от суммирования переходим к интегрированию. Элементарная сила тяжести выражается через плотность ρi элементарной частицы тела, массой , и занимающей объем :
.
Здесь g – ускорение свободного падения. Переходя от суммированию к интегрированию, имеем:
(ЦТ3) .
Центр тяжести плоской фигуры
Рассмотрим плоскую фигуру. Выберем двумерную систему координат Oxy. Тогда положение центра тяжести определяется по тем же формулам (ЦТ2) и (ЦТ3), из которых нужно убрать переменную z.
Однородная фигура
Рассмотрим плоскую однородную фигуру. Для такой фигуры, плотность ρ является постоянной; сила тяжести Δpi элементарной частицы пропорциональна площади ΔAi этой частицы: Δpi = ρΔAig. Вес P фигуры пропорционален площади A всей фигуры: P = ρAg.
Подставляя эти величины в формулы, определяющие положение центра тяжести находим:
.
Переходим от суммирования к интегрированию:
.
Мы видим, что сюда не входят плотность ρ и ускорение свободного падения g. Остались величины, зависящие только от геометрии сечения. Таким образом, для тела с постоянной плотностью, центр тяжести является геометрической характеристикой.
В этих формулах, yC есть алгебраическое расстояние от центра тяжести до оси x; yk или y – алгебраическое расстояние элементарного участка до той же оси. xC, xk и x – соответствующие алгебраические расстояния до оси y. В этой связи вводят новую геометрическую характеристику сечения, которую называют статическим моментом.
- Статический момент относительно некоторой оси
- – это сумма произведений элементарных площадей , входящих в состав фигуры, на алгебраические значения их расстояний до этой оси.
В рассматриваемом нами случае, статические моменты относительно осей x, y определяются по формулам:
.
Статические моменты широко используются при расчете конструкций. Для стандартных профилей, их значения указываются в соответствующих справочниках.
Центры тяжести простейших фигур
Параллелограмм, прямоугольник, квадрат: в точке пересечения диагоналей.
Треугольник: в точке пересечения медиан, которая делит каждую медиану в соотношении 1:2.
Дуга окружности с центральным углом 2α: .
Круговой сектор: .
Теоремы, применяемые при расчете центра тяжести
Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.
Центр тяжести фигуры, составленной из n более простых фигур, определяется по формуле:
(ЦТ4) .
Здесь – площадь всей фигуры; – площадь и координаты центра тяжести простой фигуры, входящей в состав сложной.
Способ отрицательных площадей (объемов)
Если k — я фигура вырезана из объемлющей ее части, то, в формуле (ЦТ4), соответствующая ей площадь считается отрицательной: .
Распределенная нагрузка
Равномерно (А) и линейно (Б) распределенная нагрузка.
Силу тяжести протяженных тел, на схемах, изображают в виде эпюр. Также встречаются подобные силе тяжести параллельные силы, приложенные не в определенных точках тела, а непрерывно распределенные по его поверхности или объему. Такие силы называют распределенными силами или распределенными нагрузками.
Равномерно распределенная нагрузка q (рисунок А). Ее можно заменить равнодействующей силой величины , приложенной в центре тяжести эпюры. Поскольку, на рисунке А, эпюра представляет собой прямоугольник, то ее центр тяжести находится в центре основания эпюры – в точке C: |AC| = |CB|.
Линейно распределенная нагрузка q (рисунок В). Ее также можно заменить равнодействующей. Величина равнодействующей равна площади эпюры:
.
Точка приложения находится в центре тяжести эпюры. Центр тяжести треугольника, высотой h, находится на расстоянии от основания. Поэтому .
Приведение системы сил к центру
Теорема о параллельном переносе силы (лемма Пуансо)
Сила, действующая на данное тело, эквивалентна силе, полученной параллельным переносом исходной силы в любую точку тела и паре сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.
Теорема о приведении системы сил к заданному центру
Любую систему сил, действующих на данное тело, можно привести к заданному центру O – то есть заменить одной силой, равной главному вектору, приложенной к точке приведения O, и парой сил с моментом MO, равным главному моменту относительно центра O.
Статические инварианты
- Статические инварианты
- пространственной системы сил – это такие величины, которые не зависят от центра приведения.
Такими инвариантами являются:
1) главный вектор ;
2) скалярное произведение главного вектора на главный момент .
Главный вектор равен векторной сумме всех сил и поэтому не зависит от центра приведения O. Главный момент зависит от положения центра O, относительно которого вычисляются моменты. Но величина его скалярного произведения на главный вектор не зависит от того, относительно какой точки вычисляется главный момент.
Хотя главный вектор не зависит от положения центра O, но величины его проекций на оси координат зависят от выбора системы координат. Поэтому они также не являются инвариантами. По той же причине и направление главного вектора не является инвариантом. Единственной численной величиной, которая не зависит от выбора системы координат, является модуль главного вектора. Но, в математическом отношении, проще иметь дело с квадратом модуля. Поэтому мы выберем его в качестве основного инварианта.
Итак, статическими инвариантами являются следующие величины:
– квадрат модуля главного вектора;
– скалярное произведение главного вектора на главный момент. Инвариантами также являются функции от инвариантов. Например, проекция главного момента на направление главного вектора является инвариантом:
.
Динама
Разложим главный момент на компоненту , параллельную главному вектору , и на компоненту , перпендикулярную :
(П1) .
Тогда .
Отсюда получаем упомянутый выше результат, что инвариантом является алгебраическая величина проекции главного момента на направление главного вектора:
.
Динама – одна из простейших систем сил.
То есть, при изменении положения центра O, меняется вектор , в то время как вектор остается постоянным. Выбором центра приведения O, можно обратить в нуль. Тогда мы получим систему, состоящую из главного вектора и пары сил с моментом , лежащих в плоскости, перпендикулярной главному вектору. Такая система называется динамой или силовым винтом. Система приводится к динаме, если второй статический инвариант не равен нулю.
- Динама
- – это простейшая система сил, состоящая из силы , приложенной к некоторой точке C, и паре сил, перпендикулярных . При этом момент пары параллелен линии действия силы. Динаму также называют силовым винтом, динамическим винтом, или статическим винтом.
- Ось винта
- – это линия действия силы динамического винта.
Из (П1) мы находим, что минимальное значение модуля момента равно модулю его проекции на направление главного вектора:
.
Центральная ось системы сил
Пусть и – главный вектор и главный момент относительно некоторого центра O, который выберем за начало координат. И пусть второй инвариант отличен от нуля:
.
Найдем положение такой точки C, относительно которой система сил приводится к динаме. Для этого преобразуем главный момент от центра O к C:
.
Отсюда
(П2) .
Для динамы, векторы и направлены вдоль одной прямой. Поэтому
, где λ – некоторое число. Отсюда получаем два уравнения:
(П3) .
Пусть – компоненты вектора . Тогда подставив (П2) в (П3), имеем:
.
Это уравнение прямой в пространстве, которую называют центральной осью системы сил. Относительно точек этой прямой, система сил приводится к динаме, а главный момент имеет наименьшее по модулю значение.
- Центральная ось системы сил
- – это прямая, обладающая тем свойством, что при приведении системы сил к любой из ее точек, система сил является динамой. При этом главный вектор и главный момент динамы параллельны этой прямой, а главный момент имеет наименьшее по модулю значение.
Приведение системы сил к простейшему виду
Пара сил
Пусть .
Тогда . Второй инвариант также равен нулю: . В этом случае, вектор главного момента не зависит от положения центра O. Система сил приводится к паре с моментом .
Если и , то это уравновешенная система сил. Она эквивалентна отсутствию сил.
Равнодействующая сила
Пусть .
В этом случае существует прямая, относительно точек которой главный момент равен нулю:
.
То есть система приводится к одной силе – равнодействующей, равной главному вектору приложенному к любой из точек упомянутой выше прямой. Эта прямая является линией действия главного вектора. Примеры: система сходящихся сил, система параллельных сил. Это системы, которые имеют равнодействующую.
Динама
При , как показано выше, система сил приводится к динаме.
Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
Автор: Олег Одинцов. Опубликовано: Изменено:
Авторская статья «Хонингование» на сайте инженерной-технологической компании Механика
Не так давно искал в Яндексе (не сочтите за рекламу) картинки и наткнулся на давно забытый «дрынохон». Решил заглянуть на сайт, где была размещена фотка. Вот, что там было изложено:
…Перед сборкой двигателя в обязательном порядке проводится хонингование зеркал цилиндров с целью достижения правильной посадки на них поршневых колец, обеспечивающей должную герметичность камер сгорания…
…Выпускаются два типа хонов для обработки зеркал цилиндров: хон типа «бутылочный ершик» и, более традиционный, поверхностный хон в виде насадки с подпружиненными точильными камнями. Оба инструмента обеспечивают необходимое качество обработки зеркал цилиндров, хотя использование первого для неопытного механика предпочтительнее. Потребуется также достаточное количество ветоши, специального хонинговочного или просто жидкого машинного масла, а также электродрель в качестве привода для хонинговочных насадок. Действуйте в следующем порядке….
|
Дрынохон как он есть и в действии |
Далее описана процедура гаражного хонингования. Неужели и сейчас кто-то производит восстановление цилиндров подобными методами. Я полагал, что к подобным текстам уже давно приписали что-то типа «устаревший метод, сейчас так никто не делает». Текст как водится размножен на многих сайтах (эдакий сетевой бэкап коллективного разума) и кто-то сочтёт, что этот метод вполне современен. Однако ж, технологии давно ушли вперёд и теперь дороже будет найти дрынохон, чем сделать хон на соответствующем станке. Преимущество «дрынохона» только в том, что поцарапать цилиндр можно не снимая блок с автомобиля. Фактически так можно только «освежить», но не сделать нормальный хон в изношенном цилиндре. Уж поверьте.
Немного теории и технологии
Хонингование — (от англ. honing, от hone — хонинговать, буквально — точить). Вид абразивной обработки материалов с применением хонинговальных головок (хонов). В основном применяется для обработки внутренних цилиндрических отверстий путём совмещения вращательного и поступательно-возвратного движения хона с закреплёнными на нём раздвижными абразивными брусками с обильным орошением обрабатываемой поверхности смазочно-охлаждающей жидкостью. Хотя также встречается и наружное хонингование, но выполняется такая операция на специализированных станках. Наружное хонингование применяется на деталях большой длины, обработка которых в обычных металлообрабатывающих станках не представляется возможным. Например, штоки гидротормозов артиллерийских орудий. Хонингование наружных поверхностей может осуществляется на модернизированных (шлифовальных, горизонтально-расточных) станках. Хонинговать можно детали как из черных материалов (стали и чугуны), так и из цветных (латуни, бронзы, алюминиевые цинковые и магниевые сплавы).
Хонингование применительно к деталям двигателя внутреннего сгорания
При ремонте двигателя, как это было сказано ранее, хонингуют в основной своей массе внутренние цилиндрические поверхности — отверстия. Это втулки верхней головки шатуна, отверстия нижней головки шатуна, втулки коромысел привода клапанного механизма, постели коленчатого вала и конечно же цилиндры двигателя.
|
Хонголовка с хонбрусками в цилиндре |
Если считать, что цилиндры — это сердце мотора, то знания о хонинговании, свойствах получаемой поверхности и методах её получения — это кардиология.
Для нормальной работы поршневых колец (кардиологический аналог каждый может себе придумать сам) на стенке цилиндра необходимо обеспечить определённый микропрофиль поверхности — совокупность пересекающихся рисок. Глубина и взаимное расположение этих рисок в значительной степени определяет такие эксплуатационные параметры как компрессия, мощность, расход масла, расход топлива, износ цилиндро-поршневой группы и ресурс двигателя. Нанесение этих рисок как раз и происходит при работе хонинговальной головки с установленными в неё брусками по поверхности цилиндра. Одновременное вращение инструмента и его возвратно поступательные движения (это Вам не туда-сюда дрынохоном:) определяет угол взаимного пересечения рисок на поверхности цилиндра — угол хонингования. Вид применяемого абразива, его зернистость и связка определяет шероховатость поверхности цилиндра, глубину и размер рисок. Соответственно не сложно догадаться, что следует различать черновое и чистовое хонингование, а следовательно и применяемые при хонинговании бруски. «Законодатель моды» в данном вопросе — фирма KOLBENSCHMIDT (KS) — дает чёткие рекомендации по выполнению данной операции. Поэтому я решил не ловить в цеху момент для съемки процесса хонингования и даже не пошел на склад за брусками. Я просто отсканировал картинки из буклета KS. Так вот, рекомендации распространяются на применение абразивных и смазочных материалов, настройку оборудования, припуски на обработку и самое главное — методы контроля качества выполненной работы. Для контроля шероховатости немцы применяют тестер Hommel с возможностью вывода на печать диаграммы микропрофиля и параметров шероховатости в оценочных единицах. Для контроля угла хонингования — применяется специальная пленка-шаблон. На фото она приложена к стенке цилиндра.
|
Пленка-шаблон для проверки линий хона и наглядный рисунок самих линий из рекомендаций KS |
|
Прибор для контроля шероховатости Hommel |
О практическом влиянии параметров хонингования или разрушение мифа, о «зеркальной», абсолютно гладкой поверхности цилиндра
Для надёжного удержания масла на поверхности цилиндра (чего ради собственно и затеяна вся эта вращательно-поступательная «возня»), стенка последнего должна иметь определённую шероховатость абсолютно гладкая стенка не способна удержать на себе масло, в количестве необходимом для нормальной смазки колец. С абсолютно гладкой, зеркальной, поверхности масло будет сниматься почти полностью, оставшееся масло будет сгорать, а нового масла, необходимого для нормальной смазки поступать не будет. Таким образом будут формироваться условия для сухого трения, которое вызывает повышенный износ. Поверхность, обладающая высокой шероховатостью, способна значительно лучше задерживать на себе масло и соответственно воспринимать более высокие механические нагрузки. Низкая шероховатость удерживает масло несколько хуже. Больший угол хонингования влияет на расход масла (угар), но в этом случае меньше проявляется волнистость поверхности цилиндра. Маленький угол влияет на снижение расхода масла. Вот такие закономерности. Поэтому требуется подбор режимов хонингования и применяемых материалов, которые и обеспечивают необходимый результат.
Грубая поверхность (глубокие риски — высокая шероховатость) получаются после применения крупно зернистого абразива, на первой стадии чернового хонингования. Здесь применяют алмазные бруски на медной основе. Хонингование ведётся с избытком СОЖ. Для выноса из зоны резания продуктов износа, как материала цилиндра, так и материала бруска. Получаемая после чернового алмазного хонингования поверхность непригодна для работы по ней колец, поршня да и работы вообще. В некоторых случаях алмазное (силовое) хонингование служит заменой расточки цилиндра, с той лишь разницей, что процесс хонингования более производительный и легче поддаётся автоматизации.
На второй стадии полученная поверхность обрабатывается более мелкозернистым абразивом, но не чистовым. При этом формируется новый микропрофиль поверхности. На данном этапе применяют абразивные материалы с размером зерна 1/150 мм.
Окончательное хонингование ведется материалами с зерном от 1/300 — 1/500 мм, до достижения окончательного размера цилиндра.
Финишная операция при хонинговании — хонинговое крацевание. При этой операции не происходит изменение размера цилиндра (отверстия) полученного при чистовом хонинговании. При этой операции полученный микропрофиль полностью очищается от остатков хонинговального абразива, обнажаются графитовые зёрна (для чугунных цилиндров), что влияет на снижение трения, а следовательно на механические потери и износ. При крацевании используют специальные щётки, из нейлоновых нитей с добавлением кристаллов кремния.
|
Щётки для крацевания |
Используя оборудование для хонингования можно проводить также нанесение анифрикционных покрытий на стенки цилиндров, обрабатывать цилиндры алюминиевых блоков (правда не всех) и выполнять плосковершинное хонингование. Данные операции принципиально не отличаются от обычного хонингования. Для их проведения необходимы специальные материалы и хонинговальные бруски.
|
Специальные хонинговальные бруски |
Применяется хонингование закалённых зубчатых колёс хонинговальной головкой в форме косозубого долбяка находящейся в зацеплении с обрабатываемым колесом и совершающей одновременно вращательное и колебательное движения. Н это уже экзотика:
P.S. С начала 2011 года желающие могут сходит на экскурсию по цеху механобработки в техцентре «Дзержинский». Записаться можно по электронной почте. Вам покажут и
расскажут в том числе и о хонинговании. Бутербробы и термос брать не обязательно — обещаем накормить.
отзывы, фото и характеристики на Aredi.ru
Мы доставляем посылки в г. Калининград и отправляем по всей России
- 1
Товар доставляется от продавца до нашего склада в Польше. Трекинг-номер не предоставляется.
- 2
После того как товар пришел к нам на склад, мы организовываем доставку в г. Калининград.
- 3
Заказ отправляется курьерской службой EMS или Почтой России. Уведомление с трек-номером вы получите по смс и на электронный адрес.
!
Ориентировочную стоимость доставки по России менеджер выставит после оформления заказа.
Гарантии и возврат
Гарантии
Мы работаем по договору оферты, который является юридической гарантией того, что мы выполним
свои обязательства.
Возврат товара
Если товар не подошел вам, или не соответсвует описанию, вы можете вернуть его, оплатив
стоимость обратной пересылки.
- У вас остаются все квитанции об оплате, которые являются подтверждением заключения сделки.
- Мы выкупаем товар только с проверенных сайтов и у проверенных продавцов, которые полностью отвечают за доставку товара.
- Мы даем реальные трекинг-номера пересылки товара по России и предоставляем все необходимые документы по запросу.
- 5 лет успешной работы и тысячи довольных клиентов.
Кафедра машиноведения
Учебная работа
Кафедра осуществляет обучение по направлению подготовки:Кроме того, кафедра проводит подготовку кадров высшей научной квалификации через аспирантуру и докторантуру по специальности «Машины, агрегаты и процессы (легкая промышленность)».
- Дисциплины, преподаваемые на кафедре
- основы автоматизированного проектирования
- вычислительные методы для инженеров
- компьютерные системы инженерных расчетов
- математические модели механизмов машин и моделирование на ЭВМ
- расчет и конструирование типовых узлов машин
- расчет и конструирование робототехнических комплексов
- динамика узлов и механизмов машин
- надежность машин
- гидравлика
- монтаж, эксплуатация и ремонт текстильных машин
- машины и агрегаты прядильного производства
- машины и аппараты ткацкого производства
- машины трикотажного производства
- конструкции узлов и механизмов текстильных машин
- монтаж, эксплуатация и ремонт машин легкой промышленности
- машины и аппараты швейной промышленности
- машины, аппараты и технологические линии кожевенной и обувной промышленности
- технология кожевенной и обувной промышленности
- машины и аппараты производства химических волокон
- конструкции узлов и механизмов машин легкой промышленности
- лифты и подъемно-транспортное оборудование
- монтаж, наладка, эксплуатация и ремонт лифтов и подъемно-транспортного оборудования
- проектирование лифтов и подъемно-транспортного оборудования
- основы системного проектирования
- технология машиностроения
- оборудование механообрабатывающего производства
- исполнительные элементы узорообразующих механизмов
- Оборудование швейного производства и основы проектирования оборудования
- проектирование текстильных машин
- нелинейные задачи динамики механизмов машин отрасли
- математическое моделирование узлов машин и аппаратов отрасли
- компьютерная система научных расчетов
- синтез рычажных механизмов машин отрасли
- основы научных исследований
- современные проблемы науки в области технологии машиностроения
- история и методология науки в области технологии машиностроения
- компьютерные технологии в науке и образовании
- компьютерные технологии в инженерной графике
- технический рисунок
Научная работа
В составе кафедры работают: 4 профессора и 8 доцентов.
Сотрудниками кафедры получено более 100 авторских свидетельств, 10 патентов на изобретения, опубликовано более 12 монографий.
Под руководством профессоров Мазина Л.С. и Полякова В.К. выполняются научные исследования в области анализа и разработки узлов и механизмов машин отрасли, математического моделирования динамики механизмов машин, исследования быстровращающихся роторных узлов машин отрасли и др.
- Основные научные направления
- Математическое моделирование задач механики
- Разработка методов и средств проектирования узлов и механизмов машин отрасли
- Нелинейные проблемы колебаний и динамической устойчивости механизмов с переменными параметрами
- Механика нити, ткани и гибких оболочек
- Разработка методов решения актуальных нелинейных задач механики мягких оболочек, армированных текстильными структурами
Оснащенность
Кафедра имеет компьютерный класс с мультимедийным комплексом, методический кабинет инженерной графики и технического рисунка, специализированные учебные классы для выполнения графических работ по инженерной графике и техническому рисунку. Также кафедра располагает компьютерным классом, с программным обеспечением, разработанным сотрудниками кафедры. Программы предназначены для выполнения расчетов по РГР и курсовому проектированию.
При кафедре имеется лаборатория механики машин
Руководство по дизайну: инженерные чертежи и зарисовки | Связанные ресурсы | Дизайн и производство I | Машиностроение
Чтобы увидеть анимированную версию этого руководства, обратитесь к разделу «Черчение и черчение» в компьютерной системе обучения инженерного проектирования Массачусетского технологического института. (EDICS)
Указатель раздаточных материалов
Изометрический чертеж
Ортогональные или многовидовые чертежи
Нанесение размеров
Разрез
Инструменты для рисования
Сборочные чертежи
Виды поперечных сечений
полусекций
объектов , Ребра и т. Д.Дополнительные размеры
Где разместить размеры
Введение
Один из лучших способов передать свои идеи — это использовать какую-либо форму изображения или рисунка. Особенно это актуально для инженера. Цель этого руководства — дать вам основы инженерного эскиза и рисования.
Мы будем рассматривать «зарисовку» и «рисование» как одно целое. «Набросок» обычно означает рисование от руки. «Рисование» обычно означает использование чертежных инструментов, от компасов до компьютеров, для повышения точности чертежей.
Это всего лишь введение. Не беспокойтесь о понимании каждой детали прямо сейчас — просто почувствуйте язык графики в целом.
Мы надеемся, что вам понравится объект на Рисунке 1, потому что вы будете часто его видеть. Прежде чем мы приступим к каким-либо техническим чертежам, давайте внимательно рассмотрим этот странный блок с нескольких точек зрения.
Рисунок 1 — Обработанный блок.
Изометрический чертеж
Изображение объекта на рисунке 2 называется изометрическим рисунком.Это одно из семейства трехмерных изображений, называемых графическими рисунками. На изометрическом чертеже вертикальные линии объекта нарисованы вертикально, а горизонтальные линии в плоскостях ширины и глубины показаны под углом 30 градусов к горизонтали. При построении в соответствии с этими рекомендациями линии, параллельные этим трем осям, имеют истинную (в масштабе) длину. Линии, которые не параллельны этим осям, не будут иметь их истинную длину.
Рисунок 2 — Изометрический чертеж.
Любой инженерный чертеж должен показывать все: полное представление об объекте должно быть возможным из чертежа.Если изометрический чертеж может отображать все детали и все размеры на одном чертеже, это идеальный вариант. В изометрический рисунок можно упаковать большой объем информации. Однако, если бы объект на рисунке 2 имел отверстие на обратной стороне, он не был бы виден при использовании одного изометрического чертежа. Чтобы получить более полное представление об объекте, можно использовать ортогональную проекцию.
Ортогональный или многоракурсный чертеж
Представьте, что у вас есть объект, подвешенный на прозрачных нитях внутри стеклянной коробки, как на рисунке 3.
Рисунок 3 — Блок, подвешенный в стеклянном ящике.
Затем нарисуйте объект на каждой из трех граней, если смотреть с этого направления. Разверните коробку (рисунок 4), и вы получите три вида. Мы называем это «орфографическим» или «многовидовым» рисунком.
Рисунок 4. Создание ортогонального многоракурсного чертежа.
Рисунок 5 — Мультиэкранный рисунок и его объяснение.
Какие виды следует выбирать для многоракурсного чертежа? Виды, раскрывающие каждую деталь объекта.Три представления не всегда необходимы; нам нужно ровно столько представлений, сколько требуется для полного описания объекта. Например, для некоторых объектов требуется только два представления, а для других — четыре. Круглый объект на рисунке 6 требует только двух видов.
Рисунок 6. Объект, которому требуется только два ортогональных вида.
Определение размеров
Рисунок 7 — Изометрический вид с размерами.
Мы «измерили» объект на изометрическом чертеже на рисунке 7.В качестве общего правила для определения размеров постарайтесь представить себе, что вы могли бы сделать объект и измерить его наиболее удобным способом. Уложите ровно столько размеров, сколько необходимо мастеру, чтобы сделать его — ни больше, ни меньше. Не добавляйте лишних размеров. Они не только загромождают чертеж, но и, если включены «допуски» или уровни точности, избыточные размеры часто приводят к конфликтам, когда допуски допусков могут быть добавлены по-разному.
Многократное измерение от одной точки до другой приведет к неточностям.Часто лучше измерять от одного конца до разных точек. Это дает размеры эталона. Полезно выбрать размещение размера в том порядке, в котором механик будет создавать деталь. Это соглашение может потребовать некоторого опыта.
Секционирование
Часто внутренние детали объекта не видны снаружи (рис. 8).
Рисунок 8 — Изометрический чертеж, на котором не показаны все детали.
Мы можем обойти это, притворившись разрезающим объект на плоскости и показав «вид в разрезе».Вид в разрезе применим к таким объектам, как блоки двигателя, внутренние детали которых сложны и их очень трудно понять из-за использования «скрытых» линий (скрытые линии, по соглашению, пунктирные) на ортогональном или изометрическом чертеже.
Представьте, что объект разрезан посередине (рисунок 9):
Рисунок 9 — «Разделение» объекта.
Рисунок 10 — Разделение объекта на рисунке 8.
Снимите переднюю половину (рисунок 10), и вы получите полный разрез (рисунок 11).
Рисунок 11. Изометрические и ортогональные виды в разрезе.
Поперечное сечение выглядит как на рисунке 11, если смотреть прямо.
Инструменты для рисования
Чтобы подготовить чертеж, можно использовать инструменты для рисования вручную (рис. 12) или компьютерное черчение или конструирование, или САПР. Основные стандарты и условные обозначения для чертежей одинаковы, независимо от того, какой инструмент дизайна вы используете для создания чертежей.Изучая черчение, мы подойдем к нему с точки зрения ручного черчения. Если рисунок сделан без инструментов или без САПР, он называется наброском от руки.
Рисунок 12 — Инструменты для рисования.
«Собрание» Чертежи
изометрический вид в «собранном» система подушки блок подшипника показан на рисунке 13. Это близко соответствует тому, что вы реально увидеть при просмотре объекта от определенного угла. Мы не можем сказать, как выглядит внутренняя часть детали с этого вида.
Мы также можем показать изометрические виды на подушку-блока, который они разобрали или «разобранном» (рисунок 14). Это позволяет увидеть внутренние компоненты подшипниковой системы. Изометрические чертежи могут ясно показать общую компоновку, но не детали и размеры.
Рисунок 13 — Подушка-блок (эскиз от руки).
Рисунок 14 — Подушка-блок в разобранном виде.
Виды в разрезе
Вид в разрезе отображает вырезанную часть объекта и является еще одним способом показать скрытые компоненты в устройстве.
Представьте себе плоскость, которая вертикально разрезает центр подушки подушки, как показано на рисунке 15. Затем представьте себе удаление материала с передней части этой плоскости, как показано на рисунке 16.
Рисунок 15 — Подушка Блокировать.
Рисунок 16 — Блок подушки.
Так будет выглядеть оставшаяся задняя часть. Диагональные линии (штриховка) показывают области, где материалы были разрезаны плоскостью разреза.
Рисунок 17 — Разрез «А-А».
На этом виде в разрезе (разрез A-A, рис. 17), перпендикулярном направлению взгляда, лучше видно соотношение длины и диаметра. Эти рисунки сделать проще, чем изометрические. Опытные инженеры могут интерпретировать ортогональные чертежи без изометрического чертежа, но это требует некоторой практики.
Вид подшипника «снаружи» сверху показан на рис. 18.Это ортогональная (перпендикулярная) проекция. Обратите внимание на направление стрелок на плоскости сечения «A-A».
Рисунок 18 — Вид подшипника «снаружи» сверху.
Полусечения
Полусечение — это вид объекта, показывающий половину вида в разрезе, как на рисунках 19 и 20.
Рисунок 19 — Изометрические виды в целом и в разрезе.
Рисунок 20 — Вид спереди и половинный разрез.
Диагональные линии на чертеже разреза используются для обозначения теоретически вырезанной области. Эти линии называются сечением накладки или перекрестной штриховкой . Линии тонкие и обычно рисуются под углом 45 градусов к основному контуру объекта. Расстояние между строками должно быть равномерным.
Второе, более редкое использование перекрестной штриховки используется для обозначения материала объекта. Одна форма перекрестной штриховки может использоваться для чугуна, другая — для бронзы и так далее.Как правило, тип материала указывается в другом месте на чертеже, что делает ненужным использование различных типов штриховки.
Рисунок 21 — Половина разреза без скрытых линий.
Обычно скрытые (пунктирные) линии не используются на поперечном сечении, если они не нужны для целей определения размеров. Кроме того, некоторые скрытые линии на неразрезанной части чертежей не нужны (рис. 12), поскольку они становятся избыточной информацией и могут загромождать чертеж.
Разделение объектов с отверстиями, ребрами и т. Д.
Поперечное сечение справа на рис. 22 технически правильное. Однако на чертеже принято показывать вид слева в качестве предпочтительного метода разделения этого типа объекта.
Рисунок 22 — Поперечное сечение.
Нанесение размеров
Назначение размеров — дать четкое и полное описание объекта. Полный набор размеров допускает только одну интерпретацию, необходимую для построения детали.Размеры должны соответствовать этим рекомендациям.
- Точность: должны быть указаны правильные значения.
- Четкость: размеры должны быть размещены в соответствующих положениях.
- Полнота: ничего нельзя упускать и ничего не дублировать.
- Читаемость: для разборчивости необходимо использовать линии соответствующего качества.
Основные сведения: определения и размеры
Размерная линия представляет собой тонкую линию, разорванную посередине, чтобы можно было разместить значение размера, со стрелками на каждом конце (рис. 23).
Рисунок 23 — Чертеж с размерами.
Наконечник стрелы имеет длину примерно 3 мм и ширину 1 мм. То есть длина примерно в три раза больше ширины. Выносная линия продолжает линию объекта до размерной линии. Первая размерная линия должна находиться на расстоянии примерно 12 мм (0,6 дюйма) от объекта. Выносные линии начинаются на 1,5 мм от объекта и проходят на 3 мм от последней размерной линии.
Выноска — это тонкая линия, используемая для соединения размера с определенной областью (рисунок 24).
Рисунок 24 — Пример чертежа с выноской.
Выноска также может использоваться для обозначения примечания или комментария о конкретной области. Когда пространство ограничено, стрелки могут быть заменены толстой черной точкой, как на рисунке 23. Также на этом рисунке два отверстия идентичны, что позволяет использовать обозначение «2x» и размер, указывающий только на одно из круги.
Где разместить размеры
Размеры должны быть размещены на грани, которая наиболее четко описывает элемент.Примеры подходящего и несоответствующего размещения размеров показаны на рисунке 25.
Рисунок 25 — Пример подходящего и несоответствующего размера.
Чтобы понять, что такое определение размеров, мы можем начать с простого прямоугольного блока. Для полного описания этого простого объекта необходимы только три измерения (рис. 26). Выбор места для размещения размеров невелик.
Рисунок 26 — Простой объект.
При измерении размеров блока с выемкой или вырезом необходимо сделать несколько вариантов (рисунок 27). Обычно лучше всего проводить измерения от общей линии или поверхности. Это можно назвать базовой линией поверхности. Это исключает добавление неточностей измерения или обработки, которые могут возникнуть из-за «цепного» или «серийного» определения размеров. Обратите внимание, как размеры берут начало на опорных поверхностях. Мы выбрали одну базовую поверхность на рисунке 27, а другую — на рисунке 28. Пока мы последовательны, это не имеет значения.(Мы просто показываем вид сверху).
Рисунок 27 — Пример наземной базы.
Рисунок 28 — Пример наземной базы.
На рисунке 29 мы показали отверстие, которое мы выбрали для измерения размеров на левой стороне объекта. Ø означает «диаметр».
Рисунок 29 — Пример отверстия с заданными размерами.
Когда левая сторона блока представляет собой «радиусы», как на рисунке 30, мы нарушаем наше правило, что мы не должны дублировать размеры.Общая длина известна, потому что указан радиус кривой с левой стороны. Затем, для ясности, мы добавляем общую длину 60 и отмечаем, что это эталонный (REF) размер. Это означает, что на самом деле это не требуется.
Рисунок 30 — Пример отверстия с прямым размером.
Где-то на бумаге, обычно внизу, должна быть размещена информация о том, какая система измерения используется (например, дюймы и миллиметры), а также масштаб чертежа.
Рисунок 31 — Пример отверстия с прямым размером.
Этот рисунок симметричен относительно горизонтальной средней линии. Осевые линии (пунктирные) используются для симметричных объектов, а также для центров окружностей и отверстий. Мы можем наносить размеры непосредственно по средней линии, как на рисунке 31. В некоторых случаях этот метод может быть более понятным, чем простое нанесение размеров между поверхностями.
Машиностроительные чертежи: руководство к пониманию и работе с ними
Машиностроение — одна из наших страстей в BMR Solutions.Это одна из старейших инженерных дисциплин, которая включает изучение и применение инженерии, проектирования и обслуживания механических систем и проектов.
Машиностроительные чертежи — это то, с чем должен ознакомиться каждый инженер-механик. Независимо от того, создаете ли вы их, понимание того, почему они полезны, поможет создать для вас больше возможностей для карьерного роста. Многие ведущие инженерные работодатели будут искать кандидатов, которые хорошо разбираются в технических чертежах.Это руководство призвано продемонстрировать, как они производятся, почему они полезны, и советы, как произвести впечатление на потенциальных работодателей, а также все остальное, что вам нужно знать о технических чертежах.
Что такое машиностроительные чертежи?
Машиностроительные чертежи — это технические чертежи, которые помогают определить и проиллюстрировать конкретные механические требования и процессы. Это инженерные чертежи специально для механических целей.
Эти технические чертежи помогают сообщать о проблемах и решениях, с которыми сталкиваются инженеры-механики.Эти чертежи могут стать неотъемлемой частью проекта и помочь определить, что необходимо сделать. Они помогают передавать сложные процессы и структуры ясным и кратким образом.
В отличие от художественных чертежей, инженерные чертежи должны быть очень ясными и не допускать двусмысленности. Рисунки не должны интерпретироваться разными людьми по-разному, вместо этого они должны быть ориентированы на передачу информации простым способом. Это устраняет риск искажения того, что рисунок пытается проиллюстрировать, и гарантирует, что каждый, кто работает над проектом, имеет четкое понимание требований и ожиданий.
Основы инженерного черчения
При работе над проектом в области машиностроения вам может потребоваться использовать более одного технического чертежа. Для больших проектов с множеством различных компонентов может быть несколько чертежей, разработанных для определенных групп над проектом. В результате всегда лучше убедиться, что вы знакомы с рядом рисунков, чтобы вы могли понять, какой информации следят разные команды.
Инженерные чертежимогут различаться по сложности от проекта к проекту, поэтому полезно постараться изучить как можно больше чертежей, чтобы быть уверенным в использовании любых чертежей, которые могут возникнуть в вашей карьере.Некоторые мелкомасштабные рисунки могут просто обрисовывать то, что создается, в то время как другие могут включать очень сложные идеи и процессы.
Технические чертежи можно создавать традиционными методами, такими как ручка и бумага, но чаще они создаются с помощью программного обеспечения САПР (автоматизированного проектирования). Компьютерные чертежи могут быть намного более эффективными и значительно упрощают редактирование и внесение изменений.
Великобритания следует стандартам BS 8888, установленным BSI. Это гарантирует, что существует эталон и измерение качества для всех, кто создает техническую документацию на продукт, геометрическую спецификацию продукта, спецификацию геометрических допусков и инженерные чертежи.
Чтобы быть в курсе любых изменений в технических чертежах в Великобритании, рекомендуется посетить группу BSI. Эта статья от февраля 2017 года иллюстрирует некоторые недавние изменения.
Чем полезны машиностроительные чертежи?
Технические чертежи могут быть юридическим документом. Они могут предложить официальное руководство для других (в том числе других предприятий). Это помогает гарантировать, что все, кто участвует в проекте, следуют одним и тем же указаниям, приведенным на этих чертежах.
Законность этих чертежей также означает, что если в проекте действительно возникают какие-либо ошибки, чертежи могут использоваться для определения виновных. Это также означает, что инженерные чертежи должны быть созданы в соответствии со стандартом, который сводит к минимуму риск ошибок.
Эти рисунки также очень полезны для международных проектов. Ошибки, вызванные языковым барьером или недопониманием культурных традиций, не могут служить оправданием для крупных проектов стоимостью в несколько миллионов фунтов стерлингов. Вместо этого следуя рисункам, все участники могут следовать одному и тому же плану, а ошибки, вызванные общением, могут быть ограничены.
Советы по использованию машиностроительных чертежей
Машиностроительные чертежи, вероятно, будут включать следующие детали:
Используемые материалы — жизненно важный компонент всего проекта. На чертежах должно быть четко указано, какой материал используется в каждой части проекта.
Геометрия предполагает использование точных математических уравнений и фигур для создания точных форм объектов, используемых в проекте. Это поможет проиллюстрировать, как разные предметы смотрятся под разными углами и подходят ли они друг к другу должным образом.Использование нескольких видов помогает превратить одномерные чертежи в четкие всеобъемлющие чертежи.
Размеры, используемые на технических чертежах, помогут проиллюстрировать размер каждого используемого объекта. Это помогает обеспечить масштаб проекта и убедиться, что все понимают, на что будет похож каждый компонент.
Также вероятно, что чертежи машиностроения будут сопровождаться примечаниями и вещами, относящимися именно к этому чертежу. Это может помочь убедиться, что любой, кто читает чертеж, полностью понимает, каковы намерения такого механического проекта.
Машиностроительные чертежи эволюционировали в том, как они создаются с момента развития технологий. По мере того, как 3D-печать и алгоритмы машинного обучения становятся все более распространенными (включая механику), те, кто принимает изменения и понимает, как инженерные чертежи могут развиваться в будущем, будут оставаться на вершине потребностей работодателей в найме.
В ближайшие несколько лет способность алгоритмов машинного обучения создавать эти чертежи станет реальной возможностью.Это может означать, что изучение того, как использовать конкретное программное обеспечение, может стать будущим того, как инженеры будут использовать такую информацию.
Машиностроение и решения BMR
Если вы инженер-механик, обязательно свяжитесь с нами сегодня. Мы специализируемся на поиске и размещении лучших технических специалистов в ведущих компаниях страны. Мы помогли таким же людям, как вы, найти потрясающие возможности трудоустройства, которые резко повысили их карьеру.
Чтобы поговорить с одним из наших сотрудников, свяжитесь с нами сегодня или просто загрузите свое резюме, и один из наших экспертов свяжется с вами.
| Курс элементарного механического рисования 1882 | PDF 3 мб |
| Курс механического черчения 1921 | PDF 3 мб |
| Курс проектирования конструкций 1907 | PDF 5 мб |
| Курс основ механического черчения 1912 | PDF 3 мб |
| Руководство по механическому чертежу 1903 | PDF 6 мб |
| Расширенный механический чертеж 1905 | PDF 3 мб |
| Введение в механический чертеж 1881 | PDF 3 мб |
| Appletons Cyclopedia of Technical Drawing 1896 | PDF 82 мб |
| Архитектурный чертеж 1888 | PDF 15 мб |
| Конструктивный чертеж 1908 | PDF 2 мб |
| Циклопедия рисунков 1907 | PDF 12 мб |
| Методы чертежной 1918 | PDF 5 мб |
| Изгибы в гостиной 1908 | PDF 607 кбайт |
| Элементарный механический чертеж для школы и магазина 1886 | PDF 5 мб |
| Elements of Mechanical Drawing — Энтони 1904 | PDF 5 мб |
| Элементы механического чертежа — Джемисон 1911 | PDF 11 мб |
| Элементы механического чертежа — Салливан 1893 | PDF 3 мб |
| Элементы перспективы 1898 | PDF 3 мб |
| Основы механического черчения 1917 | PDF 3 мб |
| Сельхозтехника и рисование 1911 | PDF 1 мб |
| Базовый курс измерения и механического рисунка 1916 | PDF 6 мб |
| Рисование и конструирование от руки 1919 | PDF 3 мб |
| Геометрический чертеж 1898 | PDF 3 мб |
| Промышленный чертеж 1877 | PDF 4 мб |
| Промежуточный курс механического черчения 1889 | PDF 2 мб |
| Младший курс механического рисования 1888 | PDF 2 мб |
| Машинный чертеж — Практическое руководство по стандартным методам 1920 | PDF 12 мб |
| Система чтения рабочих чертежей или синих отпечатков McLains 1921 | PDF 10 мб |
| Механический чертеж 1898 | PDF 5 мб |
| Копировальные пластины для механических чертежей 1918 | PDF 809 кб |
| Механический чертеж для промышленных и средних школ 1917 | PDF 3 мб |
| Механический чертеж для торговых школ 1909 | PDF 4 мб |
| Современная разработка 1911 | PDF 2 мб |
| Примечания к курсу элементарного механического рисования 1 1905 | PDF 5 мб |
| Примечания к механическому чертежу 1922 | PDF 3 мб |
| Примечания к практическому механическому чертежу 1907 | PDF 7 мб |
| Сведения об инструментах для рисования 1889 | PDF 3 мб |
| Практические задачи механического рисования и чтения чертежей 1921 | PDF 2 мб |
| Механический чертеж самопомощи 1914 | PDF 7 мб |
| Старший курс механического черчения 1897 | PDF 4 мб |
| Учебник по механическому черчению 1895 | PDF 3 мб |
| Книга практических рисовальщиков по промышленному образцу 1871 | PDF 35 мб |
| Практика механического рисования для самостоятельного обучения 1895 | PDF 1 мб |
| Теория инженерного рисунка 1915 | PDF 17 мб |
| Теоретическая и практическая графика 1892 | PDF 10 мб |
| Деревообработка и механический чертеж 1914 | PDF 5 мб |
| Рабочие чертежи и способы их создания и использования 1881 | PDF 2 мб |
Механические чертежи Fit-PC2 / i — fit-PC wiki
Из вики-сайта fit-PC
(Перенаправлено с механических чертежей)Страница перенаправления Перейти к: навигация, поиск
Перенаправление на:
- Линия продуктов Fit-PC: fit-PC2 / 2i
fit-PC2
- fit-PC2 механические чертежи (DXF)
- fit-PC2
- SBC-FITPC2
- fit-PC2 3D модель (.x_t Parasolid)
- SBC-FITPC2 3D модель (.x_t parasolid)
fit-PC2i
- fit-PC2i 3D модель (.x_t parasolid)
- SBC-FITPC2i 3D модель (.x_t parasolid)
Принадлежности
- Монтажный кронштейн VESA
- Фиксированный монтажный кронштейн (DXF) | PDF
- Радиатор (.x_t parasolid)
Меню навигации
Персональные инструменты
- Войти
Пространства имен
- Стр.
- Обсуждение
Варианты
Просмотры
- Читать
- Просмотреть источник
- Посмотреть историю
Подробнее
Поиск
Основной
Текущие продукты
- Тензор-ПК
- Airtop3
- фитлет2
- ДИКИЙ
Прочие товары
- Airtop2
- Airtop1
- IPC3
- IPC2
- IPC1
- фитлет1
- фитлет1-H / T
- подходит-PC4
- fit-PC3 / 3i
- fit-PC2 / 2i
- УСВР
Расширения
- Модули FACE
- Карты FACET
Принадлежности
- fit-statUSB
- Fit-Безголовый
- fit-Uptime
- Все аксессуары
Ссылки
- сайт fit-IoT
- Форум пользователя
Инструменты
- Какие ссылки здесь
- Связанные изменения
- Специальные страницы
- Версия для печати
- Постоянная ссылка
- Информация о странице
- Цитировать эту страницу
- Последнее изменение этой страницы: 2 июля 2014 г. в 07:30.
- Политика конфиденциальности
- О программе fit-PC wiki
- Заявление об отказе от ответственности
- Мобильный просмотр
Механические чертежи — Строительные нормы
Титульный лист механических чертежей должен содержать соответствующие примечания, легенды (таблица или таблица символов и сокращений) и подробности. В механическом плане указывается конструкция или модификации механической системы, компоновка и размеры воздуховодов, расположение механического оборудования, расположение заслонок, расчетная скорость подачи воздуха, расположение диффузоров, расположение термостатов и, при необходимости, дополнительные системы охлаждения.Механические схемы обычно обозначаются как M-1, M-2, M-3 и т. Д. Некоторые консультанты предпочитают, чтобы чертежи отопления, вентиляции и кондиционирования, обычно называемые чертежами HVAC, были последовательно пронумерованы и снабжены префиксом буква «Н»; чертежи сантехники должны быть помечены буквой «P»; а чертежи противопожарной защиты должны иметь префикс FP. Большая часть работ, показанных на этих типах чертежей, представлена в плане. Из-за схематического характера механических чертежей вид сверху лучше всего иллюстрирует расположение и конфигурацию работы.
Из-за большого объема информации, необходимой для механических работ, и непосредственной близости трубопроводов, клапанов и соединений, инженер использует различные символы и сокращения, чтобы передать замысел проекта. Примеры этих символов и их значения можно найти в главе 8.
- Рис. 6.15. План фундамента жилого дома.
- Рисунок 6.16 Типичные примеры структурных деталей.
Механические системы предназначены для обогрева и охлаждения зданий или помещений.Два основных метода нагрева и охлаждения используют воздух или воду. В воздушной системе горячий или холодный воздух транспортируется в помещение по приточным и возвратным воздуховодам. Типичный пример — бытовая печь с приточным воздухом. В печи используется газ или масло для нагрева воздуха. Воздух прогоняется через воздуховоды с помощью вентилятора с электроприводом в печи. Для холодного воздуха установлен отдельный кондиционер. В большинстве коммерческих зданий большой блок, часто расположенный на крыше, приводит в действие воздушную систему.Приточные воздуховоды, регистры и решетки вытяжного воздуха необходимы во всех помещениях в здании.
В системе водяного отопления используется змеевик, через который циркулирует горячая вода. Самый распространенный пример — радиатор с ребристыми трубами, который можно найти в старых домах, обычно расположенный перед окном. Сегодня самая распространенная система — это теплые полы с подогревом.
Полностью электрическая система обогрева использует электричество для нагрева элементов внутри радиатора. Самым распространенным считается утеплитель плинтуса.Применяется, когда печь не установлена. Например, во многих небольших коттеджах используются обогреватели для плинтусов. Небольшие старые коммерческие здания полагаются на установку плинтусов. Эту систему также можно найти в больших коммерческих зданиях в качестве дополнения к другим системам. Электрический радиатор со встроенным вентилятором может быть расположен у внешней входной двери, чтобы обеспечить дополнительное тепло внутри.
Механические чертежи предоставляют заказчику, строителю и разрешительному отделу полную схему HVAC для работы.Эти чертежи обычно являются частью набора строительных чертежей. Они предоставляются вместе со строительными чертежами для заявки на получение разрешения на строительство (Рисунок 6.17). Они также являются частью пакета для ценообразования проекта. Их используют для строительства. Все воздуховоды, вентиляторы, вытяжные вентиляторы, а также блоки нагрева и / или охлаждения должны поставляться и устанавливаться в соответствии с утвержденными чертежами.
Консультант по машиностроению производит чертежи. Часто электрические и сантехнические чертежи готовит одно и то же лицо или компания.Эти чертежи должны соответствовать различным строительным нормам, включая все провинциальные и местные нормы.
Обычно инженер использует эти планы и включает свою схему воздуховодов. Диффузоры, решетки возвратного воздуха и вытяжные вентиляторы изображены символами. Указаны системы отопления и / или охлаждения и указано их расположение. Добавляются легенды, расписания, подробности и примечания, относящиеся к проекту.
В небольших проектах вся необходимая информация содержится на одном или двух чертежных листах.Для больших или сложных проектов необходимо много страниц для рисования, чтобы охватить все области проекта.
Как правило, на чертежах инженера должны быть указаны тип, расположение и количество блоков отопления и / или кондиционирования воздуха. Указаны соединения HVAC и электрические соединения, а также любые соединения с газовыми линиями или системами водоснабжения. Также указываются тип, расположение и номер термостата. На рисунке 6.18 показана подробная схема трубопроводов хладагента
.Многие проекты требуют расчетов теплопотерь и притока тепла.Информация о балансировке воздуха или графики устройства распределения воздуха обычно включаются. Требуемая информация зависит от типа строящегося проекта.
Во многих городах действуют правила энергосбережения. Чертежи инженера должны соответствовать всем кодексам и постановлениям, относящимся к городу, поселку или провинции, где расположен проект.
В комплект механических чертежей обычно входят:
• Планы с указанием размеров, типа и расположения воздуховодов
• Диффузоры, регистры тепла, решетки возвратного воздуха и заслонки
• Поворотные лопатки и изоляция воздуховодов
• Типы, количество и расположение агрегатов HVAC
• Типы, количество и расположение термостатов
• Подключение к электричеству, воде или газу
- Рисунок 6.17A Типовой план этажа HVAC с изображением воздуховодов в масштабе 1/8 дюйма = 1 фут 0 дюймов. Примечания по HVAC, а также код и условия проектирования включены в лист.
• Вентиляторы приточно-вытяжные
• Условные обозначения символов, общие примечания и особые ключевые примечания
• Сводная информация о тепловой и / или охлаждающей нагрузке
Другая информация, в зависимости от сложности проекта, может включать:
• Подключение к существующим системам
• Снос части или всех существующих систем
• Детектор дыма и пожарный датчик для воздуховодов
• Программирование термостата
- Рисунок 6.17B Схема, показывающая размеры, соединения и расположение воздуховодов HVAC.
• Расчет теплопотерь и притока тепла на площадь
• Детали круглого воздуховода, поворотной заслонки и вставного диффузора
• Особые условия, например, коды сейсмостойкости
Чертежиинженера требуются для всех коммерческих проектов, связанных с работами по ОВК, включая пристройки, реконструкцию или новое строительство. Перед началом любых работ на объекте требуется разрешение.
Чертежи и разрешения также необходимы для жилых проектов, когда должны проводиться какие-либо существенные работы, связанные с HVAC.Для небольших проектов лицензированный подрядчик по механическому оборудованию может предоставить информацию, необходимую для получения разрешения.
Концепция и дизайн — это первый этап любого проекта. Когда установлено, следующий этап — строительные чертежи. После того, как планы пола и отраженного потолка завершены, они передаются инженеру для создания механических чертежей. Чертежи инженера становятся частью набора строительных чертежей.
Рисунок 6.18 Принципиальная схема трубопровода хладагента для кондиционирования воздуха.
ДЕТАЛЬ ТРУБОПРОВОДА ХЛАДАГЕНТА (КОНДИЦИОНЕР ВОЗДУХА)
Рисунок 6.18 Принципиальная схема трубопровода хладагента для кондиционирования воздуха.
Прочтите здесь: Чертежи сантехники
Была ли эта статья полезной?
Инжиниринг — Механика Drawing
Доступно:
AfghanistanÅland islandsAlbaniaAlgeriaAmerican samoaAndorraAngolaAnguillaAntarcticaAntigua и barbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBonaireBosnia и herzegovinaBotswanaBouvet islandBrazilBritish IO territoryBrunei darussalamBulgariaBurkina fasoBurundiCambodiaCameroonCanadaCape verdeCayman islandsCentral африканских republicChadChileChinaChristmas islandCocos (Кокосовые) islandsColombiaComorosCongoCongoCook islandsCosta ricaCôte d’ivoireCroatiaCubaCuraçaoCyprusCzech republicDenmarkDjiboutiDominicaDominican republicEcuadorEgyptEl salvadorEquatorial guineaEritreaEstoniaEthiopiaFalkland islandsFaroe islandsFijiFinlandFranceFrench guianaFrench polynesiaFrench южный territoriesGabonGambiaGeorgiaGermanyGhanaGibraltarGreeceGreenlandGrenadaGuadeloupeGuamGuatemalaGuernseyGuineaGuinea-bissauGuyanaHaitiHeard & острова Макдональд urasHong kongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle из manIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKuwaitKyrgyzstanLaoLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall islandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesiaMoldovMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNew caledoniaNew zealandNicaraguaNigerNigeriaNiueNorfolk islandNorth KoreaNorthern Мариана islandsNorwayOmanPakistanPalauPalestinian territoryPanamaPapua новых guineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto ricoQatarRéunionRomaniaRussian federationRwandaSaint barthélemySaint helenaSaint Киттс и nevisSaint luciaSaint martinSaint пьер и miquelonSaint Венсан SamoaSan marinoSao фолиант и principeSaudi arabiaSenegalSerbiaSeychellesSierra leoneSingaporeSint maartenSlovakiaSloveniaSolomon islandsSomaliaSouth africaSouth georgiaSouth KoreaSouth sudanSpainSri ланка SudanSurinameSvalbard и Январь mayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor-lesteTogoTokelauTongaTrinidad и tobagoTunisiaTurkeyTurkmenistanTurks и Кайкос islandsTuvaluUgandaUkraineUnited араб emiratesUnited kingdomUnited statesUruguayUS Малого отдаленных островов islandsUzbekistanVanuatuVaticanVenezuelaViet namVirgin, BritishVirgin остров, USWallis и futunaWestern saharaYemenZambiaZimbabwe
конвенциичерчения
МЕХАНИЧЕСКИЙ ЧЕРТЕЖ
КОНВЕНЦИИ О РАБОЧЕМ ЧЕРТЕЖЕ
Общие
Принципы механического черчения основаны на проверенных временем практиках, основанных на стандартах, установленных Американским институтом стандартов (ANSI). Техника механического рисования относится к стилю или качеству рисунка, который индивидуальный составитель передает работе. Он характеризуется четкими черными линиями , надписью, последовательностью и единообразием. Механические чертежи должны отражать жесткий контроль линий механически созданного чертежа. Разработка хороших подробных чертежей — настоящее инженерное достижение и искусство. Студенты должны разработать стилизованную технику рисования, которая соответствует жестким правилам рисования линий с добавлением вариаций художественных приемов для создания очень индивидуализированного законченного рисунка.
Рабочие чертежи или производственные чертежи — это полный набор чертежей, используемых для доведения разработанного проекта до готового состояния производства. Рабочие чертежи обычно состоят из чертежей деталей и сборочных чертежей. С помощью подробных чертежей чертежник должен передать на техническом языке всю информацию, необходимую для изготовления каждой отдельной детали. Сборочные чертежи показывают, как все части соединяются вместе в готовом изделии.
Чтобы иметь возможность точно подготовить необходимые чертежи, чертежник должен хорошо разбираться в новейших технических спецификациях, быть знаком с новейшими технологиями производства, а также обладать знаниями и навыками в области механического черчения.Поэтому абсолютно необходимо, чтобы рисовальщик-механик разработал хорошую технику рисования.
Выбор ракурсов
Чертеж должен содержать только те виды, которые необходимы для четкого и полного описания формы объекта. Выбираются виды, которые лучше всего отображают основные контуры или формы и содержат наименьшее количество скрытых линий. Чертежи деталей и сборочные чертежи могут использовать любое количество необходимых видов, включая виды в разрезе, вспомогательные виды и частичные виды.Цель сборочного чертежа — показать, как детали подходят друг к другу, и предложить функцию. Следовательно, виды, выбранные для отображения сборки, должны отображать взаимосвязи деталей, а не отображать подробные формы.
Номера чертежей
Все рисунки будут пронумерованы. В отрасли используется множество различных систем нумерации, поэтому не существует единой стандартной системы. Нумерация будет зависеть от стандартов компании и практики составления документов.Номера чертежей очень важны, поэтому они обозначаются большими буквами. Высота варьируется от 3/8 дюйма до 5/16 дюйма.
Список деталей
Список деталей — это список всех составных частей сборки. Список деталей включает номер детали, название детали, требуемый номер, материал детали, а иногда и другой описательный текст. Список деталей включен на все сборочные чертежи или может быть на отдельном листе. Обычно список деталей отображается вместе с чертежами сборки и включает только те детали, которые показаны на листе чертежей сборки.
Ревизионные блоки
Блоки редакций всегда появляются на чертеже для записи любых изменений, внесенных после утверждения чертежа. Внесение изменений в чертеж вызвано изменениями в конструкции, изменениями, внесенными заказчиком, или изменениями из-за ошибок в конструкции. Изменения следует отметить на чертеже и записать в блок доработок. Следует указать краткое описание изменения вместе с датой и инициалами лица, внесшего изменение.
Разрез:
Сечения широко используются в сборочных чертежах, чтобы исключить необходимость рисовать скрытые детали. Можно использовать любой вид сечения, такой как полные сечения, половинные сечения, выровненные сечения, смещенные сечения. Чтобы различать соседние части в разрезе, линии сечения проводятся в противоположных направлениях. Облицовка секций также может различаться по расстоянию, чтобы различать соседние части.
Для общего применения применяется чугунная секционная футеровка общего назначения. Тонкие детали на сборочных чертежах должны быть сплошным черным цветом вместо использования облицовки секций. Закругленные детали, такие как болты, валы, штифты, шпонки, гайки и т. Д., Не заштриховываются, даже если плоскость среза проходит через них. Эти части принято показывать без разрезов или «по кругу».
Скрытые линии:
Следует выбирать виды, которые показывают как можно больше элементов с видимыми линиями.Там, где это необходимо, чтобы сделать рисунок четким, следует использовать скрытые линии. Если они не нужны для ясности, их следует опустить. Скрытые линии на сборочных чертежах, как правило, не нужны в результате широкого использования разрезов. Их следует использовать везде, где это необходимо для ясности.
Размеры:
Размеры указаны на всех подробных чертежах. Применяются все правила и методы определения размеров, указанные в ANSI.Размеры могут быть однонаправленными или выровненными, но не в одном и том же наборе чертежей.
Размеры обычно не приводятся на сборочных чертежах. Если размеры включены, они ограничиваются некоторой функцией объекта в целом. Сюда может входить отображение минимального или максимального размера, размера, необходимого, когда в процессе сборки требуется механическая обработка, или общие примечания, относящиеся к сборке в целом.
Центральные линии:
Центральные линии используются для обозначения оси симметрии, показывают траектории движения или используются в качестве выносных линий при нанесении размеров.Центральные линии используются в основном при нанесении размеров, и их не следует указывать на несущественных формах. На сборочных чертежах следует использовать центральные линии, чтобы показать симметрию между сопрягаемыми деталями, выравнивание деталей и траектории движения, чтобы предложить функцию.
Обозначение детали
Кружки, содержащие номера деталей, используются для обозначения деталей на чертежах деталей и сборочных чертежах. Опознавательные круги имеют диаметр от 7/16 «до 1/2». Обозначения на сборочных чертежах располагаются рядом с деталями, выноски заканчиваются соприкасающимися с деталями стрелками.Линии выноски могут различаться по стилю, например выноски с плечами, без плеч, прямые выноски или изогнутые выноски. Изогнутые линии выноски рисуются с использованием параметра СПЛАЙН. Знаки конца выноски могут быть либо стрелками, касающимися детали, либо точками, проходящими внутрь детали.
Заголовки
Все объекты на чертеже должны иметь заголовок, будь то сборка, разрез, деталь, столбец примечаний, условные обозначения символов и т. Д. Заголовки достаточно крупные, чтобы привлекать внимание зрителя.Обычно высота надписи составляет от 1/4 дюйма до 3/4 дюйма. Чтобы еще больше подчеркнуть заголовки, их можно подчеркнуть. Подчеркивание может состоять из одной линии, двойной линии или комбинации толстых и тонких линий. Подчеркивание может быть центрировано с надписью, расположено заподлицо или прервано при использовании выноски в виде круга.
Надпись
Высота букв будет соответствовать рекомендациям стандартов ANSI. Для общих букв и размеров используются буквы высотой от 3/32 «до 1/8», причем 1/8 «является предпочтительным размером.
Масштаб для чертежей
Стандартная единица измерения механических величин — дюйма, или миллиметра. Масштаб всегда обозначается как ДЮЙМЫ, например 1 «= 1» или 1/2 «= 1», или МИЛЛИМЕТРЫ, например, 1 мм = 1 мм. Слово SCALE всегда пишется для обозначения того, что читается, например SCALE: 1 «= 1».
Когда чертежный лист содержит детали, нарисованные с использованием разных масштабов, в основной надписи используется обозначение МАСШТАБ: КАК УКАЗАНО .Если деталь или рисунок не выполнены в каком-либо масштабе, обозначение N.T.S. используется, чтобы указать, что рисунок НЕ В МАСШТАБЕ.
Титульные блоки
Основные надписи — очень важная часть всего рисунка. Они содержат информацию, не указанную непосредственно на чертеже, с размерами или примечаниями. Титульные блоки для чертежей конструкций подготавливаются в соответствии со спецификациями, установленными компанией. В основной надписи обычно содержится следующая информация:
Название проекта / наименование чертежа
Имя и адрес клиента.
Название и адрес компании-производителя.
Дата завершения рисования пакета.
Масштаб рисунка.
Номер чертежа.
Надпись должна быть простой и соответствовать общему стилю надписи на рисунке. Все буквы должны быть прописными.
Высота букв должна соответствовать их относительной важности. Номер чертежа должен получить наибольшее внимание и иметь высоту более 1/4 дюйма.Модель
Название чертежа, название проекта, имя клиента и название компании должны следовать высотой букв 3/16 дюйма. Адреса, дата и масштаб должны иметь высоту букв 1/8 дюйма. Случайные слова, такие как ДАТА и МАСШТАБ , должны иметь наименьшее выделение и иметь высоту буквы 1/16 дюйма.
Надпись в основной надписи должна быть либо по центру, либо с заподлицо. Вариация высоты букв добавляет общий приятный эффект к рисунку и разрушает монотонность рисования линий, а поля связаны с общим стилем рисунка, добавляя непрерывности и согласованности рисунку.
Общие примечания
| |
Банкноты классифицируются как общие и местные. Примечания пишутся на листе горизонтально и систематически. Следует по возможности избегать сокращений в общих примечаниях. При составлении заметки используются правильная грамматика, структура предложения и пунктуация. Все буквы написаны заглавными буквами.
Столбцы примечаний названы так, чтобы их можно было отличить от других частей чертежа. Высота букв для заголовков больше, чем высота букв, используемых для общих букв, и должна быть той же высоты, что и другие заголовки на листе.
Каждая заметка в столбце заметок имеет номер. Поля используются для выравнивания номеров заметок и заметок. Расстояние между строками в заметке должно быть одинарным. Расстояние между нотами должно быть двойным, чтобы каждая нота отличалась от других нот.Помните, что единообразие и последовательность играют важную роль в построении колонки примечаний.
Макет листа
Чертежную бумагу нужно оформить рамкой. Блок заголовка, список деталей и блок изменений добавляются и помещаются вдоль нижней и / или правой стороны границы.
В общем, вся область рисования должна быть заполнена. Основной рисунок должен быть доминирующим изображением на листе с подробными чертежами и общими примечаниями, относящимися к основному рисунку, размещенными вокруг него.Виды сборок и чертежи деталей могут быть объединены на одном листе или детали показаны вместе, а сборки показаны на отдельных листах. Составитель должен определить необходимые виды для каждой сборки и детали. Следует оставить достаточно места для всех размеров и примечаний. Виды одной детали не должны перекрывать взгляды другой.
Все чертежи, детали и примечания должны иметь заголовок. Заголовки размещаются под картинкой.
Если вы являетесь автором приведенного выше текста и не соглашаетесь делиться своими знаниями для обучения, исследований, стипендий (для добросовестного использования, как указано в авторских правах США), отправьте нам электронное письмо, и мы удалим ваши текст быстро.Добросовестное использование — это ограничение и исключение из исключительного права, предоставленного законом об авторском праве автору творческой работы. В законах США об авторском праве добросовестное использование — это доктрина, которая разрешает ограниченное использование материалов, защищенных авторским правом, без получения разрешения от правообладателей. Примеры добросовестного использования включают комментарии, поисковые системы, критику, репортажи, исследования, обучение, архивирование библиотек и стипендии. Он предусматривает легальное, нелицензионное цитирование или включение материалов, защищенных авторским правом, в работы других авторов в соответствии с четырехфакторным балансирующим тестом.(источник: http://en.wikipedia.org/wiki/Fair_use)
Информация о медицине и здоровье, содержащаяся на сайте, носит общий характер и цель , которая является чисто информативной и по этой причине не может в любом случае заменить совет врача или квалифицированного лица, имеющего законную профессию.
Тексты являются собственностью их авторов, и мы благодарим их за предоставленную нам возможность бесплатно делиться своими текстами с учащимися, преподавателями и пользователями Интернета, которые будут использоваться только в иллюстративных образовательных и научных целях.
.
 Размещают татуировку механика, эскиз которой предполагается разместить на предплечье, с внутренней стороны. Также популярно расположение от кисти рук, до локтевого или плечевого сустава. Подобный рисунок отлично смотрится благодаря тому, что руки часто находятся в движении;
Размещают татуировку механика, эскиз которой предполагается разместить на предплечье, с внутренней стороны. Также популярно расположение от кисти рук, до локтевого или плечевого сустава. Подобный рисунок отлично смотрится благодаря тому, что руки часто находятся в движении; Эскиз пришлось выбирать очень долго, еще больше времени ушло на то, чтобы найти хорошего мастера, который и помог мне воплотить в жизнь мою задумку. Идеальным местом для татуировки мне показалось бедро. Так у меня и появилось изображение проглядывающего сквозь кожу металла, кости, капилляров и проводов. Выполняли все в черно-белом варианте, с четкими контурами. По площади татуировка небольшая, ее легко прикрыть даже шортами или юбкой.
Эскиз пришлось выбирать очень долго, еще больше времени ушло на то, чтобы найти хорошего мастера, который и помог мне воплотить в жизнь мою задумку. Идеальным местом для татуировки мне показалось бедро. Так у меня и появилось изображение проглядывающего сквозь кожу металла, кости, капилляров и проводов. Выполняли все в черно-белом варианте, с четкими контурами. По площади татуировка небольшая, ее легко прикрыть даже шортами или юбкой.
 Раздел посвящен игре Universe Life. Раздел про авиамоделизм пополнился новой информацией. Еще один раздел готовится к открытию
Раздел посвящен игре Universe Life. Раздел про авиамоделизм пополнился новой информацией. Еще один раздел готовится к открытию ru. Либо воспользоватся системой полуавтоматического голосования, размещенной на этом сайте по этой ссылке (http://gadget-mechanic.narod.ru/2009/)
ru. Либо воспользоватся системой полуавтоматического голосования, размещенной на этом сайте по этой ссылке (http://gadget-mechanic.narod.ru/2009/) Общая высота — около 15 см) 🙂
Общая высота — около 15 см) 🙂
 Подробнее о конкурсе можно почитать на сайте Штаба Спасателей.
Подробнее о конкурсе можно почитать на сайте Штаба Спасателей. 04.2006.
04.2006.
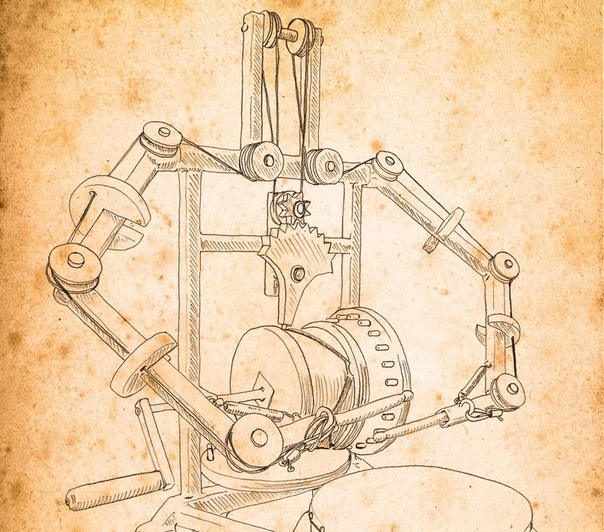 ..
.. 2006.
2006. 10.2006.
10.2006. Теперь у меня есть в чем рисовать! 🙂
Теперь у меня есть в чем рисовать! 🙂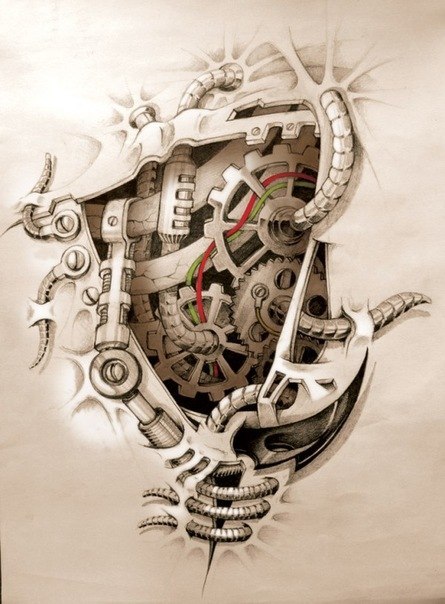 06.2006.
06.2006. Жаль только, что нашел только обложку…
Жаль только, что нашел только обложку…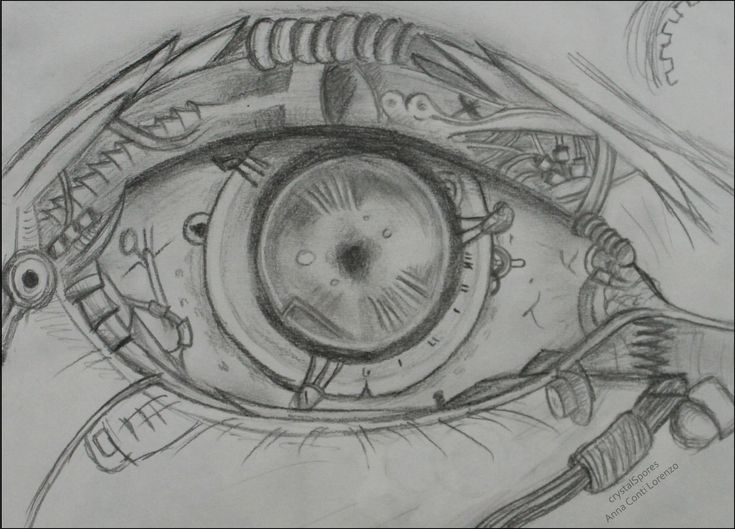 04.2006.
04.2006. Дата создания: 08.04.2006.
Дата создания: 08.04.2006. 03.2006.
03.2006.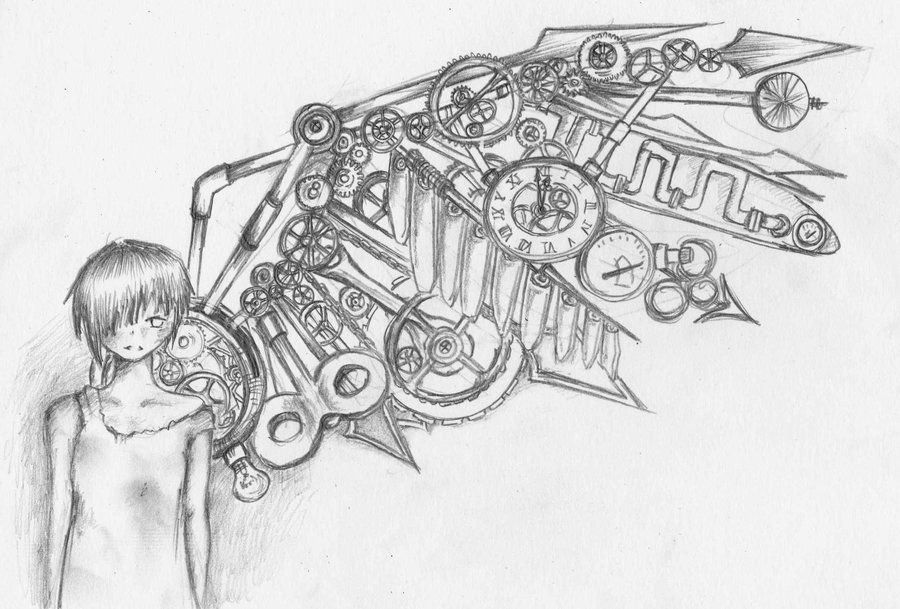 Как то непривычно рисовать Гаечку, не видя ее лица…
Как то непривычно рисовать Гаечку, не видя ее лица… Дата создания: 07.10.2005.
Дата создания: 07.10.2005. И попался мне в руки кусочек
мела… 🙂
И попался мне в руки кусочек
мела… 🙂 ..
Дата создания: 16.09.2005, 10:09.
..
Дата создания: 16.09.2005, 10:09.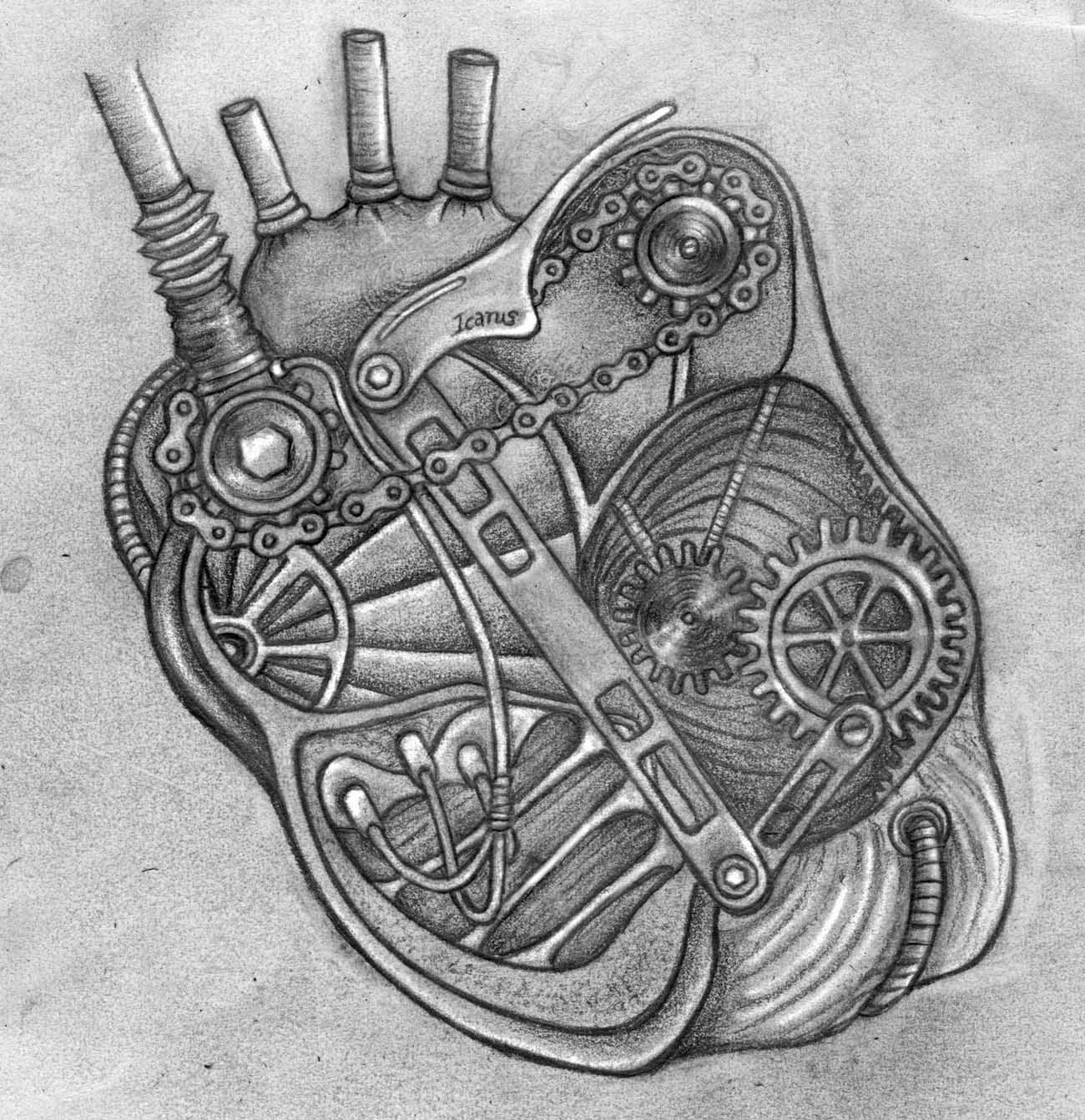 Дата
создания: 24.08.2005.
Дата
создания: 24.08.2005. Честно! 🙂
Честно! 🙂 .. просто Гаечка 🙂
Конечно же, опять — перерисовка из моделшита.
.. просто Гаечка 🙂
Конечно же, опять — перерисовка из моделшита. 08.2005.
08.2005. Дата создания: 01-02.08.2005.
Дата создания: 01-02.08.2005. Перерисовка моделшита
Перерисовка моделшита
 Дата создания: 25.06.2005.
Дата создания: 25.06.2005. Дата создания:
20.04.2005, 01:29.
Дата создания:
20.04.2005, 01:29.