Многоугольник вогнутый: Вогнутый многоугольник - что это такое, определение и понятие

Содержание

Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей

Многоугольники. Выпуклый многоугольник. Четырехугольник.

Треугольник – это частный случай многоугольника.

В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник – фигуру с пятью углами.

Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.

Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.

Иными словами, например, когда говорят о пятиугольнике А₁А₂А₃А₄А₅, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника.

Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).

Периметр многоугольника – сумма длин сторон многоугольника.

Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника.

Многоугольники делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на рисунке выше, является выпуклым, а на рисунке ниже – невыпуклым.

Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.

Существенное отличие четырехугольника от треугольника в том, что он может быть выпуклым или невыпуклым.

Очень важное различие, о котором знает каждый плотник, состоит в том, что треугольник – «жесткая» фигура, а четырехугольник (как и все остальные многоугольники) – «нежесткая».

У треугольника невозможно изменить его форму, не изменив длин сторон. При этом у любого четырехугольника можно изменить его форму, не меняя длины сторон. На практике это будет означать, что треугольник, сколоченный из трех дощечек, будет жестким, не будет сминаться даже при сильных воздействиях, а четырехугольник при достаточной нагрузке со стороны изменит свою форму.

Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольникаитеорема о сумме внешних углов выпуклого многоугольника.

Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).

Сумма углов n-угольника равна 180°·(n-2).

Математическая запись: ∠A1+∠A2+…+∠An=180°(n-2), где n – количество его углов (сторон).

Вспомним, что любой четырехугольник состоит из двух треугольников (достаточно провести диагональ). Но сумма углов каждого из них одинакова и равна 180⁰, значит, сумма углов четырехугольника 360⁰.

Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).

∠1’+∠2’+…+∠n’=360°, где n – количество его углов (сторон), а ∠1′,…,∠n’ – внешние углы, по одному от каждой вершины.

Что такое многоугольник, выпуклый многоугольник, четырехугольник

В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.

Поговорим подробнее о видах многоугольников и их характеристиках.

Определение

Многоугольник — это замкнутая ломаная линия.

Многоугольник — это простое понятие: Если в замкнутой ломаной линии соседние стороны имеют общую точку и любые две стороны не являются продолжением друг друга, то фигура называется многоугольником.

При изучении темы, что такое многоугольники, применяются следующие термины:

Вершины многоугольника.
Стороны замкнутой ломаной.
Углы, образованные между смежными сторонами.
Отрезки между несмежными вершинами называются диагоналями.
Сумма длин всех сторон фигуры является периметром.
Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.

Наименования данных фигур зависят от количества сторон:

Треугольник – это 3 стороны.
Четырехугольник имеет 4 стороны.
Пятиугольник – это 5 сторон и пр.

Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.

Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.

Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.

Виды многоугольников

Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.

Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.

Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.

Что такое правильные многоугольники

Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.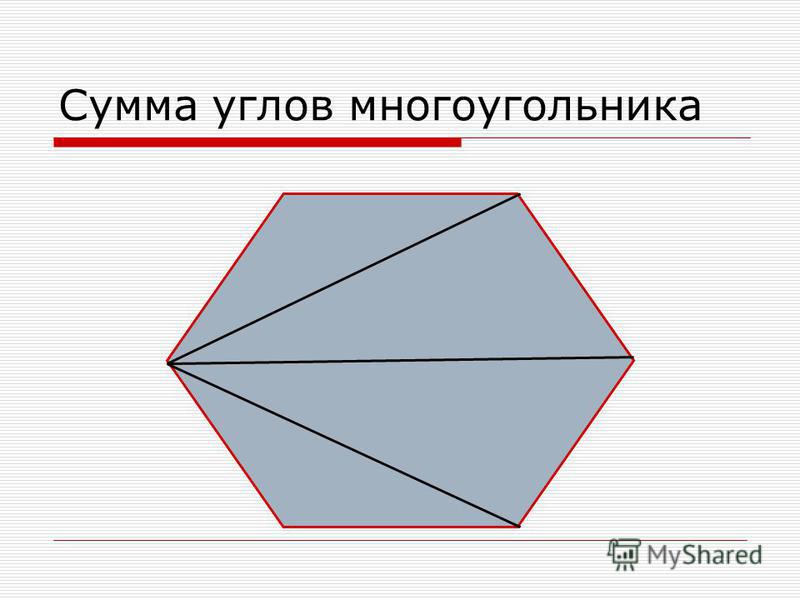

На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали

Периметром многоугольника называется сумма длин его сторон.

Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.

Пример

Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти
периметр четырехугольника.

Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см

Ответ: периметр четырехугольника ABCD равен 12 см.

Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.

Например, отрезок AD будет являться диагональю фигуры ABCDEF:

Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.

Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:

Количество треугольников будет на 2 меньше, чем число сторон:

Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.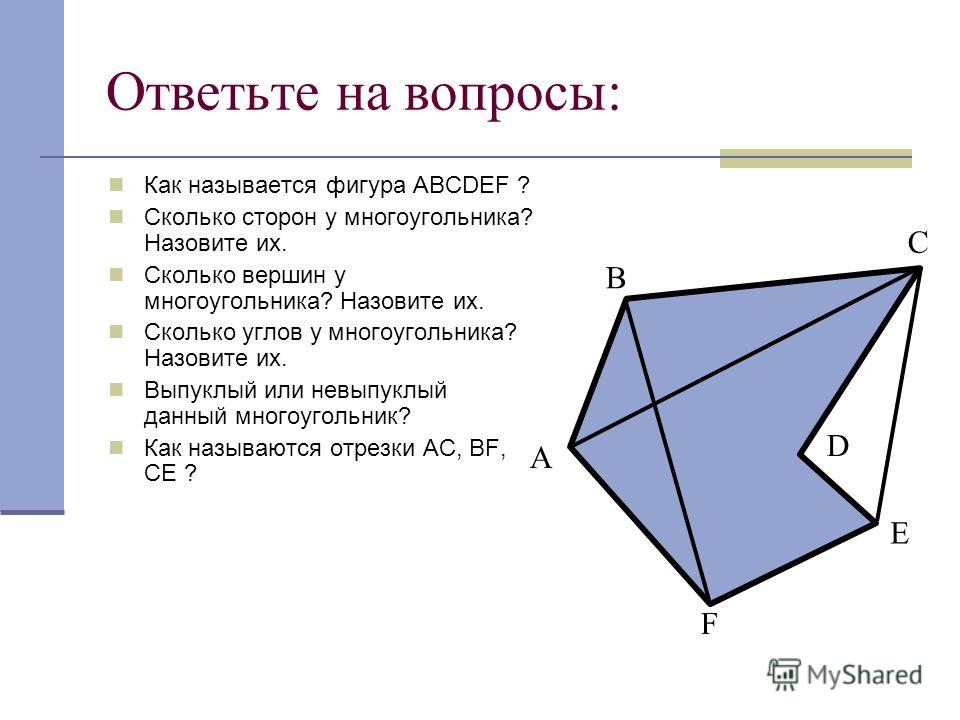

Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.

Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.

Сумма углов выпуклого многоугольника

Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.

Внутренним называется угол между смежными сторонами.

Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.

Например, ∠LBC является внешним углом для ABCDEF.

Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.

Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.

Сумма внутренних углов

Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.

Обозначения выглядят следующим образом:

сумма углов – s;
число сторон – n;
два прямых угла (2 · 90 = 180°) – 2d.

Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).

Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).

Пример:

Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.

Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Сумма внешних углов

Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.

Где:

s — сумма внешних углов;
4d — четыре прямых угла (4 · 90 = 360°).

Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).

Например, ∠1 и ∠2:

Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.

Пример

Задание: Найдите сумму углов выпуклого двенадцатиугольника.

Решение: Для выпуклого n-угольника сумма углов равна 180° (n -2).

Если имеется 12 вершин, то сумма всех углов будет рассчитываться следующим образом: 2 · 90 · (12 – 2) = 1800°.

Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.

Вогнутые многоугольники — определение, свойства, примеры

Вогнутые многоугольники — это такие многоугольники, в которых хотя бы один внутренний угол является углом отражения и направлен внутрь. У них минимум 4 стороны, и несколько диагоналей вогнутого многоугольника могут частично или полностью выходить за его пределы. Все вогнутые многоугольники неправильные, потому что внутренние углы не равны. Давайте узнаем больше о вогнутых многоугольниках в этой статье.

1.	Что такое вогнутый многоугольник?
2.	Вогнутый и выпуклый многоугольник
3.	Вогнутые многоугольники в реальной жизни
4.	Часто задаваемые вопросы о вогнутом многоугольнике

Что такое вогнутый многоугольник?

Многоугольник, который не является выпуклым, является вогнутым многоугольником. Если какой-либо внутренний угол в многоугольнике больше 180°, то это вогнутый многоугольник. Вогнутый многоугольник выглядит как многоугольник, в котором по крайней мере две стороны кажутся вдавленными внутрь. Например, звезда — это вогнутый многоугольник.

Определение вогнутого многоугольника

Вогнутый многоугольник определяется как многоугольник, в котором один или несколько внутренних углов больше 180°. Если какая-либо из диагоналей многоугольника частично или полностью выходит за пределы многоугольника, то такой многоугольник называется вогнутым. Обратите внимание на следующий рисунок, на котором показаны вогнутые многоугольники.

Свойства вогнутого многоугольника

Вогнутый многоугольник имеет некоторые отличительные свойства, которые помогают отличить его от других многоугольников.

Вогнутый многоугольник имеет по крайней мере один угол, который является углом отражения, то есть он больше 180° и меньше 360°.
Некоторые диагонали вогнутого многоугольника могут частично или полностью лежать за его пределами.
В вогнутом многоугольнике есть по крайней мере одна вершина, которая кажется вдавленной внутрь, чтобы придать многоугольнику отчетливую форму «пещеры».
Если отрезок пересекает вогнутый многоугольник, он касается более двух сторон.
Правильные многоугольники никогда не могут быть вогнутыми.
Все вогнутые многоугольники неправильные, потому что внутренние углы имеют разную величину.

Вогнутый и выпуклый многоугольник

Выпуклый и вогнутый многоугольник можно легко отличить по их свойствам. Обратите внимание на следующий рисунок и таблицу, чтобы увидеть разницу между выпуклыми и вогнутыми многоугольниками.

Выпуклые многоугольники	Вогнутые многоугольники
Выпуклый многоугольник не имеет внутреннего угла больше 180°	Вогнутый многоугольник имеет по крайней мере один угол отражения (более 180°).
Выпуклый многоугольник может иметь 3 стороны.	Вогнутый многоугольник имеет по крайней мере 4 стороны.
Когда линия проводится внутри выпуклой фигуры с любой стороны, она касается только двух сторон.	Когда линия проведена внутри вогнутой формы с одной стороны, она касается более чем двух сторон.
Диагонали выпуклого многоугольника не лежат вне его.	Некоторые диагонали вогнутого многоугольника могут частично или полностью лежать за его пределами.

Углы вогнутого многоугольника

Вогнутый многоугольник имеет внутренние и внешние углы, как и другие многоугольники. Единственное свойство вогнутых многоугольников, о котором здесь следует помнить, заключается в том, что один или несколько внутренних углов образуют угол отражения, который делает его похожим на вогнутый многоугольник. Другими словами, этот рефлекторный угол делает вершину направленной внутрь, что придает ей своеобразную форму. Давайте узнаем больше о сумме внешних и внутренних углов вогнутого многоугольника.

Сумма внешних углов вогнутого многоугольника

Сумма внешних углов вогнутого многоугольника равна 360°. Это означает, что, как и у всех других многоугольников, сумма внешних углов всегда составляет 360° для всех вогнутых многоугольников.

Сумма внутренних углов вогнутого многоугольника

Чтобы найти сумму внутренних углов вогнутого многоугольника, мы используем ту же формулу, которая применяется для других выпуклых многоугольников. Сумма внутренних углов = (n — 2) × 180°, где n представляет количество сторон многоугольника.

Вогнутые многоугольники в реальной жизни

Вогнутые многоугольники имеют заметную форму, в которой хотя бы одна из вершин направлена внутрь. Мы можем заметить вогнутые многоугольники в нашей повседневной жизни. Например, звездочка, наконечник стрелки, знак плюс и многое другое.

☛ Похожие темы
Типы полигонов
Неправильные многоугольники
Полигон Формула
Площадь полигонов

Примеры на вогнутом многоугольнике
Пример 1:
Напишите верно или неверно для следующих утверждений.
а.) Все внутренние углы вогнутого многоугольника меньше 180°.
b.) Вогнутые формы — это фигуры, у которых хотя бы одна вершина направлена внутрь.
Решение:
а.) Неверно, хотя бы один внутренний угол вогнутого многоугольника больше 180°.
b.) Верно, вогнутые формы — это те фигуры, у которых хотя бы одна вершина указывает внутрь. Это придает отчетливую форму вогнутому многоугольнику.
Пример 2:
Какие из следующих фигур представляют вогнутый многоугольник?
а.) Звезда

б.) Стрелка
в.) Ромб
Решение:
а.) Звезда — Вогнутый многоугольник
б.) Стрелка — Вогнутый x2 многоугольник
ромб полигон
Пример 3: Заполните пропуски правильным словом.
а.) В _____ многоугольнике некоторые диагонали могут частично или полностью выходить за его пределы.
b.) Многоугольник ______ может иметь 3 стороны.
Решение:
а.) В вогнутом многоугольнике некоторые диагонали могут частично или полностью лежать вне его.
b.) Выпуклый многоугольник может иметь 3 стороны.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок
Практические вопросы по вогнутому многоугольнику

перейти к слайдуперейти к слайду
Часто задаваемые вопросы о вогнутом многоугольнике
Что такое вогнутый многоугольник в геометрии?
Вогнутый многоугольник определяется как многоугольник, в котором один или несколько внутренних углов больше 180°. Если какая-либо из диагоналей многоугольника частично или полностью выходит за пределы многоугольника, то такой многоугольник называется вогнутым. В вогнутом многоугольнике есть по крайней мере одна вершина, которая, кажется, вдавлена внутрь, чтобы придать многоугольнику отчетливую «пещерную» форму.
Чему равна сумма внешних углов вогнутого многоугольника?
Сумма внешних углов вогнутого многоугольника равна 360°. Это означает, что, как и у всех других многоугольников, сумма внешних углов всегда составляет 360° для всех вогнутых многоугольников.
Какова сумма внутренних углов вогнутого многоугольника?
Чтобы найти сумму внутренних углов вогнутого многоугольника, мы используем ту же формулу, которая применяется для других выпуклых многоугольников. Сумма внутренних углов = (n — 2) × 180°, где n представляет количество сторон многоугольника.
Что является примером вогнутого многоугольника?
Мы сталкиваемся с множеством реальных примеров вогнутых многоугольников, таких как звезда, наконечник стрелы и многие другие, которые имеют особую форму и удовлетворяют всем характеристикам вогнутого многоугольника.
Как найти периметр вогнутого многоугольника?
Периметр вогнутого многоугольника можно вычислить так же, как находится периметр других выпуклых многоугольников. Все стороны многоугольника складываются, чтобы найти периметр.
Как найти площадь вогнутого многоугольника?
Поскольку вогнутые многоугольники имеют неправильную форму, специальной формулы для нахождения площади нет. Вогнутый многоугольник можно разделить на треугольники или другие меньшие многоугольники в соответствии с формой. Затем площадь этих фигур можно рассчитать по соответствующим формулам, и эти площади можно сложить вместе, чтобы получить площадь вогнутого многоугольника.
В чем разница между вогнутым и выпуклым многоугольником?
Различие между вогнутыми и выпуклыми многоугольниками можно перечислить следующим образом.
Выпуклый многоугольник не имеет внутреннего угла больше 180°, тогда как вогнутый многоугольник имеет по крайней мере один угол отражения больше 180°.
Диагонали выпуклого многоугольника не лежат вне его. Некоторые из диагоналей вогнутого многоугольника могут частично или полностью лежать за его пределами.
Выпуклый многоугольник может иметь 3 стороны, тогда как вогнутый многоугольник имеет по крайней мере 4 стороны.
Является ли звезда вогнутым многоугольником?
Да, звезда является вогнутым многоугольником, потому что она удовлетворяет всем свойствам вогнутого многоугольника. У него более 4 сторон, углы больше 180°, а диагонали звезды лежат вне формы.
Является ли стрелка вогнутым многоугольником?
Да, стрелка является вогнутым многоугольником, потому что она удовлетворяет всем условиям вогнутого многоугольника. У него внутренние углы больше 180°, а одна диагональ в стрелке лежит вне формы.
Является ли треугольник выпуклым или вогнутым многоугольником?
Треугольник является выпуклым многоугольником, потому что это трехсторонняя фигура. Вогнутый многоугольник имеет по крайней мере 4 стороны.
Является ли квадрат вогнутым многоугольником?
Нет, квадрат не является вогнутым многоугольником, это выпуклый многоугольник, потому что все диагонали квадрата лежат внутри него и нет внутреннего угла больше 180°.
Всегда ли вогнутый многоугольник правильный?
Нет, все вогнутые многоугольники неправильные, потому что один из их углов является углом отражения. Другими словами, внутренние углы вогнутого многоугольника не равны, следовательно, все вогнутые многоугольники неправильные.
Скачать БЕСПЛАТНЫЕ учебные материалы
Вогнутые многоугольники
Выпуклые и вогнутые многоугольники — определение, различия, примеры
В зависимости от внутренних углов все многоугольники можно разделить на две группы: выпуклые и вогнутые.
Выпуклые и вогнутые многоугольники
Что такое выпуклый многоугольник
Выпуклый многоугольник — это многоугольник, все внутренние углы которого меньше 180°. Все диагонали выпуклого многоугольника лежат внутри замкнутой фигуры. Выпуклый многоугольник может быть как правильным, так и неправильным. Правильные выпуклые многоугольники имеют все стороны одинаковой длины и все внутренние углы одинаковой величины (меньше 180°). Выпуклые многоугольники, которые не являются правильными, называются неправильными выпуклыми многоугольниками.
Примеры : Треугольники, все выпуклые четырехугольники, правильный пятиугольник и правильный шестиугольник — все это выпуклые многоугольники. Квадрат – это правильный выпуклый многоугольник.
Выпуклый многоугольник
Свойства
Все внутренние углы меньше 180°; ∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFA и ∠FAB меньше 180°
Все девять диагоналей лежат внутри замкнутой фигуры; диагонали AC, AD, AE, BD, BE, BF, CE, CF и CA лежат внутри фигуры.
Сумма всех внешних углов равна 360°
Сумма всех внутренних углов, имеющих n -сторон, равна ( n – 2) x 180°
В данном пятиугольнике ABCDE все внутренние углы равны. Укажите, является ли он выпуклым многоугольником.
Решение:
Как мы знаем,
Внутренний угол правильного многоугольника = (n-2) × 180°/n, здесь n = 5
= (5-2) x 180°/5
= 3 x 180° /5
= 108°
Поскольку все пять внутренних углов в данном пятиугольнике меньше 180°, это выпуклый многоугольник.
Формулы
Площадь
Это общее пространство внутри полигона. The formula is given below:
Area ( A ) = ½|(x ₁ y ₂ – x ₂ y ₁ )+(x ₂ y ₃ – x ₃ у ₂ )+……. .+(х _н у ₁ – х ₁ у _н )|, здесь (х ₁ , у 1 , у ₂ ), (х ₃ , у ₃ ),…….., (х _n , y _n ) — вершины многоугольника на координатной плоскости )
Solution:
As we know,
Area (A) = ½|(x ₁ y ₂ – x ₂ y ₁ )+(x ₂ y ₃ – x ₃ y ₂ )+(x ₃ y ₁ – x ₁ y ₃ )|,
здесь (x ₁ , у ₁ ) = (5, 2), (х ₂ , у ₂ ) = (12, 8), (х ₃ , у ₃ ) = (5, — 2)
= ½|(40-24)+ (-24-40)+ (10)-10)|
= ½|16-64|
= 48/2
Внутренние углы
Внутренние углы многоугольника — это углы внутри многоугольника. У многоугольника столько же внутренних углов, сколько и сторон.
Сумма внутренних углов
Это общая мера всех внутренних углов, объединенных в многоугольнике. Формула для определения суммы всех углов любого выпуклого правильного многоугольника приведена ниже:
Сумма внутренних углов = ( n -2) × 180°, здесь n = общее количество сторон многоугольника выпуклый правильный многоугольник.
Решение:
Как известно,
Сумма внутренних углов = (n-2) × 180°, здесь n = 22
= (14-2) x 180°
= 2160°
Один внутренний угол
Все внутренние углы правильного выпуклого многоугольника имеют одинаковые размеры и могут быть получены путем деления суммы внутренних углов на общее количество сторон. Формула приведена ниже:
Внутренний угол выпуклого многоугольника = ( n -2) × 180° / n , здесь n = общее количество сторон многоугольника
Найти меру внутренних углов выпуклый правильный многоугольник с 12 сторонами.
Решение:
Как мы знаем,
Внутренний угол правильного многоугольника = (n-2) × 180°/n, здесь n = 18
= (18-2) x 180°/18
= 16 x 180° /18
= 160°
Внешние углы
Внешний угол многоугольника — это угол, образованный одной стороной и продолжением соседней стороны.
Теорема о сумме внешних углов утверждает, что сумма внешних углов любого выпуклого многоугольника равна 360°. Для правильных выпуклых многоугольников с n сторонами каждый внешний угол определяется по следующей формуле:
Внешний угол выпуклого правильного многоугольника = 360°/ n , здесь n = общее количество сторон многоугольника
Вычислите внешний угол в 15-стороннем правильном выпуклом многоугольнике.
Решение:
Как известно,
Внешний угол правильного многоугольника = 360°/n, здесь n =15
= 360°/15
= 24°
Что такое вогнутый многоугольник
2 многоугольник, также известный как невыпуклый многоугольник, имеет по крайней мере один из внутренних углов, превышающий 180°. Некоторые диагонали вогнутого многоугольника лежат вне замкнутой фигуры.
Все вогнутые многоугольники неправильные, так как все внутренние углы имеют разную величину. Таким образом, вогнутые многоугольники никогда не бывают правильными.
Примеры : Дротик или наконечник стрелы в четырехугольниках, некоторых неправильных пятиугольниках и шестиугольниках
Вогнутый многоугольник
Свойства
Имеет по крайней мере один угол отражения больше 180° и меньше 360°; ∠DEF больше 180° и меньше 360°
Имеет хотя бы одну вершину, направленную внутрь; вершина C направлена внутрь
Имеет одну или несколько диагоналей, лежащих вне замкнутой фигуры; диагональ DF лежит вне замкнутой фигуры
Если провести отрезок, пересекающий вогнутый многоугольник, он пересечет границу более двух раз
Сумма внутренних углов данного шестиугольника ABCDEF равна 720°. Если ∠ABC = 78°, ∠BCD = 140°, ∠CDE = 80°, ∠EFA =88°, ∠FAB = 130°. Найдите ∠DEF и укажите, является ли многоугольник ABCDEF вогнутым.
Решение:
Как известно,
Сумма углов шестиугольника ABCDEF = 720°
Итак, ∠ABC + ∠BCD + ∠CDE +∠DEF + ∠EFA + ∠FAB =
78° + 140° + 80° +∠DEF + 88° + 130° = 720°
=> ∠DEF = 720° – 516°
=> ∠DEF = 204°
Поскольку ∠DEF больше 180°, многоугольник ABCDEF является вогнутым многоугольником. Также, если мы проведем линию, соединяющую точки D и F, мы обнаружим, что диагональ DF лежит вне замкнутой фигуры, что еще раз доказывает, что ABCDEF — вогнутый многоугольник.
Формулы
Площадь
Поскольку все стороны и внутренние углы вогнутого многоугольника не равны, стандартной формулы для определения их площади не существует. Чтобы определить площадь вогнутого многоугольника, мы должны разбить многоугольник на фигуры, такие как треугольник, прямоугольник, параллелограмм или другие фигуры, найти площадь каждой такой фигуры и, наконец, сложить их, чтобы получить общую площадь многоугольника. Таким образом, площадь вогнутого многоугольника равна:
Площадь ( A ) = сумма площадей всех фигур, доступных в пределах многоугольника
Периметр
Это общее расстояние, пройденное вокруг границы многоугольника. Таким образом, периметр вогнутого многоугольника получается простым сложением длин всех сторон. Таким образом, периметр равен:
Периметр ( P ) = сумма всех сторон многоугольника
Давайте разберемся с этими понятиями на примерах.
Найдите площадь и периметр вогнутого многоугольника с заданными размерами сторон.
Решение:
Данный многоугольник разбит на три прямоугольника. Нахождение площади каждого прямоугольника и их сложение даст площадь многоугольника.
Таким образом, площадь многоугольника = Площадь прямоугольника ABCD + Площадь прямоугольника GDHF + Площадь прямоугольника EFIJ
= (14 x 4) + (6 x 4) + (14 x 4)
= 56 + 24 + 56
= 136 квадратных единиц
Периметр многоугольника = AB + BD + DF +FJ + IJ+ EI + EH + GH + CG + AC
= (14 + 4 + 6 + 4 +14 + 4 +10 + 6 +10+ 4)
= 76 единиц
Найдите все стороны данного вогнутого многоугольника. Затем найдите его площадь и периметр. (Уловка: Разделите данный неправильный многоугольник на два правильных многоугольника)
Решение:
Данный многоугольник разделен на один прямоугольник и один квадрат. Нахождение площади прямоугольника и квадрата и их сложение даст площадь многоугольника.
Таким образом, площадь многоугольника = Площадь прямоугольника ABGF + Площадь квадрата CDEG
= (22 x 12) + (8x 8)
= 264 + 64
= 328 квадратных единиц
Периметр многоугольника = AB + BC + CD + DE + FE + AF
= (12 + 14 + 8 + 8 + 20 + 22)
= 84 единицы
Внутренние углы
Для определения суммы внутренних углов воспользуемся следующей формулой: = общее количество сторон многоугольника
Внешние углы
Как и для всех других многоугольников, теорема о сумме внешних углов, утверждающая, что сумма всех внешних углов равна 360°, верна для всех вогнутых многоугольников.
Часто задаваемые вопросы
Q1. Сколько сторон у выпуклого многоугольника?
Ответ . Многоугольник должен иметь как минимум три стороны и может иметь любое максимальное количество сторон.