Нарды, удвоение ставок и броуновское движение
Май 2001
Нарды: игра
Нарды считаются одной из старейших игр в мире. Его корни вполне могут уходить на 5000 лет назад, в бывшую Месопотамию. Оттуда он в различных вариантах распространился в Грецию и Рим, а также в Индию и Китай. В нее играли в Англии в 1743 году, когда Эдмонд Хойл установил правила игры в нарды в Европе. После пересмотра в 1931 году в США эти правила используются до сих пор.
То, что превратило ее в тонкую и искусную игру, которую мы знаем сегодня, было блестящим нововведением в правилах начала 20-го века: кубом удвоения. Кто его изобрел, неизвестно, но он появился в американских игорных клубах где-то в 1920-х годах. В этой статье мы рассмотрим некоторые свойства куба удвоения.
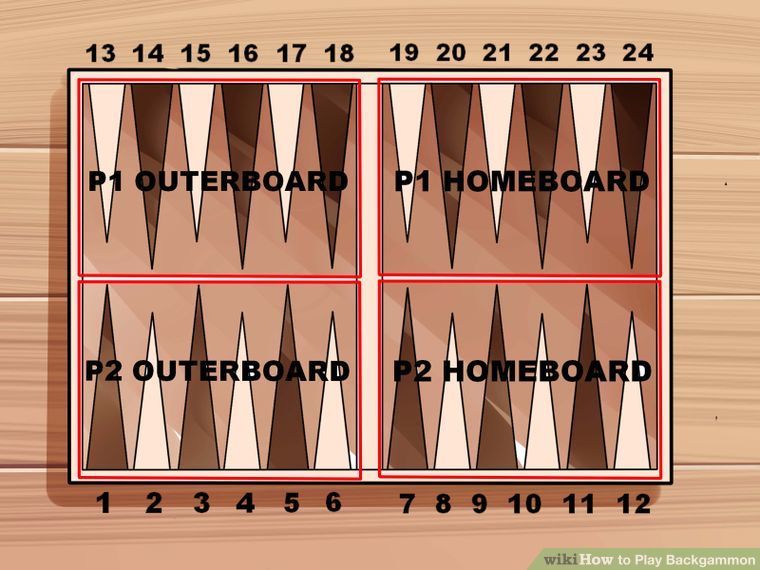
Доска для игры в нарды и несколько шашек
Нарды — это игра на удачу и мастерство. В нее играют два игрока по 15 шашек у каждого – один игрок играет черными, другой белыми.
Шашки игроков ходят в противоположных направлениях на доске с 24 клетками.
Задача каждого игрока — первым привести все свои шашки «домой» (в свою четверть доски), а затем «унести их» (полностью убрать с доски). Движение шашек следует результату броска двух костей, числа на двух костях представляют собой отдельные ходы. Правила игры см., например, на
Нарды — азартная игра, скажем, покер. В нем есть элемент случайности (представленный игральными костями), и есть понятие 9.0019 ставка за которую играют игроки. (Конечно, это не обязательно должны быть настоящие деньги; например, в турнире это могут быть очки.) Однако реальная сумма, которая переходит из рук в руки, может быть больше, чем ставка. Например, в определенных выигрышных позициях называется gammon и нарды , ставка соответственно удваивается или утраивается. Другой способ изменения ставки — это куб удвоения.
Кубик удвоения
Если один из игроков считает, что он в состоянии выиграть игру, он может перевернуть кубик удвоения и объявить двойной
, что означает, что общая ставка будет удвоена.
Если ее противник отказывается от удвоения , он немедленно теряет свою (неудвоенную) ставку, и игра заканчивается. Если он принимает удвоение , ставки удваиваются и в качестве компенсации куб удвоения
передается ему, и он получает исключительное право объявить следующий дубль. (Теперь говорят, что куб принадлежит .) Если удача в игре изменится так, что позже он решит, что теперь выигрывает, он сможет объявить так называемую 9-ку.0019 удвоить , что означает, что ставка снова удваивается. Если первый игрок отказывается от удвоения, он теряет удвоенную ставку; если она
принимает, игра продолжается с удвоенной ставкой, в четыре раза превышающей первоначальную стоимость. Количество удвоений ставки не ограничено, но право объявить об удвоении переходит от одного игрока к другому каждый раз, когда оно используется. (Изначально любой игрок может удвоить — ни у кого нет куба.) Эта приятная тонкость приводит к множеству тактических возможностей и проблем. В этой статье мы рассмотрим этот элемент игры с математической точки зрения.
Стратегия удвоения задается парой вероятностей и , с . Если ваши шансы на победу достигают (высокого) уровня, то, пока ваш противник не владеет кубом, вы объявляете дубль. Однако, если ваш противник объявляет удвоение, вы принимаете его, если ваши шансы на победу не ниже (меньшей) суммы . Мы хотели бы найти оптимальные значения для и, то есть значения, которые максимизируют ожидаемый выигрыш игрока.
Для этого мы будем использовать Броуновское движение для моделирования эволюции шансов игрока А на победу.
Математическая модель игры
Конечно, в этой статье (или вообще!) мы не можем дать четкую математическую модель игры на доске с учетом всех возможных позиций и бросков костей. Наша цель более скромная, а именно — смоделировать влияние на игру куба удвоения. Для этого предположим, что мы советуем опытному игроку, который является экспертом в игре за доской и может хорошо ее оценить.
вероятность выигрыша на каждом этапе игры. Мы будем основывать наши советы по обращению с кубом только на этом единственном числе от 0 до 1 или от 0% до 100%, если вы предпочитаете.
По ходу игры оценка игроком своих шансов на победу будет постоянно пересматриваться с каждым последующим броском кубиков. Мы будем рассматривать эволюцию шансов на победу игрока А как зависящий от времени процесс (технически называемый стохастическим процессом ), принимающий значения от 0 до 1. Чтобы нам было легче эффективно моделировать игру, этот процесс должен: как минимум, удовлетворяют следующим условиям:
Правила эволюции шансов
- Увеличиваются или уменьшаются шансы на победу игрока А после следующего хода независимо от предыдущих ходов . Это естественно, потому что броски костей не влияют друг на друга.
- Обратите внимание, что игрок А выигрывает игру точно в том случае, если его шансы на победу достигают 1 (определенность) до того, как упадут до 0 (вообще нет шансов). Следовательно, процесс, который мы используем для моделирования игры, должен быть остановлен , как только он достигнет 0 или 1.
- Эволюция шансов на победу должна быть справедливо в каком-то смысле: в некотором (небольшом) временном интервале шансы игрока А должны с одинаковой вероятностью увеличиться на определенную величину или уменьшиться на ту же величину.
- Процесс должен быть непротиворечивым. Это означает, например, что если шансы игрока А в определенный момент времени равны, скажем, 0,8, то процесс должен в конечном итоге достичь значения 1 с вероятностью 0,8 и, наоборот, достичь значения 0 с вероятностью 0,2.
- Процесс должен быть непрерывный. Это математическая идеализация, соответствующая тому факту, что с каждым ходом шансы меняются лишь немного. При математическом рассмотрении подобных задач очень удобно наблюдать за процессом в непрерывном времени.
Стоит отметить, что это последнее предположение очень важно. В реальной жизни шансы на победу игрока А увеличиваются на дискретную величину каждый раз, когда бросаются кости. Однако в начале игры скачки обычно довольно малы, так что это предположение о непрерывности, упрощающее анализ, будет довольно близко к истине. (С другой стороны, позднее, например, когда
шашек, оставшихся в игре, один особенно хороший или плохой бросок может изменить шансы игрока с 90% на 0%, поэтому на данном этапе игры наши результаты будут менее полезными.
Можем ли мы надеяться найти математическую модель (другими словами, стохастический процесс), удовлетворяющую этим условиям? Ответ на этот вопрос – да, и модель, которая работает, имеет долгую и интересную историю.
В 1828 году английский ботаник Роберт Браун изучил беспорядочное движение мелких частиц пыльцы на поверхности воды. Это беспорядочное движение связано с тем, что мелкие частицы (то есть молекулы воды) случайным образом попадают на пыльцу.
Случайное блуждание R
Если мы посмотрим только на вертикальные движения, мы окажемся в одномерной ситуации. Всякий раз, когда частица пыльцы сталкивается с молекулой сверху, она движется вниз и наоборот, как на рисунке слева.
Правила, описывающие это случайное движение, очень похожи на правила, которые мы сформулировали для нашей эволюции шансов выше: после каждого броска костей ваши шансы на выигрыш «ударяются» сверху или снизу и, следовательно, увеличиваются или уменьшаются на определенную величину.
Если принять во внимание, что таких шагов много и что, как мы видели, ваши шансы часто меняются лишь немного после каждого броска, то естественно спросить, существует ли непрерывный аналог этого процесса. К счастью, есть такой предел. Просто продолжайте выбирать все меньшие и меньшие размеры шага для случайного блуждания. Конечно, приращения случайного блуждания на каждом шаге становятся меньше. также. По мере того, как размеры шагов становятся все ближе и ближе к нулю, случайное блуждание все больше и больше напоминает процесс с непрерывным временем, называемый
Броуновское движение впервые было изучено как математический объект Башелье (1900) в теории фондовых рынков и Эйнштейном (1905) для проверки молекулярной теории тепла. Эти два автора также предположили многие свойства броуновского движения. Но потребовалось некоторое время, чтобы доказать, что броуновское движение действительно существует — в 1923 году американский математик по имени Винер, наконец, сделал это. не очевидно, что вы должны проверить, что свойства, требуемые от такого объекта, не противоречат друг другу. Значительно позже (в 1951) Донскер дал полное доказательство сходимости случайных блужданий к броуновскому движению. На рисунке справа показаны траектории типичного случайного блуждания и предельного броуновского движения.
Случайное блуждание (слева) и предельное броуновское движение
Броуновское движение проявляется в чрезвычайно большом количестве мест — оно играет решающую роль в физике (вспомните о диффузии частиц и теплопроводности), а также в теории финансов (представьте себе цену акции как маленькую частицу, по которой «ударяют» покупатели и продавцы: она растет, когда на нее падает покупатель, и падает, когда на нее падает продавец).
Его захватывающие свойства широко изучаются математиками.
Например, одной интересной особенностью является то, что он нигде не дифференцируем (хотя и непрерывен!) — это указывает на некую фрактальную структуру его путей.
Для наших целей достаточно знать, что броуновское движение существует — что мы можем принять наши свойства (1)–(5) без появления каких-либо тонких противоречий — и что оно действительно является пределом случайных блужданий, таких как шансов игрока А на победу под влиянием игральных костей с небольшими приращениями. Таким образом, броуновское движение началось с 1/2 и остановилось, когда оно достигло 0 или 1. разумная модель эволюции шансов на победу.
Оптимальная стратегия удвоения
Теперь мы попытаемся найти оптимальную стратегию удвоения, используя наши предположения (1)-(5) выше. Обозначим через P(t) вероятность выигрыша игрока А в момент времени t . Наша стратегия удвоения основана на одном чрезвычайно простом принципе:
Основной принцип : Если игрок А находится в неприятной ситуации, когда ее противник объявляет удвоение, то он примет удвоение, если это приведет к более высокому ожидаемому выигрышу, чем отказ.
.Поскольку это вполне разумно, ее противник, Игрок Б, будет применять ту же стратегию всякий раз, когда попадет в ту же проблему.
Используя этот принцип и непрерывность броуновского движения, ясно, что критический уровень , ниже которого Игрок А отказывается от удвоения и сдается, обладает следующим свойством:
Если , то ожидаемый выигрыш, если удвоение в момент времени принято равен ожидаемому выигрышу в случае отказа от удвоения.
Если мы назовем значение текущей ставки , то фактическая выплата в случае отказа Игрока А будет равна .
Каков ожидаемый выигрыш, если она согласится на удвоение, когда ? По сути, есть две возможности:
Первая возможность : Игрок А восстанавливается и достигает уровня до того, как проиграет игру. Затем, имея куб удвоения, она может объявить удвоение, и, применяя наш основной принцип, изложенный выше, к противнику, ее ожидаемая выплата равна ставке, которая в данном случае равна .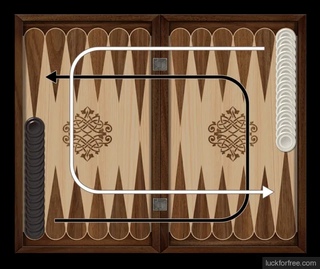
Для расчета ожидаемого выигрыша нам нужно найти вероятность того, что броуновское движение, начавшееся с, попадет на уровень до того, как достигнет 0 — см. рисунок ниже. Мы можем вычислить это, заметив, что, поскольку броуновское движение непрерывно, если оно идет от 1, оно должно сначала пройти через . Это означает, что
По свойству непротиворечивости броуновского движения вероятность в левой части равна, а второй множитель справа равен . Получаем, что
, что, следовательно, является вероятностью того, что Первая возможность сбудется.
Решение игрока А, когда игрок Б предлагает дубль
Вторая возможность: С вероятностью
Игрок А теряет ставку, не имея возможности использовать кубик удвоения.
Принимая во внимание обе возможности, ожидаемый выигрыш Игрока А при принятии равен
По нашему основному принципу это должно быть равно . Таким образом, мы получаем уравнение
Это уравнение легко решить, дав .
Когда игрок А должен объявить удвоение, если он владеет кубом удвоения? Если и она объявляет удвоение, противник примет удвоение на том основании, что его ожидаемый выигрыш больше, чем . Это так, потому что его вероятность выигрыша, которая равна , превышает . Так как ожидаемый выигрыш игрока Б меньше ожидаемого выигрыша игрока А, это нежелательно для игрока А. Следовательно, он должен ждать до тех пор, пока игрок Б не откажется от удвоения, и он выиграет ставку. Этот аргумент показывает, что обязательно .
Если Игрок А удваивает именно в этот критический момент, то Игрок Б может принять или отказаться от удвоения по своему усмотрению; его выигрыш одинаков в любом случае. Если P(t) следует пути, показанному на диаграмме ниже, и если все удвоения сделаны в критической точке и приняты, то игрок А в итоге выиграет в восемь раз больше первоначальной ставки.
Игрок А выигрывает в 8 раз больше первоначальной ставки в игре на удачу
Результат можно сформулировать как простое правило для игрока в нарды:
- Вам следует объявить дубль самостоятельно, если у вас есть на это право и вы оцениваете вероятность выигрыша с этого момента выше 80%.
- Если ваш противник объявляет дабл, вам следует сдаться, если вы считаете, что вероятность вашего выигрыша с этого момента ниже 20%.
Дополнительные примечания
Наша модель была довольно простой и допускала элегантный анализ (благодаря Киллеру и Спенсеру), но как модель игры в нарды она имеет несколько недостатков.
Ранее мы вкратце упоминали о возможности игры в гаммоны и нарды, где победитель выигрывает в два или три раза больше ставки. Хотя нарды довольно необычны, гаммоны не являются таковыми и являются важным фактором в большинстве решений удвоения. Обычный тип ситуации, когда игрок А является фаворитом, и если он выиграет, то, скорее всего, выиграет окорок. Вероятность ее победы все еще может быть далека ниже 80%, но если она удвоится, игрок Б с благодарностью откажется и уступит только одно очко, а не два, которые он уступил бы, если бы проиграл окорока. В этой ситуации игроку А уже слишком поздно удваивать. Возможно, раньше ей следовало удвоить, но сейчас ее лучшая стратегия — продолжать игру без удвоения в надежде забить гол.
Мы также видели, что предположение о непрерывности P(t) не совсем точно. В соответствии с этим предположением, если игрок Б удвоил свои ставки, а затем благодаря удачному броску костей повернул игру в свою пользу, у него всегда будет возможность удвоить ставку.
Наши расчеты основывались на расчете эквити игрока B в этот момент, если он примет первое удвоение.Однако на поздних стадиях игры может случиться так, что если В, приняв дубль, получит удачный бросок, то он немедленно выиграет игру; нет возможности удвоить первым. Это крайность, противоположная непрерывному случаю. В этом случае критическими точками являются не 80% и 20%, а 75% и 25%. (Вы можете попытаться доказать это — это несложное упражнение.)
Другим следствием непрерывности P(t) было то, что всякий раз, когда для одного игрока было правильно удвоение, для другого игрока также было правильным проигрыш! Если бы это было так в реальной жизни, то куб удвоения оказался бы не таким уж и интересным, так как на практике игры почти никогда не удваивались бы. Однако на самом деле это далеко не так. Причина в том, что, поскольку справедливость изменяется на дискретные величины, игрок А не может удвоить на ровно 80%-й балл (или 75%-й балл, или соответствующую промежуточную точку).
Поэтому часто для нее правильно удвоить до этой критической точки, особенно когда существует значительная опасность того, что ее эквити преодолеет критическую точку до ее следующего хода. С другой стороны, очевидно, что тогда для B также правильно
принять двойку.Наш вывод действителен только для двух одинаково опытных игроков, играющих в «денежную игру». Есть ситуации, в которых другие стратегии были бы лучше. Предположим, вы участвуете в турнире. В зависимости от системы подсчета очков может быть уместно избегать дублей, когда лидируете. С другой стороны, когда вы находитесь далеко позади, удвоение может быть хорошей стратегией, даже если ваши шансы на победу текущая игра плохая.
Наши расчеты основывались на расчете эквити игрока B в этот момент, если он примет первое удвоение.
Поэтому часто для нее правильно удвоить до этой критической точки, особенно когда существует значительная опасность того, что ее эквити преодолеет критическую точку до ее следующего хода. С другой стороны, очевидно, что тогда для B также правильно
принять двойку.Для получения дополнительной информации такого рода и обсуждения того, как оценить свою позицию, см. http://www.bkgm.com/articles/mpd.html и http://www.bkgm.com/articles/met.html.
Об авторах
Йохен Блат работает над докторской диссертацией по фрактальной геометрии суперпроцессов в Университете Кайзерслаутерна в Германии.
Петер Мёртерс преподает теорию вероятностей в Кайзерслаутернском университете. В сентябре он переедет в Университет Бата. Его исследования сосредоточены на взаимодействии между фрактальной геометрией и случайными процессами.
| Правила игры в нарды Windows и Android | |
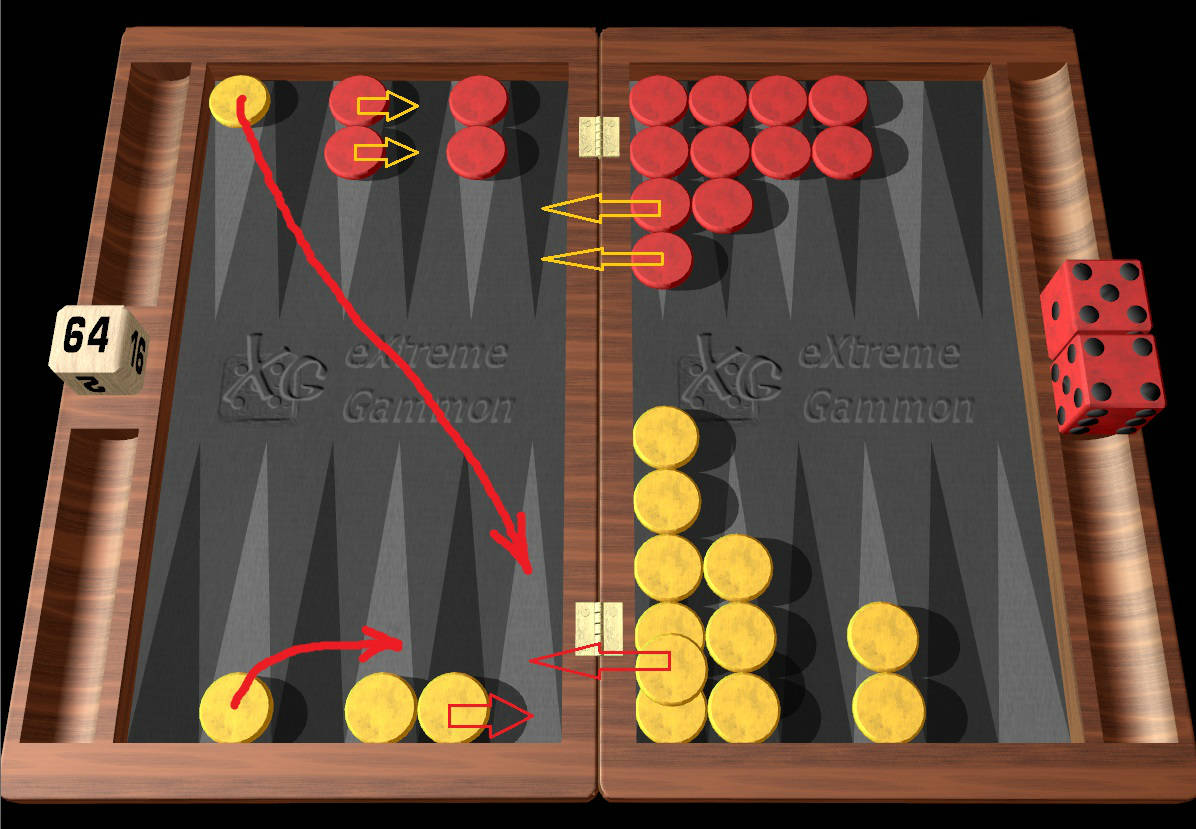
Игра в нарды в ее реальной форме ведется на
такая доска с двадцатью четырьмя треугольниками, называемыми точками, в
альтернативные цвета. Нарды – это игра для двух игроков, где
каждый должен ходить своими шашками в соответствии со значением
две кости, в свою домашнюю доску. Остальные двенадцать
треугольники представляют внешняя доска,
которая отделена от жилых домов центральной частью
доска под названием бар. | |
Доска для игры в нарды Вы видите шашки в исходном положении,
дома игроков, куб удвоения, полоса и движение
направление для белого игрока. Цель цель игры состоит в том, чтобы каждый игрок принес все свои
шашки в свою домашнюю доску, а затем уносит их.
первый игрок, сбрасывающий все свои шашки, выигрывает игру.
Во время игры вы можете применять различные стратегические ходы, такие как
блокировать ход или проникновение противника. Вы также можете
используйте кубик удвоения, чтобы увеличить ставку в игре, если это
Ваша очередь, и если это разрешено правилами применения. | |
Правила К
В начале игры каждый игрок бросает по одному кубику. Это определяет
как игрок, который будет ходить первым, так и номера, которые будут разыграны. Если
выпадают одинаковые числа, затем оба игрока снова бросают кости
пока они не получат разные числа. Игрок, получивший высшее
номер теперь перемещает свои шашки в соответствии с числами, показывающими
на обоих кубиках. После первого броска игроки бросают два кубика.
и меняй обороты. | |
Глоссарий терминов по игре в нарды A B C D E F G H I J K L M N O P Q R S | |
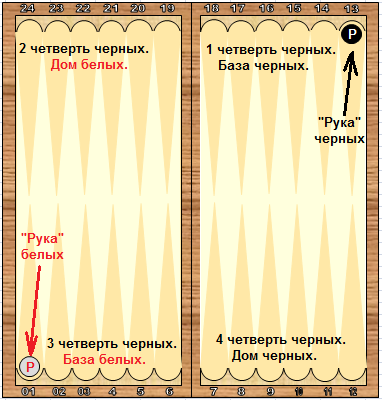Черный игрок ходит в
противоположное направление. 
Таким образом, общий победитель может быть выбран в
соревнования. Первый игрок, набравший необходимое количество
очков выигрывает матч. Очки начисляются в обычном порядке.
образом: один для одиночной игры, два для окорока и три для
нарды. Более того, используется куб удвоения, например, победитель
получает значение игры, умноженное на конечное значение
куб удвоения. 
шашки всегда есть
продвинулся вперед, к точке с меньшим номером. Точка, занятая
одна шашка любого цвета называется пятно.
Если противостоящая шашка останавливается на пятне, пятно
ударять
и размещены на
бар.
Применяются следующие правила: 
Если эти условия не выполняются, то
игрок может попытаться переместить шашку на более низкую точку. Во всяком случае, оба
кости должны быть сыграны, если это возможно. 
