Правила игры пьяница в карты: правила игры, обзор настолки или как играть

[Из песочницы] О ценности карт в игре «Пьяница»

В последнее время я много играю со своим 5-летним сыном в карточную игру «Пьяница». И он, и я радуемся, когда побеждаем, и огорчаемся, когда проигрываем.

В какой-то момент я задался вопросом: какова «финансовая» ценность каждой из карт в «Пьянице»? Так как Шестерка бьет Туза (см. вариант правил под катом), то система ценностей в «Пьянице» циклична, и ответ неочевиден. Например, ценнее ли Семерка Шестерки? Семерка бьет Шестерку — значит да! Но с другой стороны, каждая из них бьет только одну другую карту в игре (Семерка — Шестерку, а Шестерка — Туза) — значит они равны по ценности? Но Туз, побитый Шестеркой, сам по себе гораздо ценнее чем Шестерка, побитая Семеркой — значит Шестерка ценнее?!

Я решил подвести математическую модель под анализ ценности карт в «Пьянице». Результаты получились самые неожиданные.
Для начала, вот правила нашего варианта этой игры:

• В игре участвуют 2 игрока.
• 36 карт (от шестерок до тузов) раздаются поровну.
• Каждый игрок снимает верхнюю карту своей колоды и кладет ее лицом вверх — происходит «сражение». Победивший в сражении игрок кладет все карты сражения под низ своей колоды.
• Победитель в сражении определяется по обычному старшинству карт (сверху вниз): Туз, Король, Дама, Валет, Десятка, Девятка, Восьмерка, Семерка, Шестерка. Есть только одно очень важное исключение: Шестерка побеждает Туза.
• Если в сражении участвуют одинаковые карты (например, две десятки), то происходит «спор»: поверх «спорящих» карт лицом вниз кладутся еще по карте (они являются пассивными заложниками спора), и потом лицом вверх еще две карты которые вступают в сражение. Победитель забирает себе все карты спора.

Как понятно из правил, победа в этой игре зависит исключительно от везения — победитель определяется раздачей карт, так как от игроков вообще ничего не зависит.

Итак, как мы можем определить «ценность» карты в «Пьянице»? Я решил определить ценность карты через ожидаемое количество карт которые эта карта принесет если игра будет продолжаться бесконечно долго.

Начнем с простой задачи: определения ожидаемого количества карт только для Шестерки и только одного сражения. В колоде 36 карт, значит, если мы ходим Шестеркой, она вступает в сражение с другой (случайно выбранной) картой из оставшихся 35ти. Что может произойти? С вероятностью в 4/35 выпадет Туз, и тогда мы получим и Шестерку, и Туза. С вероятностью в 3/35 выпадет еще одна Шестерка, и произойдет спор —, а так как мы предполагаем абсолютно случайный расклад, то мы с равной вероятностью либо выиграем, либо проиграем его, а значит, что в среднем ожидается, что наша Шестерка останется у нас. Во всех остальных случаях мы теряем шестерку. Итого, ожидаемое кол-во карт для Шестерки после одного сражения: 7/35 Шестерки + 4/35 Туза.

Теперь, заполним матрицу для ожидаемых кол-в всех карт для одного сражения (ряд Шестерки — это ожидаемое кол-во карт получаемое после одного сражения с участием нашей Шестерки).

	Шестерка	Семерка	Восьмерка	Девятка	Десятка	Валет	Дама	Король	Туз
Шестерка	7/35	0	0	0	0	0	0	0	4/35
Семерка	4/35	7/35	0	0	0	0	0	0	0
Восьмерка	4/35	4/35	11/35	0	0	0	0	0	0
Девятка	4/35	4/35	4/35	15/35	0	0	0	0	0
Десятка	4/35	4/35	4/35	4/35	19/35	0	0	0	0
Валет	4/35	4/35	4/35	4/35	4/35	23/35	0	0	0
Дама	4/35	4/35	4/35	4/35	4/35	4/35	27/35	0	0
Король	4/35	4/35	4/35	4/35	4/35	4/35	4/35	31/35	0
Туз	0	4/35	4/35	4/35	4/35	4/35	4/35	4/35	31/35

Очевидно, что недостаточно учесть одно сражение, чтобы определить ценность карты. 2, так как Туз, потенциально выигранный в первом сражении никак не увеличивать шансов получить Шестерку во втором. Однако, тот же Туз увеличивает шансы получить каждую из остальных карт во втором сражении —, но ожидаемые кол-ва карт для Туза во втором сражении умножаются на вероятность получить Туза в первом сражении (4/35). И т.д.

Здесь можно вполне резонно возразить, что к моменту второго сражения вероятности уже не будут такими, как на момент первого, так как мы предполагаем определенные результаты первого сражения. Действительно, в идеале мы просчитали бы все пути этого сада расходящихся тропок. Но сделать это непросто, поэтому мы предположим, что изменяющееся вероятности одинаковы для всех карт и ошибки каким-то образом усредняются.

Итак, совсем немного руби кода:

require 'matrix'
# Матрица ожидаемых кол-в для одного сражения
m1 = Matrix[
     [7.0/35, 0, 0, 0, 0, 0, 0, 0, 4.0/35],
     [4.0/35, 7.0/35, 0, 0, 0, 0, 0, 0, 0],
     [4.0/35, 4.0/35, 11.0/35, 0, 0, 0, 0, 0, 0],
     [4. 0/35, 4.0/35, 4.0/35, 15.0/35, 0, 0, 0, 0, 0],
     [4.0/35, 4.0/35, 4.0/35, 4.0/35, 19.0/35, 0, 0, 0, 0],
     [4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 23.0/35, 0, 0, 0],
     [4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 27.0/35, 0, 0],
     [4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 31.0/35, 0],
     [0, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 4.0/35, 31.0/35]
]
# Матрица ожидаемых кол-в после 1000 сражений (m1 в степени 1000)
m1000 = m1 ** 1000
# (значения округлены) => Matrix[[0.0667, 0.0667, 0.0667, 0.0667, 0.0667, 0.0667, 0.0667, 0.0667, 0.0667], [0.0095, 0.0095, 0.0095, 0.0095, 0.0095, 0.0095, 0.0095, 0.0095, 0.0095], [0.0127, 0.0127, 0.0127, 0.0127, 0.0127, 0.0127, 0.0127, 0.0127, 0.0127], [0.0178, 0.0178, 0.0178, 0.0178, 0.0178, 0.0178, 0.0178, 0.0178, 0.0178], [0.0267, 0.0267, 0.0267, 0.0267, 0.0267, 0.0267, 0.0267, 0.0267, 0.0267], [0.0444, 0.0444, 0.0444, 0.0444, 0.0444, 0.0444, 0.0444, 0.0444, 0.0444], [0.0889, 0.0889, 0.0889, 0.0889, 0.0889, 0.
 
 
  0889, 0.0889, 0.0889, 0.0889], [0.2667, 0.2667, 0.2667, 0.2667, 0.2667, 0.2667, 0.2667, 0.2667, 0.2667], [0.4667, 0.4667, 0.4667, 0.4667, 0.4667, 0.4667, 0.4667, 0.4667, 0.4667]]

Обратите внимание, как через некоторое кол-во сражений все ожидаемые кол-ва карт для одной карты становятся одинаковыми — так как (из-за циркулярной системы ценностей) в конце концов мы можем выиграть все карты, то ожидаемые кол-ва для всех карт сходятся к одному числу. Теперь осталось совсем немного — складываем все числа в каждом ряду чтобы узнать «ценность» каждой из карт (т.е., ожидаемое число карт после 1000 сражений):

m1000.row_vectors.map {|row| row.reduce(&:+).round(3)}
# [0.6, 0.086, 0.114, 0.16, 0.24, 0.4, 0.8, 2.4, 4.2]

Для наглядности:

	Шестерка	Семерка	Восьмерка	Девятка	Десятка	Валет	Дама	Король	Туз
Ценность	0.6	0.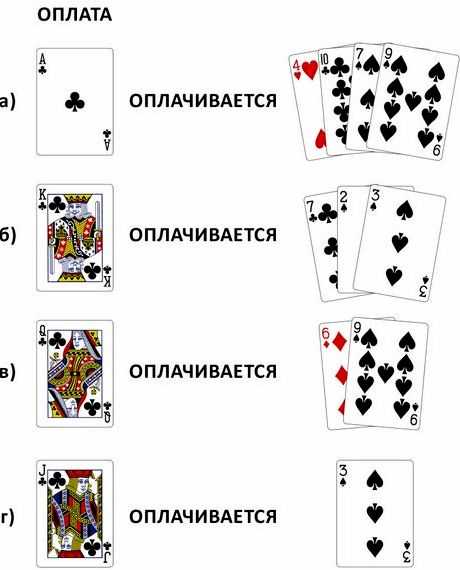 086	0.114	0.16	0.24	0.4	0.8	2.4	4.2

Неожиданные выводы:

• Ценность Шестерки лежит между Валетом и Дамой!
• Только у Короля и Туза ожидаемое конечное кол-во карт превышает 1 (то есть, ожидается позитивный ROI).

© Habrahabr.ru

Давай сыграем в пьяницу: amarok_man — LiveJournal

?

Categories:

• СССР
• Игры
• История
• Cancel

Пьяница…Нет, это не про нетрезвого человека, любящего выпить. А про карточную игру. Помните такую ?! Одна из самых простейших по правилам. Именно она вспоминается, как самая первая карточная игра, которой освоил среди них. Когда же, в каком возрасте это было ?!

Сказать, что азартный в картишки человек, так нет. Если только в детстве и юности. А с возрастом вообще потерял к игральным картам интерес. А вот игра в «пьяницу» вспоминается, как самая первая, которую узнал

Было тогда лет семь-восемь, если память не изменяет. Играли в неё с соседскими пацанами и девчонками во дворе летними вечерами на лавочке, или у нас дома с двоюродными братьями, когда те приходили в гости. Правила в неё были простейшие, насколько помню. Хотя и он уже подзабылись за давностью лет 🙂 Посмотрел в инете сейчас …

Вот и видяшка есть:

Довльно интересно было ! И азартно ) А что ещё вечерами летом делать во дворе ?! Тоже было одно из развлечений. А ещё в «дурачка» резались и спорили до хрипоты, кто мухлюет и был пойман с поличным 🙂

А потом уже были всякие «кинг», «девятка», «покер». ..

А вы помните свои игры в картишки времён детства ?!  И в какие играли ?! Вспомните их сейчас по правилам, или уже подзабылись ?!

………………………

пост отложеный

Tags: СССР, игры, утро

Subscribe

• Куда отправляются елки после праздников

  Новогодние праздники закончились. С ветвей зеленых красавиц снимают ёлочные игрушки, а сами деревца выбрасывают на мусорку. А куда отправляются…

• Арктический мороз на Волге

  У нас в регионе уже который день мороз давит. По ночам уже и под минус сорок. Хотя не только у нас. А судя по новостным сообщениям и инфолентам,…

• Блажь…

  «Блажь»…так называется спектакль нашего городского театра «Колесо», на который мы ходили 7-го января. Слоган нового…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

Previous
← Ctrl ← Alt

• 1
• 2
• 3

Next
Ctrl → Alt →

• Куда отправляются елки после праздников

  Новогодние праздники закончились. С ветвей зеленых красавиц снимают ёлочные игрушки, а сами деревца выбрасывают на мусорку. А куда отправляются…

• Арктический мороз на Волге

  У нас в регионе уже который день мороз давит. По ночам уже и под минус сорок. Хотя не только у нас. А судя по новостным сообщениям и инфолентам,…

• Блажь…

  «Блажь»…так называется спектакль нашего городского театра «Колесо», на который мы ходили 7-го января. Слоган нового…

Правила Ring of Fire — Питьевая игра Ring of Fire

Ring of Fire. Если бы нам пришлось составить список лучших игр с алкоголем, когда-либо существовавших в истории человечества, эта , вероятно, была бы довольно высоко в списке.

Классика практически на каждом предварительном приеме напитков, мероприятии Freshers и домашней вечеринке, Ring of Fire гарантированно понравится публике. К тому же, в отличие от таких игр, как бир-понг, здесь требуется немного оборудования или подготовки. Просто возьмите колоду карт, огромный пивной стакан, группу желающих и вуаля.

И хотя изучение новых игр для званых обедов , чтобы немного перепутать вещи, может быть забавным, нет ничего лучше, чем застрять в старой любимой игре. Радость быть мастером большого пальца и видеть, что никто еще не заметил? Бесподобный. Вытащить туза и все кричат ​​» водопад «? Просто прекрасный момент, тбх. Более того, определенно нет другой игры, которая гарантированно напоит вас так сильно, как Ring of Fire (ответственно, конечно). Ах, смутные воспоминания.

tabsprint.com

Тем не менее, как бы нам это ни нравилось, есть одна проблема. Учитывая, что на самом деле нужно запомнить 13 разных карт (и их значения), иногда бывает сложно вспомнить правила по требованию. Кроме того, вы, вероятно, выпьете коктейль или два, прежде чем даже начнете играть, что, знаете ли, тоже не помогает.

Итак, в час нужды, подведем итоги…

Высокий стакан ставится в центр стола, вокруг него лежат игральные карты лицевой стороной вниз в большом круге (см. рисунок выше). Это становится «огненным кольцом». Игроки по очереди берут карту из колоды, стараясь не разбить круг – например, убедившись, что каждая карта касается хотя бы одной другой, оставшейся в круге. Если ты разорвешь круг, ты должен выпить. Для каждой карты, которую вы берете, есть определенное правило —

• 2 — Вы , игрок, вытащивший карту, выбирает кого-нибудь выпить.
• 3 — Я , игрок, вытащивший карту, пьет.
• 4 — Все, кто идентифицирует себя как женщина, пьют.
• 5 — Thumbmaster, игрок, вытащивший карту, должен положить большой палец на стол в выбранное время (до того, как будут выбраны следующие пять, иначе они потеряют право). Тот, кто последним положит большой палец на стол, должен выпить.
• 6 — Все, кто идентифицирует себя как мужчина, пьют.
• 7 — Небеса, игрок, вытащивший карту, должен указать на небо (в любой момент до того, как будут вытянуты следующие 7 карт). Последний человек, указывающий на небо, должен выпить.
• 8 — Помощник , игрок, вытащивший карту, выбирает собутыльника, который должен пить каждый раз, когда выпивает. В качестве вторичного правила вы можете решить, означает ли это, что вы всегда должны пить, когда они тоже пьют.
• 9 — Рифма , игрок, вытащивший карту, произносит слово, и вы ходите по кругу, рифмуя это слово, пока кто-нибудь не ошибется и ему не придется пить.
• 10 — Категории , игрок, вытащивший карту, думает о категории (например, собаки, машины, виды алкоголя), и вы ходите по кругу, называя слова в этой категории, пока кто-нибудь не ошибется и не будет вынужден выпить.
• Джек — Составьте правило. Игрок, вытащивший карту, устанавливает новое правило (например, вы не можете сказать слово «да» или вы не можете поставить свой напиток), и любой, кто нарушает правило в любой момент до конца игры, должен пить. .
• Королева — Мастер вопросов. Вы становитесь мастером вопросов, и если кто-нибудь ответит на вопрос, заданный вами (игроком, вытянувшим карту), он должен выпить. Это касается ЛЮБОГО вопроса.
• Король — игрок, вытащивший карту, должен налить немного своего напитка в чашку посередине. Тот, кто нарисует последнего короля, должен выпить то, что находится в чашке посередине.
• Туз — водопад. Начиная с игрока, вытянувшего карту, каждый игрок должен постоянно пить свой напиток. Вы можете остановиться только тогда, когда человек справа от них перестанет пить.

Приготовьтесь к очень веселому (и, вероятно, очень пьяному) вечеру. Пожалуйста, пейте ответственно.




Дасти Бакстер-Райт Исполняющий обязанности редактора отдела развлечений Cosmopolitan Дасти Бакстер-Райт (она/она) — редактор отдела развлечений в Cosmopolitan UK по печатным, цифровым и видеоматериалам.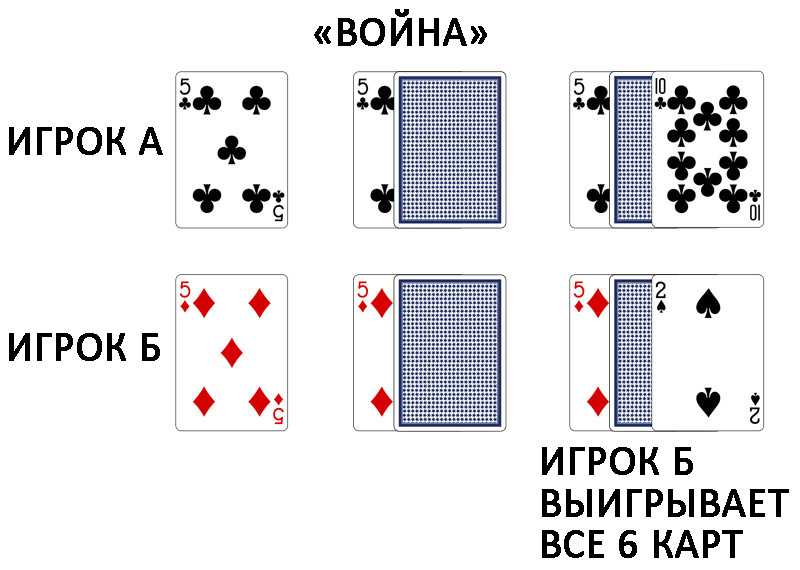

Realbeer.com: Пивная игра: питье UNO #1

Realbeer.com: Пивная игра: пить UNO #1

ГЛАВНАЯ | ПИВО.ЕДУ | СООБЩЕСТВО | РАЗВЛЕЧЕНИЕ | НОВОСТИ | РОЗНИЧНАЯ РОЗНИЦА | ПИВОВАРЕННЫЕ И ПАБЫ | ССЫЛКИ | СОБЫТИЯ

Развлечение — Игры — Отрыжка — Тосты — Юмор — Котировки — Опрос — Конкурсы Beer.edu — Пиво к празднику — Пиво и еда — Мед — Соединенное Королевство — Германия — Этот Старый Кегератор — Содержание алкоголя в пиве — Месяц американского пива — Япония — Домашнее пивоварение — Бельгия — Канада — Ирландия — Мексика — Шотландия — Октоберфест Соревнования: — Кубок мира по пиву — Битва пива — Большой американский фестиваль пива РЕКЛАМА

Пивная игра: пить UNO #1 Категория: Карточные игры Автор: Тара Солс (tsauls@dttus. com) Игроки садятся за стол и играют в настоящую игру. Каждый раз, когда разыгрывается «дикая» карта, это социальный напиток. Каждый раз, когда вам нужно взять карту, вы пьете. Например, если кто-то кладет «Draw Two», а вы тот, кто должен рисовать, вы также делаете два глотка пива. Если у вас нет карты для розыгрыша и вам нужно продолжать тянуть, вы выпиваете количество карт, которые должны были взять. Когда другой игрок кладет карту «Пропустить» или «Обратно», и вы тот, кто пропускает ход, вы пьете. Когда у игрока остается одна карта, он должен сказать «УНО». Если «Уно» не сказано, а другой игрок это замечает, игрок с одной картой должен опорожнить свое пиво и взять 5 карт. В конце игры, когда у одного из игроков закончились карты, все игроки, у которых в руках остались карты, должны выпить столько карт, сколько у них на руках.   Далее >  Beer. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт