Как решать судоку?
Данную методику решения судоку подготовила Nekonyash
Цель судоку – расставить все цифры так, чтобы в квадратах 3х3, строках и столбцах не было одинаковых цифр. Вот пример уже решенного судоку:
Можно проверить, что в каждом из девяти квадратов, а и так же во всех строках и столбцах нет повторяющихся чисел. Решая судоку нужно пользоваться этим правилом «уникальности» числа и, последовательно исключая кандидатов (маленькие числа в клетке обозначают какие числа, по мнению игрока, могут стоять в этой клетке), находить места, где может стоять только одно число.
Открыв судоку, мы видим, что в каждой клетке проставлены все маленькие серые числа. Можно сразу убрать отметки с уже выставленных чисел (отметки убираются щелчком правой мыши по маленькому числу):
Начну с числа, которое в данном кроссворде есть в одном экземпляре — 6, чтобы было удобнее показать исключение кандидатов.
Числа исключаются в квадрате с числом, в строке и столбце, убираемые кандидаты отмечены красным – по ним мы и кликнем правой кнопкой мыши, отметив,
что здесь шестерок в этих местах быть не может (иначе получится две шестерки в квадрате/столбце/строке, что противоречит правилам).
Теперь, если вернуться к единицам, то картина исключений будет следующей:
Мы убираем кандидаты 1 в каждой свободной клетке квадрата, где уже есть 1, в каждой строке, где есть 1 и в каждом столбце, где есть 1. Итого для трех единиц будет 3 квадрата, 3 столбца и 3 строки.
Далее перейдем сразу к 4, цифр больше, но принцип тот же. И если присмотреться, то видно, что в левом верхнем квадрате 3х3 остается всего одна свободная клетка (отмечена зеленым), где может стоять 4. Значит, ставим туда цифру 4 и стираем всех кандидатов (других чисел там стоять больше не может). В простых судоку таким образом можно заполнить довольно много полей.
После того, как выставлено новое число – можно перепроверить предыдущие, ведь добавление нового числа сужает круг поиска, например, в этом кроссворде благодаря выставленной четверке, под единицу в этом квадрате осталась всего одна клетка (зеленая):
Из трех доступных клеток под единицу не занята всего одна, туда единицу и ставим.
Таким образом убираем всех очевидных кандидатов для всех чисел (от 1 до 9) и проставляем числа по возможности:
После удаления всех очевидно неподходящих кандидатов получилась клетка, где остался всего 1 кандидат (зеленая), значит, там это число – тройка,
и стоит.
Так же числа ставятся, если кандидат остался последним в квадрате, строке или столбце:
Это примеры на пятерках, можно увидеть, что в оранжевых клетках пятерок нет, а в зеленых клетках остается единственный кандидат в области, значит, пятерки там и стоят.
Это самые начальные способы простановки чисел в судоку, можно уже опробовать их, решая судоку на простой сложности (одна звезда), например: Судоку № 12433, Судоку № 14048, Судоку № 526. Указанные судоку полностью решаются с использованием информации выше. Но в случае, если не получается найти следующую цифру, можно прибегнуть к методу подбора – сохранить судоку, и попробовать наугад проставить какую-нибудь цифру, а в случае неудачи загрузить судоку.
Если хочется освоить более сложные методы, читайте далее.
Запертые кандидаты
Запертый кандидат в квадрате
Рассмотрим следующую ситуацию:
В квадрате, выделенном синим, кандидаты цифры 4 (зеленые ячейки) располагаются в двух клетках на одной линии.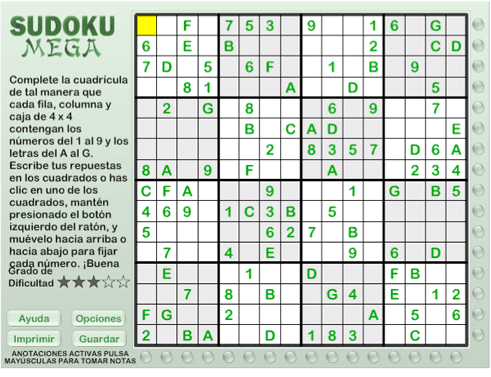 Если на этой линии (оранжевые клетки)
будет стоять цифра 4, то в синем квадрате некуда будет поставить 4, значит – исключаем 4 из всех оранжевых клеток.
Если на этой линии (оранжевые клетки)
будет стоять цифра 4, то в синем квадрате некуда будет поставить 4, значит – исключаем 4 из всех оранжевых клеток.
Аналогичный пример для цифры 2:
Запертый кандидат в строке
Этот пример похож на предыдущий, но здесь в строке (синяя) кандидаты 7 располагаются в одном квадрате. Это значит, что из всех оставшихся клеток квадрата (оранжевые) удаляются семерки.
Запертый кандидат в столбце
Аналогично предыдущему примеру, только в столбце кандидаты 8 расположены в одном квадрате. Так же убираются все кандидаты 8 из других клеток квадрата.
Освоив запертых кандидатов, можно решать судоку средней сложности без подбора, например: Судоку № 11466, Судоку № 13121, Судоку № 11528.
Группы чисел
Группы увидеть сложнее, чем запертых кандидатов, но они помогают пройти многие тупиковые ситуации в сложных кроссвордах.
Голые пары
Самый простой подвид групп – это две одинаковые пары чисел в одном квадрате, строке или столбце. Для примера голая пара чисел [7, 8] в строке:
Для примера голая пара чисел [7, 8] в строке:
Если в любой другой клетке в оранжевой строке будет 7 или 8, то в зеленых клетках останется 7 и 7, либо 8 и 8, но по правилам невозможно, чтобы в строке было 2 одинаковых числа, значит все 7 и все 8 убираются из оранжевых клеток.
Еще пример:
Голая пара [5, 8] одновременно в одном столбце и в одном квадрате. Удаляются лишние кандидаты (красные) и из столбца и из квадрата.
Важное замечание – группа должна быть именно «голой», то есть не содержать других чисел в этих клетках. То есть [5, 8] и [5, 8] являются голой группой, а [5, 6, 8] и [5, 8] – нет, так как группа уже не голая, есть лишнее число — 6. Так же [5, 8] и [5, 7] не являются голой группой, так как числа должны быть одинаковы, а здесь 3 разных числа в группе.
Голые тройки
Голые тройки похожи на голые пары, но обнаружить их сложнее – это 3 голых числа в трех клетках.
В примере числа [1, 2, 6] в одной строке повторяются 3 раза. В группе всего 3 числа и они располагаются на 3-х клетках, значит лишние числа 1, 2, 6
из оранжевых клеток удаляются.
Голая тройка может не содержать числа в полном составе, например, подошла бы комбинация: [1, 6], [1, 2] и [2, 6] – это все те же 3 типа чисел в трех клетках, просто в неполном составе.
Голые четверки
Следующее расширение голых групп – голые четверки.
Числа [2, 5], [2, 5, 6, 7], [5, 6, 7], [5, 6] образуют голую четверку из четырех чисел 2, 5, 6 и 7, расположенных в четырех клетках. Эта четверка расположена в одном квадрате, это значит, что все числа 2, 5, 6, 7 из оставшихся клеток квадрата (оранжевые) удаляются.
Скрытые пары
Следующая вариация групп – скрытые группы. Рассмотрим пример:
В самой верхней строке числа 6 и 9 расположены только в двух клетках, в других клетках этой строки таких чисел нет. И если в одной из зеленых клеток поставить другое число (например 1), то в строке не останется места для одного из чисел: 6 или 9, значит нужно удалить все числа в зеленых клетках, кроме 6 и 9.
В итоге, после удаления лишнего, должна остаться только голая пара чисел.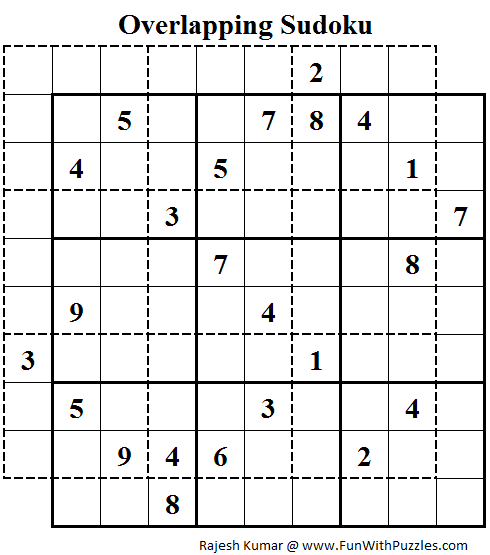
Скрытые тройки
В примере скрываются числа 4, 8 и 9. В других клетках столбца этих чисел нет – значит удаляем лишних кандидатов из зеленых клеток.
Скрытые четверки
Аналогично со скрытыми тройками, только 4 числа в 4-х клетках.
В примере четыре числа 2, 3, 8, 9 в четырех клетках (зеленые) одного столбца образуют скрытую четверку, так как в других клетках столбца (оранжевые) нет этих чисел. Удаляются лишние кандидаты из зеленых клеток.
На этом закончим рассмотрение групп чисел. Для тренировки попробуйте решить следующие кроссворды (без подбора): Судоку № 13091, Судоку № 10710
X-wing и рыба меч
Эти странные слова – названия двух похожих способа исключения кандидатов в судоку.
X-wing
X-wing рассматривается для кандидатов одного числа, рассмотрим 3:
В двух строках (синие) расположены всего 2 тройки и эти тройки лежат всего на двух линиях.
Аналогично для кандидатов на 2 и столбцов.
По факту X-wing встречается довольно часто, но не так часто встреча с этой ситуацией сулит исключение лишних чисел.
Рыба-меч
Это усложненная вариация X-wing для трех строк или столбцов:
Рассматриваем так же 1 число, в примере это 3. 3 столбца (синие) содержат тройки, которые принадлежат к одним и тем же трем рядам.
Числа могут содержаться не во всех клетках, но нам важно пересечение трех горизонтальных и трех вертикальных линий. Либо по вертикали, либо по горизонтали должны отсутствовать числа во всех клетках, кроме зеленых, в примере это вертикаль – столбцы. Тогда все лишние числа в строках должны быть убраны, чтобы 3 остались только на пересечениях линий – в зеленых клетках.
Дополнительная аналитика
Взаимосвязь скрытых и голых групп.

А так же ответ на вопрос: почему не ищут скрытые/голые пятерки, шестерки итд?
Давайте рассмотрим следующие 2 примера:
Это один судоку, где рассматривается один числовой столбец. 2 числа 4 (отмечены красным) исключаются 2 разными способами – при помощи скрытой пары или при помощи голой пары.
Следующий пример:
Другой судоку, где в одном квадрате одновременно голая пара и скрытая тройка, которые удаляют одни и те же числа.
Если вы присмотритесь в примеры голых и скрытых групп в предыдущих параграфах, то заметите, что при 4-х свободных клетках с голой группой оставшиеся 2 клетки обязательно будут голой парой. При 8-и свободных клетках и голой четверке – оставшиеся 4 клетки будут скрытой четверкой:
Если рассмотреть взаимосвязь голых и скрытых групп, то можно выяснить, что при наличии голой группы в оставшихся клетках обязательно будет скрытая группа и наоборот.
И из этого можно сделать вывод, что если у нас свободны 9 клеток в строке, и среди них точно есть голая шестерка – то проще будет найти скрытую
тройку, чем выискивать взаимосвязь между 6-ю клетками.
И еще один вывод – искать группы чисел имеет смысл только при наличии хотя бы восьми свободных клеток в квадрате, строке или столбце, при меньшем количестве клеток можно ограничиться скрытыми и голыми тройками. А при пяти свободных клетках и меньше можно не искать тройки – двоек будет достаточно.
Заключительное слово
Здесь приведены самые известные методы разрешения судоку, но при решении сложных судоку далеко не всегда применение этих методов ведет к полному решению. В любом случае метод подбора всегда придет на помощь – сохраняете судоку в тупиковом месте, подставляете любое доступное число и пытаетесь решить головоломку. Если эта подстановка приводит вас к невозможной ситуации, то значит, что нужно загрузиться и убрать подставленное число из кандидатов.
Судоку средние — играть в судоку среднего уровня
Game loading …
На начальном этапе каждый игрок знакомится с правилами и принципами игры и имеющимися стратегиями, получает первый опыт достижения победного результата не зависимо от того, за какое время он его достигает: быстро или значительно дольше. Ознакомившись с принципами, поняв логику работы игрового интерфейса и закрепив результаты и скорость нахождения решения на первом уровне, любой пользователь может перейти на еще одну ступень выше, начав улучшать свои математические навыки, логические рассуждения и умозаключения в онлайн играх судоку средней сложности.
Ознакомившись с принципами, поняв логику работы игрового интерфейса и закрепив результаты и скорость нахождения решения на первом уровне, любой пользователь может перейти на еще одну ступень выше, начав улучшать свои математические навыки, логические рассуждения и умозаключения в онлайн играх судоку средней сложности.
В самом начале игрового процесса перед каждым игроком на экране находится поле размером 9х9 ячеек, состоящее из девяти строк (1х9) и девяти столбцов (9х1). В некоторых ячейках расположены цифры. В игре задействованы только 1, 2, 3, 4, 5, 6, 7, 8, 9. Также визуальное поле разбито на сектора (группы), размеры которых составляют 3 на 3 клетки.
Цель игры
Цель та же — заполнить пустые ячейки недостающими цифрами, соблюдая одно основное правило — не должно быть повторений одной и той же цифры в строке, столбце и секторе. Однако, в средних Судоку, в самом начале игры, поле содержит меньше заполненных ячеек, что усложняет поиск правильного положения недостающих.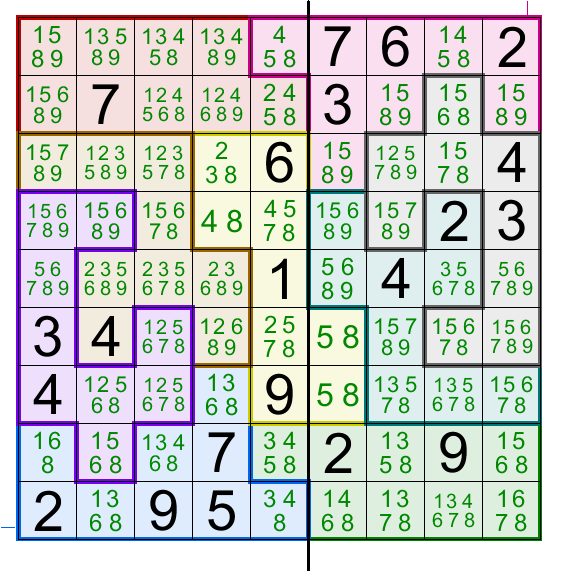 Тут на первое место выходят заметки и тактика.
Тут на первое место выходят заметки и тактика.
Стратегии
Чтобы решить Судоку среднего уровня сложности, необходимо воспользоваться функцией «карандашных» заметок. Они могут быть использованы либо для поиска решения для конкретной клетки, либо для устранения кандидатов и удаления ненужных заметок из сетки. Существует четыре основных метода достижения этой цели. На жаргоне они называются naked single (неприкрытый одиночка), hidden single (скрытый одиночка), naked pair (неприкрытая пара) и hidden pair (скрытая пара). Все эти методы требуют, чтобы пользователь записал каждого кандидата, которого он хочет применить, для каждой ячейки.
Неприкрытый одиночка
У вас есть неприкрытый одиночка, когда Вы находите одну клетку с одним единственным возможным кандидатом. В этом случае Вы нашли решение для этой ячейки, независимо от того, является ли эта цифра также кандидатом для других ячеек в той же строке, столбце или секторе.
Скрытый одиночка
Скрытые одиночки следуют той же логике, но в обратном направлении.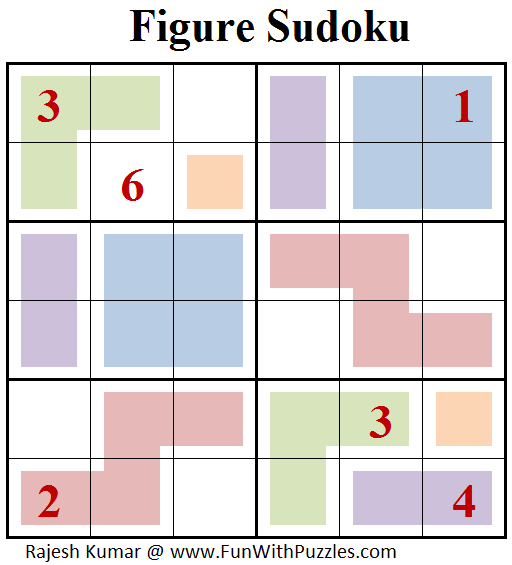 В этом случае у вас может быть несколько кандидатов на ячейку, но только одна цифра является решением в этой строке, столбце или секторе. Она называется «скрытой», потому что другие кандидаты создают «шум» (помехи, отвлекают внимание), затрудняющий ее обнаружение.
В этом случае у вас может быть несколько кандидатов на ячейку, но только одна цифра является решением в этой строке, столбце или секторе. Она называется «скрытой», потому что другие кандидаты создают «шум» (помехи, отвлекают внимание), затрудняющий ее обнаружение.
С помощью парных методов игрок может только исключить кандидатов.
Неприкрытая пара
Когда у пользователя есть одна и та же пара кандидатов в одной строке или столбце, то он обнаружил «неприкрытую пару». На этом этапе можно быть уверенным в их общем положении в сетке, даже если еще не возможно определить конечное положение каждой цифры. Это позволяет исключить этих кандидатов из любой другой клетки в этой строке или столбце.
Скрытая пара
Скрытые пары встречаются внутри секторов и, опять же, они скрыты, потому что они делят свои ячейки с другими кандидатами. Принцип прост. Если внутри группы у вас есть две идентичные пары, цифры которых не являются кандидатами ни в одной другой ячейке этой группы, то эти ячейки будут их конечной позицией, даже если решение все еще неизвестно.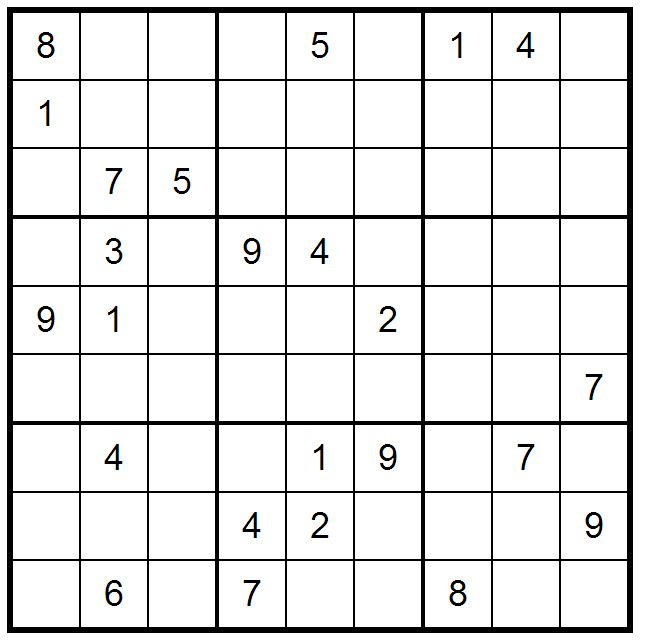 Таким образом, можно исключить оставшихся кандидатов, которые разделяют ячейки с этими цифрами.
Таким образом, можно исключить оставшихся кандидатов, которые разделяют ячейки с этими цифрами.
Преимущества пазла
Когда Вы начинаете играть в Судоку среднего уровня (бесплатно онлайн на этой сайте), то получаете ряд преимуществ для себя:
- Улучшает логическое мышление. Это не математическая игра. Она не требует абсолютно никаких арифметических навыков, но для ее решения требуется уметь логически рассуждать. По мере того, как человек учится правильно расставлять числа, его навыки логического мышления улучшаются.
- Улучшает память. Логическое мышление и память идут рука об руку. По мере того, как логическое мышление улучшается, человек начинает вспоминать конкретные стратегии и вспоминать, что работало в предыдущих головоломках. Это может быть использовано для запоминания и вспоминания вещей в других областях жизни.
- Доказано, что игра замедляет негативное влияние болезни Альцгеймера. Что замедляет потерю памяти при болезни Альцгеймера? Поддержание регулируемого кровяного давления, ежедневные физические упражнения, упражнения для тренировки памяти.
 Такие головоломки являются ключом к замедлению негативного воздействия этой болезни.
Такие головоломки являются ключом к замедлению негативного воздействия этой болезни. - Помогает развить навыки быстрого мышления. Поиграв в течение нескольких недель, вовлекая мозг в процесс решения головоломок, игра помогает научить мозг думать быстрее. Чем больше вы играете в нее, тем быстрее будут развиваться ваши навыки мышления, и Вы перейдете на более сложные Судоку.
- Учит находчивости. Пазл заставляет игроков использовать все свои ресурсы и учит быть изобретательными в своих методах решения.
CTC — взлом Cryptic
веб-приложение CTC — взлом загадочностиЭто приложение для судоку и головоломок было создано Свеном Нойманном . Вы можете связаться со мной или узнать больше о том, как поддержать текущую разработку, на svencodes.com.
Cracking The Cryptic
Cracking The Cryptic — самый популярный канал судоку на YouTube, где каждый день можно попробовать новые головоломки мирового уровня! Играйте в головоломки на своем устройстве, ссылки в описании каждого видео и инструкции ниже.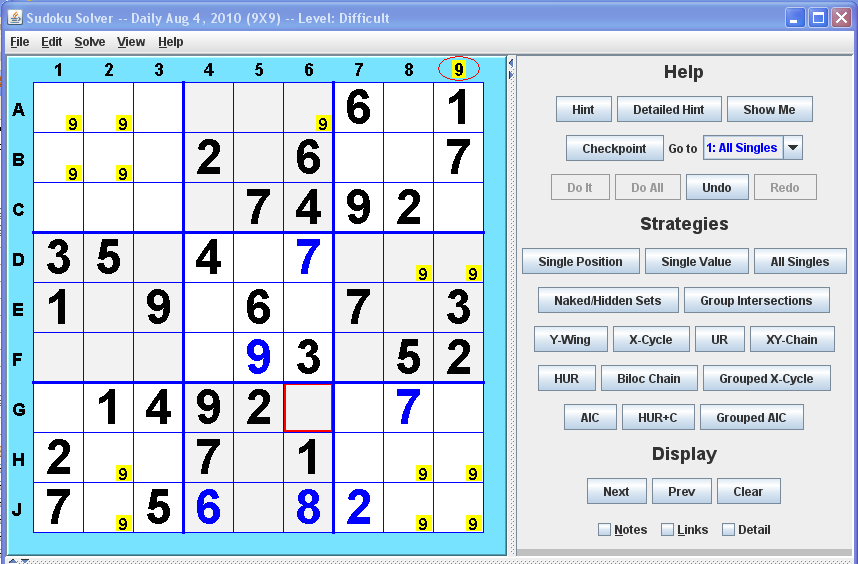 Наслаждаться!
Наслаждаться!
Горячие клавиши
Выбор
- <Щелчок/перетаскивание мышью>
- Выбрать ячейки
-
+ щелчок/перетаскивание мышью - Добавить или удалить из текущего выбора
- <клавиши со стрелками>
- Переместить выделение
-
+ <клавиши со стрелками>, + <клавиши со стрелками> - Добавить к текущему выбору
-
+ - Выделить все ячейки
-
+ + - Отменить выбор всех ячеек
-
+ - Инвертировать выделение
- <ДВОЙНОЙ ЩЕЛЧОК/КАСАНИЕ>, <ДОЛГИЙ ЩЕЛЧОК/КАСАНИЕ>
- Выбор с учетом инструмента
Ввод номера
- <0-9>
- Вставить значение, отметку карандашом, вариант или цвет
-
- Вставить значение, отметку карандашом, кандидата или цвет
- [0-9] Кнопка
- Вставить значение, отметку карандашом, вариант или цвет
Сменить инструмент
- <ПРОБЕЛ>,
- Следующий режим
-
+ <ПРОБЕЛ>, - Предыдущий режим
-
- «Цифровой» режим (
на немецкой раскладке клавиатуры) -
- Режим «Угол»
-
- Режим «Центр»
-
- Режим «Цвет»
-
+ <ЦИФРА> - Введите цифру в «центральном» режиме
-
+ - Ввод цифры в режиме «угол»
-
+ + - Ввод цифры в «цветном» режиме
Отменить/Повторить
-
+ - Отменить последнее действие
-
+ - Повторить последнее действие, если оно было отменено
Проверка готовой головоломки
- Кнопка [Проверить]
- Нажмите кнопку проверки, чтобы проверить основные правила судоку.
 Может не работать с сетками, не являющимися судоку, или со специальными ограничениями.
Может не работать с сетками, не являющимися судоку, или со специальными ограничениями.
Ссылки
Cracking The Cryptic на YouTube
Cruptic на Twitter
, взломав Cryptic в Instagram
Пример загадков
ARAF Sudoku по Phistomefel
, размещенные SIMON
888.9013KEL NALMER
3KER3. Сетка должна быть разложена на разные области. Каждая ячейка принадлежит ровно одной области. Каждая область содержит ровно две подсказки. Сумма всех цифр в области лежит между двумя подсказками, но может не достигать их. Например, если подсказки для области 21 и 24, сумма цифр в области равна 22 или 23. Цифры не могут повторяться в пределах области.16 чашек чая от Суманты Мукерджи
Организатор: Саймон
Правила
Применяются обычные правила судоку. В клетках сумма цифр должна соответствовать небольшой подсказке, указанной в верхнем левом углу клетки. Цифры не могут повторяться в клетке. Подсказки вне сетки дают сумму ячеек по указанной диагонали. Знаки неравенства в сетке указывают на меньшую из двух задействованных ячеек.
Знаки неравенства в сетке указывают на меньшую из двух задействованных ячеек.
Судоку Battlefield от Big Tiger
Организатор: Саймон
Правила
Применяются обычные правила судоку. Рассмотрим первые X ячеек и последние Y ячеек строки или столбца, где X — число в первой ячейке, а Y — число в последней ячейке. Подсказка за пределами сетки дает сумму цифр, где эти группы перекрываются, или сумму цифр в промежутке между группами, если они не перекрываются.
С.Т.С. by Prasanna Seshadri
Hosted by Simon
Rules
Применяются обычные правила судоку-убийцы (сумма ячеек в клетках должна равняться общему количеству, указанному в верхнем левом углу каждой клетки). Общее количество клеток закодировано. Каждая буква представляет собой уникальную цифру. Заштрихованы четные числа внутри клеток.
Частично закодированный убийца, Скотт Стросал
Организатор: Саймон
Правила
Применяются обычные правила судоку.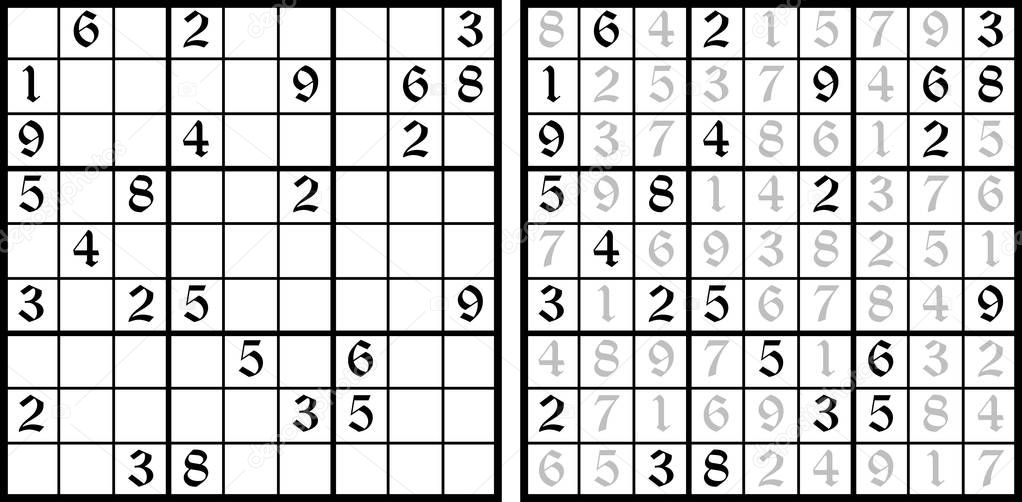 Рассмотрим первые X ячеек и последние Y ячеек строки или столбца, где X — число в первой ячейке, а Y — число в последней ячейке. Подсказка вне сетки дает сумму цифр, где эти группы перекрываются, или сумму цифр в промежутке между группами, если они не пересекаются.
Рассмотрим первые X ячеек и последние Y ячеек строки или столбца, где X — число в первой ячейке, а Y — число в последней ячейке. Подсказка вне сетки дает сумму цифр, где эти группы перекрываются, или сумму цифр в промежутке между группами, если они не пересекаются.
японских сумов? Махо Йокота
Ведущий: Марк
Правила
Применяются обычные правила судоку. Рассмотрим первые X ячеек и последние Y ячеек строки или столбца, где X — число в первой ячейке, а Y — число в последней ячейке. Подсказка вне сетки дает сумму цифр, где эти группы перекрываются, или сумму цифр в промежутке между группами, если они не пересекаются.
Arrow Sudoku от Эрика Фокса
Hosted by Mark
Rules
Применяются обычные правила судоку, и цифры вдоль стрелок суммируются с числами в кругах – некоторые из «кружков» содержат двузначные числа.
Связанные судоку из шести пакетов от Genomico (Tom Groot Kormelink)
Организатор: Марк
Правила
Это одна большая головоломка, состоящая из шести различных вариантов судоку 6×6, соединенных кругами. Круг является внешней подсказкой для обеих соседних головоломок.
Круг является внешней подсказкой для обеих соседних головоломок.
Обычные правила судоку 6×6 применяются ко всем судоку, поэтому каждая строка, столбец и область должны содержать 1-6. Внешние подсказки для варианта шоу:
Разница судоку: разница первых двух цифр в соответствующем направлении.
Судоку снаружи-2: Должен быть помещен в одну из первых двух ячеек в соответствующем направлении.
Сумма ближайших к 6 судоку: сумма всех непосредственных соседей цифры 6 в строке или столбце.
Небоскреб Судоку: количество видимых небоскребов с этой стороны. Более высокие небоскребы закрывают вид на более низкие, размер которых определяется цифрой.
MaxAscending Sudoku: длина самого длинного ряда возрастающих цифр в соответствующем направлении. (Например, длина серии 1-3-6 равна 3.)
Первое увиденное нечетное/четное судоку: если нечетное, первое нечетное число в соответствующем направлении; или, если четное, первое четное число.
Классический судоку от Cracking The Cryptic
Организатор: Марк
Правила
Применяются обычные правила судоку.
Тестовая головоломка Extra Margins
A+BOOOOOOOOOOOOOOOEOEEEEEEOOOOOOOOOOEOEOEOEOEEEEAth+BthТестовая головоломка Extra Busy
Создано Свеном Нойманном (© 2020-2022) | Поддержите меня на ПатреонеПрактический семинар — Судоку — Урок
Правила
Как объяснялось ранее, идея головоломок Судоку состоит в том, чтобы заполнить сетку числами, по одному числу на квадрат, всего с тремя ограничениями:
- Каждая строка сетки должна содержать все числа от 1 до 9
- Каждый столбец сетки должен содержать все числа от 1 до 9
- Каждая ячейка 3 на 3 внутри сетки должна содержать все числа от 1 до 9
Сочетание этих трех правил, согласно которым каждое число должно появляться один раз и только один раз в строке, столбце и поле, позволяет вы, чтобы выяснить, где числа разрешено идти. Пример показан справа.
Техники
Есть несколько техник, которые вы можете использовать, чтобы решить головоломки и выяснить, куда должны идти числа. Eсть
очень широкий диапазон сложности головоломок, поэтому для некоторых потребуются только простые приемы, а для более сложных
им потребуется гораздо больше размышлений.
Eсть
очень широкий диапазон сложности головоломок, поэтому для некоторых потребуются только простые приемы, а для более сложных
им потребуется гораздо больше размышлений.
Здесь мы рассмотрим несколько техник, начиная с самых простых.
Не хватает только одного
Пожалуй, самое простое из правил, если в любом столбце, строке или поле есть только один пустой квадрат, то можно сразу сказать, какой из них отсутствует, и может заполнить его с абсолютной уверенностью! Например, на картинке справа вы должен быть в состоянии сказать, какое число должно быть введено в пустой квадрат:
Также обратите внимание, что это правило может быть применено к строкам и столбцам точно таким же образом. Если вы используете вспомогательный апплет здесь, в Activity Workshop, то вы должны увидеть зеленый маркер на поле (или на краю строки или столбец) после его заполнения. Красный маркер будет означать, что вы допустили ошибку и ввели одно и то же число более один раз.
Исключение
Этот метод, также известный как штриховка , включает в себя просмотр всех вхождений заданного числа и
рисуя воображаемые линии по горизонтали и вертикали от этих чисел.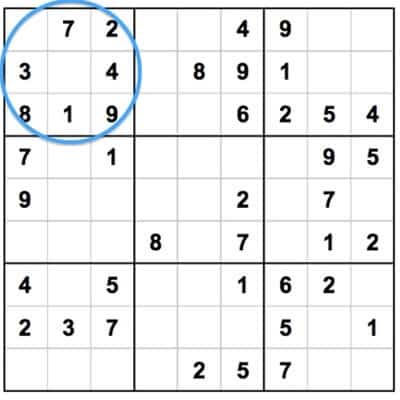 Каждое число может появляться только в каждой строке или
столбец один раз, поэтому эти строки исключают возможность появления числа в других полях.
Каждое число может появляться только в каждой строке или
столбец один раз, поэтому эти строки исключают возможность появления числа в других полях.
В примере, показанном справа, позиции четырех четверок уже известны, и мы пытаемся найти, где должна стоять четверка. зайдите в верхнее правое поле. Здесь показаны только 5 из 9 блоков, чтобы упростить задачу.
Поскольку в любом ряду не может быть более одной четвёрки, мы можем провести (в уме) горизонтальную линию из первых 4, означающих что где бы ни была цифра 4 в верхнем правом поле, она определенно не может быть в верхнем ряду. Точно так же из вторых 4 мы можем сказать что он не может быть и в среднем ряду — значит, он должен быть где-то в нижнем ряду.
Мы также знаем, что в любом столбце не может быть больше одной 4, так что мы можем нарисовать (опять же в уме) вертикаль
строки из известных четверок и уверенно заявляют, что и там больше четверок быть не может. Потому что в верхнем правом поле
определенно нужно где-то 4, и поскольку мы убрали верхнюю строку, среднюю строку, левый столбец и ,
средний столбец, мы можем уверенно поместить 4 в единственную оставшуюся возможность, нижний правый квадрат.
Возможности маркировки
Часто бывает полезно отметить возможные варианты того, куда может пойти число, и если вы решаете головоломку на бумаге, это легко чтобы отметить маленькие заметки в углах квадратов. Апплет судоку здесь позволяет сделать то же самое, щелкнув правой кнопкой мыши квадрат — введенные вами числа отмечены меньшим и серым цветом, чтобы показать, что в данный момент они просто возможны.
То, как вы используете маркеры, зависит от вас, но рекомендуется быть очень четким и последовательным в том, что вы имеете в виду. Например, в показанном здесь примере с 3 и 9отмечено, это может означать одно из двух:
- 3 может быть здесь или где-то еще. 9 также может пойти сюда или куда-то еще.
- Этот квадрат определенно равен либо 3 , либо 9.
Это хорошая идея, чтобы решить, что вы хотите, чтобы эти маркеры означали, и придерживаться этого. Как вы интерпретируете влияние других
номера зависят от того, как вы используете маркеры. Например, предположим, что вы нашли 9 в другом месте в той же коробке. Это значит
что это нерешенное поле теперь точно 3? Может быть, и нет, если бы эти 3 тоже могли пойти куда-нибудь еще. Это определенно означает
это не 9, но, возможно, есть и другие возможности, которые вы еще не отметили.
Например, предположим, что вы нашли 9 в другом месте в той же коробке. Это значит
что это нерешенное поле теперь точно 3? Может быть, и нет, если бы эти 3 тоже могли пойти куда-нибудь еще. Это определенно означает
это не 9, но, возможно, есть и другие возможности, которые вы еще не отметили.
Также рекомендуется не злоупотреблять этими маркерами, чтобы не загромождать сетку цифрами и сделать общий картина менее четкая. Используйте их экономно после того, как вы сузили возможности.
Исключение с использованием возможностей
Иногда можно использовать технику исключения, описанную выше, даже если вы точно не знаете, где находится одно из чисел.
ложь. Например, если все возможности в ячейке имеют общую строку, вы можете использовать эту строку, чтобы исключить квадраты в других полях.
коробки. На картинке, показанной здесь, положение 2 в левом поле еще неизвестно, но обе возможности лежат
в нижнем ряду. Это означает, что в правом поле не может быть двойки в нижнем ряду. Из-за 2 в
В среднем поле верхняя строка также удаляется, в результате чего в правом поле остается только один оставшийся квадрат, а остальные 2 остаются.
Из-за 2 в
В среднем поле верхняя строка также удаляется, в результате чего в правом поле остается только один оставшийся квадрат, а остальные 2 остаются.
Требуемый номер
Вы можете использовать следующее правило, когда для строки или столбца требуется определенный номер, но количество свободных номеров ограничено. квадраты, в которые он может пойти. Доступные квадраты могут быть уменьшены другими вхождениями этого числа в том же поле, строке или столбец.
На приведенном здесь примере мы смотрим на первый столбец квадратов и пытаемся понять, куда могла бы пойти единица в этом столбце.
Числа, отличные от 1, только что были обозначены здесь как «X», чтобы их было легче увидеть. В этом столбце пять пустых квадратов,
и один из них должен иметь номер 1. Однако мы знаем, что 1 не может быть ни в одном из трех верхних квадратов, потому что верхний квадрат
уже имеет свою 1. Точно так же пустой квадрат во втором поле также не может иметь 1, потому что в этой строке уже есть 1.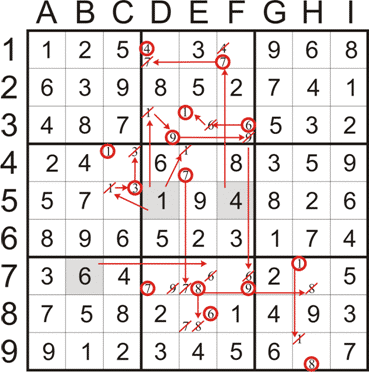 значит всего один квадрат в этом первом столбце, в котором может быть 1, и мы можем поместить 1 в этот нижний квадрат.
значит всего один квадрат в этом первом столбце, в котором может быть 1, и мы можем поместить 1 в этот нижний квадрат.
Существует альтернативный способ взглянуть на эти единицы, который также допустим. Вы можете использовать перекрестную штриховку, как и раньше, с двумя единицами чтобы исключить пять квадратов в среднем левом поле. Это означает, что 1 в этом поле может быть только в среднем столбце. Использование этого и 1 в верхнем поле означает, что в нижнем поле 1 должна быть в левом столбце, в данном случае в нижнем левом квадрат. Думать таким образом точно так же, но просто смотреть на это под другим углом.
Полные триплеты
Если в ячейке есть строка из трех уже заполненных квадратов, это, очевидно, препятствует попаданию туда любых других чисел. Если соседний в двух других столбцах есть номера, вы можете использовать метод перекрестной штриховки, чтобы сузить возможные варианты.
По сути, это ничем не отличается от описанной выше штриховки, но линия из трех очень помогает, ограничивая
возможности в одну строку или столбец.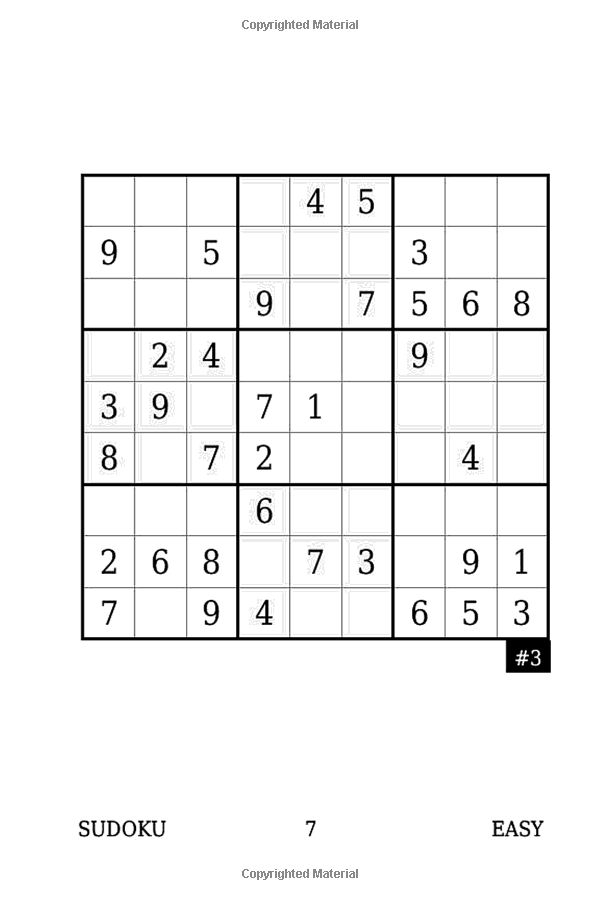 Если вы видите один из этих трех рядов, значит, стоит еще раз взглянуть на
соседние коробки, чтобы увидеть, есть ли такие штриховки.
Если вы видите один из этих трех рядов, значит, стоит еще раз взглянуть на
соседние коробки, чтобы увидеть, есть ли такие штриховки.
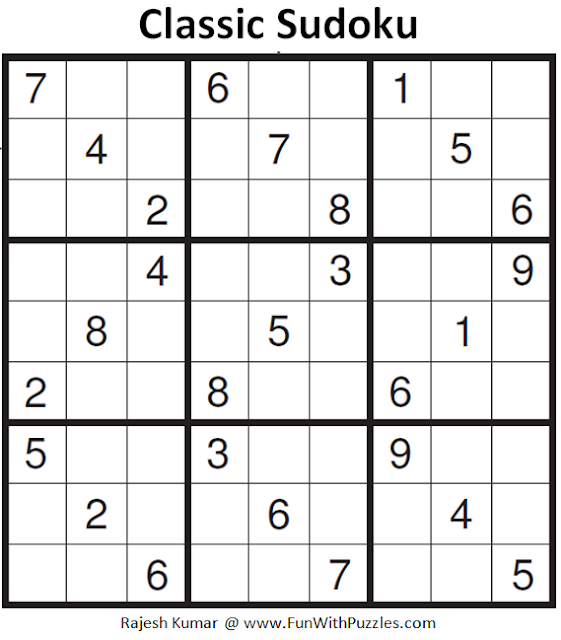
Пары
Иногда числа могут образовывать пары, при этом два числа должны стоять в двух заданных квадратах, и только порядок еще не известен. Например, на этой картинке известно, что 3 и 6 находятся в среднем ряду верхней-средней коробки, но мы пока не можем этого сказать. будь то 3,6 или 6,3. Однако мы все еще можем использовать эти маркеры, чтобы сообщить нам информацию о семерках.
По маркерам мы знаем, что это определенно либо 3,6, либо 6,3 — в зависимости от того, какие два квадрата заняты, и есть там нет места для 7. Таким образом, несмотря на то, что наша перекрестная штриховка с 7 оставляет нас с двумя возможными квадратами, один из них уже занято (либо 3, либо 6), и поэтому 7 должен пойти в другой, нижний левый квадрат верхней средней коробки.
Будьте осторожны с этим правилом, в зависимости от выбранных вами значений маркеров. Если бы было три возможных квадрата для
3 и 6, и все три квадрата были отмечены цифрой «36», это не означало бы, что 7 не может войти ни в один из них.
Аналогичный шаблон можно использовать для троек, когда в трех ячейках появляются три числа, например, «34», «36» и «46».
в этом случае все три квадрата были бы заняты.
Если бы было три возможных квадрата для
3 и 6, и все три квадрата были отмечены цифрой «36», это не означало бы, что 7 не может войти ни в один из них.
Аналогичный шаблон можно использовать для троек, когда в трех ячейках появляются три числа, например, «34», «36» и «46».
в этом случае все три квадрата были бы заняты.
Следуйте по цепочке
На первый взгляд может показаться, что в этой сетке недостаточно информации, чтобы найти больше восьмерок. Только двое из них
известны, и они не дают хороших возможностей для перекрестной штриховки в верхнем левом поле. Однако, если вы внимательно присмотритесь, вы
найдите полную тройку в среднем правом поле, что позволит вам сузить число 8 до двух правых квадратов. Хотя вы
до сих пор не знаю, в каком из них находится 8, зная, что он находится в правом столбце, вы можете использовать исключение в правом нижнем углу
поле и определите, что 8 в нижнем поле должно быть в левом столбце. Это становится частью цепочки, где вы можете использовать
этот новый 8, чтобы найти еще больше.
Используя эти вторые 8, мы можем использовать перекрестную штриховку в нижнем среднем поле и найти только две оставшиеся возможности для
8 там — оба в средней колонке. Используя , эти вместе с 8 в верхней средней ячейке говорят нам, что 8 в
средне-средний квадрат должен быть в правой колонке, а так как там только один пустой квадрат, мы можем поставить 8 в
там.
Теперь мы можем проследить цепочку обратно к среднему правому квадрату и исключить одну из наших двух возможных восьмерок, оставив только один возможный квадрат в правом верхнем углу этого поля. Это показывает важность маркеров — они начали эту цепочку. а затем привести к собственному решению.
Используя восьмерки в среднем-среднем и среднем-правом прямоугольниках, мы можем посмотреть на средне-левый квадрат и найти другой из недостающие 8s.
С этого момента это просто прямая штриховка, сначала глядя на нижний левый прямоугольник и исключая все возможности
кроме нижнего правого квадрата.

 Такие головоломки являются ключом к замедлению негативного воздействия этой болезни.
Такие головоломки являются ключом к замедлению негативного воздействия этой болезни.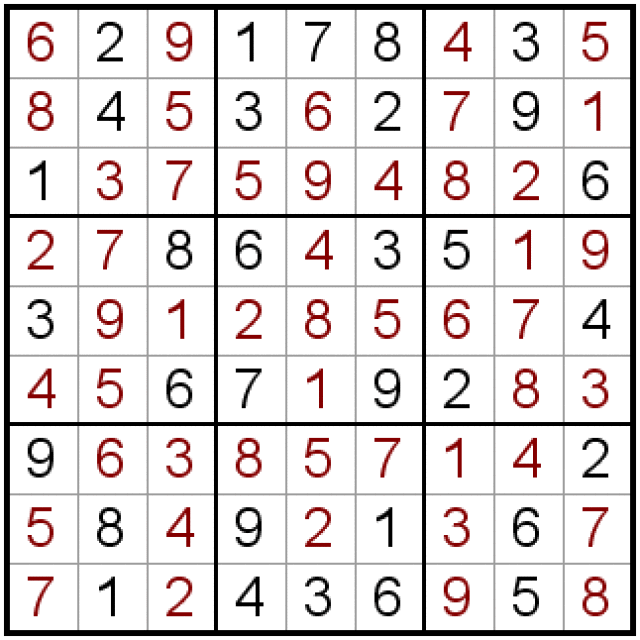 Может не работать с сетками, не являющимися судоку, или со специальными ограничениями.
Может не работать с сетками, не являющимися судоку, или со специальными ограничениями.