Правила игры в судоку с примерами: Правила судоку – стратегии, методы решения и приемы

Содержание

Как играть в Судоку? Правила и полезные советы

Как решать Судоку с помощью математики?

Цифры от 1 до 9 должны быть помещены в 81 ячейку так, чтобы ни одна цифра не могла повторяться ни в одном из секторов 3×3, ни в одной из строк или столбцов из 9 ячеек.

10 главных преимуществ игры в Судоку

Существует множество преимуществ Судоку, но в этой статьей будет рассмотрено лишь десять основных плюсов пользы игры для человека

Что такое правило 45 в Судоку?

Правило 45 в Судоку — это базовая стратегия решения, которая исходит из того факта, что цифры в каждой строке, столбце и поле 3×3 всегда будут равняться 45

Техника «скрытых троек» Судоку с примерами

Подробный разбор техники «скрытых троек» в Судоку с примерами, а также демонстрация признаков, по которым можно вычислить такие подмножества в ячейках

Метод «Голые тройки» в Судоку: базовые правила решения головоломки

«Голые тройки» — это базовая техника решения Судоку, очень похожая на «голые пары».

Метод «Голые пары» в Судоку: научитесь решать головоломки быстрее

«Голые пары» – это базовая техника Судоку, которую легко освоить и использовать, чтобы быстрее решать головоломку

Метод «Скрытые пары» в Судоку. Как определить, объяснение техники

Детальное описание метода «Скрытые пары» в Судоку с примерами, наглядно демонстрирующими в чем заключается суть этой техники и почему она так называется

Метод «Рыба-меч» для решения Судоку

Метод «Рыба-меч» («Swordfish») — это метод решения Судоку, который используется для решения более сложных головоломок путем исключения кандидатов.

Как решать Судоку? Правила игры, простые объяснения

Простые правила и советы о том, как играть в Судоку, чтобы любой желающий научился решать подобные головоломки простого и среднего уровней

10 советов и приемов судоку, которые помогут вам решать быстрее

Приемы и советы по решению Судоку, которые помогут игроку любого уровня разобраться в правилах и принципах решения головоломок

Разгадывание судоку / Статьи — Математическая составляющая

Приложения: интеллектуальные игры

Математика: логика

Популярные в XX веке кроссворды в веке XXI сменило новое увлечение — пришедшая из Японии игра судоку. Существуют различные варианты игры и множество «патентованных» рекомендаций игрокам. Удивительно, но знание математических терминов, даже только по названиям, позволяет создавать эффективные приёмы разгадывания судоку.

Задание в классическом варианте судоку — заполнить цифрами от 1 до 9 клетки квадратной таблицы $9\times 9$, которая разделена на девять квадратов $3\times 3$. В каждой строке и в каждом столбце таблицы, в каждом квадрате $3\times 3$ цифры должны быть различными.

Ряд вариантов игры получается из классического простым добавлением условий, например: «диагонали» — в каждой из двух диагоналей таблицы цифры также не должны повторяться; «неравенства» — соседние клетки таблицы связаны знаками «больше» и «меньше», которые относятся к «обитателям» этих клеток; «суммы» — вся таблица разделена не только на девять квадратов $3\times 3$, но и на области, для каждой из которых приведена сумма всех её цифр.

Начальные условия могут отличаться числом заранее «прописанных» цифр. Как правило, уменьшение числа начальных цифр усложняет задачу, но для «cумм» и иногда для «неравенств» их нет вообще.

Игровое поведение начинающего любителя судоку можно сравнить с методикой начинающего шахматиста, быстро тонущего в океане расчётов по принципу «он — туда, я — сюда…». Умение отбрасывать лишние, ненужные варианты в расчётах — проводить перебор с ограничениями — одно из главных преимуществ «обученного» игрока и в шахматах, и в судоку.

Перебирать варианты всё равно придётся, без этого не обойтись, но с помощью ряда приёмов можно сократить объём работы во много раз. Разберём несколько таких приёмов на примерах.

Метод крайнего элемента. Это словосочетание известно каждому, кто посещал занятия в математическом кружке. В нашем случае слово «крайний» будет означать «экстремальный» (т.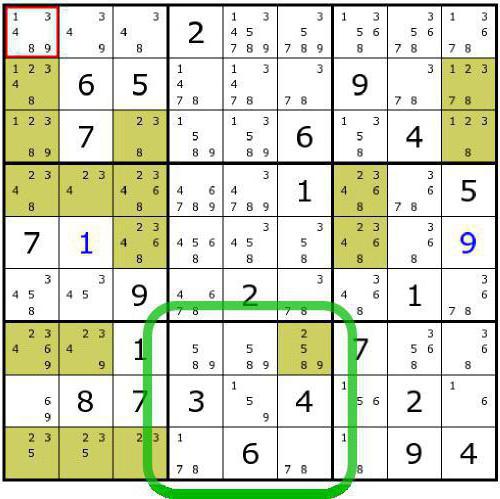 е. наименьший или наибольший).

Например, при разгадывании судоку «суммы» ограничения в переборе можно получить, отметив в таблице все блоки из двух клеток, суммы в которых равны 3, 4, 16, 17. Это и есть «крайние» элементы, наименьшие и наибольшие. Каждое из этих чисел единственным образом представляется в виде суммы двух разных цифр (отличных от нуля): $$ 3=1+2,\quad 4=1+3,\quad 16=7+9,\quad 17=8+9. $$

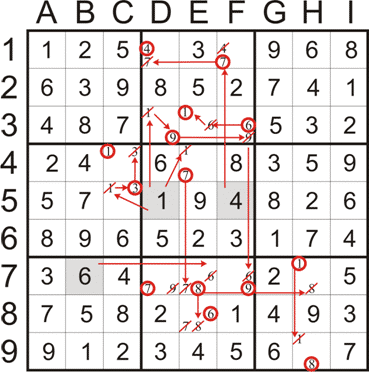
А для других чисел вариантов было бы больше, например, $7=1+6=2+5=3+4$.

На рисунке, иллюстрирующем подобный пример, две такие «крайние» области, в соответствующих клетках будут находиться (в неизвестном нам пока порядке) цифры 1, 3 и 8, 9. Это сразу даёт «ограничение» для выделенного квадрата — числа 7 и 10 из неиспользованных цифр можно сложить единственным образом: $7=2+5$, $10=4+6$. Теперь в этом квадрате $3 \times 3$ осталась неиспользованной только цифра 7, которая и отправляется в правый нижний угол.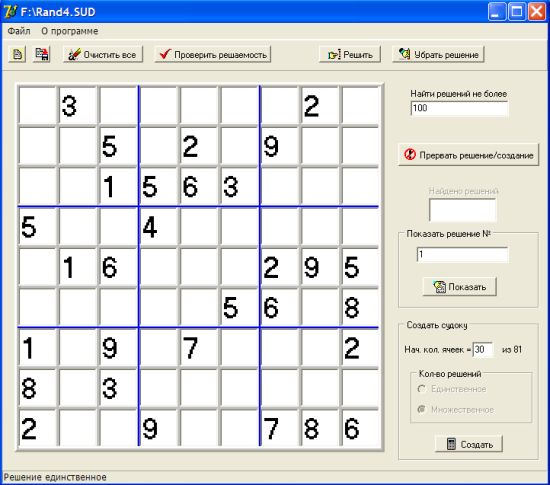 После этого определяется и сосед цифры 7 по выделенной области — цифра 6.

Переход к дополнению. Идея состоит в том, что для изучения части данного множества может быть полезным изучение дополняющей части. Вот поясняющий пример, навеянный знаменитой историей про Архимеда. Даны мерный стаканчик и шарик, объём которого надо быстро определить. Кладём шарик в стакан, заливаем водой с верхом, запоминаем отметку на шкале, вынимаем шарик, смотрим на новую отметку. Разность объёмов, определяемых первой и второй метками, равна объёму шарика.

Вернёмся к разобранному ранее примеру. Цифру 7 в правом нижнем углу квадрата $3\times 3$ можно «поставить на место» и с помощью приёма «переход к дополнению».

Правая нижняя клетка квадрата является частью «языка», уходящего в соседний квадрат, а все остальные области с обозначенными суммами за пределы квадрата $3\times 3$ не выходят. Cумма цифр по всем клеткам любого квадрата разбиения $3\times 3$ равна $$1+2+…+9=45,$$ а сумма цифр во «внутренних» областях с суммами данного квадрата равна $10+4+17+7=38$. Эти цифры «дополняют» цифру в правом нижнем углу квадрата, она равна $45-38=7$.

Блочный метод. В нашем случае блоки — это одинаковые наборы цифр.

В следующем примере из классического варианта судоку блок (2, 3) встречается в первой строке и в четвёртом столбце. В правом верхнем квадрате $3\times 3$ упомянутые строка и столбец «закрывают» для цифр блока $(2, 3)$ все клетки, кроме двух. Затем, в этом квадрате последовательно определяем место 1, место блока $(6, 7)$, место 9.

Можно считать, что место для 9 было найдено методом перехода к дополнению — другими цифрами были заняты восемь из девяти мест в квадрате $3\times 3$.

Связность. В математике линейная связность множества — свойство, означающее, что любые две его точки можно связать непрерывной кривой, не выходящей за границы множества.

В судоку «неравенства» такой линией можно считать цепочку неравенств, связывающую группу подряд идущих цифр. Идею метода иллюстрирует приведённый пример. Такая ситуация в расчётах должна быть исключена, так как между 3 и 4 цифр нет, связность нарушается.

В судоку «неравенства» важен и метод крайнего элемента, в частности 1 и 9 играют особую роль. Комбинируя эти методы, можно решать задачи, в которых в начальной позиции нет ни одной цифры!

Сначала определим крайние элементы. Единственная клетка, из которой выходят только знаки «больше», — левая нижняя клетка, значит, в ней находится цифра 9. Это своеобразный источник, вершина горы. Аналогично, средняя клетка — единственная, обитатель которой меньше соседей, — в ней находится 1. Теперь становится очевидным то, что клетки с 9 и с 1 связывает «ручей», который заполняют цифры 8, 7, …, 2.

Конечно, в реальных задачах вида «неравенства» (как, впрочем, и во всех других видах) учитываются и соображения, связанные с неповторяемостью цифр в строках и столбцах таблицы $9\times 9$.

Приведённые примеры превращений математических терминов в игровые приёмы судоку подтверждают справедливость латинского изречения nomen est omen: имя — уже значение.

Как играть в судоку {правила и руководство по решению головоломки}

Этот пост может содержать партнерские ссылки. Это означает, что Bailey’s Puzzles может получать комиссию за продажу определенных предметов. Это БЕЗ дополнительных затрат для вас. Посетите страницу правил, чтобы узнать больше.

Основные правила игры в судоку

Игра в судоку проводится на сетке 9×9.
Внутри сетки 9 больших квадратов (каждый 3×3), 9 рядов (каждый 9×1) и 9 столбцов (каждый 1×9).
Каждая строка, столбец и квадрат (из 9блоков каждый) должен содержать числа от 1 до 9 без повторения каких-либо чисел в одной и той же строке, столбце или квадрате.

Логика и разум

Судоку — это не игра в угадайку!
Логика и разум должны использоваться, чтобы определить число, которое идет в каждом пробеле.
Я покажу, как решать головоломку судоку на этом примере:

Методы решения головоломки судоку

Существует несколько методов решения головоломки судоку.

Решение для каждого числа

Начните с выбора числа (мне нравится выбирать такое число, на котором уже много чисел на доске).
Найдите все уже заданные числа.
Исключите везде, где этот номер не может быть.
Теперь, есть ли какие-нибудь очевидные блоки, которые вы можете заполнить своим номером? Если да, то сделайте это!
Если вы добавляете числа, повторите шаги 4 и 5. Если вы ничего не добавляете, пора двигаться дальше.
Необязательно: отметьте любые возможные номера (подробнее об этом далее).

В этом примере мы попытаемся заполнить все двойки.

Сначала мы нашли все существующие двойки (обведены оранжевым).
Затем мы убрали все места, куда не может попасть 2 (оранжевые линии).
Затем мы заполнили две двойки (оранжевые, верхний правый и нижний левый квадраты).
Затем мы повторили синим цветом (что дало нам еще одну цифру 2).

Дополнительно: отметьте возможные номера

Когда вы просматриваете номер, вы можете захотеть отметить, где этот номер мог бы потенциально иди.
Вы можете сделать это для любого метода решения головоломки судоку.

Для нашего примера нам нужны еще две двойки, и есть только 4 блока, в которые они потенциально могут войти. Я добавил маленькие двойки в верхней части этих полей зеленым цветом.

Решение по квадрату

Один из способов решения головоломки судоку состоит в том, чтобы делать это по одному квадрату за раз.

Начните с выбора квадрата (мне нравится выбирать квадрат, для которого нужно всего несколько цифр).
Определите, какие числа вам нужны.
Найдите эти числа в столбцах и строках.
Заполните цифры, где это возможно.
Если вы больше не можете добавлять числа, пора двигаться дальше.
Необязательно: отметьте любые возможные номера.

Это легче увидеть на примере. Мы собираемся сделать нижний левый квадрат.

Сначала мы выбрали квадрат (внизу слева).
Затем мы определили недостающие числа (6, 8, 9)
Я начал с самого левого столбца.
- У него 6, 8 или 9? ДА, на нем стоит 9, а это значит, что я могу поставить 9 на своем квадрате только в одном месте. (оранжевый)
Нет больше столбцов, которые я могу проверить, поэтому я посмотрю в верхней строке.
- 6 или 8? ДА! В верхнем ряду есть 8, поэтому в моем верхнем блоке должна быть 6. (синий)
Таким образом, у меня остается только один свободный блок в квадрате, который должен содержать 8. (фиолетовый)
Этот квадрат полностью заполнен! УРА!

Решение по ряду

Другой метод игры в судоку — решение по ряду.

Начните с выбора строки (мне нравится выбирать строку, для которой нужно всего несколько чисел).
Определите, какие номера вам нужны.
Найдите эти числа в столбцах и квадратах.
Заполните цифры, где это возможно.
Если вы больше не можете добавлять числа, пора двигаться дальше.
Необязательно: отметьте любые возможные номера.

Давайте проверим наш пример. Делаем третий ряд сверху.

Сначала мы выбрали строку (третью сверху).
Затем мы определили недостающие числа (4, 5, 9)
Я начал с крайнего левого столбца. У него есть 4, 5 или 9?
- ДА, у него есть 5 и 9, что означает, что блок должен иметь 4. (оранжевый)
Я проверю следующий столбец, там нужен номер. В столбце есть 5 или 9?
- Нет. На этом квадрате 5 или 9?
- Да, у него есть 5, поэтому мы поместим 9 в этот блок. (синий)
У меня остается только один свободный блок в ряду, который должен содержать 5. (фиолетовый)
Этот ряд полностью заполнен! УРА!

Решение по колонкам

Вы также можете попытаться решить головоломку судоку по колонкам.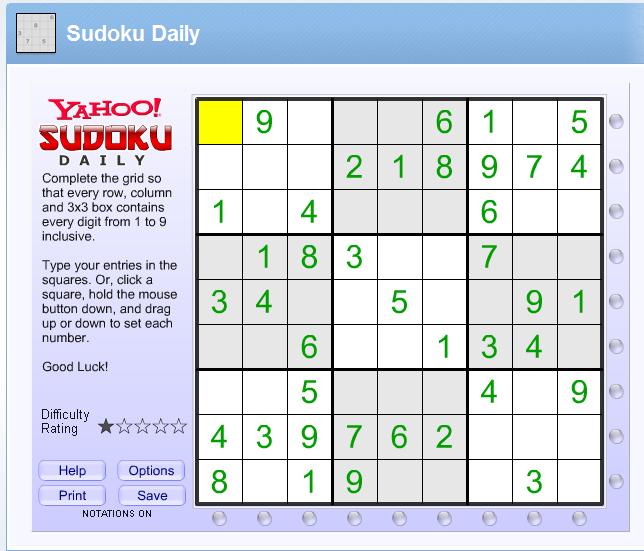

Начните с выбора столбца (мне нравится выбирать столбец, для которого нужно всего несколько цифр).
Определите, какие номера вам нужны.
Найдите эти числа в строках и квадратах.
Заполните цифры, где это возможно.
Если вы больше не можете добавлять числа, пора двигаться дальше.
Необязательно: отметьте любые возможные номера.

Давайте посмотрим на наш пример. Мы собираемся сделать крайнюю левую колонку.

Сначала мы выбрали столбец (самый левый).
Затем мы определили недостающие числа (1)
Недостающее число только одно, поэтому просто заполним его. (оранжевый)

Это было слишком просто! Давайте сделаем еще один пример столбца (средний столбец).

Сначала мы выбрали столбец (средний столбец).
Мы определили недостающие числа (3, 5, 6, 9)
Я начну сверху и буду двигаться вниз, выполняя ряд и квадрат одновременно.
В верхнем пустом блоке не может быть 3, 5 или 9, поэтому он должен содержать 6. (синий)
Во втором пустом блоке нет 3, 5 или 9 ни в квадрате, ни в ряду, поэтому он может быть любым из них.
В третьем пустом блоке есть 5 и 9 в ряду, поэтому он должен быть 3. (фиолетовый)
В четвертом пустом блоке есть 9 в ряду, поэтому он должен содержать 5. Это означает, что наш второй пустой блок должен содержать 9. (розовый)
Этот столбец полностью заполнен!

Можете ли вы закончить пример?

Мы сделали много нашего примера судоку. Попробуйте закончить его самостоятельно (нажмите здесь для версии для печати)!

Вы можете использовать метод числа, квадрата, строки или столбца (или комбинацию всех методов).

Есть еще один метод

А как насчет тех потенциальных чисел, которые вы (необязательно) отметили? Давайте посмотрим, как они могут быть полезны, заполнив средний квадрат.

Сначала мы выбрали квадрат (центр).
Затем мы определили недостающие числа (2, 5, 6, 7)
Беглый взгляд показывает, что обе нижние строки квадрата содержат 5, что означает, что наша 5 должна находиться в верхнем правом блоке. (оранжевый)
В правом столбце не может быть 6 (поскольку в столбце есть единица) или 2 (поскольку мы уже отметили все потенциальные двойки), поэтому здесь должно быть 7. (синий)
Теперь мы знаем, что оставшиеся две коробки должны быть 2 и 6, но мы не знаем, какая из них какая (пока).

Проверим 6-й ряд сверху (или 4-й ряд снизу).

Сначала мы выбрали ряд (4-й снизу).
Затем мы определили недостающие числа (2, 4, 6)
Самый дальний столбец содержит 4, что означает, что этот блок должен быть 2 или 6. Мы также знаем, что пустой левый блок должен содержать 2 или 6. Это означает, что средний блок может быть только 4.
В правом столбце не может быть 6 (поскольку в столбце есть единица) или 2 (поскольку мы уже отметили любые потенциальные двойки), поэтому здесь должно быть 7. (синий)
Теперь мы знаем, что оставшиеся два поля должны быть 2 и 6, но мы не знаем, что есть что (пока).

Давайте закончим пример

Я буду работать (в основном) квадратом, потому что это мой предпочтительный метод.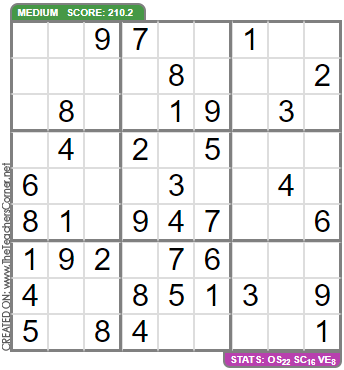 Но вы можете начать с любого места (по строке, столбцу или номеру).

Верхний левый квадрат

Отсутствуют: 5, 7, 8
В крайнем правом столбце есть 5, поэтому для 5 остается только один свободный блок.
В верхнем ряду есть 7, поэтому для 7 остается только один свободный блок. 7 заполнено, мы знаем, куда идет 8.

Верхний средний квадрат

Отсутствуют: 1, 4, 8
В верхнем ряду есть 8, что оставляет только один свободный блок для 8.
В правом столбце есть 1 , что оставляет только один свободный блок для 1,
Заполнив 1 и 8, мы знаем, куда идет 4.

Верхний правый квадрат

Пропущено: 3, 6, 9
В верхнем ряду есть 3, поэтому остается только один свободный блок для 3.
Но мы не знаем, где 6 и 9 пойдет, поэтому мы отметим их как потенциальные.

Третий столбец справа

Отсутствуют: 1, 6, 7, 9
В нижнем квадрате есть 9, а в среднем ряду 9, так что единственный блок, который может быть 9является верхним.
В нижнем ряду есть 1 и 7, поэтому блок должен быть 6. (синий)
В среднем квадрате стоит 1, поэтому этот блок должен быть 7.
Заполнив 6, 7 и 9, мы знаем, куда идет 1. (розовый)

БОНУС! Потенциальные числа, которые мы отметили, могут быть здесь действительно полезны.

Верхний правый квадрат: мы заполнили 9, поэтому мы знаем, что блок в верхнем углу должен быть 6. (оранжевый)
Средний правый квадрат: мы видим один блок, который должен быть 2 или 6. Поскольку мы добавили 6 в этот столбец, это должно быть 2. (синий)
Центральный квадрат: мы знаем, что нижний блок должен быть 6 (потому что мы только что заполнили 2 в этой строке). (фиолетовый)
Наконец, мы можем заполнить оставшийся средний квадрат цифрой 2. (розовый)

Средний левый квадрат

Пропущено: 3, 4, 6, 7
в верхнем ряду и 7 в правом столбце, что оставляет только один свободный блок для 7. (оранжевый)
В правом столбце есть 6, что оставляет только один свободный блок для 6. (синий).
В среднем ряду есть 4, поэтому для 4 остается только один свободный блок. (фиолетовый)
Заполнив 4, 6 и 7, мы знаем, куда идет 3. (розовый)

Средний правый квадрат

Отсутствуют: 3, 6, 9
В средней колонке есть 9, что оставляет только один свободный блок для 9. (оранжевый)
Есть 6 в верхнем ряду, что оставляет только один свободный блок для 6. (синий)
Заполнив 6 и 9, мы знаем, куда идет 3. (фиолетовый)

Нижний правый квадрат

Отсутствуют: 4, 5, 7
В нижнем ряду есть 7, что оставляет только один свободный блок для 7. (оранжевый)
Здесь 4 в правом столбце, что оставляет только один свободный блок для 4. (синий)
Заполнив 4 и 7, мы знаем, куда идет 5. (фиолетовый)

Нижний средний квадрат (ПОСЛЕДНИЙ!)

Отсутствуют: 3, 4, 7, 9
В нижнем ряду и верхнем ряду есть 7, что оставляет только один свободный блок для 7. (оранжевый)
В верхнем ряду есть 9, что оставляет только один свободный блок для 9. (синий)
В левом столбце есть 3, что оставляет только один свободный блок для 3. (фиолетовый)
Заполнив 3, 7 и 9, мы знаем, куда идет 4. (розовый)

Завершенная головоломка судоку

Каждому числу я присвоил уникальный цвет, чтобы вы могли видеть закономерности чисел. В каждом квадрате есть числа от 1 до 9, в каждой строке — от 1 до 9, в каждом столбце — от 1 до 9.

Собери судоку

Теперь, когда вы знаете, как решить головоломку судоку, пришло время взять несколько головоломок и приступить к их решению!

Чувствуете, что готовы перейти к более сложным или другим головоломкам? Проверьте

Happy Puzzling,

Решение судоку — Уникальность

Решение судоку — Уникальность Пред. Уровень выше След. У правильно сформулированной головоломки судоку есть уникальное решение. Можно предположить, что данная головоломка на самом деле правильно сформулирована, и использовать это в рассуждениях, чтобы исключить ответвления, которые не привели бы к единственному решению.

Принцип ЖУКА

Теорема (ср. nick67) Предположим, что кто-то записывает несколько (более 0) чисел-кандидатов в некоторых из изначально открытых ячеек данной диаграммы судоку, 0 или 2 в каждой ячейке, так что каждое значение встречается 0 или 2 раза в любой строке, столбце или поле. Тогда эта диаграмма судоку имеет четное число дополнений, которые согласуются между собой. хотя бы с одним из кандидатов в каждой ячейке, где кандидаты были даны. В частности, если диаграмма судоку имеет единственное решение, то это единственное решение отличается от обоих кандидатов хотя бы в одном клетка.

Терминология Кажется, что BUG сокращает «Двузначная универсальная могила».

Доказательство Для любого завершения данной диаграммы, имеющего одно из два значения кандидатов в каждой ячейке, где были даны кандидаты, сделать новое завершение, заменив каждый номер кандидата на другой кандидат в этой ячейке.

Аргумент уникальности

В качестве приложения у вас есть аргумент уникальности: Всякий раз, когда есть непустой набор изначально открытых ячеек, и два кандидата в каждой из этих ячеек, так что среди этих кандидатов каждое значение встречается ноль или два раза в каждой строке, столбце и блоке, тогда фактическое решение отличается по крайней мере в одной ячейке от обоих кандидатов.

Люди говорят об уничтожении прямоугольников уникальности, но такое невозможно. Единственное требование к кандидатам заключается в том, что они находятся в изначально открытых ячейках, а не в том, что они ничего общего с вашим текущим состоянием решения. С другой стороны, это означает, что аргумент уникальности становится все слабее если не помнить начальное состояние и просто иметь Текущее состояние.

Пример глобальной ошибки

Цо привел следующий пример.

Здесь позиция (5,5) не может быть 7 из-за пары 37 слева и 17 пара вправо. Если желтый квадрат не 7, то мы получить ситуацию, когда применима теорема BUG. То есть существует четное количество решений, предположительно нулевое, где желтый квадрат не равен 7. Итак, если это правильная головоломка (а так оно и есть), желтый квадрат равен 7.

Локальное приложение

Самый простой пример — это, конечно, прямоугольник, соединяющий два прямоугольника. с теми же двумя возможностями на каждом углу — не может быть уникальное решение.

Терминология Говорят об уникальности Прямоугольник» (UR), которого следует избегать. Может быть, «Прямоугольник неуникальности» было бы более уместно.

Следовательно, если эта последняя диаграмма является частью головоломки с единственным решением, тогда желтая ячейка должна быть 2.

То есть, если три угла такого прямоугольника содержат одну и ту же пару цифр, то можно вычеркнуть элементы пары из возможностей в четвертый угол.

Если два угла содержат одну и ту же пару, а два других угла содержат дополнительные возможности, то можно использовать хотя бы одну из этих на самом деле должны иметь место другие возможности. Например, в

один из двух желтых квадратов должен содержать 2, и поэтому ни один из оранжевые квадраты могут содержать 2. Другими словами, аргумент уникальности дает здесь пару.

Другой пример, с дополнительными вещами в большем количестве углов:

По крайней мере один из углов равен 2, поэтому (5,6) равно 9.

Уникальный прямоугольник как элемент заблокированного набора

Вот пример, данный tso. Очень трудно без аргумента уникальности и очень легко с.

Желтый прямоугольник подразумевает уникальность, что есть 3 или 6 в одном из положений (3,4) и (5,4). И другое явление из 3,6 должно быть в (6,4). Но тогда (7,4) не может быть 3 и должно быть 4.

Или по другому аргументу (не используя пару 36 в зеленом квадрате) но с тем же выводом: единственные девятки в столбце 4 — это те, что в желтый прямоугольник. Следовательно, ни один из желтых квадратов в столбце 4 может быть 4 (по аргументу уникальности), так что 4 должно быть в сером квадрат.

Уникальный прямоугольник с парами

Этот последний аргумент относился к случаю, когда две стороны на одном углу прямоугольника являются парами для одной из двух цифр в противоположном углу. В этом случае другая цифра может быть удалена. Например,

Х-образное крыло с ребрами для цифры 2: (8,9)-(5,9)=(5,6)-(7,6)=(7,[79])-(8,9) показывает, что (8,9)!2, и тогда следует, что в строке 8 цифры 2,3,8 должны быть на 3-х позициях 2,5,7, чтобы больше ничего не было.

Теперь посмотрите на зеленый прямоугольник. Если (7,7)3, то (7,5)8 и (8,7)8 так что (8,5)3 и у нас есть запрещенный прямоугольник со структурой 83-38. Итак, (7,7)!3, значит перед нами крестокрыл: цифра 3 в столбцах 2,7 может быть только в строках 8,9 и больше нигде в этих строках не встречается — в частности (9,4)!3, так что (6,4)3, и теперь все следует только одиночными числами.

Неуникальные головоломки

Люди задавались вопросом, что происходит с головоломками, не имеющими уникального решение. Возможно ли, что с помощью этого аргумента уникальности найдено единственное решение?

Ситуация такова: каждое применение приведенного выше аргумента уникальности отбрасывает четное число решений. Итак, если головоломка имеет четное число решений, никогда не будет найдено единственное решение, используя приведенное выше аргумент уникальности. С другой стороны, если число решений нечетное, можно выбрать любое из решений и прийти к этому решению после использования приведенный выше аргумент уникальности несколько раз.