Правила игры в жизнь: Настольная Игра в жизнь — цена 2 590 руб. в Новосибирске. Можно купить или заказать. Отзывы. Характеристики. Описание.

Жизнь — это игра. Инструкция по прохождению

11 февраля 2014 Жизнь Советы

Жизнь — это самая увлекательная игра, которая длится от момента рождения до самой смерти. И как в каждой игре, здесь есть свои правила, ресурсы и способы прохождения. Вот несколько инструкций по игре в жизнь.

Ия Зорина

Автор Лайфхакера, атлет, КМС

Реальная жизнь — это игра, в которую мы все с увлечением играем. Она может быть прекрасной или жестокой, и каждый сам выбирает, какой она будет. Вот небольшой гид по самой интересной игре под названием «Жизнь».

Основы игры

Вы можете не осознавать этого, но реальная жизнь — это игра в жанре стратегии. В её состав входят разные мини-игры, типа танцев, вождения, бега или секса, а ключ к победе целой игры — это правильное распределение ресурсов.

Различие между профи и лузерами состоит в том, на что они тратят свое время, свой самый ценный ресурс.

А как же деньги? Да, это тоже очень ценный ресурс, но всё равно главный приоритет остается у времени, и чтобы выиграть, вы всегда должны знать, на что оно уходит.

Детство

Ваша игра начинается с того, что ваш персонаж (то есть, вы) рождается с рандомным характером, в случайных обстоятельствах. После этого, первые 15 лет жизни вы проходите учебные миссии, которые нельзя пропустить.

Начало серьезной игры

Как у каждого молодого игрока, у вас есть много энергии и времени, но почти никакого опыта. Много вещей, таких как лучшая работа, дорогое имущество и партнеры, до поры до времени для вас недоступны.

Это время, когда вы постоянно повышаете свой уровень, а ваш опыт быстро растет. У вас никогда больше не будет столько свободного времени для обучения и столько энергии, как в этом возрасте.

Ваша главная задача — использовать время настолько плодотворно, насколько это возможно.

Помните, каждое дело, которым вы занимаетесь, прокачивает ваши навыки и меняет положение в игре:

Может показаться, что это слишком просто для жизни: выбрал нужные навыки, прокачал их, и порядок, можно побеждать. Конечно, в жизни всё немного сложнее, ведь вы не видите ветку талантов и не можете точно предсказать, какой навык для чего пригодится, об этом вы только догадываетесь. Кроме того, ваше тело не всегда слушается и выполняет всё, что вы запланировали. Почему? Давайте разберемся.

Как заставить свое тело слушаться

Вы отличаетесь от персонажа компьютерной игры тем, что ваше тело не всегда слушается повелений разума. Например, когда вы приказываете себе пойти в спортзал, тело полностью игнорирует этот замечательный, по сути, порыв.

Это не баг в игре, всё продумано и логично. У вас есть особая «шкала состояния», которую вы, к сожалению, не видите. Выглядит она примерно так:

Если какой-то критерий вашего состояния на слишком низком уровне, ваше тело не соглашается выполнять то, что вы хотите. Например, попробуйте учить что-нибудь, когда вы обессилены или голодны, и увидите, как это будет трудно, практически невозможно.

Также очень важна ваша шкала силы воли. У вас есть определенное количество силы воли на день, она немного повышается во время еды и полностью восстанавливается во время глубокого ночного сна. Если вы израсходовали свою силу воли, и она находится на очень низком уровне, у вас получается делать только то, что действительно нравится.

Помните, что каждое решение в пользу менее привлекательного варианта (например, пойти в тренажерный зал вместо того, чтобы посмотреть интересный фильм дома), забирает какое-то количество силы воли.

Есть несколько уловок, которые помогут поддерживать свое поведение в заданной линии игры:

1. Поддерживайте тонус. Если вы устали, хотите есть или грустите, ваша сила воли будет на низком уровне. Так что стоит позаботиться о своем персонаже, чтобы он был на что-то способен.
2. Рационально распределяйте задачи. Помните, что сила воли — это ресурс, который надо пополнять, и не расходуйте его слишком сильно. Если у вас есть несколько задач, которые требуют много силы воли, раскидайте их на разные дни, перемешав с более приятными для вас.
3. Делайте самые важные задачи в первую очередь. Если у вас есть реально важное дело, стоит потратить большую часто своей силы воли на него. Вам будет труднее выполнять другие задачи, но зато главные задачи будут выполняться идеально и в срок.
4. Уберите соблазны. Если у вас остается соблазн переключиться со сложной работы на легкую развлекательную, вам потребуется больше силы воли, чтобы это сделать. В итоге, соблазн вытянет из вас больше ценного ресурса, и вы не сможете закончить работу в срок. Например, вы составляете отчет, а в соседней вкладке открыта страница в соцсети. Вам постоянно хочется переключиться, полазить по чужим страницам и пабликам, и это изматывает вас больше, чем вы можете представить.

Получается, что ключ к успеху в игре — правильно сочетать состояние вашего тела и выполнение нужных задач.  

Выбор правильных задач

Выбирать правильные задачи в правильное время — это один из главных пунктов в игре. Одни задачи больше влияют на ваше состояние:

Другие задачи — на ваши навыки и умения:

Вы должны уделять время тому, что поможет вам оставаться в отличном состоянии, например, хорошо питаться и высыпаться, чтобы поддержать силу воли. А после этого вы должны тратить этот ресурс (силу воли) на прокачку своих навыков и способностей.

Некоторые навыки более ценные, а какие-то из них могут даже открыть вам целый путь, как ветка талантов:

 

Другие являются самостоятельными и не имеют продолжения:

 

Самое эффективное — приобретать несколько навыков и комбинировать их между собой. Очень трудно стать лучшим в какой-то сфере, развивая всего один навык, практически невозможно. Гораздо проще выбрать несколько смежных навыков, связанных между собой, и прокачивать их все.

Окружение

Ваше окружение имеет большое значение для вашего статуса, навыков и шансов поднять уровень. Вообще-то, можно играть в любом месте, но в определенных местах — гораздо проще. Например, если вы играете за женщину в ряде стран, некоторые возможности для вас будут закрыты.

Шансы полностью раскрыть себя именно в том месте, где вы оказались первоначально, могут быть весьма посредственными. Поэтому, после того, как вы определите для себя задачи, рассмотрите вариант смены локации. Если на новом месте вы сможете добиться большего, лучше развить навыки и улучшить состояние, почему бы и нет?

Поиск партнеров

Привлечение партнеров — это дополнительная мини-игра в рамках основной, и успех в ней, чаще всего, зависит от того, насколько хорошо вы проходите основную сюжетную линию.

Если у вас хорошее состояние и прокачанные навыки, вы уже имеете неплохие шансы выиграть мини-игру.

В начале игры вы можете отвергать партнеров и быть отвергнутыми.

Это нормально, но иногда негативный опыт плохо влияет на состояние игрока. Для того чтобы дальше продвигаться в этой мини-игре, игроку надо накопить достаточно силы воли и продолжать двигаться вперед.

80% успеха в поиске партнера зависит от привлекательности игрока, а если она есть, значит он тратит время на правильные вещи. Если вы любите свое дело, излучаете доброжелательность и оптимизм, вы автоматически становитесь привлекательным.

Остальные 20% успеха зависят от возможности оказаться в нужном месте, чтобы встретить свою вторую половину. То есть, если вы весь из себя привлекательный, но кроме работы и дома нигде не бываете, вряд ли вы найдете себе партнера.

Деньги, деньги, деньги

Позже в игре вам нужно будет управлять ресурсом «деньги». Большинство игроков понимают, что можно увеличить количество денег вначале игры (взять кредит или одолжить), но, на самом деле, от этого больше проблем, чем преимуществ.

Самое главное правило денег: никогда не занимайте деньги, если не планируете в результате получить ещё больше. Например, если вы берете кредит на обучение, инвестируете в свою профессию, которая обеспечит вам хороших доход, это рационально. А если вы берете кредит на новые туфли или новую модель смартфона — это нерационально и не принесет вам ничего, кроме убытков.

Вот несколько стратегий обращения с финансами:

1. Не думает о деньгах. Это стратегия сниженного напряжения: вы просто живёте в пределах своих доходов и имеете немного «на черный день». Убедитесь, что свое свободное время вы тратите правильно, тогда не будет никаких сожалений.
2. Богатый. Тщательно выбираете карьеру и окружение, и готовитесь быстро двигаться вверх. Вам приходится много инвестировать в соответствующие навыки, что заберет много вашего времени, и тщательно следить за своим состоянием, чтобы не сгореть на работе.
3. Очень богатый. Вы начинаете собственный бизнес, потому что вы не можете стать очень богатым, работая на кого-то (в принципе, в наших реалиях стать просто богатым без своего бизнеса тоже очень трудно). Если правильно распределять свои ресурсы, вам, в конце концов, вообще не нужно будет работать.

Старость

Ваши возможности меняются в течение игры. Свадьба и дети будут отнимать ваше время и энергию, а также привносить много случайных элементов в вашу игру. Это замедляет ваше развитие и прокачку навыков, но дает и свои преимущества.

У старых персонажей много развитых навыков, ресурсов и опыта, так что для них открыты квесты, которые пока недоступны для более молодых игроков. Например, у них хватает ресурсов, чтобы написать хороший роман (опыт+время) или купить дом (не у всех конечно, тут важно, какую стратегию насчет денег вы выбрали).

После 80-ти лет игроки, как правило, выбывают из игры. Если у вас прокачаны навыки здоровья, вы можете протянуть гораздо дольше, но читерских методов для этого ещё не придумали.

В самом начале игры вы никак не влияете на то, в каком окружении и с какими способностями начинаете. То же касается конца игры: всё уже определено тем, как вы вели себя на протяжении игры. Именно от этого зависит, как вы закончите свою игру: здоровым, благополучным и счастливым, или нет.

Поэтому ваша стратегия очень важна: к тому времени, как вы понимаете, как надо играть, большинство лучших моментов уже позади.

Вот и всё. Продолжайте играть.

Предложение по модификации правил игры Жизнь / Хабр

Доброго времени чтения, уважаемые пользователи Хабра! Игра Жизнь предложена Джоном Конвеем в 1970 году, и неоднократно обсуждалась на habrahabr.ru. Основные использованные теги приведены в метках к данной статье.

Предлагается ряд изменений, которые могут привести к новому направлению в развитии.

Предложение 1. В оригинальной игре предложено бесконечное поле, однако в реализациях обычно используется правило развертки тора — горизонтали и вертикали замкнуты в циклы.

Предлагается вариант, при котором горизонтали прямоугольного поля конечного размера замкнуты в цилиндр, а вертикали попарно соединены с шагом в половину размера поля по горизонтали. Таким образом можно получить легкий для расчетов аналог сферы.

Для моделирования изотропии предлагается использовать треугольную сетку, которая в расчетах подменяется оценкой близости по горизонтали, вертикали, и одной из диагоналей.

Для изменения среды могут использоваться горизонтальные слои:
один слой высотой 20% у экватора — с хорошими условиями жизни (3-4 соседа для сохранения, 4 для зарождения)
два слоя по 10% — с плохими условиями для жизни (1-2 соседа для сохранения, 2 — для зарождения жизни)
для остальной части действуют обычные правила (2-3 соседа для сохранения, 3 — для зарождения жизни)

Предложение 2.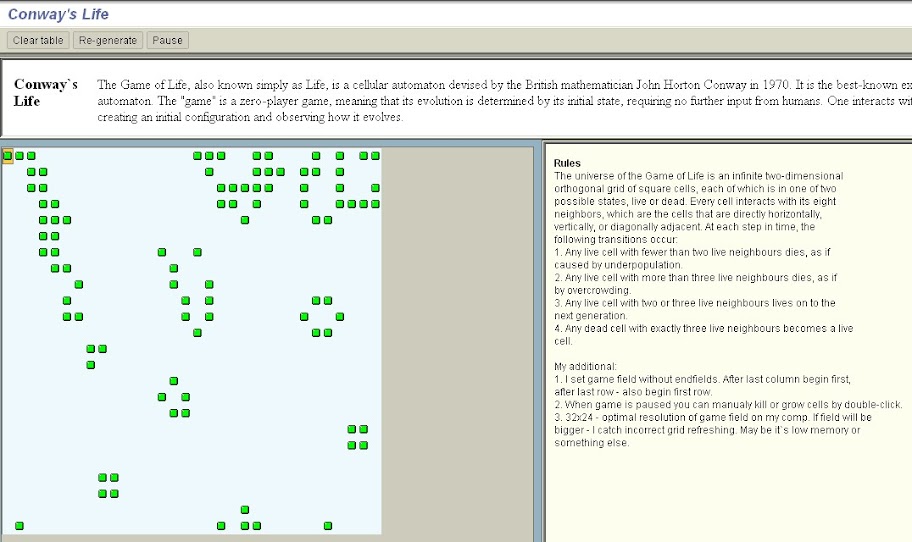 Для организмов предлагается добавление уровней сложности, возможностей объединения, генетической модификации и обучения. Каждому организму назначается до 10-ти уровней сложности, каждый уровень представлен как в материальной, так и в абстрактной области.

Уровень сложности в материальной области влияет на максимальную скорость (количество клеток, на которые организм передвигается в одном направлении за один ход). Таким образом, организмы с первым уровнем сложности (индекс массива 0) неподвижны. Целостный организм передвигается целиком.

Уровень сложности в абстрактной области влияет на количество обозреваемых по прямой соседних клеток. Предлагается удвоенный по сравнению с возможностью перемещения радиус обзора: для первого уровня — 1, для второго уровня — 3 и т.д. Видимость определяется от самых крайних клеток организма.

Реализация подобных игр может быть интересна современным студентам, изучающим обработку больших данных и алгоритмы обучения. Собственного варианта реализации на данный момент нет.

Рекомендуется генетическая эволюция алгоритмов из верховного алгоритма

Upd: вариант в разрезе групп сложности туннельного моделирования https://habrahabr.ru/post/259291/:

в разрезе природных систем

вероятностный вывод (Байес) — хаотическое
генетический поиск (эволюция) — фрактальное
оптимизация с ограничениями (аналогии) — энергетическое
обратная дедукция (символисты) — информационное
градиентный спуск (коннекционисты) — статическое

далее системы начинают проявлять поведение, и цепочка повторяется на уровне живого:

вероятностный вывод (Байес) — динамическое (процессы)
генетический поиск (эволюция) — синергетическое (рынок)
оптимизация с ограничениями (аналогии) — корпоративное (роды)
обратная дедукция (символисты) — бюрократическое (регламенты)
градиентный спуск (коннекционисты) — экологическое

Литература: Педро Домингос, Верховный алгоритм. Как машинное обучение изменит наш мир.

Ссылки:
https://habr.com/ru/post/435670/ — Верховный алгоритм — распределение алгоритмов по уровням сложности

Вариант на Python

Исходники на Python:
life.py

import pygame
import field
import numpy as np
running = True
v = field.area()
step=0
pygame.init()
screen = pygame.display.set_mode([640, 550])
font = pygame.font.Font(None, 50)
while running:
    screen.fill([0, 0, 0])
    clr = 0
    for r in range(1, v.height):
        for c in range(1, v.width):
            if v.val[r, c] != 0:
                clr=clr+64
            if r % 2 == 0 and c % 2 == 0:
                if clr > 255:
                    clr = 255
                screen.set_at([r/2, c/2], [clr, clr, clr])
                clr = 0
    step_text = font.render(str(step),1, (255, 255, 0))
    screen.blit(step_text, [10, 520])                        
    pygame.display.flip()
    for event in pygame.event.get():
        if event.type == pygame. QUIT:
            running = False
    v.generate()
    step=step+1
pygame.quit()
print "Done"

field.py

import numpy as np
import random
class area:
    def __init__(self):
       self.width = 1000
       self.height = 1000
       self.debug = False
       self.val = np.zeros((self.height, self.width), dtype = int)
       self.val1 = np.zeros((self.height, self.width), dtype = int)
       self.val[250, 140] = 1
       self.val[250, 141] = 1
       self.val[251, 140] = 1
       self.val[251, 141] = 1
       self.val[252, 140] = 1
       self.val[252, 141] = 1
       self.rw = range(1, self.width-2)
       self.rh = range(1, self.height-2)
       self.r3 = range(-1, 2)
       self.dh = int(self.height/10)
       self.h2 = [self.dh*2, self.height-self.dh*2]
       self.h3 = [self.dh, self.height-self.dh]
    def generate(self):
        for cnt in self.r3:
            c = random.randint(0, self.width-1)
            r = random.randint(0, self.height-1)
            self.val[r, c] = 1
            c = random. randint(0, self.width-1)
            r = random.randint(0, self.height-1)
            self.val[r, c] = 0
        for c in self.rw:
            for r in self.rh:
                self.val1[r, c] = 0
                cnt = 0
                for r1 in self.r3:
                    for c1 in self.r3:
                        if not ((r1 == 0) and (c1 == 0)) and not (r1==-1 and c1==1) and not (r1==1 and c1==-1):
                            if self.val[r+r1, c+c1] != 0:
                                cnt = cnt + 1
                self.val1[r, c] = self.store_value(c, cnt, self.val[r, c])
        for r in self.rh:
            for c in self.rw:
                self.val[r, c] = self.val1[r, c]
        for c in self.rh:
            if self.val[c, self.width-2] == 1:
                self.val[0, c] = self.val[self.width-2, c]
            if self.val[1, c] == 1:
                self.val[self.width-1, c] = self.val[2, c] 
    def store_value(self, c, cnt, cur):
        val = 0
        if self.h2[0] < c < self. h2[1]:
            if 1 <= cnt <= 4:
                val = 1
            if cur == 1 and cnt < 3:
                val = 1
        else:
            if self.h3[0] < c < self.h3[1]:
                if 2 <= cnt <= 3:
                    val = 1
                if cur == 1 and 2 <= cnt <= 3:
                    val = 1
            else:
                if cnt == 2:
                    val = 1
                if cur == 1 and 1 <= cnt <= 2:
                    val = 1
        return val

Результат:

Игра жизни Конвея

	Игра «Жизнь» (пример клеточного автомата) проводится на бесконечной двумерной прямоугольной сетке ячеек. Каждая клетка может быть либо живой, либо мертвой. Статус каждой клетки меняется каждый ход игры (также называемый поколением) в зависимости от статусов 8 соседей этой клетки. Соседями ячейки являются ячейки, которые касаются этой ячейки по горизонтали, вертикали или диагонали от этой ячейки. Исходный образец — первое поколение. Второе поколение эволюционирует от одновременного применения правил к каждой клетке игрового поля, то есть рождения и смерти происходят одновременно. После этого правила итеративно применяются для создания будущих поколений. Для каждого поколения игры статус ячейки в следующем поколении определяется набором правил. Эти простые правила заключаются в следующем: Если клетка жива, то она остается живой, если у нее есть 2 или 3 живых соседа Если клетка мертва, то она оживает только в том случае, если у нее есть 3 живых соседа. жизнь или смерть. Конвей пробовал многие из этих различных вариантов, прежде чем остановился на этих конкретных правилах. Некоторые из этих вариаций вызывают быстрое вымирание популяций, а другие безгранично расширяются, заполняя всю вселенную или какую-то большую ее часть. Вышеприведенные правила находятся очень близко к границе между этими двумя областями правил, и, зная то, что мы знаем о других хаотических системах, можно ожидать, что самые сложные и интересные закономерности будут обнаружены на этой границе, где противоборствующие силы безудержного расширения и смерти тщательно уравновешивают друг друга. Конвей тщательно изучил различные комбинации правил в соответствии со следующими тремя критериями: Не должно быть исходной модели, для которой есть простое доказательство того, что популяция может расти без ограничений. Должны быть исходные узоры, которые, по-видимому, растут без ограничений. Должны быть простые начальные паттерны, которые растут и изменяются в течение значительного периода времени, прежде чем закончиться следующими возможными способами: Полное исчезновение (из-за перенаселенности или из-за того, что они становятся слишком редкими) Установление стабильной конфигурации, которая после этого остается неизменной, или вхождение в колебательную фазу, в которой они повторяют бесконечный цикл из двух или более периодов. Используя предоставленные игровые поля и правила, описанные выше, учащиеся могут исследовать эволюцию простейших узоров. Они должны убедиться, что любая отдельная живая клетка или любая пара живых клеток погибнет во время следующей итерации. Некоторые возможные паттерны триомино (и их эволюция) для проверки: Вот несколько шаблонов тетромино (ПРИМЕЧАНИЕ: учащиеся могут сделать один или два из них на игровой доске, а остальные на компьютере): Примеры натюрмортов: Квадрат: Лодка: Буханка: Корабль: Следующий узор называется «планер». Учащиеся должны проследить его эволюцию на игровом поле, чтобы увидеть, что узор повторяется каждые 4 поколения, но переводится вверх и влево на одну клетку. Планер будет вечно двигаться по плоскости. Еще одна модель, похожая на планер, называется «легкий космический корабль». Он слишком медленно и неуклонно перемещается по сетке. Вначале (без использования компьютеров) Конвей обнаружил, что F-пентамино (или R-пентамино) не превратился в стабильный паттерн после нескольких итераций. Фактически, он не стабилизируется до поколения 1103. F-пентамино стабилизируется (это означает, что будущие итерации легко предсказать) после 1103 итераций. Класс паттернов, которые начинаются с малого, но требуют очень много времени, чтобы стать периодическими и предсказуемыми, называются Мафусаилами. Студенты должны использовать компьютерные программы, чтобы увидеть эволюцию этой модели и увидеть, как и где она становится стабильной. «Желудь» — еще один пример Мафусаила, который становится предсказуемым только после 5206 поколений. Алан Хенсел составил довольно большой список других распространенных паттернов и названий для них, доступный по адресу http://radialeye.com/lifepage/picgloss/picgloss.html. Life32 — полнофункциональный и быстрый симулятор Game of Life для Windows. Скачать программу Life32 можно здесь. Есть исходные шаблоны, которые можно использовать только с Life32, которые вы можете скачать здесь. Еще одна чрезвычайно быстрая программа, которую можно установить в Windows, OS X и Linux, — это Golly, которая использует хеширование для поистине удивительного ускорения. Голли можно найти по адресу http://sourceforge.net/project/showfiles.php?group_id=139.354. Здесь есть краткое описание того, как Голли достигает такой удивительной скорости. Также существует множество реализаций The Game на Java, которые можно запускать в большинстве современных веб-браузеров, хотя обычно они работают медленнее. Один из них можно найти на http://www.ibiblio.org/lifepatterns/. Джейсон Саммерс собрал очень интересную коллекцию жизненных паттернов, которую можно запустить с помощью Life32 или Golly, которую можно скачать здесь. Если вы используете Life32, то после установки учащиеся должны перейти в каталог, содержащий исходные шаблоны, указанные выше. В этом каталоге находятся файлы с предустановленными в них стандартными паттернами Life. Предоставляются следующие шаблоны (и учащиеся должны запускать файлы в этом порядке): стандартный планер, пчелиная матка-челнок, длительная пчелиная матка, планерное ружье Госпер (первый пример бесконечно растущего шаблона, принесший создателю 50 долларов). ), LWSS (легкий космический корабль), пульсар и пятиборье. После просмотра (и попытки понять) более простых примеров учащиеся могут поэкспериментировать с некоторыми файлами в этой подборке Джейсона Саммерса из журнала Popular и посмотреть на другие интересные шаблоны. Некоторые из лучших файлов расположены в каталогах «applications» и «guns». Если вы используете Golly, то в левой части окна на видном месте находится еще один список начальных шаблонов. Активность — Игра жизни для двух игроков Называть «Игру жизни» Конвея игрой — значит преувеличивать значение слова «игра», но есть забавная адаптация, которая может привести к соревновательной и стратегической деятельности для нескольких игроков. Сделана модификация: теперь живые клетки бывают двух цветов (по одному для каждого игрока). Когда новая клетка оживает, она приобретает цвет большинства своих соседей. (Поскольку для того, чтобы клетка ожила, соседей должно быть трое, ничьи быть не может. Должно быть большинство) Игроки ходят по очереди. В свой ход игрок должен убить одну вражескую клетку, а должен заменить одну пустую клетку на клетку своего цвета. Им разрешено создать новую ячейку в том месте, где они убили вражескую ячейку. После хода игрока ячейки Жизни проходят одно поколение, и ход переходит к следующему игроку. Между действиями отдельных игроков всегда ровно одно поколение эволюции. Начальная конфигурация платы должна быть определена заранее и должна быть симметричной. Игрок выбывает, когда у него не осталось клеток своего цвета. Этот вариант жизни вполне можно адаптировать для нескольких игроков. Однако, если игроков больше двух, у новорождённой ячейки может быть три соседа, принадлежащие трём разным игрокам. В этом случае новорожденная клетка нейтральна и никому не принадлежит. Можно даже создавать шаблоны, эмулирующие логические вентили (и, не, или и т. д.) и счетчики. На их основе было доказано, что игра «Жизнь» завершена по Тьюрингу, а это означает, что с подходящим начальным шаблоном можно выполнить любые вычисления, которые можно выполнить на любом компьютере. Позже Пол Ренделл сконструировал простую машину Тьюринга в качестве доказательства концепции, которую можно найти здесь. Хотя машина Тьюринга Ренделла довольно мала, она содержит все идеи, необходимые для создания более крупных машин, которые действительно могли бы выполнять осмысленные вычисления. Один из шаблонов в коллекции Джейсона Саммерса будет вычислять простые числа, а другой будет вычислять простые числа-близнецы (два простых числа, которые отличаются только добавлением или вычитанием 2). Очень далеко от машины Тьюринга Пола Ренделла:

Игра жизни Джона Конвея

Так называемый образец космического корабля в Conways Game of Life

Что такое игра жизни?

Игра «Жизнь» — это клеточный автомат, разработанный британским математиком Джоном Хортоном Конвеем в 1970 году. Его популяризировал Мартин Гарднер. в своем 19 октября70 колонка «Математические игры» в журнале «Scientific American» [6]. Статья вызвала больше откликов, чем любая другая. его предыдущих статей в журнале, включая известную статью Гарднера о гексафлексагонах.

Примечательным свойством специального набора правил, использованного в «Игре жизни» Конвея, является его полнота по Тьюрингу. Полнота по Тьюрингу — это свойство, описывающее, что язык программирования, имитационная или логическая система в принципе подходят для решения любой вычислительной задачи. Программирование «Игры жизни» будет осуществляться с помощью паттернов, которые затем взаимодействуют между собой. друг с другом в моделировании. LifeWiki имеет большой архив таких паттернов для Game of Life. Выбор из тех реализован в апплете, показанном ниже.

Тороидальный мир

(Шаблоны предоставлены LifeWiki.)

Из-за простоты набора правил реализация Game of Life является популярной задачей для начинающих программистов. Исходный код «Игры в жизнь» Используемый здесь апплет написан на Typescript и может быть загружен с GitHub. Описание реализации Игры Жизни на Python можно в другой статье на этом сайте.

«Игра жизни» Quellcode

на GitHub по адресу

Что такое клеточный автомат?

Клеточный автомат — это дискретная модель, состоящая из регулярной сетки ячеек, в которой каждая ячейка находится в конечном состоянии. Исходное состояние клеточного автомата выбирается путем присвоения состояния каждой ячейке. Затем симуляция прогрессирует с дискретными временными шагами. Штат ячейки на временном шаге t зависит только от состояния соседних ячеек на временном шаге т-1 и набор правил, специфичных для автомата.

Окрестности сотовой связи

Клетки, влияющие на состояние автомата называются окрестностями. Существует два часто используемых типа районов: район Мура и район Ван Неймана. Окрестность Мура содержит все соседние ячейки, даже если они имеют с ячейкой только угловую точку, в то время как окрестность Ван Неймана содержит только те ячейки, которые имеют общее ребро с ячейкой.

Район Мур

Район Ван Нейман

Правила игры в жизнь

В игре «Жизнь» каждая ячейка сетки может находиться в одном из двух состояний: мертвом или живом. Game of Life управляется четырьмя простыми правилами, которые применяются к каждой ячейке сетки в области моделирования:

• Живая клетка умирает, если у нее меньше двух живых соседей.
• Живая клетка с двумя-тремя живыми соседями живет до следующего поколения.
• Умирает живая ячейка с более чем тремя живыми соседями.
• Мертвая клетка будет возвращена к жизни, если у нее будет ровно три живых соседа.

Граничные условия

Клеточные автоматы часто используют тороидальную топологию области моделирования. Это означает, что противоположные края сетки связанный. Крайний правый столбец является соседом самого левого столбца, а самая верхняя строка является соседом самой нижней строки. и наоборот. Это позволяет неограниченную передачу информации о состоянии через границы.

Противоположные ребра сетки соединяются, чтобы сформировать тороидальную топологию области моделирования

Ячейки за границей сетки всегда рассматриваются как мертвые.

Другой тип граничных условий рассматривает несуществующие ячейки так, как если бы все они находились в одном и том же состоянии. В игре «Жизнь» это означало бы что несуществующие клетки рассматриваются как мертвые (в отличие от второго состояния «живые»). Преимущество этого граничного условия в Game of Life заключается в том, что она не позволяет глайдерам облетать края области симуляции. Это предотвратит разрушение планерной пушки по производимым ею планерам (подробности о том, что такое планеры, см. в тексте ниже).

Примеры узоров

Паттерны появятся при типичном прохождении Игры Жизни. Некоторые шаблоны статичны, другие колеблются или перемещаются по экрану. Некоторые паттерны могут даже создавать другие паттерны. В следующих таблицах представлен обзор наиболее часто встречающихся паттернов в игре «Жизнь».

Натюрморты

Натюрморты — это статичные конструкции, которые не меняются со временем.

Блок

Блок — самый обычный «натюрморт». Он состоит из четырех ячеек, образующих блок 2х2. Блок — это так называемый «пожиратель». Это означает, что он может разрушать другие паттерны без структурных повреждений.

Улей:

«Натюрморт», состоящий из 6 ячеек. Второй по распространенности натюрморт.

Буханка:

Натюрморт, состоящий из 7 клеточек. Третий по распространенности натюрморт.

Осцилляторы

Осцилляторы — это структуры, которые периодически повторяются во времени, но сохраняют свое положение.

Мигалка:

Самый маленький и самый распространенный осциллятор.

Жаба:

Жаба — осциллятор с периодом 2. Это второй по распространенности естественный осциллятор.

Маяк:

Третий по частоте естественный осциллятор. Он состоит из двух диагонально соприкасающихся блоков.

Космические корабли

Космические корабли — это сооружения, которые перемещаются по игровому полю «Игры жизни».

Планер:

Планер — это рисунок, который движется по диагонали экрана. Это самый маленький, самый распространенный и первый обнаруженный космический корабль.

Легкий космический корабль (LWSS):

Это колеблющийся объект, который движется ортогонально по экрану. Это самый маленький ортогонально движущийся космический корабль.

Weekender:

Это ортогональный космический корабль, который немного больше, чем предыдущие модели.

Кем был Джон Конвей?

John Horton Conway; 26 декабря 1937, Ливерпуль, Великобритания; † 11 апреля 2020, Нью-Брансуик) — британский математик. Он работал в полях конечных групп, теории узлов, теории чисел, теории кодирования, комбинаторной теории игр и внес большой вклад в развлекательную математику.

Конвей вырос в Ливерпуле. Он провел первую часть своей карьеры в Кембриджском университете. Позже он перешел в Принстонский университет в США. где он принял от Джона фон Неймана кресло, которое занимал до конца своей карьеры. За свою работу он получил премию Бервика в 1971 г. Премия Полиа в 1987 году от Лондонского математического общества. В 1981 году он стал членом Королевского общества. В 1992 году он был избран в Американскую академию. Искусств и наук, а в 2000 году Американское математическое общество присудило ему премию Лероя П. Стила.

Одной из самых известных его работ среди нематематиков является изобретение «Игры в жизнь». Об этом заявил сам Конвей в интервью YouTube-каналу. Numberphile [7], что он не нашел его особенно интересным. Поэтому он не понимал внимания, которое это вызвало. По его мнению, «Игра в жизнь» затмила более важные математические достижения. Иногда он ненавидел, когда его об этом спрашивали. Тем не менее в дальнейшем лет он также сказал, что это то, чем он гордится. [7].

11 апреля 2020 года Конвей умер от осложнений, вызванных болезнью COVID-19.

Изобретение игры «Жизнь»

Джон Конвей дал интересное интервью на YouTube-канале Numberphile [1], в котором рассказал об истоках Игры Жизни. Если вам интересно, какое отношение терраформирование Марса имеет к игре жизни, я настоятельно рекомендую его посмотреть.

Внешний контент: «Изобретая игру жизни» от Numberphile

Видео: «Изобретая игру жизни» интервью с Youtube-каналом Numberphile.

Современные разработки

Игра «Жизнь», разработанная в 1970 году, относится к ранним годам вычислительной техники. Если вы слушали интервью Джона Конвейса, вы могли заметить, что он упомянул, что В первые годы игра «Жизнь» исследовалась на бумаге. С появлением домашних компьютеров он приобрел популярность, и теперь большинство людей начинают программировать. встретится раньше или позже. Это похоже на «Hello World» графического программирования. Что делает игру жизни увлекательной, так это простота ее правил и сложность паттернов, возникающих в результате этого простого набора правил. В следующих разделах будут обсуждаться некоторые из последних результатов эволюции сообщества. вокруг «Игры жизни».

Метапиксель OCTA

В интервью Numberphile Джон Конвей упомянул, что Game of Life можно использовать для произвольных вычислений. Если вы спросите себя, что это значит и как это должно выглядеть так, как вы должны взглянуть на следующее видео, демонстрирующее реализацию Game of Life в Game of Life.

Внешний контент: Видео предоставлено Youtube / Phillip Bradbury

Видео: «Жизнь в жизни» Филиппа Брэдбери [3]. Создано с помощью симулятора жизни Golly с помощью OCTA-Metapixels

Основным строительным блоком этой симуляции является метапиксель OCTA [3]. Это элементарная ячейка размером 2048 x 2048, разработанная Брайсом Дью в 2006 году. Элементарная ячейка представляет собой конструкцию клеточного автомата, которая способна имитировать другую автоматизировать возможно сам. Существуют и другие единичные ячейки, такие как единичная ячейка Life P5760, разработанная ранее, но метапиксель OCTA уникален своим сходством с реальной ячейкой. Насколько я понимаю, это близко к черной магии, и на это приятно смотреть.

Гладкая жизнь

Smooth Life — это расширение Game of Life до непрерывного домена. Он использует значения с плавающей запятой вместо целых чисел. Правила SmoothLife были созданы Стефаном Рафлером [5]. Видео, показанное ниже, было созданный Тимом Хаттоном с SmoothLife. Более обширную коллекцию видеороликов SmoothLife можно найти на видеоканале SmoothLife.

Внешний контент: Видео предоставлено Youtube / Тимом Хаттоном

SmoothLife показывает многие известные структуры из игры Life, такие как планеры. в потрясающе красивой визуализации, похожей на микробные формы жизни. (© 2012; Тим Хаттон)

Пустяки / Пасхальные яйца

• Если вы погуглите «Conways Game Of Life», вы увидите игру в жизнь в правом верхнем углу страницы результатов

Каталожные номера

1. «Изобретение игры жизни — Numberphile».