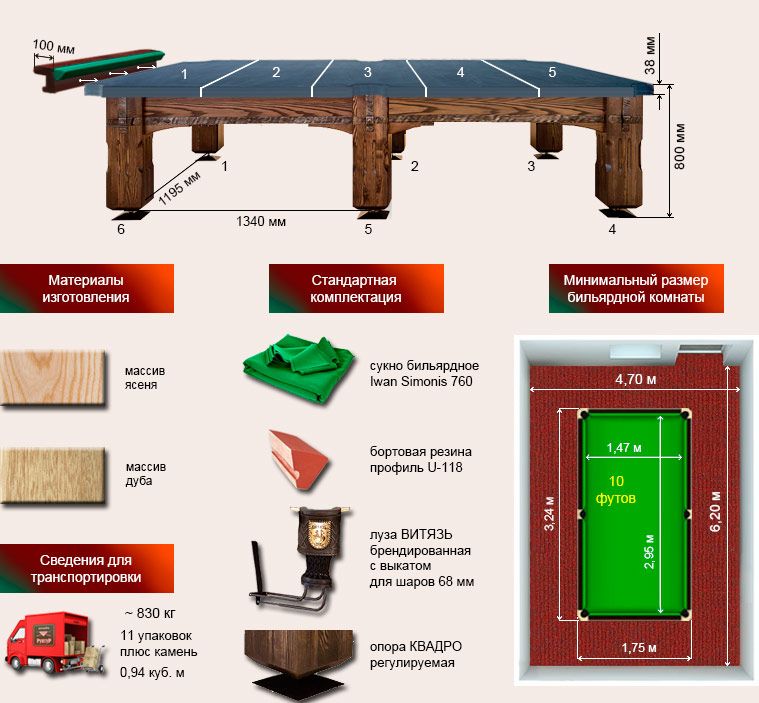
Бильярдный стол для русского бильярда
Качественный бильярдный стол от отечественного производителя.
97,265 грн.114,733 грн.97,265 грн.
114,733 грн.Бильярдный стол “KING” 12 футов, это элитный стол, сделанный с красного дерева. Ручная работа. В этом бильярдном столе идеально выдержаны все пропорции и стандарты для русского бильярда рекомендованные ФСБУ.
154,830 грн.
“KING” 12 футов — это идеальный выбор бильярдного стола, для успешного и ценящего красоту игрока. Бильярдный стол “KING” 12 футов -это профессиональный стол на котором можно спокойно проводить любое соревнование или чемпионат по бильярду. Соответствует всем нормам! Покупая Бильярдный стол “KING” 12 футов на компании Бильярдист, вы получаете не только нашу гарантию в 2 года но и полный спектр услуг, доставку бильярдного стола, установку и нивелировку.
154,830 грн.
Бильярдный стол премиум класса “LION” 12 футов, сделан с массива красного дерева. Ноги данного бильярдного стола сделаны в форме львиной головы. В “LION” 12 футов идеально выдержаны все пропорции и стандарты для русского бильярда. Это идеальный выбор бильярдного стола, для успешного и ценящего красоту игрока. Купить бильярдный стол премиум класса “LION” 12 футов Вы сможете на компании Бильярдист. Мы предоставляем гарантию на 2 года, полный спектр услуг, доставку бильярдного стола, установку и нивелировку.
170,710 грн.170,710 грн.
Бильярдный стол ROUND 10 футов — это бильярдный стол для русской пирамиды. VIP класса.
По своим техническим и игровым характеристикам идеально подходит для игры с друзьями, тренировки или обучения детей игре на бильярдном столе. Бильярдный стол ROUND 10 футов — полностью соответствует требованиям спортивных федераций по бильярду. Дизайн Бильярдного стола ROUND выполнен в классическом стиле.
109,175 грн.109,175 грн.
Бильярдный стол ROUND 12 футов это бильярдный стол для русской пирамиды. VIP класса.По своим техническим и игровым характеристикам идеально подходит для игры с друзьями, тренировки или обучения детей игре на бильярдном столе. Бильярдный стол ROUND 12 футов — полностью соответствует требованиям спортивных федераций по бильярду. Дизайн Бильярдного стола ROUND выполнен в классическом стиле.
131,010 грн.131,010 грн.
Бильярдный стол ROUND 8 футов — это бильярдный стол для русской пирамиды. VIP класса. По своим техническим и игровым характеристикам идеально подходит для игры с друзьями, тренировки или обучения детей игре на бильярдном столе.Бильярдный стол ROUND 8 футов — полностью соответствует требованиям спортивных федераций по бильярду.
91,310 грн. Дизайн Бильярдного стола ROUND выполнен в классическом стиле.91,310 грн.
Бильярдный стол Titan — это профессиональный бильярдный стол, классического типа, для русского бильярда.
131,010 грн.
Бильярдный стол Titan — идеальное сочетание игровых характеристик, цены и качества. Бильярдный стол Titan — наиболее востребован клубами и игровыми залами, где бильярдные столы используются с большой интенсивностью игры. Данный бильярдный стол будет служить своему хозяину, верой и правдой долгие годы131,010 грн.
Бильярдный стол Titan — это профессиональный бильярдный стол, классического типа, для русского бильярда.
89,794 грн.
Бильярдный стол Titan — идеальное сочетание игровых характеристик, цены и качества. Бильярдный стол Titan — наиболее востребован клубами и игровыми залами, где бильярдные столы используются с большой интенсивностью игры. Данный бильярдный стол будет служить своему хозяину, верой и правдой долгие годы.89,794 грн.
Бильярдный стол Titan это профессиональный бильярдный стол, классического типа, для русского бильярда.
61,138 грн.
Бильярдный стол Titan — идеальное сочетание игровых характеристик, цены и качества. Бильярдный стол Titan — наиболее востребован клубами и игровыми залами, где бильярдные столы используются с большой интенсивностью игры. Данный бильярдный стол будет служить своему хозяину, верой и правдой долгие годы.66,299 грн.61,138 грн.
66,299 грн.Бильярдный стол Titan — это профессиональный бильярдный стол, классического типа, для русского бильярда.
76,224 грн.
Бильярдный стол Titan — идеальное сочетание игровых характеристик, цены и качества. Бильярдный стол Titan — наиболее востребован клубами и игровыми залами, где бильярдные столы используются с большой интенсивностью игры. Данный бильярдный стол будет служить своему хозяину, верой и правдой долгие годы.79,400 грн.76,224 грн.
79,400 грн.- 95,280 грн.
95,280 грн.
Бильярдный стол Tank — разрабатывался нашими конструкторами как стол для коммерческого использования. Он вынослив и крепок как танк. По этому и получил такое название.Эти столы проверены годами и крайне надежны. Удобны, а так-же комфортные в игре.TANK — это профессиональный бильярдный стол. В TANK массивные и толстые квадратные опоры (ноги) из МДФ, вскрытые специальным грунтом-усилителем. Бильярдный стол “TANK” — идеально подойдет для любой бильярдной комнаты, соответствующего размера.
71,460 грн.
Бильярдный стол “TANK” — может использоваться для коммерческих целей, с таймером света — сауны, кафе, бары, рестораны. Много данных столов покупались в офисы, для отдыха и разгрузки сотрудников.73,445 грн.71,460 грн.
73,445 грн.
Дизайн Бильярдного стола ROUND выполнен в классическом стиле.
Дизайн Бильярдного стола ROUND выполнен в классическом стиле.
Данный бильярдный стол будет служить своему хозяину, верой и правдой долгие годы.
Бильярдный стол Старт «Домашний 2» Русская Пирамида
Оценок: 0
Сравнить к списку
Код товара: 114006
Уточнить цену
Только на заказ. Актуальную цену на момент заказа необходимо уточнять у менеджера интернет-магазина
| i | За покупку этого товара клубные баллы не начисляются. Подарочными баллами можно оплатить до 10% от стоимости этого товара. |
Варианты
Размеры стола: 6F (1,80*0,9) Размеры стола: 7F (2,0*1,0) Размеры стола: 8F (2,24*1,12) Размеры стола: 9F (2,54*1,27)
Наличие
Только на заказ
Способы получения
Способы оплаты
- Описание
- Вопросы экспертам (3)
- Отзывы
(0) +500 подарочных баллов за отзыв!
| Тип плиты | ЛДСП |
| Толщина плиты | 16 мм |
| Материал стола | Береза/сосна |
| Сукно | Kazino |
| Цвет сукна | зеленый |
| Амортизаторы | Start Super Pro (рекомендованы ФБСР) |
| Лузы | Силуминовые, х/б сетка |
| Количество ножек | 6F, 7F-4 ножки 9F-6 ножек |
| Опоры | Пластмассовые |
| Размеры комнаты | Не менее: 6F:4,90х4,00 м 7F:5,00х4,05 м 8F:5,74х4,62 мг 9F:6,04х4,77 м |
| Бренд | Старт |
| Страна производитель | Россия |
Сборка стола в указанную стоимость не входит.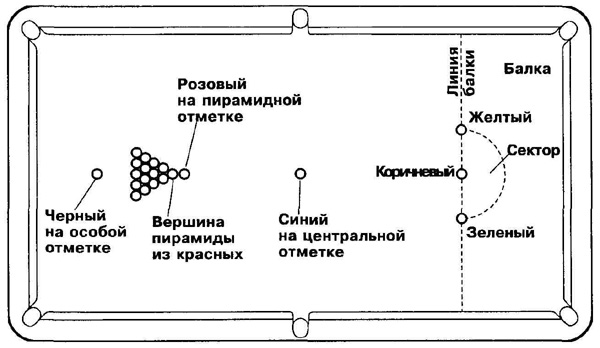
Отличие «Домашнего II» от предшествующей модели в том, что он полностью изготовлен из современного материала, обладает повышенной устойчивостью в перепадам температуры и влажности.
Стол оснащен усиленным лафетом, что обеспечивает ему повышенную статичность и жесткость конструкции. Ноги снабжены пластиковыми опорами, в которых установлена утолщенная шпилька, сохраняющая устойчивость конструкции.
Игровые характеристики и компактный внешний вид позволяют установить стол как в квартире, так и в загородном дома, а также в офисе.
Товар может иметь небольшие отличия от представленного на фотографии.
Бильярдный стол Старт «Домашний 2» Русская Пирамида — купить онлайн
Вы можете купить Бильярдный стол Старт «Домашний 2» Русская Пирамида в интернет-магазине «Чемпион» по приемлемой цене с оплатой онлайн. Бильярдный стол Старт «Домашний 2» Русская Пирамида подробное описание с фото, характеристиками, отзывами о товаре
09 дек.
2017, 07:45У стола размера 8F сколько ног? Ноги отделяются от стола? Доставка как производится?
Добрый день. 6 ног, ножки отдельно. Доставка возможна до склада в г. Екатеринбург. Затем до Уфа-Шигири транспортной компанией или самовывоз.
09 дек. 2017, 07:45
У стола размера 8F сколько ног? Ноги отделяются от стола? Доставка как производится?
Добрый день. 6 ног, ножки отдельно. Доставка возможна до склада в г. Екатеринбург. Затем до Уфа-Шигири транспортной компанией или самовывоз.
21 янв. 2018, 16:22
Размеры стола указаны по сукну?
Добрый день. Размеры указаны по игровому полю.
2017, 07:45У вас есть вопросы по товару?
Контактная информация
При необходимости вы можете оставить контактные данные, чтобы мы могли с вами связаться (оставленные данные будут использоваться только для связи с вами).
К сожалению, отзывов пока нет.
Вы можете оставить первый отзыв.
Оставьте свой отзыв
к списку
Шары для русского бильярда Start up 68 мм
4 690 ₽
4 790 ₽
к списку
Треугольник бильярдный (пластик) 57 мм
к списку
Шары для русского бильярда Start Up 60 мм
3 590 ₽
4 660 ₽
к списку
Киевница старт сосна
1 160 ₽
Геометрический подход к полудисперсионным бильярдам
Александров А.Д. Теорема о треугольниках в метрическом пространстве и некоторые ее приложения. тр. Мат. Инст. Стеклова 38 , 5–23, 1951. (рус.).
Google Scholar
Александров А.Д., Бураго Ю.Д. Квазигеодезические. проц.
Стеклов. Инст. Мат. 76 , 58–76, 1965.
Google Scholar
А.Д. Александров и В.В. Стрельцов. Изопериметрическая задача и оценки длины кривой на поверхности. проц. Стеклов. Инст. Мат. 76 , 81–99, 1965.
Google Scholar
А.Д. Александров и В.А. Залгаллер. Внутренняя геометрия поверхностей. Транси. Мат. Монографии 15, Am. Мат. Соц., 1967.
Google Scholar
В. Арнольд. Лекция на встрече в Филдсовском институте, посвященной его 60-летию.
Google Scholar
В. Баллманн. Лекции о пространствах неположительной кривизны. С приложением Миши Брина. DMV Seminar, 25. Birkhauser Verlag, Basel, 1995.
CrossRef МАТЕМАТИКА Google Scholar
М.
Берри. Квантование классической эргодической системы: бильярд Синая и метод ККР. Энн. Физика 131 , вып. 1, 163–216, 1981.
перекрестная ссылка MathSciNet Google Scholar
П. Блехер. Статистические свойства двумерного периодического газа Лоренца с бесконечным горизонтом. Дж. Стат. Физика
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Р. Боуэн. Топологическая энтропия для некомпактных множеств. Транс. амер. Мат. соц. 184 , 125–136, 1973.
Перекрёстная ссылка MathSciNet Google Scholar
Бунимович Л.А. Вариационный принцип для периодических траекторий гиперболических бильярдов. Хаос 5 , нет. 2, 349–355, 1995.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Бунимович Л.
А. Центральная предельная теорема для бильярда с рассеянием. (рус.) Мат. сб. (Н.С.) 94 , нет. 136, 49–73, 1974.
MathSciNet Google Scholar
Л.А. Бунимович, Я.Г. Синай. Основная теорема теории рассеивающих бильярдов. (рус.) Мат. сб. (NS) 90 , № 132, 415–431, 1973.
Google Scholar
Л.А. Бунимович, Я.Г. Синай. Марковские разбиения для рассредоточенных биллиардов. Комм. Мат. физ. 78 , № 2, 247–280, 1980/81.
Перекрёстная ссылка MathSciNet МАТЕМАТИКА Google Scholar
Л.А. Бунимович, Я.Г. Синай. Статистические свойства газа Лоренца с периодической конфигурацией рассеивателей. Комм. Мат. физ. 78 , № 4, 479–497, 1980/81.
Перекрёстная ссылка MathSciNet Google Scholar
Л.
А. Бунимович, Я.Г. Синай, Н.И. Чернов. Статистические свойства двумерных гиперболических биллиардов. Русская математика. Опросы 46 , № 4, 47–106, 1991.
CrossRef MathSciNet Google Scholar
Л.А. Бунимович, Я.Г. Синай, Н.И. Чернов. Марковские разбиения для двумерных гиперболических биллиардов. Русская математика. Опросы 45 , нет. 3, 105–152, 1990.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Л.А.Бунимович, К.Ливерани, А.Пеллегринотти, Ю.Сухов. Эргодические системы n шаров в бильярдном столе. Комм. Мат. физ. 146 , № 2, 357–396, 1992.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Д. Бураго, С. Ферлегер, А. Кононенко. Равномерные оценки числа столкновений в полурассеивающих бильярдах.
Энн. математики. (2) 147 (1998), вып. 3, 695–708.
Перекрёстная ссылка MathSciNet МАТЕМАТИКА Google Scholar
Д. Бураго, С. Ферлегер, А. Кононенко. Топологическая энтропия полурассеивающих биллиардов. Эргодическая теория и динамические системы, 18 (1998), нет. 4, 791–805.
Перекрёстная ссылка MathSciNet МАТЕМАТИКА Google Scholar
Д. Бураго, С. Ферлегер, А. Кононенко. Развертки и глобальные границы числа столкновений для обобщенных полурассеивающих биллиардов. Asian J. Math
MathSciNet МАТЕМАТИКА Google Scholar
Д. Бураго, С. Ферлегер, А. Кононенко. Геометрический подход к полудисперсионным биллиардам. Эргодическая теория и динамические системы, 17 , вып.
2, 1–17, 1998.
MathSciNet Google Scholar
Д. Бураго, С. Ферлегер, Б. Кляйнер и А. Кононенко. Склеивание копий трехмерного многогранника для получения замкнутого (псевдо)многообразия неположительной кривизны. проц. амер. Мат. Соц, появиться.
Google Scholar
Д. Бураго Твердые шары Газ и Александров Пространства кривизны, ограниченные сверху Труды ICM-98, том 2. Documenta Mathematica, 1998.
Google Scholar
Н.И. Чернов, Р. Макарян. Энтропия неравномерно гиперболических плоских биллиардов. Бол. соц. Бразилия. Мат. (NS) 23 , № 1–2, 121–135, 1992.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Н.И. Чернов. Топологическая энтропия и периодические точки двумерных гиперболических биллиардов.
Функц. Анальный. заявл. 25 , № 1, 39–45, 1991.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Н.И. Чернов. Новое доказательство формулы Синая для энтропии гиперболических бильярдных систем. Применение к газам Лоренца и стадионам Бунимовича. Функц. Анальный. заявл. 25 , №1, 204–219, 1991.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Н.И. Чернов. Построение поперечных расслоений в многомерных полудисперсных бильярдах. Функц. Анальный. заявл. 16 , № 4, 270–280, 1983.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Н.И. Чернов. Энтропия, показатели Ляпунова и длина свободного пробега бильярда. Дж. Стат. Физика 88 , № 1/2, 1–29, 1997.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Н.
И. Чернов. Статистические свойства периодического газа Лоренца. Многомерный случай. Дж. Стат. Физика 74 , вып. 1/2, 11–53, 1994.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Ю. Колин де Вердьер. Гиперболическая геометрия в двух измерениях и формулы следов. Chaos et physique quantique (Les Houches, 1989), 305–330, Северная Голландия, Амстердам, 1991.
Google Scholar
В. Донней. Эллиптические острова в обобщенном синайском бильярде. Эргодическая теория динам. Системы 16 , №. 5, 975–1010, 1996.
MathSciNet МАТЕМАТИКА Google Scholar
В. Донней, К. Ливерани. Потенциалы на двухторе, для которых гамильтонов поток эргодичн. Комм. Мат. физ. 135 , № 2, 267–302, 1991.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Э.
Дорон, Ю. Смиланский. Периодические орбиты и квазиклассическое квантование рассеивающих биллиардов. Нелинейность 5 , нет. 5, 1055–1084, 1992.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
К. Ефимов. Теорема типа Лившица для рассеивающего бильярда. Теор. и математика. физ. 98 , № 2, 122–131, 1994.
CrossRef MathSciNet Google Scholar
Т. Хараяма, А. Шудо. Периодические орбиты и квазиклассическое квантование рассеивающих биллиардов. Дж. Физ. А 25 , №. 17, 4595–4611, 1992.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Г.А. Гальперин. Системы с локально взаимодействующими и отталкивающими частицами, движущимися в пространстве. (Русский) Тр. ММО 43 , 142–196, 1981.
MathSciNet МАТЕМАТИКА Google Scholar
Гальперин Г.
А. Упругие столкновения частиц на прямой. (Русский) Успехи мат. наук 33 нет. 1(199), 211–212, 1978.
MathSciNet МАТЕМАТИКА Google Scholar
Г. Галлавотти, Д. Орнштейн. Бильярд и схемы Бернулли. Комм. Мат. физ. 38 , № 2, 83–101, 1974.
Перекрёстная ссылка MathSciNet МАТЕМАТИКА Google Scholar
М. Громов. «Гиперболические группы». в Очерках теории групп С.М. Герстен (ред.). М.С.Р.И. Publ., Vol.8, 75–263, Springer 1987.
CrossRef Google Scholar
М. Громов. Структурирует метрики для римских разновидностей. Под редакцией Ж. Лафонтена и П. Пансу. Textes Mathematiques, 1. CEDIC, Paris, 1981.
Google Scholar
Э. Гуткин, Н.
Гайдн. Топологическая энтропия обменов обобщенными полигонами. Bull, of AMS 32 , № 1, 50–56, 1995.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Дж. Хасс, П. Скотт. Ограниченное трехмерное многообразие допускает метрику отрицательной кривизны с вогнутой границей. Дж. Дифф. геом. 40 , № 3, 449–459, 1994.
MathSciNet МАТЕМАТИКА Google Scholar
М. Икава. Дезичность решений волнового уравнения во внешности нескольких выпуклых тел. Энн. Инст. Фурье 38 , 113–146, 1988.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Р. Иллнер. Конечность числа столкновений в системе частиц твердых сфер во всем пространстве. Статист по теории транспорта. физ. 19 , № 6, 573–579, 1990.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
А.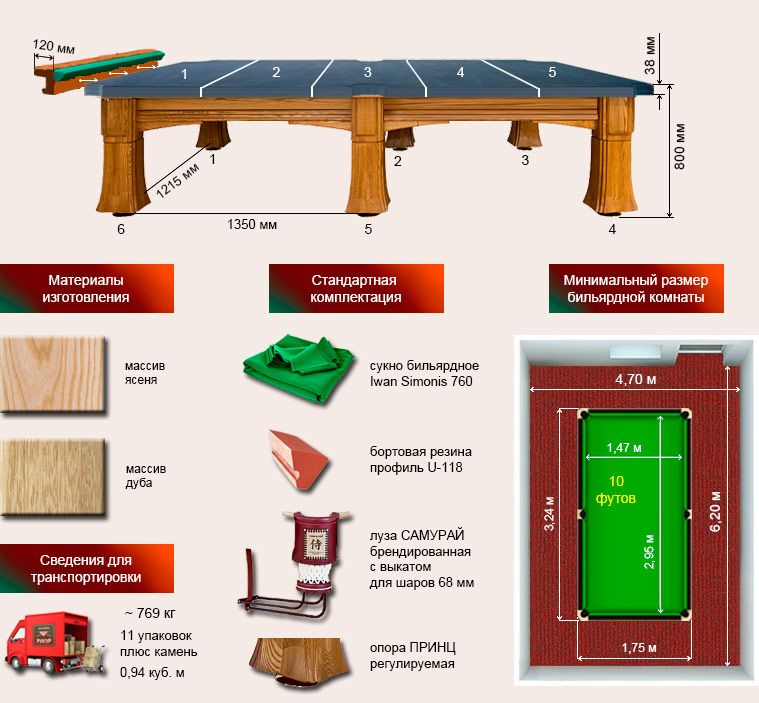
Каток. Скорость роста числа особых и периодических орбит многоугольного биллиарда. Комм. Мат. физ. 111 , 151–160, 1987.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Каток А., Стрельцын Ю.М. Гладкие отображения с особенностями: инвариантные многообразия, энтропия и биллиарды. Лект. Примечания по математике, том. 1222, Спрингер-Ферлаг, 1987.
Google Scholar
В. Козлов, Д. Трещев. «Бильярд. Генетическое введение в динамику систем с ударами». Переводы математических монографий, 89. Американское математическое общество, Провиденс, Род-Айленд, 1991.
МАТЕМАТИКА Google Scholar
Н.С. Криллов. Работает над основами статистической физики. АН СССР, Москва, 1950. Английский перевод: Принстонская серия по физике. Издательство Принстонского университета, Принстон, Нью-Джерси, 1979.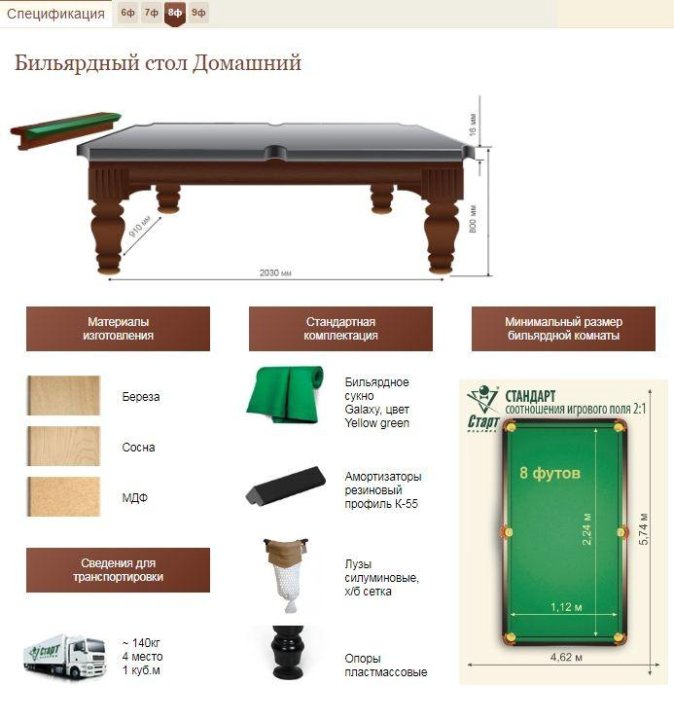
Google Scholar
А. Крамли, Н. Симаньи, Д. Сас. K -свойство трех бильярдных шаров. Энн. математики. (2) 133 , № 1, 37–72, 1991.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
А. Крамли, Н. Симаньи, Д. Сас. «Трансверсальная» фундаментальная теорема для полурассеивающих биллиардов. Комм. Мат. физ., 129, нет. 3, 535–560, 1990.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Y-E. Леви. Заметка о Синае и марковском разбиении Бунимовича для бильярда. Дж. Статист. физ. 45 , № 1–2, 63–68, 1986.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
А. Мальцев. Об изоморфных матричных представлениях бесконечных групп.
(Русский) Рек. Мат. [Мат. Сборник] Н.С. 8 , № 50, 405–422, 1940.
MathSciNet МАТЕМАТИКА Google Scholar
Т. Морита. Символическое представление бильярда без граничного условия. Транс. амер. Мат. соц. 325 , 819–828, 1991.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Дж.В. Морган, Х. Басс (ред.) «Гипотеза Смита. Доклады, представленные на симпозиуме, состоявшемся в Колумбийском университете, Нью-Йорк, 1979». Pure and Applied Mathematics, 112. Academic Press, Inc., Орландо, Флорида, 1984.
Google Scholar
Т.Дж. Мерфи, Е.Г.Д. Коэн Максимальное количество столкновений между идентичными твердыми сферами, J. Stat. физ. 71 , 1063–1080, 1993.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Ж.
-П. Отал. Гиперболизация Терстоном многообразий Хакена, препринт.
Google Scholar
Я.Б. Песин, Б.С. Пицкель. Топологическое давление и вариационный принцип для некомпактных множеств. Функц. Анальный. заявл. 18 , № 4, 307–318, 1984.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Я.Б. Песин, Я.Г. Синай. Гиперболичность и стохастичность динамических систем. Обзоры математической физики, Vol. 2. С. 53–115. Преподобный Сект. С: Математика. физ. Рев., 2, Харвуд Академик, Кур, 1981.
Google Scholar
Дж. Рехачек. Об эргодичности рассеивающих биллиардов. Случайный вычисл. Динам. 3 , № 1–2, 35–55.
Google Scholar
Ю.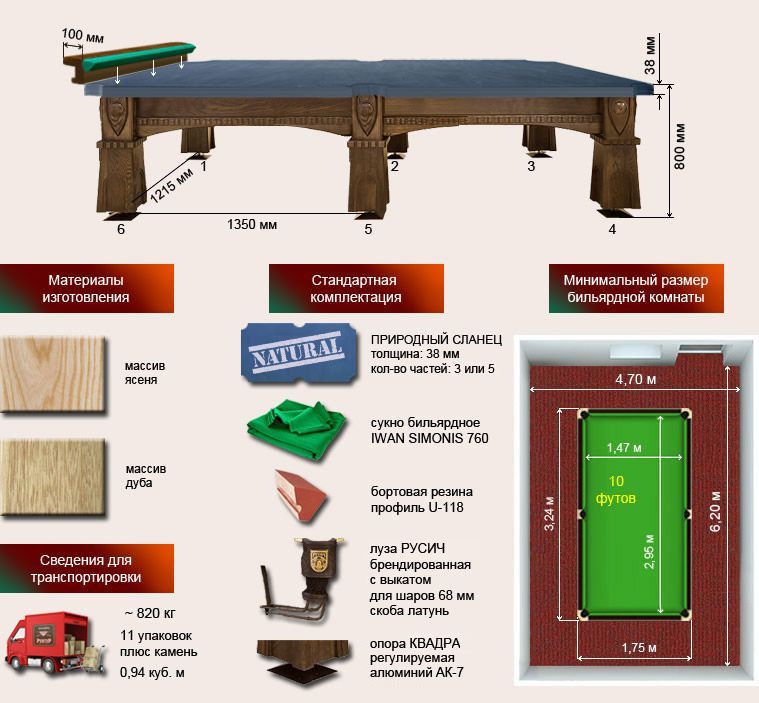
Г. Решетняк (ред.). Геометрия 4, нерегулярная риманова геометрия. Энциклопедия математических наук, Том 70, 1993.
Google Scholar
П. Сарнак. Некоторые приложения модульных форм. Кембриджские трактаты по математике, Vol. 99, 1990.
Перекрёстная ссылка МАТЕМАТИКА Google Scholar
Н. Симаньи. Свойство if N бильярдных шаров. I. Изобретать. Мат. 108 , № 3, 521–548, 1992.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Н. Симаньи. if-свойство N бильярдные шары. II. Изобретать. Мат. 110 , № 1, 151–172, 1992.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Н. Симани, Д. Сас. Лекция, прочитанная в Университете штата Пенсильвания, 1997 г.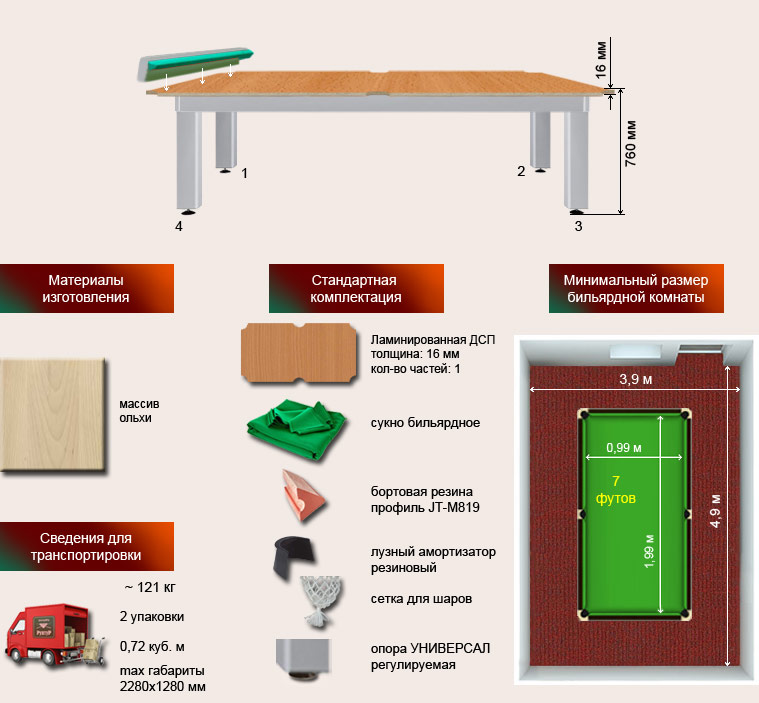
Google Scholar
Н. Симаньи, М. Войтковски. Двухчастичная бильярдная система с произвольным отношением масс. Эргодическая теория динамических систем 9 , № 1, 165–171, 1989.
MathSciNet МАТЕМАТИКА Google Scholar
Я.Г. Синай, Н. Чернов. Эргодические свойства некоторых систем двумерных дисков и трехмерных шаров. Русская математика. Обзоры 42 , 181–207, 1987.
CrossRef MathSciNet Google Scholar
Я.Г. Синай, Н.И. Чернов. Энтропия газа твердых сфер относительно группы сдвигов пространства-времени. (Русский) Труды Сем. Петровск. № 8, 218–238, 1982. Английский перевод в «Динамических системах», изд. Я. Синай, Adv. Серия по нелинейной динамике, Том 1, 373–389.
Google Scholar
Я.
Г. Синай. Энтропия на частицу для динамической системы твердых сфер. Гарвардский университет Препринт, 1978 г.
Google Scholar
Я.Г. Синай. Бильярдные траектории в многогранных углах. Успехи мат. Наук 33 , №1, 229–230, 1978.
MathSciNet МАТЕМАТИКА Google Scholar
Я.Г. Синай (ред.). Динамические системы 2. Энциклопедия математических наук, том 2, 1989.
Google Scholar
Я.Г. Синай. Об основах эргодической гипотезы динамической системы статистической механики. Советская математика. Докл. 4 , 1818–1822, 1963.
MathSciNet Google Scholar
Я.Г. Синай. Динамические системы с упругими отражениями. Эргодические свойства рассеивающих биллиардов.
Русская математика. Обзоры 25 , 137–189, 1970.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Я.Г. Синай. Развитие идей Крылова. Дополнительная статья в «Работах по основам статистической физики» Н.С. Крылов, Принстонская серия по физике. Издательство Принстонского университета, Принстон, Нью-Джерси, 1979.
Google Scholar
Я.Г. Синай. Гиперболический бильярд. Труды Международного конгресса математиков, Vol. I, II (Киото, 1990), 249–260, Math. соц. Япония, Токио, 1991.
Google Scholar
Я.Г. Синай. Эргодические свойства газа Лоренца. Функциональный анал. заявл. 13 , 192–202, 1979.
MathSciNet Google Scholar
А. Семенович, Л.
Васерштейн. Равномерные оценки числа столкновений в системах частиц, препринт.
Google Scholar
Л. Стоянов. Оценка сверху числа периодических орбит для полурассеянного бильярда. Комм. Мат. физ. 124 , № 2, 217–227, 1989.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Л. Стоянов. Экспоненциальная неустойчивость для класса рассеивающих биллиардов, препринт
Google Scholar
С. Табачников. Бильярд. Панорама. Синтезы, нет. 1, 1995. 1991.
MathSciNet Google Scholar
С. Трубецкой. Стохастическая устойчивость рассеивающих биллиардов. Теор. и математика. физ. 86 , № 2, 151–158, 1991.
Перекрёстная ссылка MathSciNet Google Scholar
В.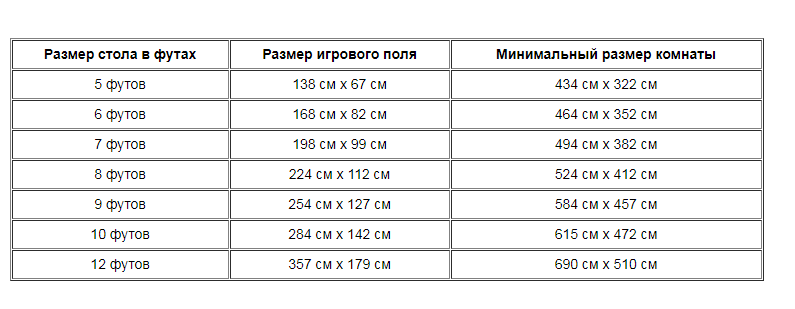
Терстон, Г. Сандри. Классическая задача трех тел на твердой сфере. Бык. амер. физ. соц. 9 , 386, 1964.
Google Scholar
У. Терстон. Трехмерные многообразия, клейновы группы и гиперболическая геометрия. Бык. амер. Мат. соц. (NS) 6 , № 3, 357–381, 1982.
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Л.Н. Васерштейн. О системах частиц с конечным пробегом и/или отталкивающими взаимодействиями. Комм. Мат. физ. 69 , 31–56, 1979.
CrossRef MathSciNet Google Scholar
А. Ветье. Синайский бильярд в потенциальном поле (конструкция устойчивых и нестабильных волокон). Предельные теоремы вероятности и статистики, Vol. I, II (Veszprem, 1982), 1079–1146, Colloq. Мат. соц. Янош Бойяи, 36 лет, Северная Голландия, Амстердам-Нью-Йорк, 19 лет84.
Google Scholar
М. Войтковски. Измерить теоретическую энтропию системы твердых сфер. Эргодическая теория динамических систем, 8 , вып. 1, 133–153, 1988.
MathSciNet МАТЕМАТИКА Google Scholar
Л.-С. Юнг, Статистические свойства динамических систем с некоторой гиперболичностью. Анналы математики, чтобы появиться.
Google Scholar
А. Земляков, А. Каток. Топологическая транзитивность биллиардов в многоугольниках. Мат. Примечания 18 , 760–764, 1975.
CrossRef Google Scholar
Брассай | Проститутка, играющая в русский бильярд, бульвар Рошшуар, Париж (1932-33/1950-е годы)
Средний
Состояние
Подпись
Сертификат подлинности
Диапазоны цен на репродукции Пабло Пикассо
Просмотрите работы в этой категории
Возможно, самый влиятельный художник 20-го века, Пабло Пикассо, возможно, наиболее известен первооткрывателем кубизма и разрушением двухмерной плоскости изображения для передачи трехмерного пространства.
Вдохновленный африканским и иберийским искусством, он также способствовал возникновению сюрреализма и экспрессионизма. Значительное творчество Пикассо выросло до более чем 20 000 картин, гравюр, рисунков, скульптур, керамики, театральных декораций и эскизов костюмов. Он написал свою самую известную работу «Герника» (1937) в ответ на гражданскую войну в Испании; тотемическое полотно гризайль остается определяющим произведением антивоенного искусства. На аукционе несколько картин Пикассо были проданы более чем за 100 миллионов долларов. Неутомимый художник был героем выставок в самых престижных учреждениях мира, от Музея современного искусства и Центра Помпиду до Stedelijk Museum и Tate Modern.
Серебряный принт в разобранном виде
11 1/4 × 8 1/8 дюйма | 28,6 × 20,6 см
Продано
Чалфонт
Хотите продать работу этого художника? Продать с искусством
Средний
Состояние
Подпись
Сертификат подлинности
Ценовой диапазон малых гравюр Пабло Пикассо
Просмотрите работы в этой категории
Пабло Пикассо, возможно, самый влиятельный художник 20-го века.
наиболее известен новаторским кубизмом и разрушением двумерной плоскости изображения для передачи трехмерного пространства. Вдохновленный африканским и иберийским искусством, он также способствовал возникновению сюрреализма и экспрессионизма. Значительное творчество Пикассо выросло до более чем 20 000 картин, гравюр, рисунков, скульптур, керамики, театральных декораций и эскизов костюмов. Он написал свою самую известную работу «Герника» (1937) в ответ на гражданскую войну в Испании; тотемическое полотно гризайль остается определяющим произведением антивоенного искусства. На аукционе несколько картин Пикассо были проданы более чем за 100 миллионов долларов. Неутомимый художник был героем выставок в самых престижных учреждениях мира, от Музея современного искусства и Центра Помпиду до Stedelijk Museum и Tate Modern.
Серия «Художник»
Портреты художников и скульпторов
113 Доступно
Портреты художников и скульпторов
113 Доступны
Портреты художников и скульпторов
113
.
Скульпторы113 в наличии
Портреты художников и скульпторов
113 в наличии
Портреты художников и скульпторов
113 Доступно
Портреты художников и скульпторов
113 Доступны
Портреты артистов и скульпторов
113
. Пабло Пикассо
Просмотреть все
Имя художника
Название произведения
Партнер
Имя художника
Название произведения
Partner
Artist Name
Artwork Title
Partner
Artist Name
Artwork Title
Partner
Artist Name
Artwork Title
Partner
Artist Name
Artwork Title
Partner
Artist Name
Название произведения
Партнер
Имя художника
Название произведения
Партнер
Другие работы Пабло Пикассо
View All
Artist Name
Artwork Title
Partner
Artist Name
Artwork Title
Partner
Artist Name
Artwork Title
Partner
Artist Name
Artwork Title
Partner
Artist Имя
Название произведения
Партнер
Имя художника
Название произведения
Партнер
Имя художника
Название произведения
Партнер
Название художника
Название искусства
Партнер
Связанные работы
Название художника
.
Скульпторы