«Бильярд. Самоучитель» читать онлайн книгу 📙 автора Николая Сергеевича Здобникова на MyBook.ru
«Бильярд. Самоучитель» читать онлайн книгу 📙 автора Николая Сергеевича Здобникова на MyBook.ruЧто выбрать
Библиотека
Подписка
📖Книги
🎧Аудиокниги
👌Бесплатные книги
🔥Новинки
❤️Топ книг
🎙Топ аудиокниг
🎙Загрузи свой подкаст
📖Книги
🎧Аудиокниги
👌Бесплатные книги
🔥Новинки
❤️Топ книг
🎙Топ аудиокниг
🎙Загрузи свой подкаст
- Главная
- Спорт, фитнес
- ⭐️Николай Здобников
- 📚«Бильярд.
 Самоучитель»
Самоучитель»
Отсканируйте код для установки мобильного приложения MyBook
Недоступна
Стандарт
(3 оценки)
Николай Здобников
162 печатные страницы
2006 год
0+
Читать онлайн
Эта книга недоступна.
Узнать, почему
О книге
Эта книга отличается от других пособий по бильярду, прежде всего, универсальностью и разноплановостью содержания, легкостью подачи материала, подробным объяснением правил и техники игры, грамотным подбором необходимых для понимания текста иллюстраций.
Книга содержит информацию не только об истории бильярда и известных игроках, но и является незаменимым практическим пособием для новичков и людей, знакомых с техникой бильярдной игры лишь поверхностно. С помощью этого самоучителя вы ознакомитесь с правилами бильярда, советами профессиональных игроков и методами тренировки, освоите основные удары и сможете применить полученные знания на практике.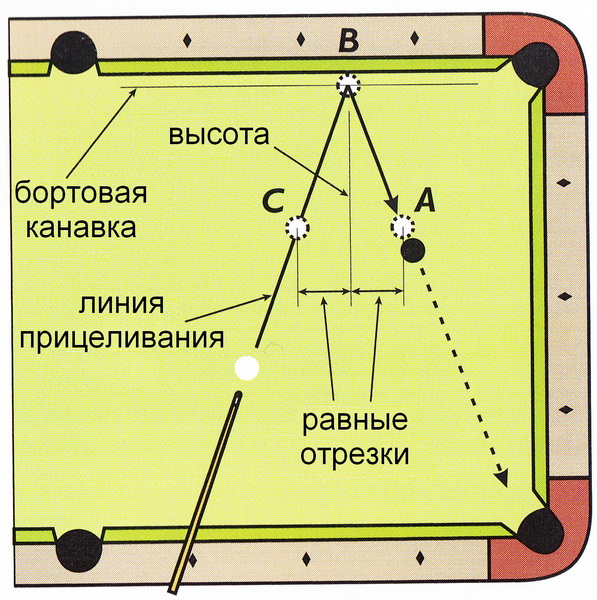 Вы научитесь правильному захвату кия, особенностям намеливания наклейки, секретам прицеливания и многому другому. Вы станете «своим» в любом бильярдном клубе и для вас не составит труда выиграть партию в «Американку», «Карамболь» или «Малую русскую пирамиду». Опытным игрокам прочтение книги позволит сделать игру более красивой и результативной. Ну а если вы никогда не были в бильярдной и не катали шары по зеленому сукну, то вам непременно захочется это сделать…
Вы научитесь правильному захвату кия, особенностям намеливания наклейки, секретам прицеливания и многому другому. Вы станете «своим» в любом бильярдном клубе и для вас не составит труда выиграть партию в «Американку», «Карамболь» или «Малую русскую пирамиду». Опытным игрокам прочтение книги позволит сделать игру более красивой и результативной. Ну а если вы никогда не были в бильярдной и не катали шары по зеленому сукну, то вам непременно захочется это сделать…
читайте онлайн полную версию книги «Бильярд. Самоучитель» автора Николай Здобников на сайте электронной библиотеки MyBook.ru. Скачивайте приложения для iOS или Android и читайте «Бильярд. Самоучитель» где угодно даже без интернета.
Подробная информация | |
|---|---|
| Дата написания: 1 января 2006 | Объем: 292677 |
| Год издания: 2006 | Дата поступления: 26 марта 2019 |
| ISBN (EAN): 985675156x | |
Спорт, фитнес
Развлечения
Правообладатель
1000 бестселлеров
215 книг
Поделиться
По жанру, теме или стилю автора
Книга ЗОЖника
Максим Кудеров
FreshLife28. Как начать новую жизнь в понедельник и не бросить во вторник
Как начать новую жизнь в понедельник и не бросить во вторник
Антон Петряков
FreshLife28. Как начать новую жизнь в понедельник и не бросить во вторник
Антон Петряков
Автобиография
Алекс Фергюсон
Бодифлекс: дыши и худей
Марина Корпан
Правило №1 – никогда не быть №2. Агент Павла Дацюка, Никиты Кучерова, Артемия Панарина, Никиты Зайцева и Никиты Сошникова о секретах побед
Дэн Мильштейн
МегаМасса. Комплекс тренировок, питания и дисциплины для достижения идеальной фигуры
Станислав Линдовер
Подслушано. Все, что вы хотели знать об окружающих, но боялись спросить
Сборник
МегаМасса. Комплекс тренировок, питания и дисциплины для достижения идеальной фигуры
Станислав Линдовер
Оксисайз: худей без задержки дыхания
Марина Корпан
О проекте
Что такое MyBook
Правовая информация
Правообладателям
Документация
Помощь
О подписке
Купить подписку
Бесплатные книги
Подарить подписку
Как оплатить
Ввести подарочный код
Библиотека для компаний
Настройки
Другие проекты
Издать свою книгу
MyBook: Истории
Николай Здобников — Бильярд.
 Самоучитель
Самоучитель12 3 4 5 6 7 …9
Николай Сергеевич Здобников
Бильярд. Самоучитель
История бильярда
Точное время возникновения бильярдной игры установить невозможно. Известно лишь, что она, так же как и шахматы, очень древнего происхождения. Родиной бильярда является Азия: по утверждению одних – это Индия, по мнению других – Китай. С уверенностью можно сказать одно: игры в мяч или шары были одними из первых, придуманных человеком.
Существует несколько версий названия игры. Англичанин Джон Вильк, к примеру, считал, что первоначально бильярдная игра называлась ball-yerds, от древнесаксонских слов ball (мяч) и yerd (палка). В других источниках упоминается о том, что слово «бильярд» происходит от франц. bille (шар).
Надо полагать, что первые «китайские» бильярды появились в Европе в XV—XVI веках. Однако игры по принципу современного бильярда были известны европейцам гораздо раньше. Например, в народной немецкой игре «Balkespiel», популярной в Германии еще в средние века, применялись длинные столы с грубыми бортами и углублениями, куда игрок при помощи дубинки старался загнать каменный шар противника.
Наиболее правдоподобными кажутся две версии возникновения бильярда в Европе. По одной – «пионерами» бильярда являются англичане, по другой – французы. Сторонники первой версии обычно приводят сохранившееся письмо Марии Стюарт к архиепископу Глазго, написанное в день ее казни, 17 февраля 1587 года. Лишенная трона шотландская королева (и неудачная претендентка на английский трон) упоминает о своем личном бильярде и просит приготовить для него место в другом помещении.
Французы с первенством англичан не соглашаются. Они вспоминают короля Франции Людовика XI (1461– 1483), который однажды приказал установить в своих апартаментах бильярдный стол. Другие авторы приписывают изобретение бильярда своему соотечественнику Генриху Делинье, жившему в период правления короля Карла IX (1560—1574), который сам, по мнению историков Франции, был страстным любителем этой игры.
Во Франции при короле Людовике XIV бильярд, так же как и в Англии, был очень моден в среде дворянства. Отдавал ему дань и сиятельный монарх. Интересно, что превосходной игрой в бильярд можно было получить доступ к королевскому двору. Постоянным партнером Людовика XIV был некий Шамильяр. Ему удалось сделать быструю карьеру: сначала он из писарей был произведен в советники при Парижском парламенте, потом сделался контролером государственных финансов, а в 1707 году стал военным министром.
В XVII веке бильярд приобретает широкую популярность в Германии и других европейских странах, совершенствуется и инвентарь.
Попытки улучшения бильярдного стола привели к изменению его формы. Вначале квадратный, потом шести-, восьмиугольный и даже круглый, он, в конце концов, получает твердо установившуюся современную четырехугольную форму, в которой утверждается строгая, независимо от величины бильярда, пропорциональность: длина стола всегда вдвое больше его ширины. Изменилась и величина бильярдных столов. Опыт показал, что большие размеры столов способствуют интересной игре.
Опыт показал, что большие размеры столов способствуют интересной игре.
Следует особо отметить, что в России, где бильярд развивался автономно, в конце концов, выработался свой, отечественный тип лузного бильярда. Еще в 30—40-х годах прошлого века бильярдный инвентарь отличался большим разнообразием и непропорциональностью деталей. Попадались шары намного меньшего по сравнению с шириной луз диаметра; борта были или очень низки, или слишком высоки; на многих столах лузы имели длинное устье, в результате чего не идеально точно пущенные шары не отталкивались от луз, а, наоборот, часто застревали в них. При состязании на таких столах шансы плохих и хороших игроков уравнивались, и борьба между ними теряла всяческий интерес.
Только в 1850 году хороший игрок и управляющий бильярдной фабрикой в Петербурге А. Фрейберг создал образец русского шестилузного бильярда, который удовлетворял необходимым требованиям. Вместе с формой стола, конструкцией луз совершенствовалась и форма выступа бортов в той их части, которая обтягивается резиной.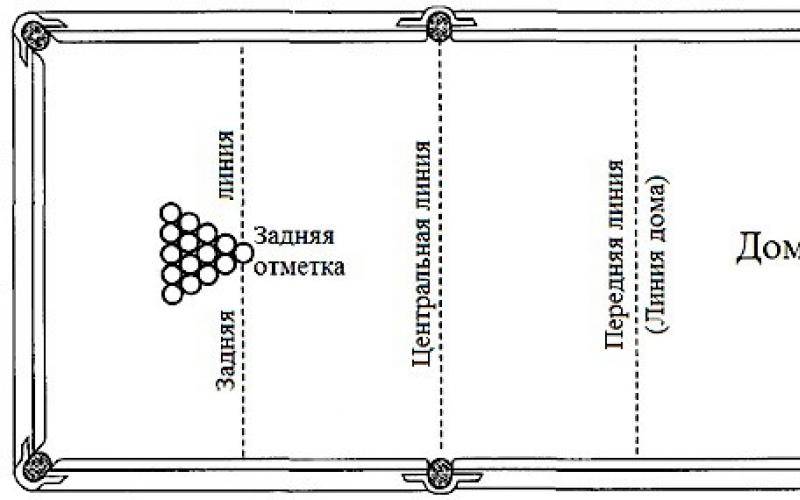 На первых лузных бильярдах этот выступ по всей высоте представлял собой как бы сплошную вертикальную стенку. Шар имел много точек соприкосновения с резиной, из-за чего отражался в непредсказуемом направлении, да и технически изготовить совершенный борт было трудно.
На первых лузных бильярдах этот выступ по всей высоте представлял собой как бы сплошную вертикальную стенку. Шар имел много точек соприкосновения с резиной, из-за чего отражался в непредсказуемом направлении, да и технически изготовить совершенный борт было трудно.
Позднее московские бильярдные мастера Щульц и Бригген предложили низкий борт и ограничили его наклонной плоскостью с заостренным закруглением резины – так было удобнее для игры. Но заостренность закругления и то, что точка соприкосновения шара с резиной находилась против его центра, и даже несколько ниже, таили «сюрпризы»: при сильном ударе шар часто подскакивал вверх и затем падал на поверхность стола, быстро теряя при этом данную ему силу движения. В дальнейшем усилиями многих бильярдных специалистов, и особенно А. Фрейберга, был выработан так называемый «нормальный» борт. Ему соответствуют умеренное закругление резины и высота, обеспечивающая прикосновение шара в точке, расположенной чуть выше его центра. Такая форма бортов сохраняется и до настоящего времени.
В 1875 году профессиональный игрок и фабрикант Гердерс изобрел передвижные борта: с помощью специальных винтов их можно было поднимать вверх и опускать вниз. Таким образом, высота бортов регулировалась в зависимости от размеров шаров. Однако практика игры выявила существенный недостаток: при любом изменении высоты бортов ширина луз оставалась постоянной, что при разных шарах создавало очевидные неудобства. Хотя это изобретение и было запатентовано в ряде западных государств, оно не получило широкого распространения.
Не дремали пытливые умы и в других странах. Например, в германском городе Мюнхене в 1901 году появился «бильярд с зеркалами». В журнале «Нива» № 43 за 1902 год была опубликована заметка об этом изобретении: «Сущность нового бильярда заключается в следующем: на нем ставятся под известным углом несколько зеркал (выставленный в Мюнхене бильярд имеет их шесть) и играющий, глядя на них, может сейчас же узнать, каким манером и на сколько ладов может быть пущен данный шар.
Фотографии, сопровождающие журнальный текст, говорят, как минимум, об одном серьезном недостатке – возможности повреждения зеркал шарами, случайно вылетевшими за борт. Не исключено, что именно это стало препятствием к распространению данного изобретения.
С середины XVIII века в связи с ростом популярности бильярда в ряде стран вводятся ограничительные законы, по которым часть прибыли от игровых залов отчислялась в казну государства. В какой-то степени эти налоги тормозили развитие бильярдного спорта.
Франция раньше других освоила особый тип безлузного бильярда. В 70—80-е годы XVIII века впервые вошла в обиход трехшаровая игра «Карамболь».Первые правила бильярдной игры издал в 1674 году в городе Лионе француз Этьен Луазон. Но его трактовка различных игровых моментов была сложной и недостаточно ясной. В этих первых правилах автор подчеркивал, что бильярдная игра не только «приятна для ума», но и полезна для здоровья.
Но его трактовка различных игровых моментов была сложной и недостаточно ясной. В этих первых правилах автор подчеркивал, что бильярдная игра не только «приятна для ума», но и полезна для здоровья.
Вплоть до конца 20-х годов XIX столетия действия главным инструментом бильярда – кием – не отличались замысловатостью. Их диапазон ограничивался простым ударом в центр шара, посредством которого невозможно было дать шару-битку произвольное направление. Причиной тому служило залитое гипсом углубление в тонком конце кия. При попытке ударить такой нашлепкой в любую точку шара, кроме центра, происходил сбой или, как его называют профессионалы, «кикс». Помимо того, каждый игрок имел в своем распоряжении несколько киев, которые регулярно макал в жидкий гипс. Столы пачкались и выглядели неопрятно. Гипсовые кии часто рвали сукно.
Изобретателем гипсового кия (все же неплохого для своего времени) считается французский офицер, майор Дуга. За бильярдным столом ему не было равных. Но невозможность хорошо владеть «своим» шаром из-за несовершенства кия побудила игроков искать способы улучшения этого орудия игры.
В 1827 году французский виртуоз бильярда – Минго – изобрел круглую кожаную наклейку для кия. Это простое, на первый взгляд, новшество произвело своего рода революцию. При игре гипсовым кием требовался лишь механический навык – после удара в центр шар катился строго по прямой. Теперь, с помощью кожаной наклейки, ее изобретатель стал демонстрировать несравненно более сложные удары: шар вращался и двигался по искривленной траектории, неожиданно останавливался сам собой и откатывался назад, перескакивал через другие шары и т. д.
12 3 4 5 6 7 …9
На Facebook
В Твиттере
В Instagram
В Одноклассниках
Мы Вконтакте
Подписывайтесь на наши страницы в социальных сетях.
Будьте в курсе последних книжных новинок, комментируйте, обсуждайте. Мы ждём Вас!
Уважаемый посетитель, Вы зашли на сайт как незарегистрированный пользователь.
Мы рекомендуем Вам зарегистрироваться либо войти на сайт под своим именем.
Интернет-ресурсы VEEB — Учебные ресурсы доктора Дэйва по бильярду
Интернет-ресурсы VEEB
- Веб-сайт онлайн-ресурсов доктора Дэйва по бильярду и веб-сайт учебных материалов
- ответы на часто задаваемые вопросы (FAQ) по различным темам пула и бильярда
- глоссарий терминов и фраз о пуле и бильярде
- онлайн-руководство по пулу, охватывающее основы
- The Illustrated Principles of Pool and Billiards (отличная книга, охватывающая все основные принципы и приемы игры в пул и бильярд).

- How To Aim Pool Shots (HAPS) (3-томная серия, посвященная тому, как прицеливаться при каждом типе удара и как эффективно использовать боковое вращение).
- Бильярдный университет (BU) Экзамены на игровые способности и серия обучающих видео для оценки навыков и недостатков игры в бильярд, а также для отслеживания прогресса с течением времени ” охватывающий каждый тип удара, принцип и технику, важные в игре)
- Видеоэнциклопедия тренировок в бассейне (VEPP) (серия из 5 томов, представляющая организованную и методическую программу тренировок и тренировки в бассейне… наиболее полную коллекцию упражнений из когда-либо опубликованных) Shots (VEPS)
- Как прицеливаться при стрельбе из пула (HAPS)
- Инструкции, информация о продукте и советы по покупке
- How To Aim Pool Shots (HAPS)
- прицеливание комбинированным выстрелом
- страница ресурса броска
- Десяти-времена-искоренная система
- 7
- 9 7-Kick и Bank Shots:
- 7
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 9
- 7 .

- Как прицеливаться при бросках в пул (HAPS)
- Видеоэнциклопедия бросков в пуле (VEPS)
- Видеоэнциклопедия тренировок в пуле (VEPP)
- бросок (CIT и SIT)
- эффекты разбрызгивания, поворота и броска
- Plus Система для прицеливания двухрельсовых ударов с короткого рельса
8
5
- Советы по технике броска в прыжке0008
- Консультации по технике прыжков
- Техника выстрела и совет по оборудованию
- 7
- 7 16 — Правила. страница ресурсов правил пула
- страница ресурсов двойного удара-фола
- Интуитивное кодирование задачи
- Высокая производительность без каких-либо действий
- Простое метапрограммирование для увеличения производительности
- Расширяемость с минимальными усилиями
- Расширяемость распространяется на все аспекты системы (множественная отправка)
- 9
Моделирование бильярда в Джулии — Nextjournal
Статьи Джулии / 19 октября 2018 г.

от GDGeorge Datseris и Simon Danisch
1
.
Автор
Джордж Дацерис, автор материалов JuliaDynamics и JuliaMusic
2
.
Этот урок
В этом уроке мы будем моделировать динамический бильярд. Это очень простая система, в которой точечная частица распространяется внутри домена с постоянной скоростью. При столкновении с границей частица испытывает зеркальное отражение.
Существует пакет Julia для моделирования таких систем,
DynamicalBilliards. В этом руководстве мы просто создаем упрощенную версию этого пакета, которая имеет меньше функций, меньшую производительность и меньший «управление безопасностью». Кроме этого, основная часть того, как работаетDynamicalBilliards, идентична настоящему руководству.
3
.
Особенности Юлии выделены
5 9.0178 4 9.0008
- 4 9.
- Частицы, которые распространяются внутри биллиарда
- Препятствия, из которых состоит биллиард
- Процессы, осуществляющие распространение
- Вычислить столкновения
pсо всеми препятствиями в бильярде - Найти первое по времени столкновение и препятствие, которому оно соответствует
- Промыть и повторить!
Система и алгоритм
Бильярд состоит из трех частей:
Важно, чтобы эти три вещи, «частицы», «препятствия» и «процессы» оставались независимыми . Это позволит расширять наш код!
Это позволит расширять наш код!
5
.
Алгоритм
Для имитации бильярда нужно следовать очень простому алгоритму. Предполагая, что частица p уже инициализирована в бильярде, шаги
Самой центральной частью этого алгоритма является функция, которая по заданной частице и препятствию возвращает столкновение (точку и время, если они существуют). Важно то, что эта функция нигде не «принадлежит». Это процесс, не зависящий от того, какое препятствие и частицу мы ему даем. Эта независимость позволяет значительно расширять код (см. ниже).
ниже).
Эта независимость возможна только при многократной отправке. Без него, так или иначе, этот метод был бы «принадлежит» либо к «классу» Препятствий , либо к «классу» Частиц . Однако это помешало бы расширяемости! Отсутствие необходимости «присваивать» процесс определенному «классу» — огромное преимущество Джулии.
6
.
Базовая структура s нам понадобится
Все векторы, которые мы будем использовать, двумерны. Таким образом, мы можем воспользоваться Статические массивы . Для упрощения я определю SV как 2D-вектор Float (все векторы, которые мы будем использовать, будут этого типа)
с использованием StaticArrays.const SV = SVector{2,Float64}
Теперь мы определяем частицу struct . Для расширяемости лучше всего определить его на основе абстрактного типа.
абстрактный тип AbstractParticle конец
изменяемая структура Particle <: AbstractParticle
поз::СВ
вел::СВ
конец
Частица(x0, y0, φ0) = Particle(SV(x0, y0), SV(cos(φ0), sin(φ0))) Затем мы определяем препятствие struct s. Опять же, чтобы обеспечить расширяемость, абстракцию и обобщение, лучше всего определить все препятствия как подтип абстрактного типа.
абстрактный тип Конец препятствия
структура Стена <: Препятствие
сп::СВ
эп::СВ
нормальный :: СВ
конец
структура диска <: препятствие
c::СВ
р::Float64
end "Бильярд" в дальнейшем будет просто Tuple из Obstacle подтипов. В частности, тип бильярда
В частности, тип бильярда NTuple{N, Препятствие} где {N} , поэтому удобно определить:
const Billiard = NTuple{N, Препятствие} где N 7
.
Столкновения
Как было сказано во введении, наиболее важной частью является функция, которая находит столкновения между частицами и препятствиями. Вот как это выглядит для столкновения стандартной частицы со стеной:
с помощью LinearAlgebra: точка, нормализация
"""
столкновение(p::AbstractParticle, o::Obstacle) → t, cp
Найдите столкновение (если есть) между данной частицей и препятствием.
Возвращает время до столкновения и предполагаемую точку столкновения `cp`.
"""
Коллизия встроенной функции @(p::Particle, w::Wall)
n = normalvec(w, p.pos)
denom = точка (p.vel, n)
если номинал ≥ 0,0
возврат без столкновений()
еще
t = точка (w. sp - p.pos, n)/denom
вернуть t, p.pos + t * p.vel
конец
конец
normalvec(w::Стена, позиция) = w.normal
sp - p.pos, n)/denom
вернуть t, p.pos + t * p.vel
конец
конец
normalvec(w::Стена, позиция) = w.normal а вот та же функция, но вместо коллизий с дисками:
@inline function Collision(p::Particle, d::Disk)
dotp = точка (p.vel, normalvec (d, p.pos))
dotp ≥ 0.0 && вернуть отсутствие столкновений()
dc = p.pos - d.c
B = dot(p.vel, dc) # указывает на центр круга: B < 0
C = dot(dc, dc) - d.r*d.r #нахождение вне круга: C > 0
Δ = В*В - С
Δ ≤ 0,0 && вернуть без столкновений()
sqrtD = sqrt(Δ)
# Ближайшая точка:
t = -B - sqrtD
вернуть t, p.pos + t * p.vel
конец
normalvec(d::Disk, pos) = normalize(pos - d.c) Вы можете видеть, что есть случаи, когда коллизии невозможны или они происходят в обратном направлении во времени. По соглашению, это значение, которое мы тогда возвращаем:
@inline nocollision() = (Inf, SV(0.0, 0.0))
next_collision — полезная функция, которая находит «истинное» следующее столкновение. Он просто обходит препятствия в бильярде. Он просто проверяет, какое препятствие имеет наименьшее время столкновения:
function next_collision(p::AbstractParticle, bd)
j, ct, cp = 0, Inf, SV(0,0, 0,0)
для i в каждом индексе (bd)
t, c = столкновение (p, bd [i])
если t < ct
дж = я
кт = т
ср = с
конец
конец
вернуть j, ct, ср
конец 8
.
Эволюция частицы в бильярде
Нам нужна простая функция для распространения частицы до найденной точки столкновения. Мы также дадим количество времени, которое «должно» занять распространение, для расширяемости. Для стандартных частиц, у которых вектор скорости постоянен при движении, это не имеет значения.
распространение!(p::Particle, pos, t) = (p.pos = pos)
Это встроенная функция (примечание ! в конце)
Мы также должны определить функцию, которая выполняет зеркальное отражение, т.е. изменяет скорость частицы (после столкновения)
function resolvecollision!(p::AbstractParticle, o::Obstacle)
n = normalvec(o, p.pos)
p.vel = p.vel - 2*точка(n, p.vel)*n
end Теперь мы готовы подвести итоги. Давайте определим функцию, которая берет частицу и эволюционирует в бильярде (кортеже препятствий) и возвращает временные ряды положений частицы.
Для удобства стоит определить следующую функцию:
"""
подпрыгнуть! (р, бд)
Эволюционируйте частицу за одно столкновение (на месте).
"""
@inline function bounce!(p::AbstractParticle, bd)
i::Int, tmin::Float64, cp::SV = next_collision(p, bd)
если tмин != Inf
распространять!(p, cp, tmin)
разрешить столкновение!(p, bd[i])
конец
возврат i, tmin, p. pos, p.vel
end
pos, p.vel
end Затем мы можем использовать его внутри более крупной функции, которая вызывает bounce! до указанного времени:
"""
временной ряд!(p::AbstractParticle, bd, n) -> xt, yt, t
Эволюционируйте частицу в бильярде `bd` для `n` столкновений
и вернуть временной ряд позиций `xt, yt` вместе с вектором времени `t`.
"""
временной ряд функций!(p::AbstractParticle, bd, n::Int)
т = [0,0]; xt = [p.pos[1]]; yt = [p.pos[2]]; с = 0
в то время как c < n
предыдущая = п.поз.; prevvel = p.vel
i, ct = отскок!(p, bd)
xs, ys = экстраполировать (p, prevpos, prevvel, ct)
толчок! (т, кт)
добавить! (xt, xs)
добавить!(yt, ys)
с += 1
конец
вернуть xt, yt, t
конец экстраполировать просто создает временные ряды позиций между двумя столкновениями. Для стандартной частицы «экстраполяция» не требуется, просто используется конечная позиция:
экстраполировать (p::Particle, prevpos, prevvel, ct) = p.pos
Почему существует эта функция экстраполировать ? Смотрите ниже, когда мы расширяем наш код для магнитных частиц!
9
.
Запустив код
давайте проверим это прямо сейчас! Мы создадим знаменитый Синайский бильярд
х, у, г = 1,0, 1,0, 0,3 зр = [0,0,у]; эп = [0,0, 0,0]; п = [х, 0,0] leftw = Стена (sp, ep, n) зр = [х, 0,0]; эп = [х, у]; п = [-х, 0,0] rightw = Стена (sp, ep, n) зр = [х, у]; эп = [0,0, у]; п = [0,0,-у] topw = Стена (sp, ep, n) сп = [0,0,0,0]; эп = [х, 0,0]; п = [0,0, у] botw = Стена (sp, ep, n) диск = Диск([x/2, y/2], r) bd = (botw, rightw, topw, leftw, disk) bd isa Billiard
, а также инициализировать частицу
p = Particle(0.1, 0.1, 2π*rand())
и развить ее
xt, yt, t = временные ряды!(p, bd, 10)
10
.
Построение графика
Давайте определим несколько простых методов построения графика и построим результат!
с использованием PyPlot
импортировать PyPlot: сюжет
const EDGECOLOR = (0,0.6,0)
график функции (d :: Disk)
цвет лица = (КРАЙЦВЕТ..., 0,5)
круг1 = PyPlot.plt[:Круг](d.c, d.r;
edgecolor = EDGECOLOR, facecolor = facecolor, lw = 2.0)
PyPlot.gca()[:add_artist](круг1)
конец
график функции (w :: Стена)
PyPlot.plot([w.sp[1],w.ep[1]],[w.sp[2],w.ep[2]];
цвет = ЦВЕТ КРАЯ, lw = 2,0)
конец
График функции (bd:: Billiard)
для o ∈ bd; участок (о); конец
gca()[:set_aspect]("равно")
конец
фигура(); участок (бд)
gcf() Отлично! Теперь посмотрим на орбиту
figure(); участок (бд) xt, yt, t = временные ряды!(p, bd, 10) сюжет (хт, ут) gcf()
Постройте 10 орбит!
цифра(); участок (бд)
p = частица (0,1, 0,5, 2π*rand())
для j в 1:10
xt, yt = временные ряды!(p, bd, 20)
график (xt, yt, альфа = 0,5)
конец
gcf() 11
.
Витрина 1: производительность и метапрограммирование
с использованием BenchmarkTools p = частица (0,1, 0,1, 2π*rand()) @btime bounce!($p, $bd)
Уже очень быстро разнести частицу за одно столкновение, однако есть некоторые выделения (хотя функция на месте).
Эти выделения происходят из-за нестабильности типа в next_collision , поскольку кортеж содержит элементы разных типов. Однако с помощью метапрограммирования легко решить эту нестабильность типа, потому что Кортеж имеет известный размер!
В следующем определении мы используем метапрограммирование, чтобы «развернуть» цикл
@сгенерированная функция next_collision(p::AbstractParticle, bd::Billiard)
L = length(bd.types) # обратите внимание, что здесь bd означает ТИП bd!
выход = :(ind = 0; tmin = Inf; cp = SV(0,0, 0,0))
для j=1:L
push!(out. args, цитата
пусть х = bd[$j]
tcol, pcol = столкновение (p, x)
# Установить минимальное время:
если tкол < tмин
tмин = tкол
индекс = $j
ср = пкол
конец
конец
конец
)
конец
push!(out.args, :(return ind, tmin, cp))
вернуться
конец
@btime bounce!($p, $bd)
args, цитата
пусть х = bd[$j]
tcol, pcol = столкновение (p, x)
# Установить минимальное время:
если tкол < tмин
tмин = tкол
индекс = $j
ср = пкол
конец
конец
конец
)
конец
push!(out.args, :(return ind, tmin, cp))
вернуться
конец
@btime bounce!($p, $bd) Этот номер безумный !!! Обратите внимание, что этот код не зависит от бильярда! Вы можете пройти любой набор препятствий, и это все равно будет так же эффективно!!! Время отказов! масштабируется линейно с количеством препятствий в бильярде.
12
.
Витрина 2: Расширяемость
Допустим, мы хотим добавить еще одно препятствие к этому «бильярдному набору», который мы делаем. Мы должны переписать все для него? Неа! В конце концов нам нужно расширить только два метода! Только два !
Чтобы показать это, давайте создадим эллипс как препятствие с полуосями a, b
struct Ellipse <: Obstacle
c::СВ
а::поплавок64
б::поплавок64
end Нам нужно расширить следующие методы:
normalvec столкновение
Да!!! Только два! Итак, приступим! normalvec довольно просто:
function normalvec(e::Ellipse, pos)
х₀, у₀ = поз.
ч, к = эк
return normalize(SV((x₀-h)/(e.a*e.a), (y₀-k)/(e.b*e.b)))
конец
используя LinearAlgebra: норма
функция столкновения (p::Particle, e::Ellipse)
dotp = точка (p. vel, normalvec (e, p.pos))
dotp ≥ 0.0 && вернуть отсутствие столкновений()
а = э.а; б = е.б
pc = p.pos - ec
μ = p.vel[2]/p.vel[1]
ψ = пк[2] - мк*пк[1]
номинал = а*а*μ*μ + b*b
Δ² = номинал - ψ*ψ
Δ² ≤ 0 && возврат без столкновений()
Δ = квадрат (Δ²); f1 = -a*a*µ*ψ; f2 = b*b*ψ # просто множители
I1 = SV(f1 + a*b*Δ, f2 + a*b*μ*Δ)/деномин
I2 = SV(f1 - a*b*Δ, f2 - a*b*µ*Δ)/деномин
d1 = норма (pc - I1); d2 = норма (pc - I2)
вернуть d1 < d2? (d1, I1 + д.к) : (d2, I2 + д.к)
конец
vel, normalvec (e, p.pos))
dotp ≥ 0.0 && вернуть отсутствие столкновений()
а = э.а; б = е.б
pc = p.pos - ec
μ = p.vel[2]/p.vel[1]
ψ = пк[2] - мк*пк[1]
номинал = а*а*μ*μ + b*b
Δ² = номинал - ψ*ψ
Δ² ≤ 0 && возврат без столкновений()
Δ = квадрат (Δ²); f1 = -a*a*µ*ψ; f2 = b*b*ψ # просто множители
I1 = SV(f1 + a*b*Δ, f2 + a*b*μ*Δ)/деномин
I2 = SV(f1 - a*b*Δ, f2 - a*b*µ*Δ)/деномин
d1 = норма (pc - I1); d2 = норма (pc - I2)
вернуть d1 < d2? (d1, I1 + д.к) : (d2, I2 + д.к)
конец Хорошо, теперь давайте создадим биллиард с эллипсом и диском, ради удовольствия
el = Ellipse([0.4, 0.2 ], 0.3, 0.1) ди = Диск ([0,6, 0,7], 0,25) bd2 = Billiard((bd[1:4]..., el, di))
и построить его
function plot(e::Ellipse)
цвет лица = (КРАЙЦВЕТ..., 0,5)
эллипс = PyPlot.matplotlib[:patches][:Ellipse](e.c, 2e.a, 2e.b;
edgecolor = EDGECOLOR, facecolor = facecolor, lw = 2. 0)
PyPlot.gca()[:add_artist](эллипс)
конец
фигура(); сюжет(bd2)
gcf()
0)
PyPlot.gca()[:add_artist](эллипс)
конец
фигура(); сюжет(bd2)
gcf() Теперь мы готовы создать частицу в этом совершенно новом бильярде:
p = Particle(0.1, 0.1, 2π*rand()) xt, yt, t = временной ряд!(p, bd2, 20) фигура(); сюжет(bd2) сюжет (хт, ут) gcf()
нарисуйте еще кучу!
цифра(); сюжет(bd2)
для j в 1:10
p = частица (0,1, 0,1, 2π*rand())
xt, yt = временной ряд!(p, bd2, 20)
график (xt, yt, альфа = 0,5)
конец
gcf() 13
.
Витрина 3: Снова расширяемость.
Итак, оказалось почти тривиально добавить дополнительное препятствие в наш код. А как насчет лишней частицы?
Я не говорю о еще одном экземпляре Частицы . Я говорю о новой частице типа , которая движется по-другому.
В этой части мы создадим этот новый тип, MagneticParticle , который движется по кругу, а не по прямой линии! Но сколько функций нам нужно определить? Если вы уже определили тип MagneticParticle , тогда столько:
столкновения # для каждого препятствия, которое мы хотим поддерживать распространять! экстраполировать
и да, вот и все. Может быть трудно поверить, что это занимает так мало, но это правда!!!
13.1
.
Тип
изменчивая структура MagneticParticle <: AbstractParticle
поз::СВ
вел::СВ
ω :: Float64
конец
MagneticParticle(x0, y0, φ0, ω) = MagneticParticle(SV(x0, y0), SV(cos(φ0), sin(φ0)), ω) Эта частица движется по окружности с угловой скоростью ω .
13,2
.
Продление столкновения
Чтобы расширить столкновение , нам просто нужно найти пересечения круг-линия и круг-круг для столкновений с Стена и Диск . Я не буду вдаваться в подробности того, как это сделать, а вместо этого скопирую и вставлю функции из DynamicalBilliards . Версии DynamicalBilliards также имеют множество комментариев, поясняющих, что происходит.
Вот столкновение со стеной: 92 -4*а*в Δ ≤ 0,0 && вернуть без столкновений()
u1 = (-b - sqrt(Δ))/2a
u2 = (-b + sqrt(∆))/2a
cond1 = 0,0 ≤ u1 ≤ 1,0
услов2 = 0,0 ≤ и2 ≤ 1,0
θ, I = без столкновений ()
если условие1 || условие2
dw = w.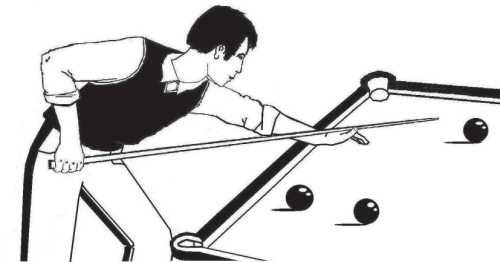 ep - w.sp
для (u, cond) в ((u1, cond1), (u2, cond2))
Y = w.sp + u*dw
если условие
φ = реальный угол (p, w, Y)
φ < θ && (θ = φ; I = Y)
конец
конец
конец
возврат θ*pr, I
конец
ep - w.sp
для (u, cond) в ((u1, cond1), (u2, cond2))
Y = w.sp + u*dw
если условие
φ = реальный угол (p, w, Y)
φ < θ && (θ = φ; I = Y)
конец
конец
конец
возврат θ*pr, I
конец
и вот столкновение с диском: 92) I1 = СВ( pc[1] + a*(p1[1] - pc[1])/d + h*(p1[2] - pc[2])/d, pc[2] + a*(p1[2] - pc[2])/d - h*(p1[1] - pc[1])/d ) I2 = СВ( pc[1] + a*(p1[1] - pc[1])/d - h*(p1[2] - pc[2])/d, pc[2] + a*(p1[2] - pc[2])/d + h*(p1[1] - pc[1])/d ) θ1 = реальный угол (p, o, I1) θ2 = реальный угол (p, o, I2) вернуть θ1 < θ2 ? (θ1*rc, I1) : (θ2*rc, I2) end
Функции cyclotron и realangle являются вспомогательными функциями. Первый находит центр и радиус циклотрона, описываемого частицей.
циклотрон(p) = (p.2)) d2r > 2 && (d2r = 2,0) θпростое = acos (1,0 - d2r) ПИ = я - Р0 сторона = (PI[1]*PC[2] - PI[2]*PC[1])*ω сторона < 0 && (θпростое = 2π-θпростое) возврат конец
Сложность функций столкновения и реального угла существует исключительно из-за геометрии пересечений между окружностями. На что мы хотим обратить внимание, так это на то, как мало
13,3
.
Распространение и экстраполяция
распространение! для MagneticParticle должен развить его по дуге окружности, так что, как видите, мы должны изменить вектор скорости!
функция распространения!(p::MagneticParticle, pos, t) φ0 = atan(p.

 Самоучитель»
Самоучитель»



 const SV = SVector{2,Float64}
const SV = SVector{2,Float64}  sp - p.pos, n)/denom
вернуть t, p.pos + t * p.vel
конец
конец
normalvec(w::Стена, позиция) = w.normal
sp - p.pos, n)/denom
вернуть t, p.pos + t * p.vel
конец
конец
normalvec(w::Стена, позиция) = w.normal  0, 0.0))
0, 0.0))  pos, p.vel
end
pos, p.vel
end  pos
pos  args, цитата
пусть х = bd[$j]
tcol, pcol = столкновение (p, x)
# Установить минимальное время:
если tкол < tмин
tмин = tкол
индекс = $j
ср = пкол
конец
конец
конец
)
конец
push!(out.args, :(return ind, tmin, cp))
вернуться
конец
@btime bounce!($p, $bd)
args, цитата
пусть х = bd[$j]
tcol, pcol = столкновение (p, x)
# Установить минимальное время:
если tкол < tмин
tмин = tкол
индекс = $j
ср = пкол
конец
конец
конец
)
конец
push!(out.args, :(return ind, tmin, cp))
вернуться
конец
@btime bounce!($p, $bd)  vel, normalvec (e, p.pos))
dotp ≥ 0.0 && вернуть отсутствие столкновений()
а = э.а; б = е.б
pc = p.pos - ec
μ = p.vel[2]/p.vel[1]
ψ = пк[2] - мк*пк[1]
номинал = а*а*μ*μ + b*b
Δ² = номинал - ψ*ψ
Δ² ≤ 0 && возврат без столкновений()
Δ = квадрат (Δ²); f1 = -a*a*µ*ψ; f2 = b*b*ψ # просто множители
I1 = SV(f1 + a*b*Δ, f2 + a*b*μ*Δ)/деномин
I2 = SV(f1 - a*b*Δ, f2 - a*b*µ*Δ)/деномин
d1 = норма (pc - I1); d2 = норма (pc - I2)
вернуть d1 < d2? (d1, I1 + д.к) : (d2, I2 + д.к)
конец
vel, normalvec (e, p.pos))
dotp ≥ 0.0 && вернуть отсутствие столкновений()
а = э.а; б = е.б
pc = p.pos - ec
μ = p.vel[2]/p.vel[1]
ψ = пк[2] - мк*пк[1]
номинал = а*а*μ*μ + b*b
Δ² = номинал - ψ*ψ
Δ² ≤ 0 && возврат без столкновений()
Δ = квадрат (Δ²); f1 = -a*a*µ*ψ; f2 = b*b*ψ # просто множители
I1 = SV(f1 + a*b*Δ, f2 + a*b*μ*Δ)/деномин
I2 = SV(f1 - a*b*Δ, f2 - a*b*µ*Δ)/деномин
d1 = норма (pc - I1); d2 = норма (pc - I2)
вернуть d1 < d2? (d1, I1 + д.к) : (d2, I2 + д.к)
конец  0)
PyPlot.gca()[:add_artist](эллипс)
конец
фигура(); сюжет(bd2)
gcf()
0)
PyPlot.gca()[:add_artist](эллипс)
конец
фигура(); сюжет(bd2)
gcf()  2))
d2r > 2 && (d2r = 2,0)
θпростое = acos (1,0 - d2r)
ПИ = я - Р0
сторона = (PI[1]*PC[2] - PI[2]*PC[1])*ω
сторона < 0 && (θпростое = 2π-θпростое)
возврат
конец
2))
d2r > 2 && (d2r = 2,0)
θпростое = acos (1,0 - d2r)
ПИ = я - Р0
сторона = (PI[1]*PC[2] - PI[2]*PC[1])*ω
сторона < 0 && (θпростое = 2π-θпростое)
возврат
конец .jpg)