Сколько доминошек: Сколько костяшек в игре Домино? Правила классического развлечения. Рыба (в домино) Комбинации беспроигрышных ходов домино

«Квантик» — журнал для любознательных

Задача 36.

Учительница попросила Васю выписать все целые числа от 1 до 100 в любом порядке. Вася решил выписать их подряд, но поскольку он всегда путает цифры 6 и 9, получилось вот что: 1, 2, 3, 4, 5, 9, 7, 8, 6, 10, 11, 12, 13, 14, 15, 19, 17, …, 67, 68, 66, 100. Выполнил ли Вася задание учительницы?

Задача 37.

Обведём в красный кружок каждое число от 1 до миллиарда, у которого все цифры нечётные, а у следующего за ним числа все цифры чётные. Обведём в синий кружок каждое число от 1 до миллиарда, у которого все цифры чётные, а у следующего за ним числа все цифры нечётные. Каких чисел больше — красных или синих, и во сколько раз?

Задача 38.

В комнате собралось несколько человек, каждый из которых либо рыцарь, либо лжец (рыцари всегда говорят правду, а лжецы всегда лгут). Затем каждый сказал остальным одно и то же: «Среди вас всего 5 рыцарей и 7 лжецов». И вдруг один из присутствующих сказал: «Мы все солгали». Сколько же всего было человек в комнате, и сколько из них лжецов, а сколько рыцарей?

Задача 39.

Изображённую на рисунке фигуру разрежьте на четыре одинаковые части.

Задача 40.

а) Дана клетчатая полоска 1×9, клетки которой раскрашены в шахматном порядке. За одну операцию надо выбрать в ней любую одну или несколько подряд идущих клеток и перекрасить их в противоположный цвет. Сделайте полоску одноцветной за 4 операции.
б) А можно ли сделать её одноцветной за 3 операции?
в) Теперь дана доска 9×9, клетки которой раскрашены в шахматном порядке. За одну операцию надо выбрать на доске любой клетчатый прямоугольник и во всех его клетках изменить цвет на противоположный. Сделайте доску одноцветной, потратив всего 8 операций.
г) А можно ли сделать её одноцветной за 7 операций?

Задача 31.

Двадцать пять ребят пошли в лес и стали ловить кузнечиков. Несколько ребят поймали по одному кузнечику, половина оставшихся ребят поймали по два кузнечика, а остальные не смогли поймать ни одного. Сколько всего кузнечиков поймали ребята?

Задача 32.

а) На рисунке изображена салфетка из 13 клеток. Какое наибольшее количество неперекрывающихся доминошек 1×2 можно уместить на этой салфетке?
б) А какое наименьшее количество доминошек потребуется, чтобы покрыть салфетку целиком, если доминошки могут перекрываться?

Задача 33.

На доске написаны в ряд четыре четвёрки: 4 4 4 4. Между каждыми двумя соседними четвёрками надо поставить один из знаков «+», «–», «x» или «:», затем расставить скобки (если потребуется) и вычислить значение. Получите таким способом каждую из цифр от 0 до 9.

Задача 34.

Разрежьте какой-нибудь куб на одинаковые кубики и переложите их так, чтобы получилось 49 кубов, не обязательно одного размера.

Задача 35.

Дорожки парка расположены так, как показано на рисунке: угол ACB прямой, дорожка BD делит угол ABC пополам. Точка B – вход в парк, а точка D – ларёк с мороженым. Буратино и Мальвина решили купить мороженое, но пошёл сильный дождь, и дорожку BD размыло (по ней нельзя пройти), а на дорожке BC образовалась огромная лужа. Поэтому Мальвина пошла по сухой дороге через точку A, а Буратино, любящий лужи, побежал по дороге через точку C. На сколько метров путь Буратино короче пути Мальвины, если AD = 1000 м, а DC = 800 м?

Задача 26.

За круглым столом сидят десять человек: рыцари и лжецы (и те, и другие присутствуют). Рыцари всегда говорят правду, а лжецы всегда лгут. Каждого спросили, кто сидит справа от него – рыцарь или лжец. Могло ли число ответов «справа от меня сидит лжец» равняться а) двум; б) одному?

Задача 27.

Ноутик нарисовал на плоскости несколько отрезков, которые не пересекаются друг с другом. Всегда ли Квантик сможет соединить некоторые из их концов другими отрезками так, чтобы получилась одна несамопересекающаяся ломаная?

Задача 28.

Найдите какие-нибудь два различных натуральных числа, больших пяти, которые и в сумме, и в произведении дают число-палиндром. (Напомним, что число называется палиндромом, если цифры в нём идут слева направо в том же порядке, что и справа налево, например: 717, 55, 3223.)

Задача 29.

Если одну из сторон квадрата уменьшить на 4 см, а вторую увеличить на 5 см, площадь получившегося прямоугольника станет меньше площади квадрата. Уменьшится или увеличится площадь, если одну из сторон этого квадрата уменьшить на 1 см, а вторую увеличить на 2 см?

Задача 30.

а) Двенадцать ребят решили сыграть в волейбол. На каждую игру тренер разбивает их на две команды по 6 человек. Он хочет провести несколько игр, чтобы в итоге каждый сыграл с каждым в одной команде. Какое наименьшее число игр потребуется?
б) Тут прибежало ещё 10 человек, и ребята решили сыграть в футбол. Теперь тренер разбивает их на две команды по 11 человек и снова хочет провести несколько игр, чтобы в итоге каждый сыграл с каждым в одной футбольной команде. Какое наименьшее число игр потребуется?

Задача 21.

На одной чашке весов лежат 6 апельсинов, а на другой – 2 дыни. Если добавить одну такую же дыню к апельсинам, то весы уравновесятся. Сколько апельсинов уравновесят дыню?

Задача 22.

Квантик заменил некоторые знаки умножения на знаки сложения и расставил скобки так, что равенство 1·2·3·4·5·6·7·8·9 = 2016 стало верным. А сможете ли вы это сделать?

Задача 23.

Петя и Вася вписали в круги одного и того же радиуса 5 см по прямоугольнику. Затем каждый из них соединил середины сторон своего прямоугольника и получил ромб (как на рисунке). Докажите, что стороны этих ромбов одинаковы, и найдите их длины.

Задача 24.

В 8 «А» классе усиленно изучают физику, математику и химию. Известно, что не всем любителям математики нравится и физика, а также что всем любителям химии, которым не нравится физика, не нравится и математика. Правда ли, что не всем любителям математики нравится химия?

Задача 25.

Отметьте на листе бумаги 9 точек и проведите 10 прямых так, чтобы на каждой прямой оказалось ровно по три отмеченных точки.

Задача 16.

В коробке лежали спички. Их количество удвоили, а затем убрали 8 спичек. Остаток спичек снова удвоили, а затем снова отняли 8 спичек. Когда эту операцию проделали в третий раз, то в коробке не осталось ни одной спички. Сколько их было сначала?

Задача 17.

Прямоугольник разделён двумя отрезками, параллельными его сторонам, на 4 прямоугольника. Площади трёх из этих кусочков равны 4, 8 и 12 см². Найдите площадь четвёртого кусочка (укажите все варианты).

Задача 18.

На столе лежит кучка одинаковых с виду монет, одна из которых фальшивая (то ли легче, то ли тяжелее обычной). Барон Мюнхгаузен положил часть монет в карман, оставив на столе не менее двух монет, и заявил, что фальшивая монета осталась на столе. Как проверить слова барона с помощью чашечных весов без гирь, потратив как можно меньше взвешиваний? (Доступны только монеты на столе, на весы можно класть любое число монет. Решение может зависеть от количества оставшихся монет.)

Задача 19.

Один мудрец заметил: «Наконец настал такой год, что количество зёрен, равное номеру года, можно разложить по клеткам шахматной доски так, чтобы ни на каких двух клетках не было поровну зёрен». В каком году произошла эта история?

Задача 20.

Квантик рисует в тетради четырёхклеточные буквы «Г» так, чтобы они не накладывались друг на друга. Из двух таких букв «Г» Квантик составил фигуру, имеющую ось симметрии, и даже несколькими способами (см. рисунок 1). Помогите Квантику составить фигуру, имеющую ось симметрии, из любого количества таких букв «Г», большего 2.

Задача 11.

Когда Петя, Коля, Вася и Дима играли в мяч, один из ребят разбил окно. На вопрос «Кто разбил окно?» все, кроме Димы, ответили «Не я», а Дима ответил «Не знаю». Оказалось, что двое мальчиков сказали правду, а двое соврали. Сказал ли Дима правду?

Задача 12.

Вася получил за год несколько оценок по математике, всего их было меньше 100. Ровно треть из них – тройки, ровно четверть – четвёрки, ровно пятая часть – пятёрки. А сколько Вася получил двоек? Назовите точное количество.

Задача 13.

Белоснежка испекла на праздник торт, разграфлённый на клеточки и украшенный вишенками, как показано на рисунке. Отрезав себе угловую клеточку (правую нижнюю), она хочет разделить оставшуюся часть торта на 7 одинаковых по размеру и форме кусков так, чтобы каждому из семи гномов досталось по целой вишенке. Помогите Белоснежке это сделать.

Задача 14.

На доске в строчку написаны двадцать пятёрок. Поставив между некоторыми из них знак «+», Толя обнаружил, что сумма равна 1000. Сколько плюсов поставил Толя? Укажите все возможные варианты и докажите, что других нет.

Задача 15.

На одной известной картине изображены 4 бурых медведя. Петя и Вася, двое ценителей искусства, по очереди перекрашивают по одному медведю, начинает Петя. Если медведь был бурым, он становится белым, а если был белым – становится бурым. Делая ход, игрок может выбрать любого медведя (в том числе и ранее перекрашенного), но при условии, что после смены цвета картина не станет точно такой же, какой она была в какой-то предыдущий момент. Проигрывает тот, кто не может сделать ход. Кто из игроков может гарантировать себе победу, как бы ни играл его соперник?

Задача 6.

Шесть кузнечиков сидят в вершинах двух квадратов с общей стороной, как показано на рисунке. Три кузнечика прыгнули каждый на новое место, все прыжки были одинаковой длины. Могли ли после этого все шестеро кузнечиков вновь оказаться в вершинах двух квадратов с общей стороной другого размера?

Задача 7.

Рыцари двух кланов собрались в замке на переговоры и расселись в каком-то порядке за большим круглым столом. Оказалось, что рыцарей, справа от которых сидит рыцарь из другого клана, столько же, сколько и рыцарей, справа от которых сидит рыцарь из его же клана. Докажите, что общее число рыцарей делится на 4.

Задача 8.

Четырёхугольник, изо­бражённый на рисунке, можно разрезать одним прямолинейным разрезом на 3 треугольника.
а) Нарисуйте шестиугольник, который можно разрезать одним прямолинейным разрезом на 3 треугольника.
б) Нарисуйте семиугольник, который можно разрезать одним прямолинейным разрезом на 3 треугольника.
в) Сколько углов может быть у многоугольника, если известно, что его можно разрезать одним прямолинейным разрезом на 3 треугольника?

Задача 9.

Можно ли записать по кругу несколько чисел (не обязательно положительных) так, чтобы среди них не было одинаковых и чтобы каждое число равнялось сумме двух своих соседей?

Задача 10.

Одна большая капля ртути и ещё несколько одинаковых маленьких капель на горизонтальной поверхности подтекли друг к другу и слились в одну огромную каплю. Диаметр большой капли в 2 раза больше, чем диаметр каждой из маленьких капель, а диаметр возникшей огромной капли в 5 раз больше диаметра каждой из маленьких капель. Сколько было маленьких капель? Считайте, что все капли строго шарообразные.

Задача 1.

Город разделён рекой на две половины, в каждой половине живёт по миллиону человек. В первый год 2015 человек переселились из левой половины в правую; во второй год 2016 человек переселились из правой половины в левую; в третий год опять 2015 человек переселились слева направо; в четвёртый год – 2016 человек переселились справа налево, и так далее.
Докажите, что в какой-то год в каждой из половин снова окажется по миллиону жителей. Через сколько лет это случится?

Задача 2.

Барон Мюнxгаузен утверждает, что может нарисовать две пересекающиеся прямые и 15-угольник так, что каждая вершина 15-угольника будет лежать на одной из этих прямых. Не хвастает ли барон?
(Ответ обоснуйте: либо нарисуйте пример, либо докажите, что такого примера нет.)

Задача 3.

а) Квадратную таблицу размером 3×3 можно разными способами заполнить натуральными числами. Петя и Коля рассматривают суммы чисел по трём строкам, трём столбцам и двум большим диагоналям. Петя убеждён, что если семь из восьми указанных сумм равны между собой, то и восьмая сумма им равна. Коля считает, что не обязательно. Кто прав?
б) Ответьте на тот же вопрос, если квадрат заполнен не просто натуральными числами, а строго числами от 1 до 9 включительно.

Задача 4.

На столе лежит треугольник периметра 10. На стол положили окружность длины 1 так, чтобы она касалась извне одной из сторон треугольника, и прокатили по его контуру, сделав один оборот вокруг треугольника. Какой путь прошёл при этом центр окружности? (Окружность катится без проскальзывания, оставаясь вне треугольника.)

Задача 5.

На доске в ряд написаны 100 произвольных целых чисел, их сумма нечётная. Ноутик и Кватик по очереди забирают себе по числу, но брать можно только число с краю. Начинает Ноутик. Когда каждый наберёт по 50 чисел, игра заканчивается. Тот, у кого сумма чисел окажется больше, выигрывает. Может ли Ноутик действовать так, чтобы всегда выигрывать у Квантика, как бы тот ни сопротивлялся и какие бы числа ни были написаны на доске?

Файлы

Входные данные для всех задач записаны в файле input.txt, результат работы нужно вывести в файл output.txt.

A: Числа могут быть где угодно

Во входном файле записано два целых числа, которые могут быть разделены пробелами и концами строк. Выведите в выходной файл их сумму.

Указание. Считайте весь файл в строковую переменную при помощи метода read() и разбейте ее на части при помощи метода split().

  2
 2

4

B: Обращение строки

Во входном файле записана одна текстовая строка, возможно, содержащая пробелы. Выведите эту строку в обратном порядке.

Строка во входном файле заканчивается символом конца строки

hello world

dlrow olleh

C: Построчное обращение

Выведите все строки данного файла в обратном порядке. Для этого считайте список всех строк при помощи метода readlines().

Последняя строка входного файла обязательно заканчивается символом '\n'.

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.

Complex is better than complicated.
Simple is better than complex.
Explicit is better than implicit.
 Beautiful is better than ugly.

D: Обращение всего файла

Выведите в обратном порядке содержимое всего файла полностью. Для этого считайте файл целиком при помощи метода read().

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex. 
Complex is better than complicated.

.detacilpmoc naht retteb si xelpmoC
.xelpmoc naht retteb si elpmiS
.ticilpmi naht retteb si ticilpxE
.ylgu naht retteb si lufituaeB

E: Длинные строки

В выходной файл выведите все строки наибольшей длины из входного файла, не меняя их порядок.

В данной задаче удобно считать список строк входного файла целиком при помощи метода

One
Twenty one
Two
Twenty two

Twenty one
Twenty two

F: Поиск символа

Определите, есть ли во входном файле символ '@'. Выведите слово YES или NO.

Входной файл может быть очень большим, поэтому считывать файл нужно посимвольно.

Valid email:
Bilbo. [email protected]

YES

Hello, world!

NO

G: Сумма чисел в строкaх

Дан файл, каждая строка которого может содержать одно или несколько целых чисел, разделенных одним или несколькими пробелами.

Вычислите сумму чисел в каждой строке и выведите эту сумму (для каждой строки выводится сумма чисел в этой строке).

В данной задаче удобно считывать данные построчно.

2 2
3    4
1       5

4
7
0
6

H: Сумма чисел в файле

В файле могут быть записаны десятичные цифры и все, что угодно. Числом назовем последовательность цифр, идущих подряд (т.е. число всегда неотрицательно).

Вычислите сумму всех чисел, записанных в файле. В данной задаче удобно считывать данные посимвольно.

 123
aaa456
1x2y3 4 5 6

600

I: Статистика по файлу

Дан файл. Определите сколько в нем букв (латинского алфавита), слов, строк. Выведите три найденных числа в формате, приведенном в примере.

Для экономии памяти читайте файл посимвольно, то есть не сохраняя целиком в памяти файл или отдельные его строки.

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.

Input file contains:
108 letters
20 words
4 lines

J: Шифр Цезаря — 2

Зашифруйте данный текстовый файл шифром Цезаря, при этом символы первой строки файла должны циклически сдвигаться на 1, второй строки — на 2, третьей строки — на три и т.

В этой задаче удобно считывать файл построчно, шифруя каждую строку в отдельности.

Hello
Hello
Hello
Hello

Ifmmp
Jgnnq
Khoor
Lipps

K: Анаграммы

Даны две строки. Определите, можно ли получить одну из другой перестановкой букв.

Программа получает на вход две строки, содержащие только ASCII-символы, не содержащие пробелы.

Программа должна вывести слово YES, если одна строка может быть получена из другой перестановкой букв или NO.

eleven_plus_two
twelve_plus_one

YES

Eleven_plus_two
Twelve_plus_one

NO

L: Числа

Саша и Катя учатся в начальной школе. Для изучения арифметики при этом используются карточки, на которых написаны цифры (на каждой карточке написана ровно одна цифра). Однажды они пришли на урок математики, и Саша, используя все свои карточки, показал число A, а Катя показала число B. Учитель тогда захотел дать им такую задачу, чтобы ответ на нее смогли показать и Саша, и Катя, каждый используя только свои карточки. При этом учитель хочет, чтобы искомое число было максимально возможным.

Во входном файле записано два целых неотрицательных числа A и B (каждое число в одной строке). Длина каждого из чисел не превосходит 100000 цифр.

Выведите одно число — максимальное целое число, которое можно составить используя как цифры первого числа, так и цифры второго числа. Если же ни одного такого числа составить нельзя, выведите -1.

280138
798081

8810

123
456

-1

M: Палиндром

Дана строка, состоящая только из заглавных латинский букв. Используя все или некоторые символы этой строки составьте строку максимальной длины, являющуюся палиндромом (то есть одинаково читающуюся слева направо и справа налево). Если таких строк несколько, то выведите минимальный в лексикографическом порядке палиндром.

PARALLELOGRAM

ALRARLA

ONE

E

N: Семипроцентный барьер

В Государственную Думу Федерального Собрания Российской Федерации выборы производятся по партийным спискам. Каждый избиратель указывает одну партию, за которую он отдает свой голос. В Государственную Думу попадают партии, которые набрали не менее 7% от числа голосов избирателей.

Дан список партий и список голосов избирателей. Выведите список партий, которые попадут в Государственную Думу.

В первой строке входного файла написано слово PARTIES:. Далее идет список партий, участвующих в выборах.

Затем идет строка, содержащая слово VOTES:. За ним идут названия партий, за которые проголосовали избиратели, по одному названию в строке. Названия могут быть только строками из первого списка.

Программа должна вывести названия партий, получивших не менее 7% от числа голосов в том порядке, в котором они следуют в первом списке.

PARTIES:
Party one
Party two
Party three
VOTES:
Party one
Party one
Party three
Party one
Party one
Party three
Party two
Party one
Party three
Party three
Party one
Party one
Party three
Party three
Party one

Party one
Party three

O: Упорядочить список партий по числу голосов

Формат входных данных аналогичен предыдущей задаче. Выведите список всех партий, участвовавших в выборах, отсортировав его в порядке убывания количества голосов избирателей, а при равном количестве голосов — в лексикографическом порядке.

PARTIES:
Party one
Party two
Party three
VOTES:
Party one
Party two
Party three
Party two
Party three

Party three
Party two
Party one

P: Выборы Президента

В выборах Президента Российской Федерации побеждает кандидат, набравший свыше половины числа голосов избирателей. Если такого кандидата нет, то во второй тур выборов выходят два кандидата, набравших наибольшее число голосов.

Каждая строка входного файла содержит имя кандидата, за которого отдал голос один избиратель. Известно, что общее число кандидатов не превосходит 20, но в отличии от предыдущих задач список кандидатов явно не задан.

Если есть кандидат, набравший более 50% голосов, программа должна вывести его имя. Если такого кандидата нет, программа должна вывести имя кандидата, занявшего первое место, затем имя кандидата, занявшего второе место.

Полуэкт Варфоломеев
Варфоломей Полуэктов
Полуэкт Варфоломеев

Полуэкт Варфоломеев

Полуэкт Варфоломеев
Варфоломей Виссарионов
Виссарион Полуэктов
Варфоломей Виссарионов
Варфоломей Виссарионов
Полуэкт Варфоломеев

Варфоломей Виссарионов
Полуэкт Варфоломеев

Q: Выборы Государственной Думы

Статья 83 закона “О выборах депутатов Государственной Думы Федерального Собрания Российской Федерации” определяет следующий алгоритм пропорционального распределения мест в парламенте.

Необходимо распределить 450 мест между партиями, участвовавших в выборах. Сначала подсчитывается сумма голосов избирателей, поданных за каждую партию и подсчитывается сумма голосов, поданных за все партии. Эта сумма делится на 450, получается величина, называемая “первое избирательное частное” (смысл первого избирательного частного — это количество голосов избирателей, которое необходимо набрать для получения одного места в парламенте).

Далее каждая партия получает столько мест в парламенте, чему равна целая часть от деления числа голосов за данную партию на первое избирательное частное.

Если после первого раунда распределения мест сумма количества мест, отданных партиям, меньше 450, то оставшиеся места передаются по одному партиям, в порядке убывания дробной части частного от деления числа голосов за данную партию на первое избирательное частное. Если же для двух партий эти дробные части равны, то преимущество отдается той партии, которая получила большее число голосов.

На вход программе подается список партий, участвовавших в выборах. Каждая строка входного файла содержит название партии (строка, возможно, содержащая пробелы), затем, через пробел, количество голосов, полученных данной партией – число, не превосходящее 10⁸.

Программа должна вывести названия всех партий и количество голосов в парламенте, полученных данной партией. Названия необходимо выводить в том же порядке, в котором они шли во входных данных.

Party One 100000
Party Two 200000
Party Three 400000

Party One 64
Party Two 129
Party Three 257

R: Проходной балл

Для поступления в вуз абитуриент должен предъявить результаты трех экзаменов в виде ЕГЭ, каждый из них оценивается целым числом от 0 до 100 баллов. При этом абитуриенты, набравшие менее 40 баллов (неудовлетворительную оценку) по любому экзамену из конкурса выбывают. Остальные абитуриенты участвуют в конкурсе по сумме баллов за три экзамена.

В конкурсе участвует N человек, при этом количество мест равно K. Определите проходной балл, то есть такое количество баллов, что количество участников, набравших столько или больше баллов не превосходит K, а при добавлении к ним абитуриентов, набравших наибольшее количество баллов среди непринятых абитуриентов, общее число принятых абитуриентов станет больше K.

Программа получает на вход количество мест K. Далее идут строки с информацией об абитуриентах, каждая из которых состоит из имени (текстовая строка содержащая произвольное число пробелов) и трех чисел от 0 до 100, разделенных пробелами.

Программа должна вывести проходной балл в конкурсе. Выведенное значение должно быть минимальным баллом, который набрал абитуриент, прошедший по конкурсу.

Также возможны две ситуации, когда проходной балл не определен.

Если будут зачислены все абитуриенты, не имеющие неудовлетворительных оценок, программа должна вывести число 0.

Если количество абитуриентов, имеющих равный максимальный балл больше чем K, программа должна вывести число 1.

Решение должно использовать O(1) памяти, то есть нельзя использовать списки, длина которых зависит от длины входных данных

5
Иванов Сергей 70 70 70
Сергеев Петр 100 100 0
Петров Василий 70 60 70
Васильев Андрей 70 60 70
Андреев Денис 100 30 100
Денисов Роман 50 50 50
Романов Иван 60 70 70
Ким Чен Ир 50 50 50
Ким Ир Сен 40 40 40

200

1
Иванов Сергей 40 40 40
Сергеев Петр 100 100 39

0

1
Иванов Сергей 60 60 60
Сергеев Петр 100 40 40

1

S: Полупроходной балл

В условиях предыдущей задачи определите полупроходной балл, то есть такое значение балла, что количество абитуриентов, набравших балл выше полупроходного, меньше K, а количество абитурентов, набравших балл выше или равный полупроходному, больше K.

Программа должна вывести значение полупроходного балла, если полупроходного балла не существует, программа должна вывести одно число 0.

Решение должно использовать O(1) памяти, то есть нельзя использовать списки, длина которых зависит от длины входных данных

5
Иванов Сергей 70 70 70
Сергеев Петр 100 100 0
Петров Василий 70 60 70
Васильев Андрей 70 60 70
Андреев Денис 100 30 100
Денисов Роман 50 50 50
Романов Иван 60 70 70
Ким Чен Ир 50 50 50
Ким Ир Сен 40 40 40

150

1
Иванов Сергей 50 50 50
Сергеев Петр 100 100 100
Ким Ир Сен 100 0 100

0

T: Призеры олимпиады

В олимпиаде участвовало N человек, каждый из которых мог набрать от 0 до 100 баллов. По положению об олимпиаде жюри может наградить не более 45% от числа участников, округляя их число до целого при необходимости вниз.

При этом если последний участник, попавший в 45% набирает столько же баллов, сколько первый участник, не попавший в 45%, то решение по этим участникам, и всем участникам, набравшим такой балл принимается следующим образом:

Все данные участники объявляются призерами, если набранный ими балл больше половины от максимально возможного балла.

Все эти участники не объявляются призерами, если набранный ими балл не больше половины от максимально возможного.

Программа получает на вход информацию об участниках олимпиады (один участник — в одной строке). Строка содержит имя участника (текстовая строка с произвольным числом пробелов) и набранный данным участником балл через пробел.

Программа должна вывести минимальный балл, который получил участник олимпиады, ставший ее призером.

Решение должно использовать O(1) памяти, то есть нельзя использовать списки, длина которых зависит от длины входных данных

Иванов Сергей 70
Сергеев Петр 30
Петров Василий 40
Васильев Андрей 80
Андреев Денис 50
Денисов Роман 90
Романов Иван 70
Ким Чен Ир 60
Ким Ир Сен 100

70

Иванов Сергей 50
Сергеев Петр 70
Петров Василий 40
Васильев Андрей 10
Андреев Денис 50
Денисов Роман 20
Романов Иван 30
Ким Чен Ир 70
Ким Ир Сен 100

70

Иванов Сергей 30
Сергеев Петр 60
Петров Василий 20
Васильев Андрей 100
Андреев Денис 30
Денисов Роман 80
Романов Иван 20
Ким Чен Ир 40 
Ким Ир Сен 10

40

домино (игра): 20 стран, где в нее играют | Где домино популярно?

Домино — древняя игра, распространившаяся по всему миру. Эта игра имеет многовековую историю и стала обычным явлением во многих странах, но некоторые придают ей особое значение. Распространено ли домино во всех странах мира? Какие страны активно играют в Домино?

Есть много стран, где играют в домино, и эта игра стала любимой во всем мире. Такие страны, как Китай, США, Куба, Италия, Франция, Южная Африка, Бразилия, Канада, Колумбия и Мексика, любят играть в домино; и это стало привычным зрелищем почти везде.

Большинство людей слышали о домино, и большинство из них играло в эту игру, но есть несколько стран, где эта игра практически не оказала влияния, хотя во многих других местах она является жизненно важной социальной практикой. Давайте определим страны, в которых играют в домино, и узнаем больше об отношениях этих стран с игрой.

Вот 20 стран, где играют в домино:

Домино зародилось в Китае много веков назад, и в него до сих пор играют. В Китае есть несколько способов играть в домино, и плитки называются по-разному, но основы игры одинаковы и остаются неизменными на протяжении тысячелетий.

В Нидерландах есть оживленная сцена домино, и она наиболее известна в мире домино благодаря Дню домино, когда многие люди собираются вместе, чтобы играть в игру и создавать произведения искусства домино. . Это ежегодное мероприятие проводится с 1986. 

В США в домино играют по-разному. В традиционное домино играют и по сей день, но есть несколько итераций игры, которые превращаются в форму карточной игры. Эта страна также является домом для многих художников и новаторов Домино.

Домино очень популярно в Латинской Америке, в том числе на Кубе, где эта игра рассматривается как способ общения и общения с близкими и друзьями во время развлечения. Известно, что кубинцы берут с собой свои плитки домино, куда бы они ни пошли, и их можно увидеть играющими в домино в каждом городе, где они проживают на международном уровне.

Считается, что современная версия игры возникла в Южной Европе, а именно в Италии, в середине 18 века. Сегодня в домино все еще играют в Италии, и она остается очень популярной как казуальная социальная игра.

Франция также считается местом, где наряду с Италией в 18 веке была развита современная игра в домино. Домино распространилось из этих южноевропейских стран на север примерно в конце 18 века.

Бельгия и Франция были одними из самых выдающихся игроков в домино в 1800-х годах, и эта игра была хорошо известна как любимая в бельгийских кафе и общественных местах. Эта игра до сих пор популярна в стране, и в нее обычно играют все поколения.

Домино очень популярно в таких странах, как Пуэрто-Рико, где местные жители собираются большими группами для игры. Домино стало важным социальным элементом в Пуэрто-Рико, и в него играют с большой энергией и азартом в стране.

Жители Ямайки стали популярными игроками в домино и разработали сложные стратегии игры. Каждый игрок в ямайское домино изо всех сил старается предсказать стратегию своего противника, чтобы победить его в игре, и победа в шести играх подряд считается окончательной победой.

Домино – важная культурная игра в Аргентине. Здесь есть несколько способов играть в эту игру, но, к сожалению, игра не продолжается молодым поколением и поддерживает игру, которая нравится старшим поколениям и несколько игнорируется молодыми людьми.

Небольшая страна Гаити хорошо известна в Карибском бассейне своей любовью к домино, и в каждом доме есть набор костяшек домино, которые регулярно используются. В этой игре есть несколько разновидностей на Гаити, как и в других странах Карибского бассейна, но в большинстве итераций играют с французским, испанским или ямайским вариантом игры.

Очень часто можно увидеть игру в домино в общественных парках и других зонах отдыха в Доминиканской Республике. Эта игра особенно любима пожилыми людьми. Тем не менее, он по-прежнему нравится многим людям из молодого поколения. Это ценно как здоровая социальная активность для поддержания социальных связей.

Известно, что бразильские семьи вместе играют в домино, и у большинства домохозяйств есть несколько наборов костяшек домино.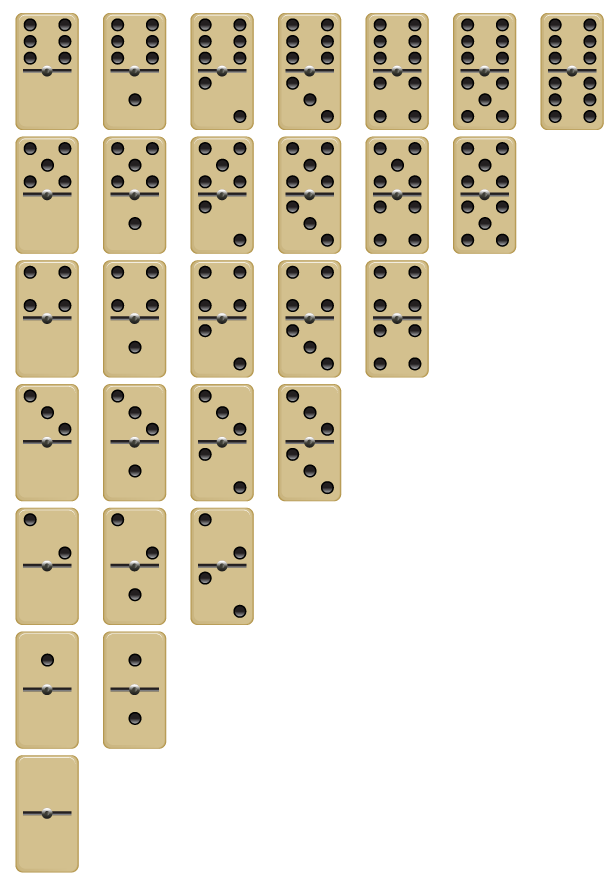 Эта игра является любимой формой семейной связи и нравится всем поколениям. Парки и другие общественные места являются обычными местами для игры в домино в Бразилии.

Домино — популярная игра, в которую играют на семейных мероприятиях, больших семейных собраниях и семейных встречах. Эта игра особенно нравится пожилым людям в этой стране, но в нее играют все, когда семья собирается вместе.

Колумбийцы, как известно, играют в домино в социальных сетях. Люди в этой стране наслаждаются домино на вечеринках, играя в несколько итераций игры с различными правилами и вариантами игры. Как и во многих странах Латинской Америки, в домино играют преимущественно пожилые колумбийцы.

Инуиты, живущие на севере Канады, играют в свою версию домино с плитками, которые обычно делаются из костей. В этих играх используются наборы до 148 плиток, и они, как правило, отличаются от обычных домино, но в конечном итоге это игра с той же предпосылкой.

В Южной Африке существует несколько клубов и союзов домино, и некоторые из этих клубов в Кейптауне, Южная Африка, очень конкурентоспособны и называют домино любимым видом спорта. . Домино является неотъемлемой частью жизни многих южноафриканцев.

Небольшие рестораны и кафе в Египте — обычное место, где можно найти группы, играющие в домино, общающиеся с друзьями и обедающие вместе. В этих условиях в Египте часто играют в домино, а также в шахматы, нарды и карточные игры.

Игра в домино довольно распространена в Англии, и в нее играют все поколения. Эта игра прибыла в Англию в 18 веке благодаря французским игрокам в домино. Существуют клубы и союзы, посвященные игре, и для многих британцев это веселое, но структурированное времяпрепровождение.

В домино играют представители старшего поколения в Турции, особенно в южных регионах страны. Мужчины будут играть в эту игру в барах и ресторанах, и часто среди друзей организуются еженедельные игры в домино.

Игра в домино – это международная деятельность. Некоторые страны относятся к игре более серьезно, чем другие, но это любимая настольная игра почти во всем мире. Игра зародилась в Восточной Азии и за последние несколько столетий стала обычным явлением почти в каждой стране.

Mexican Train Dominoes Обзор, правила и руководство по стратегии

Мы считаем, что Mexican Train Dominoes — одна из настольных игр, которая возродила в нашей семье любовь к ночным играм. Хотите верьте, хотите нет, но несколько лет назад мы довольно долго не играли всей семьей в настольные игры. За последние годы наша семья влюбилась в эту игру, и она стала одной из наших любимых настольных игр. Мы расскажем, как сильно мы любим эту настольную игру, в наших Обзор мексиканского поезда домино и руководство по стратегии . Мы также рассмотрим наши правила домино в мексиканском поезде и то, как мы играем.

Прежде чем мы углубимся в наш обзор и руководство по стратегии в мексиканском поезде домино, вот небольшая предыстория. Мы с сестрой сделали неизбежное… мы выросли из детей во взрослых; мы были слишком заняты работой, учебой и общением с друзьями.

Мы упустили возможность оставаться дома и проводить время всей семьей. Однако по мере того, как мы становились старше и привыкали к рутине, мы поняли, как сильно скучали по нашим семейным игровым вечерам.

Мы научились играть в домино благодаря бабушке нашего лучшего друга. Пройдя несколько раз по ее дому, чтобы поиграть, мы зацепились.

Однажды мы посмотрели друг на друга и решили, что нам нужно познакомить наших родителей с мексиканским поездом домино.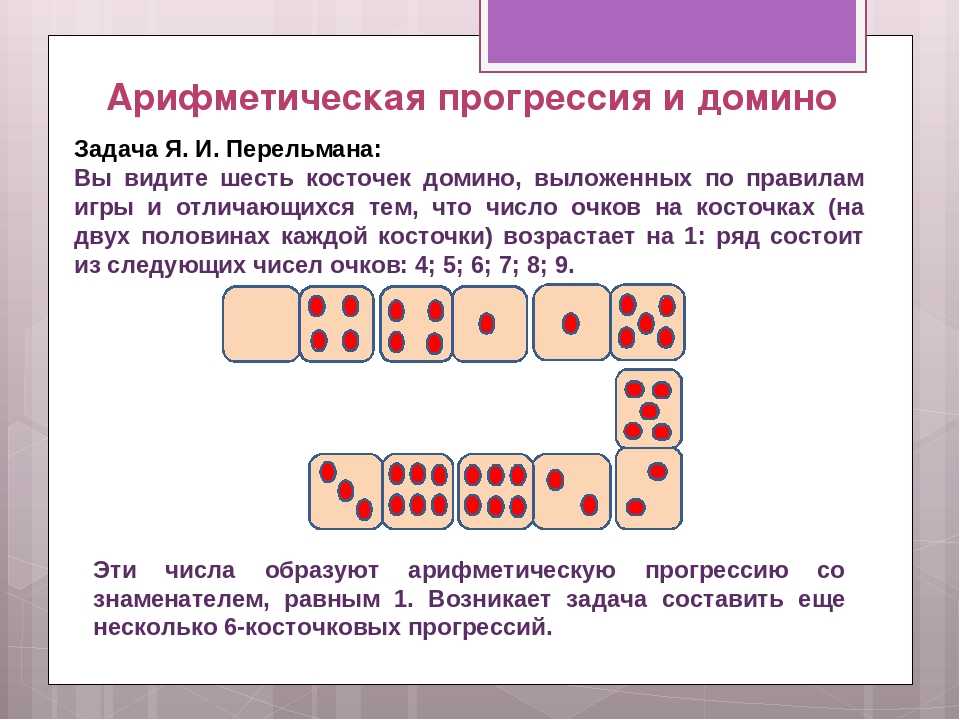 Поэтому мы купили набор 12-гранных домино для мексиканского поезда, чтобы мы могли принести его на следующий вечер семейных игр.

С того дня мы играем почти каждые выходные! Это была единственная игра, в которую хотели играть наши родители (до недавнего времени они были готовы попробовать несколько новых игр), и мы ни разу не пожаловались. Почему? Потому что мы наконец-то вернули себе семейное время!

Что такое мексиканский поезд домино?

Mexican Train Dominoes — это игра, в которую играют двухсторонними пронумерованными костяшками домино, где цель каждого раунда состоит в том, чтобы разыграть все домино/плитки из вашей руки раньше, чем это сделают другие игроки.

Игроки размещают свои плитки на различных цепях или «поездах», которые исходят из центрального узла или «железнодорожного вокзала». У каждого игрока есть свой поезд, однако есть универсальный поезд, принадлежащий всем игрокам, который называется «Мексиканский».

Mexico Train Dominoes Review & History

Правила «Игры в поезд» были разработаны парой, Роем и Кэти Парсонс, в Калифорнии в начале 90-х годов.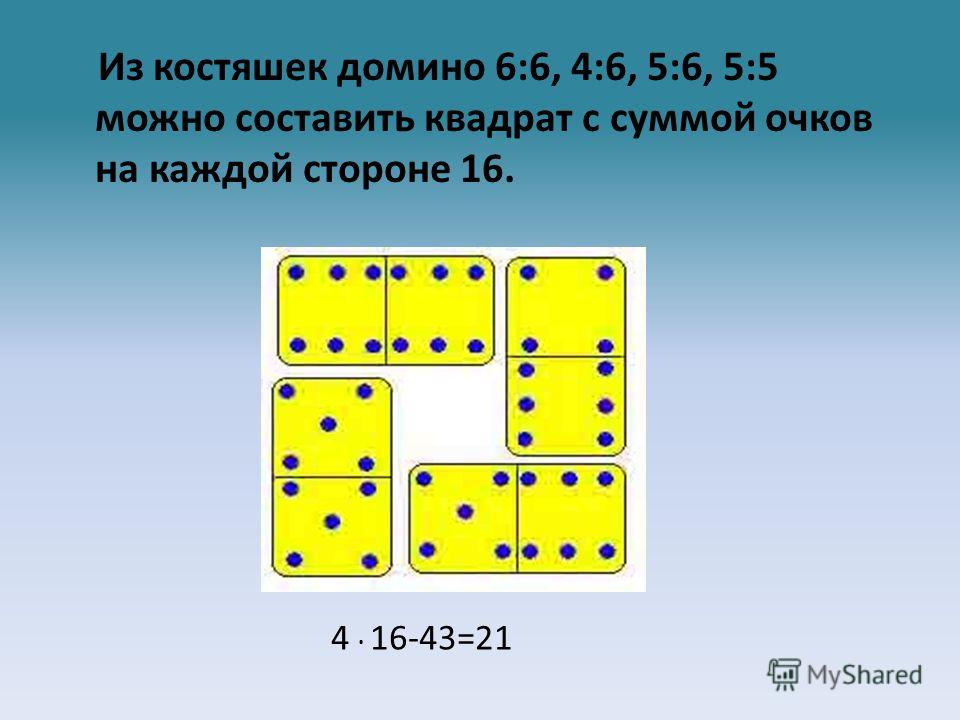 Получив более широкую известность, компания Puremco приобрела права на игру и превратила ее в игру, которую мы знаем и любим сегодня, «Мексиканское домино».

Считается, что идея игры была вдохновлена ​​несколькими китайскими играми в домино, включая Tien Gow, также известную как Heaven-Nine, Pai Gaw и Kap Tai.

Мексиканский поезд также включает в себя некоторые функции «просто для развлечения», такие как:

• Всякий раз, когда игрок запускает свой поезд, раздается свисток
• Когда разыгрывается двойная игра, ударяйте две плитки вместе, как сигнал, издаваемый двумя поездами, проезжающими мимо. двойной набор дорожек
• Когда у игрока заканчиваются кости домино, он может издать звук Чу-Чу, чтобы объявить о своей победе в раунде.

Существуют различные версии этой любимой игры про поезда. Нам нравится играть в двухсторонний набор из 12, который содержит числа, варьирующиеся до 12. Если вы играете с набором «двойное-двенадцать», то всего будет 12 раундов, начиная с двойного 12 и заканчивая двойным 0. Другое версии включают двойную шестерку и двойную девятку.

Как играть в домино в мексиканском поезде

В этом обзоре домино в мексиканском поезде мы расскажем, как настроить игру и как в нее играть! Оставайтесь с нами до конца, и мы покажем некоторые из наших любимых стратегий.

Оборудование:

• Набор из 12 костяшек «Мексиканский поезд» с костяшками домино, центральной втулкой и маркерами поездов
• Деревянные подставки для домино (дополнительно, но рекомендуется)

Комплектация:

3

6

6

6

6

6

6

6

60173 Чтобы начать первый раунд,

перетасуйте все костяшки на столе лицевой стороной вниз . Убедитесь, что они хорошо перемешаны.

Если вы используете, раздайте каждому игроку стойку для домино, а также их маркер поезда (обычно бусину в форме поезда другого цвета).

Затем каждый из игроков берет костяшки домино из смешанной стопки и добавляет их на свою стойку. В игре с двумя двенадцатью сетами игроки тянут домино следующим образом:

• 2–4 игрока : по 15 костяшек каждый
• 5–6 игроков : по 12 костяшек в каждом
• 7–8 игроков : по 10 костяшек в каждом

Все оставшиеся костяшки домино кладутся лицевой стороной вниз и будут использоваться на протяжении всей игры. Держите их подальше от игроков небольшими кучками.

Правила мексиканского поезда домино

Ознакомьтесь с нашими правилами мексиканского поезда и геймплеем ниже…

Игровой процесс:

1. выбрать из смешанной кучи. Если никому не удалось подобрать двенадцать, то решите, кто ходит первым, и начинайте по очереди собирать костяшки из лишней стопки, пока кто-нибудь не найдет двенадцать.
2. Игрок, который имеет или находит двойную двенадцатую, начинает с размещения двойной двенадцати в центре узла или «железнодорожного вокзала» и начинает свой поезд с двенадцати костяшек домино. Если у них нет двенадцати, чтобы положить вниз, им придется взять плитку из дополнительной стопки. Если он содержит двенадцать, то они должны сыграть в это домино, чтобы начать свой поезд. Если нет, то он должен оставить себе эту плитку, и игра продолжится следующим игроком слева. Затем этот игрок начнет свой поезд, либо положив домино со своей стойки, либо вытянув из лишней стопки.
3. Мексиканский поезд: это универсальный поезд, на котором может ехать КАЖДЫЙ. Он не принадлежит конкретному игроку. Обычно он отмечается специальным маркером поезда на центральном узле.
4. Каждый игрок по очереди размещает плитки на своем поезде, «общественном» поезде соперника (подробнее об этом чуть позже) или на мексиканском поезде. Игрок может открыть мексиканский поезд, если он уже открыл свой собственный поезд. Все игроки могут разместить любую свою плитку на мексиканском поезде. Мексиканский поезд должен быть открыт домино с номером, на котором идет раунд, точно так же, как вы запускаете свой собственный поезд.
5. Домино в любом поезде должны быть соединены соответствующими номерами. Например, если я начал свой поезд с домино 12 / 6, то мое следующее домино должно содержать 6, чтобы прикрепить его к моему поезду. Так что, если я выкладываю костяшку 6/2, моя следующая костяшка должна содержать двойку. И так далее!
6. Игроки могут продолжить свой поезд впереди себя или сесть на мексиканский поезд. Если игрок не может поехать на своем собственном поезде ИЛИ на мексиканском поезде И вытащить плитку из лишней стопки, которая не может никуда ехать, тогда он должен поместить свой маленький поезд в центральный узел, и он считается «открытым».
7. Общественные поезда: Когда поезд игрока открыт, это означает, что любой может сесть на поезд этого человека. Теперь у игроков есть возможность поехать на собственном поезде, мексиканском поезде или любом общественном поезде. Поезд игрока остается общедоступным до тех пор, пока он не сможет поместить одну из своих плиток на свой собственный поезд, чтобы снова «закрыть» его. Как только они смогут сесть на свой собственный поезд и закрыть его, они могут удалить свою игровую фигуру из центрального узла, и они больше не будут считаться общественным поездом.
8. Парные: Двусторонние плитки (например, 2/2 или 10/10) разыгрываются по-разному. При игре двусторонней плиткой с тем же номером вы должны положить другую плитку с тем же номером сразу после того, как будет сыграна двойная. Таким образом, если я выкладываю плитку 2/2, то я должен разыграть плитку сразу после того, как она содержит 2. Если вы кладете двустороннюю плитку и не можете положить другую плитку, чтобы закрыть двойную, вам придется взять плитку, чтобы закрыть ее. посмотрите, получите ли вы число, которое можно поместить после двойного числа. Если выбранный вами тайл не сработает, то вы считаетесь «открытым». Однако на этом все не заканчивается! Дубль должен быть закрыт, прежде чем можно будет продолжить нормальную игру. .
9. Если игрок, разместивший двойную плитку, не может ее закрыть, то вы будете ходить по столу, по одному игроку, пока кто-нибудь не положит плитку с соответствующим номером. Если следующий человек не может положить плитку, он берет другую плитку из лишней стопки и либо кладет ее. Если он не берет плитку, которая работает, то следующий человек пытается закрыть двойную. Продолжайте, пока дубль не будет закрыт. Вот сценарий: я играю двусторонней двойкой. У меня нет другой плитки с двойкой на моей стойке. Я беру костяшку костяшки из лишней стопки, но у меня по-прежнему нет цифры 2. Меня считают «открытой», и я ставлю свой поезд, чтобы отметить, что мой поезд открыт. Следующий человек должен поставить 2 на мой поезд, чтобы закрыть дубль. Они заявляют, что у них нет двойки, и продолжают брать еще одну плитку из лишней стопки. В этом костяшке нет двойки, поэтому их ход пропускается, и ходит следующий игрок (им не нужно открывать свой поезд, так как они не поставили двойку в первую очередь). Этот человек все еще должен поставить 2 на мой поезд, потому что дубль все еще открыт. У них есть домино с номером 2 на стойке. Они помещают его в мой поезд и закрывают моего двойника. Игра продолжается как обычно.
10. Обратите внимание: кости домино, оставшиеся с самого начала, используются на протяжении всей игры. Однако, если лишнее домино закончилось, то это нормально. Вы просто не берете костяшку, так как ее нет, и ваш ход технически пропускается.
11. Мертвые поезда:  поезд считается «мертвым», если никто не может ничего положить на конец поезда и не осталось лишних плиток. Просто игнорируйте этот поезд до конца раунда, так как его нельзя использовать.
12. Раунд заканчивается, когда игрок кладет все свои костяшки домино на стол, при этом ни одной кости не осталось перед ним/на подставке.
13. Остальные игроки подсчитывают свои костяшки и сообщают счет секретарю. Убедитесь, что каждый игрок считает оба числа на каждой костяшке домино. Секретарь должен записывать в блокнот счет каждого, чтобы вести учет. Будет несколько раундов, так что не пытайтесь запоминать баллы!
14. Следующий раунд начинается со следующего числа, считая от последнего, в нашем случае это будет Double Eleven. Затем, после этого раунда, двойная десятка и так далее.
15. Вся игра заканчивается, когда заканчивается раунд Double Zero.
16. Подсчет очков: Затем секретарь подсчитывает очки каждого игрока во всех раундах, и игрок с наименьшим результатом выигрывает ! Всего в наборе двойных 12 домино будет 13 раундов.

Сколько времени нужно, чтобы играть в мексиканский поезд домино?

Благодаря нашему опыту игры в двойное домино с 12 мексиканскими поездами, у нас были игры, которые обычно длятся от 2 до 3 часов. Это действительно зависит от версии, в которую вы играете, количества людей и времени, которое требуется каждому игроку, чтобы подумать/разыграть свою руку.

С 5 игроками игра в двойные 12 мексиканских домино занимает около 3 часов.

Стратегии мексиканского поезда в домино

Когда вы играете в игру столько же, сколько мы играли в домино, вы начинаете понимать, как люди играют в эту игру. Вот три стратегии, которые мы используем чаще всего, чтобы помочь нам выиграть!

#1 Запланировано и организовано:

Это стратегия, которую я (Кейт) использую! Подняв плитки на раунд, я сразу же выстраиваю их на своем подносе и пытаюсь составить самый длинный поезд. Обязательно попробуйте разные комбинации, когда у вас есть несколько чисел, которые могут выстроиться в линию, вы никогда не знаете, какая комбинация создаст самый длинный поезд на вашей стойке!

Если есть костяшки домино, которые не помещаются в запланированный поезд, я кладу их на дно подноса. Когда начнется раунд, я буду класть костяшки домино на свой поезд из запланированного поезда на свою стойку. Если у меня будет много лишних плиток, не являющихся частью моего поезда, я постараюсь как можно скорее открыть «мексиканский» поезд. Если в какой-то момент у меня появляется лишняя костяшка домино, которую можно положить на другой поезд, я так и делаю. Логика этого заключается в том, что я знаю, что могу положить в свой поезд в любое время с запланированными костяшками домино, поэтому я хочу попытаться избавиться от лишних костяшек домино как можно скорее!

Единственный раз, когда Я НЕ БУДУ класть лишнюю костяшку на другой поезд, это если это двойная костяшка, которую мне не закрыть!!! Для меня это слишком рискованно: если я выложу двойную ставку без костяшки в качестве подкрепления, я буду вынужден взять костяшку из запасной стопки. Если мне повезет, он совпадет с нужным мне номером, а если нет, то теперь я должен открыть свой поезд для других игроков, по сути разрушив запланированный поезд!

#2 Рискни хаосом:

Это стратегия Брандена. Хотя он использует некоторую организованность, планируя свой поезд заранее, Бранден полагается на риск и создание хаоса, чтобы победить.

Он будет постоянно играть в парном разряде без костяшки домино. Он скорее рискнет открыть свой поезд и избавится от двойника как можно скорее (и, надеюсь, испортит чью-то жизнь в процессе), чем будет держаться за этих надоедливых двойников! Его манера игры не всегда работает в его пользу, но мы обнаружили, что время от времени его риск окупается.

#3 Подлый и крупный игрок:

В этой стратегии вы начинаете с того, что выкладываете плитки поезда на решетку и расставляете их таким образом, чтобы другие игроки не могли сказать, сколько плиток у вас на начальном поезде. . Попробуйте использовать поддельные перерывы, чтобы они не думали, что у вас непрерывный поезд.