Танграм размеры – Как сделать танграм.

Содержание

Как сделать танграм.

Двусторонний танграм 10см*10см в 8-ми вариантах: разноцветный, красный, синий, голубой, зеленый, оранжевый, желтый и бесцветный

Скачать материал ( 3.97 МБ )

Танграм всемирно известная головоломка, состоящая из 7 фигур (танов), из которых необходимо собрать какой-либо объект, животное или человека.

Сделать танграм самостоятельно совсем не трудно.

1 вариант.

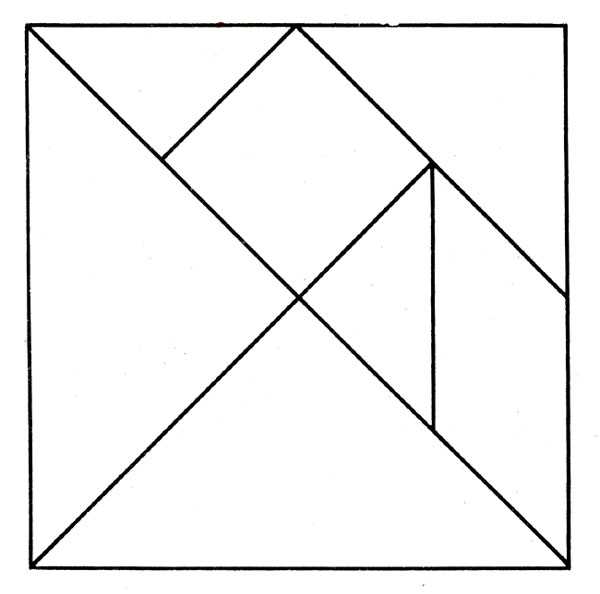
Начертите на картонном листе или листе пористой резины квадрат 10см*10см и расчертите его как показано на схеме.

2 вариант.

Распечатайте готовую схему на бумаге. Можно взять цветную двустороннюю. Рекомендуем бумагу брать поплотнее или после распечатки наклеить танграм на картон.

3 вариант.

Распечатать двустронний танграм на плотной бумаге (желательно фотобумаге). Согнуть, склеить его и разрезать по линиям. При склеивании лучше использовать двусторонний скотч.

Схему такого танграма можете скачать ниже.

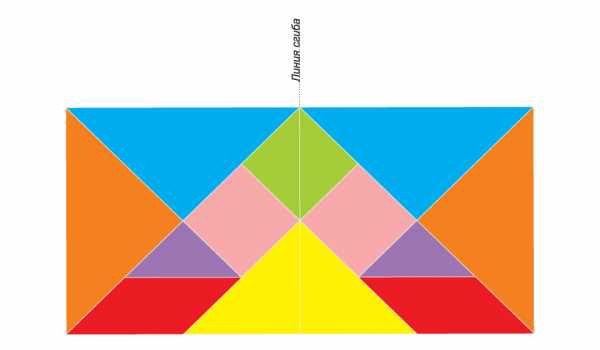
4 вариант.

Распечатать двустронний танграм на плотной матовой фотобумаге (плотность не менее 190 г/м₃. Взять лист пористой резины (на фото он белый).

Отрезать половину танграма и наклеить ее на лист пористой резины с помощью двустроннего скотча.

Аккуратно разрезать полученный танграм по линиям и также разрезать оставшийся второй танграм.

На детали второго танграма приклеиваем двустронний скотч. Каждую детальку приклеиваем к соответсвующей на сторону со вспененной резиной.

Да, работа не быстрая, но зато результат прекрасный.

Такой танграм удобнее брать ручкам Вашего ребенка и срок службы его дольше, чем обычного бумажного танграма.

Играйте, развивайтесь весело и увлекательно!

Особенности бумажной версии

1 танграм 10см*10см двусторонний, распечатанный на матовой фотобумаге плотностью 190 г/куб.м и приклеенный к декоративной пенке.

Цвет танграма укажите, пожалуйста, в комментарии к заказу.

Возможны следующие цвета танграма для заказа: разноцветный, синий, красный, голубой, зеленый, оранжевый, желтый или черно-белый.

По этой теме Вы можете еще посмотреть:

Комлект-раскраска с загадками «Фигурки-отгадайки» для малышей.

Комлект-раскраска со стихами «Циферки и фигурки» для малышей.

Комлект-раскраска со стихами «Чудо-фигурки» для малышей.

Схемы к Танграм с картинками (180 схем и 108 реалистичных картинок к ним).

Карточки со схемами к танграм (180 схем).

Контурные схемы к Танграм для наложения.

Скачать материал ( 3.97 МБ )

Оставлять комментарии могут только зарегистрированные пользователи

razvivalo4ki.ru

Танграм: геометрические головоломки для детей

Танграм (кит.七巧板, пиньинь qī qiǎo bǎn, букв. «семь дощечек мастерства») — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать

два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга.

Танграм-онлайн

Танграм можно сделать из картона или бумаги, распечатав шаблон и разрезав по линиям. Вы можете скачать и распечатать схему, кликнув по картинке и выбрав «печать» или «сохранить картинку как…».

Схемы танграма — 1 уровень — 1

Распечатать задания с ответами

Цветные картинки — задания (контуры), черно-белые картинки — ответы к ним.

Схемы и фигуры игры танграм

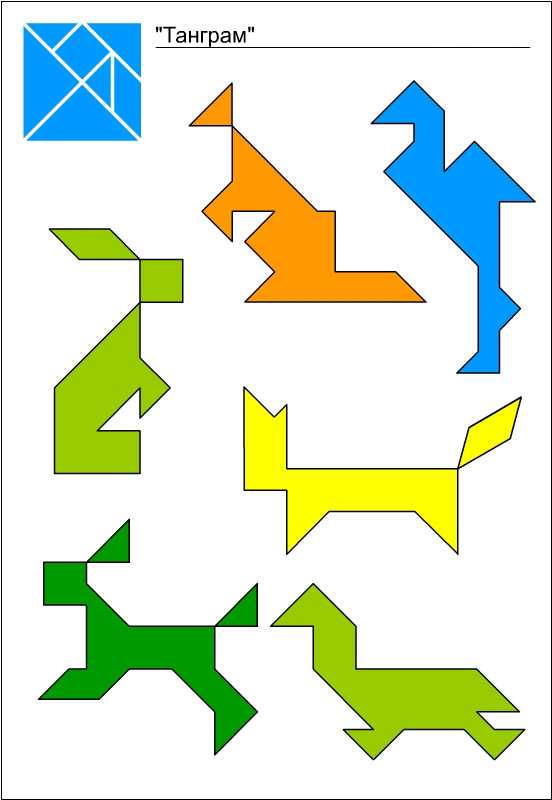
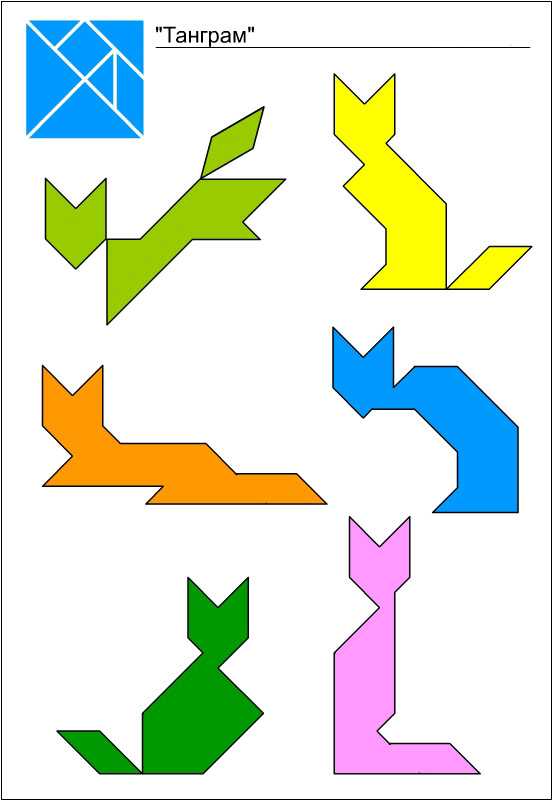
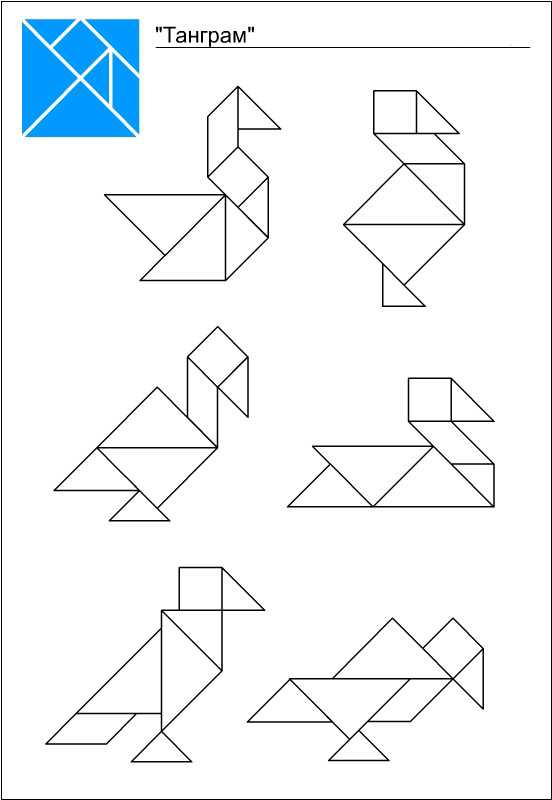
nitforyou.com

Подборка схем для игры танграм

Подборка схем

Танграм (букв. «семь дощечек мастерства») — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга.

Игра очень проста в изготовлении. Квадрат (величина его практически может быть любой: 5×5, 7×7, 10×10, 12×12 см и т.д

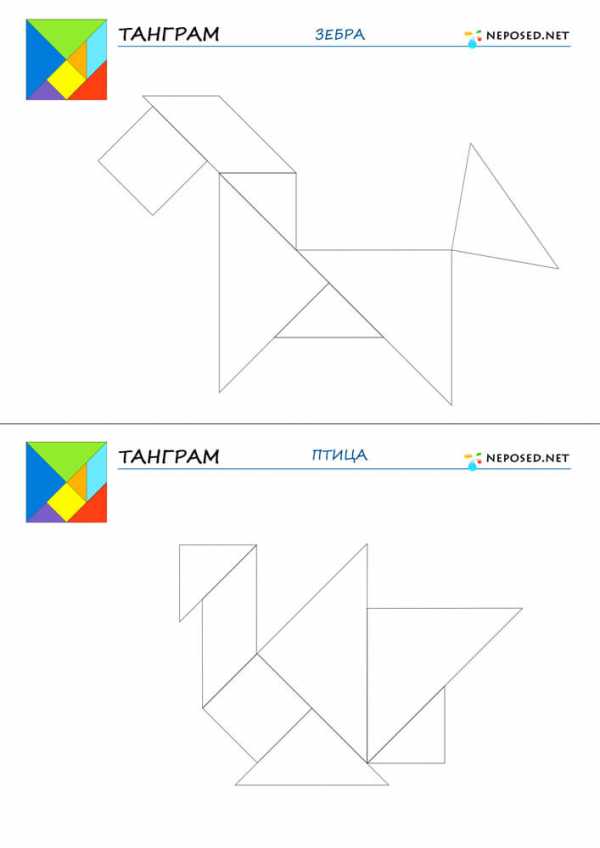
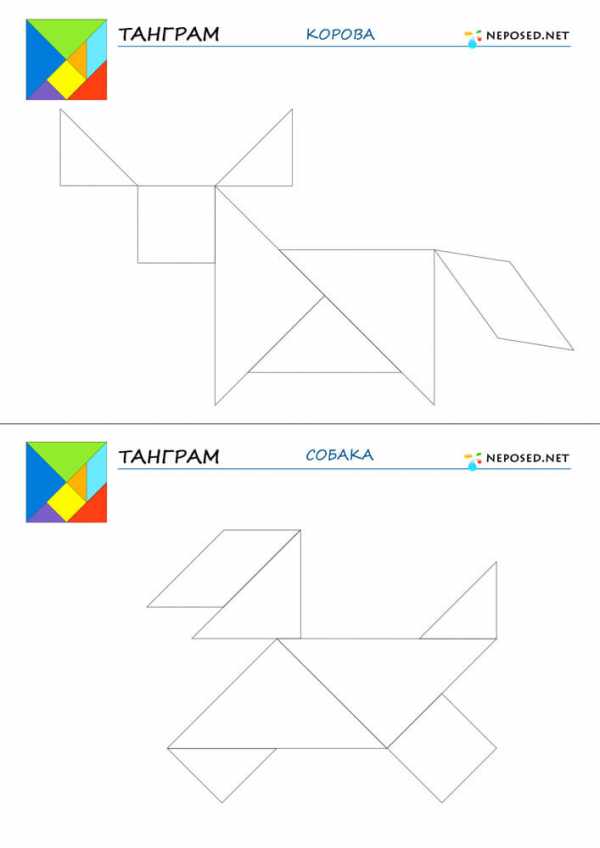
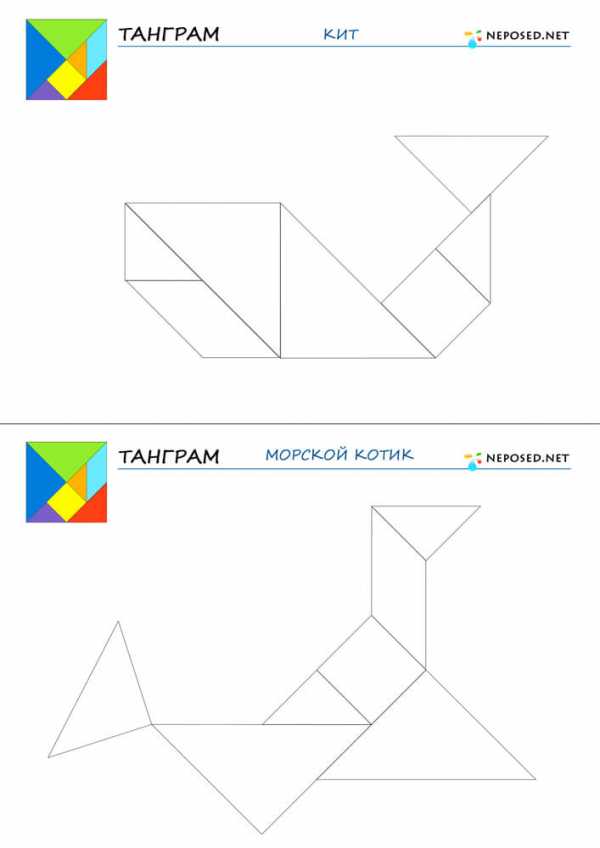
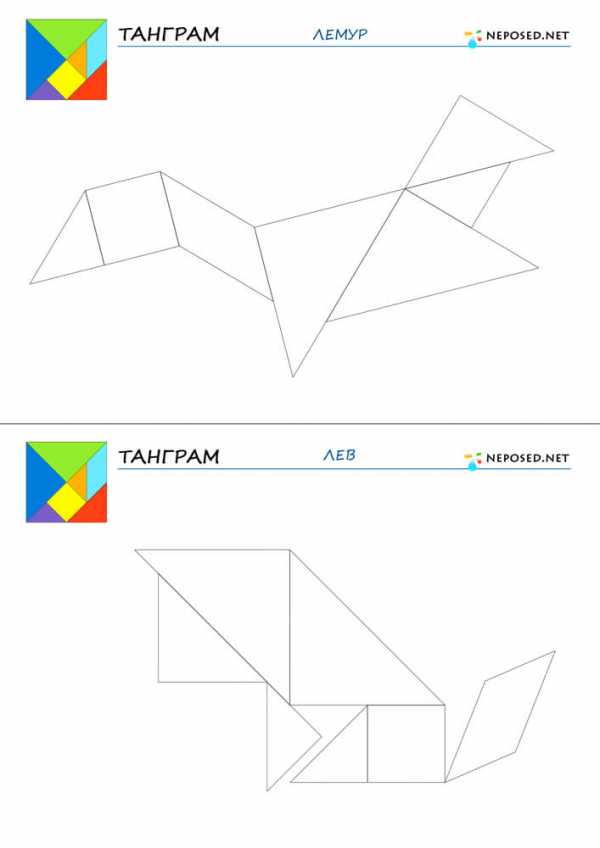
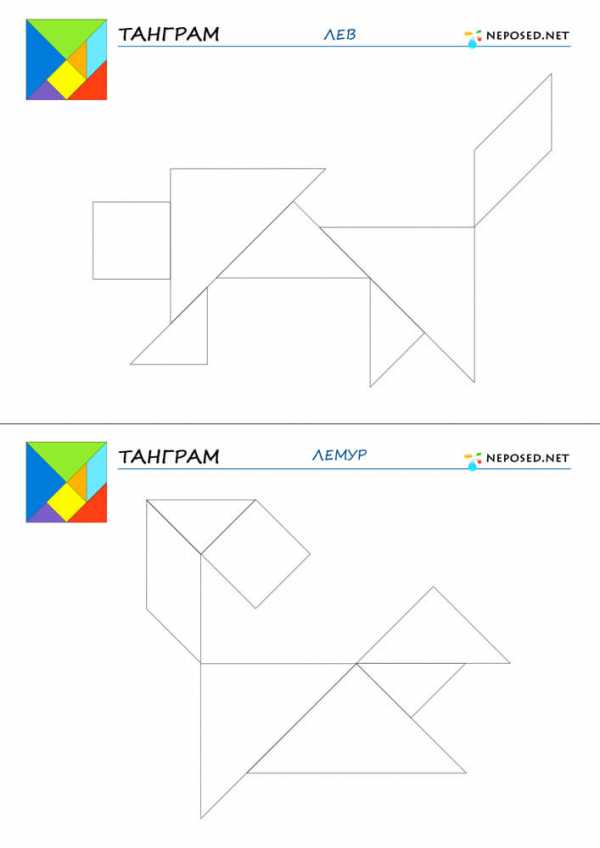
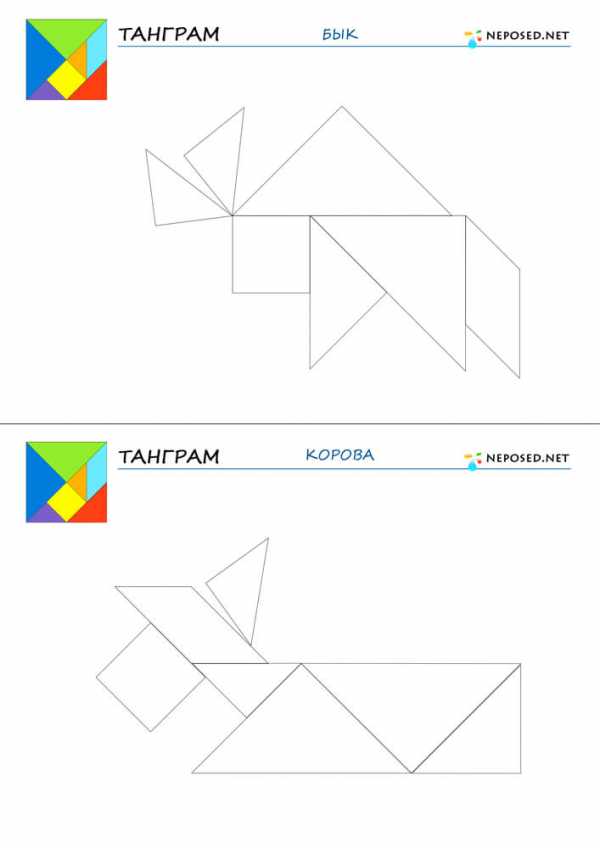
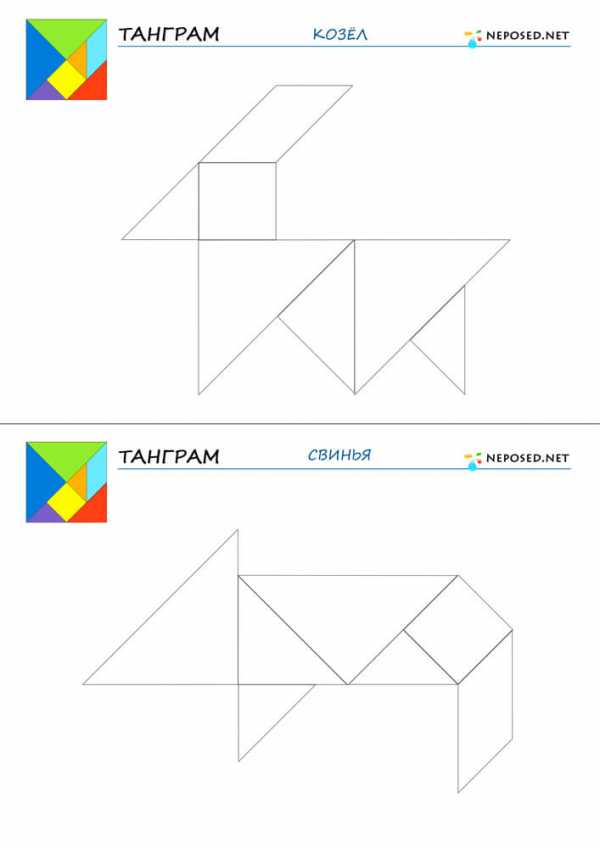
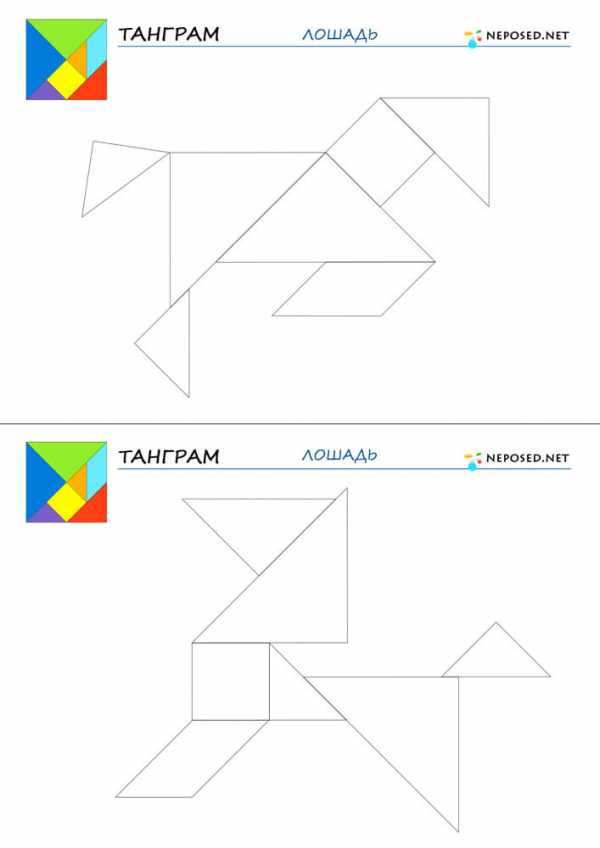
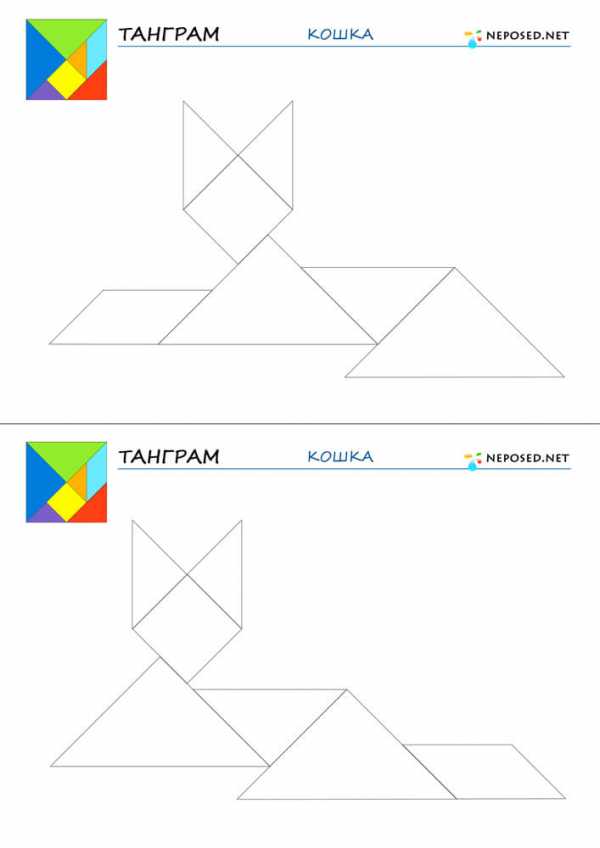
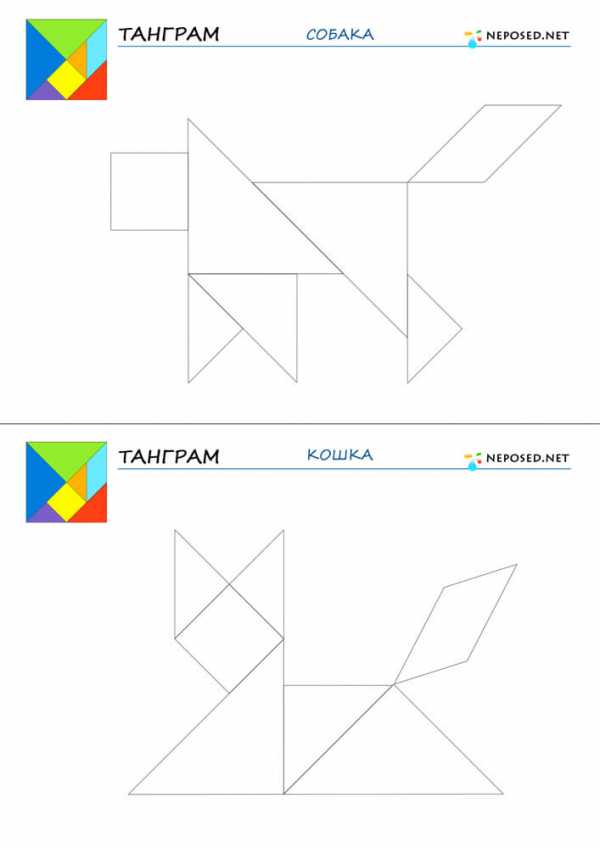
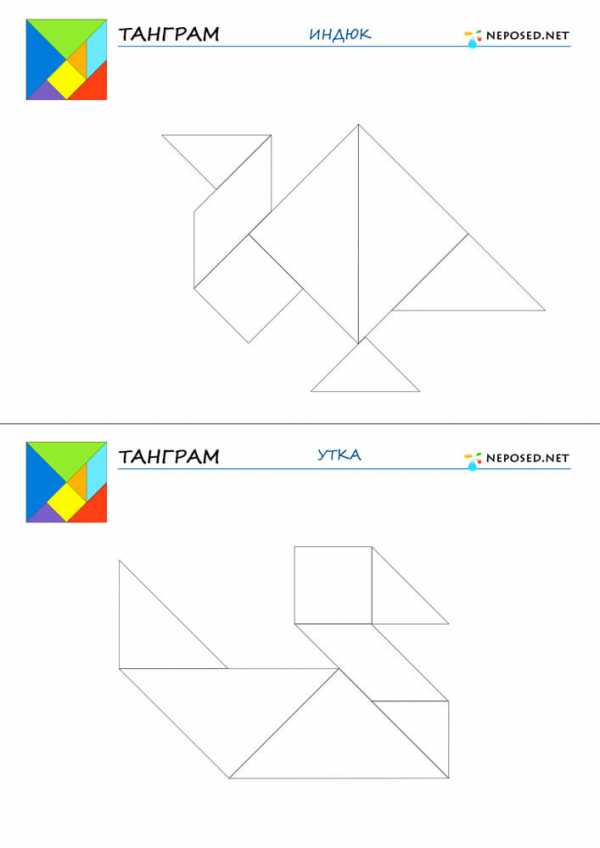
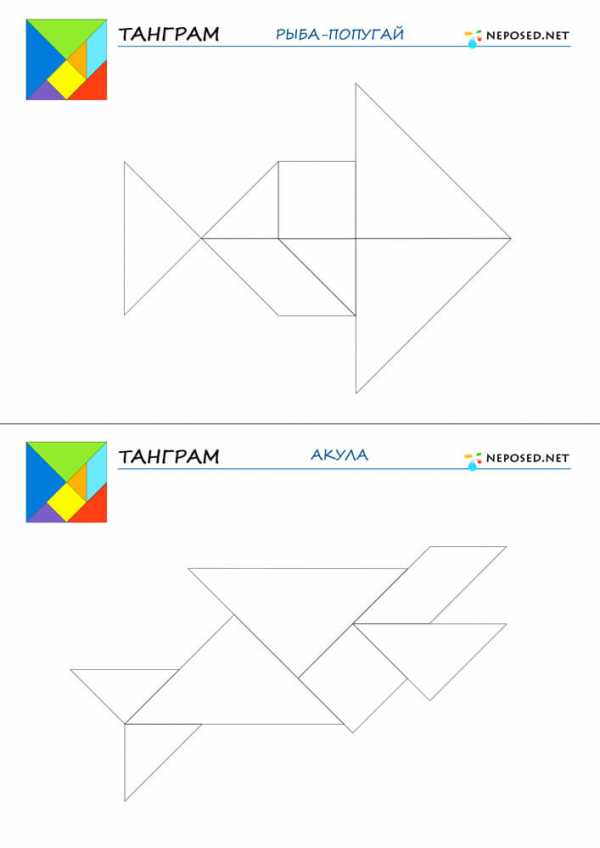
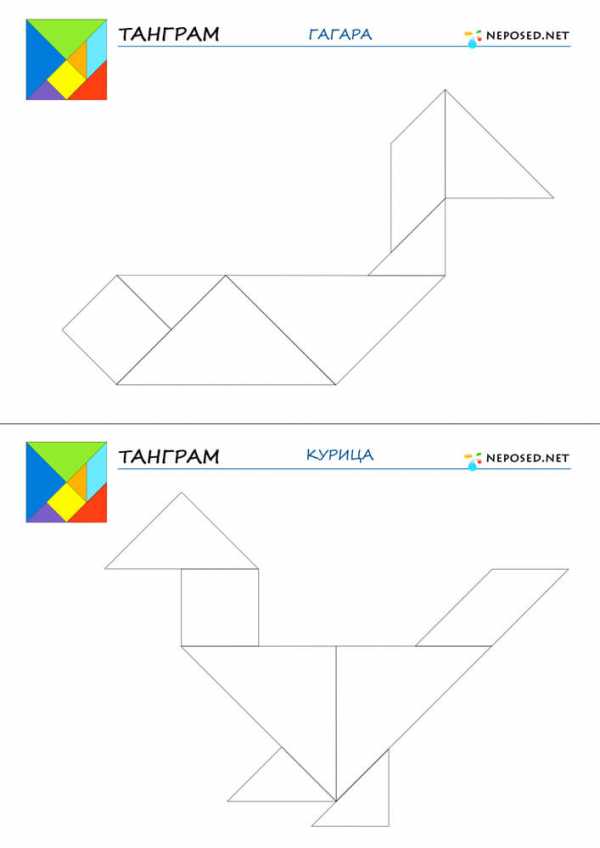
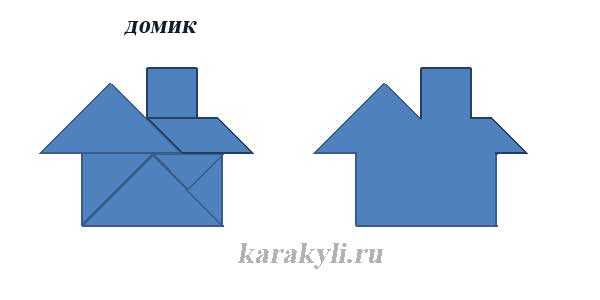
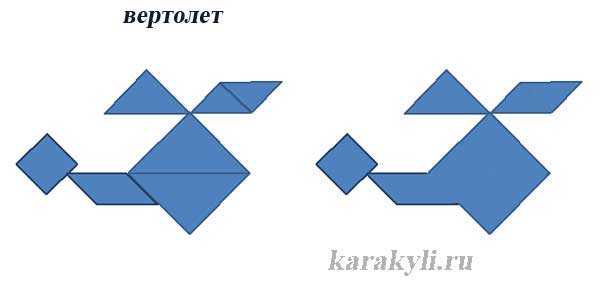
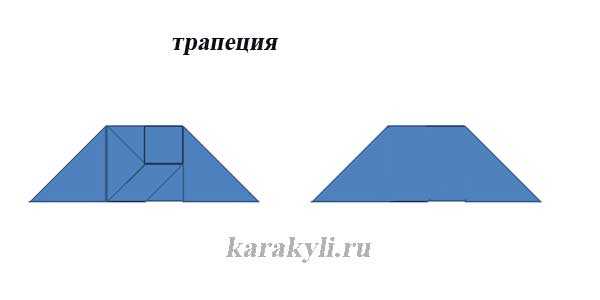
infourok.ru

Танграм

Разделы: Математика

Ход урока

I. Вступительное слово учителя.
Здравствуйте, ребята! Как ваше настроение? Настроены ли вы на занятие? Садитесь!
Я услышала о старинной китайской игре — головоломке танграм. Меня очень заинтересовала эта игра. Мне захотелось, как можно больше узнать о танграме. Я решила подробно изучить историю возникновения этой головоломки и исследовать возможности этой игры, применение ее в форме игры. Поэтому, целью данного урока является: изучить историю возникновения игры – головоломки «Танграм» и исследовать ее применение.
Головоломки – игрушки на все времена. До появления компьютерных и бурного развития настольных игр, одним из основных развлечений для большинства людей была игра — головоломка «Танграм». В наше время очень много людей увлекаются головоломками. Они любимы не только детьми, но и взрослыми. Игра помогает развивать логическое мышление, геометрическую интуицию. Это способ отвлечения от повседневных проблем и направлен на развитие различных мыслительных процессов — сопоставление, обобщение, установление последовательности, определение отношений «целое» — «часть». Все эти умения необходимы будущим математикам.

Что такое танграм? Слайд 1
Буквально слово танграм означает «семь дощечек мастерства». Танграм — головоломка, состоящая из семи танов (плоских геометрических фигур), полученных делением квадрата на семь частей – два больших (1, 2), два маленьких (3, 4) и один средний треугольник (5), один квадрат (6) и один параллелограмм (7), которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться между собой.

Базовым элементом танграма является тан. Таны возможно получить при разрезании квадрата первоначально на два больших равных треугольника, далее согласно рисунка. Минимальное количество базовых фигур равное семи приводит к гениальной простоте комбинаций.

Легенды появления танграма

II.Выступления учащихся:
Танграм — очень древняя игра – головоломка. Она появилась в Китае более
4000 лет назад. Существует целый ряд версий и гипотез возникновения игры “Танграм”.
Легенда первая: версия про разбитую плитку.
Более 4000 тысяч лет назад у одного человека из рук выпала фарфоровая плитка и разбилась на семь частей. Расстроенный, он в спешке старался ее сложить, но каждый раз получал все новые интересные изображения. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости.

Легенда вторая: три мудреца придумали «Ши-Чао-Тю».
Появление этой китайской головоломки связано с красивой легендой. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло большее удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали «Ши-Чао-Тю»- квадрат, разрезанный на семь частей.

Легенда третья:семь книг Тана.
«В записках покойного профессора Челленора, попавших в руки автора, — утверждал Лойд, — имеются сведения о том, что семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур, были составлены в Китае более 4000 лет назад. Эти книги ныне стали столь большой редкостью, что за те сорок лет, которые профессор Челленор провел в Китае, ему лишь раз удалось видеть первое издание первого из семи томов (сохранившихся полностью) и несколько разрозненных фрагмента второго тома».
Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа «инь и ян». Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудию труда, мебель, одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция, философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить. Встречаются у Лойда и ссылки на «известные» китайские пословицы типа «Только глупец взялся бы написать восьмую книгу Тана».
Первое изображение танграма (1780) обнаружено на ксилографии японского художника Утомаро, где две девушки складывают фигурки. Название «танграм» возникло в Европе, вероятнее всего, от слова «тань» (что означает «китаец») и корня «грамма» (в переводе с греческого «буква») На первых порах им пользовались не для развлечения, а для обучения геометрии.

Танграм в литературных произведениях

III.Выступление учителя
Льюис Кэрролл
Все мы хорошо знаем книгу “Алиса в стране чудес” Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге “Модная китайская головоломка” он пишет, что танграм был любимой игрой Наполеона Бонапарта, который, лишившись трона, в изгнании на Острове Святой Елены проводил долгие часы за этой забавой, “упражняя свое терпение и находчивость”.
Эдгар А. По
Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм, сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке.
Известный писатель и дипломат Роберт Ван Гулик в романе “Убивающие ногтями” построил весь сюжет книги вокруг танграма

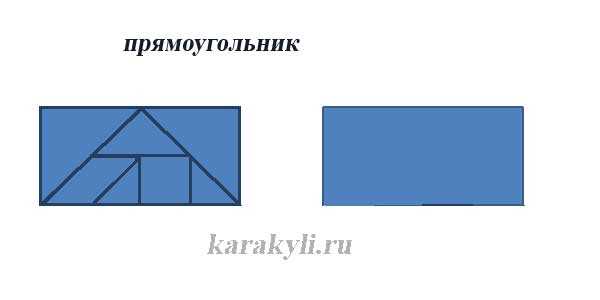
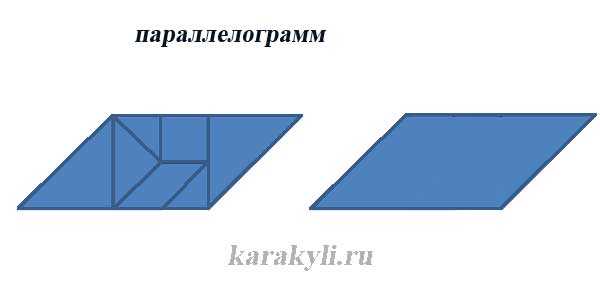
Сфера применения танграма гораздо шире, чем просто игра. Из частей головоломки можно составлять изученные геометрические фигуры (треугольник, квадрат, параллелограмм, трапеция, прямоугольник), вычислять их площади, а также сравнивать эти фигуры с помощью наложения.
Нас заинтересовала головоломка «Танграм», как игра, так как можно творчески провести время. Увлекает то, что из простых геометрических фигур можно сделать более сложные композиции.
Суть игры заключается в конструировании на плоскости разнообразных предметных силуэтов, напоминающих животных, людей, предметы быта, транспорт, буквы, цифры, цветы и т.д. Всего насчитывают более 7 000 различных комбинаций. Самые распространенные из них — фигуры животных, птиц и человека.
Правила игры: Слайд 2
 В каждую собранную фигуру должны входить все семь элементов.
 При составлении фигур элементы не должны налегать друг на друга.
 Элементы фигур должны примыкать один к другому.
 Начинать нужно с того, чтобы найти место самого большого треугольника.
В результате игры получается плоскостное силуэтное изображение. Оно условно, схематично, но образ легко угадывается по основным характерным признакам предмета: его строению, пропорциональному соотношению частей и форме.
Типы задач, решаемых танграмом. Слайд 3-5
1. Нужно сложить фигуру по контурному рисунку.
2. Нужно сложить фигуру по рисунку со сплошной заливкой, при котором не видно границ элементов.
Затем можно попрактиковаться самостоятельно, создавая свои — простейшие изображения. Тем самым развивается собственная фантазия.
Можно не останавливаться лишь на конструктивной части игры. Увлекает перенесение получившихся силуэтов на бумагу. Можно сделать подрисовку, создать и проработать фон, придумать сюжет. А удачные композиции вполне можно использовать для украшения интерьера комнаты или игрового уголка.
3. Составление более сложного двойного или тройного танграма (для этого используются два или три комплекта из семи «танов»). В качестве иллюстрации можно предложить рисунок «Игра на бильярде», приведённый в книге Я.И. Перельмана «Весёлые задачи»
Применение танграма

Танграм может применяться на уроках математики дляполучение начальных сведений о геометрии. Знакомство с простейшими геометрическими фигурами: квадрат, треугольник, ромб, знакомство с углами. Сравнение фигур по форме, размеру, площади.

Составление из нескольких фигур новой геометрической фигуры: из двух треугольников – ромб, большой треугольник, квадрат, из трёх – треугольник,
трапецию, параллелограмм и т.д.

Играя, мы запоминаем названия геометрических фигур, их свойства, отличительные признаки, обследуем формы зрительным и осязательно-двигательным путем, свободно перемещаем их с целью получения новой фигуры. У нас развивается умение анализировать простые изображения, выделять в них и в окружающих предметах геометрические формы, практически видоизменять фигуры путем разрезания и составлять их из частей.

Танграм во всех его проявлениях можно встретить начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном.

IV.Работа в группах.
Слайд 6-10

Учитель математики: —
Сегодня я предлагаю составить фигуру семью танами одного танграма, на каждой парте конверт с танграмом.

V.Выступление учителя

Парадокс Слайд11
откуда взялась нога у человечка: парадокс, обнаруженный Г. Дьюдени. Как видно из схемы, первая фигура чуть толще второй; площадь «ноги» в точности равна площади избыточной полоски на животе, обозначенной отрезком АВ).

VI.Выступление учителя
Другие головоломки Слайд 12- 15
Головоломка Пифагора
Головоломка Пифагора — это квадрат, разделенный на семь частей — 2 квадрата, 4 треугольника и параллелограмм. Изобразительные возможности игры достаточно велики — можно создавать силуэты различной степени сложности и сложные геометрические фигуры, напоминающие предметы быта, животных, птиц и т.д.

Игра «Стомахион»
Древние греки занимались геометрией, не только измеряя земельные участки и расстояния до кораблей в море. Они любили геометрические игры. Одна из них называлась «СТОМАХИОН». В этой игре надо было из 14 частей квадрата складывать различные фигуры. Создателем ее считали Архимеда. В 1899 г. Швейцарский историк Генрих Зютер обнаружил в книгохранилищах Берлина и Кембриджа арабскую рукопись «Книга Архимеда о разбиении фигуры стомахиона на 14 частей, находящихся в рациональных отношениях». Позже датский историк математики Гейберг подтвердил, что создателем игры является Архимед.
Получают разбиение стомахиона на 14 частей из прямоугольника, одна сторона которого в два раза больше другой.
Да, игра «Стомахион» требует большего терпения. Ведь она намного сложнее игры»Танграм», недаром слово «стомахион»переводится как «приводящая в ярость».
Игра «Пентамино»
Пентамино (от древне – греческого пeнта пять, и домино – полимино) – 12 фигур, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами («ходом ладьи»). Этим же словом иногда называют головоломку, в которой такие фигуры требуется укладывать в прямоугольник или другие формы.

Игра «Колумбово яйцо»
Жил-был в 16 веке итальянецДжироламо Бенцони. Он любил путешествовать. И однажды на обеде у кардинала Мендосы он встретил Колумба. Там и произошла эта история. Христофор Колумб рассказывал о своем открытии Америки. И вдруг слышит от одного из гостей: «Как просто открываются новые земли!» Тогда Колумб предложил «просто поставить яйцо на стол вертикально?» Никто не смог это сделать. Тогда Колумб ударяет яйцо об стол, сплющивая один конец, и яйцо встает вертикально. Все возмутились, что так бы и они смогли. На что Колумб ответил: « Вы бы смогли, а я сделал это». С тех пор выражение «колумбово яйцо» применяют, когда говорят о простом и неожиданном решении сложной задачи.
Колумбово яйцо – это яйцо, разрезанное на 10 частей. Сейчас эту головоломку продают в разных исполнениях – и деревянную, и бумажную, и пластиковую. На плоскости необходимо выкладывать любые фигуры, какие придумаешь или можно использовать образец. При этом нельзя накладывать части, чтобы они перекрывали друг друга. А также необходимо использовать все детали

VII. Работа на компьютере Слайд 16
Учитель: Вы составляли танграм из кусочков бумаги, а теперь поиграем в компьютерную мозаику.
При сборе мозаики на компьютере вам потребуется выделять и перемещать фрагменты рисунка, отображать и поворачивать его. Поэтому познакомимся с алгоритмами выделения, перемещения, отображения и поворота фрагмента рисунка.
Как выделить фрагмент?

Установить указатель мыши немного выше и левее выделяемого фрагмента;
Двигая мышь с нажатой кнопкой, заключить нужную область в пунктирный прямоугольник.

Каким выделением будем пользоваться?
Как правило, удобнее использовать выделение без фона.
Как переместить фрагмент?

Установит указатель мыши внутри выделенного фрагмента;
Двигать мышь с нажатой кнопкой к нужному месту.

Как отразить фрагмент рисунка?

Выделить фрагмент рисунка.
В строке меню выбрать пункт Рисунок.
Из раскрывшегося меню выбрать пунктОтразить/Повернуть.
В диалоговом окне установить требуемое действие.
Ок.

Как повернуть фрагмент рисунка?

Выделить фрагмент рисунка.
В строке меню выбрать пункт Рисунок.
Из раскрывшегося меню выбрать пунктОтразить/Повернуть.
В диалоговом окне выбрать пунктПовернуть на угол.
Выбрать необходимый угол поворота.
Ок.

Заключение
Что интересного было на занятии?
Что особенно запомнилось?
Какой композиции вы бы отдали предпочтение, и почему?

Исследовав практическое применение «Танграма», мы пришли к выводу, что комбинируя на плоскости элементы разрезанного на части квадрата, можно создавать множество новых фигур, как геометрических, так и жанровых — очертания животных, людей, бытовых предметов и т.д. Эта головоломка развивает умственные и творческие способности, пространственное воображение, комбинаторные способности, логическое мышление, сообразительность, смекалку, а также усидчивость и мелкую моторику, формирует внимательность, упорство в достижении цели, способствует творческому поиску чего – то нового, учится терпению и последовательности.
Вообще, игры — головоломки – это хорошая разрядка от трудных ежедневных проблем и они просто интересны!
Закончить о танграмах можно словами М. Гарднера: «Очарование танграма состоит в простоте материала и в кажущейся его непригодности для создания фигурок, обладающих эстетической привлекательностью»

Домашнее задание: изготовить танграм и придумать свои фигуры.

Презентация

18.12.2012

urok.1sept.ru

Игра «Танграм» — Сайт воспитателя Новак Елены Валентиновны

Это древняя китайская игра. Если разделить квадрат на семь геометрических фигур, как это показано на рисунке, то из них можно составить огромное количество (несколько сотен) самых разнообразных силуэтов: человека, предметов домашнего обихода, игрушек, различных видов транспорта, цифр, букв.

Игра очень проста в изготовлении. Квадрат (величина его практически может быть любой: 5×5, 7×7, 10×10, 12×12 см и т.д.) из картона или пластика, одинаково раскрашенный с двух сторон, разрезают на 7 частей. В результате получается 2 больших, 1 средний и 2 маленьких треугольника, квадрат, равный по размерам двум маленьким треугольникам, и параллелограмм, по площади равный квадрату.

Правила игры:

1. В каждую собранную фигуру должны входить все семь элементов.
2. При составлении фигур элементы не должны налегать друг на друга.
3. Элементы фигур должны примыкать один к другому.

При составлении силуэтов взрослый постоянно напоминает детям, что необходимо использовать все части набора, плотно присоединяя их друг к другу.

Взрослый может применять некоторые приёмы, которые помогут дошкольнику достичь наилучших результатов: предложить анализ образца в целом или наиболее сложной его части, указать на расположение одной-двух фигур в составляемом силуэте, начать выкладывание, а затем предложить ребёнку закончить силуэт или, наоборот, завершить то, что начато ребёнком. Следует постоянно подтверждать правильность хода мысли и действий ребёнка, побуждать его планировать ход своей работы, обсуждать способы выкладывания и результаты, поощрять стремление доводить начатое дело до конца, преодолевая трудности в достижении поставленной цели, выполнении задуманного.
Помощь ребёнку должна быть тактичной, побуждающей к самостоятельности, активности, настойчивости, инициативным действиям, ведущим к достижению результата. Прямых указаний, что и как делать, лучше избегать. Уместны такие советы детям: «Посмотри (рассмотри) картинку внимательно. Из каких фигур она составлена?», «Попробуй сделать ещё раз, но по-другому», «Вспомни, как ты выкладывал в прошлый раз, и начни так же», «Вначале хорошо подумай, а потом делай».

Игра «Танграм» вызывает у детей огромный интерес, способствует развитию аналитико-синтетической и планирующей деятельности, открывает новые возможности для совершенствования сенсорики, развития творческого, продуктивного мышления, а также нравственно-волевых качеств личности.

Интересна история появления этой игры. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Мальчику доставляло большое удовольствие целый день забавляться игрушками. И тогда император призвал к себе трёх мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом. И повелел он им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, а также и понял, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали «Ши-Чао-Тю» – квадрат, разрезанный на семь частей.

Этапы освоения игры «Танграм»

Первый этап — ознакомление с набором фигур к игре, преобразование их с целью составления из 2-3 имеющихся новой.

I.
Цель. Упражнять детей в сравнении треугольников по размеру, составлении из них новых геометрических фигур: квадратов, четырехугольников, треугольников.
Материал: у детей наборы фигур к игре «Танграм», у воспитателя фланелеграф и набор фигур к нему.
Ход работы. Воспитатель предлагает детям рассмотреть набор фигур, назвать их, сосчитать и определить общее количество. Дает задания:
1. Отобрать все треугольники, сосчитать. Сравнить по размеру, накладывая один на другой.
Вопросы для анализа: «Сколько больших, одинаковых по размеру треугольников? Сколько маленьких? Сравните этот треугольник (среднего размера) с большим и маленьким. (Он больше самого маленького и меньше самого большого из имеющихся.) Сколько всего треугольников и какого они размера?» (Два больших, 2 маленьких и 1 средний по размеру.)
2. Взять 2 больших треугольника и составить из них последовательно: квадрат, треугольник, четырехугольник. Один из детей составляет фигуры на фланелеграфе. Воспитатель просит назвать вновь полученную фигуру и сказать, из каких фигур она составлена.
3. Из 2 маленьких треугольников составить те же фигуры, располагая их по-разному в пространстве.
4. Из большого и среднего по размеру треугольников составить четырехугольник.
Вопросы для анализа: «Какую фигуру составим? Как? (Присоединим к большому треугольнику средний или наоборот.) Покажите стороны и углы четырехугольника, каждой отдельной фигуры».
В итоге воспитатель обобщает: «Из треугольников можно составлять новые различные фигуры — квадраты, четырехугольники, треугольники. Фигуры присоединяются одна к другой по сторонам». (Показывает на фланелеграфе)

II.
Цель. Упражнять детей в умении составлять новые геометрические фигуры из имеющихся по образцу и замыслу.
Материал: у детей — наборы фигур к игре «Танграм». У воспитателя — фланелеграф и таблицы с изображенными на них геометрическими фигурами.
Ход работы. Дети, рассмотрев фигуры, делят их по заданию воспитателя на 2 группы: треугольники и четырехугольники.
Воспитатель поясняет, что это набор фигур к игре, называется она головоломка или танграм; так ее назвали по имени ученого; придумавшего игру. Можно составить много интересных изображений.
1.Составить четырехугольник из большого и среднего треугольников.
2.Составить новую фигуру из квадрата и 2 маленьких треугольников. (Сначала — квадрат, затем — четырехугольник.).
3.Составить новую фигуру из 2 больших и среднего треугольника. (Пятиугольник и четырехугольник.)
4.Воспитатель показывает таблицы и просит детей составить такие же фигуры (см. рис.). Дети последовательно составляют фигуры, рассказывают, как они делали, называют их.
Воспитатель составляет их на фланелеграфе.

Дается задание на составление нескольких фигур по собственному замыслу детей.
Итак, на первом этапе освоения игры «Танграм» проводится ряд упражнений, направленных на развитие у детей пространственных представлений, элементов геометрического воображения, на выработку практических умений в составлении новых фигур путем присоединения одной из них к другой, соотношение сторон фигур по размерам. Задания видоизменяют. Дети составляют новые фигуры по образцу, устному заданию, замыслу. Им предлагают выполнить задание в плане представления, а затем — практически: «Какую фигуру можно составить из 2 треугольников и 1 квадрата? Сначала скажите, а затем составьте».

Второй этап — составление фигур-силуэтов по расчлененным образцам. Второй этап работы с детьми является наиболее важным для усвоения ими в дальнейшем более сложных способов составления фигур. Игры должны быть эффективно использованы воспитателем не только с целью упражнения в расположении частей составляемой фигуры, но и в приобщении детей к зрительному и мысленному анализу образца.

Составление фигуры-силуэта зайца
Цель. Учить детей анализировать способ расположения частей, составлять, фигуру-силуэт, ориентируясь на образец.
Материал: у детей — набор фигур к игре «Танграм», образец.

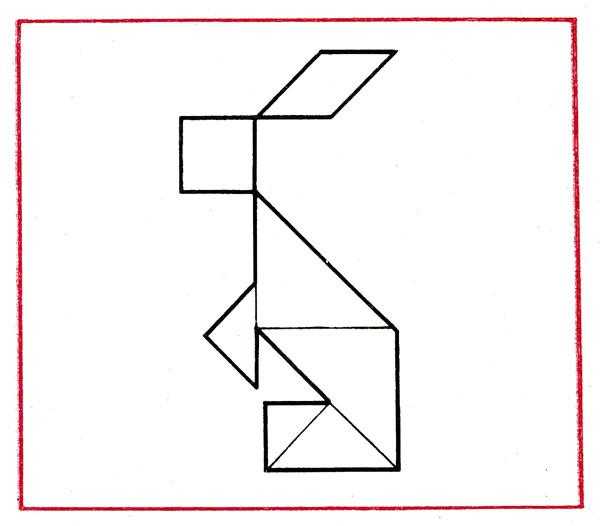
Ход работы. Воспитатель показывает детям образец фигуры-силуэта зайца (см. рис.) и говорит: «Посмотрите внимательно на зайца и расскажите, как он составлен. Из каких геометрических фигур составлены туловище, голова, ноги зайца?» Надо назвать фигуру и ее величину, так как треугольники, из которых составлен заяц (показывает), разных размеров; предлагает нескольким детям ответить.

Р. Голова зайца составлена из квадрата, ухо — из четырехугольника, туловище — из двух треугольников, а лапы — тоже из треугольников.

В. Правильно ли рассказал Коля? Если заметили ошибки, исправьте их.
Воспитатель просит рассказать другого ребенка.

Р. Туловище надо составить из 2 больших треугольников, лапу (вот эту) — из среднего треугольника и маленького, а другую — из маленького треугольника.

В. Теперь посмотрите, какую геометрическую фигуру образуют 2 больших треугольника. Покажите стороны, углы этой фигуры.

Р. Это четырехугольник (показывает его контур, считает углы, стороны).

В. А какую фигуру образует вместе средний и маленький треугольник?

Р. Это четырехугольник, вот здесь (показывает) не как у прямоугольника.

В. Вот мы и рассмотрели, как составлен заяц, из каких фигур составлены туловище, голова, лапы. А теперь возьмите свои наборы и составляйте. Кто выполнит задание, проверьте, правильно ли составил.
После того как фигура составлена, воспитатель просит двоих детей рассказать, как они составили фигуру, т. е. назвать расположение составных частей по порядку.

Р. Я составила так: голову и ухо — из квадрата и четырехугольника, туловище — из 2 больших треугольников, лапы — из среднего и маленького и 1 лапку — из маленького треугольника.

Р. У меня ухо составлено из четырехугольника, голова — из квадрата, лапа — из треугольника, туловище — из больших треугольников, лапы — вот эти — из 2 треугольников.
Анализ образца в данном случае проводился под руководством педагога. В дальнейшем следует предлагать детям самостоятельно провести анализ фигуры и составить ее.

Третий этап освоения игры — воссоздание фигур по образцам контурного характера (нерасчлененным)

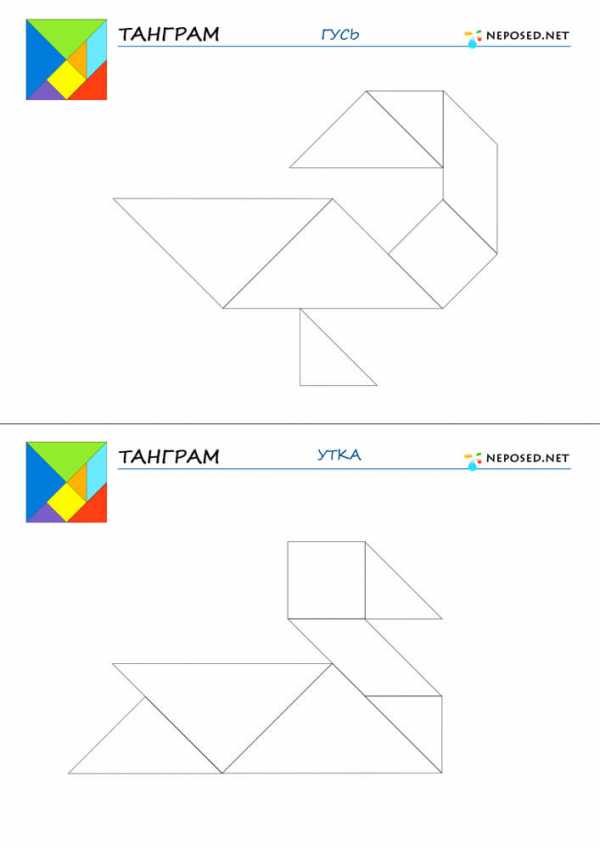
Воссоздание фигуры-силуэта бегущего гуся
Цель. Учить детей предположительно рассказывать способ расположения частей в составляемой фигуре, планировать ход составления.
Материал: наборы, фигур к игре «Танграм», фланелеграф, образец, доска и мел.

Ход работы. Воспитатель обращает внимание детей на образец: «Посмотрите внимательно на этот образец. Фигуру бегущего гуся можно составить из 7 частей игры. Надо сначала рассказать, как это можно сделать. Из каких геометрических фигур можно составить туловище, голову, шею, ноги гуся?»

Р. Я думаю, что туловище составлено из 2 больших треугольников, голова — из маленького треугольника, шея — из квадрата, лапы — треугольники.

Р. Я думаю, что голова из среднего треугольника составлена, а дальше все так же, как Лена говорила.

Р. Голова из среднего треугольника, шея — из квадрата, а туловище — из 2 больших треугольников, вот так они лежат (показывает), и четырехугольника, а ноги — из маленьких треугольников.

В. Возьмите фигуры и составляйте. И мы узнаем, кто из ребят прав.

После того как большинство детей составят силуэт гуся, воспитатель вызывает одного ребенка, который мелом на доске рисует расположение частей. Все дети сверяют составленные ими фигуры с изображением на доске.

В дальнейшем возможно проведение анализа образца составляемой фигуры не в начале занятия, а в ходе его, когда дети апробируют различные пути составления на основе предположительного самостоятельного анализа.

Четвертый этап — упражнения в составлении изображений по собственному, замыслу. Задумав составить какое-либо изображение, мысленно, в плане представления, членят его на составные части, соотнося их с формой танграмов, затем составляют.

Пятый этап — составление силуэтов из 2-3 одинаковых наборов фигур к игре «Танграм»

Руководство процессом составления должно быть направлено на развитие умения предвидеть сочетание фигур, изменения в их расположении и форме составляемого силуэта.

Итак, в обучении детей воссозданию фигур-силуэтов из частей игры «Танграм» последовательность усложнения заданий можно представить следующим образом: от овладения элементарными способами зрительного анализа дети переходят к усвоению способов мысленных действий.

ПРИЛОЖЕНИЯ

Игра «Танграм» Скачать в формате DOC

Танграм шаг за шагом Скачать в формате PDF (размер 22,1 Мб)

НАБОРЫ ФИГУР

Для скачивания – кликнуть на соответствующем рисунке.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

novakelena.wordpress.com

Проект «Геометрические соотношения танграм»(8 класс)

ОБОШИ «Лицей-интернат поселка имени Маршала Жукова»

Вторая школьная научная конференция

Тема:

«Геометрические соотношения ТАНГРАМ»

Выполнили: Болдаков Владислав и

Измайлов Сергей 8А класс

Руководитель: Курдюмова Елена Валерьевна

Содержание

Введение
История возникновения Танграм
Геометрические соотношения сторон и углов фигур, площадей
Правила танграма
Доказательство теоремы Пифагора
Парадоксы
Практическое применение танграм
Список литературы
Приложение

Когда китайская головоломка «Танграм» попала в наши руки, мы задумались – это просто игра или что-то большее? Чтобы разобраться в этом вопросе, нам предстояло изучить все комплектующие фигуры: измерить их размеры, вычислить площади, найти соотношения, установить возможности применения танграм, выяснить, почему не угасает интерес к этой игре и сейчас.

Что это такое? В переводе с китайского языка Танграм – семь дощечек мастерства, это головоломка, состоящая из семи плоских фигур «танов»: квадрата, параллелограмма, двух больших одинаковых треугольников, среднего треугольника и двух одинаковых маленьких треугольников.

Существует целый ряд версий и гипотез возникновения как слова «танграм», так и самой головоломки. Последние исследования Джерри Слокума подтвердили, что танграм был изобретен в Китае в 1796 – 1801 гг. Появление танграма на западе относят не ранее чем к началу XIX столетия, когда эти головоломки попали в Америку на китайских и американских судах. Старейший такой экземпляр, подаренный сыну американского судовладельца в 1802 году, сделан из слоновой кости.

Писатель и математик Льюис Кэрролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.

У Наполеона во время его изгнания на остров Святой Елены был набор для танграма и книга, содержащая задачи и решения.

Слово «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии».

И нас головоломка танграм заинтересовала как набор геометрических фигур.

Как гласит легенда, однажды китайский император заказал лист стекла гигантских размеров. Пока этот хрупкий квадратный груз везли во дворец императора, лист упал, но не разбился вдребезги, а раскололся на семь геометрически правильных фигур. При попытке сложить их вместе выяснилось, что это можно сделать множеством способов, и при этом получаются всевозможные фигуры. Создатели стеклянного листа продолжили путь, а во дворце показали императору свое изделие как удивительную головоломку. Император с восторгом принял подарок.

В легенде сказано, что лист стекла был квадратный, поэтому первая из задач танграма – составление квадрата.

Выполняя эту задачу, фигуры переворачивались, прикладывались друг к другу и мы заметили, что некоторые из них имеют одинаковые стороны. А когда квадрат получился, было понятно, что площади всех фигур равны площади всего квадрата.

Мы провели исследования: измерили стороны и углы плоских фигур, вычислили их площади.

Квадрат:

DF=FO=OM=MD=3,5см

S=3,5·3,5=12,25см²

F=D=M=O=90˚

Параллелограмм:

EM=CK=5см, CE=MK=3,5см, h=2,5см

S= 2,5·5=12,5см²

С=М=45˚, Е=К=135˚

Большие треугольники:

∆ADB = ∆ADC

AD=DB=DC=AD=7см

AB=AC=10см

S_ADB= S_ADC= ·7·7=24,5см²

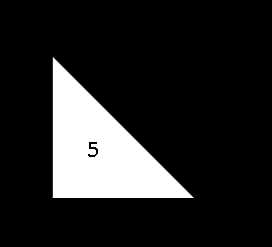
Средний треугольник:

KP=OP=5см

KO=7см

S= ·5·5=12,5см²

Маленькие треугольники:

∆EDM = ∆BFO

ED=DM=BF=FO=3,5см

EM=BO=5см

S_EDM=S_BFD= 3,5·3,5=6,125см²

По результатам нашей работы мы пришли к выводу: между деталями танграма существует ряд геометрических соотношений.

Соотношение сторон и размеры углов:

Длина катета большого треугольника равна длине гипотенузы среднего треугольника.
Длина катета среднего треугольника равна длине гипотенузы маленького треугольника, диагонали квадрата и одной из сторон параллелограмма.
Длина катета маленького треугольника равна длине стороны квадрата, а его гипотенуза – стороне параллелограмма.
У параллелограмма два угла по 45˚ и еще два по 135˚.
Пять треугольников равнобедренные и прямоугольные, поэтому у каждого из них есть угол в 90˚ и два угла по 45˚.
У квадрата, разумеется, четыре угла по 90˚.

Соотношение площадей:

Площадь большого треугольника вдвое больше площади среднего треугольника.
Средний треугольник, квадрат и параллелограмм имеют одинаковую площадь.
Площадь среднего треугольника вдвое больше площади маленького треугольника.
Площадь квадрата вдвое больше площади маленького треугольника.
Площадь параллелограмма вдвое больше площади маленького треугольника.

Установленные нами соотношения между танов позволяют заменить средний треугольник или квадрат или параллелограмм двумя маленькими треугольниками, большой треугольник заменить средним и двумя маленькими треугольниками или квадратом и двумя маленькими треугольниками или параллелограммом и двумя маленькими треугольниками. Прикладывая острым углом любой треугольник к острому углу параллелограмма, мы получим прямой угол, а прикладывая треугольник острым углом к прямому углу любой фигуры, мы получим угол в 135˚, т.е. тупой угол параллелограмма.

Всё это даёт возможность строить из них различные фигуры, которые задаются в виде силуэта или внешнего контура, буквы. При этом необходимо соблюдать правила.

В каждую фигуру должны входить все семь деталей.
Фигуры должны соприкасаться между собой (не должны перекрываться).

Исследуя детали танграма, заполняя пустоты силуэтов, мы пришли к выводу:

infourok.ru

Танграм — геометрическая головоломка

29 октября, 2012

Комментариев нет »

Игра служит для тренировки внимания, восприятия цвета, формы; способствует развитию у детей наглядно-образного мышления, воображения, комбинаторных способностей.

Танграм (кит.«семь дощечек мастерства») — древняя китайская головоломка, состоящая из семи плоских геометрических фигур, которые выкладывают в определенном порядке с целью получить различные более сложные фигуры в виде человека, животного, предмета домашнего обихода и т. д. Фигура, которую необходимо сложить, задаётся в виде силуэта или внешнего контура (в заданиях для взрослых и детей старше 7-ми лет) или в цвете с разложением на простые фигуры (для маленьких детей до 7-ми лет). При решении любого задания головоломки необходимо соблюдать два основных правила:

1- использовать все семь фигур танграма

2- фигуры не должны перекрываться между собой

Этот танграм изготовлен в домашних условиях из куска дощечки размером 15 x 15 см, толщиной 1 см путем распила на кусочки, шлифовки и окраски акриловыми красками.

Распиливаем большой квадрат, стороны которого равными 15 см, на части:
2 маленьких прямоугольных треугольника (с гипотенузой, равной 15/2=7.5 см катетами 15/2√2≈5.3 см ),
1 средний прямоугольный треугольник (гипотенуза 15/√2≈10.6 см и катеты 15/2=7.5 см),
2 больших прямоугольных треугольника (гипотенуза 15 см и катеты 15/√2≈10.6 см),
1 квадрат (со стороной 15/2√2≈5.3 см ),
1 параллелограмм (со сторонами 15/2=7.5 см и 15/2√2≈5.3 см и углами 45° и 135º).

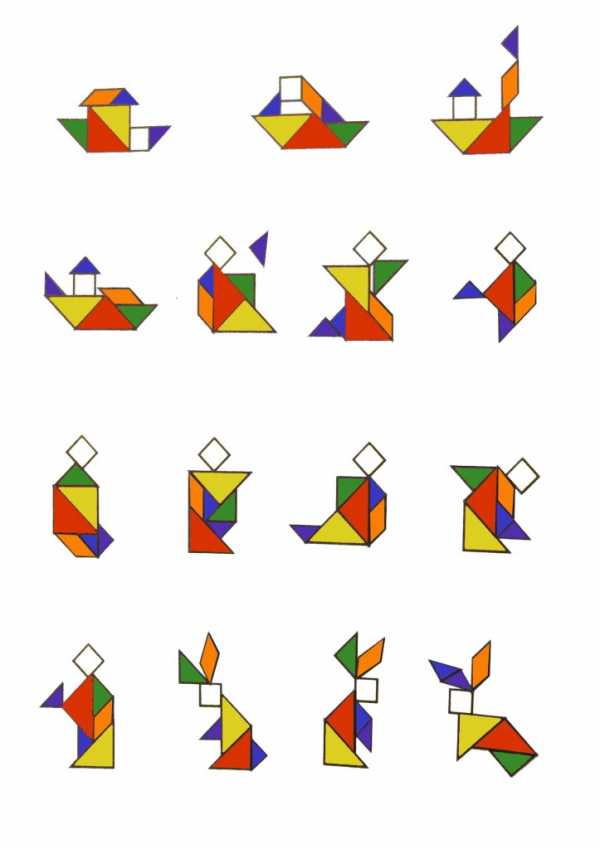
Прилагаются задания для детей до 7-ми лет:

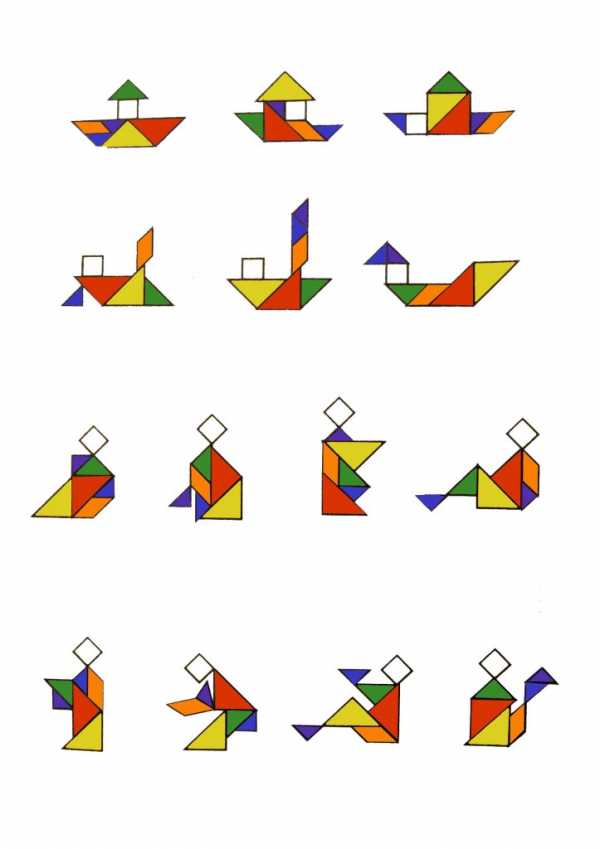
Задания для взрослых и детей старше 7-ми лет:

Комментариев нет.

mirdetey.by