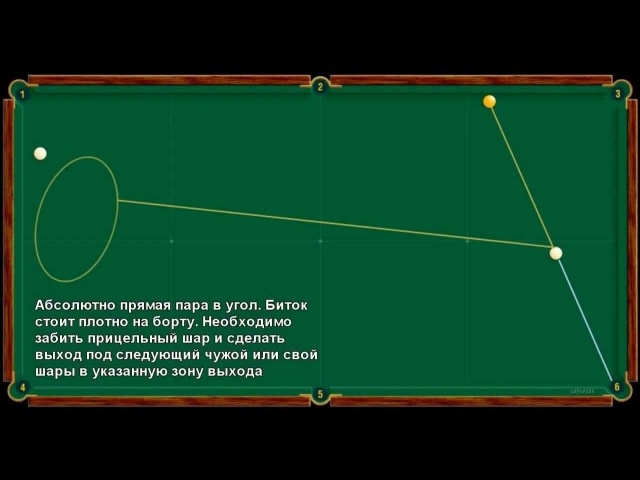
|
Теория удара в бильярде shram.
kiev.uaПо теме:- Теория прицеливания в бильярде
Бильярд (фр. billard, от фр. bille — шар или фр. billette, billart — палка) — собирательное название нескольких настольных игр с разными правилами, а также специальный стол, на котором происходит игра.
Характерной особенностью всех бильярдных игр является передвижение шаров с помощью кия.
Помещение, специально оборудованное для игры на бильярде, — Бильярдная.
Родиной бильярдной игры считают Индию или Китай.
Хороший бильяр
Плоскость бильярда состоит из двух квадратов, сложенных вместе. Эта древняя форма очертаний бильярда основана на глубоком изучении бильярдной игры. Разумеется, если бы бильярд имел очертание строгого квадрата, то дуплеты, триплеты и вообще все «отраженные» шары шли бы с замечательною правильностью. Тоже было бы на круглом бильярде. Но только бильярд в виде четырехугольника дает массу разнообразных положений шара, и вот почему эта форма сохраниться на веки.
Хороший бильярд должен быть, прежде всего велик. Это основное достоинство имеет такое большое значение, что как бы маленький бильярд ни был точен, изящен и строг, иной отличный игрок играть на нем не станет.
И это справедливо. На малом бильярде другой удар, другой расчет. Игрок, превосходно играющий на большом бильярде, играя на маленьком также уверенно и свободно, часто подставляет шары и с раздражением видит, как партию выигрывает заведомо слабейший игрок. А это легко понять, ибо что на большом бильярде отыгрыш, то на малом подставка. Одним словом, здесь наиболее очевиден основной закон бильярдной игры: чем фальшивее, легче и меньше бильярд, тем силы хорошего и дурного игрока более уравновешенны. Вот почему первоклассный игрок никогда не станет играть на скверном бильярде.
Бильярд должен быть строг и правилен — не только в смысле фабрикации его бортов и луз, но и относительно подбора шаров к лузам.
Ведь всякий бильярд на первый взгляд нетрудно сделать строгим: стоит лишь взять шары, которые едва бы входили в лузы.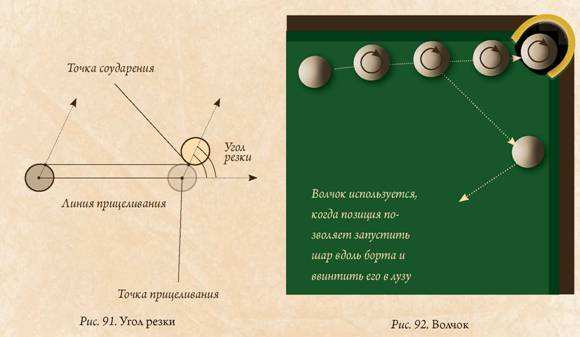
Правда это будет относительная строгость. Истинная строгость заключается в соблюдении математической пропорциональности между размерами бильярда, величиною луз и диаметров шаров. При этом должно иметь ввиду следующий важный закон всех русских партий: требуется, чтобы всякий шар в любую лузу падал при сильном ударе, по борту в среднюю лузу играть было бы невозможно.
Удовлетворить этому закону в техническом смысле очень трудно, но возможно. Впрочем некоторые мастера не признают, что бортовой шар, один из самых блестящих ударов на бильярде, мог падать идя по борту. Другие мастера и большинство из них стремятся, напротив, облегчить делание бортовых шаров. Для этого они понижают плоскость бильярда у бортов, вследствие чего шар тянет к борту, и потому шары, даже неверно взятые, при тихом ударе непременно сваливаются в лузу.
В настоящее время даже почти невозможно встретить строгого бильярда, на котором шар шел бы по борту. Теперь таких бильярдов не умеют делать.
Бильярды наследников Фрейберга часто так строги, что партию хорошие игроки играют около часу. Значит, на этих бильярдах учтены все разнообразные элементы игры и все принесено в жертву только одной точности прицела. Эту игру следует называть грубой. Такой бильярд по своей односторонности приближается к кегельбану.
На точном бильярде вся чистота и прелесть игры зависит от разумной вырезки бильярдных луз, а поэтому обращаю внимание бильярдных фабрикантов на этот вопрос.
Техника игры
Техника бильярдной игры заключается: в умении играть равно успешно сильным и тихим штосом, делать прямые удары, резать, уметь дуплетировать и наконец — владеть выходом и отыгрышем.
В самом деле даже для самого невнимательного наблюдателя очевидно, что у всякого бильярдного игрока хорошего или плохого, все равно, своя манера играть, свой удар. Повсюду слышны выражения: у него красивый удар, у того-то смелый удар и т.д. Следовательно, качество зависящее от талантливости или бездарности каждой отдельной натуры.
Нет сомнения, что путем долгих и беспрерывных упражнений можно изощрить до поразительности глаз, усвоить неимоверную точность удара, но удара артиста этого свободного, смелого и широкого размаха нельзя приобрести ничем, если нет его от природы.
Если вы не имеете от природы красивого удара, не гонитесь за ним. Лучше работайте упорно, развивайте философское хладнокровие, и вы, пожалуй, никогда не пожалеете о том, что природа обошла вас в другом отношении.
Игроки, играющие постоянно на большие деньги привыкают играть ровным, умеренным и беспощадно правильным ударом. В этом ударе нет резких ни forte, ни piano — он очень сам по себе однообразен и самоуверен. Такой удар называется коммерческим. Игрок, привыкший играть подобным образом, никогда не станет рисковать, никогда из вредной хвастливости не пренебрежет подставкой и лишь разве случайно сам сделает подставку. Такая игра, разумеется, очень поучительна, но она и суха и, если можно так выразиться, слишком машинна.
В ней нет огня, аристократического выполнения и вкуса. Притом, когда с коммерческим игроком сойдется артист, с блестящей техникой и разумным риском, хотя и равной силы, то первый обескураживается, что подряд начинает проигрывать все партии.
Совершенно прямой удар на значительном расстоянии между шарами справедливо считается самым трудным ударом на бильярде. Легче всего сделать прямой шар накатом. Так это и советую делать новичкам. Значительно труднее играть прямого клапштосом и еще труднее оттяжкой. Однако этими тремя штрихами не должен довольствоваться артист. Он должен пользоваться иногда и французским ударом.
Физика бильярда
Как известно в физике рассматриваются весьма подробно законы упругих тел и выводятся формулы, выражающие силу удара шаров, скорость после удара и т.д.
К сожалению, все эти формулы выведены только для шаров, имеющих одно движение — поступательное, т.е. вперед. В бильярдной же игре приходится постоянно рассматривать удары шаров, имеющих два или даже три движения.
При разборе этих ударов условимся называть свой шар красным и положим, что на бильярде произвольное число белых шаров, необходимые для разъяснения той или иной вариации игры — обобщим таким образом все бильярдные партии для изучения законов ударов шаров.
Не трудно заметить, что шары соприкасаются с собой в точках. Надо добавить, что при сильном ударе, вследствие значительной упругости слоновой кости, эти точки являются далеко не геометрическими. Поэтому шары легко передают друг другу не только поступательное, но и вращательное движение. Затем, выше было сказано, что такое «истинная точка прицела», и что для каждого частного случая положения шаров она одна, и когда ее видно, говорят: «шар виден»; когда не видно, то говорят: «шара не видно». Переходим теперь собственно к эффектам бильярдной игры.
Клапштос
Точка удара при клапштосе
Физика учит, если шары имеют одинаковый размер, то когда один шар ударит другого, то последний отскочит, а ударившийся остановится неподвижно на месте.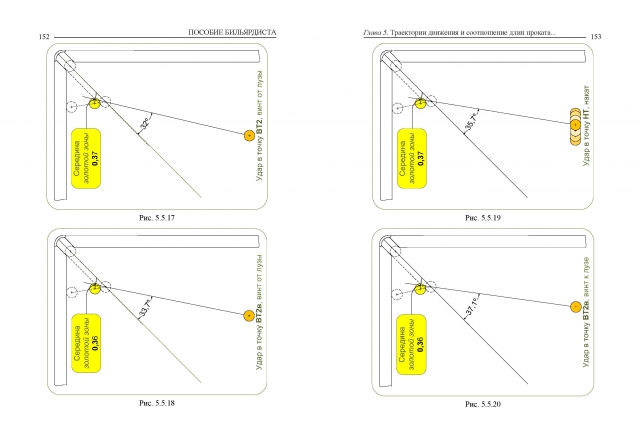
То же самое всегда бывает на бильярде, но для этого надо так ударить кием красного, чтобы он получил только одно поступательное движение (центральный удар). Тогда после удара белый полетит в лузу, а красный остановится на месте. Это и есть «клапштос».
Таким образом, если ударить кием в центр шара «в плоскости параллельной бильярду», то получится клапштос.
Клапштос очень красивый и полезный удар. Он очень легок на коротком расстоянии и очень труден на дальнем. Вообще ко всем штрихам (за исключением наката) применяется следующий закон: трудность исполнения штриха пропорционально расстоянию между шарами. Особенное значение имеет клапштос в игре a la guerre, что увидим далее.
Накат
Точка удара при накате
Часто бывает нужно, чтобы биток после удара пошел вперед. Для этого ударяют красного протяжным длинным ударом плавно в плоскости, параллельной бильярду, в верхнюю часть шара.
Тогда биток, двигаясь вперед, завертится еще и сверху вниз, и когда он ударит по белому шару, то передаст последнему только свое поступательное движение, движение же сверху вниз сохранит и поэтому, задержавшись на мгновение на месте, после удара двинется вперед. Подобный удар называется «накат».
Накат самый обыкновенный и самый легкий штрих. Все новички начинают играть только накатом. Притом при накате вернее всего прицел и удар, так что есть весьма сильные игроки, употребляющие исключительно этот удар. Особенно важное значение имеет накат при игре на польском бильярде. Но при всем том искусство выхода и отыгрыша требует употребление других ударов, которые необходимо изучить.
Оттяжка
Точка удара при оттяжке
Иногда требуется, чтобы после удара свой шар ушел назад. Для этого необходимо сообщить ему два движения: одно поступательное, а другое — вращательное снизу вверх. Тогда свой шар после удара передаст чужому поступательное движение, сохранив вращение снизу вверх, и, постояв на месте, двинется назад.
Этот удар называется оттяжкой.
Оттяжка самый красивый и самый трудный удар. Многие весьма искусные удары немыслимы без оттяжки. Применение этого удара весьма обширно.
При оттяжке наибольшее значение имеют мгновенность и мягкость удара. Притом, очень важна наклейка — до известной степени эластичная и шероховатая.
Если игрок хочет сделать очень крутую оттяжку, или если два шара стоят слишком близко, необходимо наносить удар сверху вниз под углом в 45°. Этот короткий и быстрый удар в высшей степени труден.
Боковые или французские удары (француз)
Все рассмотренные удары — обыкновенные штосы, употребляемые игроками средней и высокой силы. Они производятся ударом кия в вертикальной плоскости в центр шара, выше или ниже его. Но игроки превосходной силы для разнообразия выхода и отыгрыша употребляют еще и так называемые «боковые» удары, которые наносятся киём по точкам, находящимся справа или слева от центральной вертикальной линии шара.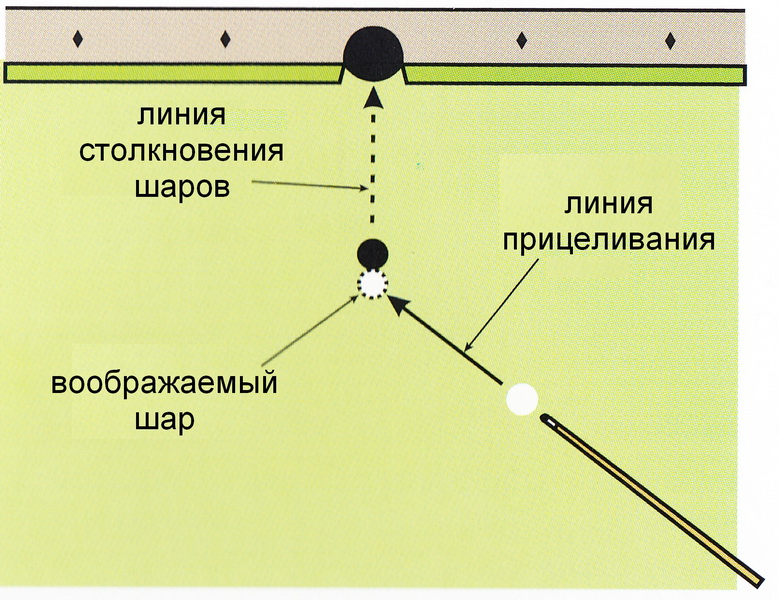
Эти удары довольно трудны, особенно в плане оценки силы удара кием. Употребление их весьма разнообразно.
Правый боковик
Точка удара при клапштосе «французом вправо»
Это удар в среднюю точку на правой стороне битка. При таком ударе биток кроме поступательного движения вперед получает также вращательное движение вокруг вертикальной оси, которая проходит через центр шара, против часовой стрелки и, столкнувшись с играемым шаром, передав ему поступательное движение, завертевшись волчком и увлекаемый своим вращательным движением, шар пойдет только вправо.
Левый боковик
Точка удара при клапштосе «французом влево»
Удар в среднюю точку на левой стороне битка. Действие данного удара аналогично предыдущему, только биток получает вертикальное вращение по часовой стрелке и после столкновения с другим шаром пойдет только влево.
Накат французом
тоже эффективный и оригинальный удар.
Этот накат употребляется в случае, когда после удара по белому красный должен перейти влево или вправо и притом вперед. Для этого ударяют кием по красному плавно и протяжно в верхнюю часть, отступая вправо или влево от вертикальной линии центра. Накат французом самый легкий из всех французских ударов.
Оттяжка французом
также один из трудных ударов. Она употребляется тогда, когда требуется, чтобы красный после удара по белому ушел назад и еще вправо или влево. Достигают этого, ударяя коротко и быстро красного вниз, но вправо или влево от вертикальной линии центра.
Все эти боковые удары называют французскими, потому что наиболее широкое применение имеют на французском бильярде без луз в карамбольной партии. Эти удары получили огромное значение тогда, когда усовершенствовали кий и наклейку. Главное достоинство их заключается в удобном достижении посредством их отыгрыша или выхода.
Дуговик
Предположим, что один чужой шар стоит над лузой, а другой загораживает его.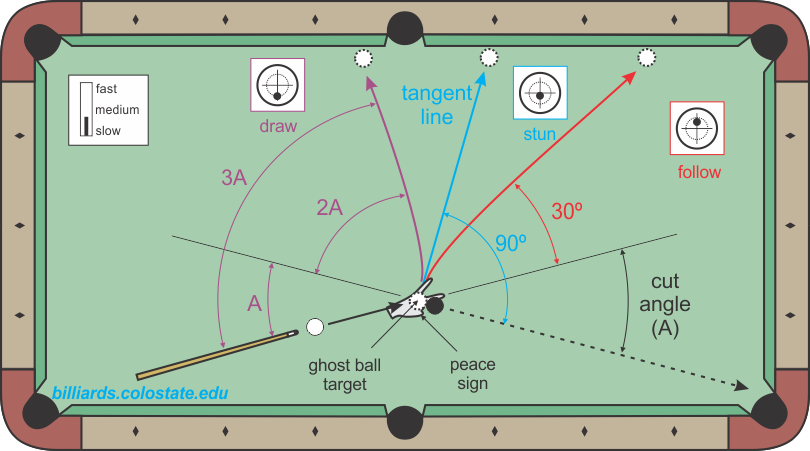
Тогда, чтобы сыграть чужого над лузой, необходимо играть дуговиком. Для этого наносят удар по своему шару кием влево (вправо) и вниз, сообщая ему сильное вращение вокруг вертикальной оси слева направо, и в то же время сообщая ему поступательное движение вправо от линии между центрами своего и первого чужого. Тогда сложение этих двух движений в результате даст движение по дуге (парабола).
Если бы свой шар, пущенный вправо от упомянутой линии между центрами шаров, не имел бокового вращения вокруг оси, то он пошел бы по прямой линии. Но, т. к. боковое вращение слева направо беспрерывно увлекает его влево, то он пойдет и вправо, и влево, т. е. по дуге.
Перескок
Это такой удар, когда свой шар, перескакивая через загораживающий чужой, кладет в лузу другой чужой. Для достижения этого штоса, по своему шару наносится протяжный и сильный удар под углом в 30° вниз шара. Тогда свой, оттолкнувшись от поверхности стола, подскочит и покатится по прямой линии.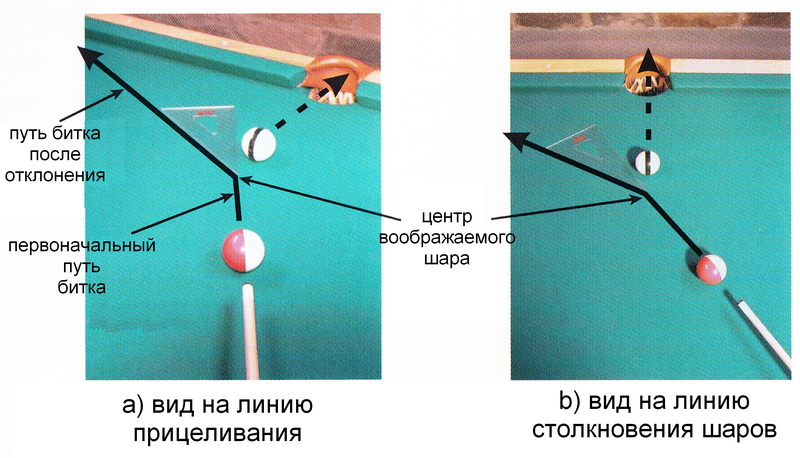
Этого результата можно достигнуть и другим способом. Держа кий в плоскости, параллельной поверхности бильярда, подводят конец кия под нижнюю часть своего. Затем вскидывают этот шар и перебрасывают его через чужой. Этот способ легче, но не так надежен, как предыдущий.
Лемановский удар
Кием быстро и легко надавливают на игральный шар, после чего бортовой падает в лузу.
Физика бильярда
Источник: http://www.flickr.com/photos/ventsislav/2222807833
Физика бильярда – столкновение шаров
Физика бильярда (или физика пула) в значительной степени связана со столкновениями бильярдных шаров. При столкновении двух бильярдных шаров столкновение почти упругое. Упругое столкновение — это столкновение, при котором кинетическая энергия системы сохраняется до и после удара. Поэтому для простоты можно считать, что при ударах бильярдных шаров удар абсолютно упругий.
При столкновении шаров импульс всегда сохраняется (как и при любом другом столкновении).
Для упрощенного случая, предполагающего отсутствие трения (обсуждается ниже), мы можем объединить этот факт с предположением об упругом столкновении, чтобы найти траекторию двух сталкивающихся бильярдных шаров после удара. На рисунке ниже показано столкновение двух бильярдных шаров. В общем случае столкновение не лобовое, что и показано на рисунке.
Предполагается, что шары A и B имеют одинаковую массу и что шар B изначально находится в состоянии покоя (скорость равна нулю). Начальная скорость мяча А равна В 1А . После удара мяч А движется со скоростью V
Линия L 1 проведена по касательной к обоим шарам в точке соприкосновения. Из-за геометрии L 1 перпендикулярен линии, проходящей через центр двух шариков и точку контакта CP. Из-за геометрии L 1 также составляет угол θ с вертикалью, а линия, проходящая через центр шаров, составляет угол θ с горизонталью.
После удара в точке СР мяч В движется в направлении линии, соединяющей центры двух мячей, как показано на рисунке. Это связано с тем, что сила (импульс), передаваемая шаром A шару B, действует нормально к поверхности шара B, если предположить, что между шарами нет трения (хорошее предположение, поскольку бильярдные шары гладкие). Таким образом, шарик B движется в направлении этого импульса.
Анализ столкновения мячей
Для двух сталкивающихся шаров общее векторное уравнение сохранения импульса имеет вид:
Поскольку массы m A и m B считаются равными, это уравнение упрощается до:
При упругом столкновении кинетическая энергия сохраняется, и уравнение выглядит так:
С массы м А и m B равны, это уравнение упрощается до:
По теореме Пифагора это последнее уравнение говорит нам, что векторы 15 образуют прямоугольный треугольник.
Следовательно, векторное уравнение сохранения импульса можно нарисовать, как показано ниже.
Таким образом, после удара мяч А движется в направлении, перпендикулярном направлению мяча В. Это очень плавный результат.
Необходимо рассмотреть два дополнительных особых случая, связанных со столкновением мячей.
В случае, когда целевой шар B необходимо ударить под углом θ, очень близким к нулю (например, чтобы погрузить его в боковую лузу), шар A должен двигаться с высокой скоростью V 1A ( это означает, что вам придется довольно сильно ударить кием по шару А). Это связано с тем, что только очень небольшая часть импульса мяча A (и, следовательно, скорости) передается мячу B из-за косого удара.
Для случая, когда удар направлен в лоб (θ = 90°), приведенное выше решение не применяется. В этом случае В 2А = 0 и В 2В = В 1А . По существу это означает, что скорость мяча А полностью передается мячу В.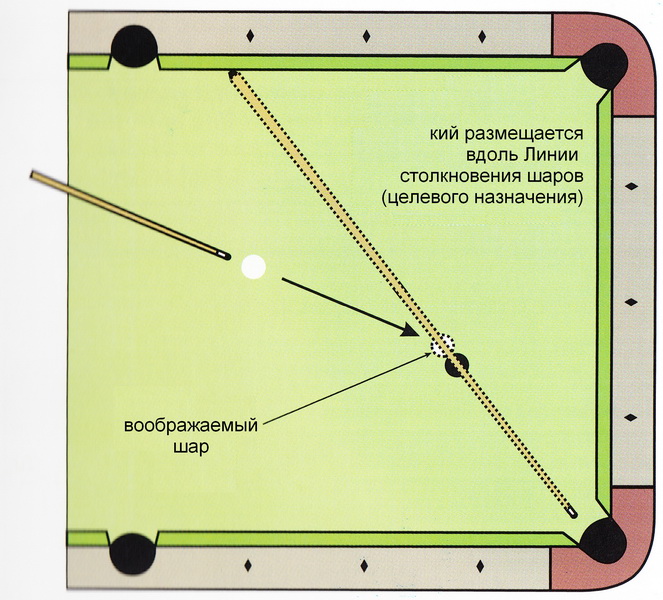
Более подробный и полный анализ, в котором рассчитывается траектория шара А (после удара) под действием трения между шаром и бильярдным столом, см. в задаче Траектория битка при трении о стол.
Сладкое место
Физика бильярда похожа на физику удара по бейсбольному мячу в том смысле, что на бильярдном шаре также есть игровая зона, где вы можете ударить кием, чтобы между шаром и бильярдным столом не возникало силы трения. Знание местоположения этой точки наилучшего результата может дать вам представление о том, куда ударить по мячу, чтобы он развернулся назад или вперед, что может быть полезно при выполнении удара.
Рассмотрим рисунок ниже, показывающий положение кия на высоте ч .
Мы хотим найти высоту h , чтобы в точке P не возникала (горизонтальная) сила трения при ударе кием по шару.
Анализ зоны наилучшего восприятия
В этом анализе мы можем представить систему шар + кий с помощью диаграммы свободного тела, как показано ниже.
Где:
F сила, с которой кий действует на мяч при ударе
r радиус шара
G — центр масс мяча
g ускорение свободного падения, равное 9,8 м/с 2
P точка контакта шара с бильярдным столом
F Px x-компонента силы, действующей на шар со стороны бильярдного стола, в точке P . Это сила трения.
Ф Py — y-компонента силы, действующей на шар со стороны бильярдного стола в точке P .
Согласно второму закону Ньютона, общее уравнение силы в направлении x:
Где:
м масса мяча
a Gx ускорение центра масс в направлении x
Это уравнение становится
Начиная с F Px = 0 получаем
Согласно второму закону Ньютона, общее уравнение силы в направлении y имеет вид:
где a Гр ускорение центра масс в направлении y.
Поскольку бильярдный шар движется только в направлении x a Гр = 0, то приведенное выше уравнение принимает вид
Поэтому
Теперь мы должны написать общее уравнение моментов для вращения твердого тела вокруг его центра масс Г .
Где:
ΣM G сумма моментов относительно центра масс G
I G — момент инерции мяча относительно его центра масс относительно оси, направленной за пределы страницы.
α — угловое ускорение мяча
Поскольку между шариком и столом не возникает силы трения, относительное скольжение в точке P 9 отсутствует.0016 . Это означает, что мы имеем дело с чистой прокаткой. Таким образом, мы можем написать следующее:
В приведенном выше уравнении знак минус соответствует правилам, используемым в этой задаче.
Уравнение моментов становится
Объединяем уравнения (1) и (2) и получаем
Для твердого шара
Поэтому
Это высота удара по мячу, чтобы в точке 9 не возникало трения0013 Р .
Как бы сильно вы ни ударили по мячу в этом месте, в точке P не возникнет силы трения (реакции). Таким образом, после удара всегда будет происходить чистое качение мяча (без относительного проскальзывания).
В тех случаях, когда кий бьет выше или ниже этой высоты h , необходимо трение для предотвращения скольжения шара по поверхности бильярдного стола. А если по мячу ударить достаточно сильно (выше или ниже высоты ч ), произойдет относительное проскальзывание из-за недостаточного трения между мячом и столом.
В случаях проскальзывания имеем следующее неравенство:
Это означает, что существует относительное движение между шаром и бильярдным столом в точке P сразу после удара. Другими словами (сразу после удара) тангенциальная скорость мяча в точке P равна , а не , равной по величине и противоположной по направлению скорости центра масс мяча G .
В случае чистого качения тангенциальная скорость мяча в точке P равна по величине и противоположна по направлению скорости центра масс шара G .
Следовательно, скорости уравновешиваются, и в точке P нет относительного проскальзывания.
Анализ относительного проскальзывания
Относительное проскальзывание между шаром и бильярдным столом является интересным моментом анализа. Полезно понять, как движется мяч в зависимости от того, куда он попал, относительно h .
Рассмотрим рисунок ниже.
При достаточно сильном ударе по мячу с силой, направленной влево, в области A 1 мячу придается скорость влево, и он получает обратное вращение в направлении по часовой стрелке. Относительное проскальзывание происходит в точке P , и результирующая сила трения в этом месте направлена вправо. Скорость мяча влево уменьшается, а вправо он ускоряется из-за направления силы трения. Скорость обратного вращения уменьшается из-за направления силы трения. Это происходит до относительного проскальзывания в точке 9.0013 P останавливается и происходит чистая прокатка.
При достаточно сильном ударе по мячу с направленной влево силой в области A 2 мячу придается скорость влево и вращение вперед в направлении против часовой стрелки. Относительное проскальзывание происходит в точке P , и результирующая сила трения в этом месте направлена вправо. Скорость мяча влево уменьшается, а вправо он ускоряется из-за направления силы трения. Скорость вращения вперед увеличивается из-за направления силы трения. Это происходит до относительного проскальзывания в точке 9.0013 P останавливается и происходит чистая прокатка.
При достаточно сильном ударе по мячу с направленной влево силой в области A 3 мячу придается скорость влево и вращение вперед в направлении против часовой стрелки. Относительное проскальзывание происходит в точке P , и результирующая сила трения в этом месте направлена влево. Левая скорость мяча увеличивается, и он ускоряется влево из-за направления силы трения. Скорость прямого вращения уменьшается из-за направления силы трения.
Это происходит до относительного проскальзывания в точке 9.0013 P останавливается и происходит чистая прокатка.
Таким образом, характер проскальзывания будет меняться в зависимости от того, в какой из областей (А 1 , А 2 , А 3 ) кий ударяет по шару.
Обратите внимание, что в трех вышеприведенных случаях сила трения, возникающая из-за относительного скольжения, известна как кинетическое трение . Кинетическое трение возникает при «трении» между двумя поверхностями. Этот тип трения всегда противоположен направлению движения. Так, например, если ящик скользит по полу влево, кинетическое трение между ящиком и полом действует вправо. В тех случаях, когда у нас есть этот тип трения, вы должны учитывать направление относительного проскальзывания, а затем назначить направление трения в в противоположном направлении .
С другой стороны, когда нет относительного скольжения между двумя поверхностями, сила трения между ними известна как статическое трение .
Таким образом, в общих случаях, когда бильярдный шар не испытывает относительного проскальзывания в точке P , мы имеем статическое трение, поддерживающее чистое качение. Учет статического трения отличается от кинетического тем, что вам не нужно знать направление, в котором оно действует. Направление решается в уравнениях динамики. Так что в этом смысле легче объяснить статическое трение, чем кинетическое трение.
Пристальный взгляд на относительное проскальзывание (дополнительно)
Это продолжение предыдущего раздела с более подробным рассмотрением относительного проскальзывания. Этот раздел является необязательным, поэтому вы можете пропустить его, если хотите.
На рисунке ниже показана диаграмма свободного тела бильярдного шара в общем случае относительного проскальзывания.
Где:
V G скорость центра масс мяча. (С практической точки зрения, когда кто-то говорит о скорости мяча, он имеет в виду скорость центра масс мяча).
w — угловая скорость мяча
Пусть w i представляют начальную угловую скорость мяча сразу после удара.
Пусть V Gi представляют начальную скорость мяча сразу после удара.
Не ограничивая общности, мы можем предположить, что V Gi слева (отрицательное, согласно соглашению о знаках), а w i — либо по часовой стрелке (отрицательное), либо против часовой стрелки (положительное).
Если кий ударяет по шару в области A 3 и происходит относительное проскальзывание, то
w i r > — V Gi .
Если кий ударяет по мячу ниже высоты h и происходит относительное проскальзывание, то w i r < - V Gi .
Набор
Это равно +1 или -1. Этот фактор определяет направление относительного скольжения, что важно знать, поскольку мы имеем дело с кинетическим трением.
Такие коэффициенты математически очень удобны при учете направления кинетического трения. (Обратите внимание, что |x| означает абсолютное значение x).
Раньше
Это нормальная сила, действующая на шар в точке P .
Общее уравнение силы в направлении x:
Кинетическое трение, действующее на P , определяется по формуле:
где μ k — коэффициент кинетического трения между шариком и столом.
Сейчас,
Общее уравнение моментов для вращения твердого тела вокруг центра масс Г это:
Становится
Из уравнений (3) и (4) получаем:
Линейная скорость мяча:
где t время
Угловая скорость мяча:
Мы хотим найти время, за которое мяч перестанет скользить и начнет катиться. Таким образом, используя уравнения (5) и (6), можно сформулировать следующее равенство, справедливое при чистой прокатке:
Отсюда мы можем найти время t .
Для твердого шара
Поэтому
Теперь найдем расстояние, пройденное мячом до начала чистого качения, используя время t сверху.
Расстояние d равно:
Последнее соображение заключается в нахождении скорости мяча до того, как начнется чистое вращение. Для этого вычисляем скорость V G используя время t сверху.
Обратите внимание, что приведенные выше три уравнения действительны только при наличии относительного проскальзывания в точке P .
Пример расчета относительного проскальзывания
Это пример расчета с использованием результатов предыдущего раздела.
В Gi = -1 м/с (начальная скорость влево)
w i = -20 рад/с (обратное вращение, вращение по часовой стрелке)
г = 0,028 м
мк к = 0,3
г = 9,8 м/с 2
δ = 1
a Gx = 2,94 м/с 2 — рассчитано по уравнению (3)
Следовательно, время, необходимое мячу, чтобы перестать скользить, равно
t = 0,15 с
Расстояние, пройденное мячом при скольжении, равно
d = -0,12 м (мяч переместился влево)
Скорость мяча непосредственно перед началом чистого качения равна
В G = -0,56 м/с (скорость влево)
Заключительные замечания
Как видите, физика бильярда может стать довольно сложной, если вы начнете учитывать все, что может произойти в типичной игре в бильярд.
Вы можете поспорить, что профессиональные игроки очень хорошо разбираются в практическом использовании представленной здесь физики, а также в других аспектах игры, которые здесь не обсуждаются.
Вернуться на страницу Физика спорта
Вернуться на домашнюю страницу Real World Physics Problems
сообщить об этом объявлении
Понимание хаотической динамики с помощью бильярда, цветов и… грибов?
Нильс Берглунд, профессор математики Орлеанского университета во Франции, снимает видеоролики, используя методы Бунимовича для визуализации динамических систем.
Рядом с именем Леонида Бунимовича часто упоминаются такие слова, как бильярд, цветы и стадион. Однако в данном контексте ни один из этих терминов не относится к бильярдным столам, ботанике или местам, где проходят матчи чемпионата мира — наряду с грибами бунимовичами, которых вы (к счастью и надежде) не найдете ни в пицце, ни в салатах.
Вместо этого эти термины относятся к визуализации математических понятий — и они сделали Бунимовича, профессора Регентов в Школе математики Технологического института Джорджии, весьма известным среди своих сверстников.
Понятия исследователя используются физиками и математиками всего мира для описания способов изучения динамических систем, основной области исследований Бунимовича. Теория динамических систем использует математические инструменты для моделирования многих компонентов явлений, которые существуют и нуждаются в объяснении, и состояние которых меняется с течением времени.
«Текущее состояние объекта описывается некоторыми характеристиками — положениями и скоростями частиц, например, или концентрациями некоторых видов вирусов, — поясняет Бунимович. Их эволюция может быть регулярной — фиксированной и относительно легко предсказуемой, или сложной (хаотической = квазислучайной) и предсказать ее не так легко, или и тем, и другим.
Динамические системы могут моделировать изменения во времени чисел в данных, внося некоторую ясность в экономические теории. Они могут моделировать явления в области здравоохранения и медицины, погодные условия, планетарные тела и квантовую механику; любая сложная система с множеством движущихся частей, которую необходимо наблюдать, понимать и предсказывать.
Знание того, как эти частицы отскакивают от стен стадиона Бунимовича, друг друга и их траекторий, может помочь математикам и физикам обеспечить лучшую предсказуемость этих движений.
Бунимович скромно отзывается о своей славе в поле. «В основном бильярд дает людям представление о хаотической динамике. Все эти стадионы Бунимовича, грибы, цветочки, дают такие наглядные примеры, которые демонстрируют, что могут происходить какие-то невообразимые прежде виды эволюций (изменений) и как они происходят». Он говорит, что старая поговорка доказывает его точку зрения: лучше один раз увидеть, чем сто раз услышать.
Выяснение этих закономерностей помогло исследователям разработать теорию хаоса, «одно из главных открытий 20 века», — объясняет Бунимович. Теория хаоса исследует случайное или непредсказуемое поведение динамических систем, управляемых фиксированными детерминированными правилами, и применяется в ряде научных и математических дисциплин.
Обновление математических представлений для 21 го века
Бунимович отмечает, что он не был первым, кто использовал концепцию бильярда для изучения динамических систем.
Ю.Г. Синай, бывший советник Бунимовича в настоящее время в Принстонском университете, написал 1970 статья, в которой представлена концепция динамического бильярда, где точечная частица прыгает внутри прямоугольной формы с удаленным кругом, как в игре в бильярд, но без потери скорости.
Синай сам был учеником А.Н. Колмогорова, одного из крупнейших русских математиков, проведшего пионерские исследования в области вероятностей, теории функций, теории турбулентности и теории сложности. Именно Колмогоров «в частности построил мост между случайными и детерминированными мирами, а также случайными и детерминированными системами», — сказал Бунимович.
Дэн Маргалит, коллега-профессор Школы математики Технологического института Джорджии, добавляет, что Бунимовичу приписывают использование этих понятий, введенных другими русскими математиками, и обновление их для использования в 21 -м -м веке в теории вероятностей и квантовой теории, а также физика. «Основная идея заключается в том, что у вас есть бильярдный стол определенной формы, и вы хотите знать, если я выстрелю бильярдным шаром без трения в каком-либо направлении, будет ли он в конечном итоге перемещаться по всему столу», — сказал Маргалит.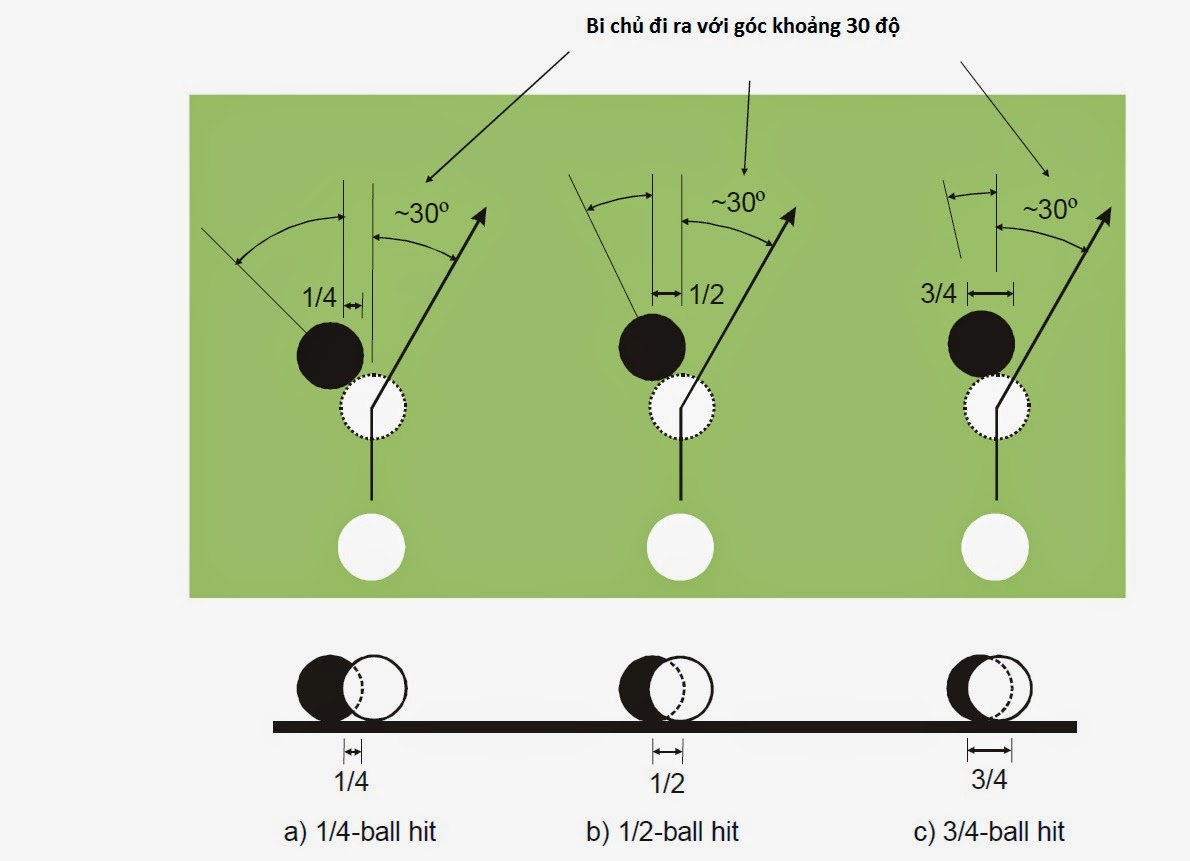
Еще один способ визуализировать динамические системы — использовать грибовидный бильярд Бунимовича, который получил свое название из-за формы шляпок и стеблей, которые формируются при визуализации, изображающей движения частиц. «Это общее мнение, хотя и не доказанное, что типичные динамические системы имеют области с регулярным движением/динамикой или стабильные острова, расположенные в хаотических морях, где динамика хаотична», — сказал он. «Грибы — единственный большой класс бильярдов, где доказано такое сосуществование. Кроме того, они очень наглядны и их легко построить, что и было сделано в различных физических лабораториях».
Происхождение стадиона Бунимовича и эллиптических цветов Бунимовича
Траектории любой частицы, напоминающей бильярдный шар, также играют роль в разработке стадиона Бунимовичем, которую он представил в статье 1974 года. Американское математическое общество определяет стадион Бунимовича как «прямоугольник, увенчанный полукругами, в котором частица движется с постоянной скоростью по прямым линиям, отражаясь от границы таким образом, что угол падения равен углу отражения».
Стадион Бунимовича показал, что в целом хаотическая динамика гораздо более характерна для всех динамических систем, чем считалось ранее. «Это просто более глубокое понимание хаоса, а стадион позволяет получить строгое математическое доказательство открытия, в которое физики не верили, пока не провели эксперименты и не увидели его».
Недавнее открытие Бунимовича: эллиптический цветочный бильярд, который может помочь в экспериментальных исследованиях в физических лабораториях, а также в математических, согласно реферату статьи Бунимовича 2021 года по этому вопросу. Эллиптический цветочный бильярд учитывает другие факторы, которые могут повлиять на траектории бильярда.
«Эллиптические цветы — единственные, где строго доказано сосуществование хаотических и нехаотических областей, а нехаотические области не имеют очень специфической формы, как в грибовидном бильярде», — сказал Бунимович. Эти изменения формы могут помочь исследователям лучше понять классические системы, переменные которых строго определены и могут быть точно измерены, и квантовые системы, в которых действие происходит на атомном или субатомном уровне.
«Математика и физика могут быть красивыми»
Нильс Берглунд, профессор математики из Орлеанского университета во Франции, выпустил на YouTube видеоролики, демонстрирующие эллиптические цветочные бильярды Бунимовича, которые он называет «примерами систем, которые, как можно доказать, имеют смешанную динамику, как с правильными, так и с хаотическими траекториями». ». Полученные анимации представляют собой красочные представления инноваций Бунимовича и других математиков.
«С помощью этих анимаций я пытаюсь показать, что математика и физика могут быть красивыми», — делится Берглунд на своем канале. «Все они основаны на реальных моделях в физике и математике, обычно описывающих эволюцию во времени какой-либо системы: частица или волна в замкнутом домене, растущая поверхность раздела, популяция животных».
Открытию Бунимовичем эллиптического цветка нет и двух лет, поэтому он не ожидает, что многие физики уже знают об этом. «Но я полностью ожидаю, что они будут строить эллиптические цветы в лабораториях физики, как это было со стадионом и грибами».