Теория настольных игр: Статья Анатомия настольных игр | все о настольных играх

Как балансируются настольные и разные другие игры – краткий обзор способов / Хабр

Неделю назад я пообщался с разработчицей развивающих детских игр, психологом, прекрасной леди Сьюзен, похоже, даже не подозревающей про математику. Она подарила мне один из самых красивых методов игрового баланса за практику, объясняя, как делала одну из своих игр. Но об этом чуть позже, там много букв.

Конечная цель любой балансировки игры – увеличение возврата игроков или времени партии. То есть играбельности механики:

• Не должно быть однозначной ультимативной стратегии победы, иначе игра потеряет вариативность и интерес.
• Игрок должен чувствовать, что от его действий и навыков зависит игра. Иначе получится Mass Effect, который, скорее, фильм, нежели RPG.
• Баланс должен быть «амортизированным», то есть прощать некоторые ошибки – иначе запоздалый на миллисекунду клик в Starcraft по первому рабочему из-за «эффекта бича» вызывал бы проигрыш через 4 часа идеальной партии. Наша настольная формула – 5-7 важных решений за игру, в двух можно ошибиться.
• У настолок есть ещё социальное условие: игроки не должны выпадать по ходу пьесы – интересно должно быть всем и до конца.

Теперь – методы.

Ограничения модели

Настольные игры крайне редко покрываются автоматизированными тестами. Делают такие вещи из известных мне личностей, пожалуй, только Сид Мейер, Влаада Хватил и ещё пара не таких известных геймдизайнеров. В остальных случаях происходит следующее:

1. Эмпирическая балансировка. Как правило, разработчик игры знаком с математикой, интуитивно понимает прикладные аспекты либо теории игр или дискретной математики, и, в целом, принимает правильные решения.
2. Затем идут игровые тесты в ограниченном кругу «профи». Тут задача – найти уязвимости баланса. В целом, те же эмпирические тесты, только уже толпой пентестеров. Как правило, это сотня партий, то есть для статистических методов маловато, но для эмпирических – в самый раз.
   При этом автор что-то докручивает в процессе, поэтому редко когда один набор правил играется больше 30 партий.
3. После игра выносится в публичную бету на «людей с улицы», чтобы проверить кривую обучения. Здесь уже можно собрать статистику, но, как правило, это не требуется.

Пример такой ручной балансировки – «Улей» мистера Янни. Когда он делал дополнение, добавляющее мокрицу в улей (действие примерно сопоставимо с добавлением новой фигуры в шахматы), то сначала он тестировал с друзьями около двух месяцев, потом показал всем знакомым геймдизайнерам и собрал мнения, потом запустил в электронной турнирной системе бета-турнир для тестов, а уже потом выпустил непосредственно пластиковую фигурку для продажи и ввёл её в стабильный релиз в электронных версиях.

Отмечу, что у настольной игры средний срок жизни – 6 партий. 10 человек сыграют по 3-4 партии за год, ещё двое будут резаться каждые выходные, а примерно каждый сотый будет готовиться к турниру. Поэтому основная задача баланса – не турнирная, как в онлайн-играх, а именно социальная – чтобы никто не выпал, и чтобы все чувствовали, как они принимают решения. Баланс связан и с кривой обучения – учитывая крайне ограниченный ресурс внимания и дикий дефицит времени, нужно применять для балансировки интуитивно-понятные игрокам вещи (а-ля «дробовик не может быть слабее пистолета»).

Методы

Жоп-филинг автора
Этот метод мы рассмотрели выше. Он часто остаётся базовым на практике.

Отпиливание того, что высовывается
Последовательное тестирование и ручное убивание самых манчкинистых стратегий. Это «выравнивание» очень напоминает отладку алгоритмов группы Монте-Карло или генетики на неполной подборке, и даёт примерно такой же результат. То есть помогает в 90-95% случаев.

Ресурсный баланс
Это уже более интересная вещь. Для каждого объекта в игре рассчитывается единая цена в некотором ресурсе. Естественно, самое сложное – придумать оценочную функцию. Та же MTG, к примеру, совершенно точно выросла из эмпирики (I и II редакции) к non-domination (III и IV редакции) и уже к шестой редакции пошла по ресурсному пути. Грубо говоря, вы знаете, что зверёк ценой 2 единицы маны будет иметь атаку 2 и защиту 2 по умолчанию в любом окружении. Например, можно сделать его 3/3? Конечно, можно, только надо повесить свойство, что он 1/1, если в предыдущем ходу противнику не был нанесён урон. За каждую «плюшку» от стандарта мы даём «дроубек» — какой-то недостаток. Хотите 2/2 и полёт? Ок, только скотина на входе в игру заберёт у вас 2 хита. Хотите 7/1? Можно, но жить оно будет один ход, и придётся убить другое существо для его вызова. И так далее. Вы берёте эталон и начинаете плясать вокруг него, создавая плюсы и минусы, чтобы в итоге они попадали примерно в 85% коридор от эталона.

Сюжетно-связанный баланс
Это когда сюжет «вытаскивает» слабые балансные состояния. Например, у вас в RPG есть ветка прокачки пистолетов и, скажем, плазменных пулемётов. В том же Shadowrun (новом) варианты развития одинаковы. На поздних уровнях навыка пистолет даёт двойной-тройной выстрелы, повышенный урон и быструю перезарядку. Урона за ход столько же, сколько от хорошей очереди из пулемёта в упор. Игрок, типа, не окажется к финалу игры неумелым лохом. Это баланс — ресурсный.

А сюжетный заключается в том, что вы можете оставить пистолет слабым, но скомпенсировать его тем же, чем в реальном мире. Например, сильно усложнить поиск патронов к пулемёту или повысить их цену в игровом мире, затем понаделать миссий на проникновение, куда пистолет пронести можно, а пулемёт – уже нет, сделать мгновенные дуэли как в вестернах, когда важнее, что быстрее выхватывается из кобуры – и так далее.

Каждый раз, когда от вашего навыка механики или взлома замков в ролевой игре зависит сюжетная ветка – это тоже оно.

Камень-ножницы-бумага
Основа баланса – принятие решений игроками. Когда баланс «слишком ровный», невозможно добиваться формирования индивидуальных стратегий и стилей игры. Поэтому баланс должен сходиться только в целом, но не в деталях. В деталях нужен некоторый хаос, и его должно быть довольно много. Самый частый пример такого баланса – это построение трёх базовых стратегий («маг, боец, вор», «агрессия, контроль, комбинация», «разработчик, дизайнер, тестировщик», «дробовик, винтовка, снайпер»). Они бьют друг друга по кругу, и поэтому задача игрока – фактически, в некотором смысле блефовать и угадывать действия противника. Эта же стратегия вносит случайность в игру и даёт возможность новичкам иногда побеждать профессионалов при угадывании.

Пример самой эффективной и самой «несбалансированной» штуки в шутерах часто – дробовик. Это оружие ближнего боя. Используя ресурсные методы и статистику для построения оценочной функции для вычисления ресурса, мы, например, знаем, что оружие должно наносить 100 единиц урона в минуту на расстоянии 100 метров. Делаем 500 единиц, но в «дроубек» даём 5 метров, и ещё делаем оружие тяжелым, неуклюжим, медленно перезаряжающимся и с малым боезапасом. Здесь запускаются сразу две ветки – выбор стратегии (задача «папика» с дробовиком — неожиданно появляться строго вплотную к потенциальным фрагам) и навык (нужно очень точно и спокойно целиться). Аналогично – хорошая снайперка. Создаёт те же требования к стратегии и навыку, но определяет уже другую стратегию поведения игрока.

Ещё одна разновидность риск-контроля – это методика выравнивания проигрывающего и выигрывающего игроков рандомом. Это нужно, например, когда игрок уже серьёзно проигрывает, но остаётся ещё половина партии. Либо он выйдет из игры и сдастся без интереса… либо вы дадите ему какие-то инструменты восстановиться. Чаще всего это — сильный риск. Проигрывающий игрок может использовать приёмы и стратегии, которые дают высокий шанс (больше 50%) критической ошибки, но при этом она-то ему не страшна, поскольку он и так проигрывает. Получилось – повезло, они снова с победителем на равных. Не получилось – ну ок, было интересно и весело. Причём как только игроки выравниваются, использовать рисковые приёмы не будут оба – ведь «дроубек» в данной ситуации становится значимым для исхода партии.

Довольно хорошо про эти нюансы есть у Сирлина в его «Играй на победу» (которую мы как-то перевели — почитайте, он копался в балансе тогда, когда игры были без патчей вообще).

В спорте эта ситуация чем-то похожа на историю, когда даже вратарь используется как один из атакующих игроков на последних минутах матча. Да-да, вы уже догадываетесь – это не только возвращает игрока в игру, но и очень героически-зрелищно. О таком потом рассказывают истории.

Ещё одна важная вещь в недетерменизме или роли рандома – чтобы не было готовых стратегий победы. В тех же шашках невозможно выиграть в игре за чёрных при математически оптимальной игре белых. В Го, по идее, тоже, но там пока наших вычислительных мощностей для такого не хватает, поэтому именно в Го есть неопределённость, а в шашках – нет. Если помните автоматы с Пакманом – там специально вводили рандом для выбора призраками направления, чтобы игроки в аркадах не заучивали оптимальные пути хождения по уровням. При написании AI врагов тоже часто используется рандом для выбора между двумя похожими решениями.

Автобалансировка
Обычно игра всеми силами стремится быть в равновесии, а игроки нагло раскачивают её состояние. В механике автобалансировки – наоборот.

Игровая ситуация часто достаточно разнообразна, и разные стратегии будут оптимальными в текущей партии. Соответственно, как правило, в сложные игры вводится ещё один пример «автобалансировки» — это когда игроки сами определяют, что сейчас важнее.

Пример. В базовой ресурсной стратегии вы знаете, например, вот такую градацию наград: 20 патронов = 100 монет, аптечка = 50 монет. На уровне ресурсов 20 патронов всегда важнее аптечки просто потому что они дороже статистически. Но в конкретной ситуации аптечка может оказаться нужнее. Создаётся ситуация аукциона, когда игроки сами назначают цену за нужный им ресурс. В итоге может оказаться, что именно в нашей партии аптечка стоит 150 монет, а патроны вообще никому не нужны.

Такие вещи могут делаться драфтами (два капитана стоят перед залом на физкультуре и выбирают по одному игроку для своих команд по очереди), аукционами (игроки делают ставки на экипировку), расположением предметов на уровне (за нужным побежало больше людей – автоматически больше конкуренция) и так далее.

Альтернатива автобалансировке – ресурсная балансировка «подтягиванием» отстающих, например, созданием отрицательной обратной связи. Чем выше уровень героя – тем меньше опыта дают монстры. Чем ниже – тем больше. Соответственно, ошибки и нелепые ситуации на первых уровнях амортизируются тем, что в конце у героев разница в 3-4% при расхождении показателя опыта в 2 раза. Это нравится не всем, но это путь онлайновых игр чаще всего.

Ещё одна интересная механика автобаланса – это предоставление выбора не между игровыми ценностями, а между игровыми и реальными (IRL). Например, драфты с ценными на вторичном рынке картами, выбор в сторону игровой валюты (которую можно перепродать на вторичном рынке или ей оплатить аккаунт) и так далее.

Следующий тип автобалансировки – это дипломатия. Если в игре есть транзакции между игроками, то они смогут объединяться в союзы. Это значит, что самый «высовывающийся» рискует получить по шапке ото всех сразу, недовольных тем, что он побеждает.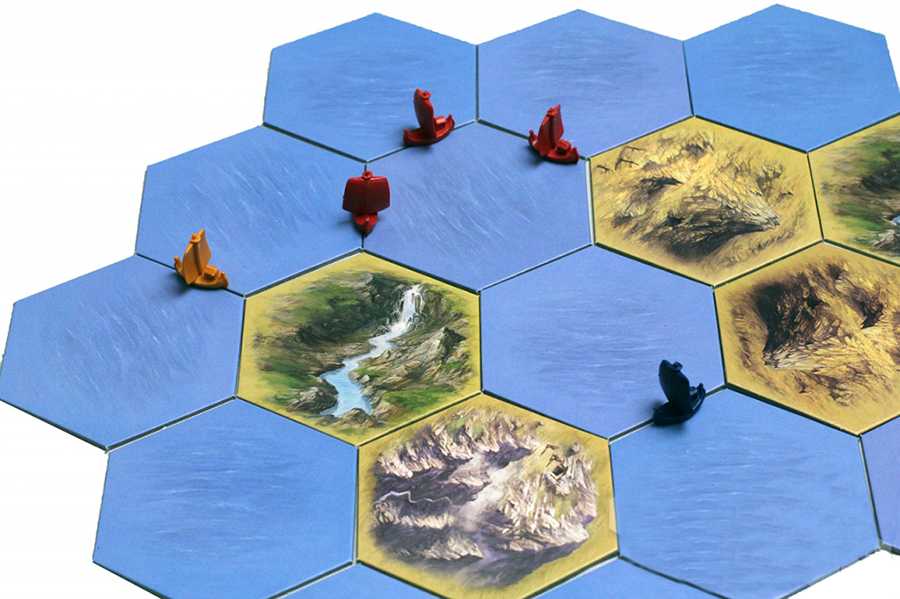

В этом плане особенно крута та же «За бортом!» — там в общем случае персонажи на лодке сначала «разведывают» друг друга, потом оставшуюся партию находятся в двух связках-союзах – одна контролирует ресурсы, вторая недовольна. Время от времени в контролирующей связке возникает раскол из-за условий победы («А почему Сноб столько захапал? Пусть даст мне бриллант, который он забрал!»), что тут же меняет местами связки и создаёт новый более сложный конфликт. Связки чисто из-за «физики» игры постоянно рекомбинируются и меняются местами, и игроки в них тоже. То есть самый сильный получает веслом по башке просто потому, что он сильный. И даже друг-союзник поможет его бить, потому что ведь задача у него – чтобы побитый друг выжил, а не чтобы он победил. Победу каждый бережёт для себя.

Разгадывание намерений и блеф

Суть стратегии – оптимизация набора параметров. Соответственно, предвидя оптимальные действия противника, вы можете принимать эффективные контрмеры. Однако противник может подозревать это и использовать не те параметры, что вы ждёте. Так образуется схема «разгадываемости» игры, когда понятно, какое действие к чему ведёт, и блефа. Это один из самых сильных факторов баланса и кривой обучения – сначала игроки повышают навыки, пытаясь предсказывать результаты тюнинга параметров (обучаются искусству игры, раскрывают скрытую информацию по поведению других игроков), а потом играют уже не с механикой, а друг с другом, используя игру только как язык.

Кривая обучения

Вернёмся в самое начало топика к диалогу с прекрасной леди и тому, что баланс связан с кривой обучения. Связан, он, в частности, тем, что при изменении состояния системы вы должны увидеть обратную связь от игры. Например, легко обучить собаку делать правильные вещи, сразу давая ей косточку. Но очень сложно обучить её, давая ей гору косточек через сутки-двое – она просто не уловит связи, несмотря на увеличенный размер награды. Так же и с игроками, и про это есть просто прекрасная статья у Данилы Кука из Epic – вот мы её на новый год перевели тут.

Так вот, задача. Есть игра «Совушки, ау!», где дети должны привести сов в гнездо, пока не наступит рассвет. Совы стоят на треке, состоящим из цветных кружков:

У игроков есть карточки с кружками. Вот у левого игрока красный, оранжевый и зелёный кружки. Соответственно, он может выбрать любую сову и двинуть её на ближайший свободный кружок этого же цвета.

Если ближайший кружок занят, сова ставится на следующий такого же цвета.

Оптимальная стратегия этой игры – не «рассыпать» сов на большую дистанцию, но при этом занимать одинаковые клетки, чтобы дальняя делала прыжки по пол-поля.

Как быстро выяснилось, дети это не понимают. Фигня, когда я тестировал, это ещё и некоторые гуманитарные взрослые не понимали. Один дядька, например, выбирал у нас на тестах самый длинный тактический шаг совы, но не просчитывал следующие 2-3 хода. В рамках своего хода горизонт планирования трагически заканчивался. Дети же берут «любимую» сову (и пофиг, что они одинаковые) и ведут именно её.

А задача игры – научить детей делать что-то в команде, то есть так, чтобы полезно было всем сразу. То есть показать им, что ход короче, но полезный другим может в перспективе быть лучше длинного, но только для себя.

Но даже после объяснений словами, проигрышей и демонстрации оптимальных игр совсем маленькие дети и некоторые особо одарённые взрослые не понимали. И снова вели либо любимую сову, либо делали длинные ходы.

Проблема в том, что из-за случайности примерно в 10-20% случаев это всё же давало победу. Сюзен, автор игры, попробовала ужесточить условия победы, чтобы включить автобалансировку по стратегии. Но столкнулась с тем, что при неверных ходах дети проигрывают, и не успевают научиться – их расстраивает цепочка проигрышей. Проблема, очевидно, в том, что цикл обратной связи слишком длинный. Нужна какая-то вещь, которая даёт положительную обратную связь сразу в течение хода, а не в конце игры. Оценочная функция, чтобы понять, сильный ход ребёнок сделал или слабый.

Остановитесь и подумайте, что бы вы сделали в этом раскладе.

А решение Сюзен под спойлером

Она выявила самый важный элемент оптимальной стратегии – прыжки через других сов. В целом, чем больше таких прыжков за игру, тем лучше. Это значит, что нужно было поощрять игроков делать именно прыжки через сов, а не думать о том, как дойти всем в гнездо, уложившись во время. И придумала новое правило: во время каждого такого прыжка дети должны были громко ухать как сова. Естественно, ухать им было куда веселее, чем просто двигать фишку. И они начали специально создавать ситуации длинных прыжков – то есть, да, учиться оптимальной стратегии. Особенно детей радовало, когда ухали их родители, играющие с ними – отсюда и возможность создать такую ситуацию не для себя, а для кого-то ещё.

В общем, Сюзен прекрасна, а мы научились балансировать введением мгновенного внеигрового вознаграждения.

Резюме

Итак, чаще всего:

1. Эмпирически и на основе небольшого набора тестов строится оценочная функция для баланса.
2. Выявляется ресурсный эталон для каждого объекта, а затем объекты подравниваются и варьируются для глубины игры, то есть возможности построения индивидуальных стратегий.
3. Вводится некоторая недетерменированность (чаще всего – случайность) для разнообразия игры и ухода от автоматизации победы. Because life is a random.
4. Вводятся реактивные методы для уравнивания игроков: дипломатия, отрицательная обратная связь, рисковый баланс.
5. При необходимости устанавливается внеигровая мотивация для совершения каких-то действий.

Но, конечно же, практика суровее. На практике один хрен до появления service pack 2 вы всё равно играете в позднюю бету.

Ещё конкретные механики есть, например, в Вики – смотрите патчи баскетбола и принцип «золотого века», плюс походите по ссылкам. Очень хорошая подборка по околобалансовым вещам есть у Денка (с точки зрения геймдизайнера) и Сирлина (с точки зрения игрока-турнирщика).

Опасна власть, когда с ней совесть в ссоре. Обзор игры 12-0-12: Теория власти

Сегодня я хочу рассказать вам об игре, которая, на мой взгляд, незаслуженно прошла мимо большинства настольщиков. Речь пойдет о «Теории Власти» за авторством Владимира Коршунова и Тимофея Никулина, которую выпустило издательство Muravey Games осенью 2020-го года.

По сюжету, коротко обрисованному в правилах комиксом, в далеком будущем человечество создало антропоморфных животных, отправив их в космос – видимо, с целью поиска миров, пригодных для заселения людьми. Но путь оказался намного длиннее планируемого, система дала сбой, и звери пробудились от криосна. Теперь игрокам предстоит возглавить различные группы животных, чтобы установить свой порядок на корабле, разработав дальнейший план действий.

«Теория власти» это карточная игра со всеми вытекающими. Если вы заядлый «картежник», вам легко будет освоиться с механиками и взаимодействием различных персонажей. Для менее опытных игроков авторы предусмотрели обучающий вариант правил. Но, в любом случае вам придется потратить немного времени на усвоение иконографики и свойств животных. Потому что уже со старта придется выбирать каких из них вы оставите в руке, а каких сбросите.

Основной игровой процесс довольно прост. Для победы необходимо первым набрать 8 победных очков и выполнить личную цель доставшегося вам лидера животных. В свой ход вы выполняете одно из четырех возможных действий.

• Получить еду. Сбросьте любое количество карт из руки, чтобы получить по 1 еде за каждую. Если было сброшено две карты одной фракции, получаете еще 1 дополнительный жетон еды.
• Привлечь сторонника. Выложите одну карту животного перед собой, оплатив ее стоимость едой и/или влиянием. Любая лежащая перед вами карта, кроме лидера, приносит одно победное очко. Вдобавок все звери обладают особыми свойствами, которые могут быть как одноразовыми, так и постоянными.
• Переманить сторонника. Выберите любую сыгранную другим игроком карту животного, оплатите ее стоимость влиянием и положите перед собой. Таким образом вы перекупаете чужого сторонника. Сделать это можно только за очки влияния, которое довольно трудно получить. Плюс на сторонников с помощью некоторых свойств можно накладывать жетоны еды, которые увеличивают их стоимость, делая их более защищенными от переманивания.
• Искать контакты. Самое простое действие – добираете из колоды в руку карты до 5, получаете за это штрафной жетон компромата, отнимающий одно победное очко. Естественно, в игре есть способы избавиться от компромата.

Но, как и полагается, глубину процессу придают различные особенности карт.

Все карты в игре делятся на четыре фракции-масти – птиц, рептилий, травоядных и плотоядных млекопитающих. Каждая категория имеет определенные черты, стиль игры. Но особым свойством отличаются только птицы – их можно разыгрывать, частично или полностью оплачивая едой не из собственных запасов, а с карт своих сторонников.

Помимо этого, часть животных являются хищникам и не все они относятся к фракции плотоядных, хищными могут быть и рептилии, и птицы. Особенность хищников заключается в том, что в момент их розыгрыша вы можете скормить им другого своего сторонника равной или меньшей стоимости, чтобы получить соответствующую скидку. К примеру, вы играете Рысь ценой 4, съедаете ей Страуса за 1 – вам остается доплатить 3 еды. Я уже слышу вопрос – «А в чем смысл, если каждое сыгранное животное дает победное очко, приближая к победе?».

Способности животных комбинируются друг с другом, позволяя извлекать дополнительную выгоду из различных действий. Тот же Страус обладает свойством, позволяющим сбросить жетон компромата при его гибели или переманивании другим игроком. А если на съеденном животном лежали жетоны еды или влияния, вы получаете их в свой запас! Это бывает очень полезно, потому что в игре много способов разместить дополнительную еду на сторонниках, а Страус, что с одним, что с двумя жетонами все равно остается легкой добычей для влиятельных оппонентов. Так что вы и скидку получаете, и победное очко не теряете (-1 очко за потерю сторонника, +1 очко от сброса компромата), так еще и пополняете свой запас ресурсов. И, поверьте, это далеко не самая эффективная комбинация.

Но и это еще не все! На картах некоторых животных также могут присутствовать половинки символов Тайных сообществ, напечатанные на краях карты – либо крылья, либо пирамиды. Стыкуя несколько карт одного из Тайных сообществ, вы получаете целые символы, активируя дополнительные бонусы. К примеру, за три собранных символа пирамиды вы получаете 2 победных очка, что может мгновенно закончить партию. За этими символами нужно следить особенно внимательно, чтобы вовремя перекупить последнего необходимого вам сторонника или притормозить нацелившегося на сбор пирамид игрока.

Что мне в этой игре понравилось, чем она меня заинтересовала? Во-первых, тут интересный игровой баланс, который строится на том, что любое животное дает вам одно победное очко. И можно играть как в раш – каждый ход выкладывая недорогих зверей, но рискуя, что в один прекрасный момент оппоненты их просто перекупят, так и нацелиться на более медленную игру, выкладывая дорогих сторонников и защищая их дополнительными жетонами еды. Логично, что более дорогие звери при этом обладают еще и более мощными способностями.

Во-вторых, в игре очень кризисный движок – ресурсы получать трудно, запас карт ограничен, а за добор новых прилетает штраф. Поэтому каждое действие нужно тщательно взвешивать и планировать ходы наперед – кого в какой последовательности разыграть, а кого сбросить.

Эта гонка за победой и дорогие мощные карты, задающие направление развития, напомнили мне «Борьбу за галактику». А ее я, как вы знаете, очень люблю. По времени партии «Теория власти» тоже сопоставима, но за счет лимита на добор карт и возможности перетягивания победных очков длиться чуть дольше. Минут 30-35.

К недостаткам игры можно отнести разве что не самые структурированные правила и вординг. Наиболее частый вопрос, который я слышал – «Почему розыгрыш карты называется привлечь сторонника?». Действительно, это действие очень созвучно с «переманить» и слабо ассоциируется с эффектом.

Почему же «Теория власти» не на слуху? Я думаю, что свою роль сыграла и пандемия, и предвзятость к отечественным разработкам, и подход к оформлению. У игры очень непростое название, которое, к тому же, легко спутать с «Тайной властью», так еще и обложка, не дающая никаких намеков на игровой процесс. Надеюсь, что мой обзор хоть немного повлияет на эту ситуацию. Обидно за ребят – игра-то действительно достойная внимания.

• Об авторе
• Недавние публикации

Сергей Афанасьев

Основатель Бородатого блога. Увлекаюсь настольными играми с 2010 года. Предпочитаю стратегии, кооперативные и карточные игры. В играх ценю вариативность, разные способы достижения цели, оригинальность и художественное исполнение.

Сергей Афанасьев недавно публиковал (посмотреть все)

Запись опубликована в рубрике Карточная игра, Обзор, Стратегия с метками Теория власти. Добавьте в закладки постоянную ссылку.

Теория игр и win-win взаимодействие

Одним из первых, кто заинтересовался этой темой, стал  немецкий математик Эрнст Цермело. С 1913 года он взялся за вычисление оптимальных стратегий для игры в шахматы. Десятилетие спустя этой же темой, но в применении ко всем настольным играм, занялся французский ученый Эмиль Борель. В 1928 году венгерско-американский математик Джон фон Нейман доказал, что для каждой игры с нулевой суммой (то есть, игры, в которой выигравший получает все, а проигравший – ничего[2]) может быть найдено оптимальное решение с помощью математических инструментов.  Переломным моментом в становлении теории игр стал выход в 1944 году в свет книги Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение», выведшей применение теории игр далеко за пределы анализа настольных игр.

Начав с математического анализа стратегий, используемых в классических играх, Фон Нейман достаточно быстро предложил его применение также и для анализа различных форм социального взаимодействия. А именно, речь здесь шла о предложении рассматривать различные формы социального взаимодействия через призму игры[3]. Под игрой в таком случае понимается некая социальная ситуация или сформировавшаяся на определённый момент система взаимоотношений, обуславливающая существование двух или более сторон, выбирающих те или иные стратегии поведения. Каждая из сторон, вовлеченная в социальную ситуацию, преследует те или иные цели, обладает теми или иными интересами[4], а также распоряжается на начало взаимодействия теми или иными ресурсами. В результате протекания игры, то есть, осуществления социального взаимодействия, положение каждой из сторон меняется по отношению к их исходному положению: каждая из них может что-то получить или что-то потерять. Каждая из сторон (каждый игрок) заинтересована в защите собственных интересов и максимизации выигрыша.  То или иное разрешение ситуации, то есть взаимное изменение положения игроков, определяется выбором каждым игроком той или иной стратегии поведения.  Исход игры, то есть, тот или иной вариант баланса между выигрышем/проигрышем различных сторон, может быть отрицательным, положительным или равным нулю. В том случае, если каждый из игроков проигрывает (или теряет возможный выигрыш), речь идет об игре с отрицательным исходом. В том случае, если каждый из игроков выигрывает (то есть, возникает win-win баланс), речь идет об игре с положительным исходом. Тогда же, когда выигрыш одной стороны равен проигрышу другой, речь идет, как уже упоминалось выше, об игре с нулевой суммой.

Именно на выявление наиболее оптимальных и/или наиболее вероятных стратегий поведения различных сторон в рамках той или иной социальной ситуации нацелено применение теории игр в экономике, социологии и других социальных науках. Важно отметить, что не меньшей, чем изначально, остается связь между теорией игр и математической наукой. Математический инструментарий позволяет выявить все возможные последствия каждого решения, которое может принять социальный субъект в рамках выбора той или иной стратегии поведения. В том случае, если мы знаем, чем руководствуются игроки в рамках выбора своей стратегии поведения – например, защитой своих эгоистических интересов и максимизацией собственного возможного выигрыша –мы можем, опираясь на предлагаемые теорией игр математические инструменты,  предсказать вероятный исход того или иного взаимодействия. Речь при этом, может идти о совершенно различных социальных ситуациях. Так, в качестве сторон в контексте экономической теории могут выступать, например, коммерческие компании, выбирающие ту или иную стратегию собственного продвижения на рынке. В контексте геополитики или военной стратегии, речь может идти, например, о взаимной выработке стратегий поведения двумя странами, вовлеченными в гонку вооружений. В способности не только объяснить, но и предсказать стратегии социальных субъектов, просчитать все возможные варианты поведения каждого игрока, а также наиболее вероятный исход социального взаимодействия в рамках выбора той или иной стратегии – особенная притягательность теории игр для экономистов, также как и для военных стратегов, нацеленных на формулирование определенной политики в соответствующей сфере.

Теория игр представляет собой, таким образом, язык[5], переведение на который собственных специфических вопросов, позволяет различным дисциплинам, в той или иной мере затрагивающим тематику стратегического поведения,  искать ответы, опираясь на мощный и в значительной степени универсальный математический инструментарий[6].

Развитие теории игр достаточно быстро привело к ее разветвлению на 2 разных направления: того, что изучает оптимальные и наиболее вероятные стратегии поведения в рамках, так называемых, некооперативных игр и того, что анализирует стратегии социальных субъектов в рамках кооперативных игр. Разделение на некооперативные и кооперативные игры является базовым в теории игр и обуславливает фундаментально разные выводы о возможных стратегиях игроков и возможных исходах игры.

Базовым условием некооперативной игры является отсутствие возможности у игроков согласовывать друг с другом свои стратегии. То есть, иначе говоря, теория некооперативных игр анализирует стратегии поведения социальных субъектов в контексте, где каждый из игроков должен вырабатывать собственную стратегию в одиночку, ориентируясь на свои представления о других игроках, их интересах, ресурсах и возможных стратегиях поведения, но  не имея ни точного знания о них, ни возможности согласования совместной, обоюдно приемлемой стратегии. Одним из наиболее классических примеров некооперативных игр может считаться дилемма заключенного, более детально рассмотренная ниже. Невозможность согласовать свою стратегию с другими игроками является важным ограничением, резко сужающим круг решений, которые игрок может принять в рамках стремления к достижению искомого им результата взаимодействия. Язык кооперативной игры используется, в свою очередь, наоборот для анализа ситуации, в которой различные стороны, оказавшиеся в той или иной социальной ситуации, могут согласовывать свои линии поведения и заниматься выработкой совместной стратегии.

Так, теория некооперативных игр является, например, особенно актуальной в рамках анализа поведения экономических субъектов в контексте свободной конкурентной рыночной среды, где, зачастую, игроки выступают как атомизированные единицы. Выработка решений социальными субъектами здесь зачастую происходит на индивидуальном уровне, без их согласования с другими участниками  игры. Каждый игрок вынужден делать выбор в пользу той или иной стратегии поведения, опираясь лишь на собственные представления о возможных вариантах поведения других игроков. Актуальность теории некооперативных игр для анализа экономических процессов в условиях доминирования во второй половине XX века в западном мире рыночной экономики, вероятно, и обусловила доминирование теории некооперативных игр в общем развитии теории игр.

Так, интерес к изучению кооперативных игр, заданный фон Нейманом и Моргенштерном, был довольно быстро вытеснен в пользу развития теории игр некооперативных, в том числе под влиянием работы американского математика Джона Нэша, обратившего внимание многих ученых именно на некооперативные игры.[7]

Разделение на кооперативные и некооперативные игры актуально при анализе факторов,  определяющих исход игры, а именно итоговую сумму, которая, как упоминалась выше, может быть равна или неравна нулю.  Так, игра с положительным исходом, то есть ситуация win-win взаимодействия, зачастую расценивается как маловероятная в рамках некооперативной игры, как показывает дилемма заключенного[8].  Рассмотрение социальной ситуации через призму кооперативной игры позволяет, однако, более оптимистично смотреть на вероятность  ситуации win-win взаимодействия. В качестве иллюстрации значимости выбора того или иного инструмента анализа будет кратко рассмотрен вопрос о, так называемой, трагедии общин Гарретта Хардина, выход из которой был предложен Элинор Остром за счет перехода от рассмотрения ситуации через призму некооперативной игры к ее рассмотрению через призму игры кооперативной.

Разделение на кооперативные и некооперативные игры отражает, по сути, базовое противопоставление между индивидуальным и коллективным действием. Обращая внимание на это разделение и его влияние на вероятность игры с положительной суммой, мы можем сделать некоторые, пусть и осторожные, выводы об эффективности коллективного действия для реализации индивидуальных интересов.

Дилемма заключенного и win—win взаимодействие.

Одной из наиболее классических некооперативных игр является, несомненно, дилемма заключенного. Несмотря на то, что речь идет об описании конкретной ситуации, сделанные на основе ее анализа выводы могут рассматриваться как актуальные для широкого круга ситуаций, в которых возникает вопрос об отстаивании общих интересов двумя (или более) социальными субъектами, вынужденными вырабатывать собственную индивидуальную стратегию поведения.

Дилемма заключенного сводится к следующему. Двое преступников, А и Б, оказываются в ситуации, когда каждый из них был пойман полицией примерно в одно и то же время, и они обвиняются в сходных преступлениях. У полиции есть основания полагать, что два преступника действовали по сговору. Изолировав их друг от друга, она предлагает каждому из них следующую сделку: если один свидетельствует против другого, а тот хранит молчание, то первый освобождается за помощь следствию, а второй получает 10 лет тюрьмы. Если оба сохраняют молчание, то их преступления проходят по более легкой статье, и каждый из них получает 6 месяцев тюрьмы. Наконец, если оба свидетельствуют друг против друга, каждый из них получает 2 года тюрьмы. Каждый из преступников должен выбрать молчание или свидетельствование против другого. При этом каждый из них не может знать точно, что сделает другой, и механизм согласования действий отсутствует.

	Б  хранит молчание	Б дает показание
А  хранит молчание	Каждый получает по 6 месяцев	А получает 10 лет Б выходит на свободу
А  дает показание	А выходит на свободу Б  получает 10 лет тюрьмы	Каждый получает по 2 года

 

Объективно наиболее выгодным для обоих заключенных было бы молчать и действовать, таким образом, с позиции коллективных действий. Однако, не обладая уверенностью в том, что другой заключенный поступит также, а не захочет максимизировать свой выигрыш за чужой счет, выбрав предательство (и, соответственно, выход на свободу), каждый заключенный сделает выбор в пользу свидетельствования против другого, как наиболее оптимальной стратегии с позиции индивидуального действия. Так как, если партнер молчит, то выгодно его предать и выйти на свободу (а не получить срок в 6 месяцев тюрьмы). А если партнер дает показания, то наиболее выгодно также давать  показания, чтобы получить 2 года (а не 10 лет). Стратегия давать показания доминирует, таким образом, над стратегией молчать, несмотря на то, что с точки зрения объективных общих интересов, двоим заключенным выгодно выступать  с позиции коллективных действий и выбрать стратегию молчать. Результатом игры является отрицательная сумма: наиболее оптимальная стратегия (давать показания), выбранная с индивидуалистических позиций, в действительности не является оптимальной для обоих заключенных. То есть, каждый из них, выступая с индивидуалистических позиций, получает 2 года тюрьмы, а не возможные 6 месяцев. Каждый из них оказывается проигравшим, пренебрегая win-win стратегией молчать.

Одним из многочисленных примеров «срабатывания» дилеммы заключенного в реальной жизни является, например, гонка вооружений между двумя враждующими странами, каждая из которых не может гарантированно рассчитывать на соблюдение формальных обещаний обеих сторон прекратить обоюдное наращивания военного потенциала. Каждая из стран вынуждена продолжать гонку вооружений, неся при этом разрушительные издержки. При этом, из-за отсутствия доверия и надежных механизмов согласования стратегии между враждующими сторонами выбор наиболее оптимальной для обеих сторон стратегии (заключающейся в прекращении гонки вооружения) – то есть, стратегии, возникающей в рамках коллективных действий —  является маловероятным.

Важно отметить, что, несмотря на то, что вероятность выбора win-win стратегии в рамках дилеммы заключенного является с точки зрения классиков теории игр маловероятным, научные эксперименты, направленные на проверку истинности этого вывода показали, что выбор участниками win-win стратегий был намного более частым, чем это можно было предположить на основании теории.

Некоторыми учеными в этой связи был обозначен ряд факторов, делающих возможной win-win стратегию даже в случае некооперативной игры, то есть в условиях необходимости осуществления индивидуального действия[9].  Среди таких факторов следует выделить влияние социальных норм, обеспечивающих предрасположенность людей к выбору индивидуальной стратегии, направленной на сотрудничество с другой стороной и защиту коллективных интересов. Выбор win-win стратегии становится также в значительной степени более вероятным в случае не разового, а многократного проведения игры. Так, выбор сотрудничества, а не предательства будет обусловлен опасениями человека быть в дальнейшем, в рамках следующей игры, наказанным за эгоистическое «асоциальное» поведение.  Таким образом, даже в рамках некооперативных игр существуют механизмы, способные обеспечить большую вероятность win-win взаимодействия.

Кооперативная игра как выход из тупика «трагедии общин» (tragedy of the commons[10]).

Несколько более надежным механизмом обеспечения win-win взаимодействия между людьми, чем те, что существуют в рамках некооперативных игр, является механизм согласования совместной стратегии между игроками — возможный в рамках  кооперативных игр.  Внедрение механизмов согласования стратегий является, согласно американскому ученому Элинор Остром, тем самым инструментом, который способен обеспечить  переход от отрицательного к положительному исходу игры.

В своей работе Элинор Остром опровергла влиятельный тезис о неизбежности трагедии общин, сформулированный в конце 1960-ых годов известным американским  экологом Гарреттом Хардином[11]. Изучая проблему перенаселения планеты, Хардин поставил вопрос о последствиях коллективного владения ограниченными природными ресурсами и сделал вывод о том, что использование ограниченных ресурсов, находящихся во всеобщем владении, неизбежно является расточительным и небрежным. Результатом такого неразумного использования, обусловленного стремлением каждого индивида к максимизации собственной выгоды, является, в конечном итоге, исчерпание ресурса и, соответственно, ситуация в которой каждый индивид оказывается в положении проигравшего – то есть речь идет об игре с отрицательной суммой.

Трагедия общин, согласно Хардину, заключается в том, что  свободный доступ к ограниченному ресурсу (Хардин предлагает в качестве примера использование пастбища, находящегося в общем владении), приводит в конечном итоге к его чрезмерному использованию и исчерпанию. Так, говорит Хардин, преследуя свои индивидуальные интересы, каждый скотовод будет стараться максимально увеличить собственную выгоду, выводя на пастбище, находящееся в общем владении, максимальное количество животных. Однако результатом получения каждым игроком максимальной выгоды сегодня станет уничтожение возможности получения выгоды в дальнейшем.  Проблема небрежного использования ресурсов, находящихся в общем пользовании,  таких как вода, воздух и т.д., особенно в рамках активного загрязнения окружающей среды, стала особенно остро ощущаться в конце XX — начале  XXI века, поэтому описанная Хардином проблема трагедии общин вряд ли может считаться надуманной или неактуальной.

Элинор Остром, в свою очередь, не отрицает существования этой проблемы. Однако, идея неизбежности печального сценария, описанного Хардином, является, согласно Остром верной только в рамках рассмотрения ситуации через призму некооперативной игры[12]. В том же случае, когда к анализу ситуации применяется теория кооперативной игры, из нее появляется выход, способный обеспечить win-win взаимодействие между пользователями ресурса. Так, Остром показала, что в истории существует много примеров, когда внедрение различных механизмов согласования стратегий использования ограниченного ресурса выступало в качестве альтернативы индивидуалистическим и  разрушительным стратегиям поведения. Выстраивание социального взаимодействия в формате кооперативной игры, то есть, внедрение механизмов согласования индивидуальных стратегий или выработки совместной стратегии может рассматриваться, таким образом, как важный  инструмент обеспечения win-win взаимодействия.

Литература:

1. Фон Нейман Джон, Моргенштерн Оскар, Теория игр и экономическое поведение, Москва, Наука, 1970, 707 с.  
2. Batifoulier Philippe, « Chapitre 4. Le décideur en interaction : égoïste et calculateur », in Bénédicte Vidaillet , La décision, De Boeck Université, « Méthodes & Recherches », 2005 p. 105-123.
3. Cabon-Dhersin Marie-Laure et Ramani Shyama, « La rationalité des agents économiques va-t-elle toujours à l’encontre de la coopération ? Le jeu de la poule mouillée», Revue d’économie politique, 2007/2, Vol. 117, p. 271-284.
4. Eber Nicolas, Le dilemme du prisonier, Paris, Repères, La Découverte, 128 p.
5. Garapin Alexis, « Rapprocher l’Homo Oeconomicus de l’Homo Sapiens. Vers une théorie des jeux réaliste et prédictive des comportements humains », Revue d’économie politique, 2009/1, Vol. 119, p. 1-40.
6. Godbout Jacques T., « Ni égoïsme ni altruisme. Don et théorie des jeux», Revue du MAUSS, 2002/2, No 20, p. 286-299.
7. Hardin Garrett, «The Tragedy of the Commons», Science, New Series, Vol. 162, No. 3859, Dec. 13, 1968, pp. 1243-1248.
8. Laskar Daniel. Accords régionaux : une approche en termes de jeux coopératifs, Revue économique, Vol. 47, No 3, 1996, pp. 797-806. 
9. Latouche Serge, « 1. Malaise dans l’association ou pourquoi l’économie plurielle et solidaire me laisse perplexe », in Jean-Louis Laville, Association, démocratie et société civile, La Découverte « Recherches », 2001, p. 17-26. 
10. Lengaigne Benoît, « Nash : changement de programme ? », Revue d’économie politique, 2004/5, Vol. 114, p. 637-662.
11. Ostrom Elinor, Gardner Roy, Walker James, Rules, Games, and Common-Pool Resources, The University of Michigan Press, 1994, 392 p.
12. Schmidt Christian, « Deux prix Nobel pour la théorie des jeux », Revue d’économie politique, 2006/2 Vol. 116, p. 133-145.
13. Schmidt Christian, « Du jeu aux joueurs : sur quelques extensions de la théorie des jeux», Psychotropes, 2007/3 Vol. 13, p. 55-75.
14. Schmidt Christian, « La révolution tranquille de la théorie des jeux », Le Débat, 2005/2,  No 134, p. 176-192.

---

[1] Schmidt Christian, « La révolution tranquille de la théorie des jeux », Le Débat, 2005/2,  No 134, p. 176-192

[2] Настольные игры как раз являются прекрасным примером игры с нулевой суммой – обычно в них есть однозначно выигравший и однозначно проигравший. 

[3] Schmidt Christian, « La révolution tranquille de la théorie des jeux », art. cit.

[4] Интересы двух сторон могут пересекаться или быть, например, наоборот, взаимоисключающими.

[5] Schmidt Christian, « La révolution tranquille de la théorie des jeux », art. cit.

[6]Введение понятия игры и совместно с ним ряда производных от него понятий (таких как игрок, стратегия, выигрыш, проигрыш и других), иначе говоря, позволяет, анализировать социальные явления с помощью  стандартизированного и поддающегося математической обработке языка. Так, наверное, уместным было бы проведение параллели между использованием терминологии теории игр в экономике, политологии или биологии и использованием языков программирования в информатике.   То есть, речь идет о переходе от игры как объекта анализа к игре как инструменту анализа различных объектов.

[7] Важно отметить, что за свой вклад в развитие теории игр, а именно за формулирования в начале 1950 годов понятия, получившего название равновесие Нэша, Джон Нэш получил Нобелевскую премию по экономике.

[8] В отсутствии механизмов согласования решений, как показывает дилемма заключенного, ситуация в который каждый проигрывает (по сравнению с возможным оптимальным вариантом) более вероятна, чем ситуация в которой каждый выигрывает. Хотя, как будет показано в дальнейшем, положительный исход игры становится возможным и в рамках дилеммы заключенного при вмешательстве ряда специфических факторов несколько трансформирующих конфигурацию.

[9] Batifoulier Philippe, « Chapitre 4. Le décideur en interaction : égoïste et calculateur », in Bénédicte Vidaillet La décision De Boeck Université « Méthodes & Recherches », 2005 p. 105-123.

[10] Классическим является перевод понятия на русский язык как трагедии общин, однако более точным и отражающим сущность понятия был, наверное, перевод трагедия коллективной собственности (коллективного владения).

[11] Hardin Garrett, «The Tragedy of the Commons», Science, New Series, Vol. 162, No. 3859, Dec. 13, 1968, pp. 1243-1248.

[12] Ostrom Elinor, Gardner Roy, Walker James, Rules, Games, and Common-Pool Resources, The University of Michigan Press, 1994, 392 p.

Настольные игры. 12-0-12. Теория власти. Съешь ближнего своего.

Космос безграничен, поэтому колонизация отдалённых планет связана с огромными трудностями: даже с использованием передовых межпространственных нанотехнологий перелёт займёт десятилетия, во время которых команда состарится, и в момент посадки по трапу спустятся лишь глубокие старцы, толку от которых будет не много. Выход прост – заморозить экипаж в криогенной камере, авось кто-то потом очухается и сможет водрузить флаг конфедерации на неизведанной земле. Главное, чтобы проснулись все вовремя и в одно и то же время, иначе быть беде…

Транспорт Genesis 13 дрейфовал в созвездии Гамма Центавра третье десятилетие, давно потеряв связь с Центром управления. Метеоритные дожди основательно потрепали судно, выведя из строя несколько энергетических блоков. Для поддержания защитного щита компьютерная система приняла единственно правильное решение – отключить питание от бесполезных отсеков, чтобы спасти электронную начинку корабля.

Несложно догадаться, что криогенные камеры были обесточены (кому нужны эти пассажиры), что вызвало преждевременное пробуждение разношёрстного экипажа. Учитывая ограниченные запасы продовольствия, на борту стали творится необъяснимые вещи…

Сегодня вам предстоит стать лидером и повести за собой верных соратников, уничтожая по пути ненавистных конкурентов. Для этого потребуется небольшая коробочка от издательства Muravey Games, внутри которой вы найдёте: горсть жетонов, стопку карт, несколько планшетов и буклет наставлений начинающему диктатору.

Жетоны пригодятся для прокорма единомышленников, обеспечат вам влияние в обществе, а также станут компроматом, дурно влияющим на репутацию.

Индивидуальные планшеты максимально информативны – здесь кратко изложены правила поведения на корабле, указаны регалии и расшифрованы специальные символы, встречающиеся на шевронах команды.

Экипаж на корабле разнообразный, состоящий из четырёх фракций животных-мутантов, выведенных специально для колонизации диких планет: парящие в небе птицы, вечно голодные хищники, травоядные млекопитающие и рептилии питают друг к другу чувство искренней ненависти.

Каждая фракция состоит из пятнадцати соратников, каждый из которых имеет свои особые свойства и знает себе цену.

Безусловно, присутствуют лидеры, готовые вести за собой единозверцев к светлому будущему, процветанию, и Великой Победе над конкурентами.

За еду и влияние!

Итак, вы оказались на злосчастном корабле, затерянном в безбрежном космосе. Криогенные камеры открыты, звероподобные существа заполонили отсеки, все постепенно осознают, что еды на всех не хватит, да и конечная цель пути практически недостижима. Задача проста – сколотить вокруг себя команду единомышленников, захватить власть над звездолётом, затем… Хотя, это уже другая история, пока займёмся вербовкой экипажа.

Претендент на звание капитана корабля располагает перед собой индивидуальный планшет, на который помещает три жетона еды. Колода животных перемешивается, первый игрок берёт пять карт, второй – шесть, третий – семь, четвёртый – восемь. Просматриваем полученных соратников по партии, оставляем пятерых, остальных отправляем в общий сброс. В дополнение (по продвинутым правилам) оппоненты получают по две карты лидеров, выкладывают перед собой одного, второй уходит в коробку.

Обратите внимание, что выполнение условий, указанных на картах лидеров, обязательно для победы над противниками (помимо базового правила завершения партии). Также некоторые личности наделяют своих хозяев преимуществами на старте. Гадюка, например, приносит один жетон влияния.

Борцы за власть ходят по очереди, выполняя в свой ход одно из четырёх действий, указанных на планшете (бывают исключения, обусловленные свойствами сыгранных карт). Первое действие – получение еды. Для этого «перерабатываем» в консервы любое количество карт с руки: один неугодный сочувствующий приносит соответствующую единицу пищи, пара представителей одной фракции – три.

Второе возможное действие – найм приспешника. Тут пригодятся еда и очки влияния в любой комбинации, требуемое количество указано в левом верхнем углу портрета претендента. Во время вербовки желаемый представитель вашей команды выкладывается перед планшетом, потраченные жетоны уходят в общий резерв. Не забудьте, что отныне работают свойства, указанные в нижнем блоке карточки.

Пять типов значков определят время и место активации свойств: во время поиска контактов, выполнения условий на карте, вербовки или предательства вашего сторонника, времени кормления. Памятка на планшете придёт на помощь в трудную минуту…

Крылья и пирамиды – тайные сообщества, примкнув к которым игрок получает определённые привилегии. Чем больше символов, тем больше влияние на ситуацию и тем выше шансы на победу!

Кстати, если у вас нет еды для привлечения хищного сторонника, то… скормите ему примкнувшего к вам ранее собрата по партии с меньшим или равным аппетитом. Также ориентируйтесь на символы в правом верхнем углу карты: снабженцы обеспечивают ваших соратников дополнительным пропитанием (его можно использовать для вербовки птиц), хищники съедают менее слабых.

Третье действие – переманивание в свой клан соратников оппонента (увы, каждый мечтает предать своего хозяина, переметнувшись в более сильный клан). Для этого используются исключительно очки влияния, количество которых должно перекрывать потребности в пище желаемого претендента. Помните, что все лежащие на карте жетоны пропитания также должны быть компенсированы!

Каким образом пополнить руку? Очень просто – четвёртое действие называется «Поиск контактов». Вы добираете руку до пяти карт, но получаете за это жетон компромата, отнимающий одно победное очко. Безусловно, некоторые свойства позволяют также добирать карточки из общей колоды.

 

Для победы необходимо выполнить два условия: сделать всё, что указано на карте лидера, а также набрать восемь (или более) победных очков. Учитываются жетоны компромата, количество сторонников, участие в тайных обществах и особые условия на картах. Победитель захватывает власть над кораблём, становится диктатором, оппонентов преобразует в консервы и безуспешно пытается отыскать планету с пригодными для жизни условиями…

Соратник соратнику – вкусная и здоровая пища

Стильная по оформлению (на любителя), быстрая по времени партии, глубокая по тактическим решениям, подразумевающая большое количество комбинаций карт, и, как следствие, высокую реиграбельность, при этом имеющая несложные правила и минимальный порог вхождения. Удивительно, но всё это создано отечественными авторами, сумевшими найти золотую середину между огромным количеством свойств и простотой их использования. Также виден задел на дополнения, которые прекрасно впишутся в игровой процесс.

Возможность забирать карты у оппонентов, а также свойства, срабатывающие в определённые фазы игрового процесса, превращают «Теорию власти» в карточную головоломку, в которой необходимо постоянно быть на стороже, внимательно следить за соперниками и стараться предвидеть дальнейшее развитие событий. В противном случае вы рискуете лишиться всего буквально в шаге от победы…

Для широкого круга поклонников карточных игр: здесь есть над чем поразмышлять, есть место коварству и холодному расчёту. Короткие партии, низкий порог вхождения, возможность дуэльного режима (он хорош) – отличная  «настолка» для вечера в кругу друзей.

Мои благодарности магазину Cardplace и издательству Muravey Games за возможность принять участие в космическом заговоре.

Японская теория пикапа. Обзор настольной игры Путь лепестка — Марафон настолок

Обзор настольной игры Путь Лепестка/Hanamikoji.

Сакуры цвет,
Веер под зонтом —
Выбор из трёх.

Признаюсь, пул настольных игр в нише карточных филлеров у меня занят очень малым количеством коробок. А потому, что мало мы такие игры достаём. С трудом туда проникают новинки, а уж если это игры на двоих — то и подавно. Так вышло, что с женой вдвоём в дуэли мы играли во времена, когда только вышли Пэчворк и 7 Wonders Duel. В коллекции есть ещё несколько игр на двоих, но чаще мы играем большой компанией. Поэтому до данной дуэльки я добрался только сейчас

Да и сесть за игровой стол с Путём лепестка я смог, когда для этого «звёзды сошлись». Я пришёл в гости раньше остальных, надо было разложить что-то быстрое, на 15 минут, потому что «вот-вот придут остальные». С собой ничего не было, а у хозяйки дома лежал на виду «Путь лепестка» Остальные задержались чуть дольше, что позволило познакомиться с игрой чуть глубже. Примечательно: я был доволен этим фактом и после первой партии попросил продолжения.

Что из себя представляет Путь лепестка? Это карточная абстрактная дуэль. Теоретически, мы ней боремся за внимание гейш, одаривая подарками, но на деле всё это напускное. Как минимум, способ одаривания в тему я вписать не смог. Хотя, именно в нём вся фишка игры.

Перед игроками раскладывается ряд из семи гейш, которые отличаются друг от друга цифрой и внешним видом. Цифра говорит о редкости запрашиваемого подарка в колоде. На колоду из двадцати одной карты это очень большая информация. Например, пять карт цветов — это почти четверть колоды. Кроме количества карт, эти числа обозначают ещё и победные очки, которые получит игрок, заманив девушку на свою сторону. В центр каждой плашки кладётся деревянный жетончик, дублирующий символ подарка и показывающий в последующем, на чьей стороне гейша сейчас.

Каждый игрок получает по четыре жетона действия и по шесть карт. Это старт, на котором игрок должен распланировать чуть ли ни всю свою будущую игру. По крайней мере, за раунд. Потому что одна карта из колоды выбрасывается, и игрок в этом раунде получит ещё всего четыре карты в начале каждого своего хода. Более того, совсем не обязательно, что он оставит их себе.

Это не факт потому, что в свой ход он должен добрать карты и разыграть один из своих жетонов, выполнив указанное. И самый простой жетон из четырёх указывает — сбрось две карты. Уходят они из раунда насовсем. Остаётся восемь (пока) карт, которыми как-то распорядится игрок. Пока, потому что ещё два жетона дают выбор карт не только хозяину, но и противнику.

Жетон с равным выбором — игрок показывает четыре карты, разделённые на пары. Соперник выбирает одну пару, а оставшуюся уже разыгрывает хозяин. Иногда выбор очевиден, а иногда проблемен — когда все карты на руке, как их не разбей, несут выгоду противнику. Если жетон не последний, в такой момент его бы не разыгрывать.

Похожий жетон — игрок показывает три карты, и соперник берёт себе всего одну. Его выгодно разыгрывать когда у тебя несколько (хотя бы две) одинаковых карт. Выкладывая их, игрок напротив будто слышит — «Если ты оставишь мне две карты для одной гейши, велик шанс что она мне и достанется; если ты оставишь мне карты для разных гейш, то борьба сохранится на двух фронтах». Немного блефа в довольно замкнутом пространстве.

Напомню, что эти два жетона разыграет и противник, и уже с его руки карты придут на сторону игрока. То есть на каждой стороне будет по семь карт.

Ну и четвёртый, эгоистичный жетон — сохранить одну карту, которая вскроется после розыгрыша всех карт и ляжет восьмой. Этот жетон, как раз позволяет люфтить в моменты выбора и возможного блефа, ведь соперник может только догадываться, какую карту ты сохранил. Единственный жетон, который я смог вписать в сеттинг, как самый ценный подарок, который игрок приберёг напоследок.

После розыгрыша всех карт игроки сравнивают, кто больше подарил каждой гейше. При ничьей, девушка остаётся холодна к обоим сторонам. Если игрок завоевал внимание четырежды, или ценность этого внимания больше одиннадцати — он победил. Если этих условий никто не достиг, начинается новый раунд. Таким перетягиванием каната в правилах рекомендуют всего три раза, по истечении которых, подсчитать всё-таки очки и закончить партию. У нас в сыгранных партиях получилось определить победителя на втором раунде. Но я совершенно не вижу помех перетягивать канат и после третьего раунда, если, конечно, игра не наскучила. Потому что победа с минимальным перевесом, который возможен , не воспринимается полноценной.

Хотя, в таком случае, игра может затянуться. На коробке написано, что полноценная партия займёт 20-30 минут, и эта длительность достаточно честная. Главное, не растянуть до такой длительности раунд. Казалось бы, всего то разыграть пару-тройку карт, но не вовремя разыгранный номинал может стоить игроку всей партии. Поэтому над каждым ходом надо чуть-чуть покорпеть.

Японский геймдизайн отличается от мирового своей лаконичностью. Kota Nakayama не изменил этому принципу и сделал маленькую игру, однако, не обделил её глубиной. Более того, по процессу игра ближе к каким-нибудь абстрактным филлерам Книции (не просто так игру сравнивают с Баталией), чем к японским малюткам от Jun Sasaki (Kobayakava, Deep Sea Adventure) или Seiji Kanai (Love Letter и гора других микро-игр). Уверен, играй я в японскую версию, и коробка была бы раза в четыре меньше (размером с колоду карт, например), но издательство Звезда, локализовавшая её в России, подарило игре коробку от души, да ещё и гейш в двух экземплярах — и для уютной игры на столе, и для партий в дороге.

На мою полку, Путь лепестка не попадёт, так как не будет пользоваться спросом. Для игр в дорогу, по мне, она имеет всё тот же минус — ограничение в два человека, не больше. Ситуация может поменяться, когда подрастут дети, но так далеко пока смотреть не буду. Однако я рад, что она есть в компании, и её можно разложить в гостях перед тем, как начнётся основная игротека. Если, конечно, ещё не пришёл третий.

Понравилось это:

Нравится Загрузка…

История появления настольных игр

Цель: познакомить с разнообразными настольными играми.  Рассмотреть настольные игры в культурно-историческом аспекте и подчеркнуть основное влияние настольных игр на развитие интеллектуальных способностей и формирование личности ребенка.

Ход классного часа

Вступление:

Строгого определения настольной игры не существует. Обычно к этой категории относят игры, состоящие в манипуляциях с относительно небольшим набором предметов, которые можно целиком разместить на столе (или на чём-нибудь, что может заменить стол) и/или в руках играющих. Такие игры могут вестись в небольшом закрытом помещении, в поезде или другом транспортном средстве, и, вообще, в любом месте, где имеется стол. Они не требуют специальных сооружений, зданий, крупногабаритного оборудования. Игроки в таких играх, как правило, могут оставаться на одном месте, им не требуется активно перемещаться. Чаще всего настольные игры рассчитаны на несколько человек, хотя есть и исключения, например пазлы.

Основная часть:

Настольная игра — игра, в которую можно играть в помещении, с помощью инвентаря, размещаемого на обычном или специально сделанном столе.

Увлечение настольными играми, в которые, впрочем, играли не только на столе, но и на земле, и на полу, первоначально возникло как забава для элиты Римской империи, а затем распространились по всей  Европе благодаря римским легионам.

Ну а голландский философ Йозеф Хайзенга эту теорию углубил. По мнению Хайзенги люди превращают в игру весь свет и человек только потому человек, что умеет играть. По этой теории вполне понятно отчего настольные игры зародились так давно, что уже и не узнать, откуда произошла эта забава.

Итак, вот некоторые вехи в истории настольных игр мира:

До нашей эры.

Самой древней настольной игрой считается сенет. Развлечение это было популярно еще 4000 лет до нашей эры в Древнем Египте и по своим правилам напоминала шашки.

Три тысячи лет до нашей эры были изобретены игральные кости, а вместе с ними и знаменитые нарды. Нарды — игра шашечного типа, появившаяся на арабском Востоке и сохранившаяся до сих пор, хотя и в изменённом виде. Тогда кстати в нарды играли по немного другим правилам.

В это время в Индии уже играли в чаупар, тоже игру шашечного типа. Известно, что в это же время зарождается игра наподобие шашек в Испании и России.

Две тысячи лет назад зарождается знаменитая и по сей день настольная игра Го.

2 тысячелетие до нашей эры

Го и Го-моку — игры шашечного типа, в которых фишки не передвигаются по доске, а лишь выставляются и убираются с неё. Появились в древнем Китае и сохранились по сей день, с минимальными изменениями.

Многие классики и военные деятели поклонялись шашкам. Игра, которая развивает логику и стратегию. Великие Пушкин, Державин, Лев Николаевич Толстой были приверженцами этой игры. Даже такие полководцы, как Суворов и Наполеон увлекались шашками и во многом полагались на свой опыт благодаря умению играть в эту занимательную и интересную, всегда новую игру.

Правила древней игры были очень похожи на современные: игровая доска уже состояла из 64 клеток, шашки были, как и сейчас, белыми и черными. Правда, ходить они могли, подобно наступающим на противника солдатам, только вперед. Если одна из шашек прорывалась в тыл врага, получала преимущества, становясь дамкой, и могла вести нападение не по прямой траектории.

1723 год 

Английский шашист польского происхождения, оставшийся в истории под прозвищем Поляк, предложил увеличить шашечную доску до 100 клеток и немного изменить правила игры — появились стоклеточные (польские) шашки. Широкое распространение и отсутствие расхождений в правилах игры сделало этот вариант шашек международным.

V век

В истории настольных игры ознаменован появлением первой игры шахматного типа. В Индии тогда появилась игра чатуранга, напоминающая современные шахматы.

XII век 

Стал одним из важнейших в истории развития настольных игр. Именно этим веком датированы первые найденные игральные карты. Найдены они были на востоке.

XVIII век. 

В эту пору из Азии в Европу привозят домино. Первой страной, где полюбилась эта игра мазаичного типа стала Италия.

1870 год стал годом игры маджонг. Приблизительно в этом году в Китае зарождается знаменитая азартная игра, с применением игральных костей.

1880 год в этом году в Великобритании изобретают знаменитую игру реверси (настольная игра шашечного типа на доске 8*8 клеток).

1934 год в этом году Чарльз Дэрроу явил миру знаменитую монополию. Тогда это была экономическая настольная игра, что-то вроде экономической стратегии. Впоследствии появились тысячи разновидностей этой игры. Полагают, что причиной для создания этой игры стала Великая депрессия 1930-х в США.

1938 год 

Придумана знаменитая игра «Скрэббл». В России она более известна как «Эрудит». Впрочем, аналогом этой игры можно считать русскую игру под названием «Балда».

Игра “Мафия” придумана весной 1986 года студентом факультета психологии МГУ Дмитрием Давыдовым, уроженцем Каменска-Уральского. Вначале в неё играли в общежитиях, аудиториях и коридорах МГУ, но после того как некоторые студенты университета провели каникулы в летних студенческих лагерях, где отдыхали студенты и других советских ВУЗов, игра вместе с новыми игроками стала распространяться по другим учебным заведениям СССР.

В 1998 году игра “Мафия” и ее европейский прототип — игра “Убийца” были использованы калининградской Высшей школой МВД РФ для курса “Визуальная психодиагностика”. Игры легли в основу учебно-методического пособия, с помощью которого развивали навыки курсантов в отношении различных приёмов и методов чтения языка телодвижений.

В Китае “Мафия” используется для лечения азартных людей от игровой зависимости, а в США — как средство перевоспитания “трудных” подростков в летних христианских лагерях. А еще, с помощью “Мафии” к роли будущих присяжных готовятся японские старшеклассники.

Мафия признана одной из “50 наиболее исторически и культурно существенных игр, появившихся с 1800 года”.

Заключение:

«Что наша жизнь? Игра» написал однажды А. Пушкин в своей «Пиковой даме».

Знаете ли вы, что настольных игр для старших школьников значительно больше, чем для детей? Казалось бы должно быть наоборот. Несмотря на то, что в последнее время настольные игры приобретают всё большую популярность, многие из них по-прежнему малоизвестны. 

Настольные игры — уникальное средство от скуки, способное разнообразить домашний досуг во время непогоды, объединить всех членов семьи и стать настоящим спасением для большой заскучавшей компании гостей.

Проектирование с помощью теории игр | UX Collective

От настольных игр до стратегии бренда и ядерной войны. Стратегия, которая нам нужна для завтрашних проблем, и как ее изучить.

Теория игр — это не дизайн игр. Это многогранное исследование, подобное архитектуре, которое смешивает экономику, психологию, социологию, философию и дизайн в одну академическую практику. Другими словами, теория игр — такой же актив, как и все остальное в наборе инструментов творческого профессионала. Это то, что вы можете оттачивать и искать в качестве формы профессионального развития, как чтение романов улучшает копирайтинг, просмотр фильмов улучшает художественное оформление, а импровизация помогает лучше выступать.

Эта статья познакомит вас с теорией игр — загадочным искусством Наполеона и Джеффа Безоса. И это защитит мое хобби от советов креативных директоров о том, что теория игр — это «то, чем вы должны бросить ради более крупной и актуальной деятельности».

На нем можно читать учебники. Вы можете получить степень в нем. Вы даже можете посмотреть отмеченный наградами фильм об этом.

Или вы можете повысить уровень своего мастерства так же, как мы это делали с данными, ИИ и человеческими истинами, с чем-то меньшим. Смешнее. И многое другое доступно.

Позвольте мне объяснить с помощью быстрой параллели…

Спросите любого редуктора, почему он любит автомобиль, и фанатик откроет капот и покажет вам его нутро. Потому что большинство автолюбителей со временем становятся любителями автозапчастей.

А эти части: легкие, артерии и стальные органы автомобиля — это ворота к чему-то большему, чем просто автомобили. Потому что среднему водителю нравится ощущение вождения, а автомобилистам нравится то, что вызывает это чувство.

В конце концов, автолюбители не играют с двигателями и коробками передач; они используют двигатели и коробки передач, чтобы играть с физикой.

Владение автомобилем означает работу с гравитацией, материей и химией. Другими словами: мощность, крутящий момент и пробег.

Я понял это, бесцеремонно, при сборке дверей автослесарем. Слушая, как солидные люди шутят о машинах на перекурах.

И это заставило меня спросить: Что мы обнаружим, когда приподнимем капот над моими увлечениями? С какими скрытыми силами мы играем, когда начинаем перестраивать эти элементарные части игрового дизайна?

Все эти крошечные правила и математические разноцветные точки на костях называются механикой. Механические части автомобилей сделаны из стали, но на фундаментальном уровне они представляют собой чистую, необработанную физику. В глубине настольных игр эти деревянные и пластмассовые детали — не правила, а теория игр.

Вот официальное определение теории игр:

Теория игр — это академическое исследование, в котором мы анализируем и проверяем варианты действий человека на основе мотивов и действий других. Итак, будь то сотрудничество или конкуренция, теория игр — это изучение стратегического взаимодействия, живя во взаимосвязанном мире.

Стратегическое взаимодействие также является основным двигателем большинства настольных игр, поэтому исследование заимствовало свое название от них. В последний раз вы, великолепный дилетант, занимались теорией игр, вероятно, играя в настольную игру.

Шахматы, крестики-нолики и современные игры, такие как Ticket to Ride — все это системы стратегического взаимодействия. Но теория игр для геймеров так же важна, как физика для автолюбителей, она выходит далеко за пределы мира материальных объектов.

В глобальная экономика , национальные государства ведут торговлю, вводят эмбарго и воюют с планами и стратегиями других стран. Вот почему некоторые страны являются синонимом производства, в то время как другие могут производить культуру для мировой торговли.

В политология , политические партии соревнуются за контроль над различными местами и политиками, разделяя землю и согласовывая свои правила, как в реальной игре Риск . В контексте теории игр идея политических партий, пытающихся «обыграть» систему, часто кажется слишком реальной; например, мошенничество — коррумпированное поведение в американской системе, но это не значит, что это не оптимальная стратегия для победы на выборах.

В Управление бизнесом , Фирмы и агентства изучают своих конкурентов, чтобы определить возможные возможности или позиции, где они могут получить прибыль. Как креативный копирайтер, я сравниваю слоганы и сообщения бренда моего клиента с существованием других.

Но это человеческие взаимодействия, а изучение стратегического взаимодействия выходит далеко за рамки социальных взаимодействий:

В биология , животные конкурируют за ресурсы, истощают свою экосистему ресурсов, когда слишком агрессивны, перенаселены, когда слишком успешны, и вымирают, когда проигрывают. Теория игр используется биологами и защитниками природы для сохранения баланса в среде обитания.

В теоретическая физика , теория игр моделирует вселенную. Он изучает Большой взрыв, расширение галактик и энтропию Вселенной. Знаете ли вы, что количество возможных перестановок в вашей стандартной колоде из 52 игральных карт больше, чем атомов на Земле?

Подводя итог, можно сказать, что область применения теории игр безгранична. И его сюжеты часто слишком сложны для обычного наблюдения. Именно здесь теория игр и настольные игры воссоединяются.

Вот некоторые заимствования теории игр из настольных игр:

Теория игр определяет всех лиц, принимающих решения, как «игроков», а все действия — как «ходы». Чтобы понять сложные сценарии, такие как экономики или группы людей, теория игр превращает их в более простые абстрактные модели, называемые «играми».

Эта абстракция превращает сложные вещи в двигатели. Сложный, но его можно разобрать, переставить, а когда это настольная игра — играть, учиться и получать удовольствие.

Дизайн игр, особенно дизайн настольных игр, представляет собой среду и практику, которая включает в себя больше, чем теорию игр. Например, такая игра, как «Монополия », — это не просто модель для изучения капитализма. Потому что если бы это было так, то оно было бы больше, сложнее и менее затенено рандомизацией, названиями свойств или картами шансов.

Однако эти формы обфускации делают игру играбельной. В большинстве игр оптимальная стратегия для победы никогда не бывает ясной или постоянной — она всегда развивается по ходу игры.

Таким образом, игровой дизайн отличается от целей теории игр. Включение таких вещей, как обман, случайность, эмоции, язык тела и скрытая информация — вот что делает игру увлекательной. Но они же и делают его несовершенным соотношением 1 к 1 в теории игр.

Это предостережение к тому, что я собираюсь предложить. Геймдизайн — это не теория игр. Однако теория игр является фундаментальной частью игрового дизайна. И это одна из самых веских причин для его изучения.

Я люблю многие настольные игры, потому что они моделируют удивительные, сложные сценарии, которые никто не может или никогда не сможет контролировать. Но за столом вы можете попробовать. Подобно автомобильным фанатикам, которые выжимают науку, чтобы двигаться быстрее, вы можете выжать из теории игр игру, чтобы командовать армиями и строить нации с помощью кубиков и деревянных фигур.

Все игры в некотором роде являются моделью теории игр с одним или двумя геймифицированными дополнениями. Разница между дизайном видеоигр и настольных игр заключается в дистанции между игроками и системой, которой они управляют.

Видеоигры — это прошедшее время с той же базовой механикой, что и у их аналоговых аналогов, но они маскируют эти механические рычаги и шестеренки графикой, интерфейсами и звуковым оформлением. Они могут позволить себе роскошь добавлять дополнительные сложности, не обременяя игрока.

Между тем, в настольных играх такой роскоши нет. Если бы настольные игры были автомобилями, их капоты всегда оставались бы открытыми. Все движущиеся части перемещаются исключительно игроком. Вся математика делается исключительно в их голове. И единственный камуфляж, который внезапно делает деревянную фигуру наполеоновской армией, — это символизм, которым ее наделяют игроки.

Любой, кто хочет восхищаться и изучать стратегическое взаимодействие, должен играть в настольные игры, потому что настольные игры делают основы интересными и доступными для всех.

Чем больше вы понимаете и восхищаетесь настольными играми, тем больше вы знаете теорию игр, вот лишь некоторые из моих любимых: договориться о выходе из нехватки ресурсов. В сеансе с высококвалифицированными игроками побеждает не тот, кто удачливее или хитрее, а тот, кто может успешно договориться о сделке, которая принесет ему победу.

Это потому, что на турнирном уровне лучшие игроки могут увидеть оптимальную стратегию за много миль, даже при случайных отклонениях в бросках кубиков. Но расстояние, которое они видят, является оптимальной стратегией, когда один игрок может действовать более стратегически, чем другие, и совершать более выгодные сделки.

Тайный Гитлер — это игра на социальную дедукцию, в которой игрокам предлагается построить обреченный на провал немецкий парламент 1933 года, в то время как другие игроки, играя за скрытых фашистов, вступают в сговор с целью его подкупа. Дизайн ставит перед хорошими парнями такие же вопросы, как и перед реальными либералами 19-го века.33 и бросает им вызов, чтобы выиграть его.

Тем не менее, они должны оценивать альтернативные издержки своих действий и отчаянно пытаться поддерживать кворум, в то время как другие игроки пытаются скрыть его логическими ошибками.

Игра посвящена принятию стратегических решений на основе неполной (часто вводящей в заблуждение) информации. Это социальный эксперимент, имитирующий реальную жизнь. Таким образом, «Секрет Гитлера » — это наполовину настольная игра и наполовину машина времени. Смогут ли игроки победить историю? И что он говорит о нашем настоящем?

Монополия , Между тем имеет особый статус. Это об истощении и энтропии. Физика под его капотом в основном находится вне контроля игрока. Стратегические решения могут сильно повлиять на игру.

Когда Элизабет Мэги разработала игру для арендодателя (предшественницу «Монополии»), она разработала игру, в которой игроки пытаются разорить друг друга. Когда выигрывает один игрок, всем остальным кажется, что они проигрывают. В теории игр мы называем это «игрой с нулевой суммой». А в Монополия , оптимальной стратегии для управления этой игрой не существует. Игроки могут думать, что они принимают обдуманные решения, но эти решения мало что могут противопоставить изменчивой силе игральных костей и карт.

Это потому, что целью было создать не забавную игру, а образовательную. Монополия имитирует реальные сценарии, в которых игроки (арендаторы и покупатели жилья) обречены на проигрыш.

Попробуйте купить недвижимость в Сан-Франциско; это поздняя игра Монополия . Если вы не можете позволить себе проиграть, вы не можете играть. А в Монополия может быть только один победитель. Все остальные проигрывают.

Чем больше мы любим настольные игры и их механику, тем больше практикуем теорию игр. Это похоже на то, как редуктор возится с физикой, за исключением того, что настольные игроки могут играть с силами наций, экономик и культур.

Что возвращает нас к тому, кто, я надеюсь, играет больше: креативщики и стратеги.

Мы всегда старались приносить результат. Больше загрузок приложений. Больше продаж. Больше заработанных медиа. Но эти результаты становятся все более важными, например, изменение рыночной позиции всей компании с помощью ребрендинга, или сдерживание насилия с применением огнестрельного оружия, или обращение вспять изменения климата.

Чем больше проблема, тем больше нам нужно для создания результатов, манипулируя абстрактными силами, которые их вызывают. Прошли те времена, когда отсутствие осведомленности вызывало проблемы у каждого клиента.

Давайте вспомним реальные примеры из теории игр.

Мы не можем успешно изменить положение компании, не зная ресурсов и оптимальных стратегий ее конкурирующих игроков. Мы не можем остановить насилие с применением огнестрельного оружия, если другие политические игроки сфальсифицировали правила в свою пользу. И мы не сможем повернуть вспять изменение климата, если у людей, вызывающих его биологических организмов, не будет эмоциональных причин вести себя иначе.

Наша отрасль постоянно развивается. По мере того, как маржа прибыли сокращается, мы продвигаемся к неизведанным территориям, украшая наши портфели проблемами, еще более чуждыми и сложными, чем когда-либо. Наши старые инструменты и методы лишь царапают поверхность.

Настольные игры не являются решением, но то, что скрывается за ними, может помочь нам понять, что вызывает проблемы. И чем больше мы признаем и ценим теорию игр, тем больше мы можем стремиться к более масштабным и долгосрочным изменениям.

Итак, в следующий раз, когда вы захотите расширить свой кругозор, возьмите игру. Это может звучать непродуктивно, даже по-детски, но вы уже играете в больше игр, чем думаете. Почему бы не попрактиковаться в победе?

Спасибо за внимание. Меня зовут Клейтон Нотестин. Я копирайтер, дизайнер и стратегически мыслящий человек с синдромом Аспергера. Если вам понравилась эта статья, не забудьте похлопать меня за Сауроноподобный глаз алгоритма.

Я основатель игрового инкубатора под названием Ищу в MullenLowe Group, и я владелец консалтинговой компании по ролевым играм, Explorers . Вы можете найти меня на сайте LinkedIn и Работает Не работает , а рассказываю об играх на Twitter .

Теория дизайна — Лаборатория дизайна настольных игр

Как и во всех творческих начинаниях, в игровом дизайне есть бесчисленное множество теорий о том, что работает лучше всего и как это сделать. В том, что заставляет игру работать хорошо, есть так много входов и выходов, что это смешно. На этой странице вы найдете множество статей практически по всем аспектам игрового дизайна. Веселиться.

Содержание

• Начните здесь
• Искусство и графический дизайн
• Быть инклюзивным
• Весы
• Выбор
• Развлечение
• Дизайн
• Кости
• Опыт игрока
• Время
• Случайность
• Подсчет очков и окончание игры
• Подробнее Чтение

Начните здесь

Использование теории дизайна для разработки игр

Основные строительные блоки игр

Последние 10% дизайна вашей игры

Измерение успешного игрового дизайна, часть 1

Измерение успешного игрового дизайна, часть 2

Убейте своих любимых

Если вам нравится ваш дизайн, отпустите его

Различные подходы к игровому дизайну

Заимствование идей из других игр

5 Atomic Теория игрового дизайна

Хорошая игра для большой аудитории ИЛИ отличная игра для небольшой аудитории

Подтекст и опасности дизайна по умолчанию

Разрушение игр

Использовать CCG или нет? Вот в чем вопрос.

Разработка настольных игр с минимальными затратами

Итерация дизайна (аудио)

Как добавить глубины вашей игре

Создание игр как задача системной инженерии, часть 1

Создание игр как задача системной инженерии, часть 2

Общие Стратегии для ваших настольных игр

Почему гибкость необходима для разработки отличной игры

Проектирование вне себя

С чего должна начинаться игра

Удача VS Мастерство (видео)

Ешьте овощи

Смена палитры: когда разнообразие не впечатляет

Более 100 000 различных настроек!

Разработка игр для систем видеоконференцсвязи

Scoundrels: Дневник разработчиков

Иерархия потребностей, часть 1
Иерархия потребностей, часть 2 Дизайн

Дизайн игр с едой

Killing Your Darlings

4 урока шарлатанов из Кведлинбурга для геймдизайнеров

 

Пример совместной игры: диверсант

 

Стратегии первого уровня

Получение победных очков!

Время драгоценное

10 лучших настольных игр и чему мы можем извлечь уроки

Познакомьтесь с человеком, стоящим за самой известной настольной игрой в годы

Шкалы решений

Программ Больше, чем все мы

Создание сложного выбора в играх

 

Как добавить в игру переменные возможности игроков

Пример совместной игры: всего один

Не позволяйте своему искусственному противнику быть генератором случайных чисел 5 0

Трактат об иконах

Руководство Мортена по серии осадных положений

 

Создание идеальной системы подсчета очков

 

Способы проигравших победить

5  

0002 Что касается того, чтобы создать Automa

Кооперативное исследование: между двумя замками Mad King Ludwig

Руководство по товарной слепоте для дизайнеров настольных игр

Ко-о-примерные исследования: Betrayal Legacy

. Уроки Санторини для начинающих гейм-дизайнеров

 

Точность модификатора

 

Увеличивается ли вероятность того, что одиночные режимы, добавленные в дополнения, попадут под удар?

Делаем выбор важным

Проблемы и дилеммы равны великолепным игровым процессам

10 лучших игр и чему мы можем извлечь уроки

Надежда на выигрышной механизм

Double Ittheme,

Ролевая игра, и Alphas Defeat

 

Зачем существуют уровни в соревновательных играх

 

Как разработать уровни сложности для экспертов

 

Психография игрока. Почему мы играем?

GDC Board Game Talks

В конце игры

Дегеномерное поведение ботов и агентов настольных игр

Использование ботов и агентов настольных игр

---

Art & Graphic Design 9021

с

---

Art & Graphic Design 9021

---

.

художник

Что за шрифт?! Тип Советы для дизайнеров настольных игр

Переосмысление графического дизайна

Зачем вашей игре нужны вспомогательные средства для игроков

Иконки и текст (серия из 4 частей)

Использование дизайна в графическом дизайне

Графический дизайн в настольных играх

Улучшение графического дизайна на картах

---

Инклюзивность

Как сделать вашу игру легкой для понимания

Как сделать игры доступными для всех

Инклюзивность и доступность в настольных играх

---

Баланс

Количество игроков и масштабируемость

Количество игроков

Баланс

Разработка для Imbalance

Создание хорошей игры — это нечто большее, чем ее усложнение: сложность, глубина и баланс

Работа с заказами игроков

Балансировка вашей игры (видео)

Баланс между сложностью, продолжительностью игры и количеством игроков

Баланс в игровом дизайне

Баланс за пределами справедливости

10 способов справиться с беглыми лидерами (видео)

Как никогда не иметь проблем с балансом

---

Варианты выбора

Почему мне нравится иметь 2 варианта выбора

Понимание и выбор

Правильный уровень контроля игрока и игры с гидом

Управление количеством вариантов выбора в игре

Руководство для игроков с помощью поощрений

Большее погружение за счет меньшего количества вариантов

Хорошие игры — трудный выбор

Разное: получайте больше удовольствия от выбора

Разработка игр для предотвращения аналитического паралича — часть 1

Разработка игр для предотвращения аналитического паралича — часть 2

14 способов уменьшить аналитический паралич

Шкалы принятия решений

Во многих играх есть пять ресурсов

Как избежать подсчета аукционов

4 Уроки от Paladins of the West Kingdom для гейм-дизайнеров

Уровни игрового дизайна

---

Веселье

Правильный тип развлечения для вашей игры

Как организовать игру для получения максимального удовольствия

Как дать игрокам возможность получать удовольствие

Психология вознаграждений в играх

Развлечения и функции

Структура развлечений

Математика Is Hard

Подсчет очков: сокрытие проигрыша

 

8 видов развлечений

---

Дизайн

Две распространенные проблемы дизайна в соревновательных играх

Простой дизайн игры Knizia: The Simple Keeping Game Design

Простой против чистой

Минимализм против элегантности

Наименование A Game

Награды, а не штрафные

Штрафы над вознаграждениями

. Барьеры в пользу

Знайте свои кобылы

Итеративный дизайн

Проектирование для TACTICS

. Решение First Game Design

Чем хороши дизайнерские ограничения

Сложность и новый игровой процесс

Искусственный интеллект в настольных играх

Последствия в играх

Достижения как общение между дизайнером и игроком

Все, что мне нужно знать о дизайне игр, я узнал из Space Invaders

Предоставление игрокам возможности заниматься дизайном

Школы дизайна и их основные приоритеты

Анатомия Карта

Инженерные противоречия

Заповеди дизайна

3 Игры, в которых используются различные настройки

Эффект пещеры

---

Кубики

Использование кубиков в качестве инструмента дизайна

Почему в игре должны быть пользовательские кубики и когда их вводить

Почему НЕ следует использовать пользовательские кубики в игре

---

Опыт игрока

Полировка опыта

Опыт VS Механика

Хороший игровой опыт и ответственность дизайнера

Не ненавидьте игрока, часть I

Не ненавидьте игрока, часть II

Дизайн с целью: основной опыт

Атмосферное давление

4 Отличные источники напряженности в играх

Соревнования в играх

Конфликтные потребности

Игра определения концепций

Проектирование опыта вокруг игрока

Создание удовлетворяющего опыта

7 уроки монополи для игровых дизайнеров

7

Чем хорош размах крыльев?

4 Уроки острова динозавров

---

Время

Продолжительность игры и максимизация ценности времени

Фактическая длина игры против воспринимаемой длины игры

Примерно время

Управление временем простоя

Управление темпом игры

Время простоя при поддержке

---

Случайность

Случайная, выбор игрока и опыт игрока

rascomness vas vas

. Случайность и неопределенность

Случайность и игровой дизайн

Вероятность для разработчиков игр

Уменьшение случайности

14 баллов за случайность

---

Подсчет очков и окончание игры

Когда заканчивать игру

Лучшие и худшие пути подсчета очков

Мысли о победе: Психология победы

Мысли о победе: проигрыш

Сопоставленные эндшпили

Как заставить волатильность работать на вашу игру, часть 1

Как заставить волатильность работать на вашу игру, часть 2

Переосмысление выигрыша в играх

Как избежать неудовлетворительных побед

Разработка условий выигрыша (аудио)

Как избежать неудовлетворенности игровым дизайном

Можно ли решить проблему создания королей в многопользовательских играх?

---

Подробнее

Почему многие Eurogames по своей сути являются однопользовательскими играми

Работа с со-дизайнерами/партнерами

Работа с разработчиком Что делает игру сломанной (аудио)

Использование пространства в настольных играх

Разработка игр с цифровыми компонентами

Экономически жизнеспособны игры только для двух игроков

10 вещей, которые должен знать каждый дизайнер игр о «100 вещах, которые должен знать каждый дизайнер о людях»

Познакомьтесь с Человек, стоящий за самой популярной настольной игрой за последние годы

Пример совместной игры: The Dresden Files

Пример совместной игры: Pandemic Legacy Season 2

Пример совместной игры: Pandemic Legacy Season 1

4 Уроки от Spirit Island для начинающих игровых дизайнеров

Эффект целительного зелья

Треки, токены и баллы

Проектирование кривой обучения для вашей игры

Co-op.

 

6 причин, по которым квесты сделают вас лучшим гейм-дизайнером

 

Шаблоны проектирования: перпендикулярные ограничения

 

Пример совместной игры: спуск

6 (с половиной) Формы взаимодействия в играх

Образцы проектирования: случайные реакции

Как выяснить, что работает в

, а что нет

. Дизайн от Root

 

Проблема с длиной игры

 

18 Card Challenge – Время разработки

4 Уроки Everdell для начинающих гейм-дизайнеров

 

Кооперативное исследование

Кооперативное исследование: ONIRIM

Трактат на ICONS

Руководство Морена по состояниям Siege Series

Создание идеальной системы оценки

Способы проигравших выиграть

 

Нет, победные очки — это не отстой

 

Игра со стимулами

Возвращение

 

50005

4 урока от Azul для начинающих дизайнеров настольных игр

.
Примеры совместной игры: «Звездный путь» — 5-летняя миссия

4 урока от Ticket to Ride для начинающих разработчиков настольных игр

 

 Уроки терраформирования Марса для начинающих разработчиков игр

Игры

 

Облегченный сбор колод Взгляните на Great Western Trail

 

Примеры совместной игры: Star Trek — Expeditions

4 Уроки от Sagrada

5 Уроки от Catan для начинающих игровых дизайнеров

Почему Boggle лучше, чем Scrabble

. У них можно учиться

Надежда на победу0005

Какие игровые дизайнеры должны заботиться о

Процесс: бета-колония

Кооперативное исследование: Pathfinder Adventure Card Gam Основные приоритеты

 

Анатомия карты

 

Инженерные противостояния

 

Заповеди дизайна

 

Цели и условия победы

Thematic Dice Dice Rolling

Dynamics End Game и как их использовать

Что кооперативные и конкурентоспособные игры могут учиться друг от друга

сделать выбор, почувствовать

.

Присоединяйтесь к более чем 6000 других дизайнеров в стремлении создавать отличные игры, которые понравятся людям.

Подписаться

© 2021 Все права защищены.

Теория настольных игр | Морж

«Должно быть, у тебя лучшая работа в мире», — часто говорят мне люди. С ними трудно спорить, ведь моя работа — помогать людям хорошо проводить время, играя в настольные игры. Я работаю в Snakes and Lattes, которое открылось в Торонто в 2010 году и стало первым кафе с настольными играми в Северной Америке. Я помогаю нашим гостям выбирать игры, которые соответствуют их вкусам, и учу их правилам, чтобы им никогда не приходилось ломать голову над сводом правил. Для того, кто любит игры так же сильно, как и я, это отличная жизнь.

Я занимаюсь этим уже более пяти лет и могу научить игроков, как решать около 500 игр. Я помогал людям всех возрастов, профессий и настроений, от нервных пар на первом свидании до шумных групп из двадцати человек. Некоторые из наших постоянных клиентов являются опытными игроками, которые без проблем осваивают богатые, захватывающие игры, которые создают миниатюрные миры для исследования игроками. Но большинство из них новички в этом хобби, и к ним я отношусь с особой осторожностью. Я знаю, что их опыт общения со мной может сделать их игроками на всю жизнь — или полностью отключить их от игр.

Если вы проводите операцию или управляете самолетом, ошибки могут убить. Но не все является жизнью или смертью.

Некоторым настольные игры могут показаться простым хобби, но моя должность в Snakes and Lattes многому меня научила о человеческой природе и о том, как наше общество относится к неудачам. Это потому, что в мире игр неудача необходима для успеха.

Позвольте мне объяснить. Я научу тебя играть в Telestrations. Это нечто среднее между Pictionary и телефонной игрой. Каждый игрок получает небольшой пластиковый буклет, маркер для сухого стирания и секретное слово или фразу. Вы пишете свое секретное слово на обложке буклета, затем открываете его на первой странице и быстро рисуете свое секретное слово.

Когда время истекло, вы передаете свой буклет с его (возможно, ужасным) рисунком игроку слева от вас, а игрок справа передает вам свой. Вы смотрите на картинку в буклете, который вам только что вручили, а затем пытаетесь (и, возможно, безуспешно) угадать, что это должно быть. Затем вы открываете вторую страницу и записываете свое предположение, прежде чем отдать буклет игроку слева от вас.

Игрок справа от вас передает вам буклет, который открыт на второй странице и содержит слово или фразу. Вы читаете это, а затем пытаетесь нарисовать это на третьей странице. И так далее. Угадайте тему изображения, передайте его, нарисуйте изображение, передайте его, пока ваш оригинальный буклет не вернется к вам.

После того, как буклеты были разосланы по кругу и каждый снова получил свой оригинальный буклет, пришло время показать и рассказать. Вы объявляете свое секретное слово и показываете свой почти неузнаваемый набросок с первой страницы на всеобщее обозрение. Затем вы открываете вторую страницу и показываете всем, что, по мнению человека слева, вы нарисовали. Затем вы открываете третью страницу и показываете всем картинку следующего игрока, а затем переходите к четвертой странице, чтобы показать им, что следующий игрок угадал , что был и так далее.

Обычно к тому времени, когда оно возвращается к вам, вся связь с исходным словом уже полностью потеряна. И так же, как в телефонной игре, в этом суть. Это кавалькада нелепых неудач. Это также одна из самых простых игр, которую можно порекомендовать группе новичков в настольных играх.

Но Telestrations не гарантирует развлечения. Есть два способа, которыми он может упасть. Первый предполагает слишком большой успех. Если все игроки опытные художники, в игру вряд ли стоит играть. Вы можете начать со слова сыр и нарисуйте хороший маленький набросок кусочка сыра, затем передайте его следующему игроку, который правильно идентифицирует его как сыр и передает его следующему игроку, который также рисует легко узнаваемый кусок сыра. К тому времени, когда он вернется к вам, ничего не изменится. Все преуспели. И это скучно. (Некоторые изобретательные игроки установили домашнее правило: если вы хорошо рисуете, вы должны использовать не доминирующую руку. Это правило я от всего сердца рекомендую. )

Второй вариант, по которому эта игра может пойти не так, возникает из-за слишком малых усилий. Игрок, который запуган или встревожен, может попытаться избежать смущения, отказавшись даже от попытки. Они рисуют бесформенные каракули, чтобы не ошибиться в рисовании, или пишут случайные слова, чтобы не ошибиться в угадывании. Опять скучно.

Чтобы Telestrations выполнила свою задачу, нужны игроки, которые сделают все возможное, чтобы добиться успеха, но все равно потерпят неудачу. Потому что именно отсюда и приходит веселье — радостная, крутящаяся паника, вызванная вашим собственным серьезным, но некомпетентным искусством и догадками, а также мягкое злорадство, когда вы смотрите, как ваши друзья терпят неудачу.

Хотя поначалу это может показаться неочевидным, тот же принцип применим почти ко всем другим играм. Если вы требуете совершенства, нет места для веселья. Но если вы отказываетесь вкладывать достаточно своей гордости в усилия, направленные на победу, вы снимаете напряжение, а вместе с ним умирает и веселье.

Воля к успеху и свобода потерпеть неудачу — это не просто предпосылки для игривости: они также необходимы для творчества. Мы видели TED Talks и слышали известное изречение Кеннета Робинсона: «Если вы не готовы ошибаться, вы никогда не придумаете ничего оригинального». Мы на словах подтверждаем эту истину в наших родительских банальностях, наших мотивационных плакатах и ​​на наших семинарах по менеджменту.

Но реальность, с которой мы сталкиваемся в наших школах и на работе, преподает нам противоположный урок. Примените необычный подход к решению задач на экзамене, и вы рискуете получить низкую оценку. Смелая, но неудачная инициатива на работе может стоить вам работы. Поэтому, конечно, мы боимся потерпеть неудачу, даже когда дело касается нашего развлечения. У самых популярных электронных игр — от Candy Crush Saga до хардкорных игр, таких как Dark Souls — есть нечто очень показательное: игрок не может проиграть игру. Они могут продолжать играть, пока не победят.

Но на столе все иначе. Каждый вечер на работе я вижу как минимум одного клиента, который подходит к нашей огромной библиотеке игр, не зная, что выбрать. Я коротко беседую с ними, чтобы оценить их вкусы, а затем рекомендую одну из сотен замечательных новых игр, опубликованных во время ренессанса настольных игр этого столетия. Что-то привлекательное и доступное, но не слишком сложное.

И тогда это происходит. Они сутулятся, нервно оглядываются и неловко посмеиваются. Они боятся потерпеть неудачу, боятся выглядеть нелепо перед своими друзьями. Поэтому вместо того, чтобы отправиться исследовать новые миры, они поддаются страху и тянутся к унылой, знакомой безопасности Монополии.

Неудача, конечно, может иметь серьезные последствия. Если вы проводите операцию или управляете самолетом, ошибки могут убить. Но не все является жизнью или смертью. Вы не можете начать новые отношения, начать новую карьеру или создать новое искусство, не упав время от времени лицом к лицу.

Игры сильны, потому что они создают пространство, которое существует за пределами нашего обычного опыта. В этом волшебном игровом круге неудача не только недопустима, но и необходима.

Это появилось в выпуске за ноябрь 2016 года.

Джоан Мориарти

Джоан Мориарти работает инструктором в Snakes and Lattes, кафе настольных игр в Торонто.

Мэрайя Льянес

Мэрайя Льянес нарисовала для Globe and Mail , Swerve и Narratively .

Присоединяйтесь к нашему сообществу

Все еще читаете? Покажите свою поддержку.

The Walrus представляет отмеченные наградами, независимые, проверенные факты журналистские материалы и онлайн-мероприятия на thewalrus.ca. Наш контент доступен всем, но как зарегистрированная благотворительная организация мы не можем выполнять эту работу без участия таких читателей, как вы.

Всего за 10 долларов в месяц вы можете поддержать работу The Walrus онлайн. Все сторонники получат бесплатную большую сумку, получат доступ к эксклюзивным обновлениям и присоединятся к сообществу, которое поддерживает нашу работу.

Стань частью Моржа.

Ежемесячные пожертвования получают налоговую квитанцию.

Теория игр | Стратегия настольной игры

Оставить комментарий Опубликовано 29 января 2018 г. Ночь игр, Теория игр

У моего брата, склонного к математике, есть несколько дополнительных идей, которые он может добавить к стратегии игры в кости лжеца. Я попросил его вести гостевой блог о них.

Если вы хотите быть занудой, вы можете добавить следующее при расчете ставки:

Большинство игроков используют вероятность, когда они играют: число и единицы = 2 варианта из шести = 1/3 в среднем для любого числа. Это предполагает, что если в игре 15 кубиков, их должно быть около 5 с каждым числом.

Что некоторые люди не принимают во внимание, так это свои собственные кости, которые они уже знают. Обладая этими знаниями, вы можете использовать условные вероятности для расчета «более рискованной» ставки, оставаясь при этом относительно безопасным. По сути, вы используете информацию, которая у вас уже есть, чтобы вычислить, сколько потенциальных кубиков есть.

Скажем, есть 3 игрока, по 5 кубиков у каждого (всего 15), любой может чувствовать себя в безопасности, выбирая 4 или 5 любых чисел. Тем не менее, вы уже знаете 5 игральных костей, поэтому вам следует скорректировать свою математику! Вы не знаете только 10 кубиков, поэтому используйте оценку 1/3 на этих кубиках и добавьте свои собственные. Если у вас есть 4 шестерки (комбинация 1 и 6), то оцените 2-4 шестерки под чашками других игроков и добавьте свои 4. Таким образом, вы можете довольно безопасно ставить 6-8 шестерок (я бы, наверное, поставил 7). чтобы быть немного безопаснее), что кажется половиной игральных костей.

Когда кто-то делает математику быстро, 7/15 ~ 50%, в его мозгу срабатывает красный флажок. Скорее всего, они позвонят Дудо. С вашими 4 не так уж сложно получить 7, которые вам нужны, поскольку у каждого игрока, вероятно, будет 1-2.

Иногда приходится защищаться. Послушайте, что предлагают другие игроки. Если они предлагают только пятерки, а у вас есть только шестерки, это может быть хорошим раундом, чтобы довести его до единиц. Или используйте свои знания о 5 известных вам кубиках (0 пятерок) и оцените на основе ставок других игроков. Не может быть больше 10 пятерок, если у вас их нет, и, вероятно, больше 7, если они оба кажутся действительно уверенными.

Этот метод не является надежным из-за изменчивости и других людей, которые знают свои собственные кости, но вы можете заставить людей вокруг вас потерять гораздо больше костей или, по крайней мере, заставить их чувствовать себя некомфортно, поднимая число, что где начинается настоящее веселье.

Имейте в виду, когда вы называете свои ставки, чем меньше игральных костей, тем больше вариативность (именно так работают вероятности: малое N, большая вариативность), поэтому, если ваш папа говорит: «О, чувак! Святой крот! и начинает хихикать, вы, вероятно, должны просто догадаться, что у него есть по крайней мере 4 из того, над чем он смеется, и исходить из этого.

Спасибо, Натан, отличные советы.

1 комментарий Опубликовано 28 декабря 2016 г. 3 января 2017 г. Теория игр, стратегические игры

Эта часть стратегии Блокуса заслуживает отдельного поста.

Позвольте мне познакомить вас с концепцией байесовских вероятностей. Математика довольно тяжелая, поэтому я просто опишу концепцию.

В обычной вероятности вы смотрите на частоту того, как часто что-то происходит. Это работает в карточных играх. «Каковы мои шансы вытянуть алмаз».

Байесовские вероятности присваивают вероятность на основе состояния знания или убеждения. «Какова вероятность того, что кто-то сыграет в этом квадрате, учитывая другие варианты игры, которые у него есть»

Это довольно сложно, поэтому позвольте мне привести пример в Блокусе. Предположим, есть 4 разных места на доске, которые вы думаете об игре. Когда вы смотрите на каждый из них, вы получаете следующую информацию о каждом варианте.

• Вариант 1: Никто другой не может на нем играть. Это идеально подходит для вашего квадратного куска
• Вариант 2: все 4 игрока могут играть в эту клетку. После того, как вы поиграли там, он изолирован, поэтому вы больше никуда не попадете.
• Вариант 3: здесь можете играть только вы и еще один человек. Другому игроку нужно это пространство, чтобы не застрять.
• Вариант 4: Вы и еще 2 человека можете играть здесь. Он ведет к еще одному открытому пространству
.

Как вы решаете, что делать? Байесовская вероятность пытается назначить вероятности для каждого из этих сайтов, чтобы определить вероятность того, что вы не сможете играть там позже. Это кажется сложным, но ваш мозг уже делает это, когда вы продумываете, где вам следует играть. Я собираюсь назначать вероятности так, как мой мозг естественно думает об этом, без фактического вычисления вероятностей. (Ни у кого нет времени, чтобы вы достали свою доску и Beautiful Mind рассказали о реальных вероятностях. )

• Вариант 1: 0% вероятность потерять это место до вашего следующего хода. Дождитесь более позднего хода, чтобы сыграть здесь
• Вариант 2: 80% вероятность потерять это. Потенциал для этого поворота
• Вариант 3: 90% шанс потерять место. Очень обидел бы другого игрока, а у тебя потом не будет шансов
• Вариант 4: 85% шанс потерять место. Это даст вам еще одну игру, поэтому, если вам нужно дополнительное пространство, это может быть вашим лучшим выбором.

К этому моменту вы знаете, что, вероятно, потеряете два места, поэтому вы хотите использовать шанс, чтобы заблокировать кого-то или прокрасться в дополнительное пространство? Это зависит от вас, просто идите в понимании последствий.

Используете ли вы какие-либо другие методы, чтобы выяснить, где играть? Оставить комментарий.

5 комментариев Опубликовано 28 ноября 2016 г. 6 января 2017 г. Теория игр, общие стратегии

Когда я был маленьким, мой старший брат был на два года старше меня и всегда побеждал меня в играх. Однажды он создал свою игру и не сказал мне ни одного правила. Пока он бросал кости, отбивая мою базу, я сидел в замешательстве. В конце концов, он сказал: «Ты не собираешься защищаться?» В тот момент я потерял его. Я перепрыгнул через игровое поле и напал на своего брата. (Я покажу ВАМ защищаться). К сожалению, он тоже был крупнее и сильнее меня, так что добром это не кончилось. Это событие помогло мне сформироваться.

Итак, вы хотите выигрывать в играх? Устали проигрывать старшему брату, ближайшему соседу, парню, девушке, соседке?

Вам нужна стратегия. И для начала вам нужна стратегия того, как вы собираетесь получить стратегию. Вот несколько стратегий для разработки вашей стратегии.

1. Всегда читайте правила ПЕРЕД игрой
2. Обратите особое внимание на условия выигрыша
3. Настройте себя на успех позже в игре
4. Учитесь на своих ошибках
5. Будьте позитивны.

Прочитайте правила

Когда вы приходите на вечер игр, люди часто предлагают игру, в которую вы никогда не играли. Это не проблема, но если вы используете игру как «обучающую», вы не выиграете. Кроме того, если вы рассчитываете на то, что кто-то еще объяснит вам игру, вы упускаете все мельчайшие детали того, как выиграть и как взаимодействуют карты, фигуры и игроки. Вам не нужно тратить полчаса, чтобы отложить все, просто найдите время, чтобы прочитать их.

Условия выигрыша

Условия выигрыша имеют значение. Некоторые игры заканчиваются, как только вытягивается последняя карта. Некоторые заканчиваются, когда все ваши ребята мертвы. Иногда вы получаете дополнительные очки, если удержите маленькую фишку и сыграете ее последней. Вы должны знать, как побеждать, чтобы иметь возможность побеждать.

Долгая игра

Не имеет значения, если вы немного встанете в начале игры, если вы не планируете стратегию, которая будет действовать на протяжении всей игры. Вычислите следующее:

• Что нужно сделать в начале, чтобы настроить себя на оставшуюся часть игры
• Какова ваша промежуточная стратегия, как вы поддерживаете себя в игре, чтобы дойти до конца и выиграть
• Ближе к концу, когда вам нужно сделать ходы, чтобы закончить игру или набрать как можно больше очков, прежде чем она закончится.

Учитесь на своих ошибках

Вы не будете выигрывать каждый раз. Возможно, вы разработали стратегию, которую считали отличной. Может быть, это действительно было здорово, но кому-то еще повезло. Или, может быть, вам нужно изменить свою стратегию. Это нормально. Не прыгайте через доску и не атакуйте. Просто скажите: «Хорошая игра». НО, это не конец. Продолжайте корректировать свою стратегию, пока не выясните, что хорошо работает для вас, чтобы выиграть

Хорошо выигрывать и проигрывать

Если вы выиграете, скажите всем, что они хорошо сыграли. Если вы проиграете, скажите всем, что они играли хорошо. Существует тонкий баланс между доминированием в соревновании и тем, чтобы быть веселым человеком, с которым можно играть. Если с вами не весело играть; в конце концов, никто не будет играть с вами.

И это правильно.

Математика игры в гекс, настольная игра, разработанная Джоном Нэшем. Теория игр по вторникам – обдумывайте свои решения

В фильме A Beautiful Mind Джон Нэш расстроен проигрышем в го. В удаленной сцене Нэш предлагает новую игру, в которой первый игрок может гарантировать победу при идеальной игре. Как и в случае с Connect4, если вы знаете, как побеждать, вы можете побеждать каждый раз.

Игра теперь известна как Hex. Она была изобретена Питом Хейном в 1942 году, а Джон Нэш повторно изобрел игру в 1947 году. В Tipping Point Math есть видео, в котором объясняются правила игры и доказывается, почему игра никогда не заканчивается вничью.

The Joy Of Hex

Есть еще более сильный результат: у первого игрока всегда есть выигрышная стратегия! Хотя выигрышная стратегия неизвестна, можно доказать, что первый игрок может наверняка выиграть при идеальной игре.

В оставшейся части поста я кратко изложу правила игры, а затем объясню, как доказать, что у первого игрока есть выигрышная стратегия.
.
.

«Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях.» С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.

.
.

Геймплей

Типичное игровое поле представляет собой шестиугольную сетку 11×11. Два игрока, Красный и Синий, поочередно размещают камни на доске. Красный владеет двумя противоположными сторонами доски, скажем, севером и югом, а синий владеет другими противоположными сторонами, скажем, востоком и западом.

(изображение из Tipping Point Math/YouTube)

Цель состоит в том, чтобы создать связанный путь из фигур между двумя сторонами, которыми владеет игрок. Первый игрок, сделавший это, выигрывает игру. Доска, показанная ниже, является выигрышной для красных, например. Красные фигуры образуют непрерывную цепочку с северной стороны на южную.

(изображение из Tipping Point Math/YouTube)

Игра никогда не заканчивается вничью

Видео иллюстрирует доказательство примерно на 1:05.

Вот краткое текстовое резюме.

Во-первых, представьте, что вся доска заполнена красными и синими камнями из допустимого набора ходов.

Во-вторых, выделите все границы между красным и синим камнями. Для ребер на границе выделите любое ребро на границе Красного с синим камнем и выделите любое ребро на границе Синего с красным камнем. (Другими словами, представьте, что соседний камень за пределами доски имеет тот же цвет, что и цвет той стороны).

В-третьих, будет два выделенных пути, где каждый путь соединяет два угла доски, что нужно проверить через мгновение. Поскольку каждый выделенный путь соединяет камни противоположных цветов, цвет на одной из сторон будет иметь непрерывный путь от одной стороны к противоположной стороне — это победа этого игрока. Доска, показанная ниже, является победой красных.

(изображение из Tipping Point Math/YouTube)

Почему должен существовать такой выделенный путь? Рассмотрим ребра, где сходятся 3 шестиугольника. Есть 2 ³ = 8 способов разместить красные и синие камни. Если все одного цвета, выделенных ребер не будет. В противном случае будет 2 одного цвета и 1 другого, что приведет к 2 выделенным краям.

(изображение из Tipping Point Math/YouTube)

Кроме того, каждая угловая часть доски принадлежит Красному с одной стороны и Синему с другой. Если синий камень находится в углу, край на красной стороне подсвечивается. Если в угол поставить красный камень, край на синей стороне подсвечивается. Каждый угол всегда начинается с одного выделенного края.

Затем выделенный край из угла должен продолжать расти по цепочке. Почему? Каждое пересечение шестиугольников должно иметь 0 или 2 выделенных ребра. Поскольку пересечение уже имеет 1 выделенное ребро, оно не может иметь 0 ребер.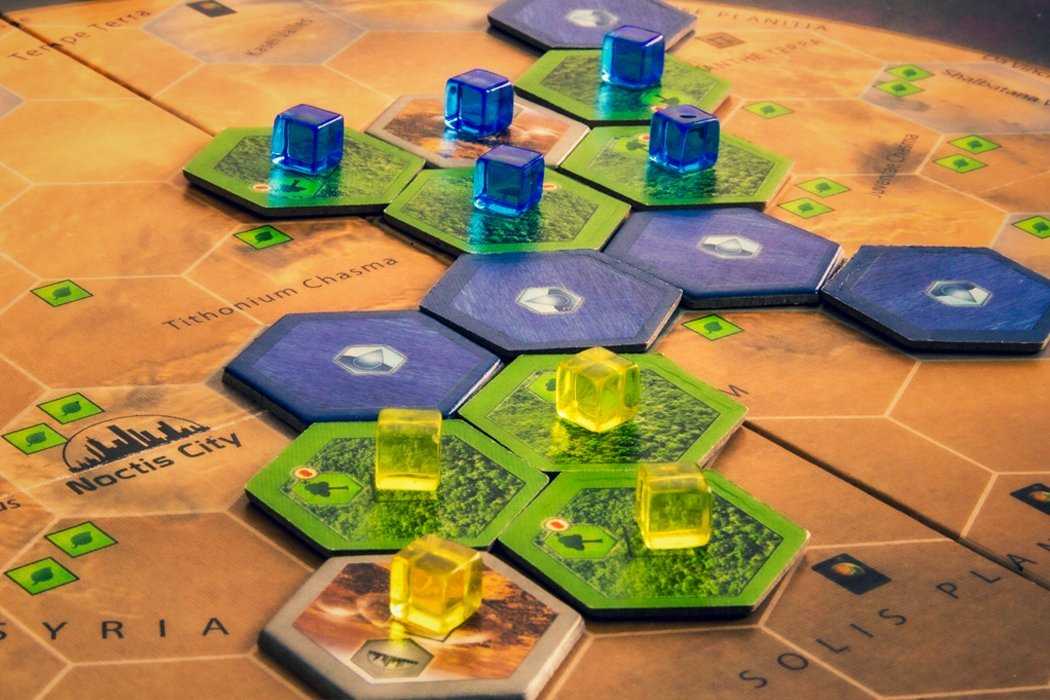 Следовательно, пересечение должно иметь 2 выделенных ребра, что означает, что цепочка продолжает расти до соединительного выделенного ребра. Также цепочка не может самопересекаться и зацикливаться, потому что это приведет к выделению 3 ребер, что невозможно. Цепочка должна заканчиваться в какой-то точке, и единственная возможность состоит в том, что она заканчивается в другом углу, у которого может быть только 1 выделенное ребро. Таким образом, у нас есть цепочка выделенных ребер между двумя углами, как и требовалось. Поскольку всего 4 угла, у нас получается 2 цепочки выделенных краев.

У первого игрока есть выигрышная стратегия

Игра в гекс имеет полную информацию, заканчивается за конечное число ходов и никогда не заканчивается ничьей. Следовательно, у одного из игроков должна быть выигрышная стратегия — это по теореме Цермело. Логика заключается в том, что с конца игры вы можете рассуждать в обратном направлении о идеальном ходе на каждом предыдущем шаге, пока не определите лучший ход. Теоретически эту логику можно применить и к шахматам; однако в шахматах слишком много ходов, поэтому идеальной стратегии еще никто не нашел.

Hex обладает еще одним интересным свойством. Поскольку наличие лишней фигуры на доске всегда выгодно, можно доказать, что у первого игрока всегда есть выигрышная стратегия. Но, как и в шахматах, игра настолько сложна, что мы не знаем идеального набора ходов.

В доказательстве используется аргумент «кражи стратегии». Предположим, что у второго игрока, Синего, есть выигрышная стратегия. Первый игрок, Красный, начинает игру, случайным образом кладя красный камень на доску. Теперь второй игрок кладет на доску синий камень. Красный теперь считает синий камень «первым» ходом в игре — красный игнорирует уже размещенный красный камень. Затем красный использует выигрышную стратегию против синего. Проблема возникает только в том случае, если красным приходится играть на месте, где уже стоит красный камень. Но это нормально, так как игра на этом месте является частью выигрышной стратегии, красный может использовать ход, чтобы случайным образом разместить камень на доске.

Если бы у второго игрока была выигрышная стратегия, Красный мог бы украсть ее с этого момента и выиграть игру. Но это означает, что у первого игрока будет выигрышная стратегия, то есть сокращение.

Следовательно, мы можем сделать вывод, что у второго игрока нет выигрышной стратегии. Поскольку игра никогда не заканчивается ничьей, в ней должна быть выигрышная стратегия для первого игрока.

Источники и дополнительная литература

The Joy Of Hex – Tipping Point Math Video
https://www.youtube.com/watch?v=2MNalT1g3m8

Удаленная сцена A Beautiful Mind
https://www.youtube.com/watch?v=pTZ3nn2Bge4

Hex Wikipedia
https://en. wikipedia.org/wiki/Hex_(board_game)

Теорема Цермело Wikipedia
https://en.wikipedia.org/wiki/Zermelo%27s_theorem_(game_theory)

Аргумент для кражи стратегии Hex
http://math.stackexchange. com/questions/856436/john-nashs-hex-proof

МОИ КНИГИ

Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

Рейтинги книг по состоянию на январь 2022 года.

(ссылки в США и других странах мира)
https://mindyourdecisions.com/blog/my-books

Принимайте решения — это сборник из 5 книг:

( 1) Радости теории игр: введение в стратегическое мышление
(2) 40 парадоксов логики, теории вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения
(4) Лучший менталитет Математические трюки
(5) Умножение чисел путем рисования линий

Радость теории игр показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (рейтинг 4,2/5 звезд в 224 обзорах)

40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд в 38 обзорах)

Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (рейтинг 4/5 звезд по 24 отзывам)

Лучшие приемы ментальной математики учит, как можно выглядеть гением математики, решая задачи в уме (рейтинг 4,2/5 звезд в 76 обзорах)

Умножение чисел путем рисования линий Эта книга является справочником руководство для моего видео, которое имеет более 1 миллиона просмотров о геометрическом методе умножения чисел. (рейтинг 4,3/5 звезд в 30 обзорах)

Размышляйте над своими головоломками представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.

Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.

Математические головоломки, том 2 — это продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)

Math Puzzles Volume 3 — третья книга в серии. (оценка 4,2/5 звезд по 22 отзывам)

KINDLE UNLIMITED

Преподаватели и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.

В настоящее время вы можете читать большинство моих электронных книг через программу Amazon «Kindle Unlimited». Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.

США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)

ТОВАРЫ

Возьмите кружку, футболку и многое другое на официальном сайте товаров: Обдумывайте свои решения в Teespring .

Сан -Луис Обиспо настольные игры (Сан -Луис -Обиспо, Калифорния)

Что мы примерно

Для людей, которые хотят играть в разные таблицы — немецкий/евро. стиль, карточные игры, игры для вечеринок, игры с плиткой, викторины и гибридные игры. Некоторые из игр в коллекции включают такие названия, как: Agricola, Settlers of Catan, Dominion, Word on the Street, Race for the Galaxy, Maori, Carcassonne и Small World. Неважно, никогда не играли в игру или не помните правила, пришли узнать или пришли освежить память.

Предстоящие события (4+)

Просмотреть все

Теория игр, глава 2: закрыто на лето. Вернется в сентябре.

Пт, 23 сентября 2022 г., 17:00 UTC

Теория игр, глава 2: закрыто на лето. Вернется в сентябре.

 
 
 

Еженедельно по пятницам игры в Cal Poly. Открыт для всех желающих. Настольные игры, РПГ и ККИ.

GTC2 проводится клубом PolyCon. Еженедельное пятничное мероприятие проводится уже более 20 лет. Парковка бесплатная после 5 в специально отведенных местах.

Когда — каждую пятницу, с 17:00 до 22:00
Где — Калифорнийский политехнический институт, корпус 8, кабинет 122
Что — настольные игры, ККИ, ролевые игры, все, что вам нравится

Если вы не слышали, забыли присоединиться или хотите пригласить другу сервера PolyCon Discord, просто перейдите по этой ссылке или поделитесь ею, чтобы присоединиться: https://discord. gg/4hv3BMpyqB

Настольные игры Atascadero

Пн, 26 сентября 2022 г., 17:30 UTC

Доска Atascadero Игры

 
 
 

Мы еженедельно собираемся каждый понедельник для людей, которые хотят иметь возможность играть в различные настольные игры. Неважно, играли вы в игру или нет, если у вас есть желание учиться, развлекаться и быть вежливым с другими. Не стесняйтесь принести игру, в которую вы хотели бы сыграть, или просто приходите и играйте в то, что есть у других, у нас обычно их много. В настоящее время мы встречаемся в пиццерии «Круглый стол» и будем либо в основной зоне сзади, либо в одной из двух боковых комнат, если они свободны.

Настольные игры SLO по вторникам

Вт, 27 сентября 2022 г., 17:00 UTC

Настольные игры SLO по вторникам

 
 
 

Примечание. когда есть возможность, заходите в игру (или начинайте новую) и получайте удовольствие!

У капитана Немо в игровой комнате с 16:00 до 21:00 вечер открытых настольных игр — иногда приходит еще несколько человек, иногда это всего лишь несколько человек из нашей группы. Несколько дополнительных деталей…

• За Капитаном Немо/Чип Трейлз есть парковка. Владельцы магазина попросили, чтобы мы не парковались на местах, прилегающих к игровому залу, или на трех местах слева от приподнятой платформы за игровым залом. Парковка на зарезервированных местах разрешена после 17:00.

• Игровая комната (отдельное здание) выходит на парковку (если вы находитесь на стоянке лицом к улице, вы идете в здание слева от основного здания — если вы заблудились, зайдите в Nemo’s и спросите у них, где игровой зал)

• Напитки/Закуски — в игровом зале есть торговые автоматы. Не стесняйтесь приносить свою еду и напитки в зал. Алкоголь в игровом зале запрещен.

• Я подтвердил у владельца Nemo’s, что нам разрешено пользоваться туалетом в магазине (в часы работы магазина)

• Несколько членов группы могут получить ключ от игрового зала, что позволяет нам остаться после закрытия магазина. Пожалуйста, относитесь с уважением к тем, кто проверил ключ, и будьте готовы закончить игру, когда они будут готовы уйти. Если вы хотите остаться позже, обратитесь к администрации магазина, чтобы получить ключ самостоятельно.

Теория игр Глава 2: Лето закрыто. Вернется в сентябре.

Пт, 30 сентября 2022 г., 17:00 UTC

Теория игр, глава 2: закрыто на лето. Вернется в сентябре.

 
 
 

Еженедельно по пятницам игры в Cal Poly. Открыт для всех желающих. Настольные игры, РПГ и ККИ.

GTC2 проводится клубом PolyCon. Еженедельное пятничное мероприятие проводится уже более 20 лет. Парковка бесплатная после 5 в специально отведенных местах.