Укажите номера верных утверждений. — КиберПедия
1) В любой ромб можно вписать окружность.
2) В прямоугольном треугольнике косинус одного из углов равен 0.
3) Отношение площадей подобных треугольников равно коэффициенту подобия.
Укажите в порядке возрастания номера неверных утверждений.
1) Ромб, диагонали которого равны, является квадратом.
2) Противоположные углы параллелограмма равны между собой.
3) тангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.
4) если в треугольнике все углы равны между собой, то это – равносторонний треугольник.
5) сумма углов треугольника равна 180 градусам.
Укажите в ответе номера неверных утверждений.
1) Около любого прямоугольника можно описать окружность.
2) В любой ромб можно вписать окружность.
3) Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.
4) Если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.
5) Если в трапецию можно вписать окружность, то эта трапеция – равнобедренная.
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его сторон.
3) Сумма углов выпуклого четырехугольника не превышает 3600 .
4) Если две стороны и три угла одного треугольника равны соответственно двум сторонам и трем углам другого треугольника, то такие треугольники равны.
5) Существует треугольник, в котором точка пересечения серединных перпендикуляров, проведенных ко всем его сторонам, лежит на одной из этих сторон.
Укажите в ответе номера неверных утверждений.
1) В любом ромбе все стороны равны.
2) Существует ромб, все стороны которого – различны.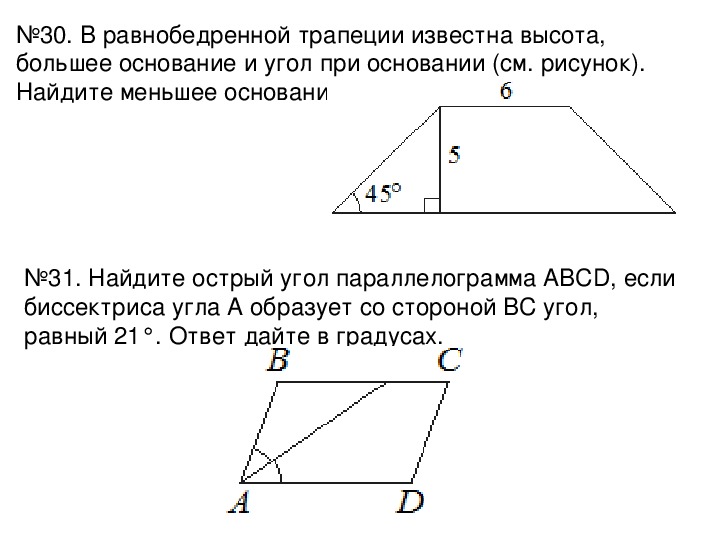
3) В любом прямоугольнике все стороны равны.
4) Существует прямоугольник, все стороны которого – различны.
5) В любой трапеции все стороны равны.
Итоговый тест по теме: Основные теоремы и факты. Вариант 2.
1. Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти прямые параллельны.
3) Точка пересечения двух окружностей равно удалена от центров этих окружностей.
2. Какие из данных утверждений верны?
1) Сумма углов любого выпуклого шестиугольника равна 940°
2) В любой параллелограмм можно вписать окружность.
3) Существует только одна точка, равноудаленная от всех вершин данного треугольника.
4) Одна из высот прямоугольного треугольника всегда делит его на два подобных треугольника.
3. Укажите в порядке возрастания номера неверных утверждений:
1) Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
2) Соседние углы параллелограмма равны между собой.
3) Сумма углов треугольника равна 90°.
4) Параллелограмм, диагонали которого равны, является прямоугольником
5) Если в треугольнике два угла равны между собой, то это – равнобедренный треугольник.
4. Укажите в ответе номера неверных утверждений.
1) В любом прямоугольнике диагонали равны.
2) Существует прямоугольник, диагонали которого различны.
3) В любом ромбе диагонали равны.
4) Существует ромб, диагонали которого различны.
5) В любой трапеции диагонали равны.
5. Какие из следующих суждений верны?
1) если в ромбе диагонали равны, то этот ромб – квадрат.
2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.
3) Сумма углов треугольника не превышает 180°.
4) Если сторона и три угла одного треугольника равны стороне и трем углам другого треугольника, то такие треугольники равны.
5) Существует треугольник, все высоты которого пересекаются в одной из его вершин.
6. Укажите в ответе номера верных утверждений.
1) В любом параллелограмме есть хотя бы один острый угол.
2) В любом параллелограмме есть хотя бы один прямой угол.
3) В любом параллелограмме есть хотя бы один тупой угол.
4) В любой трапеции есть хотя бы один острый угол.
5) В любой трапеции есть хотя бы один тупой угол.
Углы
1. В равнобедренном треугольнике угол при вершине, противолежащей основанию, равен 580.Найдите угол при основании. Ответ дайте в градусах.
2. В треугольнике АВС внешний угол при вершине А равен 125 0, а внешний угол при вершине В равен 590.Найдите угол С. . Ответ дайте в градусах.
3. В треугольнике АВС проведена высота СН, которая делит угол С на два угла, величины которых 470 и 710. Найдите наименьший из двух оставшихся углов. Ответ дайте в градусах.
Ответ дайте в градусах.
4. В параллелограмме АВСМ прямая АС делит угол при вершине А пополам. Найдите угол, под которым пересекаются диагонали параллелограмма. Ответ дайте в градусах.
5. Угол А равнобедренной трапеции АВСD с основаниями ВС и AD равен 53 0. Найдите сумму углов В и С.
6. Два угла ромба относятся как 4:6. Найдите меньший угол Ответ дайте в градусах.
7. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.
8. Найдите центральный угол АОВ, если он на 670 больше вписанного угла АСВ, опирающегося на ту же дугу.
Задачи повышенного уровня
9. Сумма углов А и В вписанного четырёхугольника АВСD равна 2040, а сумма углов В и С равна 1920. Найдите угол D.
10. Докажите, что биссектрисы смежных углов перпендикулярны.
11. Докажите, что градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу.
12. Докажите, что если биссектриса пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
13. Биссектрисы всех внутренних углов параллелограмма попарно пересекаются. Докажите, что полученный четырёхугольник является прямоугольником.
14. Биссектриса угла В треугольника АВС делит медиану, проведённую из вершины С, в отношении 7:2, считая от вершины С. В каком отношении, считая от вершины А, эта биссектриса делит медиану, проведённую из вершины А?
Тема: Углы. Вариант 1
А
1.Какой угол (в градусах) образуют
минутная и часовая стрелки часов в 5 часов?
2. .На рисунке∠1=108°, ∠2=72°,∠5=83°. а в f
Найдите угол 4. 4
1 d
c
2 5
3. .Точка О – центр окружности ∠АОВ=84°
(см. рисунок). Найдите величину
угла AСB (в градусах) С О
А В
4. Найдите ∠ С, если ∠А=62°.
А О С
5. Найдите величину угла АВС. Ответ дайте в градусах
В
А С
Тема: Углы. Вариант 2
1.Точка О – центр окружности∠ВОС=50° (см. рисунок). Найдите величину угла ВАС (в градусах) А В
О С
2.На плоскости даны четыре прямые (см. рисунок) 3
.Известно, что ∠1=130°, ∠2=50°,∠3=45°. 2
Найдите ∠5. Ответ дайте в градусах. 1 6 4
3. Точка О – центр окружности,
∠АСВ=25° (см. рисунок). Найдите С О
величину угла АОВ (в градусах). А В
4 Точка О – центр окружности∠ВАС=70°
(см. рисунок). Найдите величину В
угла ВОС (в градусах). А О
С
5. Найдите величину угла АВС. Ответ дайте в градусах
В В
А С
Тема: Углы Вариант 5
1. Величина центрального угла

Найдите величину вписанного угла ACB. Ответ дайте в градусах.
2. В треугольнике ABC AD— биссектриса, угол С равен 300,
∠ BAD =220. Найдите угол ADB.
3. Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС = 1140.
4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.
Тема: Углы Вариант 6
1. Точки А, В, С и D лежат на одной окружности так, что хорды АВ и СD взаимно перпендикулярны, а ∠АСD = 550
. Найдите величину угла ВDС.2 . Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС =1270. Ответ дайте в градусах.
Найдите угол ВАС, если ∠ВОС =1270. Ответ дайте в градусах.
3. Диагональ прямоугольника образует с одной из его сторон угол, равный 340. Найдите угол между прямыми, содержащими диагонали прямоугольника.
4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.
Итоговый тест по теме: Углы
| 1.Хорда АВ стягивает дугу, равную 1600,
а хорда АС – дугу в 600. Найдите
угол ВАС.
1)700 , 2)1000 |
| 2.Найдите угол А, если угол С равен 320. |
3.Один из углов параллелограмма на 200 больше другого. Найдите наибольший угол параллелограмма (в градусах).
Найдите наибольший угол параллелограмма (в градусах).
| 4. В окружности вписан равносторонний восьмиугольник. Найдите величину угла АВС . |
5.В угол величиной 500 вписана окружность, которая касается его
| сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АCВ. |
Вариант-1
| 6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 1230. Найдите величину угла В. Ответ дайте в градусах. |
7.Сумма двух углов равнобедренной трапеции равна 960. Найдите
больший угол трапеции. Ответ дайте в градусах.
| 8.Найдите величину угла DOB, если ОЕ – биссектриса угла АОС, OD – биссектриса угла СОВ. |
9. Укажите номера неверных утверждений:
Укажите номера неверных утверждений:
1) Если один из углов, прилежащих к стороне параллелограмма, равен 500, то другой угол, прилежащий к той же стороне, равен 400.
2) Если вписанный угол равен 240, то дуга окружности, на которую опирается этот угол, равна 480.
3) Внешний угол треугольника равен сумме двух его внутренних углов.
10. В треугольник АВС АС=18, АВ=12. Точки L и K отмечены на сторонах АС и АВ так, что АL= 6 и АК= 9. Докажите, что углы АВС и АLK равны.
Итоговый тест теме: Углы
- Хорда АВ стягивает дугу, равную 140°, а хорда ВС – дугу 60°. Найдите угол АВС. А
В С
- Найдите угол С, если АВ = ВС.
- Один из углов параллелограмма на 40° больше другого.
Найдите наименьший угол параллелограмма (в градусах).
4.В окружность вписан равносторонний восьмиугольник. Найдите величину угла АВС (см. рисунок).
Найдите величину угла АВС (см. рисунок).
|
5.В угол величиной 70° вписана окружность, которая касается его сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АСВ.
Вариант 2
| 6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 132°. Найдите величину угла В. Ответ дайте в градусах. |
7.Сумма трёх углов равнобедренной трапеции равна 234°. Найдите меньший угол трапеции. Ответ дайте в градусах.
8.Найдите величину угла АОЕ, если ОЕ – биссектриса угла АОС, ОD – биссектриса угла СОВ, угол DOВ равен 250 .
9.Укажите номера верных утверждений:
1) Если один из углов вписанного в окружность четырехугольника равен 63°, то противоположный ему угол четырехугольника равен 117°.
2) Если дуга окружности составляет 73°, то вписанный угол, опирающийся на эту дугу, равен 730 …
3) Противоположные углы параллелограмма равны…
10.В треугольнике АВС АС = 24, ВС = 12. Точки L и K отмечены на сторонах АС и ВС так, что LC = 4 и КС = 8. Докажите, что углы ВАС и LKC равны.
Тест Проверь себя ГИА Четырёхугольники 1 Укажите
Тест «Проверь себя» ГИА (Четырёхугольники)
1. Укажите в ответе номера верных утверждений. 1)В любом выпуклом четырёхугольнике все углыострые. 2)Существует выпуклый четырёхугольник, все углы которого-острые. 3)В любом выпуклом четырёхугольнике все углыпрямые. 4)Существует выпуклый четырёхугольник, все углы которого –прямые. 5)В любом выпуклом четырёхугольнике все углытупые. 6)Существует выпуклый четырёхугольник, все углы которого-тупые.
2. Укажите в ответе номера верных утверждений. 1)Есть один из углов параллелограмма — острый, то и остальные его углы — острые. 2)Если один из углов трапеции — острый, то и остальные её углы — острые. 3)Если один из углов параллелограмма-прямой, то и остальные его углы-прямые. 4)Если один из углов трапеции прямой, то и остальные её углы-прямые. 5)Если один из углов параллелограмма-тупой, то и остальные его углы-тупые. 6)Если один из углов трапеции-тупой, то и остальные её углы-тупые.
1)Есть один из углов параллелограмма — острый, то и остальные его углы — острые. 2)Если один из углов трапеции — острый, то и остальные её углы — острые. 3)Если один из углов параллелограмма-прямой, то и остальные его углы-прямые. 4)Если один из углов трапеции прямой, то и остальные её углы-прямые. 5)Если один из углов параллелограмма-тупой, то и остальные его углы-тупые. 6)Если один из углов трапеции-тупой, то и остальные её углы-тупые.
3. Укажите в ответе номера верных утверждений. 1)В любом ромбе диагонали равны. 2)В любом ромбе диагонали перпендикуляры. 3)В любом прямоугольнике диагонали равны. 4)В любом прямоугольнике диагонали перпендикулярны. 5)В любой трапеции диагонали равны. 6)В любой трапеции диагонали перпендикулярны.
4. Укажите в ответе номера неверных утверждений. 1)В любом прямоугольнике диагонали равны. 2)Существует прямоугольник, диагонали которого различны. 3)В любом ромбе диагонали равны. 4)Существует ромб, диагонали которого различны. 5)В любой трапеции диагонали равны. 6)Существует трапеция, диагонали которой различны.
5)В любой трапеции диагонали равны. 6)Существует трапеция, диагонали которой различны.
5. Укажите в ответе номера неверных утверждений. 1)В любом ромбе все стороны равны. 2)Существует ромб, все стороны которогоразличны. 3)В любом прямоугольнике все стороны равны. 4)Существует прямоугольник, все стороны которого-различны. 5)В любой трапеции все стороны равны. 6)Существует трапеция, все стороны которойразличны.
6. Укажите в ответе номера верных утверждений. 1)В любом параллелограмме есть хотя бы один острый угол. 2)В любом параллелограмме есть хотя бы один прямой угол. 3) В любом параллелограмме есть хотя бы один тупой угол. 4)В любой трапеции есть хотя бы один острый угол. 5)В любой трапеции есть хотя бы один прямой угол. 6)В любой трапеции есть хотя бы один тупой угол.
Правильные ответы 1)4 2)3 3)2, 3 4)2, 3, 5 5)2, 3, 4, 5 6)4, 6
ММО-2021 (28.03.2021)
Олимпиада для 8–11 классов прошла 28 марта 2021 года
(2 день для 11 кл. 2$). Прав ли барон?
2$). Прав ли барон?
Задача 2. Митя купил на день рождения круглый торт диаметром 36 сантиметров и 13 тоненьких свечек. Мите не нравится, когда свечки стоят слишком близко, поэтому он хочет поставить их на расстоянии не меньше 10 сантиметров друг от друга. Поместятся ли все свечки на торте?
Задача 3. В комнате находится несколько детей и куча из 2021 конфеты. Каждый из них по очереди подходит к куче, делит количество конфет в ней на количество детей в комнате (включая себя), округляет (если получилось нецелое число), забирает полученное число конфет и покидает комнату. При этом мальчики округляют вверх, а девочки — вниз. Докажите, что суммарное количество конфет у мальчиков, когда все выйдут из комнаты, не зависит от порядка детей в очереди.
Задача 4. В правильном пятиугольнике $ABCDE$ отмечена точка $F$ — середина $CD$. Серединный перпендикуляр к $AF$ пересекает $CE$ в точке $H$. Докажите, что прямая $AH$ перпендикулярна прямой $CE$.
Задача 5. В каждом из 16 отделений коробки $4\times 4$ лежит по золотой монете. Коллекционер помнит, что какие-то две лежащие рядом монеты (соседние по стороне) весят по 9 грамм, а остальные по 10 грамм. За какое наименьшее число взвешиваний на весах, показывающих общий вес в граммах, можно определить эти две монеты?
В каждом из 16 отделений коробки $4\times 4$ лежит по золотой монете. Коллекционер помнит, что какие-то две лежащие рядом монеты (соседние по стороне) весят по 9 грамм, а остальные по 10 грамм. За какое наименьшее число взвешиваний на весах, показывающих общий вес в граммах, можно определить эти две монеты?
Задача 6. В некотором государстве 32 города, каждые два из которых соединены дорогой с односторонним движением. Министр путей сообщения, тайный злодей, решил так организовать движение, что покинув любой город, в него нельзя будет вернуться. Для этого он каждый день, начиная с 1 июня 2021 года, может менять направление движения на одной из дорог. Докажите, что он сможет добиться своего к 2022 году (т. е. за 214 дней).
9 класс
Задача 1. Положительные числа $a$ и $b$ таковы, что $a — b = a / b$. Что больше, $a + b$ или $a b$?
Задача 2. Клетки бумажного квадрата $8 \times 8$ раскрашены в два цвета. Докажите, что Арсений может вырезать из него по линиям сетки два квадрата $2 \times 2$, не имеющих общих клеток, раскраски которых совпадают.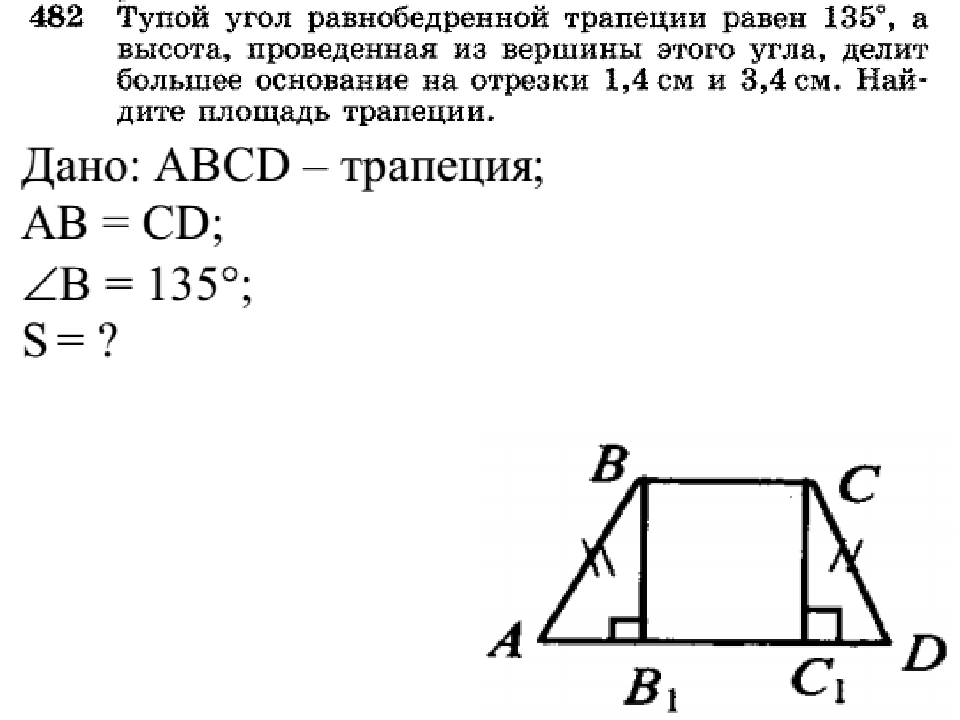 (Раскраски, отличающиеся поворотом, считаются разными.)
(Раскраски, отличающиеся поворотом, считаются разными.)
Задача 3. В узлах сетки клетчатого прямоугольника $4 \times 5$ расположены 30 лампочек, изначально все они погашены. За ход разрешается провести любую прямую, не задевающую лампочек (размерами лампочек следует пренебречь, считая их точками), такую, что с какой-то одной стороны от неё ни одна лампочка не горит, и зажечь все лампочки по эту сторону от прямой. Каждым ходом нужно зажигать хотя бы одну лампочку. Можно ли зажечь все лампочки ровно за четыре хода?
Задача 4. Точка $M$ — середина стороны $BC$ треугольника $ABC$. Окружность $\omega$ проходит через точку $A$, касается прямой $BC$ в точке $M$ и пересекает сторону $AB$ в точке $D$, а сторону $AC$ — в точке $E$. Пусть $X$ и $Y$ — середины отрезков $BE$ и $CD$ соответственно. Докажите, что окружность, описанная около треугольника $MXY$, касается $\omega$.
Задача 5. В ряд лежат $100N$ бутербродов, каждый с колбасой и сыром. Дядя Фёдор и кот Матроскин играют в игру.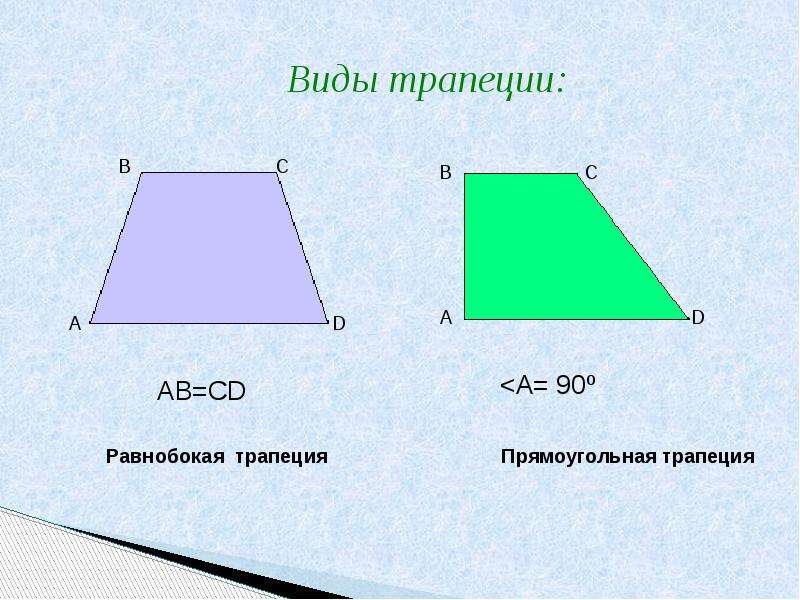 Дядя Фёдор за одно действие съедает один бутерброд с одного из краёв. Кот Матроскин за одно действие может стянуть колбасу с одного бутерброда (а может ничего не делать). Дядя Фёдор каждый ход делает по 100 действий подряд, а кот Матроскин делает только 1 действие; дядя Фёдор ходит первым, кот Матроскин вторым, далее ходы чередуются до тех пор, пока дядя Фёдор не доест все бутерброды. Дядя Фёдор выигрывает, если последний съеденный им бутерброд был с колбасой. Верно ли, что при каждом натуральном $N$ он сможет выиграть независимо от ходов кота Матроскина?
Дядя Фёдор за одно действие съедает один бутерброд с одного из краёв. Кот Матроскин за одно действие может стянуть колбасу с одного бутерброда (а может ничего не делать). Дядя Фёдор каждый ход делает по 100 действий подряд, а кот Матроскин делает только 1 действие; дядя Фёдор ходит первым, кот Матроскин вторым, далее ходы чередуются до тех пор, пока дядя Фёдор не доест все бутерброды. Дядя Фёдор выигрывает, если последний съеденный им бутерброд был с колбасой. Верно ли, что при каждом натуральном $N$ он сможет выиграть независимо от ходов кота Матроскина?
Задача 6. Пусть $p$ и $q$ — взаимно простые натуральные числа. Лягушка прыгает по числовой прямой, начиная в точке 0, каждый раз либо на $p$ вправо, либо на $q$ влево. Однажды лягушка вернулась в 0. Докажите, что для любого натурального $d < p + q$ найдутся два числа, посещённые лягушкой и отличающиеся на $d$.
10 класс
Задача 1. На доске записано натуральное число. Если у него стереть последнюю цифру (в разряде единиц), то останется ненулевое число, которое будет делиться на 20, а если первую, то на 21. \circ$.
\circ$.
Задача 3. Есть бесконечная в одну сторону клетчатая полоска, клетки которой пронумерованы натуральными числами, и мешок с десятью камнями. В клетках полоски камней
изначально нет. Можно делать следующее:
— перемещать камень из мешка в первую клетку полоски или обратно;
— если в клетке с номером $i$ лежит камень, то можно переложить камень из мешка в клетку с номером $i + 1$ или обратно.
Можно ли, действуя по этим правилам, положить камень в клетку с номером 1000?
Задача 4. Внутри четырехугольника $ABCD$ взяли точку $P$. Прямые $BC$ и $AD$ пересекаются в точке $X$. Оказалось, что прямая $XP$ является внешней биссектрисой углов $APD$ и $BPC$. Пусть $PY$ и $PZ$ — биссектрисы треугольников $APB$ и $DPC$. Докажите, что точки $X$, $Y$ и $Z$ лежат на одной прямой.
Задача 5. Пусть $p$ и $q$ — взаимно простые натуральные числа. Лягушка прыгает по числовой прямой, начиная в точке 0, каждый раз либо на $p$ вправо, либо на $q$ влево.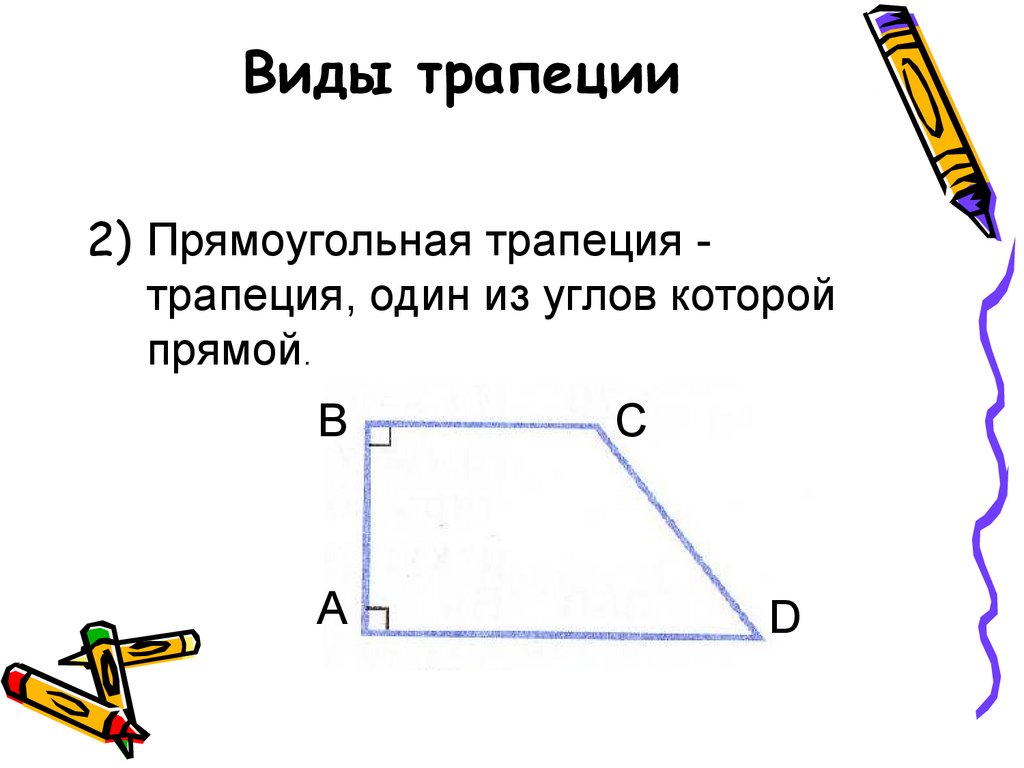 n$ до ближайшего квадрата натурального числа всегда равно 2.
n$ до ближайшего квадрата натурального числа всегда равно 2.
11 класс (1 день)
Задача 1. На доске записано натуральное число. Если у него стереть последнюю цифру (в разряде единиц), то останется ненулевое число, которое будет делиться на 20, а если первую — то на 21. Какое наименьшее число может быть записано на доске, если его вторая цифра не равна 0?
Задача 2. Существует ли функция $f$, определённая на отрезке $[-1;1]$, которая при всех действительных $x$ удовлетворяет равенству $$ 2f(\cos x)=f(\sin x)+\sin x? $$
Задача 3. Точка $M$ — середина стороны $BC$ треугольника $ABC$. Окружность $\omega$ проходит через точку $A$, касается прямой $BC$ в точке $M$ и пересекает стороны $AB$ и $AC$ в точках $D$ и $E$ соответственно. Точки $X$ и $Y$ — середины отрезков $BE$ и $CD$ соответственно. Докажите, что описанная окружность треугольника $MXY$ касается окружности $\omega$.
Задача 4. В некоторой стране есть 100 городов, которые связаны такой сетью дорог, что из любого города в любой другой можно проехать только одним способом без разворотов. 2+bx+c$ имеет три различных действительных корня, наибольший из которых равен сумме двух других. Докажите, что $c>ab$.
2+bx+c$ имеет три различных действительных корня, наибольший из которых равен сумме двух других. Докажите, что $c>ab$.
Задача 2. В остроугольном треугольнике $ABC$ точка $O$ — центр описанной окружности. Точка $B_1$ симметрична точке $B$ относительно стороны $AC$. Прямые $AO$ и $B_1C$ пересекаются в точке $K$. Докажите, что луч $KA$ является биссектрисой угла $BKB_1$.
Задача 3. Найдите наименьшее натуральное число $N>9$, которое не делится на 7, но если вместо любой его цифры поставить семёрку, то получится число, которое делится на 7.
Задача 4. Существует ли такой выпуклый четырёхугольник, у которого длины всех сторон и диагоналей в некотором порядке образуют геометрическую прогрессию?
Задача 5. В лаборатории на полке стоят 120 внешне неразличимых пробирок, в 118 из которых находится нейтральное вещество, в одной — яд и в одной — противоядие. Пробирки случайно перемешались, и нужно найти пробирку с ядом и пробирку с противоядием. Для этого можно воспользоваться услугами внешней тестирующей лаборатории, в которую одновременно отправляют несколько смесей жидкостей из любого числа пробирок (по одной капле из пробирки), и для каждой смеси лаборатория сообщит результат: +1, если в смеси есть яд и нет противоядия; −1, если в смеси есть противоядие, но нет яда; 0 в остальных случаях. Можно ли, подготовив 19 таких смесей и послав их в лабораторию единой посылкой, по сообщённым результатам гарантированно определить, в какой пробирке яд, а в какой противоядие?
Для этого можно воспользоваться услугами внешней тестирующей лаборатории, в которую одновременно отправляют несколько смесей жидкостей из любого числа пробирок (по одной капле из пробирки), и для каждой смеси лаборатория сообщит результат: +1, если в смеси есть яд и нет противоядия; −1, если в смеси есть противоядие, но нет яда; 0 в остальных случаях. Можно ли, подготовив 19 таких смесей и послав их в лабораторию единой посылкой, по сообщённым результатам гарантированно определить, в какой пробирке яд, а в какой противоядие?
Методическая разработка к уроку геометрии в 9 классе | Материал для подготовки к ЕГЭ (ГИА) по геометрии (9 класс) по теме:
5.Укажите в ответе номераневерных
утверждений
.
1)В любом ромбе все стороны равны
.
2)Существует ромб, все стороны
которого-различны
.
3)В любом прямоугольнике все стороны равны
.
4)Существует прямоугольник, все стороны
которого-различны
.
5)В любой трапеции все стороны равны
.
6)Существует трапеция, все стороны
которой-различны
.
Тест
«Проверь себя»
ГИА
(Четырёхугольники)
4.Укажите в ответе номера
неверных
утверждений
.
1)В любом прямоугольнике диагонали равны
.
2)Существует прямоугольник, диагонали которого различны
.
3)В любом ромбе диагонали равны
.
4)Существует ромб, диагонали которого различны
.
5)В любой трапеции диагонали равны
.
6)Существует трапеция, диагонали которой различны
.
Методическая разработка к уроку математики в
9
классе
Мамаева Татьяна Евгеньевна
Учитель математики
МБОУ «СОШ № 11»
г.Бологое
Тверской области
3.Укажите в ответе номера
верных
утверждений
.
1)В любом ромбе диагонали равны
.
2)В любом ромбе диагонали перпендикуляры
.
3)В любом прямоугольнике диагонали равны
.
4)В любом прямоугольнике диагонали перпендикулярны
.
5)В любой трапеции диагонали равны
.
6)В любой трапеции диагонали перпендикулярны
.
2.Укажите в ответе номера
верных
утверждений
.
1)Есть один из углов параллелограмма — острый, то и остальные его углы — острые
.
2)Если один из углов трапеции — острый, то и остальные её углы — острые
.
3)Если один из углов параллелограмма-прямой, то и остальные его углы-прямые
.
4)Если один из углов трапеции прямой, то и остальные её углы-прямые
.
5)Если один из углов
параллелограмма-тупой,то
и остальные его
углы-тупые
.
6)Если один из углов
трапеции-тупой
, то и остальные её
углы-тупые
.
Правильные ответы
4
3
2,3
2,3,5
2,3,4,5
4,6
1.Укажите в ответе номера
верных
утверждений
.
1)В любом выпуклом четырёхугольнике все
углы-острые
.
2)
Существует выпуклый четырёхугольник, все углы
которого-острые
.
3)В любом выпуклом четырёхугольнике все углы-прямые
.
4)Существует выпуклый четырёхугольник,
все углы которого –прямые
. 2 -5x +7$ на отрезке $[2, 13]$ равным $\frac{2365}{66}$.
2 -5x +7$ на отрезке $[2, 13]$ равным $\frac{2365}{66}$.
Смотрите также
Теоремы о среднем
Лимит времени: 0
Информация
Пройдите этот тест чтобы проверить свои знания по теме «теоремы о среднем».
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 4
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
- С ответом
- С отметкой о просмотре
Задание 1 из 4
Найти среднее значение функции $y=2x+3$, заданной на отрезке [2,5].

Задание 2 из 4
Выберите правильные формулировки теорем о среднем.
- Пусть функция $f(x)$ непрерывна на отрезке $[a, b]$ и дифференцируема на интервале $(a, b)$, причем $f(a)=f(b)$.
 b_{\xi} g(x)dx. $
b_{\xi} g(x)dx. $ - Пусть функция $f(x)$ дифференцируема на интервале $(a, b)$ и сохраняет непрерывность на концах этого интервала, тогда существует такая точка $\xi \in (a, b)$, что $f'(\xi) = \frac{f(b) — f(a)}{b — a}$.
- Пусть функция $f(x)$ непрерывна на отрезке $[a, b]$ и дифференцируема на интервале $(a, b)$, причем $f(a)=f(b)$.
Задание 3 из 4
Составьте верное утверждение.

Если
в условиях теоремы 1
функция $f$ непрерывна на $[a,b]$
то
найдется такая точка $\xi \in [a,b]$,
что
$\int^a_b f(x)g(x)dx = f( \xi )\int^b_a g(x)dx.
 x$, на отрезке $[0,5]$.
x$, на отрезке $[0,5]$.
Поделиться ссылкой:
Геометрия №15. Верные и неверные утверждения.
- Презентации
- Методическая разработка: ОГЭ-2016.Модуль:Геометрия №15. Верные и неверные утверждения.
Автор публикации: Самоделкина Т.Г.
Дата публикации: 31.03.2016
Краткое описание:
1
ОГЭ-2016 Часть 1 №15 Модуль «Геометрия»2
Укажите номера верных утвержденийБлагодаря этой рекламе сайт может продолжать свое существование, спасибо за просмотр.
3
Через любые три различные точки плоскости можно провести единственную прямую….4
Если угол равен 56 ,то вертикальный с ним угол равен 124˚. Существует точка п…5
Любые три различные прямые проходят через одну общую точку. Существует точка…6
Через любые две различные точки плоскости можно провести не более одной прямо…7
Через любую точку плоскости можно провести прямую. Через любую точку плоскост…8
Если две параллельные прямые пересечены третьей прямой, то соответственные уг…9
Если при пересечении двух прямых третьей сумма внутренних накрест лежащих угл…10
Если при пересечении двух прямых третьей внутренние накрест лежащие углы равн…11
Если две параллельные прямые пересечены третьей прямой, то внутренние односто…12
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест…13
Если три угла одного треугольника соответственно равны трём углам другого тре…14
Если в треугольнике АВС углы А и В равны соответственно 36˚и 64˚, то внешний. ..
..15
Составитель: Тихомирова Татьяна, 9«Б» Учитель: Самоделкина Т.Г МОУ «Гимназия…16
ОГЭ-2016 Часть 1 Модуль «Геометрия»17
Укажите в ответе номера верных утверждений 1.Если две касательные к окружност…18
Укажите в ответе номера верных утверждений 1.В любом выпуклом четырёхугольник…19
Укажите в ответе номера верных утверждений 1.Если один из углов параллелограм…20
Укажите в ответе номера верных утверждений 1.Если два угла трапеции равны, то…21
Укажите в ответе номера верных утверждений 1.Центром вписанной окружности тре…22
1.В любом ромбе диагонали равны. 2.В любом ромбе диагонали перпендикулярны. 3…23
Укажите в ответе номера неверных утверждений. 1.Около любого прямоугольника м…24
1.В любом прямоугольнике диагонали равны. 2.Существует прямоугольник, диагона…25
1.В любом ромбе все стороны равны. 2.Существует ромб, стороны которого –разли…26
1.В любом параллелограмме есть хотя бы один острый угол. 2.В любом параллелог…
2.В любом параллелог…27
Составитель: Самоделкина Т.Г МОУ «Гимназия №1» г.Печора, РК28
ОГЭ-2016 Часть 1 №15 Модуль «Геометрия»29
Верные и неверные утверждения.30
Какие утверждения НЕВЕРНЫ? 1.Средняя линия трапеции с основаниями 2см и 8см р…31
Укажите номера ВЕРНЫХ утверждений: 1.Сумма двух вертикальных углов равна 180°…32
Укажите номера ВЕРНЫХ утверждений: 1.Через любые две точки можно провести не…33
Укажите номера ВЕРНЫХ утверждений: 1.Внешний угол треугольника меньше суммы в…34
Какие утверждения НЕВЕРНЫ? 1.Если все углы многоугольника равны, то многоугол…35
Какие утверждения НЕВЕРНЫ? 1.В правильном многоугольнике все стороны равны. 2…36
Какие утверждения НЕВЕРНЫ? 1.Три медианы треугольника делят его на 6 треуголь…37
Укажите номера ВЕРНЫХ утверждений: 1.Около любой трапеции можно описать окруж…38
Укажите номера ВЕРНЫХ утверждений: 1.Середина средней линии любой трапеции яв…39
Составитель: Первак Дарья, 9«А» Учитель: Самоделкина Т. Г МОУ «Гимназия №1» г….
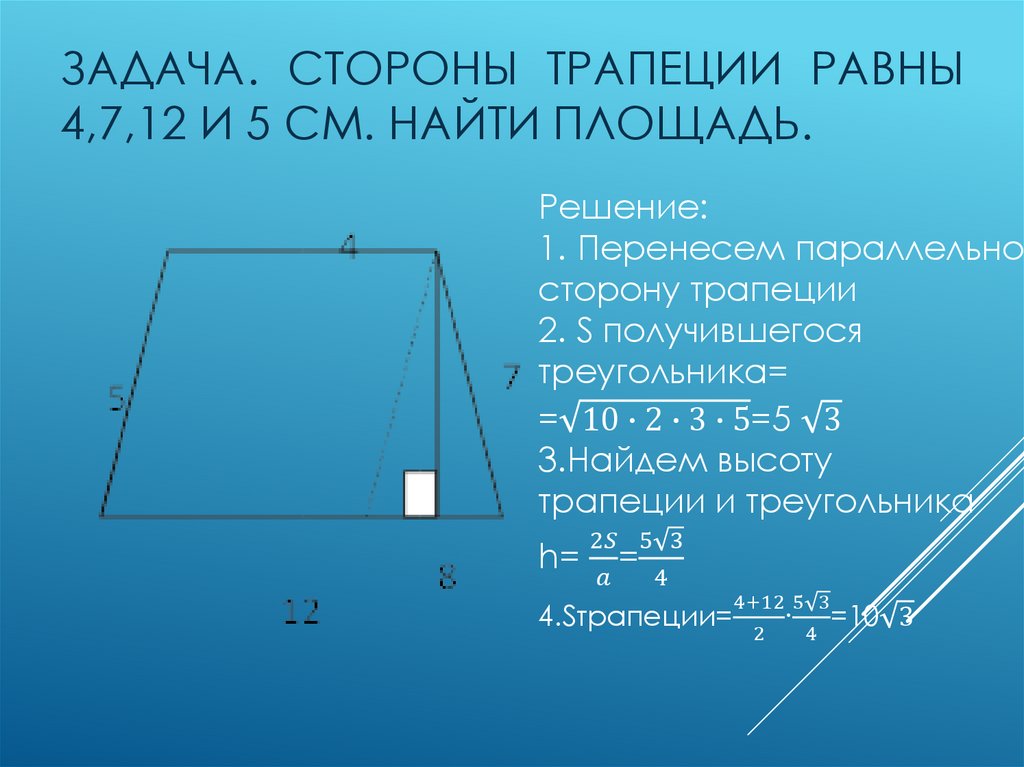
Г МОУ «Гимназия №1» г….Как высчитывается площадь трапеции. Как найти площадь трапеции: формулы и примеры
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие ;
— прямоугольные
.Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.

A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными.
 Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции - Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые .Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые , а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник , у которого линия сечения параллельна основанию треугольника.
Важно . Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.

По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.
Ответ: площадь трапеции равна 4,5 дм 2 .
№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх.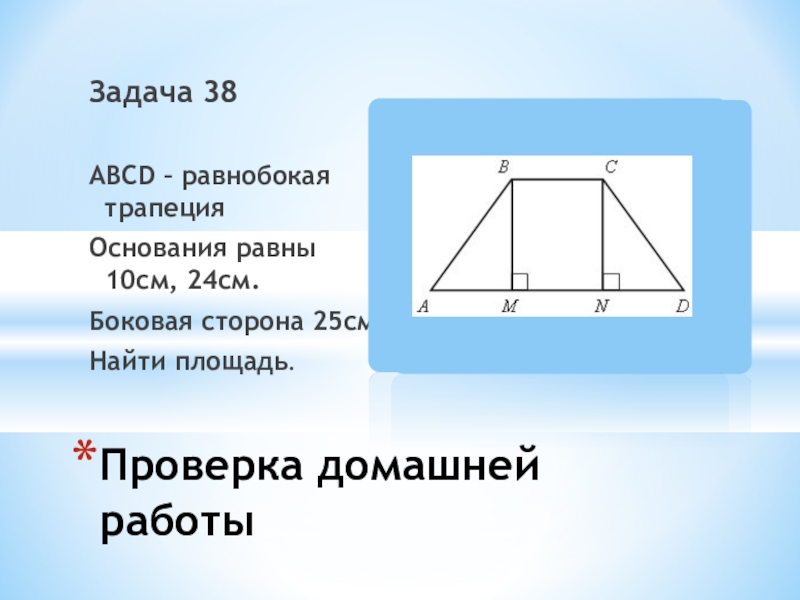 Так ЕН окажется внутри фигуры.
Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ: S = 20 см 2 .
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение. Пусть меньшее основание имеет обозначение ВС.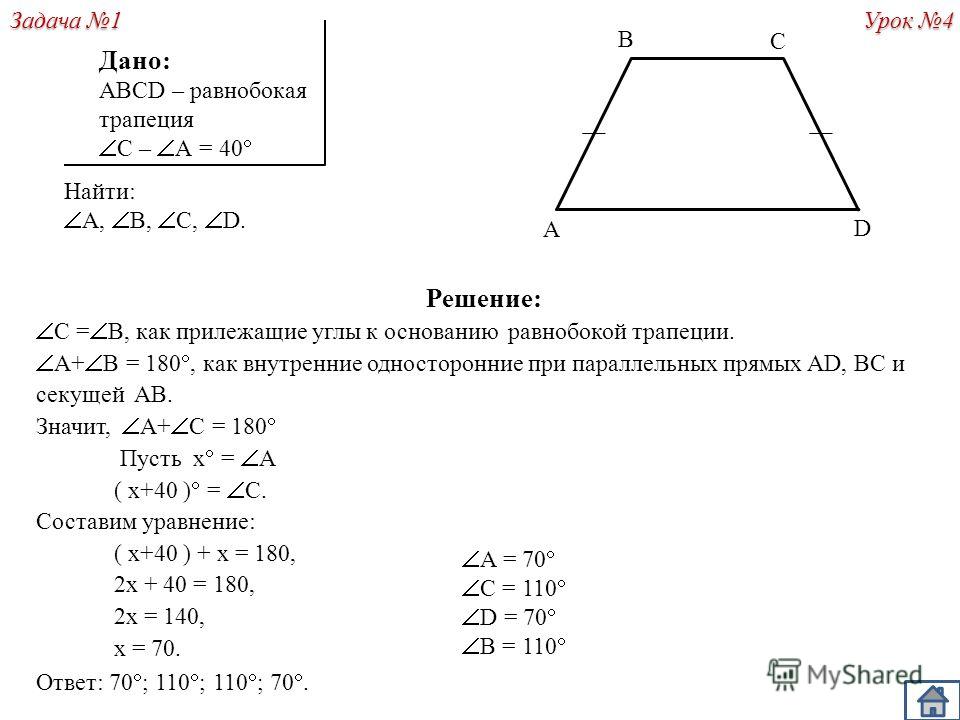 Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ: Искомая площадь равна 45 см 2 .
№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ : х = √ {(а 1 2 + 5 а 2 2) / 6}.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Прежде чем найти площадь трапеции, необходимо определится с известными элементами трапеции. Трапеция – это геометрический объект, а именно: четырёхугольник, который имеет две параллельные стороны (два основания). Другие две стороны – боковые. Если же параллельны будут и эти две стороны четырёхугольника, то это уже будет не трапеция, а параллелограмм. Если хотя бы один угол трапеции равен 90 градусов, то такая трапеция называется прямоугольной. Как найти площадь прямоугольной трапеции, рассмотрим позже. Существует также равнобедренная трапеция, название которой говорит само за себя: боковые стороны такой трапеции равны.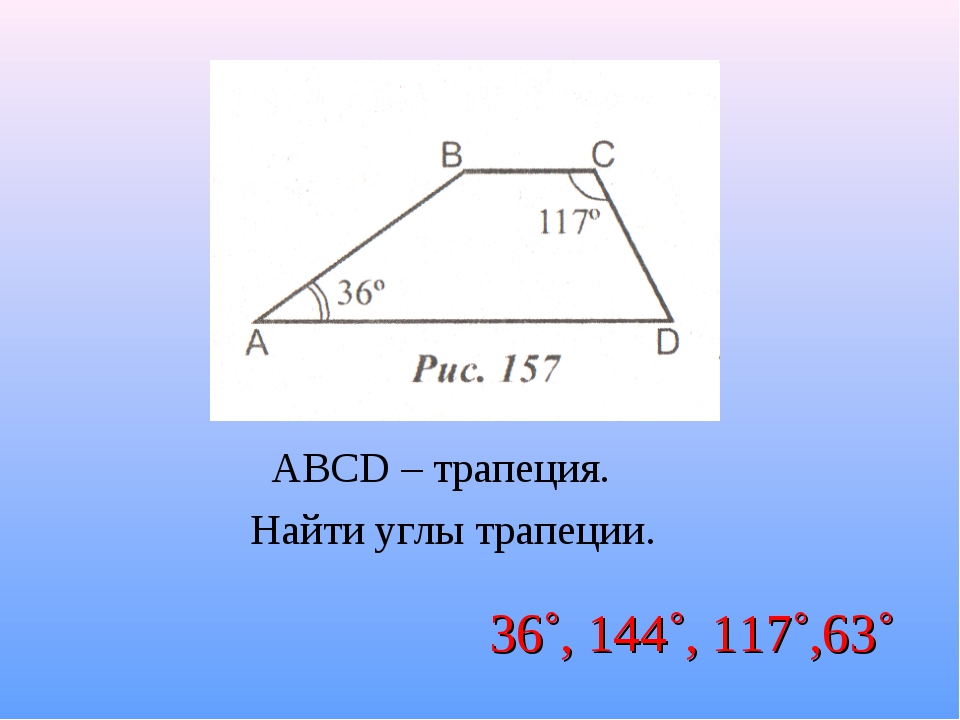 d2) – это синус угла, между диагоналями трапеции.
d2) – это синус угла, между диагоналями трапеции.
Существуют также различные формулы, выведенные из основных, а также формула для расчёта площади трапеции, когда известны все её стороны. Однако эта формула достаточно громоздкая и используется редко, ведь, зная все стороны трапеции можно просто определить высоту или её среднюю линию. Также в равнобедренную трапецию можно вписать окружность. В этом случае площадь трапеции будет высчитываться по формуле: 8*радиус окружности в квадрате.
Как найти площадь прямоугольной трапеции
Как и говорилось ранее, прямоугольной называется та трапеция, у которой хотя бы один угол прямой. Найти площадь такой трапеции очень просто. В основном, для поиска площади прямоугольной трапеции используются те же формулы, что и для обычной трапеции. Однако стоит помнить, что одна из боковых сторон такой трапеции и будет являться высотой. Также часто решение задач поиска площади прямоугольной трапеции сводится к поиску площади прямоугольника и треугольника, образованных опущенной высотой. Такие задачи достаточно просты.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Иллюстративная математика
Комментарий IM
Цель этого задания — дать учащимся определение трапеции. Есть два конкурирующих определения слова «трапеция»:
Исключительное определение трапеции гласит, что трапеция имеет ровно одну пару параллельных противоположных сторон.
Включенное определение гласит, что трапеция имеет по крайней мере одну пару параллельных противоположных сторон.
Иногда люди говорят, что у трапеций «одна пара противоположных сторон параллельна», поэтому остается неясным, может быть их больше одной или нет.Вторая часть задания подталкивает учащихся к четкому пониманию того, какую версию они намереваются. Из-за того, что учащиеся должны внимательно относиться к определениям, эта задача во многом опирается на MP6, «Заботьтесь о точности».
После того, как учащиеся сформулировали определения для себя или с партнером, класс должен обсудить определение вместе. Класс должен выбрать одно определение, с которым все согласны, поскольку смысл четко сформулированных определений состоит в том, что мы все знаем, что говорим об одном и том же.Хотя оба определения законны, преимущество инклюзивного определения состоит в том, что любая теорема, верная для трапеции, верна и для параллелограмма. Кроме того, в своем исследовании Классификация четырехугольников (Information Age Publishing, 2008) Usiskin et al. заключение,
Преобладание преимуществ всеобъемлющего определения трапеции привело к тому, что все статьи, которые мы могли найти по этому предмету, и большинство выпускаемых колледжем книг по геометрии, отдали предпочтение всеобъемлющему определению.
Инклюзивное определение устанавливает взаимосвязь между параллелограммами и трапециями, которая в точности аналогична взаимосвязи между квадратами и прямоугольниками; определение прямоугольников включает квадраты так же, как включающее определение трапеций включает параллелограммы.
Дополнительную информацию об этих проблемах см. В документе K-6 Geometry Progressions: http://commoncoretools.me/wp-content/uploads/2012/06/ccss_progression_g_k6_2012_06_27.pdf.
Решение
- Трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Он может иметь прямые углы (прямая трапеция) и равнобедренные стороны, но это не обязательно.
- Иногда люди определяют трапеции, чтобы иметь по крайней мере одну пару противоположных сторон, параллельных, а иногда говорят, что существует одна и только одна пара противоположных сторон, параллельных. Параллелограмм соответствует «по крайней мере одному» варианту определения, потому что он имеет две пары противоположных сторон, параллельных друг другу, поэтому он попадает в категорию как трапеции, так и параллелограмма.Параллелограмм не подходит под «один-единственный» вариант определения. То, как студенты ответят на это, зависит от их определения.
Примечание: если учащиеся дают разные определения, это нормально. Однако, чтобы иметь возможность обсуждать математические идеи в будущем, класс должен остановиться на одной из этих версий и двигаться дальше. См. Примечание в комментарии, поощряющее версию определения, включающую параллелограммы.
Что такое трапеция? (Определение, свойства и видео) // Репетиторы.com
Содержание
- Что такое трапеция?
- Определения трапеций
- Уголки трапеции
- Свойства трапеции
- Трапеции
- Виды трапеций
Что такое трапеция?
Трапеция — четырехугольник с одной парой параллельных сторон. Трапеция — это:
- Фигурка плоская (плоская)
- Замкнутая фигура (имеет внутреннюю и внешнюю)
- Многоугольник (прямые стороны)
- Четырехугольник (четыре прямые стороны)
Чтобы сделать трапецию, вам понадобится треугольник.Подойдет любой треугольник: прямой, тупой, равнобедренный, разносторонний. Отрежьте верхнюю часть треугольника так, чтобы разрез был параллелен нижней части треугольника. Теперь у вас есть более крошечный треугольник и трапеция.
Поскольку для определения требуется только одна пара параллельных сторон, две другие стороны можно расположить разными способами, создавая четыре внутренних угла, которые в сумме всегда составляют 360 °.
Определения трапеций
Мы уже знаем, что трапеция похожа на нижнюю часть треугольника, если от нее отрезать меньший треугольник.Вы также можете сделать трапецию из четырех отрезков или четырех прямых объектов.
Используйте все, что вам нравится: сырые спагетти, карандаши, палочки от леденцов; все, что у вас есть под рукой. Четыре прямых (линейных) объекта могут быть четырех разных длин или трех разных длин (два из них могут быть одинаковыми).
Положите два объекта вниз или нарисуйте два отрезка линии, чтобы они были параллельны (равноудалены). Сделайте их горизонтально по отношению к вам. Поместите два других объекта слева и справа от этих двух или нарисуйте их так, чтобы все восемь конечных точек соприкасались.
Вот она, трапеция! Горизонтальные части — это основания . Последние две части, которые вы нарисовали или положили (на левом и правом концах), называются ногами трапеции.
Уголки трапеции
Обратите внимание, что мы не беспокоились ни о каком из внутренних углов, поскольку сохранение двух сторон параллельными заставляет остальную часть трапеции встать на место. Углы сортируются и складываются в 360 °.
Высота трапеции — это ее высота.Пусть вас не обманывают покатые ножки — если они наклонные, то длиннее высоты. Высота всегда измеряется от основания (любой параллельной стороны) до другой стороны под прямым углом к основанию.
Вы можете провести перпендикулярную линию где угодно вдоль основания трапеции, и когда она касается противоположной, параллельной стороны, ее длина равна высоте.
Свойства трапеции
Трапеция — это параллелограмм?
Вы можете определить любую трапецию, если это четырехугольник с одной парой параллельных сторон.Многие математики включают параллелограммы как типы трапеций, потому что, конечно, параллелограмм имеет по крайней мере одной пары параллельных сторон. Другие математики исключают параллелограммы, говоря, что трапеция должна иметь ровно одной пары параллельных сторон.
Еще одним отличительным свойством всех трапеций является то, что любые два смежных внутренних угла будут дополнительными (добавить к 180 °).
Трапеции
Обычно для максимальной ясности на изображениях и рисунках трапеций показаны две параллельные стороны, идущие горизонтально, причем более длинная сторона обращена вниз в качестве основания.Однако будьте готовы увидеть трапеции в при любой ориентации . Трапецию можно нарисовать или изобразить либо с ногой внизу, либо с более короткой параллельной стороной внизу.
Поскольку параллельные стороны — единственные, которые могут быть основаниями, даже когда трапеция рисуется с ногой внизу и горизонтально, это , а не основание. Это все еще нога.
Основание обычно представляет собой более длинную параллельную сторону, но если трапеция рисуется с более короткой параллельной стороной внизу, то это основание.
Типы трапеций
Так как трапеции могут возникать как треугольники, они имеют общие названия, полученные от типов треугольников:
- Чешуйчатая трапеция — начиналась как разносторонний треугольник
- Равнобедренная трапеция — Начиналась как равнобедренный треугольник
- Правая трапеция — Когда-то был прямоугольный треугольник
- Тупая трапеция — Как тупой треугольник
- Острая трапеция — как острый треугольник
Трапеция из чешуи
Разносторонняя трапеция имеет четыре стороны неравной длины.Основания параллельны, но разной длины. Две ножки разной длины.
Равнобедренная трапеция
Равнобедренная трапеция имеет ножки одинаковой длины. Основания параллельны, но разной длины.
Трапеция правая
Прямоугольная трапеция имеет один прямой угол (90 °) между основанием и ножкой.
Тупая трапеция
Тупая трапеция имеет один внутренний угол (образованный основанием и ножкой) больше 90 °.
Острая трапеция
Острая трапеция имеет оба внутренних угла (образованные более длинным основанием и ножками ) размером менее 90 °.
Краткое содержание урока
Используя всего четыре линии и четыре внутренних угла, мы построили трапецию , узнали, что делает трапецию уникальной (пара параллельных сторон), каковы различные части трапеции и названия пяти специальных трапеций.
Следующий урок:
Как найти площадь трапеции
Четырехугольники: Классификация
А четырехугольник это многоугольник с четырех сторон.
Есть много особых типов четырехугольника.
А параллелограмм — четырехугольник, в котором обе пары противоположных сторон равны параллельный .
Параллелограмм также обладает следующими свойствами:
- Противоположные углы равны;
- Противоположные стороны совпадают;
- Смежные углы — дополнительные;
- В диагонали разделите друг друга пополам.
А прямоугольник представляет собой параллелограмм с четырьмя прямыми углами, поэтому все прямоугольники также являются параллелограммами и четырехугольниками. С другой стороны, не все четырехугольники и параллелограммы являются прямоугольниками.
Прямоугольник обладает всеми свойствами параллелограмма, а также следующими:
- Диагонали совпадают.
А ромб параллелограмм с четырьмя конгруэнтный стороны.Множественное число ромба ромбовидные . (Я люблю это слово.)
Ромб обладает всеми свойствами параллелограмма, а также следующими:
- Диагонали пересекаются под прямым углом.
А квадратный может быть определен как ромб, который также является прямоугольником — другими словами, параллелограмм с четырьмя равными сторонами и четырьмя прямыми углами.
А трапеция — четырехугольник, у которого ровно одна пара параллельных сторон.(В зависимости от того, в какой стране вы находитесь, это слово может вызывать некоторую путаницу. В Индии и Великобритании говорят трапеция ; в Америке трапеция обычно означает четырехугольник без параллельных сторон.)
An равнобедренная трапеция — трапеция, непараллельные стороны которой совпадают.
А летающий змей — четырехугольник, у которого ровно две пары смежных конгруэнтных сторон.(Это определение исключает ромбы. В некоторых учебниках говорится, что воздушный змей имеет как минимум две пары смежных конгруэнтных сторон, поэтому ромб — это частный случай воздушного змея.)
А неравносторонний четырехугольник — это четырехсторонний многоугольник, у которого нет совпадающих сторон. Ниже показаны три примера.
Диаграмма Венна четырехугольной классификации
Следующая диаграмма Венна показывает включения и пересечения четырехугольников различных типов.
полигонов — четырехугольники — в глубину
Есть много разные виды четырехугольников, но все они имеют несколько общих черт: все они имеют четыре стороны, компланарны, имеют две диагонали и сумма их четырех внутренних углов равняется 360 градусам. Вот как они похожи, но что их отличает?
Мы знаем многих четырехугольники по их особой форме и свойствам, как квадраты.Помнить, если вы видите слово четырехугольник, это не обязательно означает фигуру с особые свойства, такие как квадрат или прямоугольник! В словесных задачах будьте осторожны не предполагать, что у четырехугольника есть параллельные или равные стороны, если только что заявлено.
Специальные четырехугольники
ср может использовать диаграмму Венна, чтобы помочь нам сгруппировать типы четырехугольников.
Диаграмма Венна использует перекрывающиеся круги, чтобы показать отношения между группами объектов.Все «четырехугольники» можно разделить на три подгруппы: общие четырехугольники, параллелограммы и трапеции.
— это прямоугольник всегда ромб? Нет, потому что все четыре стороны прямоугольника не обязательно быть равным. Однако наборы прямоугольников и ромбов пересекаются, и их пересечение — это множество квадратов — все квадраты представляют собой прямоугольник и ромб.
Можем поставить квадраты на пересечении двух кругов.
Из этой диаграммы, вы можете видеть, что квадрат — это четырехугольник, параллелограмм, прямоугольник, и ромб!
— это трапеция параллелограмм? Нет, потому что у трапеции только одна пара параллельных сторон. Поэтому мы должны показать набор трапеций отдельным кружком на Диаграмма Венна.
А как насчет воздушных змеев? Воздушные змеи — это четырехугольники, которые могут быть параллелограммами . Если их две пары сторон равны, он становится ромбом, а если их углы равны, он становится ромбом. становится квадратом.
Ссылки по теме:
Формулы площади
Формулы периметра
назад наверх
Сколько прямых углов у трапеции?
Трапеция имеет два прямых угла .
У трапеций 4 прямых угла?
Трапеции. … Две стороны должны быть параллельны друг другу, чтобы получилась трапеция. У трапеции тоже четыре угла.
Может ли трапеция иметь 3 прямых угла?
У трапеции не может быть трех прямых углов.Сумма четырех внутренних углов любого четырехугольника всегда составляет 360 градусов. …
Может ли трапеция иметь 2 прямых угла?
У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла. … У острой трапеции два смежных острых угла на более длинном основании, а у тупой трапеции — по одному острому и по одному тупому углу на каждом основании.
Какие углы у трапеции?
Сумма внутренних углов всех четырехугольников составляет 360 °.У равнобедренных трапеций два верхних угла равны друг другу. Точно так же два нижних угла также равны друг другу.
Может ли трапеция иметь один прямой угол?
У правой трапеции один прямой угол (90 °) между основанием и ножкой. 29 октября 2018 г.
У параллелограмма 4 прямых угла?
Прямоугольник: параллелограмм с 4 прямыми углами.
Что такое трапеция с двумя прямыми углами?
У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла…. У острой трапеции два смежных острых угла на более длинном основании, а у тупой трапеции — по одному острому и по одному тупому углу на каждом основании.
Могут ли воздушные змеи иметь прямые углы?
Таким образом, правый змей представляет собой выпуклый четырехугольник с двумя противоположными прямыми углами. Если прямых углов ровно два, каждый должен находиться между сторонами разной длины. Все правые воздушные змеи представляют собой двухцентровые четырехугольники (четырехугольники с описанной и вписанной окружностями), поскольку все воздушные змеи имеют вписанную окружность.
Может ли трапеция иметь 2 линии симметрии?
Нет, трапеция не может иметь две линии симметрии, потому что в случае четырехугольника только одна пара параллельных сторон равны.
Что такое 4-сторонняя форма с 2-мя прямыми углами?
Трапеция должна иметь только две параллельные стороны. Однако трапеция может иметь одну из сторон, соединяющих две параллельные стороны, перпендикулярные параллельным сторонам, что даст два прямых угла.
Какие четырехугольники никогда не могут иметь прямых углов?
Другие типы четырехугольников В отличие от прямоугольника, параллелограмм не обязательно должен иметь четыре прямых угла. Ромб — это четырехугольник, у которого все четыре стороны равны по длине. В отличие от квадрата, ромб не обязательно должен иметь четыре прямых угла. 24 апреля 2017 г.
Какая форма имеет наибольшие прямые углы?
Прямоугольник Прямоугольник Прямоугольник — это четырехсторонняя форма, каждый угол которой является прямым (90 °).Также противоположные стороны параллельны и равной длины.
Конгруэнтны ли противоположные углы трапеции?
ТЕОРЕМА: (обратное) Если трапеция имеет совпадающие диагонали, это равнобедренная трапеция. ТЕОРЕМА: Если четырехугольник представляет собой равнобедренную трапецию, противоположные углы являются дополнительными. ТЕОРЕМА: (обратное) Если трапеция имеет дополнительные противоположные углы, то это равнобедренная трапеция.
Какие атрибуты есть у трапеции?
Трапеция — определение с примерами Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон.Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки.
Каковы противоположные углы трапеции?
Да противоположные углы трапеции являются дополнительными. Дополнительные углы трапеции определяются как сумма двух противоположных углов 180 …
У трапеции равные углы?
Базовые углы равнобедренной трапеции равны в меру (фактически есть две пары равных базовых углов, где один базовый угол является дополнительным углом базового угла у другого базового угла).
Каковы 3 свойства трапеции?
Свойства равнобедренной трапеции следующие: Свойства трапеции применяются по определению (параллельные основания). Ноги по определению конгруэнтны. Углы нижнего основания совпадают. Углы верхнего основания совпадают. Любой нижний базовый угол является дополнительным к любому верхнему базовому углу. Еще товары …
Сколько прямых углов у креста?
четыре прямых угла Крест имеет 4 вершины для четырех прямых углов, образованных четырьмя руками.Все 4 вершины сгруппированы вместе, как и в любом многоугольнике в центре фигуры. Как и во всех полигонах, четыре вершины в сумме составляют 360 градусов.
Может ли ромб иметь 4 прямых угла?
Ромб — это параллелограмм с четырьмя равными сторонами. Всегда ли ромб является прямоугольником? Нет, потому что у ромба не обязательно должно быть 4 прямых угла.
Все углы образуют параллелограмм 90 градусов?
Решение: Параллелограмм можно определить как четырехугольник, две стороны s которого параллельны друг другу, а все четыре угла в вершинах не равны 90 градусам или прямым углам, тогда четырехугольник называется параллелограммом.Противоположные стороны параллелограмма также равны по длине.
Какой параллелограмм не имеет прямых углов?
Этот параллелограмм ромбовидный, так как у него нет прямых углов и неравных сторон. …
Что такое ромб с двумя прямыми углами?
Ромб с прямым углом — это квадрат. Квадрат — это ромб, потому что все его стороны равны. Таким образом, ромб с прямыми углами — это особая форма ромба, называемая квадратом.3 янв.2016 г.
Сколько прямых углов у ромба?
четыре 1 Ответ. Если ромб представляет собой квадрат, все четыре его угла прямые. В противном случае все углы либо острые, либо тупые, но не прямые. 25 декабря 2015 г.
Сколько прямых углов у семиугольника?
Углы семиугольника У семиугольника семь внутренних углов в сумме составляют 900 °, а семь внешних углов в сумме составляют 360 °. 18 июн.2020 г.
Какие углы у воздушных змеев?
Воздушный змей.У воздушного змея две пары равных сторон. Имеет одну пару равных углов. Диагонали делят пополам под прямым углом.
Какие углы равны в кайте?
Воздушные змеи, которые также являются вписанными четырехугольниками (то есть воздушные змеи, которые могут быть вписаны в круг), в точности состоят из двух равных прямоугольных треугольников. То есть для этих воздушных змеев два равных угла на противоположных сторонах оси симметрии составляют каждый по 90 градусов.
Каковы 4 свойства воздушного змея?
СвойстваKite включают (1) две пары последовательных конгруэнтных сторон, (2) конгруэнтные невершинные углы и (3) перпендикулярные диагонали.Другие важные свойства многоугольника, с которыми необходимо ознакомиться, включают свойства трапеции, свойства параллелограмма, свойства ромба, а также свойства прямоугольника и квадрата.
Что такое трапеция с одной линией симметрии?
Трапеция. У трапеции одна пара параллельных сторон. Некоторые трапеции имеют одну линию симметрии. Их называют равнобедренными трапециями, поскольку они имеют две равные стороны, похожие на равнобедренные треугольники.
У всех четырехугольников две линии симметрии?
Итак, квадрат имеет четыре линии симметрии.Прямоугольник их всего два, так как его можно сложить пополам по горизонтали или вертикали: следует поощрять учащихся пытаться сложить прямоугольник пополам по диагонали, чтобы понять, почему это не работает. Трапеция имеет только вертикальную линию симметрии.
Сколько параллельных линий у трапеции?
Трапеция — это четырехугольник с одним набором параллельных сторон. У них абсолютно не может быть двух наборов параллельных сторон.
Может ли параллелограмм иметь ровно 2 прямых угла?
Конечно, может.Определение параллелограмма состоит в том, что противоположные стороны равны и параллельны. Противоположные углы равны, смежные — дополнительные. Любой прямоугольник подходит под описание параллелограмма.
Какая форма имеет два угла по 90 градусов?
Прямоугольник Название четырехугольника Описание Параллелограмм 2 пары параллельных сторон. Противоположные стороны и противоположные углы равны. Прямоугольник 2 пары параллельных сторон. 4 прямых угла (90 °). Противоположные стороны параллельны и совпадают.Все углы совпадают. Еще 2 ряда
Может ли треугольник иметь два прямых угла?
Нет, у треугольника не может быть двух прямых углов. Треугольник имеет ровно 3 стороны, а сумма внутренних углов составляет 180 °. … Таким образом, невозможно получить треугольник с двумя прямыми углами. 28 сен.2020
Какие 2 четырехугольника не имеют параллельных сторон?
В Индии и Великобритании говорят трапеции; в Америке трапеция обычно означает четырехугольник без параллельных сторон.) Равнобедренная трапеция — это трапеция, непараллельные стороны которой совпадают.
Встречаются ли в природе прямые углы?
Идеального прямого угла в природе не существует. По крайней мере, квантовая неопределенность гарантирует, что это не так. Если подумать о прямых углах в природе, на макроуровне они кажутся немногочисленными и далекими друг от друга. Большинство углов следуют некоторому соотношению числа Пи или последовательности Фибоначчи.
У всех квадратов 4 прямых угла?
Противоположные стороны квадрата параллельны и равны по длине.Все четыре угла квадрата равны (каждый составляет 360 ° / 4 = 90 °, прямой угол).
Как называется 9-гранная форма?
enneagon Нонагон также называют эннеагоном, которое происходит от греческого слова эннеагонон, что означает девять углов. Первое использование слова nonagon относится к началу 17 века и имеет латинский префикс (nona) и греческий суффикс (gon), что делает его многоугольником с девятью сторонами и девятью углами.
Есть ли у восьмиугольника прямые углы?
Восьмиугольник — это многоугольник с восемью сторонами.Если восьмиугольник — правильный восьмиугольник, то у него нет прямых углов или углов измерения 90 °.
У какой формы ровно 3 прямых угла?
пятиугольник Итак, пятиугольник имеет максимум три прямых угла, как показано.
Сколько равных углов у трапеции?
1 ответ эксперта. Трапеция — это четырехугольник с двумя параллельными сторонами. К размеру углов не предъявляется никаких требований. В равнобедренной трапеции две пары углов совпадают, они являются углами основания.28 февраля 2017 г.
Как узнать, похожи ли две трапеции?
Две трапеции с одинаковыми углами подобны, если и только соотношение между одной конкретной парой соседних сторон одинаково в двух трапециях. Если трапеция не является параллелограммом, также достаточно знать, что соотношение между двумя параллельными сторонами одинаково в двух трапециях. 27 июля 2015 г.
Какие углы трапеции совпадают?
Итак, если трапеция равнобедренная, то ноги совпадают, и каждая пара углов основания совпадают.Другими словами, углы нижнего основания совпадают, а углы верхнего основания также совпадают. Аналогично, из-за внутренних углов одинаковой стороны нижний базовый угол является дополнительным к любому верхнему базовому углу. 21 янв.2020 г.
Как определить трапецию?
Определение формы трапеции. Если форма, на которую вы смотрите, не имеет хотя бы одного набора параллельных сторон, это не трапеция; это что-то вроде трапеции. Точно так же, если у фигуры два набора параллельных сторон, это не трапеция.Это либо прямоугольник, либо форма параллелограмма, либо ромб. 22 октября 2018 г.
Трапеция — это воздушный змей?
Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. В общем, четырехугольник с двумя парами равных соседних участков (например, воздушный змей) не должен иметь пары параллельных противоположных сторон (как трапеция). … Значит, воздушный змей может быть трапецией; это тот случай, когда это ромб.
Каждый квадрат — ромб?
Квадрат — это особый случай ромба, потому что у него четыре стороны равной длины, и он выходит за пределы и имеет четыре прямых угла.Каждый квадрат, который вы видите, будет ромбом, но не каждый ромб, который вы встретите, будет квадратом. 21 сен 2018
Какова сумма всех углов трапеции?
Факты о трапециях Сумма четырех углов в градусах составляет 360 градусов. На самом деле это верно для любого четырехугольника.
Делают ли диагонали воздушного змея углами пополам?
Четырехугольник является воздушным змеем, если: одна диагональ делит пополам углы при вершине, через которые она проходит, или. одна диагональ является серединным перпендикуляром другой диагонали.
Может ли трапеция иметь 3 равные стороны?
В евклидовой геометрии такие трапеции автоматически являются прямоугольниками. … Таким образом, словосочетание «правильная равнобедренная трапеция» встречается редко. Трапеция, равная с трех сторон, — это равнобедренная трапеция, имеющая не менее трех равных сторон. Ниже изображена трапеция, равная с трех сторон. 22 марта 2013 г.
Сколько градусов у трапеции?
360 ° В трапеции 360 °. Это происходит из-за соотношения трапеций и четырехугольников.Трапеции определяются как четырехсторонние …
Может ли у трапеции равны все углы, могут ли все стороны равны, объясните?
В трапеции. Параллельные стороны могут быть равны друг другу, но не все стороны и смежные углы являются дополнительными, не все углы равны. Итак, у нас не может быть трапеции, у которой все стороны равны друг другу, а все углы равны друг другу (это может быть квадрат). 25 сен.2015
Каковы 4 свойства трапеции?
Как и у других четырехугольников, сумма всех четырех углов трапеции равна 360 °. Трапеция имеет две параллельные стороны и две непараллельные стороны.Диагонали правильной трапеции делят друг друга пополам. Длина среднего сегмента равна половине суммы параллельных оснований трапеции.
Какие правила для трапеции?
Популярные темы Основания (верх и низ) равнобедренной трапеции параллельны. Противоположные стороны равнобедренной трапеции одинаковой длины (конгруэнтны). Углы по обе стороны от оснований одинакового размера / меры (совпадают). Диагонали (здесь не показаны) совпадают.
Сколько вершин у трапеции?
4 Трапеция / количество вершин Как и в плоской геометрии, трапеция — это четырехугольник с одной парой параллельных сторон. (См. Определение трапеции). В координатной геометрии каждая из четырех вершин (углов) также имеет известные координаты.
Сколько углов у креста?
четыре угла При пересечении двух линий образуются четыре угла. Итак, у нас есть две линии, которые продолжаются вечно в обоих направлениях, они должны пересекаться, и эти четыре угла образуются.Пары углов напротив друг друга, имеющие общую вершину, называются вертикальными углами, а вертикальные углы всегда совпадают. 25 октября 2018 г.
Сколько углов у буквы H?
Если это то, что у нас здесь, то было бы еще восемь, всего 18 углов в письме.
Есть ли у шестиугольника прямые углы?
В правильном шестиугольнике все углы равны, из-за чего размер каждого угла составляет 120∘, поэтому правильный шестиугольник не имеет возможных прямых углов.
Есть ли у ромба 4 угла по 90 градусов?
Вот что нужно запомнить. У квадрата 4 стороны равной длины и 4 прямых угла (прямой угол = 90 градусов). У ромба 4 стороны равной длины, противоположные стороны параллельны и углы равны.
Как найти угол ромба?
