Пентамино: Прямоугольники
Самая распространённая задача в пентамино — сложить из всех элементов прямоугольник. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20. Очевидно, что прямоугольники 2×30 и 1×60 составить из пентамино невозможно, поскольку многие фигуры в них просто не помещаются по ширине.
Для случая 6×10 эту задачу впервые решил в 1965 году Джон Флетчер. Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника. Один из вариантов:
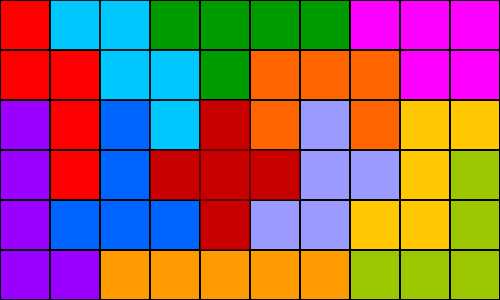 |
| Пентамино — Прямоугольник 6×10 |
Для прямоугольника 5×12 существует 1010 решений.
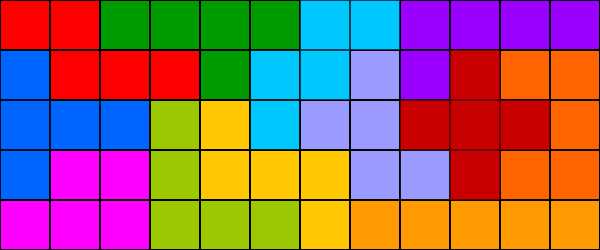 |
| Пентамино — Прямоугольник 5×12 |
| Пентамино — Прямоугольник 4×15 |
Для прямоугольника 3×20 — всего 2 решения, вот они:
| Пентамино — Прямоугольник 3×20, вариант №1 |
| Пентамино — Прямоугольник 3×20, вариант №2 |
pentamania.blogspot.com
Как играть в головоломку Пентамино? |
Your ads will be inserted here by
Easy Plugin for AdSense.
Please go to the plugin admin page to
Paste your ad code
Suppress this ad slot.
Головоломка пентамино — очень популярная логическая игра и головоломка одновременно. Элементы в игре — плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов. Всего существуют 12 элементов.
Предлагаем сделать элементы их плотного картона,а если у вас дома много стандартных кирпичиков лего, то можно попробовать сделать пентамино из них.
Детям лучше тренироваться на маленьких прямоугольниках из нескольких деталей.Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20. Так же из элементов можно складывать различные фигуры, симметричные узоры, буква алфавита, цифры.Для маленьких детей, лучше фигуры складывать по образцу, как мозаику.
Как играть в пентамино. Правила игры в пентамино.
Фигурки-пентаминошки и разлинованный черный квадрат-поле надо распечатать,
вырезать и наклеить на картон.
ПРАВИЛА.
Задача игрока – расположить все фигурки на поле, оставив четыре пустые клетки. В простом
варианте фигурки можно переворачивать (отражать зеркально), а пустые клетки – оставлять где
угодно. Усложнение: запрет на перевороты, а пустые клетки на конкретных местах (например, по
углам). Если сделать несколько комплектов, то можно собирать на время.
Еще можно без поля собирать ровные прямоугольники, стараясь, чтобы не было пустот и
ничего не торчало. Можно собирать различные фигурки по шаблонам. Это очень увлекательная игра головоломка для вашего ребенка.
Шаблон для игры в пентамино.
Оцените статью: Загрузка… Поделитесь в соц сетях:
www.mam-club.org
Пентамино. Головоломка для детей своими руками
ПентаминоИгры и игрушки своими руками |
Пентамино — очень популярная логическая игра и головоломка одновременно. Элементы в игре — плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов. Всего существуют 12 элементов пентамино, обозначаемых латинскими буквами, форму которых они напоминают (см. рисунок).

Как сделать Пентамино
Можно изготовить пентамино из кубиков, но тогда Вам нужно будет склеить и обклеить цветной пленкой 60 кубиков — трудновато. Предлагаем сделать элементы их плотного картона.
- Рисуем каждый элемент на твердом картоне, вырезаем, проверяем, чтобы элемент входил в элемент “U”. Подрезаем , если надо лишнее. Мы рисовали детали из квадратиков 2,5х2,5 см.
- Обводим готовый картонный элемент на сложенной вдвое цветной бумаге и вырезаем сразу две цветные детали. Лучше цветные детали делать меньше, чем картонные, и приклеиваются лучше, и углы поровнее будут.
- Клеим клеем-карандашом цветную бумагу с двух сторон картонки.
- Находим коробочку для хранения деталей, куда потом будем складывать также схемы и задания к игре.

Игры и задачи с Пентамино
Сложи прямоугольник.
Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20.
Один из двух способов складывания прямоугольника 3х20
Честно скажу, пыталась весь вечер сложить — не получилось, поэтому ребенку такую задачу лучше не предлагать.

Детям лучше тренироваться на маленьких прямоугольниках из нескольких деталей.
Вот нарисовали варианты складывания прямоугольников из трех деталей.
Сложи фигуру
Их элементов можно складывать различные фигуры, симметричные узоры, буква алфавита, цифры.
Фигурки можно распечатать или перерисовать на листочек в клеточку. Варианты фигур пентамино можно посмотреть здесь >>>
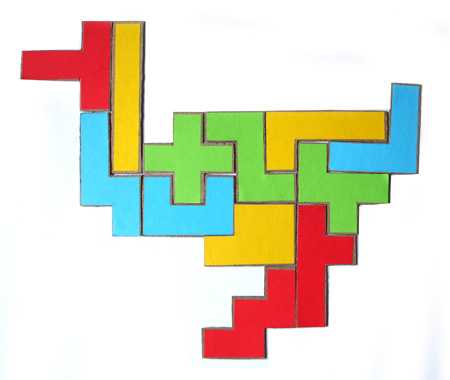
Фигура “Утка”, сложенная по образцу.
Игры с малышами.
С малышами играть лучше совсем по другому, не стоит им давать сразу сложные задания на логику, пусть играют с пентамино как с пазлами.
- Моя дочь (3,5 года) складывает их один в другой, ищет подходящий по цвету или форме, а в получившейся собранной фигуре ищет признаки сходства с животным или знакомым предметом. Например, если фигура похожа на слона, то можно пытается сделать хобот подлиннее или увеличить уши, а потом убрать пару элементов и превратить фигуру в мышь или еще кого-нибудь.
- Покажите ребенку как складывать маленький прямоугольник. Потом разломайте, как будто нечаянно. Можно перед тем как сломать, обратить внимание ребенка на то, где какие детали лежат. Попросите помочь собрать его заново, а то у вас не получается.
Да, много еще игр можно придумать с пентамино, главное, что бы ребенку и вам было интересно.
| Пентамино. Стомахион. Игра Пифагора Задания с ответами к головоломке пентамино, а также еще две интересные головоломки с тысячелетней историей. Купить >>> |
Пентамино из Лего
Кстати, если у Вас дома много стандартных кирпичиков лего, то можно попробовать сделать пентамино их них. Фигурки сложенные из Лего получаться объемные, и можно будет собирать помимо обычных, плоскостных моделей, объемные фигуры.
Схема сборки достаточно простая: два ряда кирпичиков уложенные друг на друга со смещением.
Игрушки легоИнтернет магазин: Игрушки лего |
www.babylessons.ru
Пентамино. Головоломка для детей
Пентамино — очень популярная логическая игра и головоломка одновременно.
Запатентовал головоломку “Pentomino” Соломон Вольф Голомб, житель Балтимора, математик и инженер, профессор университета Южная Калифорния. Игра состоит из плоских фигур, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами, отсюда и название. Существуют еще версия головоломок Тетрамино, состоящие из четырех квадратов, от этой игры и произошел известный Тетрис.
Всего существуют 12 элементов пентамино, обозначаемых латинскими буквами, форму которых они напоминают. При решении задач и головоломок фигурки можно вертеть и переворачивать, поэтому при изготовлении игры своими руками элементы делайте двухсторонними.

Как сделать Пентамино
- Можно изготовить пентамино из кубиков, но тогда Вам нужно будет склеить и обклеить цветной пленкой 60 кубиков — трудновато. Предлагаем сделать элементы их плотного картона.
- Рисуем каждый элемент на твердом картоне, вырезаем, проверяем, чтобы элемент входил в элемент “U”. Подрезаем , если надо лишнее. Мы рисовали детали из квадратиков 2,5х2,5 см.
- Обводим готовый картонный элемент на сложенной вдвое цветной бумаге и вырезаем сразу две цветные детали. Лучше цветные детали делать меньше, чем картонные, и приклеиваются лучше, и углы поровнее будут.
- Клеим клеем-карандашом цветную бумагу с двух сторон картонки.
- Находим коробочку для хранения деталей, куда потом будем складывать также схемы и задания к игре.

Игры и задачи с Пентамино
Сложи прямоугольник
Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20.
Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, а вот вариантов прямоугольника 3х20 всего 2.
Один из двух способов складывания прямоугольника 3х20
Детям лучше тренироваться на маленьких прямоугольниках из нескольких деталей.
Вот нарисовали варианты складывания прямоугольников из трех деталей.

Сложи фигуру
Их элементов можно складывать различные фигуры, симметричные узоры, буква алфавита, цифры.
Для маленьких детей, лучше фигуры складывать по образцу, как мозаику.
Фигурки можно распечатать или перерисовать на листочек в клеточку.
Скачать варианты фигур пентамино (657 КВ)
Ответы на задания

Игры с малышами
С малышами играть лучше совсем по другому, не стоит им давать сразу сложные задания на логику, пусть играют с пентамино как с пазлами.
Можно искать подходящий по цвету или форме, а в получившейся собранной фигуре находить признаки сходства с животным или знакомым предметом. Например, если фигура похожа на слона, то можно попытается сделать хобот подлиннее или увеличить уши, а потом убрать пару элементов и превратить фигуру в мышь или еще кого-нибудь.
Покажите ребенку как складывать маленький прямоугольник. Потом разломайте, как будто нечаянно. Можно перед тем как сломать, обратить внимание ребенка на то, где какие детали лежат. Попросите помочь собрать его заново, а то у вас не получается.
Да, много еще игр можно придумать с пентамино, главное, что бы ребенку и вам было интересно.
Пентамино из Лего
Кстати, если у Вас дома много стандартных кирпичиков лего, то можно попробовать сделать пентамино их них. Фигурки сложенные из Лего получаться объемные, и можно будет собирать помимо обычных, плоскостных моделей, объемные фигуры.
Схема сборки достаточно простая: два ряда кирпичиков уложенные друг на друга со смещением.
по материалам сайтов babylessons.ru и printplay.ru
Полезна: 2 голоса Не полезна: 0 голосов
Другие статьи на эту тему
www.detkityumen.ru
Материал для занятий кружка «Логическая математика» по теме «Пентамино»
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (2 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Полимино
В этой статье мы будем рассматривать полимино – фигуры, составленные из одноклеточных квадратов так, что каждый квадрат примыкает хотя бы к одному соседнему, имеющему с ним общую сторону.
Задачи с полимино очень характерны для комбинаторной геометрии – раздела математики, занимающегося вопросами взаимного расположения и комбинирования геометрических фигур. Это очень красивая, но еще почти не разработанная ветвь математики, поскольку общих методов в ней, по-видимому, очень мало, а известные ныне методы настолько примитивны, что не поддаются усовершенствованию. Многие встречающиеся в практике важные инженерные задачи – в первую очередь те, которые связаны в том или ином смысле с оптимальным расположением фигур заданной формы, – по существу относятся к комбинаторной геометрии.
В последующих комбинаторных задачах предполагается, что полимино можно вращать (то есть поворачивать на 90, 180 или 270) и зеркально отражать (переворачивать), не меняя формы самих фигур.
Домино
Рис. 1
Домино состоит из двух квадратов и может иметь лишь одну форму – форму прямоугольника размером 1×2 (см. рис. 1). Первая связанная с домино задача, вероятно, многим знакома: даны шахматная доска, из которой вырезана пара противоположных угловых клеток, и коробка домино, каждое из которых покрывает ровно две клетки шахматной доски (см. рис. 2). Возможно ли целиком покрыть доску с помощью 31 кости домино (без свободных клеток и наложений)? Ответ на этот вопрос гласит: «НЕТ» и имеет замечательное доказательство. Шахматная доска содержит 64 чередующиеся клетки белой и черной раскраски (имеется в виду обычная шахматная раскраска доски). Каждая положенная на такую доску и покрывающая две соседние клетки кость домино покроет одно белое и одно черное поле, а n костей домино – n белых и n черных полей, т.е. поровну и тех и других. Но изображенная на рисунке шахматная доска содержит больше черных клеток, чем белых, и потому ее нельзя покрыть костями домино. Этот результат есть типичная теорема комбинаторной геометрии.
Рис. 2
Тримино
Рис. 3
Тримино (или триомино) — полимино третьего порядка, то есть многоугольник, полученный путём объединения трёх равных квадратов, соединённых сторонами. Если повороты и зеркальные отражения не считать различными формами, то существует только две «свободных» формы тримино (см. рис.3): прямое (I-образное) и угловое (L-образное).
Тетрамино
Рис. 4
С тетрамино связано множество задач на составление из них разных фигур. Доказано, что сложить какой-либо прямоугольник из полного набора тетрамино невозможно. Доказательство использует раскраску в шахматном порядке. Все тетрамино, кроме Т-образного, содержат 2 чёрные и 2 белые клетки, а Т-образное тетрамино — 3 клетки одного цвета и 1 клетку другого. Поэтому любая фигура из полного набора тетрамино (см. рис.4) будет содержать клеток одного цвета на две больше, чем другого. Но любой прямоугольник, с чётным количеством клеток, содержит равное число чёрных и белых клеток.
Пентамино
Рис. 5
Полимино, покрывающее пять клеток шахматной доски, называются пентамино. Существует 12 видов пентамино, которые можно обозначить прописными латинскими буквами, как указано на рисунке (см. рис. 5). В качестве приема, позволяющего легко запомнить эти наименования, укажем, что соответствующие буквы составляют конец латинского алфавита (TUVWXYZ) и входят в имя FiLiPiNo. Поскольку всего имеется 12 разных пентамино и каждая из этих фигур покрывает пять клеток, то вместе они покрывают 60 клеток.
Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20 (см. рис. 6).
Рис. 6
Для случая 6×10 эту задачу впервые решил в 1965 году Джон Флетчер. Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника, но считая повороты и отражения его частей (иногда внутри прямоугольника образуется симметричная комбинация фигур, поворачивая которую можно получить дополнительные решения).
Для прямоугольника 5×12 существует 1010 решений, 4×15 — 368 решений, 3×20 — всего 2 решения (отличающихся вышеописанным поворотом). В частности, существует 16 способов сложить два прямоугольника 5×6, из которых можно составить как прямоугольник 6×10, так и 5×12.
Еще одна интересная задача о пентамино — задача об утроении фигур пентамино (см. рис. 7). Эта задача была предложена профессором Калифорнийского университета Р.М.Робинсоном. Выбрав одну из 12 фигур пентамино, необходимо построить из каких-либо 9 из 11 оставшихся пентамино фигуру, подобную выбранной, но в 3 раза бо́льшей длины и ширины. Решение существует для любого из 12 пентамино, причём не единственное (от 15 решений для Х до 497 для Р). Существует вариант этой задачи, в котором для построения утроенной фигуры разрешается использовать также и саму исходную фигуру. В этом случае число решений от 20 для Х до 9144 для Р-пентамино.
Рис. 7
Комментарии к презентации «Пентамино»
В этой работе я предлагаю несколько заданий с использованием фигур пентамино, которые можно использовать и для самых первых занятий с этой головоломкой, и для более подготовленных ребят. Они подойдут и для начальной школы, и для учащихся 5-7 классов (в зависимости от уровня обучающихся).
Для работы нам потребуется комплект, состоящий из двенадцати деталей пентамино. Его очень легко сделать самим на уроке или дома. На листе в клетку нужно нарисовать фигуры так, чтобы каждая состояла из пяти квадратов со стороной 1см. Затем следует приклеить лист в клетку на картон и вырезать по контуру получившиеся фигурки. При желании их можно раскрасить цветными карандашами или фломастерами. Пентамино готово.
Начинается презентация с самых простых заданий. Нужно из всех двенадцати фигурок пентамино отложить только те, из которых собирается данная картинка. Фигурки в презентации появляются по щелчку по одной, чтобы было удобно их находить.
На следующем слайде представлена картинка, которую нужно собрать. А на третьем слайде предложен вариант ответа. Таких задач в презентации четыре, но их количество всегда можно увеличить по мере необходимости.
Начиная с пятой задачи, учащиеся сами должны выбрать фигурки, которые будут использованы для данной картинки. В задаче №5 для «собачки» потребуются три фигурки пентамино.
В задаче №6 ребята должны не только собрать данные картинки, но и попытаться объяснить, почему может быть представлено только единственное решение этих задач.
В задачах №7 и №8 решений может быть несколько, и можно устроить соревнования «кто первый найдет все возможные решения этих задач».
Начиная с задачи №9, решений становится гораздо больше. Найти все решения на уроке не получится. Эти задачи можно предложить как вариант домашнего задания или предложить найти решения, разбив класс на группы.
В задачах №13 и №14 при решении используются все двенадцать фигур пентамино. Это уже достаточно сложные задания. С ними могут справиться не все учащиеся 5-6 классов. Поэтому те ребята, которые нашли решения этих задач, должны быть поощрены.
Очень интересный результат можно получить, предложив ребятам самим придумать различные картинки, составленные из фигур пентамино. Если это начальные классы, то нужно оговорить, что можно использовать не все фигуры сразу. В более старших классах учащиеся могут использовать весь комплект. Здесь следует напомнить, что каждая фигурка встречается ровно однажды и нельзя использовать какие-то детали более одного раза.
И вообще, очень трудно охватить такой огромный материал в одной презентации. Я предложила только малую толику того, что может быть придумано из пентамино. Творите, и результат превзойдет все ваши самые смелые ожидания. Ваши дети очень талантливы, и нужно только направить их мысль в нужную сторону. А там…
Литература:
- С.В. Голомб «Полимино», издательство «Мир», М., 1975.
- М.А. Екимова, Г.П. Кукин «Задачи на разрезание», МЦНМО, М., 2007.
- ru.wikipedia.org
20.05.2012
xn--i1abbnckbmcl9fb.xn--p1ai
ПЕНТАМИНО
Пентамино — очень популярная логическая игра и головоломка одновременно. Элементы в игре — плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов. Всего существуют 12 элементов пентамино, обозначаемых латинскими буквами, форму которых они напоминают (см. рисунок).
Как сделать Пентамино
Можно изготовить пентамино из кубиков, но тогда Вам нужно будет склеить и обклеить цветной пленкой 60 кубиков — трудновато. Предлагаем сделать элементы их плотного картона.
- Рисуем каждый элемент на твердом картоне, вырезаем, проверяем, чтобы элемент входил в элемент “U”. Подрезаем, если надо лишнее. Мы рисовали детали из квадратиков 2,5х2,5 см.
- Обводим готовый картонный элемент на сложенной вдвое цветной бумаге и вырезаем сразу две цветные детали. Лучше цветные детали делать меньше, чем картонные, и приклеиваются лучше, и углы поровнее будут.
- Клеим клеем-карандашом цветную бумагу с двух сторон картонки.
- Находим коробочку для хранения деталей, куда потом будем складывать также схемы и задания к игре.
Игры и задачи с Пентамино
Сложи прямоугольник.
Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20.
Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, а вот вариантов прямоугольника 3х20 всего 2.
Один из двух способов складывания прямоугольника 3х20
Честно скажу, пыталась весь вечер сложить — не получилось, поэтому ребенку такую задачу лучше не предлагать.
Детям лучше тренироваться на маленьких прямоугольниках из нескольких деталей.
Вот нарисовали варианты складывания прямоугольников из трех деталей.
www.baby.ru
| Пентамино. Логические игры. Головоломки. Ученик 5 класса Чекалин Илья Учитель математики: Басова Светлана Владимировна школа Интеграл Москва,2012г Цели и задачи работы • Рассказать о наиболее известных мировых головоломках, некоторым из которых более 4 000 лет. • Изучить задачи-головоломки • Провести анализ – зачем нужны головоломки и почему они так популярны до сих пор. ПЕНТАМИНО • “Пентамино” — одна из самых популярных мировых головоломок, пик популярности пришелся на конец 60-х годов. Сама игра подробно описывалась в журнале “Наука и жизнь”. • Запатентовал головоломку “Pentomino” Соломон Вольф Голомб, математик и инженер, профессор университета Южная Калифорния. • Игра состоит из плоских фигур, каждая из которых состоит из пяти одинаковых квадратов (пять – «пента»), отсюда и название. Существуют еще версия головоломок Тетрамино, состоящие из четырех квадратов, от этой игры и произошел известный компьютерный Тетрис. Элементы Пентамино • Игровой набор “Пентамино” состоит из 12 фигурок. Каждая фигура обозначается латинской буквой, форму которой она напоминает. При решении задач и головоломок фигурки можно вертеть и переворачивать. Задача : прямоугольники • Самая распространённая задача — сложить из всех фигурок прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Прямоугольники • Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20. Вариантов укладок прямоугольников множество, например, для прямоугольника 6х10 существует ровно 2339 различных способов. Задача об утроении фигур пентамино Эта задача была предложена профессором Калифорнийского университета Р.М.Робинсоном. • Выбрав одну из 12 фигур пентамино, необходимо построить из оставшихся фигуру, подобную выбранной, но в 3 раза бо́льшей длины и ширины. Решение существует для любого из 12 пентамино, причём не единственное. Головоломки : фигурки животных Компьютерные игры • С конца 1980-х годов неоднократно выходили различные компьютерные игры, основанные на пентамино. Наиболее известная — основанная на идее тетриса игра пентикс (Pentix). Один из новейших примеров — игра Dwice, которую разработал в 2006 году изобретатель Тетриса Алексей Пажитнов. Пентамино из Лего • Кстати, если у Вас дома много стандартных кирпичиков лего, то можно попробовать сделать пентамино их них. Фигурки сложенные из Лего получатся объемные, и можно будет собирать помимо обычных, плоскостных моделей, объемные фигуры. • Схема сборки достаточно простая: два ряда кирпичиков уложенные друг на друга со смещением. Выводы • Пентамино — это строительная игра, которая позволяет детям понять основы геометрии. • Пентамино — это множество головоломок с решениями, которые могут быть как очень простыми, так и экстремально сложными. Монгольская игра. Головоломка • Одна из древних классических головоломок • Головоломка представляет собой квадрат разрезанный на 11 частей: 2 квадрата, один большой прямоугольник, 4 маленьких прямоугольника, 4 треугольника. • Из элементов монгольской игры можно составить такие геометрические фигуры как ромб, трапецию, параллелограмм, прямоугольники и квадраты разного размера. Еще одна древняя игра-головоломка ТАНГРАМ • Одна из первых древних игр головоломок. Родина возникновения — Китай, возраст — более 4 000 лет. Танграм • Головоломка представляет собой квадрат разрезанный на 7 частей: 2 больших треугольника, один средний, 2 маленьких треугольника, квадрат и параллелограмм. • Суть игры — собирать всевозможные фигурки из данных элементов по принципу мозаики. Всего насчитывают более 7 000 различных комбинаций. Самые распространенные из них — фигуры животных и человека. ТАНГРАМ Жизнь в танграме • Головоломные идеи Головоломка придумана 4 000 лет тому назад, но мода на нее не проходит до сих пор. Самые современные дизайнеры используют идею складывания элементов танграма в своих модных коллекциях. • Танграм во всех его проявлениях можно встретить начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном. Самое удачное применение танграма, пожалуй в качестве мебели. Танграм • Полочки от дизайнеров по интерьерам — Lago. Выводы • Рассмотренные игры-головоломки способствуют развитию образного мышления, воображения, комбинаторных и аналитических способностей, а также умения визуально делить целое на части. |
kak.znate.ru
