Как правильно танграм или танграмм – Игра танграм: история китайской головоломки, правила, схемы, польза для детского развития

Танграм — Википедия. Что такое Танграм

Настольная версия танграм Фигурка человека

Танграм (кит.七巧板, пиньинь qī qiǎo bǎn, букв. «семь дощечек мастерства») — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга.

История

Танграм, возможно, ведёт своё происхождение от яньцзиту (燕几圖) — вида мебели, появившегося во времена империи Сун. Как мебель яньцзиту претерпела некоторые изменения за время правления династии Мин, а в дальнейшем превратилась в набор деревянных фигурок для игры.

Хотя танграм часто считают изобретением глубокой древности, первое печатное упоминание о нём встречается в китайской книге, изданной в 1813 году и написанной, очевидно, в правление императора Цзяцина.^[1]

Появление танграма на западе относят не ранее чем к началу XIX столетия, когда эти головоломки попали в Америку на китайских и американских судах. Старейший такой экземпляр, подаренный сыну американского судовладельца в 1802 году, сделан из слоновой кости и хранится в шёлковом футляре.^{[источник не указан 3041 день]}

Слово «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии».

Писатель и математик Льюис Кэрролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.

У Наполеона во время его изгнания на остров Святой Елены был набор для танграма и книга, содержащая задачи и решения. Фотографии этого набора содержатся в книге Джерри Слокума

The Tangram Book.^[2]

Книга Сэма Лойда «Восьмая книга Тан» (англ. The Eighth Book Of Tan), вышедшая в 1903 году, содержит вымышленную историю танграма, согласно которой эта головоломка была изобретена 4 тысячи лет назад божеством по имени Тан. Книга включает 700 задач, некоторые из которых неразрешимы.^[3]

Фигуры

Размеры приведены относительно большого квадрата, стороны и площадь которого принимают равными 1{\displaystyle \scriptstyle {1}}^[4].

Среди этих семи частей параллелограмм выделяется отсутствием у него зеркальной симметрии (он обладает только вращательной симметрией), так что его зеркальное отражение можно получить, только перевернув его. Это единственная часть танграма, которую требуется перевернуть, чтобы сложить определённые фигуры. При использовании одностороннего набора (в котором переворачивать фигуры запрещено) есть фигуры, которые можно сложить, в то время как их зеркальное отражение — нельзя.

Парадоксы

Парадокс танграма заключается в следующем: каждый раз полностью используя весь набор, можно сложить две фигуры, одна из которых будет подмножеством другой.^[5] Один такой случай приписывается Дьюдени: две похожие фигуры изображают монахов, но у одной из них при этом есть нога, а у другой фигуры её нет.^[6] Разрешение этого парадокса приводится во многих источниках, в том числе по ссылке^[5]. Решение состоит в том, что форма кажущихся одинаковыми частей фигур различается («безногая» фигура длиннее той, у которой есть нога), их площади также различаются ровно на площадь «ноги».

Другой парадокс предлагается Лойдом в «Восьмой книге Тан»:

Седьмая и восьмая фигуры изображают загадочный квадрат, составленный из семи частей. Затем угол квадрата срезали, но при этом всё равно используются те же семь частей.^[7]

Оригинальный текст (англ.)

The seventh and eighth figures represent the mysterious square, built with seven pieces: then with a corner clipped off, and still the same seven pieces employed.

Решение данного парадокса не приводится в книге Лойда. Другие неразрешённые задачи из этой книги обсуждаются по ссылке.^[8]

• Парадокс Дьюдени

• Парадокс Лойда

Подсчёт конфигураций

Ван Футрайн и Сюн Цюаньчжи (熊全治) доказали в 1942 году, что существуют только тринадцать выпуклых конфигураций танграма (таких, что отрезок прямой, проведённый между любыми двумя точками внешнего контура, пройдёт только через точки, заключённые внутри этого контура). ^[9][10][11]

Книга Рональда Рида «Танграм: 330 задач» (англ. Tangrams: 330 Puzzles) просит читателей присылать любые другие фигуры. Такое условие создаёт множество хотя и с гораздо большим числом элементов, чем множество выпуклых фигур, но всё же конечное.^[12]

В ответ было предложено приблизительно 6,13 миллиона возможных конфигураций,^[13] в каждой из которых при этом хотя бы одна вершина и хотя бы одна сторона любой части совпадают с вершиной и стороной другой части.

Педагогическое значение танграма

Способствует развитию у детей умения играть по правилам и выполнять инструкции, наглядно-образного мышления, воображения, внимания, понимания цвета, величины и формы, восприятия, комбинаторных способностей.

См. также

Примечания

1. ↑ Chen, Zhongying. Advances in computational mathematics: proceedings of the Guangzhou international symposium. — New York, N.Y : Marcel Dekker, 1999. — P. 466. — ISBN 0-8247-1946-8.
2. ↑ Jerry Slocum, Dieter Gebhardt, Jack Botermans, Monica Ma, Xiaohe Ma. The Tangram Book. — Sterling Publishing Company, 2003. — ISBN 1-4027-0413-5.
3. ↑ Costello, Matthew J. The Greatest Puzzles of All Time. — New York : Dover Publications, 1996. — ISBN 0-486-29225-8.
4. ↑ «Tangram» by Enrique Zeleny, Wolfram Demonstrations Project
5. ↑ ^{1 2} Tangram Paradox, by Barile, Margherita, From MathWorld — A Wolfram Web Resource, created by Eric W. Weisstein.
6. ↑ Dudeney, H. Amusements in Mathematics. — New York : Dover Publications, 1958.
7. ↑ Loyd, Sam. The eighth book of Tan — 700 Tangrams by Sam Loyd with an introduction and solutions by Peter Van Note. — New York : Dover Publications, 1968. — P. 25.
8. ↑ Unsolved Patterns by Sam Loyd, by Cocchini, Franco, From Tanzzle.com
9. ↑ (November 1942) «A Theorem on the Tangram». The American Mathematical Monthly 49 (9): 596–599. DOI:10.2307/2303340. Проверено 2009-02-06.
10. ↑ Read, Ronald C. Tangrams : 330 Puzzles. — New York : Dover Publications, 1965. — P. 53. — ISBN 0-486-21483-4.
11. ↑ А. Панов,. Загадка фигуры № 51 // Квант. — 1982. — № 12. — С. 34-37.
12. ↑
    Read, Ronald C. Tangrams : 330 Puzzles. — New York : Dover Publications, 1965. — P. 55. — ISBN 0-486-21483-4.
13. ↑ Cocchini, F. Ten Millions of Tangram Patterns. TangMath.

Литература

• Танграм // Занимательные головоломки. — Де Агостини, 2012. — № 5. — С. 13—16.

Ссылки

wiki.sc

Танграм: от истории к современности

Развитие современного общества не возможно без обращения к математическому подходу к окружающему миру, позволяющего познать его. Математические знания нужны сегодня всем — не только специалисту — математику, инженеру, учёному, но и врачу, рабочему, моряку или спортсмену, даже художнику и литератору. Особую актуальность в этой связи приобретают математические головоломки. Одной из таких головоломок, привлекших наше внимание является танграм.

Танграм — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. Наше исследование посвящено изучению возможностей применения танграма в современном мире, но полноценное исследование не возможно без обращения к истории вопроса. В связи с этим мы изучили историю возникновения танграма, которая носит довольно противоречивый характер и имеет различные версии.

Существует мнение, что история танграма насчитывает около 4000 лет. Местом где была изобретена игра несомненно является Китай. Дата создания определяется приблизительно 18 веком. Первой известной древней книгой по танграму является «Собрание фигур из семи частей» (Китай 1803 г). Издана она была на рисовой бумаге. Однако, это всеобщее заблуждение. Миф об этом создал С.Лойд, выпустивший в 1903 году книгу “Восьмая книга Тана”, в которой впервые опубликовал свою красивую версию о древнем происхождении игры. Каждая из семи книг о танграмах, насчитывает ровно тысячу фигур. Эти книги ныне стали очень большой редкостью. Одна из книг, напечатанная золотом на пергаменте, была обнаружена в Пекине английским солдатом, продавшим свою находку за 300 фунтов стерлингов одному собирателю китайской старины, который любезно предоставил некоторые наиболее изысканные фигурки для воспроизведения в этой книге. Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству [1].

Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа “инь и ян”. Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудие труда, мебель, одежда и архитектурные сооружения.

В Китае же название «Танграм» неизвестно, а игра имеет название «Ши-Чао-Тю» (семь хитроумных фигур).

Многие китайские ученые считают, что корни танграма восходят к династии Сун (960–1127), когда Хуан Боси (1079–1118) изобрел набор прямоугольных столов и схемы их расстановки на банкете (рисунок 1) [1].

Рис. 1. Схема расстановки набора прямоугольных столов на банкете

 

Во время династии Мин (1368–1644) в 1617 году Джи Шан описал расположение на банкете столов треугольной формы. Со временем, в середине династии Цин (1644–1911) столы на банкетах имели форму известных нам ныне семи частей танграма (рисунок 2).

Рис. 2. Столы формы семи частей танграма

 

В это же время появляется и головоломка «Танграм». Она пользовались большой популярностью во всех социальных слоях населения, в том числе и у императорской семьи. Головоломку начали производить и для продажи иностранным купцам. Старейший такой экземпляр, был куплен в Кантоне Робертом Валном (Robert Waln) в 1802 году. Головоломка сделана из слоновой кости. Она хранится в Ryerss Museum в Калифорнии. Хотя головоломка в Америке и Европе известна с 1802, самые ранние силуэты для сборки были опубликованы в 1813 в книге Би Ву Юши и Санг Ся Кэ (Bi Wu Jushi and Sang Xia Ke) «Сборник диаграмм танграма» (Compilation of Tangram Diagrams). В период с 1817 по 1818 год, книги о танграме были опубликованы в Англии, Франции, Швейцарии, Италии, Нидерландах, Дании, Германии и США (рисунок 3) [2].

Рис. 3. Книга Би Ву Юши и Санг Ся Кэ «Сборник диаграмм танграма»

 

В Оксфордском словаре английского языка название «Танграм» появляется с ссылкой на авторитетного Генри Э.Дьюдени, его версию принял составитель словаря Д. Мюррей. Он обнаружил, что слово «Танграм» впервые встречается в словаре Вебстерна издания 1864 г. По мнению Мюррея, само слово «Танграм» было придумано в середине прошлого столетия неким американцем, образовавшим неологизм из слова «тан», что означает на кантонском диалекте «китайский» и распространённого суффикса «грам» (как в словах анаграмма или килограмма).

Иная теория происхождения «Танграм» встречается в книге «Китайский философский и математический танграм» (1817 г.), где он трактуется как старинное английское слово, обозначающие «игрушка-головоломка» [3].

Писатель и математик Льюис Кэрролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.

Также в его книге «Модная китайская головоломка» приводятся сведения о том, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя своё терпение и находчивость». Упоминание о любимой игре Наполеона, скорее всего не соответствует действительности, однако, и нет обратных доказательств, что, в свою очередь, позволяет существовать такой красивой версии.

Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм, сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке.

Согласно еще одной из версий возникновения танграма, одним из первых научных трудов известных человечеству по решению задач на разрезание является трактат персидского астронома Абдул Вефа, жившего в десятом веке в Багдаде. Сохранились лишь отдельные части этой книги, и в том числе решение задачи как разрезать три одинаковых квадрата на 9 частей, из которых в дальнейшем возможно сложить один большой квадрат. В дальнейшем условие решение этой задачи с условием использования минимального количества элементов было сделано ранее упомянутым англичанином Генри Э.Дьюдени. Он решил задачу Абдул Вефа с использованием 6 элементов и это является минимальным решением в настоящее время. Энциклопедией решения различных задач на разрезание является книга Гарри Лингрена «Геометрия разрезаний», в которой можно найти рекорды по разрезанию многоугольников на заданные фигуры. При использовании треугольника, как базового элемента, многоугольники можно разрезать не следующие количество частей: квадрат-4, пятиугольник-6, шестиугольник-5, семиугольник-9, восьмиугольник-8, девятиугольник-9, десятиугольник-8, двенадцатиугольник-8 [3].

Таким образом, обращение к истории возникновения танграма позволяет заметить тот факт, что весьма уважаемые и умные люди относили такую совсем простую с виду игру к достойному самого пристального внимания способу развития интеллекта.

Как уже отмечалось ранее, наше исследование посвящено изучению возможностей применения танграма в современном мире.

Особую актуальность в последнее время приобретает использование танграма дизайнерами. Самое удачное применение танграма, пожалуй, в качестве мебели (рисунок 4,5).

Рис. 4. Применение танграм в мебели

 

Рис. 5. Трансформируемая мягкая мебель на основе танграм

 

Есть и столы-танграмы, и трансформируемая мягкая мебель, и корпусная мебель. Вся мебель, построенная по принципу танграма, довольно удобна и функциональна. Она может видоизменятся в зависимости от настроения и желания человека. Сколько всевозможных вариантов и комбинаций можно составить из треугольных, квадратных и четырехугольных полок. При покупке такой мебели вместе с инструкцией покупателю выдаются несколько листов с картинками на разные темы, которые можно сложить из этих полок. В гостиной можно повесить полки в виде людей, в детской из этих же полок можно сложить котов, зайцев и птиц, а в столовой или библиотеке — рисунок может быть на строительную тему — дома, замки, храмы (рисунок 6,7).

Рис. 6. Книжные полки танграм

 

Рис. 7. Книжные полки танграм

 

Интересен опыт дизайнера Даниэль Лаго, придумавшего книжные полки «Tangram» в виде танцующих человечков (рисунок 8). При этом он дает возможность пользователям самостоятельно придумывать композицию.

Рис. 8. Книжные полки «Tangram» в виде танцующих человечков

 

Другое направление примения танграм в мире мы находим в современных конструкциях зданий, в которых располагаются различные жилые объекты, офисы и т. д. (рисунок 9).

Рис. 9. Конструкции зданий на основе танграм

 

Так же на основе идеи танграм создаются различные инновационные проекты, одним из которых является проект города на воде, защищенного от землетрясений, котрый создали в дизайнерском бюро Танграм 3ДС после сокрушительных землетрясений в Чили и на Гаити (рисунок 10). Этому городу не страшны такие стихийные бедствия, при этом он защищен волнорезами от океанских волн и на его территории может произрастать достаточное для обеспечения жителей количество пищи.

Рис. 10. Проект города на воде на основе танграм

 

Таким образом, изучив историю возникновения головоломки «Танграм» и рассмотрев возможности применения данной головоломки в современном мире, мы пришли к выводу о том, что свое происхождение танграм ведет от мебели. Эти необычные предметы интерьера, носившие название «яньцзиту», со временем превратились в фигуры для игры. Отдавая дань истории, вместе со схемами для сборки танграма в современном мире существует множество иллюстраций как мебели, которую современные дизайнеры создали по принципу знаменитой головоломки, так и современных сооружений и конструкций, созданных на ее основе.

 

Литература:

 

1.                  Драко, М. В. Китайский танграм. Магический круг. Вьетнамская игра: Игры-головоломки. — Попурри, 2009. — 56 с.

2.                  Мациевский, С. В. Математическая культура. Игры: учебное пособие / С. В. Мациевский.— Калининград: Изд-во КГУ, 2003. — 120 с.

3.                  Шарыгин, И. Ф. Наглядная геометрия. 5–6 кл.: пособие для общеобразовательных учреждений / И. Ф. Шарыгин, Л. Н. Ерганжиева. — 13-е изд., стереотип. — М.: Дрофа, 2011. — 189 с.

4.                  Шарыгин, И. Ф. Математика: Задачи на смекалку: учеб. пособие для 5–6 кл. общеобразоват. учреждений / И. Ф. Шарыгин, А. В. Шевкин. — 5-е изд. — М.: Просвещение, 2000. — 95 с.

yun.moluch.ru

Танграм — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Танграм (кит.七巧板, пиньинь qī qiǎo bǎn, букв. «семь дощечек мастерства») — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга.

История

Танграм, возможно, ведёт своё происхождение от яньцзиту (燕几圖) — вида мебели, появившегося во времена империи Сун. Как мебель яньцзиту претерпела некоторые изменения за время правления династии Мин, а в дальнейшем превратилась в набор деревянных фигурок для игры.

Хотя танграм часто считают изобретением глубокой древности, первое печатное упоминание о нём встречается в китайской книге, изданной в 1813 году и написанной, очевидно, в правление императора Цзяцина.^[1]

Появление танграма на западе относят не ранее чем к началу XIX столетия, когда эти головоломки попали в Америку на китайских и американских судах. Старейший такой экземпляр, подаренный сыну американского судовладельца в 1802 году, сделан из слоновой кости и хранится в шёлковом футляре.К:Википедия:Статьи без источников (тип: не указан)^{[источник не указан 3151 день]}

Слово «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии».

Писатель и математик Льюис Кэрролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.

У Наполеона во время его изгнания на остров Святой Елены был набор для танграма и книга, содержащая задачи и решения. Фотографии этого набора содержатся в книге Джерри Слокума The Tangram Book.^[2]

Книга Сэма Лойда «Восьмая книга Тан» (англ. The Eighth Book Of Tan), вышедшая в 1903 году, содержит вымышленную историю танграма, согласно которой эта головоломка была изобретена 4 тысячи лет назад божеством по имени Тан. Книга включает 700 задач, некоторые из которых неразрешимы.^[3]

Фигуры

Размеры приведены относительно большого квадрата, стороны и площадь которого принимают равными <math>\scriptstyle{1}</math>^[4].

• 5 прямоугольных треугольников
  • 2 маленьких (с гипотенузой, равной <math>\scriptstyle{1/2}</math> и катетами <math>\scriptstyle{\sqrt{2}/4}</math>)
  • 1 средний (гипотенуза <math>\scriptstyle{1/\sqrt{2}}</math> и катеты <math>\scriptstyle{1/2}</math>)
  • 2 больших (гипотенуза <math>\scriptstyle{1}</math> и катеты <math>\scriptstyle{1/\sqrt{2}}</math>)
• 1 квадрат (со стороной <math>\scriptstyle{\sqrt{2}/4}</math>)
• 1 параллелограмм (со сторонами <math>\scriptstyle{1/2}</math> и <math>\scriptstyle{\sqrt{2}/4}</math> и углами <math>\scriptstyle{45^\circ}</math> и <math>\scriptstyle{135^\circ}</math>)

Среди этих семи частей параллелограмм выделяется отсутствием у него зеркальной симметрии (он обладает только вращательной симметрией), так что его зеркальное отражение можно получить, только перевернув его. Это единственная часть танграма, которую требуется перевернуть, чтобы сложить определённые фигуры. При использовании одностороннего набора (в котором переворачивать фигуры запрещено) есть фигуры, которые можно сложить, в то время как их зеркальное отражение — нельзя.

Парадоксы

Парадокс танграма заключается в следующем: каждый раз полностью используя весь набор, можно сложить две фигуры, одна из которых будет подмножеством другой.^[5] Один такой случай приписывается Дьюдени: две похожие фигуры изображают монахов, но у одной из них при этом есть нога, а у другой фигуры её нет.^[6] Разрешение этого парадокса приводится во многих источниках, в том числе по ссылке.^[5]

Другой парадокс предлагается Лойдом в «Восьмой книге Тан»:

Седьмая и восьмая фигуры изображают загадочный квадрат, составленный из семи частей. Затем угол квадрата срезали, но при этом всё равно используются те же семь частей.^[7]

Оригинальный текст (англ.)  

The seventh and eighth figures represent the mysterious square, built with seven pieces: then with a corner clipped off, and still the same seven pieces employed.

Решение данного парадокса не приводится в книге Лойда. Другие неразрешённые задачи из этой книги обсуждаются по ссылке.^[8]

• Monk1.GIF

  Парадокс Дьюдени

• Squares.GIF

  Парадокс Лойда

Подсчёт конфигураций

Ван Футрайн и Сюн Цюаньчжи (熊全治) доказали в 1942 году, что существуют только тринадцать выпуклых конфигураций танграма (таких, что отрезок прямой, проведённый между любыми двумя точками внешнего контура, пройдёт только через точки, заключённые внутри этого контура). ^[9][10][11]

Книга Рональда Рида «Танграм: 330 задач» (англ. Tangrams: 330 Puzzles) просит читателей присылать любые другие фигуры. Такое условие создаёт множество хотя и с гораздо большим числом элементов, чем множество выпуклых фигур, но всё же конечное.^[12]

В ответ было предложено приблизительно 6,13 миллиона возможных конфигураций,^[13] в каждой из которых при этом хотя бы одна вершина и хотя бы одна сторона любой части совпадают с вершиной и стороной другой части.

Педагогическое значение танграма

Способствует развитию у детей умения играть по правилам и выполнять инструкции, наглядно-образного мышления, воображения, внимания, понимания цвета, величины и формы, восприятия, комбинаторных способностей.

См. также

Напишите отзыв о статье «Танграм»

Примечания

1. ↑ Chen, Zhongying. Advances in computational mathematics: proceedings of the Guangzhou international symposium. — New York, N.Y: Marcel Dekker, 1999. — P. 466. — ISBN 0-8247-1946-8.
2. ↑ Jerry Slocum, Dieter Gebhardt, Jack Botermans, Monica Ma, Xiaohe Ma. The Tangram Book. — Sterling Publishing Company, 2003. — ISBN 1-4027-0413-5.
3. ↑ Costello, Matthew J. The Greatest Puzzles of All Time. — New York: Dover Publications, 1996. — ISBN 0-486-29225-8.
4. ↑ «[demonstrations.wolfram.com/Tangram/ Tangram]» by Enrique Zeleny, Wolfram Demonstrations Project
5. ↑ ^{1 2} [mathworld.wolfram.com/TangramParadox.html Tangram Paradox], by Barile, Margherita, From MathWorld — A Wolfram Web Resource, created by Eric W. Weisstein.
6. ↑ Dudeney, H. Amusements in Mathematics. — New York: Dover Publications, 1958.
7. ↑ Loyd, Sam. The eighth book of Tan — 700 Tangrams by Sam Loyd with an introduction and solutions by Peter Van Note. — New York: Dover Publications, 1968. — P. 25.
8. ↑ [www.tanzzle.com/loyd.html Unsolved Patterns by Sam Loyd], by Cocchini, Franco, From Tanzzle.com
9. ↑ (November 1942) «[www.jstor.org/stable/2303340 A Theorem on the Tangram]». The American Mathematical Monthly 49 (9): 596–599. DOI:10.2307/2303340. Проверено 2009-02-06.
10. ↑ Read, Ronald C. Tangrams : 330 Puzzles. — New York: Dover Publications, 1965. — P. 53. — ISBN 0-486-21483-4.
11. ↑ А. Панов, [kvant.mccme.ru/1982/12/p34.htm Загадка фигуры № 51] // Квант. — 1982. — № 12. — С. 34-37.
12. ↑ Read, Ronald C. Tangrams : 330 Puzzles. — New York: Dover Publications, 1965. — P. 55. — ISBN 0-486-21483-4.
13. ↑ Cocchini, F. Ten Millions of Tangram Patterns. [www.tanzzle.com/tangmath/BillionPatterns.htm TangMath].

Литература

• Танграм // Занимательные головоломки. — Де Агостини, 2012. — № 5. — С. 13—16.

Ссылки

• [www.juegotangram.com.ar The Tangram]
• [pecesjocdetangr.sourceforge.net/ Танграм]
• [tangram.op-team.ru/ Танграм онлайн]
• [www.banjen.com/Pythagoras.aspx Pythagoras puzzle (Tangram)]

Отрывок, характеризующий Танграм

Принимая все более и более мелкие единицы движения, мы только приближаемся к решению вопроса, но никогда не достигаем его. Только допустив бесконечно малую величину и восходящую от нее прогрессию до одной десятой и взяв сумму этой геометрической прогрессии, мы достигаем решения вопроса. Новая отрасль математики, достигнув искусства обращаться с бесконечно малыми величинами, и в других более сложных вопросах движения дает теперь ответы на вопросы, казавшиеся неразрешимыми.
Эта новая, неизвестная древним, отрасль математики, при рассмотрении вопросов движения, допуская бесконечно малые величины, то есть такие, при которых восстановляется главное условие движения (абсолютная непрерывность), тем самым исправляет ту неизбежную ошибку, которую ум человеческий не может не делать, рассматривая вместо непрерывного движения отдельные единицы движения.
В отыскании законов исторического движения происходит совершенно то же.
Движение человечества, вытекая из бесчисленного количества людских произволов, совершается непрерывно.
Постижение законов этого движения есть цель истории. Но для того, чтобы постигнуть законы непрерывного движения суммы всех произволов людей, ум человеческий допускает произвольные, прерывные единицы. Первый прием истории состоит в том, чтобы, взяв произвольный ряд непрерывных событий, рассматривать его отдельно от других, тогда как нет и не может быть начала никакого события, а всегда одно событие непрерывно вытекает из другого. Второй прием состоит в том, чтобы рассматривать действие одного человека, царя, полководца, как сумму произволов людей, тогда как сумма произволов людских никогда не выражается в деятельности одного исторического лица.
Историческая наука в движении своем постоянно принимает все меньшие и меньшие единицы для рассмотрения и этим путем стремится приблизиться к истине. Но как ни мелки единицы, которые принимает история, мы чувствуем, что допущение единицы, отделенной от другой, допущение начала какого нибудь явления и допущение того, что произволы всех людей выражаются в действиях одного исторического лица, ложны сами в себе.
Всякий вывод истории, без малейшего усилия со стороны критики, распадается, как прах, ничего не оставляя за собой, только вследствие того, что критика избирает за предмет наблюдения большую или меньшую прерывную единицу; на что она всегда имеет право, так как взятая историческая единица всегда произвольна.
Только допустив бесконечно малую единицу для наблюдения – дифференциал истории, то есть однородные влечения людей, и достигнув искусства интегрировать (брать суммы этих бесконечно малых), мы можем надеяться на постигновение законов истории.
Первые пятнадцать лет XIX столетия в Европе представляют необыкновенное движение миллионов людей. Люди оставляют свои обычные занятия, стремятся с одной стороны Европы в другую, грабят, убивают один другого, торжествуют и отчаиваются, и весь ход жизни на несколько лет изменяется и представляет усиленное движение, которое сначала идет возрастая, потом ослабевая. Какая причина этого движения или по каким законам происходило оно? – спрашивает ум человеческий.
Историки, отвечая на этот вопрос, излагают нам деяния и речи нескольких десятков людей в одном из зданий города Парижа, называя эти деяния и речи словом революция; потом дают подробную биографию Наполеона и некоторых сочувственных и враждебных ему лиц, рассказывают о влиянии одних из этих лиц на другие и говорят: вот отчего произошло это движение, и вот законы его.
Но ум человеческий не только отказывается верить в это объяснение, но прямо говорит, что прием объяснения не верен, потому что при этом объяснении слабейшее явление принимается за причину сильнейшего. Сумма людских произволов сделала и революцию и Наполеона, и только сумма этих произволов терпела их и уничтожила.
«Но всякий раз, когда были завоевания, были завоеватели; всякий раз, когда делались перевороты в государстве, были великие люди», – говорит история. Действительно, всякий раз, когда являлись завоеватели, были и войны, отвечает ум человеческий, но это не доказывает, чтобы завоеватели были причинами войн и чтобы возможно было найти законы войны в личной деятельности одного человека. Всякий раз, когда я, глядя на свои часы, вижу, что стрелка подошла к десяти, я слышу, что в соседней церкви начинается благовест, но из того, что всякий раз, что стрелка приходит на десять часов тогда, как начинается благовест, я не имею права заключить, что положение стрелки есть причина движения колоколов.
Всякий раз, как я вижу движение паровоза, я слышу звук свиста, вижу открытие клапана и движение колес; но из этого я не имею права заключить, что свист и движение колес суть причины движения паровоза.
Крестьяне говорят, что поздней весной дует холодный ветер, потому что почка дуба развертывается, и действительно, всякую весну дует холодный ветер, когда развертывается дуб. Но хотя причина дующего при развертыванье дуба холодного ветра мне неизвестна, я не могу согласиться с крестьянами в том, что причина холодного ветра есть раэвертыванье почки дуба, потому только, что сила ветра находится вне влияний почки. Я вижу только совпадение тех условий, которые бывают во всяком жизненном явлении, и вижу, что, сколько бы и как бы подробно я ни наблюдал стрелку часов, клапан и колеса паровоза и почку дуба, я не узнаю причину благовеста, движения паровоза и весеннего ветра. Для этого я должен изменить совершенно свою точку наблюдения и изучать законы движения пара, колокола и ветра. То же должна сделать история. И попытки этого уже были сделаны.
Для изучения законов истории мы должны изменить совершенно предмет наблюдения, оставить в покое царей, министров и генералов, а изучать однородные, бесконечно малые элементы, которые руководят массами. Никто не может сказать, насколько дано человеку достигнуть этим путем понимания законов истории; но очевидно, что на этом пути только лежит возможность уловления исторических законов и что на этом пути не положено еще умом человеческим одной миллионной доли тех усилий, которые положены историками на описание деяний различных царей, полководцев и министров и на изложение своих соображений по случаю этих деяний.

Силы двунадесяти языков Европы ворвались в Россию. Русское войско и население отступают, избегая столкновения, до Смоленска и от Смоленска до Бородина. Французское войско с постоянно увеличивающеюся силой стремительности несется к Москве, к цели своего движения. Сила стремительности его, приближаясь к цели, увеличивается подобно увеличению быстроты падающего тела по мере приближения его к земле. Назади тысяча верст голодной, враждебной страны; впереди десятки верст, отделяющие от цели. Это чувствует всякий солдат наполеоновской армии, и нашествие надвигается само собой, по одной силе стремительности.
В русском войске по мере отступления все более и более разгорается дух озлобления против врага: отступая назад, оно сосредоточивается и нарастает. Под Бородиным происходит столкновение. Ни то, ни другое войско не распадаются, но русское войско непосредственно после столкновения отступает так же необходимо, как необходимо откатывается шар, столкнувшись с другим, с большей стремительностью несущимся на него шаром; и так же необходимо (хотя и потерявший всю свою силу в столкновении) стремительно разбежавшийся шар нашествия прокатывается еще некоторое пространство.

wiki-org.ru

«Танграм» (исследовательская работа 5-6 класс)

ОКРУЖНАЯ НАУЧНАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ

СЕКЦИЯ “МАТЕМАТИКА”

ТАНГРАММ.

Автор:

Обыдённова Екатерина,

учащаяся 5 класса

ГБОУ СОШ п. Коммунарский

Научный руководитель:

Бурухина О.Ф. учитель математики

п. Коммунарский, 2014 г.

Содержание.

Введение……………………………………………………………….3 стр.

1. Историческая справка о танграме……………………………………………………………4 стр.

2. Значение танграма в жизни человека……………………………………………………………6 стр.

3. Площадь и свойства площадей с использованием танграма……8 стр

4. Математика и танграм нашем современном мире…………………………………………………………………9 стр.

Заключение…………………………………………………………….10стр.

Список источников информации…………………………………………………………….11стр.

Приложение…………………………………………………………….12 стр.

ВВЕДЕНИЕ.

Наш современный мир переполнен техническими новинками, наш быт модернизирован, роботы-«люди» научились думать и решать, а порой заменяют самих людей. Мир вокруг становится техническим, а душевная теплота уходит постепенно в небытиё.

Порой в самом простом можно найти необычное и увлекательное, даже в обыкновенной игре.

Несколько лет назад я познакомилась с волшебным игрой Танграм. Слово ТАНГРАМ в переводе с китайского 七巧板, пиньинь qī qiǎo bǎn, буквально «семь дощечек мастерства» — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). В процесс знакомства и овладения техникой складывания фигурки танграма у меня возникли вопросы: Как танграм может помочь в изучении математики? В решении логических и занимательных математических задач?

Цель: изучить взаимосвязь танграма – древней китайской игры-головоломки и математики, точной науки.

Гипотеза:

Танграм, даёт возможность, правильно понимать и решать математические задачи, связанные с измерением площадей, несложных геометрических фигур.

Задачи: на 2013-2014 уч.год

• Найти, изучить и отобрать информацию по теме.

• Изучить историю происхождения традиционной китайской игры-головоломки – ТАНГРАМ.

• Пробудить одноклассников интерес к танграму и занимательной математике.

• Оформить исследовательскую работу и подготовить презентацию.

на 2014-2015 уч.год:

• Продолжить изучение информации по теме.

• Пробудить интерес к танграму и занимательной математике учащихся 2,3 и 5 классов.

• Проведение соревнований по собиранию из танграма фигурок, между одноклассниками и классами нашей школы.

• Оформить исследовательскую работу и подготовить презентацию.

Объект исследования: танграм.

Методы исследования:

• Изучение литературы и сведений и различных информационных источников.

• Наблюдение.

• Обработка полученных данных.

• Нахождение площадей простейших фигур, с использованием танграма.

• Анкетирование учащихся и учителей.(приложение №3)

• Анализ и обобщение информации по теме.

История танграма

О названии Танграм

В Китае название Танграм неизвестно, а игра имеет название Ши-Чао-Тю (семь хитроумных фигур).
В Оксфордском словаре английского языка — название Танграм появляется с ссылкой на авторитетного Генри Э.Дьюдени, его версию принял составитель словаря Д.Мюррей. Он обнаружил, что слово танграм впервые встречается в словаре Вебстера издания 1864 г. По мнению в Мюррея, само слово танграм было придумано в середине прошлого столетия неким американцем, образовавшим неологизм из слова Тан, что означает на кантонском диалекте китайский, и распространенного суффикса -грам (как в словах анаграмма или криптограмма). Иная теория происхождения слова танграм была выдвинута Питером Ван Ноутом в предисловии к новому изданию книги Ллойда: китайские семьи, живущие на лодках, называются танка, тан по-китайски означает — падшая женщина. Американские моряки, покупавшие головоломку у девушек — танка, могли назвать ее танграмом — головоломкой доступных девушек. В книге «Китайский философский и математический транграм» (1817 г.) слово транграм — трактуется, как старинное английское слово — обозначающие игрушка головоломка.

Миф создания

Существует целый ряд версий и гипотез возникновения игры “Танграм”.

1) Наиболее распространенной и известной является та, что игра “Танграм” насчитывает около 4000 лет. Такую дату можно прочитать у Кордемского Б.А. или Котова А.Я., а так же у различных иностранных авторов. Мнение о танграме, как о самой древней головоломке является весьма распространенным. Однако, это всеобщее заблуждение. Миф об этом создал С.Лойд. В 1903 году он выпустил книгу “Восьмая книга Тана”, в которой впервые опубликовал свою красивую версию о древнем происхождение игры. Это и по настоящее время один из величайших розыгрышей в мире головоломок.

2) Местом где была изобретена игра, несомненно является Китай. Дата создания может быть определенна приблизительно XVIII век. Первой известной древней книгой по танграму является “Собрание фигур из семи частей” (Китай 1803 г.). Издана она была на рисовой бумаге. Книги, изданные в Европе, были лишь отчасти оригинальны, а в своей основе имели китайские источники.

“В записках покойного профессора Челленора, попавших в руки автора, — утверждал Лойд, — имеются сведения о том, что семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур, были составлены в Китае более 4000 лет назад. Эти книги ныне стали столь большой редкостью, что за те сорок лет, которые профессор Челленор провел в Китае, ему лишь раз удалось видеть первое издание первого из семи томов (сохранившихся полностью) и несколько разрозненных фрагмента второго тома.

В этой книге связи уместно напомнить, что части одной из книг, напечатанной золотом на пергаменте, были обнаружены в Пекине английским солдатом, продавшим свою находку за 300 фунтов стерлингов одному собирателю китайской старины, который любезно предоставил некоторые наиболее изысканные фигурки для воспроизведения в этой книге”.

Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа “инь и ян”. Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудию труда, мебель, одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция, философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить. Встречаются у Лойда и ссылки на “известные” китайские пословицы типа “Только глупец взялся бы написать восьмую книгу Тана”.

Знаменитые люди и танграм

Льюис Кэрролл

Все мы хорошо знаем книгу «Алиса в стране чудес» Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге «Модная китайская головоломка» он пишет, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость». Упоминание о любимой игре Наполеона, скорее всего не соответствует действительности, однако, и нет обратных доказательств, что, в свою очередь, позволяет существовать и такой красивой версии.

Эдгар А. По

Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке.

Роберт ван Гулик
Известный писатель и дипломат Роберт ван Гулик в романе «Убивающие ногтями» построил весь сюжет книги вокруг танграма.

Абдул — Вефа
Одним из первых научных трудов известных человечеству по решению задач на разрезание является трактат Абдул Вефа. Он являлся персидским астрономом. Жил в десятом веке в Багдаде. Сохранились лишь отдельные части этой книги и в том числе решение задачи как разрезать три одинаковых квадрата на 9 частей из которых в дальнейшем возможно сложить один большой квадрат. В дальнейшем решение этой задачи с условием использования минимального количества элементов было сделано англичанином Генри Э. Дьюдени. Он решил задачу Абдул Вефа с использованием 6 элементов, и это является минимальным решением на настоящее время.

Гарри Линдгрен
Энциклопедией решения различных задач на разрезание является книга Гарри Линдгрена «Геометрия разрезаний». В этой книге можно найти рекорды по разрезанию многоугольников на заданные фигуры. При использовании треугольника как базового элемента — многоугольники можно разрезать на следующие количество частей:
квадрат — 4
пятиугольник — 6
шестиугольник — 5
семиугольник — 9
восьмиугольник — 8
девятиугольник — 9
десятиугольник — 8
двенадцатиугольник — 8

Рассматривая решения задач на разрезание понимаешь, что универсального алгоритма или метода не существует. Иногда начинающий геометр в своем решении может значительно превзойти более опытного человека. Это простота и доступность является основой популярности игр основанных на решении таких задач. Сразу на ум приходит пример — тетрис.

Площадь и свойства площадей с использованием танграма.

Изучая тему в 5 классе «Площадь. Свойсва площадей.» Можно чётко проследить данное понятие на примере «Танграма». Собрав квадрат, становиться ясно, что измерение части занимаемой той или иной фигурой, удобно осуществлять квадратом, с заданной единицой длины стороны квадрата. Свойства площадей: 1.Равные фигуры имеют равные площади. С помощью наложения треугольников в танграме это хорошо просматривается. Треугольник аbd = треугольнику adh,

g Треугольник hfi= треугольнику dgc.

2.Чтобы найти площадь сложной фигуры надо найти сумму всех площадей входящих в неё фигур. В танграмме, площадь фигуры cbeg= площадь треуголника cgd+ площадь треугольника hti, а так как пплощадт этих треугольников равны, то площадь четырёхугольника cbeg=2 площадям треугольника cgd.Площадь треугольника iej=2площадям cgd.Таким образом площадь четырёхугольника cbeg=площади треугольника iej.

Вывод: Действительно тема площадей и свойств площадей прекрасно иллюстрируется танграмом .

Значение оригами в жизни человека.

Пазлы
Игрой внешне близкой танграму являются пазлы. В начале пазлы являлись большим набором фигур неправильной формы из которых необходимо было сложить картинку — задание. Несмотря на эту схожесть — танграм, задача противоположная, так как семь базовых элементов позволяет значительное множество фигур, а в случае пазла мы ограничены только одним решением.
Сравнительный анализ танграма с другими аналогичными играми был сделан Р.Ридом в книге «Танграмы: 330 головоломок». Для игры танграм основным требованием к человеку является логическое мышление и геометрическая интуиция, а для игры пазл — все-таки всего лишь усидчивость и терпение.

Розыгрыш Дьюдени
В своей книге «Математические развлечения» он приводит вымышленную историю о том, как один американский корреспондент приобрел набор перламутровых танов китайской работы, к которому прилагалось отпечатанная на рисовой бумаге брошюра, содержавшая более 300-х фигур. Корреспондента заинтересовал таинственный иероглиф на титульном листе, но все китайцы, к которым он обращался с просьбой объяснить, что означает этот знак, не хотели или не могли ничем ему помочь. Он воспроизвел иероглиф в своей книге и обратился к читателям за помощью. Мы знаем, что ответили Дьюдени его современники, но Рид, у которого была та же брошюра, без труда разгадал загадку. Иероглиф был просто надписью под танграмом, изображавшим двух человек. Надпись гласила — два человека лицом друг к другу пьют чай. Эта картинка свидетельствовала о больших возможностях, таящихся в игре танграм.

Танграм. Новые идеи и возможности головоломки

 

Головоломные идеи
Головоломка придумана 4 000 лет тому назад, но мода на нее не проходит до сих пор. Самые современные дизайнеры используют идею складывания элементов танграма в своих модных коллекциях.

Танграм во всех его проявлениях можно встретить начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном. Самое удачное применение танграма, пожалуй в качестве мебели. Есть и столы танграмы и трансформируемая мягкая мебель и знаменитые настенные полки фирмы Lago.

 

 

Вся мебель построенная по принципу танграма очень удобна и функциональна. Каждый раз она может видоизменятся в зависимости от настроения и желания хозяина. Интересный вариант трансформируемых диванов дизайнера Julien Bernard. Эта модель была представленна на выставке в Милане в 2009 году.

  Самая известная коллекция мебели в стиле танграм у дизайнеров по интерьерам — конечно, Lago. Сколько всевозможных вариантов и комбинаций можно составить из этих симпатичных полочек. Сами производители выпустили вместе с инструкцией по сборке несколько страниц с идеями для библиотеки, гостиной, спальни и детской.

 Заключение

1.Танграм способствует развитию у детей:

• умения играть по правилам и выполнять инструкции,

• умения наглядно-образно мыслить, воображать, вниманию,

• понимания цвета, величины и формы,

восприятия, комбинаторных способностей.

2. Тема площадей и свойств площадей прекрасно иллюстрируется танграмом .

ИСТОЧНИКИ ИНФОРМАЦИИ

Приложение №1

Приложение №2

Приложение №3

Учащихся — 2, 3, 5 и 6 классов- 42человека, взрослых -16 человек.

1. 1. Вы знаете, что такое танграм?

   2. Вы играли в эту головоломку?

   3. Вам понравилась эта игра?

1 2 3

Вопрос ы

infourok.ru

Что такое танграм? Как сделать танграм своими руками?

Танграм

Это восточная головоломка, которая состоит из 7 плоских фигур, получающихся при разрезании квадрата определённым образом.

Вот названия этих фигур:

• 2 больших треугольника.

• 1 средний треугольник.

• 2 маленьких треугольника.

• 1 квадрат.

• 1 параллелограмм.

Цель — сложить эти части друг с другом таким образом, чтобы получилась какая-либо сложная фигура (человек, животное и т.п.).

Обязательно должны быть использованы все 7 фигур танграма, их можно переворачивать как угодно. Фигуры должны примыкать друг к другу и не перекрываться (то есть накладываться друг на друга).

Танграм развивает следующие навыки и качества:

• Логическое мышление.

• Усидчивость.

• Воображение.

• Комбинаторские способности.

• Внимательность.

• Понимание цвета, формы, величины.

---

Делаем танграм своими руками

Танграм можно сделать из различных материалов — подойдут обычная бумага, цветной картон, фотобумага, пластик, дерево…

Но слишком тонкую бумагу брать не стоит.

Здесь главное — это построить квадрат определённых размеров и разделить его определённым образом на 7 частей.

Я расскажу об одном из самых простых вариантов — танграме из обычной офисной бумаги или фотобумаги.

Чтобы сделать танграм нам понадобятся:

• 1 лист бумаги / фотобумаги.

• простой карандаш.

• ножницы.

• линейка.

• цветные карандаши (для раскрашивания фигурок).

Пошаговое описание:

1) Сначала нужно начертить квадрат определённых размеров. Пусть это будет 21 на 21 сантиметр.

2) В квадрате проводим диагональ — тем самым мы разобьём его на 2 больших треугольника.

3) Найдём середины двух сторон у одного из больших треугольников (21 см / 2 = 10,5 см) и соединим их отрезком. Если говорить геометрическими терминами — построим среднюю линию треугольника.

4) У нас получился маленький прямоугольный треугольник, нужно отметить середину его самой большой стороны (гипотенузы).

Теперь проводим большую линию от правого верхнего угла к отмеченной точке (она является частью диагонали нашего квадрата).

Эта линия должна пройти через середину стороны большого треугольника — в результате он разобьётся на 2 маленьких.

5) Находим середину стороны у первого из получившихся треугольников и отмечаем точку.

Эту точку соединяем с вершиной нижнего треугольника. В результате получим квадрат и маленький треугольник.

6) Находим середину у второго большого треугольника и соединяем её с серединой гипотенузы нижнего треугольника.

Получим ещё один маленький треугольник и параллелограмм.

7) Вырезаем получившееся фигуры, и танграм будет готов.

Остаётся раскрасить все фигуры с обеих сторон цветными карандашами или, например, восковыми мелками.

Если вы хотите, чтобы каждая фигура имела свой цвет, то можно обойтись и без раскрашивания. Возьмите соответствующий лист толстого цветного картона и обведите на нём фигурку, а затем вырежете.

**

На данный момент можно найти множество готовых схем (шаблонов) для танграма.

При этом существуют схемы, где все фигурки уже на месте, а есть просто образцы-контуры.

В качестве примера приведу несколько схем, позволяющих собрать животных:

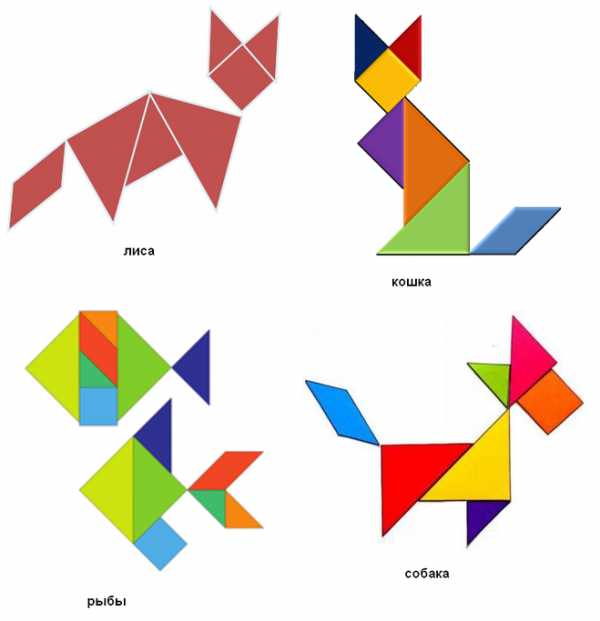
Если вы хотите найти большое количество различных схем, то это можно сделать, например, на этом развивающем сайте.

В частности, на этой странице вышеупомянутого сайта содержатся 60 различных шаблонов животных.

А здесь можно найти схемы животных и некоторых других предметов.

www.bolshoyvopros.ru

История создания — Нешарнирные головоломки

Танграм

История

Танграм, возможно, ведёт своё происхождение от яньцзиту (燕几圖) — вида мебели, появившегося во времена империи Сун. Как мебель яньцзиту претерпела некоторые изменения за время правления династии Мин, а в дальнейшем превратилась в набор деревянных фигурок для игры.

Хотя танграм часто считают изобретением глубокой древности, первое печатное упоминание о нём встречается в китайской книге, изданной в 1813 году и написанной, очевидно, в правление императора Цзяцина.

Появление танграма на западе относят не ранее чем к началу XIX столетия, когда эти головоломки попали в Америку на китайских и американских судах. Старейший такой экземпляр, подаренный сыну американского судовладельца в 1802 году, сделан из слоновой кости и хранится в шёлковом футляре.

Слово «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии».

Писатель и математик Льюис Кэрролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.

У Наполеона во время его изгнания на остров Святой Елены был набор для танграма и книга, содержащая задачи и решения. Фотографии этого набора содержатся в книге Джерри Слокума The Tangram Book.

Книга Сэма Лойда «Восьмая книга Тан» (англ. The Eighth Book Of Tan), вышедшая в 1903 году, содержит вымышленную историю танграма, согласно которой эта головоломка была изобретена 4 тысячи лет назад божеством по имени Тан. Книга включает 700 задач, некоторые из которых неразрешимы.

Парадоксы

Парадокс танграма заключается в следующем: каждый раз полностью используя весь набор, можно сложить две фигуры, одна из которых будет подмножеством другой. Один такой случай приписывается Дьюдени: две похожие фигуры изображают монахов, но у одной из них при этом есть нога, а у другой фигуры её нет. Разрешение этого парадокса приводится во многих источниках, в том числе по ссылке.

Другой парадокс предлагается Лойдом в «Восьмой книге Тан»: Седьмая и восьмая фигуры изображают загадочный квадрат, составленный из семи частей. Затем угол квадрата срезали, но при этом всё равно используются те же семь частей.

Подсчёт конфигураций

Ван Футрайн и Сюн Цюаньчжи (熊全治) доказали в 1942 году, что существуют только тринадцать выпуклых конфигураций танграма (таких, что отрезок прямой, проведённый между любыми двумя точками внешнего контура, пройдёт только через точки, заключённые внутри этого контура).

Книга Рональда Рида «Танграм: 330 задач» (англ. Tangrams: 330 Puzzles) просит читателей присылать любые другие фигуры. Такое условие создаёт множество хотя и с гораздо большим числом элементов, чем множество выпуклых фигур, но всё же конечное.

В ответ было предложено приблизительно 6,13 миллиона возможных конфигураций, в каждой из которых при этом хотя бы одна вершина и хотя бы одна сторона любой части совпадают с вершиной и стороной другой части.

Местом где была изобретена игра несомненно является Китай. Дата создания может быть определенна приблизительно 18 век. Первой известной древней книгой по танграму является «Собрание фигур из семи частей» (Китай 1803 г.). Издана она была на рисовой бумаге. Книги изданные в Европе были лишь отчасти оригинальны, а в своей основе имели китайские источники.

Все мы хорошо знаем книгу «Алиса в стране чудес» Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге «Модная китайская головоломка» он пишет, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость». Упоминание о любимой игре Наполеона, скорее всего не соответствует действительности, однако, и нет обратных доказательств, что, в свою очередь, позволяет существовать и такой красивой версии.

Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке.

Известный писатель и дипломат Роберт ван Гулик в романе «Убивающие ногтями» построил весь сюжет книги вокруг танграма.

Одним из первых научных трудов известных человечеству по решению задач на разрезание является трактат Абдул Вефа. Он являлся персидским астрономом. Жил в десятом веке в Багдаде. Сохранились лишь отдельные части этой книги и в том числе решение задачи как разрезать три одинаковых квадрата на 9 частей из которых в дальнейшем возможно сложить один большой квадрат. В дальнейшем решение этой задачи с условием использования минимального количества элементов было сделано англичанином Генри Э. Дьюдени. Он решил задачу Абдул Вефа с использованием 6 элементов, и это является минимальным решение на настоящие время.

Энциклопедией решения различных задач на разрезание является книга Гарри Линдгрена «Геометрия разрезаний». В этой книге можно найти рекорды по разрезанию многоугольников на заданные фигуры. При использовании треугольника как базового элемента — многоугольники можно разрезать на следующие количество частей:

квадрат — 4

пятиугольник — 6

шестиугольник — 5

семиугольник — 9

восьмиугольник — 8

девятиугольник — 9

десятиугольник — 8

двенадцатиугольник — 8

Рассматривая решения задач на разрезание понимаешь, что универсального алгоритма или метода не существует. Иногда начинающий геометр в своем решении может значительно превзойти более опытного человека. Это простота и доступность является основой популярности игр основанных на решении таких задач. сразу на ум приходит пример — тетрис.

Пазлы

Игрой внешне близкой танграму являются пазлы. В начале пазлы являлись большим набором фигур неправильной формы из которых необходимо было сложить картинку — задание. Несмотря на эту схожесть — танграм, задача противоположная, так как семь базовых элементов позволяет значительное множество фигур, а в случае пазла мы ограничены только одним решением.

Сравнительный анализ танграма с другими аналогичными играми был сделан Р.Ридом в книге «Танграмы: 330 головоломок». Для игры танграм основным требованием к человеку является логическое мышление и геометрическая интуиция, а для игры пазл — все-таки всего лишь усидчивость и терпение.

Миф создания

Существует целый ряд версий и гипотез возникновения игры танграм. Наиболее распространенной и известной является та, что игра танграм насчитывает около 4000 лет. Такую дату можно прочитать у Кордемского Б.А. или Котова А.Я., а так же у различных иностранных авторов. Мнение о танграме, как о самой древней головоломке является весьма распространенным. Однако, это всеобщее заблуждение. Миф о этом создал С.Лойд. В 1903 году он выпустил книгу «Восьмая книга Тана» в которой впервые опубликовал свою красивую версию о древнем происхождение игры. Это и по настоящее время один из величайших розыгрышей в мире головоломок.

О названии Танграм

В Китае название Танграм неизвестно, а игра имеет название Ши-Чао-Тю (семь хитроумных фигур). В Оксфордском словаре английского языка — название Танграм появляется с ссылкой на авторитетного Генри Э.Дьюдени, его версию принял составитель словаря Д.Мюррей. Он обнаружил, что слово танграм впервые встречается в словаре Вебстера издания 1864 г. По мнению в Мюррея, само слово танграм было придумано в середине прошлого столетия неким американцем, образовавшим неологизм из слова Тан, что означает на кантонском диалекте китайский, и распространенного суффикса -грам (как в словах анаграмма или криптограмма). Иная теория происхождения слова танграм была выдвинута Питером Ван Ноутом в предисловии к новому изданию книги Ллойда: китайские семьи, живущие на лодках, называются танка, тан по-китайски означает — падшая женщина. Американские моряки, покупавшие головоломку у девушек — танка, могли назвать ее танграмом — головоломкой доступных девушек. В книге «Китайский философский и математический транграм» (1817 г.) слово транграм — трактуется, как старинное английское слово — обозначающие игрушка головоломка.

Розыгрыш Дьюдени

В своей книге «Математические развлечения» он приводит вымышленную историю о том, как один американский корреспондент приобрел набор перламутровых танов китайской работы, к которому прилагалось отпечатанная на рисовой бумаге брошюра, содержавшая более 300-х фигур. Корреспондента заинтересовал таинственный иероглиф на титульном листе, но все китайцы, к которым он обращался с просьбой объяснить, что означает этот знак, не хотели или не могли ничем ему помочь. Он воспроизвел иероглиф в своей книге и обратился к читателям за помощью. Мы знаем, что ответили Дьюдени его современники, но Рид, у которого была та же брошюра, без труда разгадал загадку. Иероглиф был просто надписью под танграмом, изображавшим двух человек. Надпись гласила — два человека лицом друг к другу пьют чай. Эта картинка свидетельствовала о больших возможностях, таящихся в игре танграм.

nontwistypuzzles.ru

История танграм

Местом где была изобретена игра несомненно является Китай. Дата создания может быть определенна приблизительно 18 век. Первой известной древней книгой по танграму является «Собрание фигур из семи частей» (Китай 1803 г.). Издана она была на рисовой бумаге. Книги изданные в Европе были лишь отчасти оригинальны, а в своей основе имели китайские источники.

Льюис Кэрролл

Все мы хорошо знаем книгу «Алиса в стране чудес» Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге «Модная китайская головоломка» он пишет, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость». Упоминание о любимой игре Наполеона, скорее всего не соответствует действительности, однако, и нет обратных доказательств, что, в свою очередь, позволяет существовать и такой красивой версии.

Эдгар А. По

Танграм — сердце

Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке.
Известный писатель и дипломат Роберт ван Гулик в романе «Убивающие ногтями» построил весь сюжет книги вокруг танграма.

Абдул — Вефа
Одним из первых научных трудов известных человечеству по решению задач на разрезание является трактат Абдул Вефа. Он являлся персидским астрономом. Жил в десятом веке в Багдаде. Сохранились лишь отдельные части этой книги и в том числе решение задачи как разрезать три одинаковых квадрата на 9 частей из которых в дальнейшем возможно сложить один большой квадрат. В дальнейшем решение этой задачи с условием использования минимального количества элементов было сделано англичанином Генри Э. Дьюдени. Он решил задачу Абдул Вефа с использованием 6 элементов, и это является минимальным решение на настоящие время.

Линдгрен
Энциклопедией решения различных задач на разрезание является книга Гарри Линдгрена «Геометрия разрезаний». В этой книге можно найти рекорды по разрезанию многоугольников на заданные фигуры. При использовании треугольника как базового элемента — многоугольники можно разрезать на следующие количество частей:
квадрат — 4
пятиугольник — 6
шестиугольник — 5
семиугольник — 9
восьмиугольник — 8
девятиугольник — 9
десятиугольник — 8
двенадцатиугольник — 8

Рассматривая решения задач на разрезание понимаешь, что универсального алгоритма или метода не существует. Иногда начинающий геометр в своем решении может значительно превзойти более опытного человека. Это простота и доступность является основой популярности игр основанных на решении таких задач. сразу на ум приходит пример — тетрис.

Пазлы
Игрой внешне близкой танграму являются пазлы. В начале пазлы являлись большим набором фигур неправильной формы из которых необходимо было сложить картинку — задание. Несмотря на эту схожесть — танграм, задача противоположная, так как семь базовых элементов позволяет значительное множество фигур, а в случае пазла мы ограничены только одним решением.
Сравнительный анализ танграма с другими аналогичными играми был сделан Р.Ридом в книге «Танграмы: 330 головоломок». Для игры танграм основным требованием к человеку является логическое мышление и геометрическая интуиция, а для игры пазл — все-таки всего лишь усидчивость и терпение.

Миф создания
Существует целый ряд версий и гипотез возникновения игры танграм. Наиболее распространенной и известной является та, что игра танграм насчитывает около 4000 лет. Такую дату можно прочитать у Кордемского Б.А. или Котова А.Я., а так же у различных иностранных авторов. Мнение о танграме, как о самой древней головоломке является весьма распространенным. Однако, это всеобщее заблуждение. Миф о этом создал С.Лойд. В 1903 году он выпустил книгу «Восьмая книга Тана» в которой впервые опубликовал свою красивую версию о древнем происхождение игры. Это и по настоящее время один из величайших розыгрышей в мире головоломок.

О названии Танграм
В Китае название Танграм неизвестно, а игра имеет название Ши-Чао-Тю (семь хитроумных фигур).
В Оксфордском словаре английского языка — название Танграм появляется с ссылкой на авторитетного Генри Э.Дьюдени, его версию принял составитель словаря Д.Мюррей. Он обнаружил, что слово танграм впервые встречается в словаре Вебстера издания 1864 г. По мнению в Мюррея, само слово танграм было придумано в середине прошлого столетия неким американцем, образовавшим неологизм из слова Тан, что означает на кантонском диалекте китайский, и распространенного суффикса -грам (как в словах анаграмма или криптограмма). Иная теория происхождения слова танграм была выдвинута Питером Ван Ноутом в предисловии к новому изданию книги Ллойда: китайские семьи, живущие на лодках, называются танка, тан по-китайски означает — падшая женщина. Американские моряки, покупавшие головоломку у девушек — танка, могли назвать ее танграмом — головоломкой доступных девушек. В книге «Китайский философский и математический транграм» (1817 г.) слово транграм — трактуется, как старинное английское слово — обозначающие игрушка головоломка.

Розыгрыш Дьюдени
В своей книге «Математические развлечения» он приводит вымышленную историю о том, как один американский корреспондент приобрел набор перламутровых танов китайской работы, к которому прилагалось отпечатанная на рисовой бумаге брошюра, содержавшая более 300-х фигур. Корреспондента заинтересовал таинственный иероглиф на титульном листе, но все китайцы, к которым он обращался с просьбой объяснить, что означает этот знак, не хотели или не могли ничем ему помочь. Он воспроизвел иероглиф в своей книге и обратился к читателям за помощью. Мы знаем, что ответили Дьюдени его современники, но Рид, у которого была та же брошюра, без труда разгадал загадку. Иероглиф был просто надписью под танграмом, изображавшим двух человек. Надпись гласила — два человека лицом друг к другу пьют чай. Эта картинка свидетельствовала о больших возможностях, таящихся в игре танграм.

взято с www.axel.nm.ru

Купить головоломку можно в магазине, например, тут my-shop.ru или тут ozon.ru

ipuzzles.ru