Исследовательская работа «Математический бильярд» | Социальная сеть работников образования
Дистанционный конкурс творческих и исследовательских работ младщих школьников «Страна чудес — страна исследований» | |
Полное название темы работы | Как бильярд помогает решать математические задачи? |
Фамилия имя,отчество автора(ов) | Шаманов Максим Петрович |
Фото автор | |
Территория, населенный пункт | д. Тинская Саянского района Красноярского края |
Наименование образовательного учреждения | Муниципальное казенное общеобразовательное учреждение Тинская основная общеобразовательная школа |
Класс | 5 класс |
Место выполнения работы | Образовательная программа |
Руководитель e-mail (обязательно) Контактный телефон | Рулькевич Галина Ивановна, МКОУ Тинская ООШ, учитель +7 9039238834 |
ВВЕДЕНИЕ
Цель: исследовать возможности применения теории математического бильярда для решения задач на переливание жидкости.
Задачи: познакомиться с историей математического бильярда
изучить применение метода для решения задач с двумя и тремя сосудами
исследовать вопрос о разрешимости задач на переливание
найти в литературе и решить задачи на переливание, имеющие практическую направленность.
Актуальность: задачи на переливание часто встречаются в олимпиадах; их решение способствует развитию логического мышления, любознательности и творческих способностей.
Гипотеза: используя метод математического бильярда, можно решить любую задачу на переливание с двумя или тремя сосудами, или доказать, что такое переливание невозможно
Мой любимый школьный предмет – математика. Я с большим удовольствием участвую в различных олимпиадах по этому предмету, люблю решать логические задачи. Я обратил внимание, что среди занимательных задач по математике большое место занимают так называемые задачи на переливание, суть которых сводится к следующему: имеется несколько сосудов известного объема. Нужно указать последовательность действий, при которой отмеряется требуемое количество жидкости, и выполнены все условия задачи. Если не сказано ничего другого, считается, что: все сосуды без делений; нельзя переливать жидкости «на глаз»; переливать можно только полностью всю жидкость, или столько, сколько вмещается в другой сосуд;
Рассмотрим решение одной из таких задач: Можно ли, имея лишь два сосуда емкостью 3 и 5 л, набрать из водопроводного крана 4 л воды?
1 шаг: наполним водой первый сосуд;
2 шаг: перельём из первого сосуда во второй 3 л. В первом остается 2 л.
3 шаг: из второго сосуда выльем эти 3 л обратно в раковину;
4 шаг: 2 л воды из первого сосуда перельём во второй;
5 шаг: вновь наполним первый сосуд водой. Теперь в первом сосуде 5 л, а во втором — 2л;
6 шаг: перельем из первого сосуда 1 л воды во второй, наполнив его до краёв. В первом сосуде осталось 4 л воды — задача решена. Все шаги по переливаию удобно записывать в виде таблицы (табл.1).
Эту задачу я решил подбором. Но понятно, что если увеличить объем сосудов, ее решение становится затруднительным. Поэтому логично найти общий метод решения задач данного типа. Оказывается, такой метод существует. Он заключается в использовании математического бильярда.
ГЛАВА I. ИСТОРИЯ МАТЕМАТИЧЕСКОГО БИЛЬЯРДА
Билья́рд, реже биллиард (от фр.bille — шар или billette, billart — палка) — собирательное название нескольких настольных игр с разными правилами, а также специальный стол, на котором происходит игра.
Всем знакома игра бильярд за прямоугольным столом с лузами. Точное время ее появления установить невозможно. Известно лишь, что она, так же, как и шахматы, очень древнего происхождения, а родиной бильярда является Азия, по утверждению одних исследователей — Индия, по мнению других — Китай. В Европе первые упоминание о нем имеется в английских летописях VI века. В Россию бильярд был завезен из Голландии Петром I. и быстро завоевал популярность. Подобно тому, как азартная игра в кости вызвала к жизни «исчисление» вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. Идея применения этой теории к задачам на переливание очень красиво и даже эффектно описана Перельманом книге «Занимательная геометрия».
ГЛАВА II. ЗАДАЧИ С ДВУМЯ СОСУДАМИ И так, что же это такое — математический бильярд? Начнем с того, что стол для него, как уже было сказано выше, отличается от обычного. Математический бильярдный стол — не прямоугольник, а параллелограмм с углами 60 и 120 градусов (рис 1). Стороны параллелограмма должны выражаться числами, равными числу единиц объема наших сосудов. Весь стол расчерчен параллельными прямыми на равносторонние треугольники. Бильярдный шар может Рис.1 перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль линии сетки, выходящей из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов. Рассмотрим на примере уже знакомой нам задачи, какие прекрасные возможности представляет этот метод. Задача 1. Имеются два сосуда – трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 4 литра воды. В нашем распоряжении по-прежнему, водопроводный кран и раковина, куда можно выливать воду. Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом. (рис.1). Будем следить за движением шарика и расщифровывать каждую точку его удара о борт стола. Первая точка удара (5; 0) (рис.2), это значит, что мы должны наполнить водой больший сосуд. Вторая точка удара (2; 3)- она говорит о том, что шарик рекомендует нам из 5-литрового сосуда 3 литра перелить в меньший. Следующая точка удара имеет координаты (2;0). Это означает, шарик советует из меньшего сосуда вылить всю воду. Будем дальше следить за шариком и заполнять таблицу (табл. 2). Мы увидим, что после 7 переливаний наша цель достигнута: в 5-литровом сосуде получено 4 литра воды (рис. 5)
Рис.2 Рис. 3 Рис. 4 Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды за 7 шагов. Шарик решил задачу!
Рис. 5
Задача 2. Можно ли, имея в распоряжении сосуды 3 и 5 л, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды? Чтобы ответить на этот вопрос продолжим следить за движением нашего «умного шарика» и записывать все шаги, пока не придем в одну из угловых точек, или в точку на стороне параллелограмма, в которой шарик уже побывал. И на столе (рис.6), и в таблице (табл.3) видно, что можно получить любое количество жидкости от 1 до 8 л за 15 ходов .
Рис. 6. Табл. 3
Задача 3. Выясним теперь, можно ли было решить эту задачу, наполнив сначала трехлитровый сосуд? Выполним переливание (рис. 7), заполним и проанализируем таблицу (табл. 4).
Рис.7 Табл. 4
Как видим, задачи на переливание можно решать двумя способами: I.начать переливания с большего сосуда; II.начать переливания с меньшего сосуда. Какой из способов более рационален (т.е. каким способом мы быстрее получим нужное количество жидкости) зависит от условий задачи. Изначально это определить нельзя. Например, 4 литра можно получить в первом случае за 6 ходов, а во втором — за 8, а вот 6 литров мы получим уже на 4 шаге, если начнем переливание с 3-х литрового сосуда .
Задача 4 Возникает вопрос — а всякая ли задача такого типа имеет решение? Оказывается, нет. Например, имея сосуды объемом 6 и 3 литра, невозможно набрать 4 л воды, и наш умный шарик это легко обнаружит (это видно из рисунка 8). Уже на 5 шаге он оказался в углу бильярдного стола, из которого начал движение, а это значит, что никаких других вариантов по переливанию мы получить не сможем. Рис. 8 Так произошло потому, что объемы наших сосудов выражены числами, общий делитель которых отличен от 1. Значит, задача имеет решение, если объемы сосудов выражаются взаимно-простыми числами.
ГЛАВА III. ЗАДАЧИ С ТРЕМЯ СОСУДАМИ А теперь рассмотрим задачи на переливания, по условиям которых используются три сосуда, один из них заполнен жидкостью, а два других пустые. В задачах такого типа появляются дополнительные условия: выливать жидкость вне сосуда нельзя; наливать жидкость извне нельзя. В качестве примера рассмотрим самую старинную головоломку с тремя сосудами, известную еще математикам XVII века:
Задача 1. Восьмилитровый сосуд до краев наполнен водой. С помощью двух пустых сосудов емкостью 3 и 5 литров надо поровну разделить воду в два больших сосуда. Решение. Для решения этой задачи точно так же используем параллелограмм со сторонами 5 и 3 единицы. Чтобы фиксировать количество воды в третьем, восьмилитровом сосуде, дополнительно проведем главную диагональ параллелограмма (рис.9). Она делится наклонными прямыми на 8 частей. Пронумеруем эти точки числами от 8 до 0, начиная с нижней левой вершины. Первые две координаты любой точки параллелограмма, куда может попасть бильярдный шар, определяются, как и раньше, а третья координата равна величине отрезка, отсекаемого на главной диагонали соответствующей наклонной. Как и раньше, шар начинает движение от точки с координатами (0;0). Нарисовав траекторию шара, получим решение задачи за 8 шагов (табл. 5).
шаг | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
5 л | 0 | 5 | 2 | 2 | 0 | 5 | 4 | 4 |
3 л | 0 | 0 | 3 | 0 | 2 | 2 | 3 | 0 |
8 л | 8 | 3 | 3 | 6 | 6 | 1 | 1 | 4 |
Табл. 5 Рис. 9
В этой задаче объем большего сосуда равен сумме объемов двух меньших. Но, разумеется, могут быть и другие случаи, когда объем большего сосуда меньше или больше этой суммы. Метод математического бильярда применим и для них, но с дополнительными условиями. Задача 2. Имеется 11-литровый сосуд, наполненный водой и два пустых сосуда емкостью 3 и 5 литров. Как с помощью этих сосудов отлить 4 л воды?
Решение. Так как. 11 > 3 + 5, главную диагональ необходимо продлить за вершину параллелограмма Но шарик за границы нашего стола все равно не выходит, потому что при любом переливании в 11-литровом сосуде остается, как минимум, 3 литр воды Рис. 10 (11 — (5 + 3) = 3). И тогда решение выглядит следующим образом (рис.10):
. Задача 3. Имеется 6-литровый сосуд, наполненный водой и два пустых сосуда емкостью 3 и 5 литров. Как с помощью этих сосудов отлить 4 л воды? Решение. На диагонали, выражающей количество воды в третьем сосуде, должно быть отложено 6 единиц. Поэтому у параллелограмма надо отсечь верхний правый угол и продолжать следить за движением шарика (рис.11).
Рис. 11
Осталось рассмотреть вопрос о разрешимости задач с тремя сосудами. Как и в случае с двумя сосудами, если объемы двух меньших сосудов выражаются взаимно простыми числами, а объем третьего сосуда больше или равен сумме объемов двух меньших, то с помощью этих трех сосудов можно отмерить любое целое число литров, начиная с 1 литра и кончая объемом среднего сосуда. Имея, например, сосуды вместимостью 7, 8 и 15 литров, можно отмерить любое количество воды от 1 до 8 литров. Когда объем большего сосуда меньше суммы объемов двух других, задача может оказаться неразрешимой, даже если объемы двух меньших сосудов не имеют общего делителя. Например, если объемы сосудов равны 7, 9 и 12 литров, то отмерить можно любое количество воды, кроме 6 литров. Но любой вопрос о разрешимости задач такого типа легко решается, если следить за движением «умного» шарика на математическом бильярдном столе.
ЗАКЛЮЧЕННИЕ
1. Изучая литературу по истории математического бильярда, мы выяснили, что с момента появления в Европе эта азартная игра послужила предметом серьезных научных исследований, в результате которых появилась теория математического бильярда или теории траекторий
2. Теория математического бильярда нашла прекрасное применение для решения задач на переливание.
3. Используя метод математического бильярда, можно легко выяснить, имеет ли задача решение.
4. В большинстве книг по занимательной математике и среди олимпиадных задач большое место занимают задачи на переливание, многие из которых я решил, используя метод математического бильярда. В своем предположении я убедился. Используя метод математического бильярда, можно решить любую задачу на переливание или убедиться, что это не возможно. Задачи на переливание действительно часто встречаются на олимпиадах, их решение способствует культурному и интеллектуальному развитию, помогает развитию памяти, внимания, логического мышления, любознательности и творческих способностей. Именно с решением одной из сложных задач о переливаниях связывают раскрытие математических способностей выдающегося французского математика Симеона Дени Пуассона. Говорят, что эта задача сыграла решающую роль в выборе профессии. Однажды, знакомый принес юному Пуассону несколько задач на переливание, разного уровня сложности. Пуассон решил их менее чем за час, определив тем самым выбор своей будущей профессии – он стал математиком. А одна из самых известных задач подобного рода носит его имя (я ее также решил)
Список литературы
1. Мартин Гарднер. Математические досуги. Под редакцией Я. А. Смородинского. Перевод с английского Ю А. Данилова. Издательство «Мир», Масква, 1972
2. Я.И. Перельман. Занимательная Геометрия, издание одиннадцатое, стереотипное, под ред. И с дополнениями Б.А. Кордемского, государственное издательство физико-математической литературы. Москва, 1959(Я.И.Перельман.,Занимательная геометрия М.: ГИФМЛ, 1959, с.238) 3.https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BB%D1%8C%D1%8%D1%80%D0%B4 4. Ф.Ф. Нагибин, Е.С. Канин, Математическая шкатулка Москва, «Просвещение», 1984, с.160
5. Е.И. Игнатьев В царстве смекалки Москва, «Наука» ГРФМЛ, 1987, с176
nsportal.ru
Презентация по математике «Исследовательская работа на тему «Математический бильярд

Математический бильярд- бильярд для любителей?
Автор работы:
Ковалева Ирина Сергеевна.
9 «А» класс МОБУ СОШ № 35.
Научный руководитель:
Сизько Ирина Сергеевна, учитель математики
МОБУ СОШ № 35.

БИЛЬЯРД
- интереснейшая интеллектуальная игра и в то же время прекрасный вид спорта, который вырабатывает у человека такие важные качества характера,
как психологическая устойчивость,
выдержка, умение сосредоточиться .

Актуальность исследования –
популярность игры в бильярд и применение метода математического бильярда в процессе игры.

Цель исследования —
изучить и выявить на практике действие законов математического бильярда.

Задачи исследовательской работы :
1. Изучить понятие «бильярд в круге»;
2. Ознакомиться с теоремой Якоби, а именно, с ее применение к теории чисел;
3. Проанализировать теорему Пуанкаре о возвращении;
4. Изучить метод математического бильярда;
5. Опытным путём доказать или опровергнуть, что метод математического бильярда действительно возможен для применения его на практике.

Бильярд — в круге
Простейшая ограниченная выпуклая область с криволинейной границей на плоскости — круг.
Проблема бильярда в круге поддается полному исследованию.

Шар в круглом бильярде без луз
Рассмотрим шар в круге Q , ограниченном окружностью Г . Его траекториями являются вписанные в Г ломаные Po, Р1, Р2, Р3, Р4 .., обладающие свойством равенства в точках, Р1,Р2,Р3 .. углов падения и отражения, отсчитываемых от касательных или от радиусов. Из этого свойства следует, во-первых, что все звенья траектории равны между собой равны ; и во-вторых, что равны опирающиеся на них центральные углы.

Шар в круглом бильярде без луз
Шар в круглом бильярде без луз
Свойство:
любая бильярдная траектория в круге никогда не заходит внутрь некоторого концентрического круга, границы которого касаются всех ее звеньев.

Шар в круглом бильярде без луз
Получается, что вид бильярдной траектории в круге определяется числом α . А именно:
(а) если число α соизмеримо с π , т. е. α/ π является рациональным числом, то бильярдная траектория периодична;
(б) если α и π несоизмеримы, т. е. число иррационально, то отвечающая углу α траектория непериодична.

Теорема Якоби. Применение к теории чисел
Теорема 1. Если α и π несоизмеримы (т.е. число α / π иррационально), то любая траектория бильярда в круге, отвечающая углу α (т.е. каждое звено которой из центра круга под углом α ), всюду плотно заполняет кольцо К.
Теорема Якоби . Пусть α — несоизмеримое с π число
{Ро, Р1,Р2, …}= {Рк} — бесконечная последовательность точек окружности Г такая, что каждая следующая точка последовательности Рк+1 получается
из предыдущей точки {Рк} поворотом около
Тогда для любой дуги треугольника
окружности Г хотя бы одна точка
последовательности {Рк} лежит на этой дуге.

Теорема Якоби. Применение к теории чисел
Доказательство теоремы Якоби. Пусть — произвольная дуга на окружности Г , е – ее радиальная мера. Выберем такое натуральное число N , что 2π/N е . Разобьем окружность Г на N равных по длине дуг 1 , 2 ,…, N ; радианная мера каждой из них равна 2π/N и меньше е .

Теорема Пункуаре о возвращении
Появление теоремы Пункуаре о возвращении было связано с развитием классической механики, которая на рубеже XX века приобрела завершенный характер благодаря многочисленным выдающимся математическим работам как самого Анри Пункуаре, так и других математиков.
 0. Более того, почти все точки области U возвращается снова в U – объем невозвращающихся в U точек равен нулю. «
0. Более того, почти все точки области U возвращается снова в U – объем невозвращающихся в U точек равен нулю. «
Теорема Пункуаре о возвращении
Пусть Т – сохраняющее объемы взаимно однозначное преобразование пространства, переводящее ограниченную область D пространства в себя: Т (D)=D. Тогда в любой сколь угодно малой окрестности U внутри D найдется точка x, которая после нескольких применений к ней преобразования Т снова возвращается в область U при некотором n 0. Более того, почти все точки области U возвращается снова в
U – объем невозвращающихся в U точек равен нулю.

Теорема Пункуаре о возвращении
Пусть y- произвольная точка пересечения областей T и U, где n=k-l. Так как каждая точка области T получается из некоторой точки области U в результате действия преобразования и точка y, лежащая вT, получается из некоторой точки x области U таким же способом: y= T n (x). Но точка y одновременно лежит в области U. Следовательно, точка x через n
шагов вернулась опять в область
U.

Метод математического бильярда
Впервые о математическом базисе бильярдной игры заговорил известный физик Гаспар Густав Кориолис в своей книге «Математическая теория явлений бильярдной игры» 1835-го года. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа.

Результаты исследований математиков Штайнхауза и Гарднера.
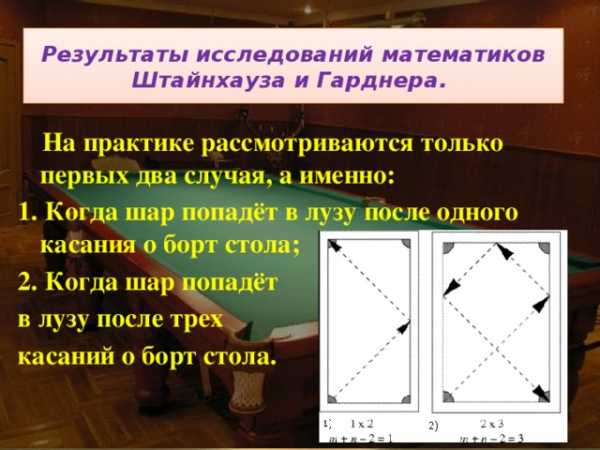
Для этого должен быть прямоугольный бильярдный стол с одними лишь угловыми лузами и целочисленными сторонами m и n (m, n — взаимно просты и обозначают ширину и длину бильярдного стола ). Шар, посланный из одной угловой лузы в другую под углом 45 градусов попадёт в другую лузу после m+n-2 касаний борта.
Результаты исследований математиков Штайнхауза и Гарднера.
На практике рассмотриваются только первых два случая, а именно:
1. Когда шар попадёт в лузу после одного касания о борт стола;
2. Когда шар попадёт
в лузу после трех
касаний о борт стола.

Применение математического бильярда
на практике
Законы о преломлении и отражении лучей из курса физики дают возможность проверить теорию математического бильярда.

Применение математического бильярда
на практике
Вместо бильярдного стола — небольшие коробочки соответствующих размеров исследований Штайнхауса и Гарднера. Вместо шара — обычный лазер и лазерный луч, отражавшийся от зеркал, т.к. зеркало- то место, где лазерный луч, т.е. шар должен касаться о борт стола. Зеркала должны стоять ровно перпендикулярно к коробочке.

Случай № 1
Случай № 2

Применение математического бильярда
на практике
Опираясь на данное правило и результат Штайнхауса и Гарднера, было определено, что действительно лазерный луч, т.е. шар, посланный из одной угловой лузы в другую под углом 45 градусов, попадёт в другую лузу после m+n-2 попаданий в зеркало, т.е. касаний о борт стола (коробочки).

Выводы
1. Метод математического бильярда возможен,
требует повышенного внимания и точных расчетов приложенной силы удара и необходим для игроков;
2. Применение рассмотренных теорем и следствий позволяют повысить уровень игры;
3. Игра в бильярд интересна, но сложна и не допускает погрешностей.

Благодарю за внимание!!!
videouroki.net
Математический бильярд
Математический бильярд
Акбаева А.А. 11Муниципальное казенное общеобразовательное учреждение «Средняя общеобразовательная школа аул Верхний Учкулан»
Джамбаева Ф.Н. 11Муниципальное казенное общеобразовательное учреждение «Средняя общеобразовательная школа аул Верхний Учкулан»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Цель: исследовать возможности применения теории математического бильярда для решения задач на переливание жидкости.
Задачи: познакомиться с историей математического бильярда
изучить применение метода для решения задач с двумя и тремя сосудами
исследовать вопрос о разрешимости задач на переливание
найти в литературе и решить задачи на переливание, имеющие практическую направленность.
Актуальность: задачи на переливание часто встречаются в олимпиадах; их решение способствует развитию логического мышления, любознательности и творческих способностей.
Гипотеза: используя метод математического бильярда, можно решить любую задачу на переливание с двумя или тремя сосудами, или доказать, что такое переливание невозможно
Мой любимый школьный предмет – математика. Я с большим удовольствием участвую в различных олимпиадах по этому предмету, люблю решать логические задачи. Я обратил внимание, что среди занимательных задач по математике большое место занимают так называемые задачи на переливание, суть которых сводится к следующему: имеется несколько сосудов известного объема. Нужно указать последовательность действий, при которой отмеряется требуемое количество жидкости, и выполнены все условия задачи. Если не сказано ничего другого, считается, что: все сосуды без делений; нельзя переливать жидкости «на глаз»; переливать можно только полностью всю жидкость, или столько, сколько вмещается в другой сосуд;
Рассмотрим решение одной из таких задач: Можно ли, имея лишь два сосуда емкостью 3 и 5 л, набрать из водопроводного крана 4 л воды?
1 шаг: наполним водой первый сосуд;
2 шаг: перельём из первого сосуда во второй 3 л. В первом остается 2 л.
3 шаг: из второго сосуда выльем эти 3 л обратно в раковину;
4 шаг: 2 л воды из первого сосуда перельём во второй;
5 шаг: вновь наполним первый сосуд водой. Теперь в первом сосуде 5 л, а во втором — 2л;
6 шаг: перельем из первого сосуда 1 л воды во второй, наполнив его до краёв. В первом сосуде осталось 4 л воды — задача решена. Все шаги по переливаию удобно записывать в виде таблицы (табл.1).
Табл. 1
Эту задачу я решил подбором. Но понятно, что если увеличить объем сосудов, ее решение становится затруднительным. Поэтому логично найти общий метод решения задач данного типа. Оказывается, такой метод существует. Он заключается в использовании математического бильярда.
1.ИСТОРИЯ МАТЕМАТИЧЕСКОГО БИЛЬЯРДА
Билья́рд, реже биллиард (от фр.bille — шар или billette, billart — палка) — собирательное название нескольких настольных игр с разными правилами, а также специальный стол, на котором происходит игра.
Всем знакома игра бильярд за прямоугольным столом с лузами. Точное время ее появления установить невозможно. Известно лишь, что она, так же, как и шахматы, очень древнего происхождения, а родиной бильярда является Азия, по утверждению одних исследователей — Индия, по мнению других — Китай. В Европе первые упоминание о нем имеется в английских летописях VI века. В Россию бильярд был завезен из Голландии Петром I. и быстро завоевал популярность. Подобно тому, как азартная игра в кости вызвала к жизни «исчисление» вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. Идея применения этой теории к задачам на переливание очень красиво и даже эффектно описана Перельманом книге «Занимательная геометрия».
1.ЗАДАЧИ С ДВУМЯ СОСУДАМИ
И так, что же это такое — математический бильярд? Начнем с того, что стол для него, как уже было сказано выше, отличается от обычного. Математический бильярдный стол — не прямоугольник, а параллелограмм с углами 60 и 120 градусов (рис 1). Стороны параллелограмма должны выражаться числами, равными числу единиц объема наших сосудов. Весь стол расчерчен параллельными прямыми на равносторонние треугольники. Бильярдный шар может Рис.1 перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль линии сетки, выходящей из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов. Рассмотрим на примере уже знакомой нам задачи, какие прекрасные возможности представляет этот метод. З адача 1. Имеются два сосуда – трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 4 литра воды. В нашем распоряжении по-прежнему, водопроводный кран и раковина, куда можно выливать воду. Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом. (рис.1). Будем следить за движением шарика и расщифровывать каждую точку его удара о борт стола. Первая точка удара (5; 0) (рис.2), это значит, что мы должны наполнить водой больший сосуд. Вторая точка удара (2; 3)- она говорит о том, что шарик рекомендует нам из 5-литрового сосуда 3 литра перелить в меньший. Следующая точка удара имеет координаты (2;0). Это означает, шарик советует из меньшего сосуда вылить всю воду. Будем дальше следить за шариком и заполнять таблицу (табл. 2). Мы увидим, что после 7 переливаний наша цель достигнута: в 5-литровом сосуде получено 4 литра воды (рис. 5)
Рис.2 Рис. 3 Рис. 4 Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды за 7 шагов. Шарик решил задачу!
Табл. 2
Рис. 5
З
адача 2.Можно ли, имея в распоряжении сосуды 3 и 5 л, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды? Чтобы ответить на этот вопрос продолжим следить за движением нашего «умного шарика» и записывать все шаги, пока не придем в одну из угловых точек, или в точку на стороне параллелограмма, в которой шарик уже побывал. И на столе (рис.6), и в таблице (табл.3) видно, что можно получить любое количество жидкости от 1 до 8 л за 15 ходов .
Рис. 6. Табл. 3
Задача 3. Выясним теперь, можно ли было решить эту задачу, наполнив сначала трехлитровый сосуд? Выполним переливание (рис. 7), заполним и проанализируем таблицу (табл. 4).
Рис.7 Табл. 4
Как видим, задачи на переливание можно решать двумя способами: I.начать переливания с большего сосуда; II.начать переливания с меньшего сосуда. Какой из способов более рационален (т.е. каким способом мы быстрее получим нужное количество жидкости) зависит от условий задачи. Изначально это определить нельзя. Например, 4 литра можно получить в первом случае за 6 ходов, а во втором — за 8, а вот 6 литров мы получим уже на 4 шаге, если начнем переливание с 3-х литрового сосуда .
Задача 4 Возникает вопрос — а всякая ли задача такого типа имеет решение? Оказывается, нет. Например, имея сосуды объемом 6 и 3 литра, невозможно набрать 4 л воды, и наш умный шари к это легко обнаружит (это видно из рисунка 8). Уже на 5 шаге он оказался в углу бильярдного стола, из которого начал движение, а это значит, что никаких других вариантов по переливанию мы получить не сможем. Рис. 8 Так произошло потому, что объемы наших сосудов выражены числами, общий делитель которых отличен от 1. Значит, задача имеет решение, если объемы сосудов выражаются взаимно-простыми числами.
ЗАДАЧИ С ТРЕМЯ СОСУДАМИ
А теперь рассмотрим задачи на переливания, по условиям которых используются три сосуда, один из них заполнен жидкостью, а два других пустые. В задачах такого типа появляются дополнительные условия: выливать жидкость вне сосуда нельзя; наливать жидкость извне нельзя. В качестве примера рассмотрим самую старинную головоломку с тремя сосудами, известную еще математикам XVII века:
Задача 1. Восьмилитровый сосуд до краев наполнен водой. С помощью двух пустых сосудов емкостью 3 и 5 литров надо поровну разделить воду в два больших сосуда. Решение.Для решения этой задачи точно так же используем параллелограмм со сторонами 5 и 3 единицы. Чтобы фиксировать количество воды в третьем, восьмилитровом сосуде, дополнительно проведем главную диагональ параллелограмма (рис.9). Она делится наклонными прямыми на 8 частей. Пронумеруем эти точки числами от 8 до 0, начиная с нижней левой вершины. Первые две координаты любой точки параллелограмма, куда может попасть бильярдный шар, определяются, как и раньше, а третья координата равна величине отрезка, отсекаемого на главной диагонали соответствующей наклонной. Как и раньше, шар начинает движение от точки с координатами (0;0). Нарисовав траекторию шара, получим решение задачи за 8 шагов (табл. 5).
|
шаг |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
5 л |
0 |
5 |
2 |
2 |
0 |
5 |
4 |
4 |
|
3 л |
0 |
0 |
3 |
0 |
2 |
2 |
3 |
0 |
|
8 л |
8 |
3 |
3 |
6 |
6 |
1 |
1 |
4 |
Табл. 5 Рис. 9
В этой задаче объем большего сосуда равен сумме объемов двух меньших. Но, разумеется, могут быть и другие случаи, когда объем большего сосуда меньше или больше этой суммы. Метод математического бильярда применим и для них, но с дополнительными условиями. Задача 2. Имеется 11-литровый сосуд, наполненный водой и два пустых сосуда емкостью 3 и 5 литров. Как с помощью этих сосудов отлить 4 л воды?
Решение. Так как. 11 > 3 + 5, главную диагональ необходимо продлить за вершину параллелограмма Но шарик за границы нашего стола все равно не выходит, потому что при любом переливании в 11-литровом сосуде остается, как минимум, 3 литр воды Рис. 10 (11 — (5 + 3) = 3). И тогда решение выглядит следующим образом (рис.10):
. Задача 3. Имеется 6-литровый сосуд, наполненный водой и два пустых сосуда емкостью 3 и 5 литров. Как с помощью этих сосудов отлить 4 л воды? Решение. На диагонали, выражающей количество воды в третьем сосуде, должно быть отложено 6 единиц. Поэтому у параллелограмма надо отсечь верхний правый угол и продолжать следить за движением шарика (рис.11).
Рис. 11
Осталось рассмотреть вопрос о разрешимости задач с тремя сосудами. Как и в случае с двумя сосудами, если объемы двух меньших сосудов выражаются взаимно простыми числами, а объем третьего сосуда больше или равен сумме объемов двух меньших, то с помощью этих трех сосудов можно отмерить любое целое число литров, начиная с 1 литра и кончая объемом среднего сосуда. Имея, например, сосуды вместимостью 7, 8 и 15 литров, можно отмерить любое количество воды от 1 до 8 литров. Когда объем большего сосуда меньше суммы объемов двух других, задача может оказаться неразрешимой, даже если объемы двух меньших сосудов не имеют общего делителя. Например, если объемы сосудов равны 7, 9 и 12 литров, то отмерить можно любое количество воды, кроме 6 литров. Но любой вопрос о разрешимости задач такого типа легко решается, если следить за движением «умного» шарика на математическом бильярдном столе.
ЗАКЛЮЧЕНИЕ
1. Изучая литературу по истории математического бильярда, мы выяснили, что с момента появления в Европе эта азартная игра послужила предметом серьезных научных исследований, в результате которых появилась теория математического бильярда или теории траекторий
2. Теория математического бильярда нашла прекрасное применение для решения задач на переливание.
3. Используя метод математического бильярда, можно легко выяснить, имеет ли задача решение.
4. В большинстве книг по занимательной математике и среди олимпиадных задач большое место занимают задачи на переливание, многие из которых я решил, используя метод математического бильярда. В своем предположении я убедился. Используя метод математического бильярда, можно решить любую задачу на переливание или убедиться, что это не возможно. Задачи на переливание действительно часто встречаются на олимпиадах, их решение способствует культурному и интеллектуальному развитию, помогает развитию памяти, внимания, логического мышления, любознательности и творческих способностей. Именно с решением одной из сложных задач о переливаниях связывают раскрытие математических способностей выдающегося французского математика Симеона Дени Пуассона. Говорят, что эта задача сыграла решающую роль в выборе профессии. Однажды, знакомый принес юному Пуассону несколько задач на переливание, разного уровня сложности. Пуассон решил их менее чем за час, определив тем самым выбор своей будущей профессии – он стал математиком. А одна из самых известных задач подобного рода носит его имя (я ее также решил)
Список литературы
1. Мартин Гарднер. Математические досуги. Под редакцией Я. А. Смородинского. Перевод с английского Ю А. Данилова. Издательство «Мир», Масква, 1972
2. Я.И. Перельман. Занимательная Геометрия, издание одиннадцатое, стереотипное, под ред. И с дополнениями Б.А. Кордемского, государственное издательство физико-математической литературы. Москва, 1959(Я.И.Перельман.,Занимательная геометрия М.: ГИФМЛ, 1959, с.238) 3.https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BB%D1%8C%D1%8%D1%80%D0%B44. Ф.Ф. Нагибин, Е.С. Канин, Математическая шкатулка Москва, «Просвещение», 1984, с.160
54. Е.И. Игнатьев В царстве смекалки Москва, «Наука» ГРФМЛ, 1987, с17611
Просмотров работы: 100
school-science.ru
Проект Математический бильярд — Saratov FIO Wiki
Автор проекта
Абасов Валерий Викторович
Ведышев Артем Андреевич
Название проекта
Математический бильярд
Краткая аннотация проекта
•Проект «Математический бильярд» разработан для учащихся 8 классов общеобразовательных школ. •Проект может быть использован при изучении темы «Число Пи» а так же на факультативных занятиях и кружках по математике.
•Главным в этом проекте является освоение учениками методов конструирования, прогнозирования и «обучение в сотрудничестве».
•В ходе проекта учащиеся самостоятельно проводят групповые исследования по различным источникам информации (печатные, картографические, Интернет) и оформляют результаты своих исследований в виде презентации и буклета.
•В процессе обучения у учащихся формируется умение анализировать, сопоставлять, рассуждать и творчески мыслить.
Направляющие вопросы
«Кто исследовал бильярд?», «И зачем?», «Где в жизни мы встречаемся с бильярдом?» , «Какие полезные свойства бильярд вам известны?»
План проекта
1.Мозговой штурм (формирование тем исследований учащихся).
2.Формирование групп для проведения исследований, выдвижение гипотез, обсуждение путей решения проблем.
3.Выбор творческого названия проекта.
4.Обсуждение плана теоретической и практической работы учащихся в группе.
5.Обсуждение с учащимися возможных источников информации.
6.Самостоятельная работа групп.
7.Подготовка учащимися презентаций и докладов по отчёту о проделанной работе.
8.Представление исследовательских работ.
Публикация учителя
Буклет «В мире бильярда»
Презентация учителя для выявления представлений и интересов учащихся
Пример ученической работы
Презентация Бильярд
Описание процедур оценивания
Формирующее оценивание
Критерий буклета
Критерий оценивания
Дидактические материалы
Кроссворд
Тест
Другие документы
Компьютерные технологии/Физмат
wiki.soiro.ru
|
sites.google.com
Исследовательская работа по математике
Муниципальное Автономное Общеобразовательное Учреждение
«Средняя Общеобразовательная Школа № 47»
Исследовательская работа на тему:
Математический бильярд
Выполнили: ученицы 8 «В» класса
Липилина Елизавета и Куприянович Ольга
Руководитель:
Карнишина Валентина Ивановна
Пермь 2016
ОГЛАВЛЕНИЕ:
Введение………………………………………………………………………3
Глава 1.
Бильярд……………………………………………………..……………..4
Появление математического бильярда. Первое его использование..…4
Подробнее о математическом бильярде………………………………….4
Глава 2.
Рассмотрение и решение задач…………………..…..…………………..5
π и бильярд…………………………………………………………………5
Правило m+n-2…………………………………………………………….5
Биллиардная задача Альхазена…………………………………….…….7
2.4. Задачи на переливание……………………………………………………….7
Заключение…..……………………………………………………………….…..10
Список используемых источников………………………………….………….11
Введение
Проблема: желание узнать, что такое математический бильярд и как его можно использовать
Актуальность: решение задач более быстрым способом.
Цели и задачи: узнать, что такое «математический бильярд» и научится пользоваться этим методом для решения задач с помощью построения бильярдного стола
Глава 1
1. Что же такое сам бильярд? Наверняка, каждый играл в него когда – либо в жизни.
Бильярд — высокотехничная игра. Выбор пары шаров на столе, прицеливание, подход к шару и, наконец, удар. Появившись до нашей эры в Индии и Китае, бильярд через много веков перекочевал в европейские страны – упоминание о нем имеется в английских летописях VI века. В России бильярд стал известен и распространился при Петре I.
1.1.Подобно тому, как азартная игра в кости вызвала к жизни «исчисление» вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. Впервые о математическом базисе бильярдной игры заговорил известный физик Гаспар Густав Кориолис в своей книге «Математическая теория явлений бильярдной игры» 1835-го года. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Для своего времени это было ничто — как правильно выразился Леман, книга не представляла интереса ни для математиков, ни для бильярдистов. Прошло более полутораста лет и математический бильярд по сути превратился в огромное дерево с тьмой отростков и гигантских ветвей. «Теория биллиардов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа π с помощью бильярда! Но с привычным нам бильярдом, математический биллиард имеет лишь общие идеологические корни. Намного ближе общеобразованному читателю результаты исследований математиков Штайнхауза, Альхазена и Гарднера.
Но обо всем по порядку.
1.2. Математический бильярд – механическая система, состоящая из горизонтального бильярдного стола (без луз – французский бильярд), и движущегося без трения точечного шара, абсолютно упруго отражающегося от бортов. Точечный шар находится в бильярдной области Q, ограниченной бортом Г (границей области Q). Траектория бильярда в области Q определяется начальным положением точки q и начальным вектором её скорости v. Математическая проблема бильярда – поиск траектории шарика. Шар в бильярде – один. Направление вектора v(t), т.е. направление движения шара, меняется только при его ударе о борт. Траектория бильярда — это вписанная в кривую Г ломаная, которая может быть однозначно построена по своему начальному звену. Бильярд — динамическая система, порожденная движением с единичной скоростью точечной частицы внутри Q с упругими отражениями от границы dQ. Первым сильную неустойчивость систем с упругими столкновениями отметил Н.С.Крылов. Бильярдные системы общего типа, характеризующиеся свойством экспоненциальной неустойчивости траектории («бильярды Синая»), введены и изучены Я. Г. Синаем. Бильярдом называют динамическую систему, порожденную свободным движением материальной точки внутри ограниченной области (сосуда) с упругими отражениями от стенок. Бильярды служат удобными моделями в ряде областей классической физики. В последнее время они используются также при исследовании квантового хаоса. Если стенки сосуда вогнуты внутрь, то бильярд называется рассеивающим. Если же вогнутость нестрогая, т. е. допускаются уплощения, то бильярд полурассеивающий. К рассеивающим и полурассеивающим бильярд сводятся известные в статистической физике модели твердых сфер, газы Лоренца и Рэлея. Эти бильярды обладают сильными стохастическими свойствами и по своей структуре схожи с геодезическими потоками на поверхностях отрицательной кривизны. А именно, они характеризуются экспоненциальной неустойчивостью траекторий. В ряде случаев для них доказана эргодичность, перемешивание, К-свойство и В-свойство. Близкими к ним являются бильярды Бунимовича. По аналогии с геодезическими потоками мы будем называть все эти бильярды гиперболическими. Важной характеристикой динамической системы, отражающей скорость расходимости ее траекторий, является метрическая (колмогоровская) энтропия, введенная в 1958. Методы вычисления энтропии интенсивно развивались в 60-х и 70-х годах. В 1970 Я. Г. Синай получил формулу для энтропии двумерного рассеивающего бильярда, а в 1978 он же обобщил её на многомерные полурассеивающие бильярды.
Глава 2
2.1. π и бильярд (автор методa, выдающийся математический биллиардист,
Гальперин Г. А., о котором сказано ранее).
Положим на числовую ось два биллиардных шара с массами M и m (M>m), и будем предполагать, что в начале координат х=0 расположена абсолютно упругая стенка, отражающая налетающий на неё шарик. При отражении от стенки скорость шарика меняется на строго противоположную. Размеры шариков несущественны, и для простоты мы будем считать их точечными частицами. Фиксируем натуральное число N. Следующая процедура позволяет определить любое наперёд заданное количество N последовательных цифр числа π.
Массы m и M подбираем так, чтобы M/m=100N.
Шар m располагаем между стенкой х=0 и шаром М.
Запускаем шар М в сторону шара m с произвольной скоростью.
Подсчитываем общее количество ударов в системе (т. е. число столкновений между шарами и число отражений шара m от стенки).
Записываем полученное число в десятичной системе и обозначаем его через π(N).
Теорема: а) число ударов в описанной динамической системе всегда конечно и не зависит от начальных положений шаров и начальной скорости шара М.
б) Число π(N) ударов в системе равно
Рис.1
2.2. Правило m+n-2.
Результат Штайнхауса и Гарднера(о которых тоже проговорено ранее).
Дано прямоугольный бильярдный стол с одними лишь угловыми лузами и целочисленными сторонами m и n (m, n — взаимно просты). Шар, посланный из одной угловой лузы в другую под углом 45 градусов попадёт в другую лузу после m+n-2 касаний борта.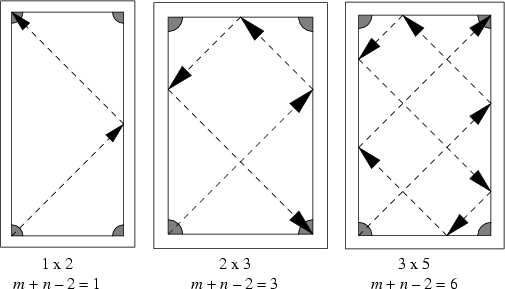
Рис.2
В одной из своих работ Штайнхаус даёт также метод ударения по шару, чтобы он коснулся всех четырёх бортов прежде, чем ударить прицельный шар. Прекрасная основа для теоретического карамболя.
2.3. Биллиардная задача Альхазена.
Постановка задачи в том, чтобы найти такую точку на борту круглого биллиардного стола, ударив в которую биток коснётся прицельного шара в другой данной точке.
Впервые задача была сформулирована Птолемеем, но названа именем Альхазена, поскольку он первым подробно исследовал её применения в оптике.
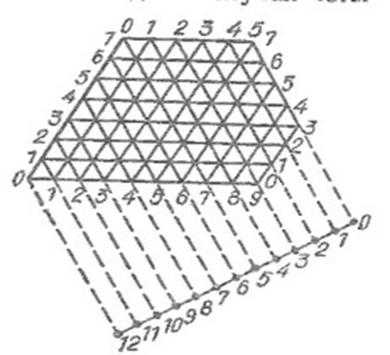
Рис. 3
2.4. В этом разделе мы приведем одно изящное применение математического бильярда к решению задач на переливание.
Задачи на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма.
Задача. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников (см. рис. 4).
Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов. Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны в точке А. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке В, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд.
Прослеживая дальнейший путь шара и записывая все этапы его движения в виде отдельной таблицы (табл.1), в конце концов, мы попадаем в точку Н, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически в таблице.
Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в пятилитровый сосуд. Если на диаграмме шар из точки О покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то получим более короткое решение задачи. Можно показать, что полученное решение с 6 переливаниями уже является самым коротким.
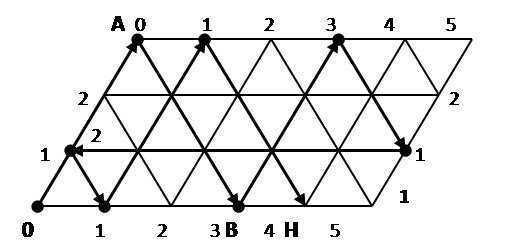
Рис. 4
Табл. 1
ЗАКЛЮЧЕНИЕ
В нашей исследовательской работе мы узнали больше про обычный бильярд, а также метод математического бильярда, как с помощью него можно решать задачи. Метод математического бильярда для решения задач на переливания удобней, чем составления таблиц, и мы надеемся, что этот метод будет использоваться в будущем.
infourok.ru
Математический бильярд | Социальная сеть работников образования
Слайд 1
МОСКОВСКИЙ ИЗДАТЕЛЬСКО-ПОЛИГРАФИЧЕСКИЙ КОЛЛЕДЖ ИМ . ИВАНА ФЁДОРОВА ТЕМА: МАТЕМАТИЧЕСКИЙ БИЛЬЯРД Автор(ы) проекта: Гусева М.С. Руководитель проекта: Епихина Е.В. Москва 2017гСлайд 2
Введение 1.Происхождение бильярда………………………………………………………………………………..3 2.Бильярдный стол…………………………………………………………………..4 4.Стратегия………………………………………………………………..……………5 5.Методы математического бильярда ……………………………………………6 5.1.Круглый стол …………………………..………………………………………………7 5.2.Эллиптический стол ……………..………………………………………………8 5.3.Произвольный овальный стол …………………………………………….9 5.4.Многоугольный стол ……………………………………………………………10 6.Исследования математиков …………………..…………………..…..……………11 Заключение…………………………………………………………………………….12
Слайд 3
ПРОИСХОЖДЕНИЕ БИЛЬЯРДА очень древнего происхождения, а родиной бильярда является Азия, по утверждению одних — Индия, по мнению других — Китай.
Слайд 4
Бильярдный стол Первый бильярдный стол (согласно сохранившимся документам) был изготовлен мастером Анри де Винемом в 1469 году для короля Франции Людовика XI
Слайд 5
Стратегия Стратегия — способ использования ресурсов, направленный на достижение цели операции. Стратегия определяется принимаемыми значениями. Задача исследования операций, обычно состоит именно в выборе оптимальной из числа альтернативных.
Слайд 6
Методы математического бильярда Математический бильярд – один из доказательств стохастических систем.
Слайд 7
Круглый стол ( Представлен эллиптический бильярд. Круглый получается совмещением фокусов.)
Слайд 8
Эллиптический стол Ситуация в целом похожа на предыдущий случай, со следующими поправками.
Слайд 9
Произвольный овальный стол Если его граница гладкая и выпуклая, то немного подумав, можно обнаружить две периодические траектории — вдоль наибольшего и наименьшего диаметров, по аналогии с эллипсом.
Слайд 10
Многоугольный стол Простейшим случаем многоугольника является бесконечный угол . Доказано, что бильярдный шарик, попадающий в любой угол, рано или поздно вылетит из него.То же можно сказать и про лазерный луч, попадающий в два поставленные пол углом зеркала.
Слайд 11
Исследования математиков Результаты исследований математиков, таких как Гарднер показали возможность теории математического бильярда.
Слайд 12
Заключение Бильярд не простая игра. Как только не обосновываются самые виртуозные и искусные удары знаменитых бильярдистов .
nsportal.ru
